Introduction

The open-framework metal phosphates of stoichiometry MIMIIIP2O7 are known in particular for MIII = FeIII materials with all the alkaline cations (Li–Cs). These materials, characterized by their ionic conductivity, have been extensively studied. It also might find applications such as prospective materials in technology, viz. in electronic devices, as solid electrolytes with high thermal resistance, and as potential devices in space application, sensors, solid-state laser materials, piezoelectrics, luminescence, ceramics, catalysis, adsorption, ionic conductors, and magnetic materials. Indeed, nowadays some of them were used as nanoparticles for remediation and decontamination of water [1–11].

As an element of this group, the present work selected AgFeP2O7 material for investigation. This is done specially for two reasons: firstly, to determine the possible conduction and dielectric relaxation mechanisms. Secondly, no papers are found to deal with the direct current (DC) and AC electrical conductivities of AgFeP2O7 as a good candidate for its higher polarizability of Ag+ which makes it more easily deformed (d10 configuration) and pass through the bottlenecks and consequently more mobile.

AgFeP2O7, to which this paper is devoted, is isostructural to MIFeP2O7 (MI = Na, K, Rb, Cs) double phosphates family [7, 12]. Its framework is built up from infinite rows of isolated iron octahedral connected to five P2O7 groups, one of them acting as “chelating” sequence around the transition metal (Fig. 1). As a result of these block's assemblage, a 3D framework is formed with hexagonal tunnels, where silver cations reside. These and the cavities associated are at the origin of alkali cations Ag+ migration within the structure [13].

Fig. 1
figure 1

Formation of hexagonal channels filled by silver atoms in the structure

Full size image

In this paper, not only electrical conductivity and dielectric properties of the title compound are reported by means of impedance spectroscopy. We have also discussed the conduction mechanism and its correlation with the crystallographic properties.

Experimental

The AgFeP2O7 was prepared from high purity (99 %) AgNO3, F2O3, and NH4H2PO4 by conventional methods. The reagents were firstly ground into fine powders using mortar and pestle, intimately mixed, and progressively heated to 573 K for 8 h to eliminate NH3, CO2, and H2O. The obtained product is again ground manually, pressed into cylindrical pellets using 3 T/cm2 uniaxial pressure, and heated at 1073 K for 8 h. Phase purity and homogeneity were determined by XRD pattern which was recorded and refined using a Phillips powder diffractometer PW 1710 with CuKα radiation (λ = 1.5405 Ǻ) in a wide range of Bragg angles (8° ≤ 2θ ≤ 80°).

The electrical conductivity measurements were performed using two platinum electrodes. As a fact, the finely grain samples were pressed into pellets with a diameter of 8 mm and thickness of about 1 mm thickness before being sandwiched between these electrodes. Moreover, the measurements were performed as a function of both temperature (553 to 698 K) and frequency (209 to 5 MHz) employing a Tegam 3550 ALF impedance analyzer.

Results and discussions

Crystalline parameter

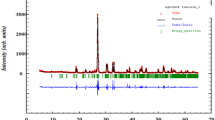
The powder X-ray diffraction pattern of the AgFeP2O7 sample, recorded at room temperature, along with Rietveld refinement is shown in Fig. 2. Profile refinements within the monoclinic space group P21/C reproduce XRD patterns reasonably well. The quality factors indicating the accord between the observed and the calculated profiles are R B = 2.71, R F = 2.43, and χ 2 = 1.13. The corresponding lattice parameters and unit cell volume obtained from Rietveld refinement are in a good agreement with those reported earlier for the AgFeP2O7 compound [10] being: a = 7.3373(4) Ǻ, b = 7.9972(5) Ǻ, c = 9.5758(6) Ǻ, β = 111.8329(12) ° V = 521.5847(4) Ǻ3.

Fig. 2
figure 2

Powder X-ray diffraction pattern and Rietveld refinement for the sample AgFeP2O7 (circle signs correspond to experimental data, and the calculated data are represented by the continuous line overlapping them: tick marks represent the positions of allowed reflection and a difference curve on the same scale is plotted at the bottom of the pattern)

Full size image

Electrical impedance analysis

The electrical conductivity generally consists of both ionic and electronic conduction. The first one is proportional to the ion concentration and mobility, while the second follows the hopping theory [14, 15]. The electronic conductivity in oxides is due to overlapping of non-completely filled d or f orbitals of cations or to electron hopping from aliovalent ions like Fe2+ and Fe3+ assisted by an oxygen anion in between. In the title compound, the conductivity should be totally ionic as iron shows only one valence state (FeIII).

Figure 3a, b shows the typical impedance plots for AgFeP2O7 sample at several temperatures. The well-defined semicircles either passing through or close to the origin were obtained at 553 K ≤ T ≤ 698 K. As temperature increases, the pattern of the arc corresponding to the bulk resistance of the sample decreases, indicating an activated thermal conduction mechanism. Indeed, such pattern tells us about the electrical process occurring within the sample and their correlation with the sample microstructure when modeled in terms of an electrical equivalent circuit [16, 17].

Fig. 3
figure 3

a–b: Complex impedance spectrum as a function of temperature with electrical equivalent circuit (inset), accompanied by theoretical data calculated with expressions (2) and (3)

Full size image

In the present case, the equivalent circuit configuration for the impedance plane plot is a parallel combination of a resistance, capacitance, and fractal capacitance (Fig. 3a inset). The impedance of CPE is presented as [18]:

$$ Z{}_{\mathrm{CPE}}=\frac{1}{{\left( Qi\omega \right)}^{\alpha }} $$
(1)

Z CPE is usually considered to be a dispersive capacitance, while α is the measure of the capacitive nature of the element: if α = 1, the element is an ideal capacitor; if α = 0, it behaves as a frequency-independent ohmic resistor.

The expressions of |Z| and phase θ related to the equivalent circuit are obtained from the real (Z′) and the imaginary (Z″) parts of the complex impedance:

\( \left|Z\right|=\sqrt{Z{\prime}^2+Z\prime {\prime}^2} \) and \( \theta ={ \tan}^{\hbox{--} 1}\left(\frac{Z\prime \prime }{Z\prime}\right) \)

Where Z′ and Z″ can be written as:

$$ Z\prime =\frac{R^{-1}+Q{\omega}^{\alpha } \cos \left(\frac{\alpha \pi}{2}\right)}{\left({R}^{-1}+Q{\omega}^{\alpha } \cos {\left(\frac{\alpha \pi}{2}\right)}^2+\left( C\omega +Q{\omega}^{\alpha } \sin {\left(\frac{\alpha \pi}{2}\right)}^2\right)\right)} $$
(2)
$$ -Z\prime \prime =\frac{ C\omega +Q{\omega}^{\alpha } \sin \left(\frac{\alpha \pi}{2}\right)}{\left({R}^{-1}+Q{\omega}^{\alpha } \cos {\left(\frac{\alpha \pi}{2}\right)}^2+\left( C\omega +Q{\omega}^{\alpha } \sin {\left(\frac{\alpha \pi}{2}\right)}^2\right)\right)} $$
(3)

Thus, the presentation of the impedance data as a Bode plot gives information that helps to ascertain more directly the different conduction processes involved in the sample. The modulus |Z| and the phase θ of the impedance are plotted against the angular frequency in subpanels a and b of Fig. 4, respectively. Those diagrams clearly show a good agreement between theoretical and experiment data. Consequently, the suggested equivalent circuit describes the crystal–electrolyte interface reasonably well. Fitted values of C are in the range of pF. This implies that the single semicircular response is from grain interior which is expected from the sample where no grain boundaries are involved. Additionally, the values of α vary in the range 0.64 confirming the weakness interaction between localized sites.

Fig. 4
figure 4

a–b: Bode plots for a AgFeP2O7: modulus of |Z| versus frequency and b AgFeP2O7: phase θ versus frequency

Full size image

The magnitude of DC conductivity, σ DC, can be calculated from the relation:

$$ {\sigma}_{\mathrm{DC}}=\frac{e}{R\times S} $$
(4)

Where S is the electrolyte–electrode contact area, e is the thickness of the sample and R is the bulk resistance obtained from the intercept of the semicircular arcs observed at higher frequency on the real axis (Z′). The temperature dependence of the conductivity Log (σT) versus 1000/T in the studied temperature range is given in Fig. 5. This plot indicates an increase in conductivity with rise in temperature. Such type of temperature dependence indicates that the electrical conduction in the sample is a thermally activated transport process governed by Arrhenius law. Besides, the obtained activation energy is about 0.89(±0.03) eV.

Fig. 5
figure 5

Temperature dependence of σ DC versus 1,000/T. In the inset, dependence of Log (fp) on temperature for AgFeP2O7

Full size image

AC conductivity analysis

The frequency-dependent conductivity of inorganic glasses, polymers, doped semiconductors, and ionic conductors exhibits universality and their behavior is scaled to master curve [19, 20]. The angular frequency dependence of the AC conductivity at various temperatures for the sample is shown in Fig. 6. In fact, the conductivity curves reveal two distinct regions: the low-frequency region and high-frequency region. At low frequencies, a plateau which characterizes the DC conductivity is present, while at high frequencies, the conductivity increases gradually with the increase in frequency. Besides, the transition region from DC to AC conductivity shifts to higher frequencies with the increase in temperature. Furthermore, the observed frequency-dependent conductivity can be described by the known augmented Jonscher's relation as:

Fig. 6
figure 6

Angular frequency dependence of the AC conductivity at various temperatures

Full size image
$$ {\sigma}_{\mathrm{AC}}\left(\omega \right)={\sigma}_{\mathrm{DC}}+A{\omega}^S+ B\omega $$
(5)

Where σ DC is the DC conductivity, A is temperature-dependent parameter, and s is frequency exponent parameter which represents the degree of interaction between mobile ions and the environments surrounding them. Additionally, B is weakly temperature-dependent term.

Two terms of Eq. (5) are denoted as, namely, universal dielectric response (UDR), in general, universal dynamic response, and nearly constant loss (NCL), respectively. These two additive terms correspond to different processes happening in the material. The power-law frequency-dependent UDR term comes from the hopping of the carriers with interactions of the inherent defects or disorder in the material. On the other hand, the linear frequency-dependent NCL term is modeled to originate from rocking motions in an asymmetric double well potential [20] and electrical loss occurring during the time regime; the ions are confined to the potential energy minimum [21]. UDR and NCL terms are also categorized to occur in the high-temperature/low-frequency and the low-temperature/high-frequency regimes, respectively.

The hopping frequency ω h of the charge carrier which represents the crossover frequency from DC to dispersive conductivity region at ω > ω h can be calculated by the following expression [22].

$$ \omega {}_{\mathrm{h}}={\left(\frac{\sigma_{\mathrm{DC}}}{A}\right)}^{\frac{1}{S}} $$
(6)

The latter is used as scaling parameter for the frequency axis. It is also expected to be more appropriate for scaling the conductivity spectra of ionic conductors since it takes into account the dependence of the conductivity spectra on structure and the possible changes of the hopping distance experienced by the mobile ions [23].

Figure 7 shows the Arrhenius plot of Logω h as function of temperature, and the corresponding activation energy value is found to be 0.89 (±0.04) eV which is close to the values obtained from analyses of impedance. In fact, this reveals that the transport properties in this material appear to be due to Ag+ ions movement along tunnel in which it resides.

Fig. 7
figure 7

Temperature dependence of the hopping frequency ω h

Full size image

Seeing that, scaling is an important feature in any data evaluation program. The study of the conductivity spectra of several materials at different temperatures leads to a scaling law which results in a time temperature superposition [24, 25]. Different authors have studied several materials [19, 26] for scaling studies with various parameters [23, 24, 27] to scale the frequency axis. Here, conductivity spectra have been scaled by a Ghosh's model [28]:

$$ \frac{\sigma_{\mathrm{AC}}\left(\omega \right)}{\sigma {}}=f\left(\frac{\omega }{\omega_{\mathrm{h}}}\right) $$
(7)

The perfect overlap of the spectra at different temperatures (Fig. 8) implies that the relaxation dynamics of charge carriers in the present compound is independent of temperature [29].

Fig. 8
figure 8

Plot of (σ AC/σ DC) versus (ω/ω h) at different temperatures

Full size image

On the other hand, Fig. 9 shows the variation of σ AC with inverse of absolute temperature (1000/T) at different frequencies. It is clear from this figure that σ AC increases linearly with the reciprocal of the absolute temperature. This dependence of AC conductivity on temperature suggests that the AC conductivity is a thermally activated process and it can be analyzed according to the well known Arrhenius equation: σT = B exp(−E σ /kT). In addition, it is observed that the AC conductivity of the material increases with rise in temperature and shows the negative temperature coefficient of resistance behavior.

Fig. 9
figure 9

Plot of AC conductivity versus 1,000/T at different frequencies

Full size image

We reported in Fig. 10 the frequency dependence of activation energy calculated at different frequencies from the slopes of the obtained straight lines of Fig. 9. Clearly, values of E σ decrease with increasing applied frequency. Such a decrease can be attributed to the contribution of the applied frequency to the conduction mechanism which confirms the hopping conduction to be the dominant mechanism.

Fig. 10
figure 10

Frequency dependence of AC activation energy

Full size image

Dielectric studies

Studies of the frequency-dependent electrical conductivity of materials are important to explain the mechanisms of conduction in these materials. Furthermore, the dielectric relaxation studies are important too. In the first place, it reveals significant information about the chemical as well as physical behavior. This, in turn, may be useful in the determination of the structure and defects in solids [30, 31].

In this case, the dielectric relaxation is described by a non-Debye model which gives the frequency-dependent complex permittivity in the form [32]:

$$ {\epsilon}^{*}\left(\omega \right)={\epsilon}_{\infty }+\frac{\epsilon_{\mathrm{S}}-{\epsilon}_{\infty }}{1+{\left( i\omega {\tau}_1\right)}^{1-\alpha }}+\frac{\sigma_{\mathrm{DC}}}{ i\omega {\epsilon}_0} $$
(8)

where σ DC represents the specific conductivity, ε S is the static permittivity, ε 0 is the permittivity of the free space, ε ∞ is the high-frequency value of ε′, and τ 1 is the relaxation time of the Debye process.

The imaginary part of ε * is [30].

$$ \epsilon \prime \prime \left(\omega \right)=\frac{\left({\epsilon}_{\mathrm{S}}-{\epsilon}_{\infty}\right){\left(\omega {\tau}_1\right)}^{1-\alpha } \sin \left(\left(\left(1-\alpha \right)\pi \right)/2\right)}{1+{\left( i\omega {\tau}_1\right)}^{1-\alpha } \cos \left(\left(\left(1-\alpha \right)\pi \right)/2\right)+{\left(\omega {\tau}_1\right)}^{2\left(1\hbox{--} \upalpha \right)}}+\frac{\sigma_{\mathrm{DC}}}{ i\omega {\epsilon}_0} $$
(9)

The first part in Eq. (5) is related to the thermal polarization, whereas the second is related to the electrical conductivity.

Figure 11 illustrates the variation of real part ε′ of the complex dielectric permittivity. It is obvious from this figure that ε′ decrease with an increase of the applied frequency which can be explained by means of the dielectric polarization mechanism of the material. This is a commonly observed feature in ceramic materials. In fact, at low frequencies due to space charge accumulation, a gradual increase has been observed. While at high frequencies, it approaches a limiting constant value ε′∞(ω) which can be interpreted as a result of a rapid polarization processes with no ionic motion contribution because the frequency is too high and the ions can only oscillate without reaching the sample–electrode interface. On the other hand, frequency dependence of the imaginary part of dielectric constant is shown in Fig. 12. Best fits using function (9) give a suitable description of the experimental data. Indeed, there are no appreciable relaxation peaks in the frequency range employed in this study. Additionally, the dielectric loss rises sharply at low frequency indicating that electrode polarization and space charge effects have occurred confirming non-Debye dependence [33, 34].

Fig. 11
figure 11

Frequency dependence of the real part ε′ of the permittivity for the AgFeP2O7 compound at several temperatures

Full size image
Fig. 12
figure 12

Variation of the imaginary part of dielectric constant versus frequency

Full size image

Electrical modulus

The complex electrical modulus formalism has been used in the analysis of the electrical properties because it gives the main response of the bulk of sample crystal and is particularly suitable to extract phenomena, such as electrode polarization and conductivity relaxation times.

The dielectric relaxation was studied by electric modulus which is defined as [35]:

$$ {M}^{*}=\frac{1}{\epsilon^{*}}= j\omega c{}_0Z^{*} $$
(10)

where C 0 is the vacuum capacitance of the cell; the variation of the imaginary part of electric modulus M″ with the frequency at various temperatures is shown in Fig. 13. In fact, each isothermal frequency spectrum exhibits a well-defined peak. The region to the left of the peak is the place in which the ions Ag+ are mobile over long distances. On the other hand, the region to the right is the place in which the ions are spatially confined to their potential wells. Moreover, when temperature increases, modulus peak maxima shift to higher frequencies.

Fig. 13
figure 13

Frequency dependence of the imaginary part of electric modulus at several temperatures

Full size image

The modulus plot can be characterized by full width at half height or in terms of a non-exponential decay function [36]. In this fact, the stretched exponential function is defined by the empirical Kohlrausch–Williams–Watts function [37]:

$$ \begin{array}{cc}\hfill \varphi (t)= \exp {\left[\left(-\frac{t}{\tau}\right)\right]}^{\beta}\hfill & \hfill 0\langle \beta \langle 1\hfill \end{array} $$
(11)

Where τ the characteristic relaxation time and β is the well-known Kohlrausch parameter, which decreases with an increase in the relaxation time distribution. Indeed, its value for a practical solid electrolyte is clearly less than 1. φ(t) is related to the modulus in the angular frequency domain by the equation:

$$ M={M}_{\mathrm{s}}\left[1-{\displaystyle {\int}_0^{\infty } \exp \left(- i\omega t\right)}\left(-\frac{ d\varphi (t)}{ d t}\right) dt\right]={M}_{\mathrm{s}}\left[1-\varPhi \left(\omega \right)\right] $$
(12)

Among these functions, the Havriliak–Negami (HN) one has been the most extensively used in literature [38]. The HN function is:

$$ {\varPhi}_{\mathrm{HN}}\left(\omega \right)=\frac{1}{{\left[1+{\left( j\omega \tau \right)}^{\alpha}\right]}^{\gamma }} $$
(13)

Where α and γ are shape parameters ranging between 0 and 1. The Cole–Cole function corresponds to the case 0 < α < 1 and γ = 1 and the Cole–Davidson to α = 1 and 0 < γ < 1. The Debye case is recovered again with α = γ = 1. Alvarez et al. established that for HN function which approximately corresponds to the Fourier transform of \( \frac{ d\varphi (t)}{ d t} \). These two shape parameters, α and γ are related as [39, 40]

$$ \gamma =1-0.812{\left(1-\alpha \right)}^{0.387} $$
(14)

being the corresponding relationship between β and HN parameters given by:

$$ \upbeta ={\left(\alpha \gamma \right)}^{\left(1/1.23\right)} $$
(15)

In this event, the modulus expression becomes:

$$ M={M}_s\left[1-{\varPhi}_{\mathrm{HN}}\left(\omega \right)\right] $$
(16)

The β parameter is most often interpreted as a result of correlated motions between ions. Its value represents the deviation from the linear exponential (β = 1). In the present case, the shape of each spectrum has been quantified with a β value obtained by fitting the curve to Eq. (16). Thus, to achieve the fit to Eq. (16) at each temperature, β, τ, and M ∞ values have been taken freely parameters. It is worthy to note that the best fits for M″ at different temperatures for the compound are shown in Fig. 13. Additionally, the obtained β parameter was found to be independent of temperature with an average value of 0.43, which suggests that all possible relaxation mechanisms occurring at different frequencies exhibit the same thermal energy and the dynamical processes are temperature independent.

On the other hand, the conductivity relaxation frequency f p is given by the relation [41], \( f={f}_0 \exp \left(-\raisebox{1ex}{${E}_{\mathrm{m}}$}\!\left/ \!\raisebox{-1ex}{$ KT$}\right.\right) \). Where f 0 is characteristic phonon frequency, E m is the activation energy for conductivity relaxation, K is the Boltzmann constant, and T is the temperature. The temperature dependence of the conductivity relaxation frequency is plotted in Fig. 5 (inset). It is well described by the Arrhenius relation. Besides, it also reveals that the experimental and the simulated values of the relaxation frequency are very close. The obtained activation energy is about 0.88 (±0.04) eV. Thus, this value is close enough to value issued from impedance measurement 0.89 (±0.03) eV suggesting that the Ag+ ion transport is probably due to a hopping mechanism [42].

Conclusions

In this work, we have synthesized the AgFeP2O7 by solid-state reaction technique. Rietveld refinement indicates that the sample is single phase. The AC conductivity and dielectric behavior of the AgFeP2O7 compound have been studied as a function of temperature, and frequency ranges 553–698 K and 209–5 MHz, respectively. Moreover, the analysis of the complex impedance allowed determining an equivalent electrical circuit for the electrochemical cell with AgFeP2O7. Continuing, the AC conductivity spectra are found to obey augmented Jonscher's power law at different temperatures. With respect to the activation energies obtained from the impedance and modulus spectra, they are proven to be close; suggesting that the Ag+ ions transport in the investigated material can be described by a hopping mechanism within tunnels presented in the structure.