Introduction

Complex dynamics is frequently modeled using attractor networks, but precise characterization of attractor basins and possible transitions between them is rarely attempted. Understanding high-dimensional neurodynamical systems is very difficult. Many methods of statistical mechanics and complex systems are applicable only to relatively simple networks and toy systems. Mathematical analysis is often focused on asymptotic properties, while in the neurodynamics properties of specific transient and quasi-stable states are interesting. Graph theory is used to show how states are linked, but similarity and spatial relations between the states are not displayed in graphs.

A general method for analysis of dynamical systems that displays some properties of the trajectory in the phase space is based on recurrence plots (Marwan et al. 2007). This technique helps to see the most important properties of trajectories and to link information about recurrences to dynamical invariants of the system. Recurrence plots (RPs) have wide applications for analysis of time series, and are frequently used to analyze simple dynamical systems, but they are less often used to analyze high-dimensional systems typical for neurodynamics. An overall qualitative view of the global properties of neurodynamics could certainly be quite useful.

Recurrence plots compare current point \(\user2{x}(t)\) at the time t to all previous points \(\user2{x}_i=\user2{x}(t_i), t_i<t\) on the trajectory, calculating their distance and displaying it using color scale, or using a threshold function of the distance and displaying black dots for points that are sufficiently close to the current point. With some experience such plots allow for the identification of many interesting behaviors of the system. Visualization approximates the density of trajectories as a function of time relatively to a point \(\user2{x}(t)\) on the trajectory. This density is close to zero in most regions of the phase space. Selecting interesting regions where it is high leaves a few reference points and displaying the distance only from these points allows for significant reduction of dimensionality. Each reference point is associated with some membership function that estimates the degree to which it belongs to its neighborhood. These membership functions could be used to approximate the sensity of the trajectory points, but for visualization only 2 or 3 functions are selected.

The recurrence rule \({\bf R}_{\bf i}(\user2{x};\epsilon) = \Uptheta(\epsilon-||\user2{x}_i-\user2{x}||)\) may be interpreted as the return of the trajectory \(\user2{x}(t)\) into the neighborhood of the vector \(\user2{x}_i\) associated with some metric function \(||\cdot||\) characterized by parameters \(\epsilon\). In particular if \(L_{\infty}\) (Chebyshev) metric is used the neighborhoods are hyperboxes and positive \({\bf R}_{\bf i}(\user2{x};\epsilon)\) entry is marked by a symbol s i , mapping vectors along the trajectory into a sequence of symbols. This approach, known as the symbolic dynamics (Hao et al. 1998) (SD), has been used to characterize statistical properties of relatively simple dynamical systems, providing a very crude view of long-term dynamics. Such discretization may be too rough for most applications.

The Fuzzy Symbolic Dynamics (FSD) technique, introduced by us recently (Dobosz and Duch 2010) replaces hard partitions of the phase space (hyperboxes) by membership functions that estimate how far is the trajectory from selected reference points. This is in fact a projection of the trajectory on a set of k basis functions \(G(\user2{x};\mu_i,\sigma_i), i=1,...,k\), with parameters σ i defining the shape of the function localized around μ i . The basis functions should be strategically placed in important points of the phase space. If k ≤ 3 plots of \([G(\user2{x}(t);\mu_i,\sigma_i)]\) points show trajectories directly, otherwise the value of each \([G(\user2{x}(t);\mu_i,\sigma_i)]\) component may be represented as color in a row of points for discretized time t.

FSD provides a non-linear reduction of dimensionality suitable for visualization of trajectories, showing many important aspects of neurodynamics, such as size and relative position of attractor basins. To analyze more precisely properties of individual attractors response of the system to different type of noise with increasing variance may be studied. The FSD plots greatly enhance qualitative information that may be derived from recurrence plots. Activity of 140 neurons of the semantic layer in the 3-way model of reading and recognition of word meaning, implemented in the Emergent simulator (O’Reilly and Munakata 2000) is used for illustration. Although this model is far from being realistic interesting conclusions about associative thinking may be drawn from visualization of its dynamics. Spontaneous transitions between attractors for different words due to the noise and neural fatigue are observed. Many properties of neurons and connectivity between them influence the character of the trajectory, as is easily seen in visualizations. Strong attractors may entrap dynamics, significantly slowing the transition to the next attractor basin. Weak attractors prevent the system from abiding longer in any state, quickly jumping to the next one. In all cases transitions are very short, so the behavior may seem quasi-discrete, but the states reached by spontaneous transitions may significantly differ from the memory states the system has been trained on.

The model of normal and disordered reading (O’Reilly and Munakata 2000), used here for illustration of new visualization techniques, is introduced in the next section. In the third section recurrence analysis is presented, section “Visualization of trajectories by FSD” introduces the FSD technique for visualization of trajectories, followed in section “Optimization of the FSD viewpoint” by some discussion on optimization of parameters that influence legibility of plots. Section “From visualization to interesting hypothesis” illustrates how visualization of trajectories may lead to interesting hypothesis: looking at the qualitative changes in neurodynamics one can speculate about the causes of autism and ADHD-like symptoms. The final section contains a brief discussion.

Model of reading

Although the visualization methods discussed here are quite general and may be applied to any dynamical system to show their potential for helping to understand complex neurodynamics we shall focus on a specific example. It is based on a modified model of normal reading and dyslexia, implemented in the Emergent simulator by O’Reilly and Munakata, originally described in chapter 10 of their book (O’Reilly and Munakata 2000) and in a more recent paper (Aisa et al. 2008). The model, presented in Fig. 1, has 6 layers, representing information about orthography (6 × 8 units), phonology (14 × 14 units) and semantics (10 × 14 units), connected to each other via intermediate (hidden) layers of neurons. Full connectivity between each adjacent layer is assumed, with recurrent self-connections within each of these layers. Neurons have excitatory, inhibitory and leak channels, and incorporate some biological effects, including calcium-dependent activity regulation that leads to accommodation or neural fatigue effects.

Fig. 1
figure 1

Model of normal reading and dyslexia implemented in the Emergent simulator (O’Reilly and Munakata 2000). Layers that represent information about orthography (6 × 8 units), phonology (14 × 14 units) and semantics (10 × 14 units) are connected to each other via additional hidden layers of neurons

Full size image

The original model has been used primarily to demonstrate the effect of various lesions on word recognition. The network has been trained on 40 words, half of them concrete and half of them abstract. Simplified phonological representations have been used, and semantics has been captured by using 67 micro-features for concrete words (an average of 18 active features per word) and 31 for the abstract words (five active features on average). Correlation dendrogram between all 40 words presented in (O’Reilly and Munakata 2000) shows that similarity between different words have been correctly learned. Half of the neurons in the semantic layer respond to the abstract, and half to the concrete features. The original model has been slightly modified by turning on the accommodation (neural fatigue) mechanism based on concentration of intracellular calcium which builds up slowly as a function of activation and opens leak channels that release potassium ions and regulate the subsequent inhibition of a neuron. In addition to this synaptic Gaussian noise with zero mean and 0.02 variance has been added to provide more energy for the system to facilitate free evolution simulating word associations (there are several types of noise that can be used in the model, here only the synaptic noise has been used).

In the learning process many attractor basins that serve as memory states have evolved. The trajectory of activity of the semantic layer, comprised of 140 neurons, is visualized below. Although interesting effects due to lesions are reflected in these visualizations they are not presented here. Also the dynamics of learning is not analyzed, as this would make the paper much longer. The network is prompted by showing it different words in the orthographic or phonological layers, and observing the activity of the neurons in the semantic layer. Some of the questions addressed below are: how does the trajectory representing the semantic layer evolves, which basins of attraction it visits, how fast it reaches them and how long the system stays in each basin, do all these basins correspond to learned words or are there spurious states, between which attractor basins transitions are made, how does the synaptic noise influence the trajectories, how the parameters that determine single neuron activation influence the global dynamics, what is the influence of inhibition? Visualization of the trajectories should help to answer these and many other questions.

Recurrence analysis

A general method for understanding the behavior of dynamical systems is based on analysis of recurrence (Eckmann et al. 1987; Marwan et al. 2007). A trajectory \(\user2{x}_i=\user2{x}(t_i)\) may return to almost the same area (within \(\epsilon\) distance) of the phase space as previously visited, creating non-zero elements of the recurrence matrix:

$$ {\bf R}_{ij}(\epsilon) = \Uptheta(\epsilon-||\user2{x}_i-\user2{x}_j||), \quad i,j = 1,\dots,n , $$
(1)

where \(\varvec{\Uptheta}\) is the step function, and n is the number of trajectory points. Because n is usually quite large it is not written but displayed graphically: non-zero elements of the recurrence matrix are plotted as black dots.

Recurrence plots depend strongly on the choice of \(\epsilon\) and the choice of the time step \(\Updelta t=t_{i+1}-t_i\). They may become irregular, the patterns in the plot may wash out, show spurious correlations or tangential motions (Marwan et al. 2007), especially if steps along the trajectory \(\user2{x}(t_i)\) are not constant for consecutive t i . Thus a lot of experience is needed in their interpretation.

Quite often original black-and-white recurrence plots introduced by Eckmann et al. (1987) are used, directly representing the binary matrix defined in Eq. 1. The information about the immediate neighborhood is obviously quite important. In analysis of high-dimensional dynamical systems it may be useful to retain more information by plotting distances between trajectory points using color scale related to the distance. The recurrence matrix elements (1) are then calculated using some function of a distance \(D(\user2{x}_i,\user2{x}_j)\) to represent similarity; this function should decrease from 1 to 0 when the distance changes from 0 to infinity. For example, an inverse function:

$$ {\bf R}_{ij} = \frac{1}{1+D(\user2{x}_i,\user2{x}_j)}, \quad i, j = 1,\ldots,n , $$
(2)

or exponential decay:

$$ {\bf R}_{ij} = \exp{\left(-D(\user2{x}_i,\user2{x}_j)\right)}, \quad i, j = 1,\ldots,n, $$
(3)

are suitable, with freedom to choose distance function \(D(\user2{x}_i,\user2{x}_j)\). A good choice is a function proportional to a square of Euclidean distance. Linear relation between the values of R matrix elements and color maps with such exponential form that decays rapidly to zero helps to smooth recurrence plots removing small variations that carry little information. The final result is a non-linear representation of distance by a color scale.

Recurrence analysis is very useful for characterization of attractor dynamics. In Fig. 2 the recurrence plot and the FSD plot of the same data (discussed in detail in the next section) are presented. The orthographic layer of the network (Fig. 1) has been prompted with a single word “flag” and allowed to evolve with clamped input. Both axes on the RP plot show time (number of iterations, restricted to 500), while the color scale represents the distance from a point on the diagonal to all other points on the trajectory. The FSD plot uses colors to represent time flow, showing non-linear distances to two or three reference points only.

Fig. 2
figure 2

Recurrence plot (top) and the FSD trajectory (bottom) of the 140-units in semantic layer for the word “flag” in the model of reading

Full size image

Interesting properties can be obtained from the recurrence plot. Blue squares along the diagonal line show that for some time the system stays in roughly the same area, exploring the basin of some attractor. The size of each square gives an estimation of time spent in each basin. Narrow blue lines connecting squares show rapid transitions between different attractor basins. In general they are rather short, lasting less than 20 iterations. The dwell time, that is the time spent by the trajectory in each basin of attraction, is proportional to the size of each diagonal block. It depends strongly on parameters controlling neural accommodation; attractor basins simply vanish due to the fatigue of neurons that are highly active when the trajectory is in that basin, and this facilitates jumps to distant attractors. In the highly dimensional phase space there are many ways to make this transition (see below).

The color intensity allows for estimation of the strength of an attractor, e.g. dark blue square indicates a very strong attraction to some prototype state, fluctuating around it with a small variance. Color distribution in each block depends on the noise level, an important factor in determining the dwell time, as more noise means more energy, larger variance and a greater chance to escape from the basin of attraction. Changing noise level helps to see the structure of this basin. Magnification of the RP plot around the third attractor basin (iterations 210–320), presented in Fig. 3, shows two subblocks, the first one (iterations ∼5–35) showing trajectory oscillating around one basin, and the second one (iterations ∼40–80) where the trajectory jumps back and forth between the two states, moving into stronger oscillations before another attractor basin is entered for a short time (iterations ∼80–90) leading to a transition state. One can identify average configurations of the semantic layer corresponding to each of these basins to see which micro-features belong to the core representation of a given concept, and which may not be present although the system still stays in the basin that is linked to the phonological and orthographic representation of the same concept.

Fig. 3
figure 3

Magnification of the third attractor basin (iterations 210–320) of the “flag” word

Full size image

Zbilut and Webber (1994), Zbilut and Webber (1992) and Marwan et al. (2002) introduced several measures for quantitative analysis of recurrence plots. These measures are defined only for binary recurrence matrices (black-and-white plots) and so far have not been generalized to the graded case (colored plots). However, some measures may readily be generalized. For example, the Probability of Recurrence (PoR) to a given point in the vicinity of \(\user2{x}(t_i)\), defined as the number of points for which \(||\user2{x}(t_i)-\user2{x}(t_j)||<\epsilon\) divided by the number of all points n, can be estimated by summing all similarities between the trajectory point \(\user2{x}(t_i)\) and all other points \(\user2{x}(t_j)\). Defining similarity as the Gaussian function of a distance \({\bf S}_{\bf ij}=\exp(-||\user2{x}(t_i)-\user2{x}(t_j)||^2/2\sigma^2)\), where the dispersion σ plays similar role as the \(\epsilon\) in the original recurrence plots, probability of finding trajectory points in the σ neighborhood of \(\user2{x}(t_i)\) is calculated as:

$$ {\bf PoR}_{\bf i}({\bf t}_{\bf i}) = \frac{1}{n} \sum_{j=1}^n {\bf S}_{\bf ij}. $$
(4)

This measure estimates likelihood of finding trajectory points near each other in a fuzzy probability sense (Zadeh 1968). Instead of the Gaussian function other localized functions with values in the [0, 1] may be used, for example sigmoidal or soft trapezoid-like functions that replace hard threshold functions (Duch 2005). The overall probability of recurrence for a given trajectory can then be estimated as the average probability PoR i for all n points:

$$ {\bf PoR} = \frac{1}{n} \sum_i {\bf PoR}_{\bf i}. $$
(5)

In Fig. 4 probability of recurrence for the word “flag” is presented. Scaling the distance by the Gaussian function leads to a better contrast of the RP plot and to a smoother probability chart. Probability PoR i for a given trajectory point \(\user2{x}(t_i)\) represents the chance of finding the trajectory of the system near this point in the course of evolution. This probability is in general significantly smaller for points at the trajectory segments outside attractor basins compared to points that lie in the attractor basins. Estimation of recurrence probability depends on the length of the trajectory but also, in a complex neurodynamical system, it may strongly depend on priming by earlier activations and initialization of the network. The same is true for estimation of transition probabilities between words. Even when the network prompted by a given word starts from zero activity synaptic noise may lead to different trajectories, because in the high-dimensional phase space there are many pathways leading out of the attractor basin. Asymptotic averaging of results will not be very useful in predicting transition probabilities in real situations, washing out important priming effects (Spivey 2007).

Fig. 4
figure 4

Smoothed version of recurrence plot (left) for the “flag” word and the corresponding probability of recurrence plot (right). Overall probability of recurrence for this word is ≈0.02

Full size image

Recurrence plots do not show information about absolute location of trajectory in the phase space, preserving only information about the neighborhood of a given point. Recreation of relative positions of attractor basins from recurrence plots is usually impossible. One way to display relative distances between all successive points on the trajectory is to use multidimensional scaling (MDS) (Cox and Cox 2001), although computational costs of such visualization are quite high. In some neurodynamical systems relative relations between attractor states may be preserved despite different distributions of neural activity (Freeman 2000). Such phenomena cannot be observed using recurrent plots or MDS plots, but can be seen using fuzzy symbolic dynamics (FSD), described in the next section.

Visualization of trajectories by FSD

Fuzzy Symbolic Dynamics may be understood from several perspectives. First, understanding complex dynamics requires drastic simplifications. Symbolic dynamics (SD) is a well-know attempt to do that (Hao et al. 1998), replacing trajectories by a list of symbols that label different regions of the phase space crossed by the trajectory at a given time. This amounts to a very crude discretization, losing most information about dynamics. The Fuzzy Symbolic Dynamics (FSD) technique (Dobosz and Duch 2010) replaces hard partitions (hyperboxes) of the phase space by fuzzy partitioning (Klir and Yuan 1995). A given point may belong to each fuzzy set to some degree, measured by a membership function that defines this set. In practice one can define a set of reference points in the phase space and use simple distance functions rescaled in a non-linear way by Gaussian membership functions. Symbols may still be used as labels for the fuzzy sets, but they must be followed by real-valued vectors that provide membership values for each trajectory point in each set; symbols for sets for which membership value is below threshold may be deleted.

Second, FSD may be seen as a simplification of recurrence plots. Averaging \(\user2{x}(t)\) in the basin of an attractor identified in the RP plot provides a good reference point P k in the phase space, and a membership function based on rescaled distance from this vector may be used as a new dimension to plot the trajectory. Distances from several such vectors map original trajectories into a low-dimensional space. Instead of the recurrence matrix containing distances between all points on the trajectory, transformed distances from selected fixed reference points are used, \({\bf R}_{\bf ki} = {\bf G}(||{\bf P}_{\bf k}-\user2{x}_{\rm i}||)\). If the number of reference vectors is two or three elements of the R ki matrix may be plotted directly, otherwise the values of each \(G_k(t_i)=G(||{\bf P}_{\bf k}-\user2{x}({\bf t}_{\bf i})||)\) function are plotted on a time line using a color code.

Third, FSD is a mapping of the high-dimensional trajectory on a set of k basis functions \(G(\user2{x};\mu_i,\sigma_i), i=1,\ldots,k\), localized around μ i with some parameters σ i , strategically placed in important points of the phase space. One can argue that this type of reduction is quite common in the brain, with one area reacting to average activity level of several other areas that estimate different aspects of the sensory signals. For FSD visualization in two-dimensions \(G_i(\user2{x})=G(\user2{x};\mu_i,\sigma_i), i=1,2\) membership functions are placed in two different parts of the phase space, defining fuzzy sets. These functions return non-zero values each time system trajectories pass near their centers, providing a sequence of membership values (G 1,G 2) for the two fuzzy sets along the trajectory.

In our example two Gaussian functions with rather large dispersions are placed in the 140-dimensional space based on activations of the semantic layer. Parameters of these functions are given in Fig. 5, showing trajectories that lead to the first attractor basin for all 40 words that the network has been trained on (orthographic inputs are clamped after presentation of each word).

Fig. 5
figure 5

FSD mapping showing trajectories and attractors of all 40 words used in the dyslexia model. Twenty abstract words fall into a lower right corner, while concrete words are more on the left side, requiring longer times to activate more neurons

Full size image

Words that belong to two semantic categories, abstract and concrete words, have quite different representations. Concrete words have on average many more properties that define them than abstract words. Abstract words reach their basins of attractors much faster due to the significantly lower number of active units, while the meaning of concrete words is established after a longer trajectory, with more complex activity distributions. It is known from experiments that recognition potentials for words, peaking in the brain around 200–250 ms after presentation of a word, are influenced by their semantic categories (Martín-Loeches et al. 2001). Information about word latency is hidden in recurrence plots in the short sectors representing transitions, but FSD plots display it quite clearly. Figure 5 shows also different shapes of attractor basins (see comments on the role of noise below).

In Fig. 6 FSD trajectories and recurrence plots for the network activity prompted by two correlated words, “deer” and “hind”, are presented. The recurrence plots look quite similar but trajectories on the FSD plots differ significantly in their middle part (the first basin of attraction is almost identical because the two concepts are only slightly different), showing that the semantic layer of the network reaches in both cases rather different states in its evolution. This information is not displayed in the recurrence plots.

Fig. 6
figure 6

Comparison of the FSD trajectories (left) and the recurrence plots (right) for two correlated words “hind” (top) and “deer” (bottom) in the model of reading

Full size image

Recurrence plots may identify interesting substructures in trajectories exploring the basins of attractors, as seen in Fig. 3 (top). FSD visualization in Fig. 2 does not show such subtle structure in the first 100 iterations, but one may move centers of Gaussian membership functions to a different location of the phase space (with dispersions remaining unchanged), in effect magnifying this area. The structure of this attractor basin is than revealed in details as shown in Fig. 3 (bottom).

The center of the attractor basin that is reached after prompting the system with a given word defines “a prototype” vector, or a specific distribution of semantic layer activations. In Fig. 7 MDS visualization of all prototypes of abstract and concrete words is presented, with the addition of five prototypes taken as centers of the attractor basins that the system visits after prompting the orthographic layer with a single word “flag”. Lines connecting these five points show the order in which they are visited and have no other meaning. The first point is the prototype of the “flag” word. After reaching this basin of attraction the system moves to the second basin that is slightly different from prototypes for words used in the training. The second and the fifth prototype are very close to each other, as can also be seen in the RP and FSD plots (see Fig. 2). They both are close to the prototype of the “rope” word. The third prototype is also quite close to the prototype of the concrete word “flea”.

Fig. 7
figure 7

MDS visualization of all prototypes of abstract and concrete words with comparison to five centers of attractor basins (represented by stars connected by lines) which the system visits in its evolution after prompting orthographic layer with a single word “flag”. Note clear separation of abstract and concrete words

Full size image

The fourth prototype is a distorted version of the “flag” word. It does not represent any word that has been explicitly learned. When longer trajectories are investigated such spurious states are seen more often. Inspection of the activity of individual neurons leads in some cases to conclusions that they are abstractions of categories, for example a simplified prototype activity for several animals, with features shared by several animals that the network was trained on.

Another interesting observation is that abstract and concrete words are well separated in the MDS and FSD plots. This agrees with results from neuroimaging studies (Wang et al. 2010), where different brain structures were identified in neural representation of abstract and concrete concepts.

The role of synaptic noise. To analyze more precisely properties of individual basins of attractors response of the system to noise with increasing variance has been studied. The model of reading without any noise is deterministic and converges to the point attractor, because the model has already been trained and starts from zero activity except for the input layer. To explore attraction basins for a given word Gaussian synaptic noise with zero mean and progressively growing variance has been introduced.

In Fig. 8 trajectories and attractor basins of eight words, grouped into pairs of correlated words, are displayed, with concrete words in the first two pairs (“flag”–“coat”, “hind”–“deer”) and abstract words in the next two pairs (“wage”–“cost”, “loss”–“gain”). The variance of the noise has been increased from 0.02 to 0.09.

Fig. 8
figure 8

FSD visualization of the semantic layer shows changes in the size of attractor basins explored by the trajectories for increasing noise variance: 0.02 in top left plot, 0.04 (top right), 0.06 (bottom left) and 0.09 (bottom right)

Full size image

In Fig. 9 the variance of the trajectory near the attractor basin center is plotted as a function of increasing noise variance. This plot helps to estimate the strength of attractors, or the depth of their basins. For small noise variance there is a small linear change of the trajectory variance, showing that attraction is quite strong around the center, but for larger synaptic noise level there is a sharp increase in the variance of the trajectory, as is also seen in Fig. 8. Probably reaching the outer parts of the attraction basin quickly weakens the attraction and the trajectory is pulled towards other attractors. This effect is stronger for concrete words because more units remain active when noise levels are high, giving competing configurations of activations the chance to pull the trajectory in their direction. However, for very high levels of synaptic noise (>0.14) strong saturation of neurons inhibits most of them and a sudden decrease of the trajectory variance is observed in all cases. It is not yet clear whether this is a single neuron property due to the resonances that may occur when strong noise is present (Muresan and Savin 2007) or is it due to the connectivity of the network.

Fig. 9
figure 9

Variance of the trajectory around centers of the basins of attraction as a function of increasing noise variance

Full size image

Analysis of the FSD plots allows for drawing of a number of interesting conclusions:

  • convergence to sparse, simple representations (abstract words) is much faster than to more complex ones; experiments that go beyond two semantic categories (abstract vs. concrete, or familiar/not familiar) could in principle confirm this;

  • some basins of attractors may be difficult (and slow) to reach—this is indicated by chaotic trajectories that lead to them;

  • similar words have quite similar basins of attraction in the semantic layer, with the pair (coat, flag) being the most distinct in our simulations;

  • shapes of attraction basins differ for different words and different noise levels—this is seen when trajectories explore larger areas with increasing noise levels;

  • noise with a small variance preserves overall stability, for stronger noise distinct attractor basins are still seen, although patterns of semantic activity are severely distorted and may start to overlap;

  • for very strong synaptic noise plots of all basins of attractors shrink, the network turns itself off.

Only the first 500 iterations have been shown in figures presented here to preserve legibility. Analysis of longer sequences shows that for most words the states tend to visit the same basins of attraction every 400 iterations, as seen in the diagonal blocks creating bands in Fig. 10, although a lot of variance is seen each time the cycle is repeated. MDS visualization shows also all prototypes that were used in the training process. Prototypes of abstract words form a dense cluster in the upper part of the plot because they all lay far from the points on the trajectory (over 2,000 trajectory and prototype vectors have been used for this MDS mapping).

Fig. 10
figure 10

Recurrence plot and MDS visualization for 2,000 iterations for the “flag” word. The system tend to visit roughly the same basins of attraction every 400 iterations. MDS visualization shows also all prototypes used in the training process

Full size image

Figure 11 displays the FSD plot in 40 dimensions, showing the distance from all prototypes that have been used in the training process. Horizontal axis represents time (i.e. iterations) whereas on the vertical axis all prototypes are listed, starting with the 20 abstract words in the upper half, and ending with the 20 concrete words in the bottom half. This figure represents the same simulation for the “flag” word with 2,000 iterations as used in Fig. 10. In the first few iterations the system searches for the basin of attraction activating abstract concepts, and after reaching correct basin (identified by the darkest strip) it slips briefly into the neighborhood of “rope”–“lock” and then “flea”, and from there somewhere in between “hind”, “deer” and “hare”. The trajectory repeats itself (due to clamping of input) with considerable variance.

Fig. 11
figure 11

FSD plot presenting distance from all prototypes used in the training process. Abstract words are listed in the upper half and concrete in the bottom half of the vertical axis; horizontal axis represents time discretized into 2,000 iterations

Full size image

Optimization of the FSD viewpoint

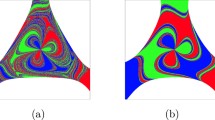
Reduction of dimensionality brings inevitably loss of information. FSD displays interesting structures only if appropriate parameters of membership functions are chosen. In Fig. 8 attractor basins for two correlated words (“deer” and “hind”) overlap almost completely. Moving centers of Gaussian membership functions to a different part of the phase space shows trajectories in all 8 basins as a separate areas, bringing forth the detailed shapes of these basins. In Fig. 12 FSD mapping was done with a different position of Gaussian function centers. From this points of view it is clear that “deer” and “hind” are represented by slightly different activity in the semantic layer.

Fig. 12
figure 12

FSD visualization for different locations of Gaussian function centers. For this visualization the same synaptic noise was used with variance equal 0.02

Full size image

FSD visualization depends strongly on parameters of membership functions. They should be optimized to reveal maximum information about neurodynamics. This requires some measure to quantify the goodness of visual representation. While many such measures have been proposed for dimensionality reduction visualization may benefit from more specific optimization. With larger number of membership functions approximation of the probability density calculated for long trajectories could be useful, but for visualization with two or three functions good approximation will not be achieved. To avoid overlaps of distinct basins of attractors the first FSD quality index is calculated as follows:

  • prototypes P i (centers of the attraction basins) are calculated in the N-dimensional phase space as average values of all iteration points that fall into well-defined blocks in the recurrence plots;

  • distances between pairs of these prototypes are calculated D ij  = ||P i  − P j ||;

  • prototype vectors P i are mapped to the d-dimensional FSD space G k (P i ) = G(P i ;Q k , σ k ), where Q k , σ k , k = 1, …, d are parameters that should be optimized;

  • points G(P i ) representing prototypes P i in FSD visualization should faithfully show distances g ij (Q k , σ k ) = ||G(P i ;Q k , σ k ) − G(P j ;Q k , σ k )||;

  • stress-like MDS measure (Cox and Cox 2001) is defined, summing differences between distances in the original and in the reduced spaces \(\mathcal{I}({\bf Q}_{\bf k},\sigma_{\bf k})=\sum_{\bf i>j} ||{\bf g}_{\bf ij}({\bf Q}_{\bf k},\sigma_{\bf k})-{\bf D}_{\bf ij}||\), and minimized over Q k , σ k .

Reference points Q k are defined in the phase space, and thus this is a rather costly minimization over dN + N parameters. Instead of the sum over all pairs of distances only minimal distances between prototypes that should be seen as separate may be used; this leads to the maxmin separation index \(\mathcal{I}_{mm}({\bf Q}_{\bf k},\sigma_{\bf k})\) based on the maximization of the minimal distance. Both the full FSD quality index and the maxmin measures give interesting results, but only the second one is used in comparisons below.

Many algorithms for multidimensional optimization may be used to optimize separation indices. Here ALOPEX (ALgorithm Of Pattern EXtraction), a simple correlation-based algorithm similar to simulated annealing, has been used. ALOPEX, developed by Harth and Tzanakou (1974), has been applied to optimization problems in many areas, including neural networks, decision trees, control, optimization of visual and auditory systems. The great advantage of ALOPEX is the simplicity of its implementation and gradient-free computation, which makes it quite useful for many purposes.

ALOPEX starts from randomly generated Q ik , k = 1,…, d variables (coordinates of Gaussian centers) over the [0, 1] range—in our model neural activations are real values from 0 to 1, so the phase space is contained in the [0, 1]d hypercube, where d = 140 is the number of neurons (only units of the semantic layer are analyzed). In every iteration each variable Q ik changes its value by adding or subtracting (with the same probability 0.5) an increment \(\Updelta\) that is decreased in every iteration by a constant value \(\Updelta=(\Updelta_0-\Updelta_f)/(\max_{it}-1)\) that depends on the maximum number of iterations max it (this is a form of annealing). Starting values \(\Updelta_0=0.3\) and the final value \(\Updelta_f=0.001\) are sufficient for our purpose. Values of variables are restricted to the [0, 1] range. At the end of each iteration the cost function value is computed and the new state is accepted if it improves the index, otherwise another stochastic iteration is run.

In Fig. 13 FSD plots for the “flag” word obtained by optimizing maxmin separation index are presented. The left plot shows FSD mapping for randomly generated Gaussian centers (the same as in Fig. 2 top), and the right plot shows the ALOPEX optimized maxmin mapping. The main advantage of optimized visualization is that basins of attractors are well separated from each other showing clearly the sequence of system transitions. Centers are now removed from data (coordinates change from 0.5 to 1, while for random parameters the range was quite small) and the basins of attractors look much smaller. Selecting centers close to the main clusters shows more detailed structure with a lot of jitter due to the synaptic noise, while optimized mappings place the centers of reference functions further from the data and are sensitive to large changes, smoothing the trajectories.

Fig. 13
figure 13

Comparison of FSD visualization for randomly generated Gaussian centers (left, same as in Fig. 2) and centers optimized using ALOPEX algorithm. FSD mapping with optimized centers shows clearly the sequence of system transitions

Full size image

In Fig. 14 optimized FSD visualization is compared with multidimensional scaling (MDS). Surprisingly, the two-dimensional (2D) trajectory structure in the maxmin optimized FSD plot is very similar to that in the MDS plot. In 3D differences between the plots are more noticeable than in the 2D case; the main difference is caused by the position of the third attractor basin (iterations 250–300, middle part), which in the case of MDS visualization is not as well separated as in the FSD plot. In the MDS 3D plot the fourth (orange) attractor basin is shifted too near to the first attractor basin (dark blue), as can also be confirmed using the RP plot (see Fig. 2). In particular the distance between these two attraction basins should be larger than between the second (light blue) and the fifth (red) basin (in the RP plot off-diagonal blue square between the second and the fifth attractor is darker than the one between the first and the fourth attractor). This is preserved in the optimized FSD visualization. Comparing to MDS, optimized FSD seems to separate attractor basins in a better way, placing them far from each other in the transformed space and in consequence showing the structure of the trajectories in a more faithful way. This is quite encouraging, although there is no guarantee that it will always be so.

Fig. 14
figure 14

Comparison between optimized FSD visualization (left) and multidimensional scaling (right). In 3D visualization differences between the plots are more noticeable than in 2D case but in general the mappings looks quite similar

Full size image

From visualization to interesting hypothesis

Visualization of trajectories of biologically-motivated complex networks may lead to deep insights into the relation between cognitive processes and the properties of networks and neurons. The development of phenomics (Consortium for Neuropsychiatric 2011), systematic study of phenotypes on a genome-wide scale, by integrating basic, clinical and information sciences, shows the need for such insights. The 7-level schema developed by the Consortium for Neuropsychiatric Phenomics places neural systems in the middle of the hierarchy, starting with genome, proteome, cellular signaling pathways, neural systems, cognitive phenotypes, symptoms and syndromes. Direct correlations between genomes and syndromes are quite weak and without intermediate steps there is no chance to link phenotypes to genotypes (Bilder et al. 2009). Simulations of biologically realistic neurodynamics may provide insights into possible abnormalities in signaling pathways and cognitive phenotypes, and is therefore of central interest to neuropsychiatry. However, statistical analysis of such simulations does not reveal much information about the global properties of neurodynamics. Here visualization may certainly be useful.

Even rough neural simulations can lead to interesting hypotheses that may be tested experimentally. Many specific perturbations of neural properties, at the synaptic, membrane and general connectivity level, may lead to very similar behavioral symptoms disturbing neural synchronization and leading to attention deficits. This is the reason why only weak correlation between the molecular and behavioral level are found (Pinto 2010). Brain development in such situations leads to various abnormalities, impairment of higher-level brain processes (including mirror neurons and the default network), and mistaken suggestions that these impairments are real causes of such diseases as autism (Zimmerman 2008).

Simulations of cognitive functions, such as the reading process used here as an example, allow for identification of parameters of neurons and network properties that change the nature of neurodynamics. Some of these changes may be interpreted as problems with attention shifts from one stimuli (or one thought) to another. Neurons that do not desynchronize will be active for a long time creating a persistent pattern, or an attraction basin that traps neurodynamics for a long time, as seen in Fig. 15. In this case attention remains focused on one object for unusually long time, as it happens in autism spectrum disorders (ASD) (Zimmerman 2008). On the other hand short synchronization times lead to rapid jumps from one basin of attraction to another, with short dwell times. Attention is not focused long enough, as is typical in case of Attention Deficit Hyperactivity Disorder (ADHD). A single parameter that controls the neuron accommodation mechanism may lead to such changes: increases in intracellular calcium which builds up slowly as a function of activation controls voltage-dependent potassium leak channels. This is seen in the FSD plots in Fig. 15 for the spontaneous associations of the “flag” word, with different values of the time constant controlling the accommodation mechanism (O’Reilly and Munakata 2000), from b_inc_dt = 0.005 for deep attractor basins that reduce the number of states in neurodynamics, through b_inc_dt = 0.01 that lead to the normal associations, to b_inc_dt = 0.02 that lead to fast depolarization of neurons, shallow attractor basins and the inability to focus on a single object.

Fig. 15
figure 15

Example of effects of leak channels: a single parameter controlling accommodation (leak channel) leads to problems with attention disengagement (top) or attention focus (bottom); standard noise, “flag” word, the same parameters of FSD mappings

Full size image

Computer simulations allow for investigating the influence of neural properties on cognitive functions. FSD visualization of simulations of attention shifts in visual field, spontaneous attention shifts in activation of linguistic system (thinking process), simulations of the Posner spatial attention tasks lead to the following hypothesis that is best formulated in the language of neurodynamics (Duch 2009 and in preparation): the basic problem in mental diseases involving attention deficits (including ASD and ADHD) may be due to the formation of abnormal basins of attractors. If they are too strong, entrapping the dynamics for a long time, behavioral symptoms observed in autism will arise, with hyperspecific memories and the inability to release attention for a long time (Kawakubo et al. 2007; Landry and Bryson 2004). As a result the number of interactions between distant brain areas will be unusually small, Hebbian learning mechanisms will not form strong connections. This in turn will lead to underconnectivity between these areas, as observed in neuroimaging, poor development of the mirror neuron system, default mode system and other higher-level brain processes (see articles in Zimmerman 2008). On the other hand shallow attractor basins do not allow the system to focus, maintain working memory, reflect longer on the current experience, jumping from one state to the other, as it happens in ADHD. Optimal behavior is thus a delicate compromise that may easily be disturbed at the molecular level.

Other parameters related to individual neurons and network connectivity may also lead to similar behavior, showing how diverse the causes of some diseases may be. Identifying specific ion channels that lead to such behavioral changes should allow for identification of proteins that may be responsible for specific dysfunctions, making the search for genes that code these proteins much easier. Although this is not a simple task (there are many types of ion channels) this approach may provide the foundation of a comprehensive theory of various mental diseases, linking all levels, from genetic, through proteins, neurons and their properties, to computer simulations and predictions of behavior. Current approaches to ASD, ADHD and many other mental diseases either try to link genetic mutations to behavior using statistical approaches (Pinto 2010), or are based on vague hypotheses that—even if true—do not lead to precise predictions testable at the molecular level (Gepner and Feron 2009; Zimmerman 2008). Visualization of neurodynamics may lead to quite new hypotheses expressed in a very different language.

Discussion

In this paper two techniques for analysis of high-dimensional neurodynamical systems have been explored: first, a fuzzy version of the symbolic dynamics (FSD), and second, analysis of variance of trajectories around point-like attractors as a function of noise. We have shown here that FSD, introduced very recently (Dobosz and Duch 2010) as a dimensionality reduction technique, may be treated as a generalization of the symbolic dynamics, and that it may also be approached from the recurrent plot technique point of view with very large neighborhoods for selected trajectory points. Symbolic dynamics is obtained from its fuzzy version by thresholding the activations of membership functions, and it is likely that some mathematical results obtained for symbolic dynamics (Hao et al. 1998) may be extended to the fuzzy version. Example of such a generalization for fuzzy recurrence probability has been given in section “Recurrence analysis”.

In this paper FSD has been used primarily as a visualization technique, motivated by the desire to understand global properties of complex neurodynamics. Recurrence plots and FSD maps complement each other, both providing an overview of global dynamics. Recurrent plots depend only on the time step selected, and on the size of the neighborhood that may be arbitrarily selected by the user, or on the scaling of the color maps in the continuous case (Marwan et al. 2007). Symbolic dynamics depends also on the way the phase space is partitioned. FSD mappings depend on the choice of membership functions that provide soft partitioning of the phase space. The dependence on the time step and the size of the neighborhood is not so critical as in the case of recurrence plots. The optimization procedure presented in section “Optimization of the FSD viewpoint" automatically selects parameters maximizing information that is shown in visualization.

Cognitive science has reached the point where moving from finite automata models of behavior to continuous cognitive dynamics becomes essential (Spivey 2007). Recurrent plots and symbolic dynamics may not be sufficient to show various important features of neurodynamics in complex systems. The whole trajectory is important, not only invariants and asymptotic properties of the dynamics. As an example of such analysis FSD visualizations of the semantic layer in the model of reading have been analyzed in some details, showing many aspects of dynamics, identifying parts of the phase space where the system is trapped, showing attractor basins, their properties and mutual relations. FSD visualizations loose many details that are contained in the original trajectories, but allow to zoom on specific areas near interesting events. These areas are analyzed precisely using membership functions that are adapted to local probability density distributions. The challenge is to retain interesting information, suppressing the chaotic, random part. The choice of various membership functions and their parameters in FSD gives sufficient flexibility to achieve this.

Quantitative measures for FSD plots may be introduced along the same lines as for recurrent plots (Marwan et al. 2007). Noise level has influence on many properties of neurodynamics, including:

  • the number of attractor basins that a system may enter;

  • percentage of time spent in each basin (dwell time);

  • character of oscillations around attractor basins;

  • probabilities of transitions between different attractors.

Such measures allow for interesting characterization of dynamical systems but will not replace the actual observation of the trajectory in specific situation. Adding noise \(\epsilon\) of increasing variance and plotting the variance of trajectories \(\hbox{var}(x(t,\epsilon))\) may also helps to understand behavior of a system inside and near attractor basins. For quasi-periodic attractors variance in the direction perpendicular to the trajectory may be estimated.

FSD mappings show how attractor basins created by various learning procedures depend on the similarity of stimuli, on the context and history of previous activations, and the properties of individual neurons. Interactive visualization is the best solution for such explorations. As a result interesting hypotheses may be generated, for example connection between leaky ion channels and attention shifts, a phenomenon that may be of fundamental importance in attention deficit disorders, including ASD and ADHD. To our best knowledge this is the first time such detailed analysis has been performed for neurodynamical systems.

Static pictures of the trajectory do not express the full information about a neurodynamical system. The trajectory may leave the basin of attraction for many reasons: it may have enough energy to jump out, or find an exit path in some dimensions where attraction is weaker, or the basin of attraction itself may become quite weak for some time due to the neural fatigue. In the last case the whole landscape of accessible basins of attractors changes in time as a result of recent activity, and may only be shown on a series of snapshots or on a movie, but not in a static picture. Basins of attraction change all the time and the whole landscape may recreate itself locally only in an approximated way when the trajectory returns there. Spurious attractor basins may be observed in a trained network, resulting from complex dynamics. Their nature is worth detailed investigation and may help to understand why some ideas are quickly accepted and some cannot embed themselves in existing neurodynamics. One may connect these ideas with the vague concept of memes (Dawkins 1989; Distin 2005).

Among many potential applications of the FSD technique visualization of causal networks in simulated neural systems (Seth 2008) should be mentioned. Graph theory used for that purpose does not show the enfolding of the trajectories. The challenge here is that activity in different structures should be separated, and thus it may not be so clear in the 3 dimensions. The whole neurodynamics may then be visualized using hierarchical approach, with simplified activity of major structures in one plot, and more detailed activity of other structures in separate plots. Application to real neuroimaging signals is even a greater challenge. Decomposition of data streams into meaningful components using Fourier or Wavelet Transforms, Principal and Independent Component Analysis (PCA, ICA), and other techniques (Sanei and Chambers 2008) are very popular in signal processing. These techniques are used to remove artifacts by filtering some components, but do not capture many important properties that the global trajectory of the system reflects. Global analysis is needed to characterize different types of system’s behavior, see how attractors trap dynamics, notice partial synchronization and desynchronization events. FSD may help to inspect such behavior and complement recurrence plots in qualitative analysis.