A secure image encryption scheme based on a novel 2D sine–cosine cross-chaotic (SC3) map

Abstract

In this paper, we propose a new 2D sine–cosine cross-chaotic (SC3) map to design an image encryption scheme with high confusion and diffusion capability. We evaluate the maximum Lyapunov exponent (MLE) of the proposed SC3 map to measure its degree of sensitivity to initial conditions and perform bifurcation analysis to find the chaotic region. The proposed chaotic map generates two pseudo-random sequence $R_1$ and $R_2$, which are used in confusion (permutation) and diffusion phase, respectively. The confusion layer is designed by shuffling the image pixels, and the diffusion layer is designed by bitwise XOR operation. The strength of the proposed image encryption scheme is evaluated against resistance to the statistical attack (information entropy, correlation coefficient, and histogram analysis), differential attack (NPCR and UACI), and sensitivity to the secret key. The experimental results of both security and performance analysis show that the proposed image encryption scheme is secure enough to resist all the existing cryptanalytic attack and efficient in terms of encryption time.

1 Introduction

With the rapid increase in the number of smart devices, Internet of Things (IoT) devices, and lightweight mobile applications, a huge amount of multimedia data (images) are being generated and transmitted over the insecure public channel and stored in a trusted cloud server. The user’s data communicated over an insecure channel is vulnerable and must be protected from the existing cryptanalytic attack. The traditional block cipher such as AES [1] and DES [2], lightweight block cipher such as PRESENT, GIFT and stream cipher such as grain [3] are not efficient enough in a constrained environment due to low computational and storage capability.

To improve the performance of an image encryption scheme without compromising the security level, chaos-based cryptosystem [4,5,6,7] is a suitable choice for fast and secure transmission of multimedia data. In fact, chaos-based cryptosystems are based on the confusion and diffusion principle as proposed by Claude Shannon [8]. Confusion principle hides the relationship between key and ciphertext, whereas diffusion principle hides the relationship between plaintext and ciphertext as complex as possible. The inherent characteristics of any chaos-based cryptosystems are unpredictability and sensitivity to initial conditions, which are based on confusion and diffusion principle respectively. The existing chaotic map is of two types, i.e., 1D chaotic map [9,10,11] and multidimensional chaotic map [12,13,14]. In 1D chaotic map, only one variable and few parameters are involved to generate the pseudo-random sequence. The initial parameters are easily estimated due to small key space and less complex structure of 1D chaotic maps. So, it is not secure enough for image encryption. On the other hand, multidimensional chaotic map involves multiple initial variables, which makes it more secure than 1D chaotic map, but takes more computational time.

In this paper, we design a chaotic map called 2D sine–cosine cross-chaotic (SC3) map, which generates two different pseudo-random sequences concurrently $R_1$ and $R_2$ for confusion (permutation) and diffusion layer, respectively. The pseudo-random sequence $R_1$ is used to permute the image pixels to reduce the high correlation between adjacent pixels within the plain image. The pseudo-random sequence $R_2$ is used to modify the pixel values of the permuted image by doing bitwise XOR operation. Based on the security requirements, the encryption process can be iterated for multiple rounds to make it more secure according to the type of environment (hardware/software).

2 Our contribution

The contribution of our research work is twofold: first one is from chaotic point of view, and second one is security analysis. The performance of our proposed 2D SC3 map is evaluated by the phase diagram, bifurcation analysis, and randomness testing. The security analysis is performed on image encryption using permutation and diffusion structure.

The proposed chaotic map has achieved a much wider range of chaotic behavior. The proposed 2D SC3 map has chaotic behavior when $\alpha \in$ [0.49, 1], and $\beta \in$ [0.79, 1] and maximum Lyapunov exponent value $\lambda _1$ and $\lambda _2$ is 2.6239 and 2.6189, respectively. A higher value of LE increases its degree of unpredictability and sensitivity to initial condition. We compare our proposed chaotic map with 2D LASM [15] in terms of LE, and chaotic range. The proposed chaotic map has a higher LE value and a much wider chaotic range than 2D LASM. The NIST statistical testing results shows that the proposed chaotic map passed all the tests, which signifies the chaotic map is truly random as recommended by NIST [16].

To measure the confusion and diffusion capability of our proposed chaotic map, we design an image encryption algorithm using permutation and diffusion structure. The control parameters ($\alpha , \beta$) are chosen within their corresponding chaotic range along with initial parameter ($x_0$, $y_0$) as a secret key. The initial seed or secret key is used to generate the pseudo-random sequence to permute the image pixel followed by the bit diffusion process with XOR operation. The security analysis of the image encryption algorithm resistance to statistical attack, differential attack, and sensitivity to the secret key shows that the proposed chaotic map has high confusion and diffusion capability to attain desired security level.

3 Related work

In this section, we will discuss about the recently proposed chaotic map used in the image encryption scheme for both grayscale and color images. The main idea of designing any chaos-based image encryption scheme is to resist both statistical attack and cryptanalytic attack [17]. So, it is important to analyze cryptographic strength of the proposed chaotic map. The chaotic behavior of any chaotic map denotes the confusion and diffusion capability of the proposed scheme. First, we describe the properties used to evaluate the confusion and diffusion capability of any chaotic map and later we discuss the underlying architecture used for image encryption. The Lyapunov exponent is a quantitative measurement to check sensitivity to the initial conditions [18] of any chaotic map. To achieve the high confusion and diffusion capability, the pseudo-random sequence with chaotic behavior is not enough. The underlying architecture also plays an important role for security of the image encryption to resist both statistical and cryptanalytic attack. Basically, there are three widely known architectures for designing an image cryptosystem, such as permutation (confusion) only, diffusion only, and both permutation–diffusion structure [19]. In permutation only method, the image pixels are shuffled to reduce the high correlation among adjacent pixels. Since only pixel values are shuffled, the distribution of pixel values remains unchanged in cipher image and becomes non-uniform, which makes the cipher vulnerable against statistical attack. A study on some popular image scrambling techniques is presented in [20]. In diffusion only structure, the pixel values are modified using bit permutation or Xor operation, which results a uniform distribution of the pixel values in an encrypted image. But in diffusion structure, high correlation among adjacent pixels is not fully reduced, which leads to the correlation attack. In permutation–diffusion structure [21], the plain image is permuted first, and then the diffusion operation is performed by modifying the pixel values.

Almost all chaos-based image encryption schemes follow permutation–diffusion structure by 1D chaotic map [9], multidimensional (2D/3D) chaotic map, multiple 1D chaotic map [12, 15, 22, 23], chaotic map with DNA computing [14, 24, 25], chaotic map with cellular automata [21, 22], or chaos-based S-Box [6, 10, 26, 27]. The main goal is to design an image encryption scheme with computational complexity without compromising the security level, specially for constrained environment and lightweight mobile application.

The 1D chaotic map has a simple structure and generating only one pseudo-random sequence. It is easy to implement and takes less computational effort, but it is vulnerable to the cryptanalytic attack due to its simple structure. Zhu et al. [28] proposed a symmetric image encryption scheme based on a 1D logistic map for diffusion operation and Arnold cat map for bit-level permutation. The computational complexity is very high in this scheme. Belazi et al. [29] propose a novel image encryption scheme which is based on 1D chaotic map and S-Boxes using the substitution–permutation network. The author used a new chaotic map for diffusion using XOR operation and then performed the substitution operation using S-Boxes. The diffusion is done using the logistic map, and finally permutation is performed with a permutation function. This cryptosystem has a more complex structure, and time complexity is quite higher. Wang et al. [25] apply the logistic map for color image encryption using pixel-level permutation as a combination of row scrambling and column scrambling followed by the diffusion. The author generates two different pseudo-random sequences with length $3M \times N$ and $3M \times N$ for row and column scrambling, respectively, for RGB components.

Wu et al. [23] propose a robust color image encryption scheme using three different improved 1D chaotic maps and DNA computing such as logistic tent system, logistic sine system, and tent sine system. The security level is quite high in comparison to other image encryption schemes. The computational complexity is more, as it uses three different maps and it involves encoding and decoding process of DNA computing, which is not suitable for a lightweight application. Cao et al. [30] design an image encryption scheme based on 2D LICM hyperchaotic map using bit permutation approach for both confusion and diffusion layer. Since the bit permutation is a time-consuming approach, so this encryption scheme was also not efficient for a constrained environment. Hua et al. [15] use 2D logistic-adjusted sine map to design image cryptosystem with bit manipulation confusion and diffusion. This encryption scheme adds a random number to the surrounding pixel intensities of the plain image in every round to enhance the security level. Mondal et al. [21] propose a image encryption scheme based on cellular automata and chaotic skew tent map. The author used the skew tent map to generate the initial vector for cellular automata. The plain image then permuted using pseudo-random sequence followed by the diffusion process. Ping et al. [22] designed image cipher using life-like cellular automata and chaotic map with the permutation–substitution network. The cellular automata-based image cipher using chaotic map suffers from drawbacks such as having no explicit classification of CA rules, small rule space and low diffusion capability.

Fu et al. [31] propose an image encryption scheme with improved spatial bit-level permutation strategy using the 3D cat map. The bit-level permutation has both confusion and diffusion capability. The author generates the keystream using a function of secret key and plain image to enhance the security against chosen plaintext attack. Ping et al. [32] design an image encryption scheme with simultaneous permutation–substitution structure using discrete henon map. The plain image is scanned only once and the image pixels are shuffled with pixel positions generated by 2D discrete henon map and followed by two-point diffusion simultaneously using the keystream as a function of plain image. The proposed scheme increases the efficiency of image encryption with simultaneous confusion and diffusion operation. Kandar et al. [33] design image encryption using the sequence generated by the cyclic group for both confusion and diffusion process. The author applied both row permutation and column permutation in confusion phase, bit-level permutation and bit-level transformation in diffusion phase using the pseudo-random sequence generated by the cyclic group. Liu et al. [6] propose a color image encryption scheme using chaos-based bijective S-Box. The chaotic map used in this paper generates three different pseudo-random sequences for both confusion and diffusion. The confusion process is substituted by bijective S-Box and diffusion process done using bitwise XOR operation. Zhan et al. [34] proposed a scalable coding scheme, which performs encryption using modulo-256 addition followed by an encoding scheme. In this scheme, encoded bit streams are made of quantized subimage and remainders of Hadamard coefficients. Qin et al. [35] proposed a scheme for image encryption with compression techniques. The plain image is masked with modulo-256 addition followed by a block permutation. This scheme achieves better rate-distortion performance. Panwar et al. [36] propose an image encryption using DNA sequence and multiple 1D chaotic map. In this paper, the author analyzes how the original encryption scheme found to be low sensitivity by slight modification of plain image which leads to diffusion process becoming insecure. The author improves the existing techniques to resist these shortcomings. The same author [37] also improve the image encryption by combination of 1D chaotic map.

4 Preliminaries

A chaotic map is an evolution function which is a deterministic, and nonlinear dynamic system. It generates a pseudo-random sequence having both confusion and diffusion capability, so that it can be secured enough when applied for image encryption. The chaotic map can be defined as follows:

$$\begin{aligned} x_{n+1} = f(x_n), \end{aligned}$$

(1)

where $n = 0, 1, 2, \dots$, and so on. It determines the value of the next state based on the present state. The dynamics of the systems depends upon the composition of the nth iteration of the evolution function, i.e., $f^n(x_0)$. The most important properties of any chaotic map is its chaotic behavior, i.e., sensitive to initial condition, wider chaotic range. The sensitivity to an initial condition properties is important for image encryption. To design an evolution function, initial parameters are not enough, it requires some control parameter to become more chaotic. But the 1D chaotic map is vulnerable to cryptanalytic attack and not secure for image encryption. So the chaotic map is dependent on multiple initial values as well as multiple control parameters to increase the security level and this type of chaotic map is called multidimensional chaotic map, which can be generalized as Eq. 2:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{i+1} = f_1(y_i; \alpha _i)\\ y_{i+1} = f_2(x_i; \alpha _i). &{} \end{array}\right. } \end{aligned}$$

(2)

In the above equation, $f_1$ and $f_2$ are both inter-dependent to generate two different pseudo-random sequences and this type of chaotic map is called cross-chaotic map. In this paper, we propose a sine–cosine cross-chaotic map which demonstrates all properties of chaotic behavior. The map is used to generate two pseudo-random sequence.

5 Proposed 2D sine–cosine cross-chaotic (SC3) map

In this section, the mathematical definition of our proposed chaotic map is presented and then evaluated whether the proposed system exhibits chaotic behavior. The 2D SC3 map is defined in Eq. 3.

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{i+1} = \text{ sin }\Big (\frac{\alpha }{y_i} \Big )^{\frac{3}{2}} \\ y_{i+1} = \text{ cos }\Big (\beta ~ \text{ cos }^{-1} x_i \Big ), &{} \end{array}\right. } \end{aligned}$$

(3)

where $x_0, y_0$ are two initial parameters, ($x_0, y_0) \in [0, 1]$ and $\alpha , \beta$ are two control parameters, where $(\alpha , \beta ) \in [0, 1]$.

Fig. 1

Phase diagram of proposed chaotic map

5.1 Bifurcation analysis and phase diagram

The performance of the chaotic map is measured by the phase diagram, bifurcation analysis, and Lyapunov exponent.

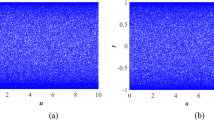
The phase diagram represents the distribution of attractors or output pairs ($x_{i+1}, y_{i+1}$) in a 2D phase plane. The attractors of our proposed 2D SC3 map is shown in Fig. 1 with initial values ($x_0, y_0$) = (0.5, 0.6). The figure denotes the distribution of data covers a much larger region, which signifies the proposed map covers the entire region. It is not clustered to a particular region, which tells the randomness and uniform distribution of the pseudo-random sequence to achieve the high diffusion capability. The phase diagram suggests it is more chaotic, and good ergodicity.

Bifurcation occurs when there is a changes in its topological structure with respect to change in control or bifurcation parameter, i.e., distribution of output values with respect to its control parameters. The bifurcation diagram are shown in Figs. 2 and 3 with respect to varying of $\alpha$ and $\beta$, respectively. Figure 2a, b represents the bifurcation diagram of X and Y sequence, respectively, when $\alpha$ varies from 0 to 1 and $\beta$ = 0.85 with step value of 0.001. The solid line represents the fixed point and periodic window, whereas the dotted line represents the chaotic region. The obtained results show that the proposed map has chaotic behavior when control parameter $\alpha \in$ [0.49, 1]. Figure 3a, b shows the bifurcation diagram of X and Y sequence, respectively, when $\beta$ varies from 0 to 1 and $\alpha$ = 0.90. The figure signifies that the system attains the chaotic behavior when $\beta \in$ [0.79, 1]. The wide chaotic range of the control parameter suggests that it has large key space which improves the security of the cipher against an exhaustive search attack.

Fig. 2

Bifurcation diagram ($\alpha$ = vary, $\beta$ = 0.85)

Fig. 3

Bifurcation diagram ($\beta$ = vary, $\alpha$ = 0.90)

Fig. 4

Lyapunov exponent ($\alpha$ = vary $\beta$ = 0.85)

Fig. 5

Lyapunov exponent ($\beta$ = vary $\alpha$ = 0.90)

5.2 Maximum Lyapunov exponent

The chaotic behavior of a dynamical system is defined by its sensitiveness to initial conditions and unpredictability. The Lyapunov exponent is a quantitative measurement to determine the dynamic system’s chaotic behavior [38]. Lyapunov exponent measures the degree of divergence between any two nearby trajectories of a dynamic system which is the stretching of an orbit. If the orbit is stable, then the maximum Lyapunov exponent is less than zero and stretching is minimal. The positive value of maximum Lyapunov exponent shows exponential stretching of an orbit. Technically, if we take two initial points which are very close together say $x_0$, $y_0 (x_0+\delta _0$) and iterate the evolution function n times to get the $x_n$ and $y_n$. The difference between two sequence $y_n - x_n$ should grow exponentially and is mathematically defined in Eq. 4:

$$\begin{aligned} |\delta _n| \sim |\delta _0| e^{\lambda n}. \end{aligned}$$

(4)

The constant $\lambda$ is called Lyapunov exponent. If the Lyapunov exponent (LE) $\lambda$ is positive, then the system is chaotic and if it is negative or zero then the systems exhibits non-chaotic behavior. Every chaotic system has at least one positive Lyapunov exponent to achieve the chaotic behavior.

$$\begin{aligned} \lambda (x_0) = \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{i=0}^{n-1} \text{ ln }|f'(x_i)|. \end{aligned}$$

(5)

A multidimensional chaotic map has more than one LE and if all the LEs are positive, then the dynamic systems possess hyperchaotic behavior. The hyperchaotic behavior is good for image encryption and it is very difficult for attacker to predict the secret key.

In this paper, we calculate the Lyapunov exponent by keeping $\alpha$ vary, $\beta$ fixed and $\beta$ vary, $\alpha$ fixed as shown in Figs. 4 and 5, respectively. Since our proposed chaotic map is 2D, it has two Lyapunov exponents ($\lambda _1$ and $\lambda _2$). Figure 4 shows the Lyapunov exponent values $\lambda _1$ and $\lambda _2$ with respect to change in control parameters, i.e., $\alpha$ varies from 0 to 1 and $\beta$ = 0.85. We observe that both $\lambda _1$ and $\lambda _2$ are positive when $\alpha \in$ [0.49, 1]. The maximum Lyapunov exponent value of $\lambda _1$ and $\lambda _2$ is 2.3218 and 2.2938, respectively. Similarly, Fig. 5 shows the Lyapunov exponent values $\lambda _1$ and $\lambda _2$ with respect to change in control parameters, i.e., $\beta$ varies from 0 to 1 and $\alpha$ = 0.90. Both $\lambda _1$ and $\lambda _2$ are positive, when $\beta \in$ [0.79, 1]. The maximum Lyapunov exponent value of $\lambda _1$ and $\lambda _2$ is 2.6239 and 2.6189, respectively. The higher value of LE denotes the system is more difficult to be predicted. The computation of maximum Lyapunov exponent is performed with different combinations of $\alpha$ and $\beta$ as shown in Table 1. We compared our results with the results obtained by the chaotic map [29] as shown in Table 2, and it shows that the proposed chaotic map has higher Lyapunov exponent.

Table 1 Lyapunov exponent value of the proposed map

Table 2 Lyapunov exponent value of the existing chaotic map [29]

5.3 NIST statistical test

The pseudo-random sequence generated by the chaotic map must satisfy the randomness property for cryptographic application. The pseudo-random sequence generated for image encryption should be unpredictable even if the initial and control parameters are known to the attacker. For cryptographic application, the sequence must be truly random or it must be indistinguishable from a random sequence in a polynomial time algorithm. Randomness in a given sequence is defined as the distribution of data in different patterns of sequence which is difficult to be predicted by the attacker. The NIST published a test battery to evaluate the randomness criteria of any binary sequence by detecting the deviation of a given binary sequence from a randomness property. There are sixteen different test criteria present in NIST test suite [39] to check the randomness property of either random or pseudo-random generator. We calculate the p value of our sequence generated by the proposed chaotic map. To evaluate any randomness testing, the p value is compared with the significance level $\alpha$. If the resulting p value is larger than the significance level $\alpha$, then the test is random and considered as passed. As recommended by NIST, $\alpha$ is commonly set to 0.01 for cryptographic application.

In our experiment, we perform NIST statistical test on 100 different sequence of length $(10)^k$, where k varies from 3 to 5 for all the test suite except binary matrix rank and Maurer’s universal statistical test. For binary matrix rank test and Maurer’s universal statistical test, the minimum length of the bit string sequence must be 38912 bits and 387840 bits, respectively, as per NIST recommendation [16, 39]. The pseudo-random sequence generated by our proposed chaotic map passed all the NIST statistical tests and the test result is shown in Table 3.

Table 3 NIST statistical test results

5.4 Discussion

In this section, we evaluate the performance of our proposed chaotic map in terms of phase diagram, bifurcation analysis, and Lyapunov exponent. The phase diagram of proposed 2D SC3 map covers whole data range in a 2D phase plane and has much larger distribution. The output pairs ($x_{i+1}, {y_{i+1}}$) become more dense as it approaches 1. We compare our phase diagram with 2D logistic map, 2D SLMM, Henon map, and 2D LASM. The comparison results shows that the output trajectory of 2D logistic map, Henon map, and 2D SLMM chaotic map clustered to a particular region, whereas the phase diagram of proposed 2D SC3 map covers entire region in 2D phase plane. The bifurcation analysis of 2D LASM has chaotic behavior when $\mu \in$ [0.37,0.38] $\cup$ [0.4,0.42] $\cup$ [0.44,0.93] $\cup$ 1, i.e., which seems to cover less range as compared to proposed 2D SC3 map. The proposed map has chaotic behavior when $\alpha \in$ [0.49, 1], and $\beta \in$ [0.79, 1]. The proposed map covers a much wider region than 2D LASM. The maximum Lyapunov exponent values $\lambda _1$ and $\lambda _2$ are 2.6239 and 2.6189, respectively, which is much higher than the Lyapunov exponent value of 2D LASM ($\lambda<$ 1.5). We also compared our Lyapunov exponent results with the chaotic map mentioned in the Table 2. The maximum value of LE has achieved by the chaotic map [29] is 1.38632, which is much lesser than our proposed chaotic map.

We perform NIST statistical testing on the pseudo-random sequence generated by the proposed chaotic map to check the randomness property. The proposed chaotic map passed 14 test out of 16 statistical testing as shown in Table 3.

6 Proposed cryptosystem based on SC3 map

Fig. 6

Architecture of proposed image cryptosystem

In this section, we apply our proposed 2D SC3 map to design the cryptosystem for image encryption to resist the brute force attack, statistical attack, and differential attack. But in permutation followed by bit-level diffusion structure, the encryption algorithm both shuffles the image pixels and substitutes with different values which can resist all types of attack like statistical attack, differential attack, and correlation attack. The architecture of our proposed cryptosystem is shown in Fig. 6. The architecture takes the plain image as input and transformed to cipher image by applying pixel shuffling and bitwise XOR using pseudo-random sequences $R_1$ and $R_2$, respectively. The pseudo-random sequences $R_1$ and $R_2$ were generated as a function of the shared secret key using the proposed 2D SC3 map. The initial parameters ($x_0, y_0$) and control parameters ($\alpha , \beta$) combined together ($x_0, y_0, \alpha , \beta$ ) and ($x_0', y_0', \alpha ', \beta '$) to form the secret key $K_1$ and $K_2$ for both confusion and diffusion layer, respectively. The encryption and decryption process is described in algorithm 1 and algorithm 2, respectively.

6.1 Confusion based on pixel scrambling

The confusion principle states that the relationship between cipher image, and secret key should be as complex as possible and sensitive to the secret key. The changes of single bit in secret key must affect the cipher image in a pseudo-random way. The pixel shuffling phase permutes the plain image using the pseudo-random sequence $R_1$ to reduce the correlation between the adjacent pixel.

6.2 Diffusion using bit manipulation

The diffusion principle hides the relationship between the plain image and cipher image by making it as complex as possible to resist the differential attack. The diffusion phase not only hides the relationship between plain image and cipher image, it also maintains the uniform distribution of pixel values of the cipher image. That means, as the pixel values of plain images are highly clustered within a particular interval, the attacker can mount the statistical attack by computing the variance of the histogram. The good diffusion methods transform the plain image into cipher image with uniform distribution of pixel values which is difficult for the statistical attack. The diffusion phase suggests that the cipher image is highly sensitive to the change in plain image pixel values, i.e., one pixel change in plain image must be changed into cipher image by at least 50%. This is called avalanche effect. In this paper, the pixel values are manipulated using bitwise XOR operation with the pseudo-random sequence $R_2$ generated by the 2D SC3 map.

7 Experimental details

We evaluate both the security aspect and performance of proposed encryption scheme by experimenting in MATLAB (R2018b) on the standard image “Lena”, “Baboon”, “Peppers”, “Nike logo”, “Airplane”, and “Barbara” of size 512 $\times$ 512. The two secret keys ($K_1$ and $K_2$) used for generating the pseudo-random sequence $R_1$ and $R_2$ for confusion and diffusion layer, respectively. The initial parameters $(x_0, y_0)$, and the control parameters $(\alpha , \beta )$ are considered as secret key $K_1$, where $x_0, y_0, x_0', y_0' \in$ [0,1], and $\alpha , \beta , \alpha ', \beta ' \in$ [0,1]. The two secret keys in our experiment are $K_1 = (x_0, y_0, \alpha , \beta )$ and $K_2 = (x_0', y_0', \alpha ', \beta ')$, where $x_0 = 0.5217649304251095$, $y_0 = 6392750215680951$, $\alpha = 0.5672104389217190$, $\beta = 0.8502175864356750$, and $x_0' = 0.7356439802176543$, $y_0' = 0.8530267952419067$, $\alpha ' = 0.5678093425186743$, $\beta ' = 0.9256810743901653$.

The experiments are conducted on the system having windows 10 operating system, 4GB RAM, Intel i5 Generation 3. We evaluate our encryption scheme against resistance to statistical attack, resistance to differential attack, key space analysis to resist brute force attack, and key sensitivity analysis. The computational complexity of our proposed encryption scheme is less than existing image encryption scheme and encryption/decryption time is quite faster. The standard test images, encrypted images, and decrypted images of Lena, Peppers, and Baboon are shown in Fig. 7a–i, respectively. The cipher images are completely noisy one and unrecognizable. So, the attacker finds it difficult to discover any hidden information to recover either secret key or plain image.

Fig. 7

a Plain image Lena; b encrypted image Lena; c decrypted image Lena; d plain image Peppers; e encrypted image Peppers; f decrypted image Peppers; g plain image Baboon; h encrypted image Baboon; i decrypted image Baboon

8 Security and performance analysis

This section presents the experimental results of six grayscale images of key space analysis, key sensitivity analysis, statistical analysis, differential cryptanalysis and encryption quality of proposed image encryption scheme.

8.1 Key space analysis

To resist the brute force attack or exhaustive search, the total key search space should be huge. In this paper, the proposed 2D SC3 map-based image encryption scheme have four parameters $(x_0, y_0, \alpha , \beta )$ to generate the secret key. In our experiment, the computational precision is allowed up to $10^{-16}$, so the total key space is $10^{64} \approx 2^{213}$. Table 4 provides the comparison results of the total search space of the secret key of our proposed encryption scheme and the existing encryption scheme. Our proposed image scheme has larger key space to resist the brute force attack.

Table 4 Comparison results of total key space of proposed and existing scheme

8.2 Key sensitivity analysis

The key sensitivity analysis suggests minor changes in key bits would have a significant impact on the cipher image that means resulting in a complete different encrypted image. A good image encryption algorithm must be sensitive to the secret key and it can be possible when the chaotic map used in the encryption scheme is highly sensitive to initial conditions. We analyze our proposed encryption scheme to evaluate the sensitivity to the secret key by modifying only one parameter and keeping other parameters unchanged.

The secret key of our proposed cryptosystem has four parameters ($x_0, y_0, \alpha , \beta$). Two different set of keys ($K_1, K_2$) are used for both confusion and diffusion, respectively. We modify the $x_0$ value of $K_1$, i.e., $x_{{\text {mod}}} = x_0 + (10^{-k})$ where $k \in$ [10, 16]. The secret key $K_1$ and $K_1^\prime$ = ($x_{{\text {mod}}}, y_0, \alpha , \beta$) is used to encrypt the Lena image in Fig. 8a. Figure 8b, c represent the cipher image obtained by $K_1$ and $K_1^\prime$, respectively. Figure 8d is the pixel-by-pixel difference between (b) and (c). To get the plain image, the receiver must decrypt with the correct key. Figure 8e, f represents the decrypted image of the Fig. 8b using correct ($K_1$) and wrong key ($K_1^\prime$), respectively. Similarly, Fig. 8g, h is the decrypted image of Fig. 8c using wrong key ($K_1$) and correct key ($K_1^\prime$), respectively. Figure 8f,  g is completely unrecognizable since it uses the wrong keys. This proves that the slight changes in key bits would make a significant impact on the encryption and decryption mechanism. The experimental results shows that the proposed image cryptosystem is highly sensitive to the secret key.

Fig. 8

a Plain image Lena; b encrypted image of Lena using $K_1$; c encrypted image of Lena using $K_1^\prime$; d the pixel-by-pixel difference between b and c; e decrypted image from b using $K_1$; f decrypted image from b using $K_1^\prime$; g decrypted image from c using $K_1$; h decrypted image from c using $K_1^\prime$

8.3 Resistance to statistical attack

8.3.1 Histogram analysis

Histogram represents the distribution of the pixel values [0, 255] of the image. The secure image cryptosystem should achieve uniform distribution of the pixel values of the encrypted image which makes the attacker very difficult to introduce the statistical attack. Basically, the distribution of pixel values is not uniform and clustered within a particular interval and the image encryption scheme having high diffusion capability encrypts the plain image by modifying the pixel values to achieve uniform distribution. If the cipher image is not uniform, then the attacker can perform statistical analysis to recover the plain image. Figures 9, 10, 11, 12, 13 and 14 shows the histogram of both plain image and cipher image of six grayscale images and the experimental results shows that histogram of all cipher images has uniform distribution of the pixel values.

Fig. 9

a Plain image Lena; b histogram of plain image Lena; c Cipher image Lena; d histogram of cipher image Lena

Fig. 10

a Plain image Peppers; b histogram of plain image Peppers; c Cipher image Peppers; d histogram of cipher image Peppers

Fig. 11

a Plain image Baboon; b histogram of plain image Baboon; c Cipher image Baboon; d histogram of cipher image Baboon

Fig. 12

a Plain image Barbara; b histogram of plain image Barbara; c Cipher image Barbara; d histogram of cipher image Barbara

Fig. 13

a Plain image Airplane; b histogram of plain image Airplane; c Cipher image Airplane; d histogram of cipher image Airplane

Fig. 14

a Plain image Nike; b histogram of plain image Nike; c Cipher image Nike; d histogram of cipher image Nike

8.3.2 Correlation analysis of adjacent pixels

In digital image, the adjacent pixels in plain image are highly correlated which is vulnerable to the correlation coefficient attack. Thus, a secure image encryption algorithm should break this correlation to resist correlation coefficient attack. To evaluate the correlation coefficient of both plain image and cipher image, we choose 3000 random pairs of adjacent pixels in horizontal, vertical, and diagonal direction. Mathematically, the correlation coefficient is computed as defined in Eq. 6. Figures 15 and 16 denote the correlation coefficient of the Airplane image and Airplane cipher image, respectively. Figures 17 and 18 denote the correlation coefficient of NIKE plane image and cipher image, respectively. The cipher image is distributed in a much larger region among the pixel values, whereas the correlation coefficient of plane image is clustered into a particular region. The experimental results of correlation coefficient are presented in Table 5. Further, a comparison of correlation coefficient of the proposed scheme with the existing scheme is presented in Table 6 using the Lena image. The comparison shows that the proposed scheme is performing comparatively better.

$$\begin{aligned} C_{xy} = \frac{{\text {Cov}}(x, y)}{\sqrt{D(x)} \sqrt{D(y)}}, \end{aligned}$$

(6)

where x and y are the gray values of two adjacent pixels.

$$\begin{aligned}&D(x) = \frac{1}{N} \sum _{i=1}^{N} (x_i - E(x))^2\\&D(y) = \frac{1}{N} \sum _{i=1}^{N} (y_i - E(y))^2\\&E(x) = \frac{1}{N} \sum _{i=1}^{N} x_i\\&E(y) = \frac{1}{N} \sum _{i=1}^{N} y_i\\&{\text {Cov}}(x, y) = \frac{1}{N} \sum _{i=1}^{N} (x_i - E(x)) (y_i - E(y)). \end{aligned}$$

Fig. 15

a Diagonal correlation coefficient of plain Airplane image; b horizontal correlation coefficient of plain Airplane image; c vertical correlation coefficient of plain Airplane image

Fig. 16

a Diagonal correlation coefficient of cipher Airplane image; b horizontal correlation coefficient of cipher Airplane image; c vertical correlation coefficient of cipher Airplane image

Fig. 17

a Diagonal correlation coefficient of plain Nike image; b horizontal correlation coefficient of plain Nike image; c vertical correlation coefficient of plain Nike image

Fig. 18

a Diagonal correlation coefficient of cipher Nike image; b horizontal correlation coefficient of cipher Nike image; c vertical correlation coefficient of cipher Nike image

Table 5 Correlation coefficient of adjacent pixels of original and encrypted image

Table 6 Comparison of Lena image

8.3.3 Information entropy analysis

Information entropy suggest the average number of bits required to represent the entire message. In image encryption, information entropy is used to measure the uncertainty or randomness or the distribution of the gray scale values of the cipher image. The higher the information entropy, more the uniform distribution of the gray scale values which becomes more difficult for the attacker to mount the statistical attack. For any random source generating the message consisting of total $2^N$ symbols, the entropy should be $H({\text {msg}}) = N$. In any grayscale image, the pixel values occurs within [0, 255] and total 8 bit required to represent the entire image. If the information entropy of cipher image attains 8 bit or very close to it, then the cryptosystem is more secure against statistical attack. Mathematically, Shanon’s entropy is defined as in Eq. 7:

$$\begin{aligned} H({\text {msg}}) = - \sum _{i=0}^{2^{N}-1} P({\text {msg}}_i)\text{ log }_2 P({\text {msg}}_i), \end{aligned}$$

(7)

where ${\text {msg}}_i$ denotes ith position grayscale value and $P({\text {msg}}_i)$ denotes the probability of value ${\text {msg}}_i$ present in the cipher image. The cipher image whose entropy is more close to 8 and is considered more secure. We have computed the information entropy of our plain images and cipher images and present the results in Table 7. From Table 7, we observed that the entropy of all cipher image is close to 8 which makes statistical attack more difficult.The comparison results are shown in Table 8.

Table 7 Information entropy results

Table 8 Comparison of information entropy

8.4 Resistance to differential attack

The differential cryptanalysis is a chosen plaintext attack. That means, the attacker chooses a plain image ($P_1$) and modifies one pixel to get a different image ($P_2$). Both the images $P_1$ and $P_2$ are encrypted using the same secret key to get the cipher image $C_1$ and $C_2$. The attacker tries to find the output differences by observing both the pairs to discover the relationship between plain image and cipher image, which leads to recovery of the key bits. The image cryptosystem having good diffusion capability is highly sensitive to changes in pixel values, i.e., one pixel change in the plain image influences the cipher image completely which becomes more difficult for the attacker to find the relationship between plain image and cipher image. The quantitative measurement to evaluate the diffusion capability of the image cryptosystem resistance to differential attack is number of pixel change rate (NPCR) and unified average changing intensity (UACI). Mathematically,

$$\begin{aligned} {\text {NPCR}} = \frac{ \sum _{i, j} D(i, \,j) }{WH} \times 100 \%, \end{aligned}$$

(8)

where W and H is width and height of the plain image and D(i, j) denotes whether the pixel values of both the encrypted image $C_1$ and $C_2$ are same or not.

$$\begin{aligned} D(i, j)= & {} {\left\{ \begin{array}{ll} 1 &{} \text{ if } C_1(i, j) \ne C_2(i, j)\\ 0 &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

(9)

$$\begin{aligned} {\text {UACI}}= & {} \frac{1}{W \times H} \sum _{i, j} \frac{|C_1(i, j) - C_2(i, j)|}{255} \times 100 \%. \end{aligned}$$

(10)

In our experiment, 200 random pixels are selected from the plain image and changed the pixel values to generate the new image. Then we encrypt both the images using the same secret key to generate the cipher image $C_1$ and $C_2$. We compute the minimum, maximum and average values of NPCR and UACI and the result is shown in Table 9. The average value of NPCR and UACI is very close to ${\text {NPCR}}_{{\text {expected}}}$ (99.61%) and ${\text {UACI}}_{{\text {expected}}}$ (33.46 %). The comparison of NPCR and UACI results is shown in Table 10.

Table 9 Results of average NPCR and UACI values of different plain images

Table 10 Comparison of NPCR and UACI results of Lena image

8.5 Encryption quality

The proposed image encryption scheme achieves lossless encryption when the plain image and decrypted image are completely identical. Both images will be identical when the mean square error (MSE) will be zero. Mean square error is used to evaluate the peak signal-to-noise ratio (PSNR), a quantitative measurement to find the similarity between the plain image and decrypted image. When the PSNR $\ge$ 30 db, the image is not able to differentiate. Mathematically, PSNR is defined as Eq. 11, while MSE is defined as Eq. 12:

$$\begin{aligned}&{\text {PSNR}} = 20 {\text {log}}_{10} \Big ( \frac{255}{\sqrt{{\text {MSE}}}}\Big ) \end{aligned}$$

(11)

$$\begin{aligned}&{\text {MSE}} = \frac{\sum _{i=1}^{W}\sum _{j=1}^{H} \Big ( P'(i, j) - P(i, j) \Big )^2 }{WH}, \end{aligned}$$

(12)

where W and H denote the width and height of the plain image, respectively, and P and $P'$ represent the plain image and decrypted image, respectively. The lesser the values of MSE, the higher the value of PSNR, and more similarity between the plain image and decrypted image. The proposed image encryption scheme achieves lossless encryption.

8.5.1 Irregular deviation

The irregular deviation is a quantitative measure of the statistical distribution of the deviation between plain image and cipher images to the uniform distribution. Mathematically, irregular deviation [29] can be defined as:

$$\begin{aligned} I_{\text {D}} = \sum _{i=0}^{N-1}H_{{\text {D}}_i}, \end{aligned}$$

(13)

where $H_{{\text {D}}_i} = |h_i - A_H|$, $h_i$ is the amplitude of histogram at index i and $A_H$ is the average sum of histogram values of deviation matrix i.e., $\frac{1}{256} \sum _{i=0}^{N-1} h_i$. The amplitude of histogram at index i is the absolute difference between plain image and cipher image pixel values. The lower value of the irregular deviation denoting the encryption quality becomes high. Table 11 presents the obtained results of our proposed cryptosystem and our results are in acceptable range.

Table 11 Irregular deviation of the proposed image cryptosystem

8.6 Speed and computational complexity

Apart from security analysis of the image encryption scheme, performance analysis is also an important aspect to evaluate the encryption/decryption time and time complexity of the algorithm. To evaluate the encryption speed of our proposed algorithm, the experiment is carried out in the system having configuration of windows 10 operating system, 4GB RAM, Intel i5 Generation 3 in MATLAB (R2018b). The encryption time taken by our proposed algorithm is shown in Table 12 of our standard image data set.

Table 12 Encryption time/decryption time (in s) of the proposed algorithm

Since the encryption and decryption time of the image cryptosystem vary according to the type of environment (hardware/software) and the system configuration, so it is not the right way to compare with the existing algorithm. So we analyze our proposed image cryptosystem based on the time complexity related to all the steps involved in encryption/decryption process. There are different steps involved generating the pseudo-random sequence, confusion phase, and diffusion phase. Since our chaotic map is 2D map, so it generates two pseudo-random sequences and the time complexity becomes $\Theta (2 \times W \times H)$. In confusion phase, computational cost includes shuffling of the pixels $W \times H$ times using the sequence $R_1$, so the time complexity becomes $\Theta (W \times H)$. In diffusion phase, it involves the bitwise Xor operation with pixel values. Since each pixel value is represented in 8 bits, the time complexity becomes $\Theta (8 \times W \times H)$. The comparison result of computational complexity is shown in Table 13.

Table 13 Encryption time/decryption time (in s) of the proposed algorithm

9 Conclusion

In this paper, a novel 2D sine–cosine cross-chaotic map is proposed. In proposed chaotic map, two pseudo-random sequences $R_1$, and $R_2$ are generated for confusion and diffusion process, respectively. The proposed scheme has a wide range of chaotic behavior, uniformity, much larger attractor distribution in 2D phase plane, and higher Lyapunov exponent value. So, the proposed chaotic map is more suitable for image encryption. We apply our proposed chaotic map in image encryption using permutation–bit diffusion structure to measure the confusion and diffusion capability. The security analysis of the encryption scheme shows that the algorithm is secure enough to resist statistical attack, differential attack, and key sensitivity analysis. The proposed chaotic map has a large key space of $2^{213}$, i.e., large search space to resist brute force attack.