Lossless data hiding for absolute moment block truncation coding using histogram modification

Abstract

This paper presents a lossless data hiding method for an absolute moment block truncation coding (AMBTC) images, which is a compressed grayscale image. It is not easy to hide secret data in an AMBTC-compressed image because it is composed of bit planes. Thus, it is very sensitive to change some pixels. Nevertheless, to improve the hiding capacity, we present an efficient extension of the histogram modification technique by counting the coefficients of the bit planes in each 4 × 4 block. In addition, our proposed scheme has low complexity and achieves a high embedding capacity with the good perceptual quality compared to the prior arts. In an experiment, we verified our proposed data hiding scheme through the comparison with previous methods.

1 Introduction

Digital contents based on block truncation coding (BTC) [1, 2] need to be protected from illegal users that can redistribute the contents anywhere. Thus, watermarking [3, 5] and data hiding [4, 6–8] techniques are used to protect them. Furthermore, these techniques are also applied to private communications when transmitting various multimedia contents across the Internet. However, data hiding techniques cannot guarantee the safety of a message. Data hiding only conceals the existence of a message in an image, while cryptography [9] protects its content.

BTC is a lossy compression, i.e., it reduces the file size but loses some information originally present in the image. Since its introduction, BTC has been used in various applications such as the compression of graphics, video signals, and color images. However, BTC has two drawbacks. First, it produces a low-level image quality. Second, its compression rate is lower than that of JPEG [10] or JBIG [11].

A data hiding scheme based on the least significant bit (LSB) can be easily changed to embed a hidden secret message. However, hiding data in a BTC image is a more challenging task, since any pixel change can be easily detected by attackers, because it is composed of bit planes. To compensate for this defect, a diffusion algorithm was introduced for a BTC image [12]. In a diffused image, colors that are not available in the palette are approximated by the diffusion of colored pixels from within the existing palette. The human eye perceives the diffusion as a mixture of the colors within it.

This paper proposes good solutions providing quality or coding gain improvements. The data hiding method for a BTC image uses the technique of flipping a bit plane in a block. Most schemes cannot recover the original image, because of the irreversible distortion introduced. This may not satisfy the requirements of some applications, where the content accuracy of the host medium must be guaranteed.

In the data hiding area, we are mainly concerned with how to hide more messages or more securely and reconstruct the original images. In 2004, Lin and Chang [13] proposed a data hiding scheme by performing LSB substitution operations on BTC high and low means and introducing the minimum distortion algorithm for BTC bit planes. In 2006, Chuang and Chang [14] embedded data in the BTC bit planes of smooth regions to obtain an improved embedded image quality. However, they did not reconstruct the original cover image. Reversible data hiding techniques are mainly classified into three main categories. The first is based on data compression [15–17], the second based on pixel value difference expansion [18–20], and the third based on histogram shifting [21–24]. As listed in Table 1, these types of techniques have advantages and disadvantages.

Table 1 Compare merits and demerits among three data hiding types

The reversible data hiding scheme for BTC images was proposed in 2008 by Hong et al. [23], where the secret data are embedded by toggling or preserving the BTC bit planes according to the secret bit and the relationship between the high mean and low mean. For each AMBTC-encoded block i with trio $(a_i, b_i, B_i)$, where the trio is composed of a high mean, low mean, and bit plane, respectively, if the embedded bit is “1,” then $(a_i, b_i, B_i)$ is changed to $(b_i, a_i, B_i')$, and otherwise, it remains the same. Although this scheme is reversible, when the high mean equals the low mean, there will be some problem in secret data extraction.

To overcome this problem [25], Chen et al. [26] recently proposed an improved reversible hiding scheme. The difference in the quantized values for each block is used to determine whether only “1” bit of the secret is hidden for the block or to toggle bits in the bitmap to hide more bits. Although this scheme is reversible, when the high mean equals the low mean, it is impossible to hide a secret bit. Sun et al. [27] proposed a reversible data hiding scheme based on the joint neighbor coding technique. BTC-compressed data can be represented by a high mean table, low mean table, and bit plane sequence. This scheme is based on the relationships between the current value and the neighboring ones in mean tables. Thus, this scheme is to average 2 bits in each mean value. Lo et al. [28] proposed a reversible data hiding scheme for BTC, where they employed a histogram shifting technique to embed the secret data into the quantization levels of the compressed codes. There was no problem with recovering the original BTC image. However, the embedding capacity was not higher than the other previous schemes [25–27].

A histogram represents the statistical distribution of the pixels in an image. It is widely applied in many research fields, e.g., image enhancement, image indexing, and pattern recognition. In addition, it is possible to apply reversible data hiding. A histogram-based reversible data hiding method was introduced by Ni et al. in [21], where the message was embedded within the coefficients of the histogram. Embedding is done by shifting the peak and zero points of the histogram. In addition, the histogram shifting technique brings about overflow and underflow problems. Overflow is the condition where the gray value exceeds 255. Underflow is the condition where the gray value falls below 0. Embedding based on histogram modification has been presented in [21–23]. One of the major issues associated with all these techniques is that the peak and zero points need to be embedded along with the data during image embedding.

However, a histogram modification scheme cannot be directly applied to AMBTC [29] images. Therefore, we propose a simple and efficient reversible data hiding algorithm, which is an improved version of the histogram modification for AMBTC images.

The rest of this paper is organized as follows: In Sect. 2, we explain the related works. The proposed AMBTC histogram modification scheme is illustrated via examples and algorithms in Sect. 3. In Sect. 4, the experimental results are given. Finally, some conclusions are made in Sect. 5.

2 Related works

2.1 Block truncation coding (BTC)

Delp and Mitchell [1] proposed BTC, which is a lossy compression technique for grayscale images. In their work, the image was divided into blocks of $M \times N$ pixels, and each block was processed independently. They then calculated the mean value ($\mu$) and standard deviation ($\sigma$) of each block.

In addition, the first two sample moments were preserved in the compression. Each original block could be encoded with “0’s” and “1’s.” When a pixel value was smaller than the mean of the block, it was set to “0,” and otherwise, it was set to “1.” Block decompression required the $\alpha$ and $\beta$ values of each block of the image. Each block B was composed of “0’s” and “1’s.” When BTC was decoded as it was uncompressed, each “0” bit of B was set to $\alpha$, and each “1” bit of B was set to $\beta$, where $\alpha$ and $\beta$ were computed according to Eqs. (1) and (2), respectively, and q and m represent the number of “1” and “0” bits in B, respectively.

$$\begin{aligned} \alpha &= \mu - \sigma \times \sqrt{q \over (m-q)} \end{aligned}$$

(1)

$$\begin{aligned} \beta &= \mu + \sigma \times \sqrt{(m-q) \over q} \end{aligned}$$

(2)

BTC is a very simple algorithm. Hence, anybody can easily implement this technique. However, it does not provide good quality.

2.2 Absolute Moment Block Truncation Coding (AMBTC)

AMBTC [29], which was proposed by Lema and Mitchell in 1984, is a version of the BTC, a lossy compression algorithm for grayscale or color images. The processing time for the BTC algorithm [1] has significant computational complexity, and therefore, it is not generally recommended for time-consuming applications. The grayscale image to be encoded is divided into non-overlapping blocks of size (4 × 4) or (8 × 8), for example, and the average of the blocks is calculated as in Eq. (3):

$$\begin{aligned} \bar{x} = \frac{1}{W \times H} \sum _{i=1}^{N} x_i \end{aligned}$$

(3)

where $x_i$ denotes the ith pixel, N is the number of pixels in the block, and W and H are the width and height of the block, respectively. A pixel of a grayscale image is composed of 8 bits, but that of a binary image is 1 bit. Therefore, we must convert the grayscale image pixels into binary values for AMBTC. Equation (4) shows how to construct a bit plane for AMBTC from the grayscale image. If $x \ge \bar{x}$ , then “1” is assigned to $b_i$, and otherwise, “0” is assigned to $b_i$:

$$\begin{aligned} b_i = \left\{ \begin{array}{ll} 1, & {\text{if}}\,(x_i \ge \bar{x}), \\ 0, & {\text{if}}\, (x_i < \bar{x}), \end{array} \right. \end{aligned}$$

(4)

The means $\alpha$ for the higher range and $\beta$ for the lower range are calculated using Eqs. (5) and (6), respectively:

$$\begin{aligned} \alpha &= \left\lfloor \frac{1}{t} \sum _{x_i \ge \bar{x} }^{} x_i \right\rfloor \end{aligned}$$

(5)

$$\begin{aligned} \beta &= \left\lfloor \frac{1}{(W \times H)-t} \sum _{x_i < \bar{x} }^{} x_i \right\rfloor \end{aligned}$$

(6)

where t is the number of pixels in a block with a gray level greater than $\bar{x}$. A binary block B contains the bit planes that represent the pixels. The values of $\alpha$ and $\beta$ are used to decode the AMBTC-compressed image; every “1” in block B is replaced by $\alpha$ and every “0” is replaced by $\beta$:

$$g_{i} = \left\{ {\begin{array}{ll} \alpha , & {{\text{if}}\quad (bi = 1)} \\ \beta , & {{\text{if}}\quad (bi = 0)} \\ \end{array} } \right.$$

(7)

where $g_i$ is a grayscale pixel, and thus, the grayscale image is reconstructed. The compression rate for AMBTC is 2 bpp, because the total number of bits required for a block is 32 bits. BTC has a complex computation, while AMBTC has a simple computation and therefore requires less computation time than BTC.

Figure 1a shows the original image block of 4 × 4 pixels. First, we compute the mean value of the block using Eq. (4). This gives a mean value of 161.25. Figure 1b shows the bitmap of an original grayscale image using Eq. (4). Then, the quantization levels for these two groups ($\alpha$ and $\beta$) are calculated using Eqs. (5) and (6), respectively. These two quantization levels are 161 = $\lfloor 160.5\rfloor$ and 162, respectively. Each compressed image block forms a trio ($\alpha$, $\beta$, bitmap) where each quantization level is stored in 8 bit. Finally, the compressed trio (161, 162, $(1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0)_2$) is sent to the receiver.

Fig. 1

Example of AMBTC encoding and decoding: a original image block, b bitmap, and c reconstructed image block

An example of the image decoding procedure is described in the following. Suppose that the compressed trio $(161, 162, (1100110011001100)_2)$ is received by the receiver. A pixel in the block is reconstructed by 161 if a corresponding bit valued “0” is found. Otherwise, it is reconstructed by 162. The reconstructed block of this example is shown in Fig. 1c.

Fig. 2

AMBTC example for “Lena” image. a Orginal Lena (512 × 512). b Bitmap. c AMBTC

According to the AMBTC algorithm, the bitmap image is shown in Fig. 2b, c is also reconstructed using Eqs. (5), (6), and (7). It becomes a grayscale image almost the same as the original “Lena.”

2.3 Histogram pairs method

Many researchers [15–23] have proposed reversible data hiding schemes that use histogram pairs of grayscale images. In the histogram, we first search for a zero point and then a peak point. A zero point corresponds to the grayscale value that is not possessed by any pixel in the given image. A peak point corresponds to a grayscale value equal to the largest number of pixels in the image. We find a peak point to raise the embedding capacity as much as possible [21]. In the following, we will refer to a data embedding scheme stage by stage. For an M × N image, each pixel a grayscale value $x \in [0, 255]$:

• Step 1: Generate its histogram H(x).

• Step 2: In the histogram H(x), find the maximum point $h(\alpha )$, $\alpha \in [0, 255]$ and the minimum point $h (\beta )$, $\beta [0, 255]$.

• Step 3: If the minimum point $h(\beta ) \ge 0$, then record the coordinates (i, j) of those pixels and the pixel grayscale value $\beta$ as overhead bookkeeping information (referred to as overhead information for short), and set $h(\beta ) = 0$.

• Step 4: Without loss of generality, assume that $\alpha < \beta$. Move the whole part of the histogram H(x) with $x \in (\alpha , \beta )$ to the right by 1 unit. The result is that all of the pixel grayscale values in the interval $(\alpha , \beta )$ are incremented by 1.

• Step 5: Scan the image until meeting the pixel whose grayscale value is $\alpha$; check the to-be-embedded bit. If the to-be-embedded bit is 1, the pixel grayscale value is changed to $\alpha +1$. If the bit is 0, the pixel value remains $\alpha$.

In this way, the actual data embedding capacity C is calculated as follows:

$$\begin{aligned} C = h(\alpha ) - O \end{aligned}$$

(8)

where O denotes the amount of data used to represent the overhead information. We refer to C as pure payload. Clearly, if the required payload is greater than the actual capacity, more pairs of maximum and minimum points need to be used.

3 Proposed data hiding scheme

Fig. 3

Block diagram for our proposed scheme

The histogram modification method is an excellent reversible data hiding technique for grayscale images. But this method cannot be directly applied to AMBTC images with existing previous schemes for grayscale images, because a BTC image is composed of bit planes. In order to apply that method to AMBTC images, the run lengths of the binary data are counted to generate and shift histogram bins. In this paper, we solve this problem and conceal a large quantity of information in an AMBTC image.

Fig. 4

Scan order of 4 × 4 image block

In this section, we shall present the proposed scheme, including embedding and extracting processes. Figure 3 shows the block diagram to explain data hiding procedure.

Fig. 5

Concept of data embedding using histogram modification for AMBTC image: a original histogram, b bitmap planes, c stego BTC block

Fig. 6

Example of data hiding with AMBTC: a original image block, b bitmap (including hidden bits), c stego image block

Figure 3 shows the procedure for our proposed scheme with AMBTC. That is, a bitmap of AMBTC is produced using Eqs. (3) and (4), and then, the histogram modification algorithm (including the embedding and extracting schemes) is applied to the bitmap image. Finally, we obtain the stego image embedded secret messages. To improve the hiding capacity, we present an efficient extension of the histogram modification technique by counting the coefficients of the bit planes in each 4 × 4 block in an image while scanning from left to right and from top to bottom, as shown in Fig. 4.

Our proposed scheme offers a high embedding capacity while maintaining low distortion. Figure 5a shows a histogram of Fig. 1b, where the number of “0” pixels is 8 and “1” pixels is 8. Exploiting the bit planes in a block, we decide to add bin 2 as shown in Fig. 5a. Thus, bin 2 would be empty. After the bins are ready, it begins data embedding by dealing out bin 1, according to the message. By doing this, we exploit “1” bits as shown in Fig. 5b. That is, if the secret bit is “0,” keep “1” (bin 1) values without moving to 2’s (bin 2). Otherwise, the “1’s” (bin 1) move to 2’s (bin 2). Figure 5b shows the result of the embedding procedure.

Figure 6 shows an example of hiding secret bits in a 4 × 4. The method used to hide secret bits in a block is explained in Fig. 5. Figure 6b shows that the hidden bits (e.g., “0 1 0 1 0 1 0 1”) are concealed in a block with histogram modification as in Fig. 5b. Figure 6c shows a reconstructed grayscale image based on AMBTC, i.e., it is possible to obtain the block using Eqs. (4), (5), (6), (9), and (10).

$$\begin{aligned} \gamma &= \left\lfloor \frac{(\alpha +\beta )}{2} \right\rfloor \end{aligned}$$

(9)

$$\begin{aligned} g_i &= \left\{ \begin{array}{ll} \alpha , & {\text{if}}\, (b_i = 1), \\ \beta , & {\text{if}}\, (b_i = 0), \\ \gamma , & {\text{if}}\, (b_i = 2), \end{array} \right. \end{aligned}$$

(10)

To reconstruct Fig. 6c, the bit planes for “1’s” and “0’s” change into $\alpha$ and $\beta$, respectively, using Eqs. (5), (6), and (10). In the case of the bit “2’s” values, it is changed into $\gamma$ using Eqs. (9) and (10).

Fig. 7

Example of extraction and reconstruction using stego AMBTC: a stego grayscale block, b bitmap (restore original bitmap from stego bitmap), and c reconstructed image block

Figure 7 shows an example of extracting the hidden bits from the stego bit planes, reconstructing the original bit planes from the stego bit planes, and then restoring the original grayscale image. That is, if a pixel in a stego block is a “1,” the extracted hidden bit is “0.” Otherwise, in the case a “2,” the hidden bit is “1,” and it could be reconstructed by changing it into a “1.” Figure 7b shows an original block of reconstructed bit planes. Figure 7c shows a grayscale image block based on AMBTC that is restored using Eqs. (4), (5), and (6).

In Sects. 3.1 and 3.2, we explain our proposed scheme, including the embedding and extraction algorithms.

3.1 Embedding method

This section shows the embedding procedure based on the bit planes of AMBTC using histogram modification, according to the hidden messages.

Input: Original grayscale image GI with $M \times N$ pixels and secret data $\delta = [b_1, b_2, \ldots ,b_n]$

Output: Stego image SI, length of secret data $|\delta |$

• Step 1: First, divide the image to be coded into small non-overlapping image blocks (typically the blocks of size 4 × 4 pixels to achieve reasonable quality). Each pixel block can be treated as a vector with a size of $M \times N$. Then, let $x_i$ be the pixel values of each vector. Next, we compute the mean value $\bar{x}$ for the pixels of each pixel block using Eq. (3). If a pixel is greater than or equal to the block mean, the corresponding pixel position of the bitmap will have a value of “1”; otherwise, it will have a value of “0.” As a result of this procedure, we could obtain a bitmap image (BI), which is composed of “0’s” and “1’s.”

• Step 2: Read a block from BI using Eq. (11), where i and j are indexes of an image, and T is a block. Count the number of “0” and “1” bits using Eq. (12). $S_0$ and $S_1$ are the sums of all the “0’s” and “1’s” in T, respectively.

  $$\begin{aligned} T&= \sum _{i=1 }^{M/4} \sum _{j=1 }^{N/4} BI_{i+3,j+3} \end{aligned}$$

  (11)
  $$\begin{aligned} {S_0, S_1} &= \left\{ \begin{array}{ll} S_0 + 1, \, & {\text{if}}\, (T_{m,n}^{4 \times 4} = 0), \\ S_1 + 1, \, & {\text{if}}\, (T_{m,n}^{4 \times 4} = 1), \end{array} \right. \end{aligned}$$

  (12)

• Step 3: If $S_0$ or $S_1$ is all “0’s” or “1’s,” go to step 2.

• Step 4: Scan every element in a block T. If the scanned value is equal to “1” and hidden bit $\delta _\varphi$ is “$0_b$,” it does not need to move. If the scanned value is equal to “1” and hidden bit $\delta _\varphi$ is “$1_b$,” move to “2” using Eq. (13).

  $$\begin{aligned} {SI_{ij}}= \left\{ \begin{array}{ll} 1, \, & {\text{if}}\,(T_{m,n}^{4 \times 4} = 1 \cap \delta _{\varphi ++} = 0), \\ 2, \, & {\text{if}}\, (T_{m,n}^{4 \times 4} = 1 \cap \delta _{\varphi ++} = 1), \end{array} \right. \end{aligned}$$

  (13)

• Step 5: Go to step 2 to continue the embedding processes until all of $\delta$ is scanned.

• Step 6: If the process of data hiding is complete, it has produced the bit planes of image SI.

3.2 Extraction and reconstruction method

The extraction and reconstruction procedures are shown below:

Input: : Stego image SI and the length of secret data $|\delta |$

Output: Original image BI and secret data $\delta$

• Step 1: Scan image SI and divide it into a $4 \times 4$ group with non-overlap.

• Step 2: Read a block from SI using Eq. (14), where i and j are indexes of an image, and T is a block, and then count the number of “0” and “1” bits using Eq. (12).

  $$\begin{aligned} T = \sum _{i=1 }^{M/4} \sum _{j=1 }^{N/4} SI_{i+3,j+3} \end{aligned}$$

  (14)

• Step 3: If $S_0$ = 16 or $S_1$ = 16, then go to step 2.

• Step 4: Scan every pixel in a block T. If the scanned pixel value is equal to “1,” the hidden bit is “0,” which is combined with a secret message $\delta$ using Eq. (15). In contrast, if the scanned pixel value is “2,” the extracted bit value is “1,” which is combined at $\delta$ using Eq. (15). In addition, if the pixel is “2,” move to “1” to reconstruct the original bit planes using Eq. (16).

  $$\begin{aligned} {\delta _{\varphi ++}}&= \left\{ \begin{array}{ll} {\delta +\textsc {'0'}}, \, \,& {\text{if}}\,\, (T_{m,n}^{4 \times 4} = 1), \\ {\delta +\textsc {'1'}}, \, \,& {\text{if}}\,\, (T_{m,n}^{4 \times 4} = 2), \end{array} \right. \end{aligned}$$

  (15)
  $$\begin{aligned} {BI_i}{(m, n)} &= \left\{ \begin{array}{ll} {\text{don't\, move}} & {\text{if}}\,\, (T_{m,n}^{4 \times 4} = 1), \\ {1} & {\text{if}}\,\, (T_{m,n}^{4 \times 4} = 2), \end{array} \right. \end{aligned}$$

  (16)

• Step 5: Repeat step 2 until $\varphi = |\delta |$.

• Step 6: At this step, most of the coefficient values are restored, and the bitmap image (BI) could be reconstructed.

4 Experimental results

In this paper, we propose a novel reversible data hiding scheme using a histogram modification method. In order to prove the performance of our proposed scheme, we need to compare its performance with those of previous methods. Six $512 \times 512$ images (“Lena,” “Airplane,” “Boat,” “Pepper,” “Baboon,” and “F16”) [30] (Fig. 8) were used in the experiment. In addition, the block size for the AMBTC compression method was set at $4 \times 4$.

The simulation environment for the experiments was a 2.66 GHz, Core 2, Quad system with 8 GB of RAM and a MATLAB compiler.

Fig. 8

Grayscale images (512 × 512) for the experiment. a Lena. b F16. c Pepper. d Baboo. e Boat. f Goldhill

To evaluate our proposed scheme, we used the peak signal-to-noise ratio (PSNR) [6] and hiding capacity. The PSNR is defined as Eq. (17), where the mean squared error (MSE) is computed by Eq. (18). A higher PSNR value indicates a better quality for the stego image. The hiding capacity denotes the number of bits that can be hidden in the AMBTC image.

$$\begin{aligned} {\text{PSNR}}&= 10log_{10} \frac{255^2}{MSE} \end{aligned}$$

(17)

$$\begin{aligned} {\text{MSE}} &= \frac{1}{M\times N} \sum _{i=1}^{M} \sum _{j=1 }^{N} (x_{ij}-x_{ij}^{'})^2 \end{aligned}$$

(18)

where $M\times N$ is the size of the image, and $x_{ij}$ and $x_{ij}^{'}$ denote the pixel values of the cover image and stego image in the same position (i, j), respectively.

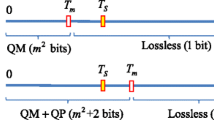
It is well known that an AMBTC image is very sensitive to flipping the bits of the pixels. Thus, in the experiments, two performance aspects were adopted to evaluate the data hiding scheme, i.e., the capacity represents the maximum number of secret bits that can be hidden and the PSNR represents the quality of the stego image.

First, we tested the performance of our algorithm under different embedding rates. Therefore, to examine the influence of flipping a large number of pixel bits, we compared the relation between the embedding rate (from 0.1 to 0.8 bpp) of the hidden bits in an image and PSNR, as listed in Table 2. As given in Table 2, the embedding rates steeply increased, while the PSNRs gradually decreased. In these cases, there were a few different PSNRs between the neighboring embedding rates, which proved that the performance of our proposed scheme was good. In addition, the PSNRs in Table 2 are relatively high values, so the quality of the stego images was very good.

Table 2 Comparison of relation between embedding rate and PSNR

Fig. 9

Comparison of embedding capacities of data hiding schemes

Afterward, using the same block size (4 × 4), we compared our algorithm with the methods of Chuang and Chang [14], Hong et al. [25], Chen et al. [26], and Sun et al. [27]. Figure 9 shows a comparison of the embedding bits with the “Lena” image using the previous schemes and our proposed scheme. According to Fig. 9, our proposed embedding scheme had the best performance. That is, the number of hidden bits in the “Lena” image based on our proposed scheme was 146,598 bits. However, the PSNR of Lo et al.’s method [28] is slightly low and its embedding capacity is lower than that of the other schemes. With respect to the embedding capacity and PSNR, our proposed scheme achieved the highest embedding capacity and good quality. The scheme of Sun et al. [27] embedded 2 bits in each mean value, including the low mean table and high mean table. Thus, it was possible to embed 4 bits in each 4 × 4 pixel block. The capacities of the schemes of Hong et al. [25] and Chen et al. [26] were normally 1 bit in each 4 × 4 pixel block.

Fig. 10

Quality comparison of Lena images, including (a) original Lena, b AMBTC, c–f stego AMBTC

Table 3 PSNR and capacity comparisons between previous schemes and proposed scheme

As listed in Table 3, the capacity of our proposed scheme is about 9 times higher than those of the other schemes (Sun et al., Hong et al., and Chen et al.). Its significant dominance in relation to the neighboring bins is important in terms of the embedding capacity.

The AMBTC $512 \times 512$ “Lena” image with Hong et al.’s method can hide a total of 16,384 bits at one time. On the other hand, it is possible to hide 146,598 bits at one time with our method. Figure 10 shows a quality comparison of the images, including the original (a) Lena, (b) AMBTC, and (c)–(f) stego images. As shown in Fig. 10, it would be difficult to detect which is original image or stego image. Therefore, it is shown that the performance of our proposed scheme is good enough for data hiding based on AMBTC.

Fig. 11

Histogram of original Lena image

After extracting the secret data from the stego image, the original AMBTC image could be reconstructed. However, this does not mean that the reconstructed AMBTC image is the original grayscale image, because there is a quality difference between them. To improve the quality of an AMBTC image, we apply a Gaussian filter to this image. It has two variations, involving the filter size and standard deviation. We performed numerous experiments to determine the size of the filter and standard deviation. In this work, the size of the filter is fixed at $7 \times 7$ with a standard deviation $\delta = 1.3$, which is used to simulate the human visual response.

Fig. 12

Histogram after Gaussian filtering

Figures 11 and 12 show histograms of the original “Lena” image and stego “Lena” image, respectively. We are interested in comparing them, because this makes it is possible to determine how much the stego is similar to the original image. If they are similar, it is not easy for an attacker to detect the stego image.

Fig. 13

“Lena” and “Peppers” images after Gaussian filtering. a Orginal Lena. b Stego 0.1 bpp, 35,448 dB. c Gaussian, 37,610 dB. d Orginal Peppers. e Stego 0.1 bpp, 35,425 dB. f Gaussian, 37,132 dB

Therefore, the usefulness of our proposed scheme has been amply proven. Figure 13 shows the stego “Lena” and “Peppers” images after Gaussian filtering. Figure 13b shows a quality improvement of about 2 dB. In addition, our method has low complexity and achieves a high embedding capacity with good perceptual quality compared to the prior arts.

The complexity of our proposed scheme mainly lies on generating histogram, determining minimum and maximum (and possibly subminimum and submaximum) points, scanning pixels, and adding or subtracting pixel grayscale values by one in the spatial domain. Hence, the execution time of the algorithm is rather short. Assume the image height is M and the width is N and a block height is H and the width is W and number of blocks is k. We need to scan the whole image one time in the embedding. Hence, the computational complexity is $O(MN+kWH)$.

5 Conclusion

In this paper, we presented an efficient reversible data hiding algorithm based on the histogram modification of AMBTC-compressed images. As listed in Table 2, the PSNR of our proposed scheme is higher than that of the original AMBTC-compressed image. In addition, we invented new scheme to exploit the bitmap coefficients of 4 × 4 blocks of an image based on histogram modification. Thus, the capacity of our proposed scheme is about 9 times higher than those of the other schemes. In the extraction procedure, the AMBTC-compressed image and secret messages can be reconstructed completely. As is generally known, most portable video devices do not need high-quality images. In addition, they need simple computation and high-speed time complexity. Therefore, our proposed scheme would be very appropriate for hiding data on portable devices.