A Nonlocal Model for Contact Attraction and Repulsion in Heterogeneous Cell Populations

Abstract

Instructing others to move is fundamental for many populations, whether animal or cellular. In many instances, these commands are transmitted by contact, such that an instruction is relayed directly (e.g. by touch) from signaller to receiver: for cells, this can occur via receptor–ligand mediated interactions at their membranes, potentially at a distance if a cell extends long filopodia. Given that commands ranging from attractive to repelling can be transmitted over variable distances and between cells of the same (homotypic) or different (heterotypic) type, these mechanisms can clearly have a significant impact on the organisation of a tissue. In this paper, we extend a system of nonlocal partial differential equations (integrodifferential equations) to provide a general modelling framework to explore these processes, performing linear stability and numerical analyses to reveal its capacity to trigger the self-organisation of tissues. We demonstrate the potential of the framework via two illustrative applications: the contact-mediated dispersal of neural crest populations and the self-organisation of pigmentation patterns in zebrafish.

1 Introduction

Cells and organisms move through their environment according to a variety of internal and external cues. Amongst these, responses due to direct contacts with others are particularly crucial: for example, the membrane to membrane adhesion contacts formed between cells generate movement forces (Palsson 2008), while an animal will frequently alter its motility according to the touch or sight of others (Potts et al. 2014). How these interactions feed into larger-scale dynamics, such as the organisation of cell populations during development, the invasion of cancerous cells into healthy tissue, or the formation of bird flocks are fundamental questions that have generated significant theoretical interest.

To start, we briefly state our definition of direct contacts. Here we consider this as some form of one to one contact between a signaller and a receiver: for example, for two cells this could be a result of direct linking between molecules on adjacent membranes, while for animals, it could be through touch or visual contact. Indirect contacts, which we do not explicitly consider here, are exemplified by the many to many contacts mediated via the secretion of a diffusible chemoattractant in a population of bacteria. Our focus in this paper will be on the impact of direct contacts on the movement and patterning of cell populations, although we note that the generic nature of the model would easily allow its adoption, for example, in modelling movement of animal populations.

In the context of cell populations, the capacity for direct contacts to dictate movement and patterning has been revealed in various examples. The classic case is cell–cell adhesion (e.g. Steinberg 2007), in which the binding of adhesion molecules on adjacent cell membranes acts to pull cells together into a cohesive tissue. In the “differential adhesion hypothesis”, it is proposed that distinct adhesive properties in the different cell types of a heterogeneous tissue can act to restructure populations into a characteristic pattern, the precise arrangement varying according to the self-adhesion (adhesion between two cells of the same type) and cross-adhesion (different type) strengths.

Cell contacts can also induce repulsion. Abercrombie and Heaysman (1953) described a process of contact-inhibited movement of fibroblast cells more than 60 years ago, a process since shown to occur in neural crest cells, where contact with another cell induces a migrating neural crest cell to arrest its migration and change direction (Carmona-Fontaine et al. 2008). Such signals have also been shown to exist between cells of distinct types, such as the interactions between xanthophores and melanophores in zebrafish pigmentation cells (Maderspacher and Nüsslein-Volhard 2003; Nakamasu et al. 2009; Yamanaka and Kondo 2014). Less specifically, inhibition of movement and the organisation of differing cell types within various tissues has been found to be regulated by Ephrin signals, which are contact dependent, and which can also promote adhesion and hence attractive movement (for a review, see Poliakov et al. 2004).

Contact-dependent signalling in cells is typically mediated through a membrane-bound signalling molecule on a signalling cell attaching to a receptor molecule on the membrane of a target cell, such that the signal is communicated directly from one to another (Alberts et al. 2013). Activation of the receptor triggers a signalling cascade, which in turn leads to a response: for example, if the instruction is to repel, the target cell does so in the direction inferred from the signal. In other instances of contact-mediated signalling, information may pass directly between cells via tunnels, such as gap or tight junctions (Zihni et al. 2014).

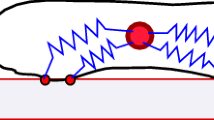
While a membrane to membrane interaction superficially suggests a short-range method of communication, capable of only contacting neighbouring cells, the fact that certain cells can extend long membrane protrusions—such as ligand/receptor carrying filopodia and cytonemes—potentially confers a longer-range element. For example, cytonemes in the imaginal disk of Drosophila are found to extend at least 100 $\upmu$m from a cell membrane (Ramírez-Weber and Kornberg 1999), while filopodia can extend some ten times an average cell diameter in newt pigment cells (Tucker and Erickson 1986). Recent findings suggest that these and other protrusions can transmit signals directly to distant cells of the same or different type, via a signalling cell contacting a receiving cell either at the bodies or tips of their respective protrusions (e.g. see the reviews in Sherer and Mothes 2008; Gradilla and Guerrero 2013; Kornberg and Roy 2014). In the more specific context of movement-based responses, in vitro cultures of liver stellate and hepatocyte cells suggest a process in which the extensions of stellate cells “pull” hepatocyte cells into forming aggregates, (Thomas et al. 2006; Green et al. 2010). Consequently, it is probable that for certain cell populations both attracting and repelling signals can be directly transmitted over different interaction ranges and across large regions of tissue (Fig. 1).

Fig. 1

Schematic showing the potential for distinct interactions and ranges between various cell types. We consider two cell types (dark and light), each with distinct forms of cell protrusions. In this theoretical model a, dark cells communicate via tip to tip protrusions, giving interaction range $\xi _{uu}$; b dark cells communicate to light cells via a tip to body interaction, with range $\xi _{vu}$; c light cells communicate to each other via a tip to tip interaction, with range $\xi _{vv}$; finally, d light cells communicate to dark cells via tip to body, with corresponding range $\xi _{uv}$

Individual-based (or agent-based) models (IBMs) offer a relatively straightforward path to model the impact of direct contacts on movement: tracking individuals allows their interactions to be easily incorporated. For example, a variety of IBMs have been applied to test the differential adhesion hypothesis and to other instances of cell contact-driven patterning. This includes discrete-lattice models based on the cellular Potts model (Graner and Glazier 1992; Glazier and Graner 1993), other discrete agent-based and cellular automaton models (e.g. Agnew et al. 2014; Hackett-Jones et al. 2011), and off-lattice models such as modelling cells as deformable ellipsoids (Palsson and Othmer 2000). Pertinent to the current study, Shinbrot and others (Caicedo-Carvajal and Shinbrot 2008; Shinbrot et al. 2009) explored cell sorting behaviour in an IBM, including both attracting and repelling interactions and applying the results to pigmentation patterning in zebrafish. IBM approaches have also been widely applied to study how contact-mediated interactions can organise animal populations, for example to explore flocking and schooling behaviour (e.g. Couzin et al. 2002).

Perhaps the greatest drawback of IBMs lies in their resistance to analytical rigour: apart from highly specific cases, it can be difficult to draw out general properties and conclusions without recourse to extensive and time-consuming numerical simulation. Continuous partial differential equation (PDE) models, while lacking the finer-scale detail of IBMs, profit from a larger repository of analytical tools and techniques, along with the ability to efficiently simulate large cellular systems; yet, including the impact of a contact-dependent interaction in these models is nontrivial. Early attempts to incorporate cell–cell adhesion utilised ideas based on surface tension (Byrne and Chaplain 1996) or non-linear diffusion (Perumpanani et al. 1996) to model restricted cell movement due to adhesion. Other approaches have explicitly included some form of nonlocal integral term to model the impact of contact-based interactions on movement and pattern formation: early examples are the integro-partial differential equation models developed in Edelstein-Keshet and Ermentrout (1990) to model contact-mediated cell alignment. Notably, solutions to such nonlocal models can demonstrate a variety of desirable dynamical traits, such as travelling waves and self-organisation. Consequently, representation via a nonlocal term has been applied in numerous contexts including cell sorting (Armstrong et al. 2006; Gerisch and Painter 2010), chemotaxis (Othmer and Hillen 2002; Hillen et al. 2007), pattern formation during development (Sekimura et al. 1999; Armstrong et al. 2009; Green et al. 2010) and cancer invasion (Gerisch and Chaplain 2008; Sherratt et al. 2009; Kim et al. 2009; Painter et al. 2010; Chaplain et al. 2011; Andasari et al. 2011). Mathematical challenges raised by these models have also been addressed, such as their boundedness and existence properties (Sherratt et al. 2009; Dyson et al. 2010; Chaplain et al. 2011; Dyson et al. 2013).

Continuous and nonlocal models have also been proposed for the self-organisation of animal populations, such as in swarming, flocking, and schooling phenomena (Mogilner and Edelstein-Keshet 1999; Lee et al. 2001; Eftimie et al. 2007a; Topaz et al. 2006; Eftimie et al. 2007b, 2009). One such model has been used to study the effect of varying interaction ranges on spatial organisation (Topaz and Bertozzi 2004), revealing that in the case of potential motion and nonlocal repulsion, a short range leads to a smoothing of the density profile, while a larger range leads to increased movement. Under attractive interactions, an increasing interaction range leads to a decrease in the number but an increase in the size of individual aggregates.

In this paper, we extend these ideas further to explore how direct contacts impact on the dynamics of cell populations. We begin with a general nonlocal PDE model that permits cells of homogeneous (one cell type) or heterogeneous (multiple cell types) tissues to directly interact via attraction or repulsion over distinct spatial ranges. This general model can easily be tailored to many of the above applications of nonlocal models and hence applied to investigate phenomena ranging from waves, as in cancer invasion, to self-organisation, such as cell sorting. A general linear stability and numerical analysis is performed to uncover the rich dynamical properties. Further, we illustrate its relevance via applications in classic examples of invasion and self-organisation: the impact of repelling interactions on the dispersal of neural crest cells and the organisation of distinct pigment cell types during zebrafish pigmentation patterning.

2 Model Formulation

2.1 Homogeneous Tissue: Single Population Model

Generally, continuous models for cell/organism movement are either (i) proposed on phenomenological grounds, using classical continuum-based arguments (e.g. see Murray 2002), or (ii) derived from an individual-based model for movement, under certain scaling arguments (e.g. see Hillen and Painter 2013). While the latter approach has the advantage that macroscopic terms and parameters can be traced to the underlying individual-based rules, we adopt here the former method, employing a mass conservation approach to describe the evolving cell density of a population $u({\mathbf{x}},t)$ at position ${\mathbf{x}} \in {{\mathbb {R}}}^n$ and time $t$. However, we note that various nonlocal models of chemotaxis and adhesion, similar to the model derived below, have been derived from an underlying discrete process, for example see Buttenschoen et al. (2015), Chauviere et al. (2012), Middleton et al. (2014).

Specifically we take

$$\begin{aligned} \frac{\partial u}{\partial t} = -\nabla \cdot \mathbf J + h(\cdot )\,, \end{aligned}$$

where $\mathbf J$ represents the cell flux and $h(\cdot )$ is a function describing cell proliferation and death. The flux describes the various factors leading to cell movement: here we suppose attractive and/or repulsive interactions between cells, together with a random motility component. We take the simplest assumption in that the latter is modelled via Fickian diffusion, $\mathbf J _\mathrm{random} = -D\nabla u$ where $D$ is a constant cell diffusion coefficient, although we acknowledge that nonlinear diffusion terms may be more appropriate in some contexts.

We assume the interaction between one cell and another generates either an attractive or repulsive force, leading to their movement towards or away from each other. These forces could be directly generated, as in the forces created through adhesion molecule binding on adjacent cell membranes, or indirectly generated, for example the activation of intracellular movement machinery due to the trigger presented by a signalling cell: in the general model, the precise mechanism is not important, we simply assume movement is initiated when two cells are within range. Specifically, we assume the force created at ${\mathbf{x}}$ due to signalling with cells at ${\mathbf{x+s}}$ is given by

$$\begin{aligned} {\mathbf{f}}({\mathbf{x}},{\mathbf{s}},t)= \frac{{\mathbf{s}}}{\left| {\mathbf{s}}\right| } \Omega (\left| {\mathbf{s}}\right| ;\xi ,\mu ) g(u({\mathbf{x+s}},t)). \end{aligned}$$

In the above $\Omega :[0,\infty ) \rightarrow {\mathbb {R}}$ is the interaction function which dictates how the strength of the force generated at ${\mathbf{x}}$ varies with distance to ${\mathbf{x+s}}$, parameterised with respect to the interaction range $\xi$ and interaction strength $\mu$; see below for further details. The functional dependence on cell density at ${\mathbf{x+s}}$, $g(u({\mathbf{x+s}},t))$, simply assumes the force exerted on cells at ${\mathbf{x}}$ varies according to the number of cells they can contact at ${\mathbf{x+s}}$. We sum all such forces through integrating over space to obtain the total force:

$$\begin{aligned} {\mathbf{F}}({\mathbf{x}},t)=\int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}}\right| } \Omega (\left| {\mathbf{s}}\right| ;\xi ,\mu ) g(u({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}}\,. \end{aligned}$$

Assuming that inertia is negligible and drag is proportional to velocity, we therefore obtain the interaction flux

$$\begin{aligned} \mathbf J _\mathrm{interaction} ({\mathbf{x}},t) = u \, p(u) \omega \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}}\right| } \Omega (\left| {\mathbf{s}}\right| ;\xi ,\mu )g(u({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}}\,. \end{aligned}$$

(1)

Note that $\omega$ is a proportionality constant that depends on factors such as the viscosity of the medium, while we also introduce a packing or volume-filling function, $p(u)$, that acts to prevent unbounded cell densities: $p$ is assumed to be a decreasing function of $u$, reflecting decreased ability to move at higher densities. Incorporating (1) into the general mass conservation equation, the one-population model becomes

$$\begin{aligned} \frac{\partial u}{\partial t} = \nabla \cdot \left( D \nabla u - u \omega p(u) \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}}\right| } \Omega (\left| {\mathbf{s}}\right| ;\xi ,\mu )g(u({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}} \right) + h(\cdot ) \,. \end{aligned}$$

(2)

The above equation clearly has great scope and to focus attention on the dynamics induced by nonlocal signalling interactions we fix functions $g$, $p$ and $h$ at this point. For $g$, we take the simplest assumption that the force increases linearly with the cell density, $g(u({\mathbf{x+s}},t))=u({\mathbf{x+s}},t)$, due to increased likelihood of forming an interaction at higher cell densities; suitable nonlinear forms could also be selected. We take $p(u) = 1 - u/P$ as a suitable packing function (e.g. see Painter and Hillen 2002), where $P$ is a parameter describing the packing density, and we adopt the standard form $h(u) = \rho u ( 1 - u/U)$ for cell kinetics, where $\rho$ is the proliferation rate and $U$ is the carrying capacity. Note that packing density and carrying capacity parameters are not necessarily the same: the former describes a density at which movement has become negligible, while the latter describes the density for which the net growth is zero. In particular, we assume here that the carrying capacity $U \le P$, i.e. movement can still continue until the tissue is ‘packed’, yet growth becomes restricted at lower densities (e.g. due to nutrient depletion). Note also that it would be possible to conceive a long-range dependent proliferation term, for example via a nonlocal form of $h(u)$: we do not consider this extension at present.

As stated above, the function $\Omega (r)$ describes how the strength of the force varies with the distance $r$ from a cell and forms our focal point. Here we specifically set

$$\begin{aligned} \Omega (r;\xi ,\mu ) = \mu \frac{\tilde{\Omega } \left( r/\xi \right) }{\xi } \end{aligned}$$

where $\tilde{\Omega }:[0,\infty ) \rightarrow {\mathbb {R}}$ is the normalised interaction function of $r/\xi$ that satisfies

$$\begin{aligned} \int _{0}^{\infty }\tilde{\Omega } (r/\xi ) \hbox {d}r = \xi \,. \end{aligned}$$

Hence the normalised interaction function is parametrised solely by $\xi$. In this formulation, each cell transmits a total signal¹ parametrised solely by the interaction strength parameter $\mu$, distributed over some region determined by $\tilde{\Omega }$ and characterised solely by the signalling range $\xi$.

The signalling range and strengths are expected to vary with cell type: for example, whether direct membrane to membrane interactions or longer (e.g. filopodia, cytoneme) protrusions form the primary mode of signalling. Note that for now we will exclusively consider nonnegative functions for $\tilde{\Omega }$ (i.e. $\tilde{\Omega }:[0,\infty ) \rightarrow {\mathbb {R}}^+$). Consequently, it is the sign of the interaction strength parameter that reflects whether a signalling interaction is attracting ($\mu > 0$) or repelling ($\mu < 0$). Of course, this precludes that two cells may attract or repel each other, according to their distance apart: such scenarios could easily be modelled by lifting the restriction on $\tilde{\Omega }$ being nonnegative.

A simple choice for $\tilde{\Omega } (r/\xi )$ would be a step function—uniform signalling within a cell’s reach and zero outside—however, given the often dynamic and flexible shape of cells and their protrusions, we would intuitively expect signalling to vary with distance from the signalling cell. Here we explicitly consider the following three functions:

$$\begin{aligned} \begin{array}{llcllcllc} \tilde{\Omega } \left( r/\xi \right) = \left\{ \begin{array}{ccc} 1 &{} \text{ if } &{} \frac{r}{\xi } \le 1 \\ 0 &{} \text{ if } &{} \frac{r}{\xi } > 1 \end{array} \right.&\text{(O1); }\quad&\,&\tilde{\Omega } \left( r/\xi \right) = e^{-\frac{r}{\xi }}&\text{(O2); } \quad&\,&\tilde{\Omega } \left( r/\xi \right) = \frac{r}{\xi } e^{-\frac{1}{2}(\frac{r}{\xi })^2}&\text{(O3). }&\end{array} \end{aligned}$$

In the above, (O1) describes the simple uniform signalling stated above, and the signalling range $\xi$ describes the outermost reach. (O2) defines a simple exponential decrease in signalling with distance from the cell, reflecting a decrease in the probability of creating a contact with distance from a cell’s centre. The third proposal (O3) assumes that peak signalling takes place some distance $\xi$ from a cell’s centre (e.g. a point reflecting the mean extent of cell protrusions from the centre) and away from there (in both directions) decreases towards zero: its precise (and analytically convenient) form follows that chosen in similar models by Mogilner and Edelstein-Keshet (1999), Eftimie et al. (2007a, (2007b) in the context of animal swarming.

Therefore, our one-population model is given by

$$\begin{aligned} \frac{\partial u}{\partial t} = \nabla \cdot \left( D \nabla u - u \omega (1 - u/P) \frac{\mu }{\xi } \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}}\right| } \tilde{\Omega } (\left| {\mathbf{s}}\right| /\xi ) u({\mathbf{x+s}},t)\hbox {d}{\mathbf{s}} \right) + \rho u (1 - u/U) \,. \end{aligned}$$

(3)

where $\tilde{\Omega }$ is given by one of the forms (O1)–(O3) above.

For initial conditions, we simply state $u({\mathbf{x}},0) = u_0({\mathbf{x}}) (\ge 0, \le P)$, discussing specific choices in applications below. Domain and boundary conditions generally require special attention: for a bounded region of space, standard boundary conditions such as zero-flux can certainly be specified, yet it also becomes necessary to modify the nonlocal term to account for how points outside the domain should be accounted for. One possibility would be to truncate the signalling function to zero for exterior points, assuming that there are no cells in that region capable of providing a signal; of course, this would be a modelling decision based on the applications under consideration. Given the primarily theoretical nature of the present analysis, we will simply consider either an unbounded domain (for analysis) or periodic boundary conditions (when it comes to numerics).

2.1.1 Example Application: Cell Invasion Waves

Models similar to Eq. (3) have been studied in various contexts, including self-organisation of a homogeneous cell population and wave invasion. For example, we trivially note that when $\mu = 0$, (3) reduces to Fisher’s equation and one therefore expects travelling wave solutions. Consequently, models based on (3) have specifically been used to explore the dynamics of invading waves of cancer cell populations (e.g. see Gerisch and Chaplain 2008; Sherratt et al. 2009; Painter et al. 2010), for example, focussing on how cell–cell adhesion impacts on the rate and form of an invasion wave. In Sect. 4 below, we extend this further in a specific application of (3) to neural crest invasion, exploring how a process of contact repulsion in a travelling wave of cells alters their rate of invasion.

2.2 Heterogeneous Tissues: Multiple Populations

We next generalise our model to examine signalling interactions between multiple populations. Specifically, for two populations $u$ and $v$, we consider a total of four interaction terms: two homotypic terms for the interactions between cells of the same type ($u$ to $u$ or $v$ to $v$), and two heterotypic terms for the interactions between cells of distinct type ($u$ to $v$ or $v$ to $u$).

The interaction function $\Omega _{mn} (r;\mu _{mn},\xi _{mn})$ now defines the impact on cell type $m$ through contacts with cells of type $n$, parametrised according to the interaction strength $\mu _{mn}$ and interaction range $\xi _{mn}$. We again assume that

$$\begin{aligned} \Omega _{mn} (r;\xi _{mn},\mu _{mn}) = \mu _{mn} \frac{\tilde{\Omega }_{mn} \left( r/\xi _{mn} \right) }{\xi _{mn}} \end{aligned}$$

where $\tilde{\Omega }_{mn}:[0,\infty ) \rightarrow {\mathbb {R}}$ is the function of $r/\xi _{mn}$ that satisfies $\int _{0}^{\infty }{\tilde{\Omega }}_{mn} (r/\xi _{mn}) \hbox {d}r = \xi _{mn}$. Extending (2) to two populations, our model is given by

$$\begin{aligned} u_t= & {} \nabla \cdot \left( D_u \nabla u - u \omega p(u,v) \frac{\mu _{uu}}{\xi _{uu}} \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}} \right| } \tilde{\Omega }_{uu} \left( r/\xi _{uu} \right) g_{uu} (u({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}}\right. \nonumber \\&\left. -\,u \omega p(u,v) \frac{\mu _{uv}}{\xi _{uv}} \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}} \right| } \tilde{\Omega }_{uv} \left( r/\xi _{uv} \right) g_{uv} (v({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}} \right) + h_u (u,v) \end{aligned}$$

(4)

$$\begin{aligned} v_t= & {} \nabla \cdot \left( D_v \nabla v - v \omega p(u,v) \frac{\mu _{vv}}{\xi _{vv}} \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}} \right| } \tilde{\Omega }_{vv} \left( r/\xi _{vv} \right) g_{vv} (v({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}} \right. \nonumber \\&\left. -\,v \omega p(u,v) \frac{\mu _{vu}}{\xi _{vu}} \int _{{\mathbb {R}}^n} \frac{{\mathbf{s}}}{\left| {\mathbf{s}} \right| } \tilde{\Omega }_{vu} \left( r/\xi _{vu} \right) g_{vu} (u({\mathbf{x+s}},t))\hbox {d}{\mathbf{s}} \right) + h_v (u,v) \end{aligned}$$

(5)

where $D_u$ and $D_v$ are the (assumed constant) cell diffusion coefficients, $\omega$ is as above and $p(u,v)$ is a packing function. Here we limit ourselves to the choice $p(u,v) = 1 - (u+v)/P$, where $P$ denotes the packing density parameter, although we note other decreasing forms could also be chosen (e.g. $p(u,v) = \exp (-(u+v)/P)$), and again we assume simple linearly increasing forms for the various functions $g_{mn}$. We note that the choice of constant diffusion coefficients represents a clear simplification when packing-type behaviour is accounted for: for interacting cell populations, diffusive-based movements can be considerably more complicated, for example driven by the multiple cell density gradients (e.g. see Painter and Sherratt 2003; Simpson et al. 2009; Painter 2009). Reducing to constants allows us to focus on the crucial contribution from the nonlocal interaction terms.

Functions $h_u$ and $h_v$ describe the cell kinetics, although we will ignore these in the analysis that follows ($h_u = h_v = 0$). Initially we set $u({\mathbf{x}},0) = u_0({\mathbf{x}}), v({\mathbf{x}},0) = v_0({\mathbf{x}})$, such that $0 \le u_0, v_0, u_0+v_0 \le P$ for all ${\mathbf{x}}$. Domain and boundary conditions are considered as given in the homogeneous tissue case.

2.2.1 Example Application: Cell Sorting

A natural application of the above model is to the patterning and sorting of cell populations during embryonic development. In particular, in Armstrong et al. (2006) and Gerisch and Painter (2010), a particular formulation of (4)–(5) was suggested to describe the differential adhesion-driven sorting of cell populations. Here, the generation of attractive forces via direct cell–cell binding imposes natural restrictions, such as $\mu _{mn} \ge 0$ and symmetry of the heterotypic interaction terms. Despite these restrictions, the model is capable of generating a diverse range of patterning, including the various sorting patterns predicted by the differential adhesion hypothesis (Steinberg 2007). Under the more general scenario here, signals are transmitted uni-directionally and via different modes of communication.

3 Pattern Formation

Given the above mentioned relevance of models (3) and (4)–(5) to the self-organisation and sorting of populations, we begin with a general analysis into pattern formation, before returning in Sect. 4 to some expository applications. We begin with the simpler situation of a homogeneous tissue, exploring the necessary relationships between parameters such as interaction range and strength for patterning to occur. The insights will be used to guide explorations into the more intricate case of a heterogeneous tissue.

3.1 Homogeneous Tissue: One-Population

3.1.1 Linear Stability Analysis

For convenience, we restrict to the one-dimensional case and nondimensionalise (3), scaling via

$$\begin{aligned} \begin{array}{ccccccc} \hat{u} = \frac{u}{P}\,,&\hat{x} = \frac{x}{L}\,,&\hat{t} = \frac{D}{L^2} t\,,&\hat{\xi } = \frac{{\xi }}{L}\,,&\hat{\mu } = \frac{\omega \mu L P}{D}\,,&\hat{\rho } = \frac{\rho L^2}{D}\,,&\hat{U} = \frac{U}{P}\,. \end{array} \end{aligned}$$

In the above, $L$ represents a reference length scale, which relates dimensional and non-dimensional values of the signalling range; this will be application-dependent. Note that since $U \le P$, we have $\hat{U} \le 1$. We substitute the above forms into (3) and drop the “hats” for notational simplicity to obtain

$$\begin{aligned} \frac{\partial u}{\partial t} = u_{xx} - \left( u (1 - u) \frac{\mu }{\xi } \int _{{\mathbb {R}}} \frac{s}{\left| s\right| } \tilde{\Omega }(\left| s \right| /\xi ) u(x+s,t)ds \right) _x + \rho u ( 1 - u/U) \,. \end{aligned}$$

(6)

We note that for $\rho > 0$ we determine a (positive) uniform steady state $0 < U \le 1$. When $\rho = 0$, the uniform steady state will be determined by the average initial density (on an infinite domain or with homogeneous boundary conditions), which we also take to be given by $U$ and will be in the range $0 < U \le 1$ by the above specified initial conditions.

To explore stability of the steady state, we set $u(x,t) = U+\tilde{u}(x,t)$ in (6), where $\tilde{u}$ describes a small perturbation. We linearise and take the standard approach (for example, see Murray 2002) of looking for solutions of the form $\tilde{u} \sim e^{ikx +\lambda t}\,$ where, for the unbounded domain case here, $k \in {\mathbb {R}}$. Here $k$ denotes the wavenumber, with corresponding wavelength = $2 \pi /k$. Note that a formal analysis under bounded domains would require care and attention to any restrictions on $k$ due to the stated boundary conditions. Straightforward rearrangement yields

$$\begin{aligned} \lambda = -k^2 + i k U(1-U) \frac{\mu }{\xi } \int _{{\mathbb {R}}} \text{ sgn }(\sigma ) \tilde{\Omega }(\left| \sigma \right| /\xi ) e^{-ik\sigma } \hbox {d}\sigma -\rho \,. \end{aligned}$$

In the above, we have set $\sigma = -s$ and taken $\text{ sgn }(.)$ to denote the sign function: the integral therefore defines the (purely imaginary) Fourier transform of the odd function $\text{ sgn }(\sigma ) \tilde{\Omega }(\left| \sigma \right| /\xi )$ and we let $\Gamma$ be the odd function defined by

$$\begin{aligned} \int _{{\mathbb {R}}} \text{ sgn }(\sigma ) \tilde{\Omega }(\left| \sigma \right| /\xi ) e^{-ik\sigma } \hbox {d}\sigma = - i \xi \Gamma (k, \xi )\,. \end{aligned}$$

(7)

A necessary condition for linear instability of the uniform steady state to spatially inhomogeneous perturbations is $\text{ Re }(\lambda ) >0$ for some $k > 0$, i.e.

$$\begin{aligned} k U(1-U) \mu \Gamma (k, \xi ) > k^2 + \rho \,. \end{aligned}$$

(8)

Note that it is sufficient to restrict to $k>0$ due to the even nature of $k \Gamma$.

To explore this instability condition further, we consider $\Gamma$ for the three representative functions $\tilde{\Omega }$ given by (O1)–(O3), see Table 1 for details. We note that for each of these functions, we have $\Gamma \ge 0$ for $k >0$ and $\Gamma \rightarrow 0$ as $k \rightarrow \infty$. Observe that $\Gamma \ge 0$ for $k >0$ and $0<U\le 1$ implies that (8) is satisfied for some $k>0$ if $\mu$ is sufficiently large (positive), and thus instability is possible under these conditions. If, however, $\mu <0$ (i.e. the repellent case) then (8) cannot hold for any $k>0$.

For the analytically convenient case of (O2), we can perform an explicit analysis by substituting the form for $\Gamma$ given in Table 1 directly into Eq. (8), rearranging and showing it holds for some $k>0$ if and only if the following condition is satisfied:

$$\begin{aligned} \mu U(1-U) > \frac{\left( 1+\xi \sqrt{\rho } \right) ^2}{2 \xi }\,. \end{aligned}$$

(9)

Note that in the specific case of zero cell proliferation, this reduces to $2 \xi \mu U(1-U) > 1$. Representations of (9) for $U=0.5$ and $\rho =0$ or $\rho =1$ are provided in Fig. 2 (middle plots).

Table 1 Table showing the functions for $\Gamma$ following the Fourier transform (7) for the interaction functions (O1)–(O3)

Fig. 2

$\xi -\mu$ parameter regions for predicted patterning in the one-population model under (left to right) different interaction functions (O1)–(O3) and (top row) $\rho = 0$ and (bottom row) $\rho = 1$. In the regions where patterning is predicted, we also indicate the expected spatial wavelength, color-coded from patterns of zero wavelength (dark blue) to wavelengths greater than 30 (dark red) (Color figure online)

Using the explicit condition (9) obtained for (O2), we can clearly see the requirement of a sufficiently large and positive $\mu$ (attractive interactions), deduced in general above: attraction generates the cohesion that pulls cells into aggregated groups. The dependence on $\xi$, on the other hand, is more subtle. For $\rho = 0$, longer signalling ranges promote instability and patterning. For $\rho > 0$, however, instabilities are optimised at a specific signalling range, with smaller and larger $\xi$ necessitating a larger value of $\mu$ to generate patterning. Intuitively, for a small interaction range, it is necessary to generate a strong signal in order to pull enough cells together to create a cluster, while for large interaction ranges, the signal becomes dispersed over a wider field and the interaction strength must also be that much larger to overcome the stabilizing effects of proliferation.

Cases (O1) and (O3) are less amenable to a direct analysis, yet the form of $\Gamma (k, \xi )$ implies similar dependencies on $\xi$ and $\mu$, with small and larger $\xi$ requiring larger $\mu$ to generate patterning. Numerical calculations of the $\xi - \mu$ instability region (fixing $U = 0.5, \rho = 1$) demonstrate this similarity, see Fig. 2.

We further consider the value $k_m$ at which $\text{ Re } \lambda (k)$ reaches its maximum value, indicating the corresponding wavelength $2\pi / k_m$ using the color code in Fig. 2. This provides an indication of the expected wavelength of patterns that emerge from perturbations of the steady state and, hence, the (initial) spacing of aggregates. As intuition would predict, we observe that the predicted wavelength increases with the signalling range.

3.1.2 Numerical Simulations

To investigate the form of the patterns, we numerically solve the equations in 1D. Up until now, we have avoided the necessary specification of boundary conditions and modification of the integral term for bounded domains: here, to limit any boundary effects, we wrap the interval $[0,L]$ onto a circle by imposing periodic boundary conditions, with the integral term itself also ‘wrapped’.

To solve the nonlocal PDEs, we follow a Method of Lines approach, using the MATLAB inbuilt integrator “ode45” to solve the resulting system of time-dependent ODEs. Note that the discretisation utilises a Fast Fourier Transform technique to calculate the integral: full details of the numerical method itself are provided in Gerisch (2010), Gerisch and Painter (2010). Exploiting the fact that for all $|s|>\xi$ all proposed forms for $\tilde{\Omega }$ are either zero or decay rapidly to zero, we set

$$\begin{aligned} \int _{{\mathbb {R}}} \frac{s}{\left| s\right| } \tilde{\Omega }(\left| s\right| /\xi ) u(x+s,t)ds \approx \int _{-N\xi }^{N \xi } \frac{s}{\left| s\right| } \tilde{\Omega }(\left| s\right| /\xi ) u(x+s,t)ds\,. \end{aligned}$$

The above provides a close approximation for large enough $N$: in simulations, where we have restricted to the forms (O1)–(O3), we use $N = 10$ and solution differences are negligible for a larger $N$. We have further verified the accuracy of simulations via running representative simulations with different absolute/relative error tolerances for the ODE integrator and different spatial discretisations.

We begin by exploring pattern formation from quasi-uniform initial conditions,² determining the impact of the interaction strength and range parameters on the form of the developing pattern. We refer to the parameter space in Fig. 2 as a guide.

Figure 3a–d demonstrates patterning under zero proliferation ($\rho = 0$) and a fixed interaction range $\xi = 1$. Patterning only develops when the interaction strength parameter lies above the critical line indicated in Fig. 2 and, in this instance, we observe the formation of aggregations as seen in previous similar models (e.g. Armstrong et al. 2006). Attraction between the aggregates leads to merging and a coarsening phenomenon, as previously reported (e.g. Armstrong et al. 2006). Note that simulations here are of the nondimensional model: to provide a reference point, we note that since $\xi =1$, the length scale $L$ is the dimensional interaction range. Based on a cell diffusion coefficient in a range $D \approx 10^{-9}-10^{-8}$ cm$^2/$s and an interaction range $L = \xi \approx 20 \upmu$m (twice a “typical” cell diameter), $t = 10$ would therefore correspond to somewhere in the range 1–10 h. Therefore, aggregates are capable of becoming well established within a few hours.

Fig. 3

Patterning for the one-population model with interaction function (O2) under a–d varying interaction strengths, and e–h varying interaction ranges. In each subplot, we plot in the top panel, the space (horizontal)—time (vertical) cell density map (black–red–orange–yellow–white indicates the increasing cell density from 0 to 1), and in the bottom panel, the cell density profile at the fixed time $t =100$. For these simulations, there is no cell growth, $\rho = 0$. For a–d we choose $\xi = 1$ and a $\mu = 1$, b $\mu = 5$, c $\mu = 10$ and d $\mu = 20$; for e–h we choose $\mu = 5$ and a $\xi = 0.25$, b $\xi = 1$, c $\xi = 2$ and d $\xi = 4$. For simulations, here we set $U = 0.5$. Numerical method as described in the text, with 2000 spatial grid points and error tolerances set at $10^{-6}$ (Color figure online)

Figure 3e–h show corresponding pattern development when the interaction strength parameter is fixed and the interaction range is increased: again, patterning requires a certain minimum interaction range. Notably, the interaction range parameter has a strong impact on the wavelength of the pattern.

Incorporating cell growth ($\rho >0$) introduces additional dynamics, as illustrated in Fig. 4. While pattern formation and the merging of existing aggregates still occurs, we now observe (for certain parameters) a renewal process, such that a new aggregate emerges in the space between existing peaks: intuitively, while the merging of two aggregates is driven by their mutual attraction, the subsequent space created allows a new aggregate to emerge, driven by cell proliferation. Note that this behaviour is highly reminiscent of that reported in chemotaxis models, see Painter and Hillen (2011) for further details. Finally, we confirm the earlier prediction of the linear stability analysis, in that only intermediate interaction ranges promote patterning: high and low $\xi$ result in a uniform distribution, see Fig. 4e–h.

Fig. 4

Patterning for the one-population model with interaction function (O2) under a–d varying interaction strengths, and e–h varying interaction ranges. In each subplot, we plot in the top panel the space (horizontal)—time (vertical) cell density map (colormap details as in Fig. 3), and in the bottom panel the cell density profile at the fixed time $t =100$. For these simulations we include logistic growth, $\rho = 1$. For a–d we choose $\xi = 1$ and a $\mu = 5$, b $\mu = 10$, c $\mu = 20$ and d $\mu = 50$; for e–h we choose $\mu = 10$ and a $\xi = 0.25$, b $\xi = 1$, c $\xi = 2$ and d $\xi = 4$. For simulations here we set $U = 0.5$. Numerical method as described in the text, with 2000 spatial grid points and error tolerances set at $10^{-6}$ (Color figure online)

While the above numerics have been presented for the interaction function (O2), very similar dynamics are observed with either (O1) or (O3) (although the exact parameters necessary for patterning vary, cf. Fig. 2). Consequently, hereafter we confine our study to the form (O2).

3.2 Heterogeneous Tissues: Two Populations

3.2.1 Linear Stability Analysis

The two population model provides a more formidable challenge, complicated by its large parameter space: the interaction functions alone require 8 parameters. Again, we consider an infinite one-dimensional domain and, to simplify the analysis further, we choose to ignore cell kinetics ($h_u = h_v = 0$). We use the nondimensional scalings

$$\begin{aligned} \begin{array}{ccccccc} \hat{u} = \frac{u}{P}\,,&\hat{v} = \frac{v}{P}\,,&\hat{x} = \frac{x}{L}\,,&\hat{t} = \frac{D}{L^2} t\,,&\hat{\xi }_{mn} = \frac{{\xi _{mn}}}{L}\,,&\hat{\mu }_{mn} = \frac{\omega \mu _{mn} L P}{D_u}\,,&\hat{D} = \frac{D_v}{D_u}\,, \end{array} \end{aligned}$$

where $L$ is again a reference length scale. Substituting and dropping the “hats”, we find

$$\begin{aligned} \begin{array}{rl} u_t &{}=u_{xx} - \left( u (1 - u - v ) \left( \frac{\mu _{uu}}{\xi _{uu}} \int _{{\mathbb {R}}} \frac{s}{\left| s \right| } \tilde{\Omega }_{uu} \left( s/\xi _{uu} \right) u(x+s,t)\hbox {d}s \right. \right. \\ &{}\quad \left. \left. +\, \frac{\mu _{uv}}{\xi _{uv}} \int _{{\mathbb {R}}} \frac{s}{\left| s \right| } \tilde{\Omega }_{uv} \left( s/\xi _{uv} \right) v(x+s,t)\hbox {d}s \right) \right) _x \\ v_t &{}= Dv_{xx} - \left( v (1 - u - v ) \left( \frac{\mu _{vv}}{\xi _{vv}} \int _{{\mathbb {R}}} \frac{s}{\left| s \right| } \tilde{\Omega }_{vv} \left( s/\xi _{vv} \right) v(x+s,t)\hbox {d}s \right. \right. \\ &{}\quad \left. \left. +\, \frac{\mu _{vu}}{\xi _{vu}} \int _{{\mathbb {R}}} \frac{s}{\left| s \right| } \tilde{\Omega }_{vu} \left( s/\xi _{vu} \right) u(x+s,t)\hbox {d}s \right) \right) _x \end{array} \end{aligned}$$

(10)

In the absence of cell kinetics, uniform steady states for the above equations are determined by the average initial densities, $U$ and $V$, which, following the scaling, satisfy $0 \le U, V, U+V \le 1$. We set $u(x,t)=U+\tilde{u}(x,t)$ and $v(x,t)=V+\tilde{v}(x,t)$ (for small perturbations $\tilde{u}$ and $\tilde{v}$), linearise and again look for solutions of the form $\sim e^{i k x + \lambda t}$ to obtain a dispersion relation of the form

$$\begin{aligned} \lambda ^2 + {\mathcal {C}}(k)\lambda + {\mathcal {D}}(k)=0 \end{aligned}$$

where ${\mathcal {C}}$ and ${\mathcal {D}}$ are given by:

$$\begin{aligned} {\mathcal {C}}(k) = k^2(1+D) - k (1-U-V) \left( U \mu _{uu} \Gamma _{uu} + V \mu _{vv} \Gamma _{vv} \right) \end{aligned}$$

(11)

and

$$\begin{aligned} \begin{array}{rcl} {\mathcal {D}}(k) &{} = &{} D k^4 - k^3(1-U-V) (D U \mu _{uu} \Gamma _{uu} + V \mu _{vv} \Gamma _{vv} ) \\ &{} &{} +\, k^2 U V (1-U-V)^2 ( \mu _{uu} \Gamma _{uu} \mu _{vv} \Gamma _{vv} - \mu _{uv} \Gamma _{uv} \mu _{vu} \Gamma _{vu} )\,. \end{array} \end{aligned}$$

(12)

In the above we have once again used the notation $\Gamma _{mn}$, where

$$\begin{aligned} \int _{{\mathbb {R}}} \text{ sgn }(\sigma ) \tilde{\Omega }_{mn}(\left| \sigma \right| /\xi _{mn}) e^{-ik\sigma } \hbox {d}\sigma = - i \xi _{mn} \Gamma _{mn} (k, \xi _{mn})\,, \end{aligned}$$

for $mn$ = $uu$, $uv$, $vu$, $vv$.

For instability, we require $Re(\lambda _+)>0$, where $\lambda _+ = 0.5(-{\mathcal {C}} + \sqrt{{\mathcal {C}}^2-4{\mathcal {D}}})$. Clearly, this can occur if and only if ${\mathcal {C}} < 0$ or ${\mathcal {D}} < 0$ for some positive $k$. A comprehensive analysis is a formidable challenge, yet with $0 \le U+V \le 1$ and assuming $\Gamma _{mn} \ge 0$ for $k>0$ (as for (O1)–(O3)) we can make some general statements. The equation for ${\mathcal {C}}$ shows that an instability is possible when at least one of the homotypic interactions is positive and sufficiently large, i.e. at least one of the populations is self-attracting to a sufficiently strong extent. Yet even if ${\mathcal {C}} \ge 0$, in particular when both homotypic interactions are negative, $\mu _{uu}, \mu _{vv} \le 0$, we can still achieve instabilities through ${\mathcal {D}} < 0$ given suitable heterotypic interactions. Specifically, given $\mu _{uu}, \mu _{vv} \le 0$, we require $\mu _{uv} \mu _{vu} > 0$ and sufficiently large to generate an instability via ${\mathcal {D}} < 0$: the two populations must either both attract or both repel each other. Thus, pattern formation can still occur in a system in which all interactions are repelling.

Summarising, we find that some form of patterning is possible under almost any generalised set of interactions, given suitable parameter values: our analysis implies that it is only when two repelling homotypic interactions are combined with one attractive and one repelling heterotypic interaction that pattern formation (from an initially uniform state) cannot occur. Table 2 summarises these general comments.

Table 2 It indicates whether pattern formation is feasible in the two population case (given suitable parameter values) for the given combinations of homotypic and heterotypic interactions

These principles can be shown more transparently through a specific analysis: therefore, we numerically calculate and plot parameter regions for patterning, along with the expected pattern wavelengths, following fixation of many of the parameters. A variety of such calculations are shown in Fig. 5, where regions of patterning are colored, with the color code indicating the expected wavelength.

Fig. 5

Parameter regimes for expected patterning in the two population case. In each plot, we vary the two indicated parameters over the axial ranges and calculate whether patterns are expected to grow, along with the color-coded expected wavelength. a Patterning under varying homotypic interactions and fixed positive heterotypic interactions. We fix $\mu _{uv}=\mu _{vu} = 10$, $\xi _{uv}=\xi _{vu} = 1$, $U = V = 0.25$ and $D = 1$ and vary $\mu _{uu}$ and $\mu _{vv}$ for (a1) $\xi _{uu}=\xi _{vv} = 1$, (a2) $\xi _{uu}=\xi _{vv} = 2$ and (a3) $\xi _{uu}=\xi _{vv} = 0.5$. b Patterning under varying heterotypic interactions and fixed negative homotypic interactions. We fix $\mu _{uu}=\mu _{vv} = -10$, $\xi _{uu}=\xi _{vv} = 1$, $U = V = 0.25$ and $D = 1$ and vary $\mu _{uv}$ and $\mu _{vu}$ for (b1) $\xi _{uv}=\xi _{vu} = 1$, (b2) $\xi _{uv}=\xi _{vu} = 2$ and (b3) $\xi _{uv}=\xi _{vu} = 0.5$. c Patterning under varying initial cell densities. We fix parameters $\xi _{uu}=\xi _{vv} =\xi _{uv}=\xi _{vu} = 1$, $\mu _{uv} = \mu _{vu} = 10$, $D=1$ and change the homotypic strengths from (c1) $\mu _{uu} = \mu _{vv} = 10$, (c2) $\mu _{uu} = \mu _{vv} = 0$, (c3) $\mu _{uu} = \mu _{vv} = -5$. The black dots in (a1) and (b1) indicate the position in parameter space for parameter values used in Figs. 7 and 8 (Color figure online)

In Fig. 5a, we vary the homotypic interaction parameters, fixing the heterotypic (and other) parameters at positive values: i.e. the two populations attract each other. In Fig. 5a1, all interaction ranges are given the same value ($\xi _{mn} = 1$): patterning covers most of the parameter space, with the strongly positive heterotypic interactions capable of driving patterning even when the homotypic interactions are zero or slightly negative. Strongly negative homotypic terms (i.e. self-repulsion) can lead to a loss of patterning, with the desire of cells to move away from cells of their own type overcoming the aggregating heterotypic attraction. Either increasing (Fig. 5a2) or decreasing (Fig. 5a3) the homotypic interaction ranges have a slight impact on these parameter regimes, while also altering the expected wavelength of patterning.

In Fig. 5b, we turn our attention to the heterotypic interaction parameters, fixing homotypic terms at negative values (i.e. self-repelling populations). In Fig. 5b1, all interaction ranges are given the same value ($\xi _{mn} = 1$) and, as expected from the earlier analysis, patterning can only occur when the product of heterotypic strengths ($\mu _{uv} \mu _{vu}$) is sufficiently large and positive: we can still expect patterning for all-repelling interactions, provided the two populations repel each other more than they repel themselves. For Fig. 5b2, b3, we respectively increase or decrease the heterotypic interaction ranges: correspondingly, we observe either expanded or contracted parameter regions, along with an overall increase or decrease of the expected patterning wavelengths.

Although the analysis primarily focuses on the interaction parameters, we briefly consider how the sizes of the respective populations affect patterning in Fig. 5c. In Fig. 5c1, we consider an all-attracting scenario, such that all interaction strengths are set to be strongly attracting: $\mu _{mn}=10$, with $\xi _{mn}=1$. Varying the population sizes $U$ and $V$ between 0 and 1 (while ensuring $U +V \le 1$), we find patterning occurs over nearly all $(U,V)$ combinations: only for $U+V$ close to zero (too few cells to collectively aggregate) or $U+V$ close to one (tissue almost at maximum packing density) does patterning fail to occur. Notably, patterning will also occur in the absence of one population, since the remaining population can aggregate via self-attraction. When homotypic terms are switched off ($\mu _{uu} = \mu _{vv}=0$) or made negative ($\mu _{uu} = \mu _{vv}=-5$), however, patterning becomes increasingly restricted and requires both populations to be present ($U,V > 0$): here, patterning is driven via the heterotypic interactions and, consequently, sufficient populations of both cell types must be present to create an appropriately strong aggregating command.

Finally, we comment very briefly on the expected patterning wavelengths. Overall, there is an unsurprising correlation between interactions ranges and expected pattern wavelengths: i.e. larger (smaller) interaction ranges tend to promote larger (smaller) wavelengths and wider (narrower) aggregates. Close to stability-instability boundaries, there is a notable increasing of expected pattern wavelengths: intuitively, within these regions there is a weak tendency to form aggregates, and consequently, cells must assemble from a broad region of space.

3.2.2 Numerical Simulations

The large parameter space precludes extensive numerical analyses for the two population case and instead we will focus our attention on a few illustrative cases. We note that a more detailed study, for differential adhesion cell sorting, has been performed elsewhere (Armstrong et al. 2006; Gerisch and Painter 2010), revealing that a rich tapestry of patterning exists even within that more limited context. The main focus of the current investigation will be to look beyond the natural restrictions of differential adhesion: for example, repelling interactions and asymmetric heterotypic terms.

To contain our preliminary study, we immediately discard cell kinetics and further restrict to the case $U = V$, such that there are equal numbers of the two cell types. We also assume $D=1$, meaning that the two cell populations have equal diffusivities, and we use the same general forms for each of the interaction functions $\tilde{\Omega }$ (using (O2)). We begin by exploring the predictions of Table 2; thus we cycle through distinct combinations of homotypic and heterotypic terms (Fig. 6). Note that for the simulations here, we stop at $t=100$, corresponding to approximately 10–100 h based on the discussion of time scales in the one-population case.

Fig. 6

Patterning in the two population model under different homotypic–heterotypic combinations, as Table 2. In each subplot, we plot the cell densities for $u$ (solid blue) and $v$ (dot-dash red) at $t=100$. Each title indicates the nature of homotypic/heterotypic interactions, with respect to the choices for $(\mu _{uu},\mu _{vv}):(\mu _{uv},\mu _{vu})$. Specific values in each row are: (top row, left) $(10,10):(10,10)$, (middle) $(10,10):(10,-10)$, (right) $(10,10):(-10,-10)$; (middle row, left) $(10,-10):(10,10)$, (middle top panel)$(20,-10):(10,-10)$, (middle bottom panel)$(20,-10):(-10,10)$, (right) $(10,-10):(-10,-10)$; (bottom row, left) $(-10,-10):(20,20)$, (middle) $(-10,-10):(10,-10)$, (right) $(-10,-10):(10,-10)$, $(-10,-10):(-20,-20)$. Note that parameters for each case are chosen within the patterning regime, if applicable. Other parameters are set at $\xi _{mn} = 1$, $D=1$ and $U = V = 0.25$. Numerical simulations solved as described in the text, with 1000 spatial grid points and error tolerances set at $10^{-6}$. Note that in all plots, the vertical axis scale ranges between 0 and 1 (Color figure online)

As expected, we find patterns for almost any parameter combination, except repelling homotypic interactions coupled with opposing heterotypic terms. Patterns fall into two principal camps: mixed/partially-mixed aggregates composed of both cell populations (e.g. as for all attractive interactions) or separated aggregates of distinct populations (e.g. attractive homotypic/repelling heterotypic). The investigation here is relatively crude, of course, and we would expect a refined investigation to yield more subtlety in the pattern variation. For example, previous investigations (Armstrong et al. 2006; Gerisch and Painter 2010) into the differential adhesion hypothesis (all non-negative interactions) reveal a variety of patterns (mixed, encapsulated etc.) according to the precise values of the interaction strengths. We note further that for opposing homotypic and opposing heterotypic, two different cases are shown according to the configuration of the interactions.

Fig. 7

Patterning in the two population model as we perturb from the attracting control. In each subplot, we plot in the top frame the total cell density $w = u+v$ as a position (horizontal)-time (vertical) density plot (colormap details as in Fig. 3) and in the bottom frame, we plot the distinct cell densities for $u$ (solid blue) and $v$ (dot-dash red) at $t=100$. a We decrease heterotypic strengths such that (a1) $\mu _{uv} = \mu _{vu} = 10$, (a2) $\mu _{uv} = \mu _{vu} = 0$, (a3) $\mu _{uv} = \mu _{vu} = -10$, and (a4) $\mu _{uv} = \mu _{vu} = -20$; other parameters are set at $\mu _{uu} = \mu _{vv} = 10$, $\xi _{mn} = 1$, $D=1$ and $U = V = 0.25$. b We decrease one of the heterotypic strength parameters, such that (b1) $\mu _{uv} = 10$, (b2) $\mu _{uv} = 0$, (b3) $\mu _{uv} = -10$, and (b4) $\mu _{uv}= -50$; other parameters are set at $\mu _{uu} = \mu _{vv} = \mu _{vu} = 10$, $\xi _{mn} = 1$, $D=1$ and $U = V = 0.25$. Numerical simulations solved as described in the text, with 2000 spatial grid points and error tolerances set at $10^{-6}$ (Color figure online)

To explore patterning further, as well as to investigate the time evolution of patterns, we set up two “controls” and explore how the patterning structure is altered as one or two key parameters are given freedom. Specifically, the control cases assume that the two populations behave identically, in that they have the same signalling and response characteristics but different “labels”; such as in an experiment where half of a homogeneous population has been tagged with some identifying label. Hence, $\mu _{uu} = \mu _{vv} = \mu _{uv} = \mu _{vu} \equiv \mu$, $\xi _{uu} = \xi _{vv} = \xi _{uv} = \xi _{vu} \equiv \xi$ and (with $D=1$) we can add the $u$-and $v$-equations in (10) to give

$$\begin{aligned} w_t = w_{xx} - \left( w (1 - w) \frac{\mu }{\xi } \int _{{\mathbb {R}}} \frac{s}{\left| s\right| } \tilde{\Omega }(\left| s\right| /\xi ) w(x+s,t)\hbox {d}s \right) _x \,, \end{aligned}$$

where $w = u + v$ defines the total density. Hence, the total population density behaves exactly as the one-population model considered earlier (excluding cell kinetics).

For the controls, we consider the following two situations.

• Attracting populations, where we set $\mu >0$ and $\xi >0$. The earlier linear stability analysis predicts that patterning will occur for sufficiently large $\mu \xi$: specifically, we consider the point represented by the black dot in Fig. 5a1. In this case, we observe aggregates forming that contain a uniform mixture of the two cell types, c.f. Fig. 7a1/b1.

• Repelling populations, where we set $\mu < 0$ and $\xi >0$. The earlier linear stability analysis predicts patterns do not emerge: specifically, we consider the point represented by the black dot in Fig. 5b1. Here we observe a spatially uniform mixing, c.f. Fig. 8a1/b1.

Fig. 8

Patterning in the two population model as we perturb from the repelling control. In each subplot, we plot in the top frame the total cell density $w = u+v$ as a position (horizontal)-time (vertical) density plot (colormap details as in Fig. 3) and in the bottom frame, we plot the distinct cell densities for $u$ (solid blue) and $v$ (dot-dash red) at $t=100$. a We vary heterotypic strengths such that ($a1$) $\mu _{uv} = \mu _{vu} = -10$, ($a2$) $\mu _{uv} = \mu _{vu} = -20$, ($a3$) $\mu _{uv} = \mu _{vu} = -50$, and ($a4$) $\mu _{uv} = \mu _{vu} = 20$; other parameters are set at $\mu _{uu} = \mu _{vv} = -10$, $\xi _{mn} = 1$, $D=1$ and $U = V = 0.25$. b We vary just one of the heterotypic strength parameters, such that ($b1$) $\mu _{uv} = -10$, ($b2$) $\mu _{uv} = -40$, ($b3$) $\mu _{uv} = -100$, and ($b4$) $\mu _{uv}= +50$; other parameters are set at $\mu _{uu} = \mu _{vv} = \mu _{vu} = -10$, $\xi _{mn} = 1$, $D=1$ and $U = V = 0.25$. Numerical simulations solved as described in the text, with 2000 spatial grid points and error tolerances set at $10^{-6}$ (Color figure online)

3.2.3 Attracting Control

We first consider a study in which the two heterotypic interaction strength parameters are simultaneously decreased from positive to negative; note that since the homotypic parameters remain large and positive, the linear stability analysis will always predict patterning in this scenario. Simulations are plotted in Fig. 7a; note that the plot in Fig. 7a1 corresponds to the attracting control.

Decreasing $\mu _{uv},\mu _{vu}$, we observe a loss of the mixed aggregates in the control case: For $\mu _{uv} = \mu _{vu} = 0$, Fig. 7a2, alternating aggregates of $u$ and $v$ form, each accumulating via the self-attracting interactions, but separated by the tissue packing term. Note that while they alternate, there is no apparent characteristic distance between aggregates of separate type: sometimes they abut one another (e.g. as indicated by the *), while others show greater spatial separation (indicated by the $\circ$). However, for $\mu _{uv}=\mu _{vu} < 0$ (Fig. 7a3–a4), an ordered structuring arises: heterotypic repulsion pushes the distinct peaks away from each other, resulting in their regular patterning.

In the next study, Fig. 7b, we examine the impact of reducing one parameter, decreasing the interaction stength $\mu _{uv}$ (i.e. the impact of population $v$ on the movement of $u$) from attracting to repelling; again, Fig. 7b1 corresponds to the control. Setting $\mu _{uv} = 0$ has relatively little impact on the form of the patterns, Fig. 7b2, with mixed (though not equally mixed) aggregates forming. However, setting $\mu _{uv} < 0$ can have a profound impact on patterning, with the potential to generate persistent spatio-temporal patterning, see Fig. 7b3, b4. While some stable aggregates form, the heterotypic terms form a run and chase behaviour, with the $u$ population ever attempting to evade the chasing $v$ population.

3.2.4 Repelling Control

We next turn our attention to the repelling control, again focussing on the impact of alterations to the heterotypic strength parameters. Figure 8a shows the effects of simultaneously altering the size of $\mu _{uv}$ and $\mu _{vu}$, while keeping the homotypic interaction strengths fixed (at $\mu _{uu} = \mu _{vv} = -10$). Figure 8a1 corresponds to the control scenario, with the populations remaining homogeneously and uniformly mixed.

As expected from the earlier linear stability analysis, decreasing the sizes of the heterotypic interaction terms, such that cross-population repulsions become stronger than the self-population repulsions, allows patterns to emerge, see Fig. 8a2–a3: here, sorting of the two populations occurs, with aggregates alternating between $u$ and $v$ populations. Changing the heterotypic interactions to be strongly attracting also allows patterning, see Fig. 8a4, although now mixed aggregates occur containing equal proportions of the two cell types. We next focus on a single heterotypic parameter ($\mu _{uv}$), again varying over negative and positive ranges. For $\mu _{uv} < \mu _{uu,vv,uv} < 0$ we can again generate patterns, via the same mechanism described above, see Fig. 8b2–b3. However, for $\mu _{uv} \ge 0$ we are unable to generate any patterning, seemingly confirming our earlier suggestion that only in the case of one attracting heterotypic interaction and all other interactions repelling do we fail to generate patterns, see Fig. 8b4.

4 Applications

The above analysis has been exploratory in scope, with the main intention being to illustrate potential dynamics of the model. We next show how the model can be adapted to model specific biological processes: the intention is not to provide detailed modelling studies, but rather to show the applicability of the model. Our two examples both derive from embryonic development, yet their formulation would also be relevant to other situations ranging from tumour growth to ecology. The first explores the capacity of contact-inhibition-induced repulsion to promote dispersal of cells from the neural crest, while the second considers a classic example of pattern formation: the organisation of pigmentation stripes in zebrafish.

4.1 Contact-Inhibition-Induced Invasion

Dispersal and invasion processes occur in numerous contexts. In ecosystems, invasion of an alien species can have a devastating impact on native species (Simberloff et al. 2013), while the transformation of tumorous cells into invasive forms can be a prelude to metastasis (Ramis-Conde et al. 2009). Positive examples include the controlled recolonisation of wounded tissue by cells (Sherratt and Murray 1990) or the dispersal of cells from the neural crest during embryogenesis.

The neural crest is a transient and essential structure of embryonic vertebrates that contributes various cell types to diverse adult tissues and organs, including the peripheral nervous system, craniofacial skeleton and skin (Le Douarin and Kalcheim 1999). Arising in a compact strip of cells along the roof of the neural tube (the developing central nervous system) and running from head (anterior) to tail (posterior), neural crest populations are characterised by their migratory characteristics: cells detach from the crest and migrate along defined pathways, predominantly dorsal (back) to ventral (front), to their eventual destination (Theveneau and Mayor 2012). Spatio-temporal coordination of this process is tightly controlled, with cells breaking their adhesive bonds, peeling off from the neural crest and shifting into a migratory form, a process highly reminiscent of the onset of cancer invasion and thereby providing a key comparative system. Further, failure of a neural crest population to reach its final destination within appropriate developmental timescales can lead to a wide range of birth defects, collectively termed neurocristopathies (Etchevers et al. 2005). It is important therefore to ask what the mechanisms and cues are that allow movement out of the crest and subsequent guidance to their destinations.

While a wide variety of mechanisms are likely to play a role in neural crest cell migration, including chemoattraction and chemorepulsion (Theveneau and Mayor 2012), here we explore the potential contribution from contact-inhibition (Carmona-Fontaine et al. 2008). Studies in Carmona-Fontaine et al. (2008) revealed that the collision of two migrating neural crest cells would result in a brief arrest in their movement before migration renews, but now bearing in the opposite direction to their pre-collision trajectory. Consequently, this contact-induced repulsion is believed to optimise the dispersion of neural crest cells away from the neural crest, accelerating their invasion into non-invaded regions.

4.1.1 Simple Model for Contact-Inhibition Repulsion

Here we model the impact of contact-induced homotypic repulsion on the effective dispersal of a homogeneous population. Specifically, we consider the one-population model (3), assuming that the neural crest cells migrate and proliferate. The latter is modelled via the simple logistic term: obviously, proliferation of neural crest cells in vivo will be significantly more complicated than that implied here; however, our intention is to focus on the role of contact-induced repulsion. In certain instances, such as pigment cell precursors migrating into the skin, invasion is predominantly restricted to a two-dimensional field consisting of the anterior–posterior and dorsal–lateral axes. However, the invasion front appears relatively uniform across the former, and therefore, we simplify into a one-dimensional situation, $x \in [-L,L]$ with periodic boundary conditions, such that $x = 0$ defines the dorsal-most and $x = \pm L$ the ventral-most points. Initially, we assume neural crest cells are confined to their pre-dispersal position along the dorsal neural tube, setting

$$\begin{aligned} u(x,0) = \left\{ \begin{array}{c@{\quad }l} u_0 &{} \text{ if } \left| x\right| < x_0 \\ 0 &{} \text{ otherwise }\,. \end{array} \right. \end{aligned}$$

Given the tendency of neural crest cells to reverse migration on contact with each other, we assume cell movement derives from random migration and a homotypic repulsion term, taking $\mu < 0$ for the interaction strength parameter. Other key parameters are the diffusion coefficient $D$, the interaction range parameter $\xi$, cell proliferation rate $\rho$, tissue packing capacity $P$ and tissue carrying capacity $U$. Given the focus on the repulsion process, we fix parameters $D, P, \rho$ and $U$ at specific values such that we can concentrate on the impact of different signalling ranges and strengths on the invasion rate. Note that there is also the proportionality constant parameter $\omega$. However, and without loss of generality, we set this at $\omega = 1$, effectively absorbing it into the interaction strength parameter $\mu$.

For the fixed parameters, we take $D = 3.6 \times 10^{-4}\,\hbox {mm}^2/\hbox {h},\, P = 10^4\,\hbox {cells/mm}^2,\, U = 10^3\,\hbox {cells/mm}^2$ and $\rho =0.07/\hbox {h}$. We initially set $x_0 = 0.05\,\hbox {mm}$ and $u_0 = U$, such that the initial strip is $100\,\mu \hbox {m}$ wide. We should stress that while these values are not rooted in solid data, they are by no means unreasonable: for example the growth rate $\rho$ corresponds to a maximum cell doubling time of approximately 10 h; the density $P$ corresponds to a tightly packed layer of cells of circa $10\,\upmu \hbox {m}$ diameter and we assume the saturating density of the population is far from a packed layer. While changing these parameters will alter specific rates of invasion, they do not impact on the general nature of the results. Of course, successful neural crest dispersal in practice may be highly dependent on each of these terms, along with other factors such as embryonic growth. Consequently, a more careful study in the context of a precise application (e.g. migration of pigment cells in zebrafish) would require more careful parameter selection.

4.1.2 Numerical Simulations of Dispersal

Note that when $\mu = 0$ (no contact repulsion), the model (2) simply reduces to Fisher’s equation and, following initial dispersion, we expect solutions to evolve to a travelling wave with invasion speed $c = 2\sqrt{\rho D} \approx 0.01$ mm/h for the above parameter set. We solve the full equations over a range of $\mu$ and $\xi$. Based on the cells in our nondescript population having a diameter of approximately $10\,\mu \hbox {m}$, we allow $\xi$ to range between $0.01$ and 0.1 mm: the lower value assumes contact-dependent interactions occur (approximately) at a membrane-membrane level, while the latter suggests much longer interactions may come into play. For neural crest cell populations either value of $\xi$ is feasible: for example, in the above cited studies, cells are observed to collide against each other before repelling (Carmona-Fontaine et al. 2008), while reports of other migrating neural crest cells suggest longer-range (filopodia-mediated) contacts may play a role (Kulesa and Fraser 1998). For the interaction strength, we have no firm guidance, so we simply consider a range from 0 (no contact repulsion) to $-0.001$ (strong contact repulsion).

In Fig. 9, we plot the results of numerical simulations as we vary (a) the interaction strength, and (b) the interaction range. Note that as we increase the magnitude of either parameter we observe a significant increase in the invasion rate, suggesting that dispersal of the population could be accelerated either via stronger repellent interactions, or via increased interaction ranges. Notably, solutions appear to evolve to travelling wave profiles, with a constant speed and shape.

Fig. 9

Numerical simulations of model for contact repulsion mediated dispersal of neural crest cells. a Invasion waves under increasing interaction strength. Cell population invades left and right from their initial localisation (at $x = 0$). Time between each curve is 1 day, and the outermost curve is 10 days following the initial dispersal. ($a1$) $\mu = -10^{-4}, \xi = 0.01$; ($a2$) $\mu = -3 \times 10^{-4}, \xi = 0.01$; ($a3$) $\mu = -10^{-3}, \xi = 0.01$. b Invasion waves under increasing interaction range, with plot details as in (a). ($b1$) $\mu = -10^{-4}, \xi = 0.01$; ($b2$) $\mu = -10^{-4}, \xi = 0.03$; ($b3$) $\mu = -10^{-4}, \xi = 0.1$. All other parameters as stated in text. c Invasion depth plotted for varying $(\mu ,\xi )$, defined as the distance from the initial dispersion site after 5 days. d Numerically calculated invasion wave speed, plotted as function of $|\mu \xi |$. Numerical simulations performed as described in the text, with an error tolerances set at $10^{-6}$ and a spatial grid resolution $\Delta x = 0.002$ (Color figure online)

To establish the dependence on $(\mu ,\xi )$ more carefully, we measure the invasion depth (Fig. 9c). Specifically, we define this as the furthest point from $x=0$ at which the cell density has reached $U/2$ at $t = 5$ days following the initial dispersal. Clearly, the results reinforce the above findings, with increases in both interaction range and repelling strength leading to deeper invasion. Moreover, the dependence on $\xi$ and $\mu$ appears to be symmetrical, suggesting that the rate of invasion depends on the size of the product $\mu \xi$. To test this, we numerically calculate the travelling wave invasion speed for different pairs $(\mu ,\xi )$ yielding the same value for $|\mu \xi |$, and over a range of $|\mu \xi |$ values. Plotting the results (Fig. 9d), the numerical simulations corroborate our hypothesis: invasion speed appears to depend solely on $|\mu \xi |$ rather than a precise pair $(\mu ,\xi )$. Note that these results are all predicated on the choice $\mu < 0$, since we are assuming a repulsive interaction.

Summarising, our results support that contact repulsion may be an important factor in enhancing the invasion or dispersal of cells, such as neural crest populations (Carmona-Fontaine et al. 2008, see also Theveneau and Mayor 2012 and references therein). Our study has been intentionally brief and general in scope, focussing on the combined actions of range and strength on the extent of invasion: while the cells studied in Carmona-Fontaine et al. (2008) interact at relatively short distances, our results suggest that if extended to cells communicating at distance via filopodia then invasion may become significantly enhanced. Given the crucial need for neural crest cell populations to successfully disperse, or the pathological consequences of rapid cancer invasion, such mechanisms clearly demand careful attention: for example, our simulations would suggest that inhibiting long-range extensions could significantly limit the invasion process. Future extensions could include a more focussed investigation based on the specific system in Carmona-Fontaine et al. (2008), thereby allowing a more precise theoretical-experimental comparison to be made.

4.2 Zebrafish Pigmentation Patterning

We next consider an example featuring multiple cell types, and a case study of embryonic self-organisation: zebrafish (Danio rerio) pigmentation patterning. As their name suggests, adult members of this species feature an alternating barcode pattern of blue/black stripes and yellow/silver horizontal interstripes, see Fig. 10a. Closer inspection of these patterns reveals a thin separation, such that stripes/interstripes are separated by a thin strip with an absence of xanthophores and melanophores.

Fig. 10

a Adult zebrafish pigmentation patterning consists of alternating black/blue stripes (melanophores and iridophores) and silver/yellow interstripes (xanthophores and iridophores). Figure “Zebrafisch” by Azul—own work. Via Wikimedia Commons—http://commons.wikimedia.org/wiki/File:Zebrafisch.jpg. b–c The simple run-chase interactions observed between melanophores and xanthophores in vitro are unable to either b organise a pattern from an initial uniform mixed distribution or c maintain an existing pattern of melanophore/xanthophore stripes. d–f A variety of homotypic interactions including d positive homotypic interactions for the melanophores, e positive homotypic interactions for the xanthophores, f positive homotypic interactions for both populations (Color figure online)

Fish (unlike mammals) possess multiple pigment cell types, or chromatophores, which organise into various configurations: in the case of zebrafish, the black stripes are dominated by black melanophores with yellowish xanthophores restricted to interstripes; a third pigment cell type, iridophores, are organised in a more subtle manner, integrated in different forms within both stripes and interstripes (e.g. Patterson and Parichy 2013). Early attempts to explain zebrafish pigmentation borrowed heavily on the seminal theoretical ideas of Turing (Turing 1952), yet, despite an impressive capacity to replicate patterns (e.g. see Asai et al. 1999), attempts at uncovering the chemical morphogens it is based on have, so far, proved fruitless. Explanations have subsequently shifted to interactions between the principal chromatophores (e.g. Maderspacher and Nüsslein-Volhard 2003; Parichy and Turner 2003), and given that melanophores and xanthophores are restricted to stripes and interstripes respectively, their interplay formed a natural focus for investigation. Melanophores and xanthophores display various short-range and long-range interactions (e.g. Hamada et al. 2014; Maderspacher and Nüsslein-Volhard 2003; Parichy and Turner 2003; Nakamasu et al. 2009; Yamanaka and Kondo 2014). In particular, recent in vitro investigations suggest that xanthophores and melanophores act out a cat and mouse game, with xanthophores chasing the escaping melanophores, leading to speculation that this interaction forms a core component of the pattern-generating mechanism (Yamanaka and Kondo 2014). In terms of the current model, this would suggest melanophores are repelled by xanthophores and xanthophores are attracted by melanophores.

In fact, adult pigmentation in wild-type zebrafish involves a significantly more complicated set of interactions, with iridophore interactions also involved (Patterson and Parichy 2013; Frohnhöfer et al. 2013; Singh et al. 2014): formulating and analysing a model to study this process in detail is far beyond the aims of the current paper, where the primary intention is to demonstrate the scope of the model. Yet, the fact that some mutants missing entire chromatophore classes can still establish some form of pattern raises the question as to what interactions form a minimal set of pattern-generating interactions, or what is the core pattern-driving mechanism? As a case in point, would the above described “run and chase” interaction between melanophores and xanthophores be sufficient to engineer the adult pattern of alternating melanophore/xanthophore bars?

The current model can easily be used to explore such questions, reinterpreting model (4)–(5) in terms of melanophores ($u$-population) and xanthophores ($v$-population). To describe the run and chase interaction, we would set:

• (RC1) xanthophores repel melanophores, i.e. $\mu _{uv} < 0$;

• (RC2) melanophores attract xanthophores, i.e. $\mu _{vu} > 0$.

We discuss homotypic interactions below; for other parameters we set $\xi _{uu} = \xi _{vv} = \xi _{uv} = \xi _{vu} = 0.1\,\hbox {mm}$, based on an average melanophore/xanthophore diameter of $100\,\upmu \hbox {m},\, D_u = D_v = 0.1\,\hbox {mm}^2/\hbox {day}$, and equal initial densities of melanophores and xanthophores, such that the total density is 75 % of the packing density. Note that altering these basic parameters does not affect the overall conclusions below, but it will impact on the rate and wavelength of any patterns that develop.

Excluding any homotypic interactions or cell kinetics, and adopting our earlier analysis (Sect. 3.2), our modelling suggests that the run and chase interactions, (RC1–RC2), would be unable to spontaneously generate a pattern: in the absence of positive homotypic terms, opposing heterotypic interactions are unable to generate a pattern. Instead, melanophores and xanthophores remain in a mixed and spatially uniform distribution, see Fig. 10b.

If not capable of generating a pattern, could run and chase maintain a previously formed pattern? We explore this by forcing the initial distribution into an alternating pattern of melanophore and xanthophore bands, but we find that the run and chase interactions (RC1–RC2) lead to dispersal of the bands and a return to the mixed uniform distribution, Fig. 10c.

Summarising, our model suggests that run and chase alone is unable to either organise or maintain alternating melanophore/xanthophore bands. The same conclusion was drawn from individual-based modelling in Woolley et al. (2014). What minimal additional interactions would be sufficient? As suggested from the earlier analysis, a simple solution would be to add a positive homotypic interaction in either or both the melanophore and xanthophore populations. We explore the impact of positive homotypic interactions in (i) the melanophore population, (ii) the xanthophore population, and (iii) both populations and examine which would generate a pattern consistent with the adult zebrafish, Fig. 10d–f.

While all three forms of added interaction certainly conspire to generate a pattern, their capacity to replicate a zebrafish-type pattern differs. Under (i) positive homotypic melanophore interactions, we simply observe the accumulation of melanophores and xanthophores into predominantly mixed aggregates: the xanthophores are pulled into the melanophore aggregates, which are unable to escape. Positive interactions in both populations (iii) create a more effective pattern, yet it is somewhat disordered in nature. Moreover, this case corresponds to the scenario where highly dynamic spatio-temporal patterning is possible, suggesting that it is a far from ‘robust’ pattern. Allowing homotypic interactions for the xanthophores, case (ii), creates a far more acceptable pattern: xanthophore and melanophore aggregates are robustly separated, and moreover, a thin strip separates the aggregates. Note that while including this homotypic interaction drives the system into pattern formation, subsequently removing the repulsive interaction (RC1) results in a loss of the zebrafish-type pattern (data not shown).

5 Discussion

In this article, we have presented and explored a general model for contact-dependent interactions within homogeneous (single cell type) and heterogeneous (multiple cell types) tissues. Cell populations have been allowed to interact in diverse (from attracting to repelling) ways, and over variable spatial ranges. The rich dynamical properties of the model were studied through a combination of linear stability and numerical analyses, along with illustrative applications to classic processes of embryonic organisation.

In previous work (e.g. Armstrong et al. 2006; Gerisch and Painter 2010), we formulated and analysed a nonlocal model for adhesion-driven sorting of cell populations. The current work extends this framework, generalising the interactions to include attractive and repelling signals and variable interaction ranges. Allowing repulsion can help create ordered, spatially-separated aggregates, yet can also introduce dynamic spatio-temporal behaviour. This rich variety of behaviour echoes behaviour found in heterogeneous chemotaxis systems, which also allow for various combinations of attracting and repelling interactions (Painter 2009). Unfortunately, the large parameter space and complex nature of the underlying system of equations here precludes the exhaustive and subtle analysis possible under more restricted scenarios, such as the differential adhesion hypothesis: future investigations would benefit from focussing the equations towards a specific experimental system, where a number of the interactions are reasonably well characterised (such as zebrafish pigmentation patterning, as discussed below).

Given the flexibility of the models presented, there is clearly significant debate over the choice of various terms: for example, the form of signalling interaction functions, the positioning and form of any “volume-filling” type terms (such as inside or outside nonlocal terms), the use of constant diffusion coefficients over non-linear forms, etc. Given the phenomenological nature of the present study, our choices have mainly been driven by a desire for simplicity: typically choosing linear forms and keeping the number of parameters manageable, while retaining sufficient complexity to study relevant questions. The greater insight into the underlying assumptions that is required by specific formulations could be obtained via derivations from an underlying microscopic model; we note a number of related models have been derived in this manner (Buttenschoen et al. 2015; Chauviere et al. 2012; Middleton et al. 2014).

We tested the model via applications to specific systems: an example of a cell invasion process, in a model of contact-induced dispersal of neural crest cells; and an example of pattern formation, for the sorting of zebrafish pigment cells into stripes. With respect to the former, we determined that contact-induced repulsion accelerates neural crest dispersal and hence may be important for migration to be achieved within the correct developmental timescales. Our results suggest that both interaction range and strength will be significant, such that longer interaction ranges or stronger repulsion will enhance the rate of invasion. Mathematically, determining the wave speed dependence on these parameters is of clear interest: our numerics imply dependence on the product, $\mu \xi$. The standard approach for calculating wave speeds—linearising ahead of the wave—does not work here: the linearised form of Eq. (3) is identical to that of Fisher’s equation, such that the interaction terms disappear entirely. Hence, the wave speed depends on nonlinear interactions behind the wavefront: intuitively this makes sense, since the contact-based repulsion requires other cells to impact on movement. A mathematical evaluation, however, remains an open problem. A natural extension of the modelling here would be to apply the ideas to specific examples of neural crest dispersal, such as dispersal of pigment cells, while also taking into account other potentially crucial aspects (e.g. embryonic growth). Also, while the focus here has been neural crest invasion, there are other natural applications where similar mechanisms could apply, such as cancer or ecological invasion processes.

In the context of zebrafish pigmentation patterning, we showed how the model could be used to test biological hypotheses for pattern formation: here, whether the run/chase interactions observed between melanophores and xanthophores in vitro (Yamanaka and Kondo 2014) are capable of either generating or maintaining a striped pattern. The fact that our model suggests that this is not the case highlights the importance of applying theoretical rigour to biological hypotheses.

Incorporating a homotypic attraction between xanthophores allowed a zebrafish-type pattern to be “recovered”, yet it is highly debatable whether this occurs in practice: we know of no evidence that would support such a mechanism. A more likely solution would be to examine other potential interactions, such as interactions affecting cell division, survival or differentiation, or by incorporating the impact of iridophore cells. In fact, recent evidence suggests that iridophores play a major (possibly leading) role in the patterning process (Patterson and Parichy 2013; Frohnhöfer et al. 2013; Singh et al. 2014): therefore, a clear area for future modelling would be to extend the framework to incorporate iridophores and their interactions.

Nonlocal models have been used to study spatiotemporal population dynamics since the 1970s (Diekmann 1978; Mollison 1977), but the last few years have seen a huge increase in research on pattern formation in such models. Some of this work concerns the differential adhesion hypothesis, which is the direct antecedent of this paper. Another active research area concerns spatiotemporal patterns in oscillatory systems with nonlocal terms (Merchant and Nagata 2011; Nagata and Merchant 2014; Sherratt 2014). But by far, the largest part of the recent literature concerns swarming in animal populations. We end this paper with a brief discussion of the relationship between that work and ours. Any meaningful review of research on swarming would require a dedicated paper and we do not attempt it—as a good starting point the reader is referred to Kolokolnikov et al. (2013) and to the special journal issue that this article introduces. The generic model for swarming is a version of (2), with $D=0$, $p(.)\equiv 1$ and $h(.)\equiv 0$ (e.g. Bertozzi et al. 2009). The form of the kernel $\Omega (.)$ clearly plays a central role in model predictions, but our kernels (O2) and (O3) are widely used in applications to swarming; for detailed discussions of predictions from other kernels, see for example Carrillo et al. (2014), Hackett-Jones et al. (2012). Also, although diffusion is omitted in most models for swarming, its inclusion has been considered by some authors (e.g. Hughes and Fellner 2013; Topaz et al. 2006). Therefore, the essential difference between our work on a single population (Sect. 3.1) and that in the swarming literature lies in our inclusion of a packing function $p(.)$ and (in some cases) of population growth $h(.)$. The effects of the latter term were explored in Sect. 3.1 (see Figs. 3, 4). The packing function reflects the fact that we are considering direct contacts, so that availability of physical space is a significant issue. By contrast, the interaction between individuals in swarms changes from attractive to repulsive at a separation distance that is large compared to the length scale of one animal. Of course, the major difference between our work and that on swarming is that much of our study concerns mixtures of two populations, a property fundamental in many areas of biology, especially developmental pattern formation. While we have concentrated on cellular populations, we note that such mixtures may also be relevant in certain types of swarming, such as the predator-prey interactions between different species of schooling fish, such as the jack (Caranx ignobilis) and Hawaiin anchovy (Stolephorus purpureus) (Major 1978). Consequently, the present model may have interesting applications and extensions beyond its current motivation from the behaviours of cellular populations.

Direct cell–cell signalling played out over long distances are increasingly viewed as a crucial property in both developing and formed tissues. The delicate nature of long cell extensions such as filopodia and cytonemes has previously hindered their systematic investigation, yet technological advances are now providing new light on their capacity to direct cellular responses (Sherer and Mothes 2008; Gradilla and Guerrero 2013; Kornberg and Roy 2014). Models that can accommodate such phenomena therefore provide a pathway towards understanding the potential dynamics in such systems.