Vegetation Pattern Formation Due to Interactions Between Water Availability and Toxicity in Plant–Soil Feedback

Abstract

Development of a comprehensive theory of the formation of vegetation patterns is still in progress. A prevailing view is to treat water availability as the main causal factor for the emergence of vegetation patterns. While successful in capturing the occurrence of multiple vegetation patterns in arid and semiarid regions, this hypothesis fails to explain the presence of vegetation patterns in humid environments. We explore the rich structure of a toxicity-mediated model of the vegetation pattern formation. This model consists of three PDEs accounting for a dynamic balance between biomass, water, and toxic compounds. Different (ecologically feasible) regions of the model’s parameter space give rise to stable spatial vegetation patterns in Turing and non-Turing regimes. Strong negative feedback gives rise to dynamic spatial patterns that continuously move in space while retaining their stable topology.

1 Introduction

The occurrence of regular vegetation patterns has been studied by plant ecologists for a long time (Watt 1947; White 1971). Different patterns, such as spots, labyrinths, gaps, and stripes, as well as plant rings and fungal fairy rings (Valentin et al. 1999; Bonanomi et al. 2012, 2013), occur in a variety of natural environments (Boale and Hodge 1964; Wickens and Collier 1971; Leprun 1999; Okayasu and Aizawa 2001). It has been hypothesized that their development is affected by global phenomena like climate change (Rietkerk et al. 2002; Dekker et al. 2009). An extensive analysis of data from 249 geographical locations supports this hypothesis by correlating the observed regular vegetation patterns with climatic variables and soil properties (Deblauwe et al. 2008). Such studies suggest that vegetation patterns in arid and semiarid environments might provide early warning signs of climate shifts and critical transitions (van de Koppel et al. 1997; Rietkerk et al. 1997, 2004; Scheffer et al. 2009).

Development of a comprehensive theory of the formation of vegetation patterns is still in progress. Phenomenological models of Lefever and Lejeune (1997) and Lejeune et al. (1999, 2002) postulate two feedback mechanisms of pattern formation: short-range facilitation of plants under their aerial structures and long-range competition between plants by overlapping root zones. A more prevailing theory identifies water availability as the main causal factor for the emergence of vegetation patterns. It is usually formulated in terms of two coupled partial differential equations (PDEs) governing the dynamics of plant biomass and (surface or soil) water (Klausmeier 1999; Hardenberg et al. 2001; Rietkerk et al. 2002; Meron et al. 2004; Ursino and Contarini 2006; Gilad et al. 2007a, b; Kealy and Wollkind 2012; Nathan et al. 2013). In these and other similar models, vegetation patterns emerge solely due to a feedback between biomass and water (e.g., water infiltration and/or evaporation, plant water uptake, and surface water runoff). Treating water availability as the only controlling mechanism of pattern formation fails to explain the occurrence of vegetation patterns in humid environments (Rietkerk and Koppel 2008, and references therein).

A plant–soil negative feedback (NF) provides an alternative mechanism of the emergence of vegetation patterns. Mechanisms involved in the NF include the presence of soilborne pathogens, the changing composition of soil microbial communities (Kulmatisky et al. 2008), and the accumulation of autotoxic compounds from decomposing plant litter (Mazzoleni et al. 2007; Bonanomi et al. 2011). The experimental evidence reported by Mazzoleni et al. (2014) suggests that litter autotoxicity and plant–soil NF are manifestations of the inhibitory effects of extracellular DNA. The large amount of evidence presented in these studies reinforces the relevance of autotoxicity in the setting of temporal and spatial dynamics of plant systems. The NF was shown to play an important role in plant-species coexistence and biodiversity (Mazzoleni et al. 2010), and in the occurrence of ring patches in clonal plants (Cartení et al. 2012; Bonanomi et al. 2014). The latter study proposed a model consisting of two coupled PDEs, which described the dynamics of biomass and toxicity. Marasco et al. (2013) supplemented this model with a third PDE, which was used to govern the dynamics of soil water. The resulting three-PDE model reproduced the emergence of vegetation patterns even when water is not a limiting resource.

Mathematical analyses of such coupled PDEs often focus on bifurcation points, which give rise to Turing patterns (Turing 1952). The latter occur when the stability of a homogeneous steady state is lost with respect to heterogeneous perturbations. Turing patterns were observed in chemical (Rovinsky and Menzinger 1993; Jensen et al. 1994; Coullet and Riera 2000), physical (Tlidi et al. 1994; Kessler and Werner 2003), and biological (Meinhardt 1995; Murray 1988) systems described by coupled reaction–diffusion equations. A key indicator of the emergence of Turning patterns is a high contrast between diffusion coefficients in the governing PDEs.

Despite its popularity, Turing instability is not the only mechanism leading to pattern formation in systems of reaction–diffusion PDEs. A number of theoretical and numerical studies (Petrovskii et al. 2001; Volpert and Petrovskii 2009; Kéfi et al. 2010; Banerjee and Petrovskii 2011) demonstrated the emergence of vegetation patterns even when the Turning condition is not satisfied. One such regime, called by Petrovskii et al. (2001) a “dynamic stabilization” leads to the formation of a transitory unstable plateau behind a diffusive front and can be thought of as an opposite of the Turing regime.

The analysis presented below explores the rich structure of a toxicity-mediated model of the vegetation pattern formation. This model consists of three PDEs accounting for a dynamic balance between biomass, water, and toxic compounds (negative feedback). Different (ecologically feasible) regions of the model’s parameter space give rise to stable spatial vegetation patterns in Turing and non-Turing regimes. It reduces to the two-PDE model of Kealy and Wollkind (2012) in the absence of toxicity feedback. Strong negative feedback gives rise to dynamic spatial patterns that continuously move in space while retaining their stable topology. In contrast to the modeling predictions of Rietkerk et al. (2002), Meron et al. (2004), and Gilad et al. (2007a, b), the distribution of biomass within the patterns is not symmetric.

Our paper is organized as follows. Section 2 contains a formulation of the toxicity-mediated model of the vegetation pattern formation. In Sect. 3, we present simulation results representative of an ecologically feasible range of the model parameters. A linear stability analysis of the model’s homogenous stationary solutions to both homogeneous and inhomogenous perturbations is presented in Sect. 4. A discussion of ecological implications of the toxicity-mediated model is presented in Sect. 5.

2 Mathematical Model

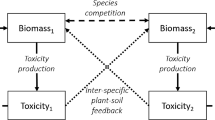
Following Cartení et al. (2012) and Marasco et al. (2013), we postulate that vegetation patterns emerge as a result of the competition between biomass $B$ (kg/m$^2$), water $W$ (kg/m$^2$), and toxic compounds $T$ (kg/m$^2$). Figure 1 provides a schematic representation of the interactions between these three quantities at any spatial point $\mathbf{x} = (x,y)^\top$ and time $t$: Growth of biomass $B$ is mediated by water availability, its intrinsic mortality, and the toxic compounds; availability of water $W$ is affected by precipitation, evaporation, and transpiration (plant water uptake); and toxic compounds $T$ are produced by the decomposition of dead plants and removed from the soil by intrinsic degradation and precipitation.

Fig. 1

A soil–plant–atmosphere system accounts for the feedback between plant biomass ($B$), toxic compounds ($T$), and soil water ($W$). The continuous lines represent transfers of matter between the compartments, while the dashed lines represent the influences

These processes are described by a system of coupled PDEs

$$\begin{aligned} \frac{\partial B}{\partial t}&= D_B \nabla ^2 B + f_B(B,W,T), \qquad f_B \equiv c B^2 W - (d+sT)B;\end{aligned}$$

(1a)

$$\begin{aligned} \frac{\partial W}{\partial t}&= D_W \nabla ^2 W + f_W(B,W), \qquad f_W = p - r B^2 W - l W; \end{aligned}$$

(1b)

$$\begin{aligned} \frac{\partial T}{\partial t}&= f_T(B,T), \qquad f_T = q (d + s T) B - (k + w p) T \end{aligned}$$

(1c)

where the real positive constants $D_B$ and $D_W$ represent dispersal and effective diffusion coefficients of biomass and water, respectively. Their values, as well as those of model parameters $c > 0$, $d > 0$, $p > 0$, $q > 0$, $r > 0$, $l > 0$, $s \ge 0$, $w \ge 0$ and $k \ge 0$, are either chosen in accordance with Klausmeier (1999) and Cartení et al. (2012) or selected from within an order-of-magnitude feasibility range. They are summarized in Table 1. Equations (1) are defined on the bounded domain $\varOmega = \{ 0 \le x \le L_x, 0 \le y \le L_y\}$ and are subject to the boundary and initial conditions

$$\begin{aligned} \partial _n B = 0, \qquad \partial _n W = 0, \qquad \partial _n T = 0, \qquad \mathbf{x} \in \partial \varOmega , \qquad t \ge 0 \end{aligned}$$

(2a)

and

$$\begin{aligned} B(\mathbf{x},0) = B_0(\mathbf{x}), \qquad W(\mathbf{x}, 0) = W_0(\mathbf{x}), \qquad T(\mathbf{x},0) = 0, \qquad \mathbf{x} \in \varOmega \end{aligned}$$

(2b)

where $\partial \varOmega$ is the boundary of $\varOmega$; $\partial _n$ is the normal derivative on $\partial \varOmega$; $B_0$ and $W_0$ are initial spatial distributions of biomass and water, respectively.

Table 1 Model parameters and their values

Three-equation model (1) accounts for the negative soil–plant feedback due to plant toxicity that is absent in the two-equation models of Klausmeier (1999) and Kealy and Wollkind (2012). The latter two models attribute the occurrence of vegetation patterns solely to competition between biomass growth and water availability. Setting $s = 0$ in (1) decouples pattern formation from the effects of toxicity and reduces the structure of our model to that introduced by Kealy and Wollkind (2012). It is worthwhile emphasizing that their simulations and analysis were carried out for an infinite domain, while we define our model on bounded domain $\varOmega$.

3 Pattern Formation: Simulation Results

The simulations reported below are performed on a square lattice of $100 \times 100$ elements, with initial biomass $B_ 0 = 0.2$ in $N_0 = 5{,}000$ randomly selected elements (or the total initial biomass $B_0^\mathrm{tot} = 1{,}000$) and $B_ 0 = 0$ in the remaining nodes. The simulation time $t_\mathrm{max} = 274$ years consists of 100,000 time steps $\varDelta t = 0.01$ days. In all simulations, eight of the eleven dimensional model parameters (i.e., two out of the five dimensionless parameters) are assigned the unique values listed in Table 1. The remaining three parameters—decay rate of toxicity ($k$), precipitation rate ($p$), and sensitivity of plants to toxicity ($s$)—define a parameter space, which determines the structure of vegetation patterns. The system of Eq. (5) was solved with forward Euler integrations of the finite-difference equations resulting from discretization of the diffusion operator with reflecting boundary conditions. This numerical scheme is identical to that used by Rietkerk et al. (2002).

Figure 2 shows the spatial distributions of plant biomass $B(\mathrm{x}, t_\mathrm{max})$ predicted with our model for several values of $p$, $k$, and $s$. Plants not affected by toxicity ($s=0$, the first row in Fig. 2) form stable spatial patterns typical of arid and semiarid environments (Rietkerk et al. 2002; Gilad et al. 2007a, b; Kéfi et al. 2010). As precipitation rate $p$ increases, spatial distributions of plant biomass transition from bare soil ($B \equiv 0$ for $p = 0.4$) to homogeneous cover (constant $B$ for $p \ge 1.2$), forming the spot ($p = 0.6$ and $0.8$), gap ($p = 1.0$), and labyrinth ($p = 1.1$) patterns in between.

Fig. 2

Spatial vegetation patterns formed at time $t_\mathrm{max} = 274$ years for several values of precipitation rate $p$ (columns), toxicity decay rate $k$ (rows), and plant sensitivity to toxic compounds $s$. Darker shades of the gray scale maps represent higher values of biomass density $B(\mathbf{x}, t_\mathrm{max})$. In the absence of toxicity feedback ($s=0$, first row), our three-equation model (5) reduces to the two-equation model of Kealy and Wollkind (2012) and reproduces steady state patterns reported for arid and semiarid environments. Weak negative feedback ($s=0.2$ with $k=0.2$, second row) gives rise to the stable patterns that are qualitatively similar to their toxicity-free counterparts. Strong negative feedback ($s=0.2$ with $k=0.01$, third row) leads to the formation of dynamic patterns that continuously evolve in time without reaching a steady state

The toxicity-induced ($s = 0.2$) negative feedback (NF), which is significantly ameliorated by a high toxicity decay rate ($k = 0.2$, the second row in Fig. 2), gives rise to the stable patterns that are qualitatively similar to their toxicity-free counterparts. The toxicity is degraded too fast to affect the fundamental characteristics of pattern formation. Its only visible effect is to shift the emergence of homogeneous cover (constant $B$) to higher values of precipitation ($p = 2.0$).

As the toxicity’s impact becomes more persistent, i.e., its decay rate is reduced to $k =0.01$ (the third row in Fig. 2), the negative feedback leads to the formation of dynamic patterns for precipitation rates $0.6 \le p \le 1.1$. In this regime, the spots ($p = 0.6$ and $0.8$) and labyrinths ($p = 1.0$ and $1.1$) continuously evolve in time, without reaching a steady state (see also the Supplementary Material, SPOT_k=0.01_p=0.6.avi, LABYRINTH_k=0.01_p=1.0.avi and GAP_k=0.01_p=1.1.avi). This dynamic behavior represents the biomass “escaping from the toxicity” that accumulates in the soil patches previously occupied by the vegetation.

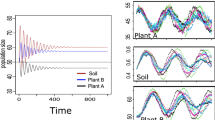
Figure 3 elucidates this phenomenon by exhibiting the temporal evolution of both biomass $B(\mathbf{x}_c, t)$ at the central pixel (black line) and the average biomass of the entire lattice $B_\mathrm{ave}(t)$ (gray line). The lack of ($s = 0$, first row) or weak ($s = 0.2$ with $k=0.2$, second row) toxicity-induced negative feedback results in stable steady state asymptotes $B_\mathrm{st}(\mathbf{x}_c)$ after exhibiting transitory fluctuations at early times. For bare soil (first column) and uniform cover (last column), the biomass values $B_\mathrm{st}(\mathbf{x}_c)$ coincide with the average values $B_\mathrm{ave}(t_\mathrm{max})$. This stable behavior is in sharp contrast to the persistent temporal fluctuations of $B(\mathbf{x}_c, t)$ introduced by strong toxicity-induced negative feedback ($s = 0.2$ with $k=0.01$ and $0.6 \le p \le 1.1$, third row). In this regime, the biomass density $B(\mathbf{x}_c, t)$ oscillates indefinitely, i.e., vegetation patterns continue to evolve without reaching a stable spatial configuration (see also videos in the Supplementary Material).

Fig. 3

Temporal evolution of biomass density $B(\mathbf{x}_c, t)$ at the central pixel of the simulation domain (black line) and of the biomass density $B_\mathrm{ave}(t)$ averaged over the entire lattice (gray line), for several values of precipitation rate $p$ (columns), toxicity decay rate $k$ (rows), and plant sensitivity to toxic compounds $s$. The time $t$ on the horizontal axis varies from 0 to $t_\mathrm{max} = 274$ years, with 100,000 time steps. The lack of ($s = 0$, first row) or weak ($s = 0.2$ with $k=0.2$, second row) toxicity-induced negative feedback results in stable steady state asymptotes after exhibiting transitory fluctuations at early times. Strong toxicity-induced negative feedback ($s = 0.2$ with $k=0.01$ and $0.6 \le p \le 1.1$, third row) gives rise to persistent temporal fluctuations of $B(\mathbf{x}_c, t)$, indicating that vegetation patterns continue to evolve without reaching a stable spatial configuration

Our model predicts asymmetric distributions of biomass within individual spots and stripes (Fig. 4). The biomass peak within each spot is shifted toward the direction of the spot’s movement, escaping the zone with the highest toxicity accumulation. The degree of asymmetry increases as toxicity decay rate $k$ decreases (right panel in Fig. 4). The biomass distribution exhibits a tail on the side opposite to the direction of the spot’s movement. The length of this tail depends on the persistence of toxicity in the soil: Low values of $k$ result in a short biomass tail due to the high toxicity left in the previously occupied soil, while higher $k$ values degrade the soil toxicity and allow a larger portion of biomass to persist in the tail. Such asymmetric biomass distributions are absent in models (e.g., Rietkerk et al. 2002; Meron et al. 2004; Gilad et al. 2007a, b; Kéfi et al. 2010; Meron 2011) that ignore plant toxicity (left panel in Fig. 4).

Fig. 4

Horizontal cross sections of a single biomass spot at different levels of toxicity decay rate $k$ and plant sensitivity to toxic compounds $s$. In the absence of the negative feedback ($s = 0$, left panel), a stable isolated vegetation spot has a symmetric distribution of biomass with a peak in its center. The negative feedback ($s = 0.2$, right panel) modifies the shape of the biomass curve within a continuously moving vegetation spot, for three levels of $k$. The arrow indicates the direction of the moving biomass front. The top-right corner of each panel shows the positioning of the plane view of simulated spots

Transition from stationary to dynamic vegetation patterns depends on the interplay between toxicity decay rate $k$, plant’s sensitivity to toxicity $s$, and precipitation rate $p$ (with other model parameters being fixed to their values in Table 1). Figure 5 shows the $(k,s)$ phase space for several values of precipitation rate $p$. The area above the $p = \mathrm{const}$ curves represents the parameter region that gives rise to dynamic vegetation patterns that continuously evolve in time; the area below the $p = \mathrm{const}$ curves represents the parameter region that gives rise to stationary vegetation patterns. The former region decreases, and the latter region correspondingly increases, with precipitation rate $p$.

Fig. 5

$(k,s)$ phase space for several values of precipitation rate $p$. The area above the $p = \mathrm{const}$ curves represents the parameter region that gives rise to dynamic vegetation patterns, which continuously evolve in time; the area below the $p = \mathrm{const}$ curves represents the parameter region that gives rise to stationary vegetation patterns. The former region decreases, and the latter region correspondingly increases, with precipitation rate $p$. The curves are obtained with numerical simulations in which the $(k, s)$ space is discretized by the $25 \times 41$ elements

Figure 6 shows the effect of the initial total biomass $B_0^\mathrm{tot}$, the precipitation $p$, and the decomposition rate $k$ on the emergence of spatial patterns. We conducted a number of simulations in which a value of $B_0^\mathrm{tot}$ is selected from the interval $[400, 1{,}600]$, and $N_0 = B_0^\mathrm{tot} / B_0$ randomly selected elements are assigned initial biomass $B_0 = 0.2$. The weak negative feedback ($k = 0.2$, Fig. 6a) causes the bare soil to emerge for precipitation rate $p=0.4$ independently of $B_0^\mathrm{tot}$ values, while the more pronounced negative feedback ($k = 0.01$, Fig. 6b) does the same for $p=0.6$ if $B_0^\mathrm{tot} < 800$ or for $p=0.8$ if $B_0^\mathrm{tot} < 600$. Regardless of the value of $B_0^\mathrm{tot}$, both the weak ($k=0.2$) and pronounced ($k=0.01$) negative feedback regimes lead to the formation of uniform vegetation cover for $p \ge 1.4$ and $p=1.2$, respectively. Non-trivial vegetation patterns emerge for all other combinations of the parameters. The toxicity acts to reduce the area of pattern formation.

Fig. 6

Effect of precipitation rate $p$, initial biomass $B_0$, and decomposition rate $k$ on pattern formation. The panels $k=0.2$ (a) and $k=0.01$ (b) show the emerged spatial pattern as a function of precipitation rate ($0.4 \le p \le 2.0$) and of initial value of the biomass $B$. White, gray, and black zones correspond to bare soil, vegetation pattern (i.e., spot, labyrinth, or gaps), and homogeneous vegetation, respectively

In order to further understand the effects of toxicity on biomass movement, we conducted one- and two-dimensional simulations in which biomass initially covers the left half of the simulation domain. Supplementary video One-dimensional.avi shows that shortly after the beginning of the one-dimensional simulations, the biomass aggregates into a single central spot and starts moving toward the half of the domain that was not occupied before since it is clear of toxicity. Moreover, the formation of a toxicity peak right behind the biomass front drives its continuous movement. The two-dimensional biomass dynamics is reflected in its temporal snapshots in Fig. 7. Shortly after the beginning of the simulation, the biomass in the left half of the domain starts to decrease, giving rise to a biomass front invading the empty half of the domain that is clear of toxic compounds (second column in Fig. 7). A toxicity peak is formed right behind the biomass front (third column in Fig. 7); it forces the front to keep traveling in the same direction and impedes the diffusion of biomass to the left. After the first front, the residual biomass in the left part of the domain starts creating new traveling fronts (fourth column in Fig. 7) until the vertical symmetry is broken and the linear fronts become continuously moving spots (fifth column in Fig. 7).

Fig. 7

Temporal evolution of the system starting from homogeneous biomass cover in the left half of the simulation domain. The first row panels show two-dimensional maps of the biomass density. The second row panels represent plots of $B$, $W$, and $T$ along the central horizontal transect of the domain. Parameter values are set to $p=0.8$, $s=0.2$, and $k=0.01$

4 Pattern Formation: Linear Stability Analysis

Systematic analysis of mathematical properties of ecological problems consisting of more than two PDEs is notoriously challenging (Sherratt 2005; Sherratt and Lord 2007; Sherratt 2010). Quasi-steady state approximations, which are often employed to perform stability analyses and to verify the presence of Turing bifurcations, are based on the phenomenological assumption that the dynamics of one state variable is much faster than those of the others (HilleRisLambers et al. 2001; Kéfi et al. 2010). Since this approach presents some drawbacks in the context of vegetation modeling (Flach and Schnell 2006), we do not adopt it here.

The subsequent analysis is facilitated by transforming model (1) into its dimensionless form. Let us introduce dimensionless independent and dependent variables

$$\begin{aligned} \tilde{\mathbf{x}} = \sqrt{\frac{k}{D_W}} \, \mathbf{x}, \qquad \tilde{t} = k t, \qquad \tilde{B} = \frac{k r}{c p} B, \qquad \tilde{W} = \frac{k}{p} W, \qquad \tilde{T} = \frac{k r }{ c p q} T \end{aligned}$$

(3)

and corresponding dimensionless parameters

$$\begin{aligned} \mu = \frac{D_B}{D_W}, \quad \alpha = \frac{d}{k + w p}, \quad \beta = \frac{\alpha ^2 c p s q}{d^2 r}, \quad \gamma = \frac{\alpha ^3 c^2 p^2}{d^3 r}, \quad \lambda = \frac{\alpha l}{d}. \end{aligned}$$

(4)

Then, Eq. (1) take a dimensionless form (unless otherwise noted we omit the tildes)

$$\begin{aligned} \frac{\partial B}{\partial t}&= \mu \nabla ^2 B + f_B(B,W,T), \qquad f_B \equiv \gamma B^2 W - (\alpha + \beta T)B;\end{aligned}$$

(5a)

$$\begin{aligned} \frac{\partial W}{\partial t}&= \nabla ^2 W + f_W(B,W,T), \qquad f_W = 1 - \gamma B^2 W - \lambda W; \end{aligned}$$

(5b)

$$\begin{aligned} \frac{\partial T}{\partial t}&= f_T(B,W,T), \qquad f_T = \alpha B - (1 - \beta B) T. \end{aligned}$$

(5c)

In this dimensionless formulation, $\mu$ is the ratio of diffusion coefficients of biomass ($D_B$) and water ($D_W$); $\alpha$ represents the intrinsic death rate (a balance between a plant’s intrinsic mortality $d$ and the rate of loss of toxicity $k + w p$ due to natural decay, $k$, and dilution by rain, $w p$); $\beta$ is the supplemental death rate caused by plant growth (as quantified by growth rate $c$ and precipitation $p$) and plant mortality (due to toxic compounds released from a fraction of dead biomass, $q$, and its sensibility to toxicity, $s$), both of which are ameliorated by the rate of loss of toxicity $k + w p$ and water uptake $r$; $\gamma$ is the ratio between the parameters controlling plant growth and toxicity loss rate $k + w p$ and water uptake $r$; $\lambda$ is the ratio between the water loss parameter $l$ and toxicity loss rate $k + w p$.

4.1 Linear Stability Under Spatially Homogeneous Perturbations

Toxicity-induced negative feedback ($s > 0$). Biologically feasible homogeneous equilibrium points of model (5) are non-negative solutions of a system of algebraic equations

$$\begin{aligned} \gamma B^2 W - (\alpha + \beta T)B = 0, \quad 1 - \gamma B^2 W - \lambda W = 0, \quad \alpha B - (1 - \beta B) T = 0. \end{aligned}$$

(6)

Within the range of ecologically relevant model parameters, this system admits three equilibrium points,

$$\begin{aligned} (B_1,W_1,T_1)&= (0,\lambda ^{-1},0) \end{aligned}$$

(7)

$$\begin{aligned} (B_2,W_2,T_2)&= \left( \frac{\gamma + \varDelta }{2(\alpha +\beta )\gamma }, \frac{2 (\alpha +\beta ) \beta \lambda + \gamma - \varDelta }{2 \lambda (\beta ^2 \lambda + \gamma )}, \frac{-2 \alpha \beta \lambda + \gamma + \varDelta }{2(\beta ^2 \lambda + \gamma )} \right) \end{aligned}$$

(8)

$$\begin{aligned} (B_3,W_3,T_3)&= \left( \frac{\gamma - \varDelta }{2(\alpha +\beta )\gamma }, \frac{2 (\alpha +\beta ) \beta \lambda + \gamma + \varDelta }{2 \lambda (\beta ^2 \lambda + \gamma )}, \frac{-2 \alpha \beta \lambda + \gamma + \varDelta }{2(\beta ^2 \lambda + \gamma )} \right) \end{aligned}$$

(9)

where $\varDelta \equiv \sqrt{\gamma [ \gamma - 4(\alpha + \beta )\alpha \lambda ]}$ introduces a constraint $\gamma \ge 4(\alpha + \beta )\alpha \lambda$.

A linear stability analysis reveals that “bare-soil” equilibrium point $(B_1,W_1,T_1)$ is stable with respect to homogeneous perturbations; “coexistence” equilibrium points $(B_2,W_2,T_2)$ and $(B_3,W_3,T_3)$ are stable and unstable (see Fig. 8), respectively.

Fig. 8

Bifurcation diagram for homogeneous stationary solutions of (5) showing biomass $B$ versus precipitation rate $p$ in the presence of negative feedback ($s=0.2$) for $k=0.01$ (a) and $k=0.2$ (b). The dotted lines denote stable equilibria of the spatial and non-spatial model. Continuous lines denote unstable equilibria for the spatially homogeneous case. The dashed lines denote equilibria which are asymptotically stable to spatially homogeneous perturbations but unstable to heterogeneous perturbations. The vertical lines $p = p^*$ and $p = p^S$ delineate the region of a Turing bifurcation; the values of $p^*$ and $p^S$ are given by Eq. (15). Two non-trivial equilibria (i.e., uniform vegetation) exist for $p>p*$. Spatial bistability occurs when $p \ge p^S$

Absence of negative feedback ($s = 0$). In this regime, our three-equation model (5) reduces to the two-equation model analyzed by Kealy and Wollkind (2012). Within the range of ecologically relevant model parameters, the resulting system admits three equilibrium points,

$$\begin{aligned} (B_1^0,W_1^0,T_1^0)&= (0,\lambda ^{-1},0) \end{aligned}$$

(10)

$$\begin{aligned} (B_2^0,W_2^0,T_2^0)&= \left( \frac{\gamma + \sqrt{\gamma ^2 - 4 \alpha ^2 \lambda \gamma } }{2 \alpha \gamma }, \frac{\alpha }{\gamma B_2^0}, \alpha B_2^0 \right) \end{aligned}$$

(11)

$$\begin{aligned} (B_3^0,W_3^0,T_3^0)&= \left( \frac{\gamma - \sqrt{\gamma ^2 - 4 \alpha ^2 \lambda \gamma } }{2 \alpha \gamma }, \frac{\alpha }{\gamma B_3^0}, \alpha B_3^0 \right) \end{aligned}$$

(12)

with a parameter constraint $\gamma \ge 4 \alpha ^2 \lambda$. This result is identical to that given by Eqs. (4) and (5) in Kealy and Wollkind (2012). A linear stability analysis suggests that bare-soil equilibrium point $(B_1^0,W_1^0,T_1^0)$ is stable with respect to homogeneous perturbations; “coexistence” equilibrium points $(B_2^0,W_2^0,T_2^0)$ and $(B_3^0,W_3^0,T_3^0)$ are stable and unstable (see Fig. 9 and Kealy and Wollkind (2012)), respectively.

Fig. 9

Bifurcation diagram for homogeneous stationary solutions of (5) showing biomass $B$ versus precipitation rate $p$ in the absence of negative feedback ($s=0$). The dotted lines denote stable equilibria of the spatial and non-spatial model. The continuous lines denote unstable equilibria for the spatially homogeneous case. The dashed lines denote equilibria which are asymptotically stable to spatially homogeneous perturbations but unstable to heterogeneous perturbations. Spatial bistability occurs when $p \ge p^S$

The trivial, bare-soil state of $(0,\lambda ^{-1},0)$ is unconditionally stable in the range of ecologically relevant parameter values, but is of limited interest. Likewise, the states $(B_3,W_3,T_3)$ and $(B_3^0,W_3^0,T_3^0)$ are unstable even to spatially homogeneous perturbations and hence are biologically insignificant (Sherratt et al. 2014). We therefore focus on the remaining equilibrium points, $(B_2,W_2,T_2)$ and $(B_2^0,W_2^0,T_2^0)$, that are stable to homogeneous perturbations. The latter equilibrium point has been shown to give rise to a Turing instability within a certain subspace of the parameter space (Kealy and Wollkind 2012).

4.2 Linear Stability Under Spatially Inhomogeneous Perturbations

Occurrence of Turing-like instabilities and resulting patterns can be deduced by analyzing the response of stable homogeneous equilibrium states to inhomogeneous perturbations (e.g., Kealy and Wollkind 2012; Sherratt et al. 2014 and references therein).

Toxicity-induced negative feedback ($s > 0$). Consider solutions of (5) composed of homogeneous stationary state $(B_2,W_2,T_2)$ and non-uniform infinitesimal perturbations,

$$\begin{aligned} B(\mathbf{x}, t) =&\; B_2 + a_B(0) \mathrm{e}^{i \mathbf{x} \cdot \mathbf{h} + \nu t}, \qquad W(\mathbf{x}, t) = W_2 + a_W(0) \mathrm{e}^{i \mathbf{x} \cdot \mathbf{h} + \nu t}, \nonumber \\ T(\mathbf{x}, t) =&\; T_2 + a_T(0) \mathrm{e}^{i \mathbf{x} \cdot \mathbf{h} + \nu t}. \end{aligned}$$

(13)

Here $i = \sqrt{-1}$, $\mathbf{h} = (h_1,h_2)^\top$ is the perturbation wave vector, $\nu$ is the growth rate, and $a_k(t) = a_k(0) \exp (\nu t)$ ($k = B, W, T$) are perturbation amplitudes. Substituting (13) into (5) and retaining the first-order terms yield an eigenvalue problem

$$\begin{aligned} \mathbf{J}(h) \mathbf{a} = \nu \mathbf{a}, \qquad \mathbf{a}(t) = (a_B, a_W, a_T)^\top \end{aligned}$$

(14a)

where $h = | \mathbf{h} |$ is the perturbation wave number and

$$\begin{aligned} \mathbf{J} = \begin{pmatrix} - \alpha + 2 \gamma B W - \beta T - h^2 \mu &{} \gamma B^2 &{} - \beta B \\ - 2 \gamma B W &{} - h^2 - \gamma B^2 - \lambda &{} 0 \\ \alpha + \beta T &{} 0 &{} \beta B - 1 \end{pmatrix} \end{aligned}$$

(14b)

The solution of this eigenvalue problem gives rise to dispersion relations, which provide information about the stability of homogeneous stationary point $(B_2,W_2,T_2)$ to heterogenous perturbations. Specifically, a Hopf bifurcation is said to occur if $Im[\mu (h)] \ne 0$ and $Re[\mu (h)] = 0$ at $h=0$, while a Turing bifurcation is characterized by $Im[\mu (h)] = 0$ and $Re[\mu (h)] = 0$ at $h \ne 0$. The occurrence of both Hopf and Turing bifurcations was investigated by solving numerically eigenvalue problem (14).

This analysis revealed that for the set of parameters specified in Table 1, state $(B_2,W_2,T_2)$ exhibits a Turing bifurcation (and becomes unstable) if precipitation rate $p$ falls within an interval $p^*(k) < p < p^S$ where

$$\begin{aligned} p^*(k) = {\left\{ \begin{array}{ll} 0.692478 &{} \text {for k=0.01} \\ 0.596614 &{} \text {for k=0.2} \end{array}\right. },\qquad p^S(k) = {\left\{ \begin{array}{ll} 1.14 &{} \text {for k=0.01} \\ 1.13 &{} \text{ for } k=0.2 \end{array}\right. }; \end{aligned}$$

(15)

otherwise, i.e., if $p \ge p^S(k)$, state $(B_2,W_2,T_2)$ does not exhibit a Turing bifurcation and remains asymptotically stable (Fig. 8). In both regimes, Hopf conditions are not satisfied.

Absence of negative feedback ($s = 0$). A linear stability analysis of homogeneous stationary point $(B_2^0,W_2^0,T_2^0)$ revealed a similar behavior: A Turing bifurcation occurs for the precipitation rates in the range $0.59 < p < 1.19$, while $(B_2^0,W_2^0,T_2^0)$ remains stable for $p \ge 1.19$ (Fig. 9). It is worthwhile emphasizing that the Turning patterns identified in the Kealy and Wollkind (2012) analysis of this system correspond to the ratio of diffusion coefficients $\mu \equiv D_B / D_W$ that is an order of magnitude smaller than that used in our study (see Table 1).

5 Discussion

We analyzed a three-equation model in which vegetation patterns emerge as a result of nonlinear dynamical interactions (“competition”) between biomass, available water, and plant toxicity. The model allows for pattern formation in both Turing and non-Turning regimes. In particular, for $\{s=0.2, k=0.2, p=0.6\}$ and $\{s=0.2, k=0.2, p=1.2\}$, stable patterns (spots and gaps, respectively) emerge in non-Turing regime (15), as also observed by Petrovskii et al. (2001). Depending on environmental conditions, i.e., for a certain range of parameter values, our model exhibits a bistability area (Figs. 8, 9) in which two stable and one unstable states coexist for the same values of infiltration rate $p$; this behavior is similar to that observed by Rietkerk et al. (2002) and Hardenberg et al. (2001). Another ecologically feasible region of the parameter space gives rise to Turing and non-Turing regimes in which vegetation patterns continuously evolve in space without ever reaching an equilibrium. This regime represents a strong toxicity-induced negative feedback between the vegetation and ambient soil, which is absent in two-equation models of vegetation patterns (e.g., Klausmeier 1999; Kealy and Wollkind 2012).

Regardless of the parameter subspace, as precipitation rate $p$ decreases the vegetation cover shifts from uniform to gaps, labyrinths, spots, and, finally, bare soil. This behavior is consistent with the simulation results reported in the literature (e.g., Gilad et al. 2007a; Kéfi et al. 2010; Meron et al. 2004; Meron 2011; Rietkerk et al. 2002). The effect of significant toxicity-induced negative feedback is to reduce the parameter subspace in which regular vegetation patterns occur (compare Fig. 6a, b). That is because toxicity enhances plant mortality, so that a larger amount of initial biomass is needed to prevent the formation of bare soil when precipitation rate is low. At higher precipitation rates, toxicity has a destabilizing effect that breaks the pattern formation and leads to homogeneous vegetation covers.

Key differences between the toxicity-induced negative feedback and the classical positive and negative feedback mechanisms (e.g., Klausmeier 1999; Kealy and Wollkind 2012) are worthwhile emphasizing. The latter refer to “short-range facilitation” and “long-range inhibition”: plants improve their local growth condition, e.g., by increasing water availability (a positive feedback); the proliferation of plants reduces resources, e.g., water, available to each plant (a negative feedback). Such dynamics are responsible for the emergence of stable patterns when the positive and negative feedbacks are balanced. By accounting for the local accumulation of toxic compounds in the soil due to biomass decomposition, our model disturbs this equilibrium. While low water availability promotes the aggregation of biomass into stable patterns due to the local facilitation, this aggregation increases local levels of toxicity and exerts a destabilizing force on the patterns.

If the toxic compounds degrade fast (high values of decay rate $k$), the toxicity-induced negative feedback is not sufficient to disrupt the formation of stationary vegetation patterns with reduced biomass productivity (Figs. 3 and 6 with $k=0.2$). If the toxic compounds persist locally in the soil (low values of decay rate $k$), they force the plants to invade the toxin-free regions, leading to the formation of dynamic vegetation spots that move in space without reaching a steady state (SPOT_k=0.01_p=0.6.avi and One-dimensional.avi in Supplementary Material). At higher precipitation rates ($p \ge 0.6$), the vegetation patterns do attain a stationary configuration, but the biomass distribution continuously change within the patches (LABYRINTH_k=0.01_p=1.0.avi and GAP_k=0.01_p=1.1.avi in Supplementary Material).

The toxicity-induced negative feedback also affects the biomass distribution within individual spots and stripes of vegetation patterns (Fig. 4). In the absence of the negative feedback, a stable isolated vegetation spot has a symmetric distribution of biomass with a peak in its center. This is the behavior predicted by a plethora of previous models (e.g., Rietkerk et al. 2002; Meron et al. 2004; Gilad et al. 2007a, b; Kéfi et al. 2010; Meron 2011). The negative feedback modifies the shape of the biomass curve within a continuously moving vegetation spot. The degree of asymmetry increases as toxicity decay rate $k$ decreases. The biomass distribution exhibits a peak shifted in the direction of the spot’s movement and a tail on the side opposite to the opposite direction. The length of this tail depends on the persistence of toxicity in the soil: Low values of $k$ result in a short biomass tail due to the high toxicity left in the previously occupied soil, while higher $k$ values degrade the soil toxicity and allow a larger portion of biomass to persist in the tail.

From an ecological point of view, both the continuous movement and the asymmetrical shape of the patterns are very relevant phenomena, although their timescale (years) makes them difficult to be observed and studied with field experiments. Model parameters used in our simulations resulted in a propagation speed of about 3 m/y which is slightly faster than observations (Valentin et al. 1999; Leprun 1999). Such overestimation can be explained by the fact that the model is set up with constant precipitation rates providing small amounts of water during each time step. This is in contrast with precipitation patterns in arid environments, which are concentrated in brief periods of time with most of the water lost to runoff.

In order to test the occurrence in nature of asymmetrical patterns, analysis of aerial photographs (Fig. 10) was carried out in two sites reported by Deblauwe et al. (2008). Using specific filters, the aerial photographs (Fig. 10, first column) have been edited to highlight zones of high (black), medium (dark gray), and low (light gray) biomass density (Fig. 10, second column), and then are compared to model simulations (Fig. 10, third column). Such analysis clearly shows a good qualitative correspondence between real vegetation spots and the ones predicted by model simulations (Fig. 10, first row). Similarly, labyrinths present a heterogeneous distribution of biomass within the stripes that was also observed in natural patterns (Fig. 10, second row).

Fig. 10

Comparison of model simulation outputs (spots and labyrinths in rows) with aerial photographs of real vegetation patterns and image interpretation. Spots and labyrinths refer to California, 26$^\circ$48$^\prime$ N, 11253$^\prime$ O and Sudan, 11$^\circ$08$^\prime$ N, 27$^\circ$50$^\prime$ E, respectively

In future work, we will further analyze the conditions for the development of dynamic patterns and their occurrence in different biological systems.