1 Introduction

Adolescent idiopathic scoliosis is characterized as a three-dimensional (3D) deformity of the spine and rib cage. To study scoliosis pathomechanisms and treatments, it is important not only to assess the geometrical deformity but also to analyze the stresses in the scoliotic spine, and particularly, the difference of compressive stresses between concave and convex sides of the scoliotic curves because of their mechanobiological importance [26, 29]. The stresses come mainly from three sources: gravity, muscle activity and dynamical effects (absent in the quasi-static approximation). Experimentally, it is difficult to measure them on patients. Meir et al. [16] measured the stress profile in the disks of scoliotic spines but patients were in a lateral decubitus position. The difference of compressive stresses in the disk annulus between concave and convex sides of scoliotic curves was up to 1 MPa.

Computer models have been used to analyze the biomechanics of asymptomatic [1, 15, 18, 24, 25, 31] and scoliotic spines [2, 6, 10, 26, 27, 29]. To compute the stresses in the scoliotic spine, the gravitational forces were generally included in the models and sometimes an assumption about the muscles contribution was made. Gravity forces were frequently applied on the spinal geometry acquired from radiographs in a standing position, so while gravity forces were already acting on the patient. Then, the resulting geometry did not correspond anymore to the real patient’s geometry.

In previous studies, gravitational forces were applied either directly on the vertebral bodies [2, 29] or on the center of gravity of each vertebral trunk slice as measured experimentally in the sagittal plane for non-scoliotic subjects [13, 20, 21]. In the coronal plane, the centers of gravity were hypothetically assumed to be positioned along the scoliotic spine curve [2, 10, 29]. The influence of this simplifying hypothesis was not evaluated.

The objectives of this article are to describe a method improving the representation of gravity in a scoliotic spine FEM and to evaluate spinal forces and compressive stresses.

2 Methods

2.1 Trunk model

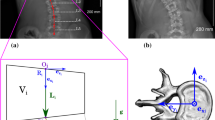
The 3D geometry of the spine, rib cage, and pelvis of each patient was acquired using a multiview radiography reconstruction technique (Fig. 1a) [5]. On three radiographs (lateral, postero-anterior, and postero-anterior with a 20° tilted down incidence), anatomical landmarks were digitized and reconstructed in 3D. An atlas of detailed reconstructed vertebrae, ribs, and pelvis along with a free-form interpolation technique were then used to obtain the final geometry. The accuracy of this reconstruction method is 3.3 ± 3.8 mm [5].

Fig. 1
figure 1

a Acquisition of the internal geometry by a multi-view x-rays reconstruction technique; b Acquisition of the external geometry by surface topography technique; c Superimposition of the two geometries; d Finite element model of the trunk

Full size image

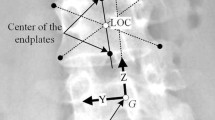
In addition, the external trunk surface of the patient was digitized using a surface topography technique (3-dimensional Capturor, Creaform, Quebec, Canada) (Fig. 1b) [19]. Using fiducial radiopaque markers visible on both the X-rays and the trunk surface, the internal and external geometries were then superimposed using a point-to-point least square algorithm [8] (Fig. 1c). A global coordinate system R g, with origin at the center of the first sacral vertebra S1, was associated with this geometry such that the z-axis was directed vertically upwards, x-axis was postero-anterior, and the y-axis was lateral (oriented from left to right) (Fig. 1c).

The method was applied to three scoliotic patients [thoracic and lumbar Cobb angles: P1 (38°, 23°); P2 (36°, 16°); P3: (20°, 33°)] (Fig. 5).

Based on the patient-specific geometry, a non linear finite element model of each patients’ torso was built using Ansys 11.0 FE package (Ansys Inc, Canonsburg, PA, USA). Main components of the model of the spine, rib cage, and pelvis have been described elsewhere [3] and are here summarized (Fig. 1d). The thoracic and lumbar vertebrae, intervertebral disks, ribs, sternum, and cartilages were represented by 3D elastic beam elements, the zygapophyseal joints by shells and surface-to-surface contact elements, and the vertebral and intercostal ligaments by tension-only spring elements. The abdominal cavity was modeled by equivalent beam elements whose nodes were interpolated from the nodes of the rib cage, vertebrae, and pelvis. The external nodes of the beam model were then projected on the torso surface of the patient, and hexahedral solid elements were created to model the external soft tissues. Geometrical and mechanical nonlinearities were taken into account.

Mechanical properties of all the components of the model were taken from experimental and published data [3]. They are summarized in Table 1. Materials were modeled as linear elastic. A second version of the model was created with softer spine stiffness (rigidity of the intervertebral disks divided by 2) to cover a range of possible stiffnesses of the spine [22].

Table 1 Mechanical properties of the main components of the model
Full size table

Finally, 17 nodes representing the centers of gravity of each trunk slice corresponding to a vertebral level were created. The center of gravity of the head and neck was associated to the center of gravity of the T1 level, and the center of gravity of upper limbs was associated to the centers of gravity of T3, T4, and T5 levels [7]. Non-deformable beam elements connected these nodes to their relative vertebra to transmit gravity forces to the spine. Their position in the sagittal plane was derived from the literature (Fig. 2) [13, 20, 21]. In the coronal plane, their position was parameterized as follow:

$$ Y_{i}^{\text{cog}} = \alpha \times Y_{i}^{\text{vc}} $$
(1)

where Y cog i  = coordinate on the y-axis (coronal plane) of the center of gravity node for each vertebral level i (i = 1..17), Y vc i  = coordinate on the y-axis of each vertebral center (vc), α = adjustable parameter. Three values of α were tested: α = 0.5, 1, or 1.5 (Fig. 3) (α = 1: original position, α = 0.5: 50% closer to the sagittal plane, α = 1.5: 50% farther from the sagittal plane).

Fig. 2
figure 2

Schematic representation of the spine and of the trunk slices gravity centers in the sagittal plane showing the different steps of the simulation process (a Initial Geometry; b Application of anti-gravitational forces; c Zero-gravity geometry; d Application of gravitational forces; e Final geometry)

Full size image
Fig. 3
figure 3

Different positions of the centers of gravity of each trunk slice in the coronal plane (Patient P2)

Full size image

2.2 Simulation process

The magnitude of the gravitational forces F g i  = m i ·g (i: vertebral level, varies from 1 (T1) to 17 (L5), m i : mass of the trunk slice corresponding to the vertebral level i, g: gravity field of 9.8 m s−2) applied on the centers of gravity of the trunk was issued from the literature [13, 20, 21] and was adapted to the patient’s specific weight (Table 2).

Table 2 Percentage of total body weight applied to the centers of gravity at the different levels
Full size table

Boundary conditions were applied on the model: the pelvis was fixed in space and the displacement of the first thoracic vertebra was blocked only in the transverse plane, allowing vertical translation. The simulation process was then divided into two steps: (i) Inverted gravitational forces F −g i  = m i ·(−g) (i = 1..17) were applied vertically upwards on the patient’s geometry acquired from X-rays (Fig. 2b) and the model was solved. At the end of this step, the geometry was updated and stresses present in the model were reset to zero (‘zero-gravity’ state of the patient, Fig. 2c); (ii) Gravitational forces F g i  = m i ·g (i = 1..17) were applied vertically downward on the zero-gravity geometry (Fig. 2d). The resulting computed geometry (Fig. 2e) did not correspond exactly to the geometry of the patient reconstructed from the radiographs (Fig. 4; Table 3). An optimization process was therefore used to find the upward forces to apply at step 1 to obtain the appropriate zero-gravity geometry. The upward forces were divided into two components (Fig. 2b): the vertical ascending forces F −g i  = A i  × m i  × ( −g) (i = 1..17, A i = adjustable parameter) and transverse forces \( {\text{Ft}}_{{y_{i} }} \) and \( {\text{Ft}}_{{x_{i} }} \) (i = 3, 6, 9, 12, 15) applied, respectively, in the y and x directions (global reference system R g) on the vertebral bodies T3, T6, T9, T12, and L3. Transverse forces were applied to only five vertebrae because, after a trial and error process, this method proved to be a good compromise between computational cost and optimization efficiency. Initially, A i (i = 1..17) was fixed to 1 and transverse forces were null.

Fig. 4
figure 4

Coronal and lateral views of the spine shape of the three patients in the initial geometry (filled diamond), in the zero-gravity geometry before (times symbol) and after the optimization process (filled square), in the final geometry before (asterisk) and after (filled triangle) the optimization process (α = 1, flexible spine model)

Full size image
Table 3 Objective function and maximal difference between the position of the vertebra centers before and after the optimization process
Full size table

The goal of the optimization process was to find the optimization variables A i , \( {\text{Ft}}_{{y_{i} }} \) and \( {\text{Ft}}_{{x_{i} }} \) that minimize the objective function Fctobj:

$$ {\text{Fct}}_{\text{obj}} = \sum\limits_{i = 1}^{17} {(\left| {X_{\text{f}} - X_{i} } \right| + } \left| {Y_{\text{f}} - Y_{i} } \right| + \left| {Z_{\text{f}} - Z_{i} } \right|) $$
(2)

where X i , Y i , Z i are the positions in Rg of the vertebral body centers acquired from radiographs and X f, Y f, Z f are the positions of the vertebral body centers in the simulated model including the gravitational forces. A gradient descent algorithm was used to solve the optimization problem. The optimization variables were not constrained. A difference smaller than 1% of the objective function between 2 iterations was used as the convergence criterion.

After the appropriate zero-gravity geometry was found, compressive stresses, forces, and moments acting on the vertebral endplates were computed in a local coordinate system R local for each vertebra. The origin of R local was located at the center of the vertebral body center. The z-axis was in the direction of the line joining the centers of the vertebral endplate centers. The x-axis was the projection of the global x-axis on the plane perpendicular to the z-axis. The y-axis was perpendicular to the x and z-axes.

3 Results

Before the optimization process, the computed objective function Fctobj ranged between 106 and 340 mm for the three cases and the maximal difference between the 3D positions of the vertebral centers acquired from radiographs and computed positions after inclusion of gravity on the model was up to 24 mm (mean: 8.0 mm) (Table 3; Fig. 4). After optimization, the objective function was inferior to 33 mm and the maximal difference between the real and simulated positions of the vertebral centers was inferior to 3 mm (mean: 1.3 mm) (Table 3).

After the optimization process, the vertical ascending forces F −g i  = A i ·m i ·(−g) were superior to the initial antigravitationnal forces F −g i  = m i ·(−g). The parameters A i ranged between 1 and 1.11 (mean: 1.07). Transverse forces \( {\text{Ft}}_{{y_{i} }} \) and \( {\text{Ft}}_{{x_{i} }} \) ranged between −15.6 and 9.3 N.

Between the geometry acquired from X-rays and the computed zero-gravity geometry obtained after optimization, the mean reduction of the thoracic and lumbar Cobb angles was, respectively, 33% (21–50%) and 36% (27–50%) and the mean reduction of the kyphosis and lordosis was, respectively, 71% (45–92%) and 21% (14–26%) (Table 4). The spine length increase was on average 27 mm for the flexible spine models (22–33 mm) and 18 mm (14–24 mm) for the stiff spine models.

Table 4 Indices of the initial, zero-gravity, and final geometries after optimization (α = 1) (all values in degrees)
Full size table

After introduction of gravitational forces, the loading of the vertebrae was a superimposition of pure compressive forces (quantified by local forces F z ) and of bending, flexion, and torsional moments (Table 5). Bending and flexion moments M x and M y quantify, respectively, the asymmetrical compressive loading of vertebrae in the coronal and sagittal planes. In the patients’ spines, M x was maximal at the level of the scoliotic curve apices (Table 5; Figs. 5, 6). Variation of M x was greater for the stiff spine models than for flexible spine models (Fig. 6). The position of the gravity centers in the coronal plane had an influence on M x : at the scoliotic curves apices, M x decreased when parameter α increased (Fig. 5). For instance, for the thoracic apex of patient P2 (stiff spine model), M x decreased of 30% when α increased from 0.5 to 1.5. The position of the gravity centers in the coronal plane had no significant influence on the other forces and moments acting on the vertebrae.

Table 5 Forces (N) and Moments (N mm) acting on the vertebral endplates for the patient P1
Full size table
Fig. 5
figure 5

Influence of the positions of the trunk slices gravity centers on the moment M x exerted on the vertebral endplates (open triangle: α = 1.5, open diamond: α = 1, open square: α = 0.5) (stiff spine model)

Full size image
Fig. 6
figure 6

Influence of the spine model stiffness on the moment M x exerted on the vertebral endplates (open square: flexible spine model, open circle: stiff spine model)

Full size image

Compressive stresses present in the stiff spine model of P2 (α = 1) after the application of gravity are shown in Fig. 7. Figure 8 gives the mean compressive stresses on the whole vertebral endplates and on their right and left sides (α = 1, stiff spine model). In these figures, a negative stress corresponds to a compression state while a positive stress corresponds to a tension state. The mean compressive stress in the spine was about 0.2 MPa (Fig. 8). The stresses were slightly higher for the stiff spine than for the flexible spine models, but the distribution was the same for the two cases. There was an asymmetry of the stress distribution relatively to the sagittal plane due to the scoliotic deformities. The compression was greater in the concavity of the thoracic and lumbar curves than in their convexity. At the levels of the apices of the scoliotic curves, the difference between the mean compressive stresses on the right and left sides of the vertebral endplates was in the range of 0.1 and 0.2 MPa. Maximal differences of compressive stresses of 1 MPa occured at these levels (Fig. 7).

Fig. 7
figure 7

Compressive stresses in the spine of P2 (α = 1, stiff spine model)

Full size image
Fig. 8
figure 8

Compressive stresses on the vertebral endplates (open diamond: global mean stress, open square: mean stress on the left side, open triangle: mean stress on the right side) (α = 1, stiff spine model)

Full size image

4 Discussion

This study shows that applying gravity on a trunk model is not trivial. Simply applying the gravity forces vertically upward is not a satisfactory way of finding the zero-gravity geometry. It is partially due to the non-linearity induced by the stress-stiffening effects. The suppression of the stresses associated to the vertical ascending forces used to compute the zero-gravity geometry introduces an asymmetry in the simulation process because it modifies the stiffness of the spine structure. It explains why the simulated geometry including gravitational forces is different from the initial geometry acquired from the X-rays when the gravity forces are applied vertically upward to find the zero-gravity geometry. This phenomenon was numerically verified on a simpler equivalent beam model subjected to a bending force. In this framework, the horizontal forces at each anatomical level added during the first step of the simulation process should be interpreted as ‘abstract forces’ that allow counteracting the non-linearity induced by the stress-stiffening effect.

An optimization process, requiring 5 iterations on average, was therefore necessary. The maximal difference between the geometries acquired from the X-rays and the simulated geometry including gravity forces was under the precision of the 3D reconstruction technique (3.3 mm [5]) after the optimization process. In order to verify the gradient descent algorithm used in the optimization process lead to a global optimum, different initial design points were tested and it did not modify the optimum found. In future studies, other alternatives to find the zero-gravity geometry could be investigated. For instance the abstract transverse forces could be replaced by different design variables in the optimization process.

The computed zero-gravity geometry is difficult to fully validate because of the unavailability of such data for scoliotic patients. The passage from the standing to supine or prone positions could be used as a first approximation of this state for the coronal curves as the vertical descending gravity forces are suppressed and applied in the sagittal plane. The reaction forces with the horizontal cushions could however have an impact on the kyphosis and lordosis. The reduction of the scoliotic curves (mean: 34.5% (21–50%)) and lengthening of the spine in the zero-gravity geometry (mean: 22.5 mm = 1.4% total body height, min: 14 mm, max: 33 mm) found in this study are similar to experimental data that compared the standing to supine spine geometry [4, 11, 12, 28].

Internal forces, moments, and stresses computed in the spine (Table 5; Figs. 6, 7, and 8) showed that relatively important moments resulting from an asymmetrical compressive loading appear in the spine when it supports pure vertical gravity forces. This phenomenon was described in previous studies [18, 24]. In a normal spine, these moments are only present in the sagittal plane (M x is null). In the scoliotic spine, gravitational forces induce also bending moments in the coronal planes (Table 5; Figs. 6, 7, and 8). The pattern of the asymmetrical compressive loading of the vertebrae in the coronal plane corresponded to what is generally assumed but was seldom quantified [23, 26, 29]. The compression was greater in the concavity of the scoliotic curves than in their convexity, especially at the scoliotic curve apices. According to the Hueter-Volkmann principle this would induce a growth modulation response aggravating the scoliotic deformities in pediatric cases [26, 29]. The difference of the mean compressive stresses between the concave and convex sides of the scoliotic curves ranged between 0.1 and 0.2 MPa, which is similar to the results of Stokes [26] and Driscoll [6].

Several limits of the model should be taken into account. Vertebrae and disks were represented as homogeneous linear elastic beam elements. This simplification of the disk model did not allow fully representing the distinction between the nucleus and the annulus. The effect of the asymmetrical loading on the disk cell metabolism, the water loss, and the subsequent change of material constants of the disk across the scoliotic curve and over time were not modeled, which obviously could have an impact on the results.

Stresses computed were purely due to gravity. The global muscles contribution to the spinal loading was indirectly and schematically considered with the applied boundary conditions at the spine extremities to maintain spine stability. These constraints could be interpreted as muscular effects. However, they introduced small reaction forces in the transverse plane (<25 N) suggesting that here the model was quite equilibrated and that, in the considered standing positions, the muscle action role is more to stabilize the spine (retroaction loop) to prevent it from buckling rather than to equilibrate the gravitational forces. However, in reality muscles cross shorter segments of the spine and might be involved as shown experimentally [17, 30]. It is also possible, as other authors suggested [9, 14], that in scoliotic patients, local muscular strategies could be adopted to reduce the scoliotic deformities and reduce the asymmetrical loading of the vertebrae, in the same way they tend to reduce sagittal flexion moments in the spine of healthy subjects [18, 24].

As very few data exist about the stress distribution in the scoliotic spine in the standing position, validation is quite difficult. Meir et al. [16] found differences of compressive stresses in the disks of scoliotic patients up to 1 MPa but the subjects were in a lateral decubitus position, and this difference was found difficult to interpret. The decubitus lateral position could have been not fully ‘neutral’ and could have imposed actually a slight bending to the spine that created these asymmetrical stresses. As the lateral bending that could have been imposed was not quantified in the study, it makes the data about the asymmetrical stresses difficult to use for validation purposes. In addition, even for the healthy spine, only hydrostatic pressure in the nucleus of a lumbar disk was measured for a subject in different positions [17, 30] [0.5 MPa in a standing position and between 0.15 and 0.2 MPa was issued from the weight of the patient (gravity)]. The mean compressive stress on the vertebra endplates of 0.2 MPa found here is similar to the experimental values.

5 Conclusion

The primary goal of this study was to develop a method to include the gravitational forces in the FEM of a scoliotic trunk while respecting the geometry of the patient in the standing position. This objective was achieved with a precision inferior to 3 mm, which is satisfactory considering it is the precision of the multi-view X-ray reconstruction technique. The developed method could be integrated in the computer modeling to study scoliosis biomechanics, where the gravitational forces and the spinal loading are of primary importance to the pathomechanisms or treatment of the deformity’s progression.