1 Introduction

Proper patient positioning is an important step in spine surgery and a general practice is to use positioning frames. A majority of the positioning frames are based on the Relton–Hall four post principle [32] which focuses on keeping the abdomen pendulous to reduce blood loss [33]. It has been reported that positioning of the patients legs can have an affect on lumbar lordosis [23, 30, 36]. More recently noted, the scoliotic spinal deformity can decrease significantly due to positioning prior to surgical instrumentation [10].

To capitalize on the reduction in deformation prior to instrumentation, a dynamic positioning frame has been designed, the details of which are presented elsewhere [22]. In summary, base cushions can be adjusted at the start of surgery to adapt to patients of various sizes and also modify kyphosis and lordosis. Positioning of the legs can be adjusted based on supports placed under the thighs. As well, there are corrective cushions that can be applied directly to the patient’s trunk at the prominence of the deformity. This system has been tested on a group of unanaesthetized scoliotic patients [15].

Because it is difficult to test different treatments on the same patient, computer models have been created. These computer models are capable of simulating various scoliosis treatments including bracing [8, 29], instrumentation [2, 13, 23] and thorocoplasty [7, 20]. Optimization techniques were applied to determine patient personalized material properties [14, 23, 31] and brace treatments [17].

The objective of this study was to simulate, with a finite element model of the trunk, the positioning of patients during spinal instrumentation surgery while testing various adjustment parameters in order to recommend optimal positioning prior to, and during spine surgery based on the results of the computer simulations.

2 Methods

A flow chart is provided to summarize the materials and methods used in order to optimize patient positioning and compare that to the position on a standard Relton-Hall (R–H) type frame (Fig. 1).

Fig. 1
figure 1

Flow chart summarizing the materials and methods. First the 3D standing geometry (1) was used to take geometric measures (2) and as input to the simulation on the R–H frame (3). From this simulation 3D geometric measures of the R–H position were obtained (4) and validated [14]. Then 32 different prone positions were simulated (5) and the geometric results (6) were used in an elaborate statistical analysis (7). The statistical analysis determined the statistically significant parameters (8) as well as a simplified model (9). The model was used to estimate the measures for the optimal simulations (10) and suggest the optimal input parameters (11). These optimal parameters were then put back into the finite element model (5) where the 3D geometric measures of the optimal simulations were determined (12) and then compared to the estimated optimal simulations (10)

Full size image

2.1 Patient

The patient used in this study was classified King II [21] or Lenke 2C+ [25]. This patient is representative of one of the most common types of adolescent idiopathic scoliosis curves [24]. Various geometric measures were taken from the three-dimensional (3-D) reconstruction of the patient’s standing calibrated X-rays; lateral, postero-anterior (PA) and tilted PA at 20° [11] (Table 1).

Table 1 Geometric measures
Full size table

2.2 Model

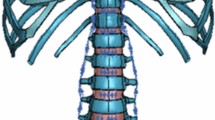
A personalized finite element model was created using ANSYS 8.0 (ANSYS inc., USA) from the 3-D geometry of the above scoliotic patient obtained from a bi-planar reconstruction technique [1, 11]. In summary, this model contains 2,974 elements and 1,440 nodes representing the osseo-ligamentous structures of the pelvis, spine, ribcage, and sternum (Fig. 2). The vertebrae, intervertebral disks, ribs, sternum, pelvis, and cartilages were represented by 3D elastic beams. The respective material properties were taken from experiments that have repeatedly tested the overall response of the functional units by comparing their behavior in the simulation model to that in experimental data [12]. This simplified representation does not permit the analysis of specific details, such as the stress in the disc components etc. Nevertheless, it allows to analyze the global response of the spine. The costo-vertebral, costo-transverse and zygapophyseal joints are modeled in greater detail with shell, multilinear and point-to-surface contact elements. Material properties were obtained from literature and experimental trials from cadaver specimens [12]. These material properties were personalized to the side bending radiographs using an optimization technique [31] and the standard prone position was simulated on a Relton–Hall type frame, as described in another study [14]. This personalized patient finite element model has been previously used in other studies to investigate various scoliosis treatments and biomechanics, particularly brace treatment [1, 17, 28, 29], lateral bending [4], thorocoplasty [6, 7, 19], muscle recruitment [16], growth [38, 39] and patient positioning [14]. When validating the simulation of patients in the prone position the largest difference observed was 4° for the lumbar Cobb angle [14], which is generally considered within standard clinical measurement error.

Fig. 2
figure 2

Postero-anterior (PA) and lateral view of a finite element model of a scoliotic patient. Various parameters were adjusted including pelvic inclination (−15° to ± 15°), chest cushion location (under ribs 6–9 or 3–6), chest cushion height (0–3.5 cm), rib hump force, lateral thoracic force, and lumbar force (all 10–150 N)

Full size image

The reference plane used in the model is that, which is defined as the global (body) coordinate system by Stokes [34]. The model was defined in the prone position using the application of gravity as a distributed load. Specific boundary conditions were applied on the most predominant nodes of the pelvic and the iliac crests and the most anterior points of 3 ribs on each side [14]. To simulate different aspects of positioning six model parameters were tested at different extremities (Figure 2). Pelvic inclination (−15° and +15°), chest cushion location (under ribs 3–6 or under ribs 6–9) and chest cushion height (0 and 3.5 cm) are boundary conditions, which represent adjustments to the base cushions of the positioning system. The flexion and extension of the legs was indirectly taken into account by allowing the inclination of the pelvis. Application of external forces on the rib hump (posterior node of ninth rib on the right hand side), the lateral thorax (lateral node of same rib) and lateral lumbar region (L3 on the left hand side), involve adjustment of external correction cushions which all varied between 10 N and 150 N. The upper limit of 150 N was selected based on a laboratory experiment where a clinician was asked to push on the trunk of a subject as done in the operating room while the applied pressure was measured using a force sensing array (Vista Medical, Winnipeg, Canada).

2.3 Validation of geometric and model parameters

Ten geometric measures were taken from the 3-D geometry of the model using the standing geometry as a base. The reference plane used in the model was defined by Stokes [34] as the global (body) coordinate system and is shown on the model in Fig. 2. Whenever possible, clinical measures outlined in the Spinal Deformity Study Group Radiographic Measurements Manual were used to assess the deformity [27].

Details of the clinically relevant geometric measures are now given. Decompensation was the horizontal distance between T1 and L5 projected onto the AP plane, positive to the left and negative to the right. Balance was the horizontal distance between T1 and L5 projected onto the sagittal plane and was positive to the front and negative to the back. Main thoracic Cobb was the difference of the tilt of the vertebra projected onto the AP plane between T6 and T12. Lumbar Cobb was measured between T12 and L4. These end vertebral levels were determined at the inflection points of the curve [20], corresponding to the most inclined vertebrae when standing and were maintained for all subsequent AP Cobb angle measurements. Apical vertebra translation (AVT) is the horizontal distance of the most laterally deviated vertebra projected onto the AP plane relative to the line joining T1 and L5 (T9 thoracic, L3 lumbar). Apical vertebral axial rotation (AVR) was calculated at T9 based on the Stokes method [35]. Kyphosis was calculated between T2 and T12 and lordosis between L1 and L5 as the difference in tilt of the vertebrae projected onto the sagittal plane. Finally, rib hump was calculated from the average angle of the double tangent lines across ribs 8, 9 and 10.

2.4 Experimental design

Six model parameters were manipulated in a controlled manner as part of a Box–Hunter experimental design with 32 runs. Results for the 32 simulations were entered into Statistica (StatSoft, USA) for an analysis of significant parameters and linear regressions coefficients. Ten equations were obtained and used to make a simplified model representing the ten geometric measurements as a function of the six model parameters. These equations were entered into a cost function (Eq. 1) and optimized in Matlab (MathWorks, USA).

$$ \begin{aligned}{} {\text{Cost}}\;{\text{function}} = & w_{1} {\left( {a_{{\text{s}}} - a_{{\text{m}}} } \right)}^{2} + w_{2} {\left( {b_{{\text{s}}} - b_{{\text{m}}} } \right)}^{2} + w_{3} {\left( {c_{{\text{s}}} - c_{{\text{m}}} } \right)}^{2} \\ & + w_{4} {\left( {d_{{\text{s}}} - d_{{\text{m}}} } \right)}^{2} + w_{5} {\left( {e_{{\text{s}}} - e_{{\text{m}}} } \right)}^{2} \\ & + w_{6} {\left( {f_{{\text{s}}} - f_{{\text{m}}} } \right)}^{2} + w_{7} {\left( {g_{{\text{s}}} - g_{{\text{m}}} } \right)}^{2} \\ & + w_{8} {\left( {h_{{\text{s}}} - h_{{\text{m}}} } \right)}^{2} + w_{9} {\left( {i_{{\text{s}}} - i_{{\text{m}}} } \right)}^{2} + w_{{10}} {\left( {j_{{\text{s}}} - j_{{\text{m}}} } \right)}^{2} \\ \end{aligned} $$
(1)

where

  • wi = weighting

  • m = desired geometric measure

  • a = decompensation

  • b = balance

  • c = main thoracic Cobb

  • d = lumbar Cobb

  • e = thoracic AVT

  • s = simulated geometric measure

  • f = lumbar AVT

  • g = thoracic AVR

  • h = kyphosis

  • i = lordosis

  • j = rib hump

Each geometric measurement was individually optimized by attributing a normalized weighting of 0.9991 while the other nine geometric measurements were given a weighting of 0.0001, for a total of 1.0. Uniform optimization was also performed with equal weighting (0.1). The cost function in Eq. 1 is a simple, equally weighted, multivariate linear regression equation that relates the ten geometric parameters. After every parameter is optimized the cost function calculates the overall correction. The optimization algorithm repeats this procedure until the error difference between the simulated and desired values of the ten geometric parameters is minimized.

It is not only difficult to establish the desired geometric measurements attainable by properly positioning the patient but also the attainable outcome is surgeon specific. Realistically, if a positioning frame could correct 50%, it would be an improvement over existing frames, which are able to correct thoracic and lumbar Cobb angles between 33 and 37% [5, 10]. To account for this an acceptable range of correction was divided into three categories; ideal correction (>50%), realistic correction (20–50%) and unsatisfactory correction (<20%). Kyphosis ranges from 10 to 40° and lordosis ranges from 40° to 60°. “Ideal kyphosis” and “Ideal lordosis” were set to be 25° and 50°, respectively [27]. Decompensation and sagittal balance are clinically very important [3] so the “ideal” was set to zero. Considerable variability is observed in balance, even in normal adolescents, so the desired range has a minimum of ±10 mm and a maximum of ±35 mm [37].

The equations, built from the regression coefficients, are in effect a simplified mathematical model. Using a Box–Hunter experimental design to determine these equations assumes a linear sensitivity. In order to validate this assumption the optimized model parameters were entered into the equations giving estimated geometric measures and re-tested in ANSYS giving optimal simulated geometric measures. Comparing these measures, the robustness of the regression equations and the optimization were tested using the initial simulations (n = 32) as a training set and the optimal simulations (n = 11) as a test set.

3 Results

For the initial prone simulation a detailed 3-D analysis of ten geometric measures is presented in Table 1. The initial prone simulation shows that decompensation moves further to the right (−5 to −10 mm). Balance moves forward, improving from −43 to −23 mm. Main thoracic Cobb and lumbar Cobb correct from 62°–47° to 42°–34°, respectively. Thoracic apical vertebral translation improves from 46 to 32 mm while lumbar apical vertebra translation was quite consistent (8–9 mm). Thoracic apical vertebral rotation remains unchanged at −40°. Kyphosis and lordosis both decrease from 45° to 38° and −37° to −32°, respectively. The rib hump improved from −5.0° to −4.4°.

Looking at the minima and maxima obtained for the 32 simulations one can see the variability and determine if the geometric measures fall within the acceptable range (Table 1). The simulated range for decompensation, balance, thoracic apical vertebral translation, apical vertebral rotation and rib hump all contain the desired ideal. Main thoracic Cobb, lumbar Cobb, lumbar apical vertebral translation, kyphosis and lordosis overlap with the realistic range but ideal correction (>50%) was never obtained in the tested area.

Statistical analysis determined which model parameter has a significant effect on the geometric measures. Table 2 shows only those parameters that have a significant (P < 0.05) effect on the geometric measures and lists their relative importance. Looking at kyphosis, for example, chest cushion location, pelvic inclination, chest cushion height and rib hump force all have a significant effect and act in that order of importance. One can also see how often a model parameter is significant. For example, rib hump force and lateral thoracic force were significant for six and eight of the geometric measures, respectively.

Table 2 Significant model parameters and their importance for each geometric measure
Full size table

From the regression coefficients ten equations representing each geometric measure with respect to the model parameters were determined. There were 22 regression coefficients for each of the ten equations representing the geometric measures for a total of 220. As an example, Eq. 2 shows the main thoracic Cobb as a function of the model parameters. The simplified equation only shows the four most significant model parameters and no intra parametric interactions. In order to minimize the main thoracic Cobb, pelvic inclination, rib hump force and lateral lumbar force should be minimized while lateral thoracic force should be maximized.

$$ {\text{MTC}} = 48.218 + 0.068{\left( {{\text{PI}}} \right)} + 0.024{\left( {{\text{RF}}} \right)} - 0.072{\left( {{\text{TF}}} \right)} + 0.008{\left( {{\text{LF}}} \right)} $$
(2)

where

  • MTC = main thoracic Cobb

  • PI = pelvic inclination

  • RF = rib hump force

  • TF = lateral thoracic force

  • LF = lateral lumbar force

The geometric measures were individually optimized using the cost function (Eq. 1) and the resulting model parameters are shown in the left portion of Table 3. Using the main thoracic Cobb, as an example, the pelvic inclination should be −15°, the chest cushions placed under ribs 6–9 and raised 3.5 cm, rib hump force, lateral thoracic force and lateral lumbar force should be 10, 150 and 10 N, respectively. There is a large range for each model parameter varying between its minimum and its maximum tested range depending on what geometric measure is optimized. For example, the main thoracic force is optimized at 150 N for the main thoracic Cobb and only 10 N for the lumbar apical vertebral translation.

Table 3 Optimized geometric measures and corresponding model parameters
Full size table

Using the equally weighted (0.1) optimization the suggested model parameters along with the resulting geometric measures are shown in the last line of Table 3. The only parameter that attained ideal correction was thoracic apical vertebral translation (−20 mm). Balance (−3 mm), main thoracic Cobb (43°), lumbar Cobb (33°), apical vertebral rotation (−24°) and kyphosis (40°) were all within the desired ideal range. Unfortunately, the decompensation (−13 mm), lumbar AVT (12 mm) and lordosis (−32°) all worsened compared to their initial standing values. As an analysis of overall correction, the cost function was 479 for the initial standing position, 216 for the original prone position and 122 for the equally weighted optimization. To obtain this correction it is recommended that the pelvis is inclined 12°, the chest cushions should be placed under ribs 4–7 and should not be raised. The rib hump force, lateral thoracic force and lateral lumbar force should be 68, 97 and 10 N, respectively.

In order to determine if the regression equations can realistically predict the finite element model output, the calculated absolute difference between the two is shown in Table 4. The largest difference for the training set (n = 32) was found in the balance at 5.4 ± 3.8 mm when looking at displacement and the rib hump 1.9° ± 1.6° when looking at angles. For the test set (n = 11) the largest difference was again found in the balance at 7.8 ± 4.8 mm. For the angles the largest difference was the apical vertebral rotation at 2.8° ± 1.3°.

Table 4 Calculated difference from linear regression predicted geometric measures and the finite-element model simulated geometric measures
Full size table

4 Discussion

The corrections simulated in this study are due only to patient positioning and not the instrumentation. Ideally, if the patient were placed in an optimal position, it is hypothesized that the act of inserting the instrumentation would be facilitated and final correction after instrumentation could be improved, compared to standard positioning frames. Optimal positioning of the patient could yield better post-operative correction and/or make the surgery easier by reducing the necessary applied forces and potentially reducing operative time and blood loss.

In a clinical study the trunk geometry of 14 patients was recorded while lying on a dynamic positioning frame allowing the capability to test various positioning parameters such as chest cushion height, lateral lumbar force and a combined thoracic/rib hump force [15]. The computer simulations of the present study are consistent with the above-mentioned clinical study since the decompensation was sometimes over corrected or negatively affected. The rib hump improved with the application of the rib hump force. However, it is recommended that these forces are applied after the hooks and screws are in place but before rod insertion. This will minimize pressure at the patient cushion interface and the external corrective forces should be removed as soon as the rods are secured to the hooks and screws. And finally, in both studies raising the chest cushions increased kyphosis.

These simulations support clinical studies [36] that show that the lordosis increases when the legs are extended (pelvis inclines towards +15°) and decreases when the legs are flexed (pelvis inclines towards −15°) [26, 30]. The original standing lumbar lordosis was only −37° and further worsened to −32° on prone positioning. The simulations showed that lordosis could be regained to −42° with the pelvic inclination at +15°. However, since there is already loss in lordosis due to prone positioning, it would be difficult to expect to correct a very hypolordotic curve and maintaining the standing lordosis or increasing it by a few degrees would be a realistic correction. When validating the simulation of patients in the prone position the largest difference observed was 4° for the lumbar Cobb angle [14], which is generally considered within standard clinical measurement error.

This is the first study that has simultaneously optimized many different geometric measurements. The most similar study is that of Gignac et al. [17] and Ghista and Viviani [18]; the former have optimized five geometric measures to determine the best type of brace treatment in adolescent idiopathic scoliosis [17] while the latter have optimized segmental spinal stiffness, distribution and magnitude of corrective forces for the surgical instrumentation of the spine. It is interesting to see the effect (sometimes negative) that optimizing a single geometric measure has on the other nine measures. This makes the task of optimizing all ten simultaneously difficult. As shown in Table 2, each of the model parameters had a significant effect on at least 5 of the geometric measures meaning that all of the model parameters need to be considered when positioning the patient. When looking at the overall correction and optimization it is important to evaluate the cost function. The patient positioned with optimized positioning had a cost function of 122 compared to 216 on the standard frame and 479 when standing. In other words, there was an overall correction of 55% when the patient was simulated on the Relton–Hall frame and 75% correction when the patient’s position was optimized.

Linear equations were obtained for each geometric measure and a simplified mathematical model was created and used for the optimization. For this simplified model to be a useful tool, the equations must accurately represent the finite element analysis. A characteristic of the Box–Hunter experimental design is that it tests at extreme limits not taking into account any non linearities in the model. We found this assumption to be valid, as shown in Table 4, since even with the test set, the difference in Cobb angles, kyphosis and lordosis were all under 2° which is below the generally accepted clinical error of 5°. Though the results are not presented here, the option exists to ignore the interactions when performing statistical analysis (Statisica, StatSoft, USA). Less accurate results were obtained since some interactions were significant, and should therefore be taken into account. The accuracy of the simplified model could be improved by increasing the experimental design to three modalities (Box–Benkhen) to account for nonlinearities. However, to obtain the same information regarding the interaction would require 243 simulations and not 32. The average time for the simulations was about 22 min (not including data analysis) using a Pentium III 557 MHz processor with 512 Mega bytes of RAM.

The experimental design was originally used to screen significant parameters (Table 2) and then to optimize cushion placement for desired geometric measures. However, these equations can be used in the reverse sense. Meaning that the simplified model of equations, representing the patient personalized finite element analysis, can be used by the surgeon to test various positioning configurations and almost instantly see the virtual resultant trunk geometry. In addition, using this experimental design method to find the optimal configuration provides an advantage of reduced computational time over using an optimization algorithm that calls the finite element software at each iteration. Dar et al noted that experimental design methods should be utilized more often in biomechanical modeling to provide a better assessment of the model to input parameters [9].

This biomechanical study showed that the patient’s geometry varied depending on cushion placement. Some of the results were obvious and well known, such as flexing the legs, and hence applying anterior rotation to the pelvic, will reduce the lordosis. This model could be used to help better position patients for any number of lumbar surgeries. External corrective forces applied to the apical vertebra and rib hump produced the desired correction but optimal rib hump correction was observed at less then the maximum force. To simultaneously optimize the geometric measures, maximum corrective forces are not recommended. There were some surprising results in that a large number of model parameters had a significant effect on the geometric measures (Table 2). Out of the ten geometric measures eight of them were significantly dependent on three or more of the model parameters. This is significant in that the surgeon may not be aware that changing one parameter can have an unexpected effect on other geometric measures. For example when the main thoracic Cobb was optimized, a correction to 35° was attained, however, other geometric measures worsened such as the decompensation which increased to −11 mm, apical vertebral rotation worsened by 1° and lordosis decreased to −25°. Most interesting was to note the effect that the location of the chest cushions has on the patient’s kyphosis and balance. It was surprising to find that the kyphosis was heavily influenced by the chest cushion location and less, but still significantly, influenced by the chest cushion height. Clinicians performing kyphosis surgery can apply this information, extracted from the model. Balance was also significantly influenced by chest cushion location. Chest cushions are normally placed as high as possible without interfering with the axilla and arms. This practice could be altered depending on the desired balance and kyphosis.

There are always certain limitations to modeling. One limitation of this study is that the muscles are not directly simulated in the model. Indirectly, the muscles are taken into account as the segmental stiffness of the spine was adjusted based on the patients bending X-rays, which incorporate the muscles [14]. The active effect of the muscles was not modeled as they were considered to be very low under anesthesia. The head and neck of the patient was not simulated and no constraints were imposed at T1 so its displacement may be slightly exaggerated. However, allowing T1 to move freely is considered an improvement over other models that have rigidly fixed T1 and, in doing so, the response of balance and decompensation cannot be observed. This model was not directly validated against a particular patient because for ethical reasons it is not permitted to subject scoliotic patients to additional X-rays in order to determine the internal 3-D geometry while subjected to various positioning cushion locations and forces. As discussed, the model results were compared to a previous clinical study examining trunk geometry [15]. Also, the base model of this patient positioned on the standard Relton–Hall type positioning system was validated against standard X-rays taken during surgery, prior to the instrumentation [14].

Another limitation is the simplified representation of the intervertebral discs that were modeled as single functional units using 3D elastic beams. While this representation limits the analysis of the stress patterns in the disc components it nevertheless allows to analyze the global response of the spine.

The results of this study are based on a single patient case, which is an important limitation to the conclusions that can be drawn. Even if the results show clearly the important impact of this patient positioning, it cannot be assumed that it would be the same for all patients. Thus it is clearly a demonstration of the feasibility and pertinence of such an approach and should be further exploited on a larger cohort of scoliotic patients.

5 Conclusion

Modifications to an existing finite element model were done such that six different patient positioning parameters could be simulated and so that ten geometric measures were optimized. Every model parameter had a significant effect on at least five of the geometric measures. Individual optimization of the geometric measures was possible but often resulted in a deterioration of other geometric measures. Simultaneous optimization of all ten geometric measures is difficult but better overall correction was achieved (75%) compared to the standard prone position (55%). The regression equations that were the result of the analysis of the experimental design adequately predicted the geometric measures and can be used instead of the finite element model for future analysis on this patient. This study reports a proof of concept that the positioning of the patient is an important step in the surgical procedure of spinal deformity surgery. Further tests, on a larger number of patients should be done to demonstrate the importance of patient positioning prior to scoliosis surgery.