Introduction

Metal/dielectric integrated structures, which overcome the diffraction limit due to the surface plasmon polaritons (SPPs), can manipulate light in the nanoscale domain and thus receive considerable interest. Metal-dielectric-metal (MDM) and dielectric-metal-dielectric (DMD) structures are the two typical kinds of subwavelength structures. Especially, those MDM structures show great potential in the integrated photonic area [1–3], owing to the advantages of deep subwavelength confinement of light and easily manufacture process, which benefits from the promising fabrication technologies of focused ion beam, lithography, etching, and template methods [4–8]. A variety of plasmonic devices based on MDM waveguides have been proposed and demonstrated, such as filters [9–12], sensors [13–17], couplers [18–20], and so on. As one of those impressive MDM structures, RR, where local SPP resonance will arise, has attracted lots of attention [21–24]. It should be noted that FP resonance is a common and basic effect in these resonators [25, 26]. Through the FP effect, plasmonic filters were firstly achieved by using single side-coupled or end-coupled MDM resonator, and then, electromagnetic induced transparency phenomenon and Fano resonance were observed by using different RR arrangements [27, 28]. However, limited by the FP effect, there will be only one or two channels in a large wavelength range. Specifically, the wavelengths of the resonance modes are fixed by the effective lengths of the resonators and meet the proportion relation of 1 :  1/2 :  1/3 : ⋯ . This character may be not suitable for the development of on-chip multi-channel filtering.

In this letter, a plasmonic tunable multi-channel filter is proposed based on the RR structure. In addition to the conventional modes in the RR, two extra resonance modes are excited by adding a groove on the side-coupled RR. Four resonance modes in a certain wavelength range are obtained. According to the magnetic field distributions of the modes in the resonator, the position of the groove is an important factor to affect the wavelengths of the forbidden bands. When the groove locates at the antinodes of the magnetic fields, red shift will occur for the band-gap wavelengths by increasing the length of groove. Instead, the mode wavelength is immune to the groove when it is placed at the nodes. The performance of the proposed structure is investigated by using the finite difference time domain method (FDTD) method.

Analyses and Results

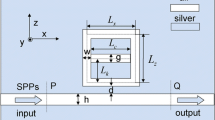
The schematic of the proposed structure is illustrated in Fig. 1, which shows that a side-coupled RR is placed above a MDM bus waveguide. Figure 1a is the cross-section (x-y plane) schematic, and the Fig. 1b is the perspective view which can show more detailed design of the 3D structure. However, 2D FDTD simulations, which have been widely demonstrated to have the comparable accuracy with the 3D simulations but save much more running time, are employed in this paper. Therefore, the parameter setup of the structure is mainly based on Fig. 1a, and the length in z-axis is ignored. A groove locates at the right side of the RR with an angle θ, which is between the groove and y-axis direction. In the following, θ is used to define the position of the groove and is firstly considered as θ  =  90o. It is well known that the perfect ring can perform as an FP resonator, and the resonance modes should satisfy the condition:

$$ \frac{2\pi Re\left({n}_{eff}\right)}{\lambda }{L}_{eff}\kern0.5em +\kern0.5em \varDelta \phi \kern0.5em =\kern0.5em 2m\pi, \kern0.5em m\kern0.5em =\kern0.5em 1,\kern0.5em 2,\kern0.5em 3,\kern0.5em \cdots $$
(1)
Fig. 1
figure 1

Schematic of ring resonator with a groove. (a) x-y plane. (b) Perspective view

Full size image

where D is the width of the waveguide, L eff   =  π(R  +  r) is the effective resonance length, R and r are the outer radius and inner radius, respectively, Δϕ is the phase change in the resonator, m stands for the integer resonance mode, and Re(n eff ) is the real part of effective index n eff , which can be obtained by the dispersion equation of the TM mode in the waveguide [29]: ε d k m   +  ε m k d  tanh (−jk d D / 2)  =  0, where \( {k}_{d,m}\kern0.5em =\kern0.5em \sqrt{\varepsilon_{d,m}{k_0}^2\kern0.5em -\kern0.5em {\beta}^2} \) and ε d ,  m are the transverse propagation constant and permittivity in dielectric and metal, respectively. It should be noted that TE surface plasmon waves do not generally exist in planar metal-dielectric structures, since continuity of Ez forbids charge accumulation at the interface. This physical mechanism and phenomenon have been deeply analyzed by J. A. Dionne [29]. Therefore, we only consider the TM mode in the MIM waveguide and obtain the effective refractive index from the dispersion equation. According to Eq. (1), the transmission-band-gap wavelengths should approximately follow the condition: λ 1 : λ 2  =  1 : 1/2, where λ 1 and λ 2 are the wavelengths of the 1st-order and 2nd-order resonance modes of M 1 and M 2, respectively. After adding a groove to the RR, the resonance condition will be changed. Parts of SPPs will be captured into the groove, and thus, extra non-integer modes will be excited. In this case, the new generated modes, which are called mode M (m + 1/2), will no longer satisfy the phase condition in Eq. (1). Besides, when the groove locates at the antinodes of the magnetic fields of the original integer modes, SPPs will also be captured into the groove, and then the effective resonance length L eff is changed. As such, the wavelengths of the corresponding modes will be linearly affected by the length of the groove. Otherwise, the wavelengths of the resonance modes should be immune to the groove when it is placed at the nodes. Based on this characteristic, one can easily manipulate the wavelengths of the specific modes by changing the position and the length of the groove.

In the following, FDTD method with PML layer is used to investigate the performance of the proposed structure. The source and the grid size are defined as plane wave and 5  ×  5 nm, respectively. The metal and dielectric are air and silver, whose optical constants are obtained from the experiment [30]. The detailed parameters are defined as follows: the widths of the bus MDM waveguide and the groove D  =  50 nm, the coupling distance s  =  15 nm, the inner radius r  =  150 nm, the outer radius R  =  200 nm, and the angle θ  =  90o.

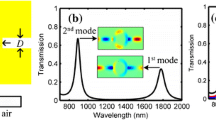
The transmission spectrum of the perfect RR is shown in Fig. 2(a), where two integer resonance modes of M 1 and M 2 arise at the wavelengths of 1544.2 and 779.6 nm, respectively. Through the magnetic field distributions in Fig. 3(a), (b) for M 2 and M 1, it can be clearly seen that even antinodes are distributed along the RR (i.e., four in Fig. 3(a) and two in Fig. 3(b)), respectively. Interestingly, the magnetic field intensities for the two modes share the same nodes at the left or right side of the RR. Therefore, we firstly place the groove on the right side of the groove (i.e., θ  =  90o) to investigate the performance. By setting L = 100, 150, and 200 nm, the transmission spectra are shown in Fig. 2(b)–(d), respectively. In addition to the integer resonance modes of M 1, 2, non-integer modes of M 1.5 and M 2.5 are excited, and thus four transmission band gaps are obtained. Figure 3(c)–(n) shows the magnetic field intensity distributions of M 1, 1.5, 2, 2.5 in detail. Obviously, the groove locates at the nodes of M 1, 2, and thus none of SPPs are distributed in the groove (Fig. 3(d), (f), (h), (j), (l), (n)). That is to say the modes M 1, 2 are immune to the length variation of the groove; therefore, the wavelengths of M 1, 2 are always uniform as 1544.2 and 779.6 nm (see the red-dotted line in Fig. 2(b)–(d)), respectively. On the contrary, the wavelengths of M 1.5, 2.5 can be linearly manipulated by changing L, as illustrated in Fig. 2(b)–(d) with red-dotted line. More details can be found in the magnetic field intensity distributions at the dip wavelengths in Fig. 3(c), (e), (g), (i), (k), (m). In this case, SPPs for M 1.5, 2.5 are captured and distributed in the groove, leading to the transform of the effective resonance length. Therefore, the wavelengths of M 1.5, 2.5 have red shift by increasing L. Generally, for the perfect ring structure, if the radius of the ring is increased, the wavelengths of both integer modes will red shift, but no new modes will be generated. However, there are four modes, including two integer modes and two extra generated non-integer modes, that are obtained by adding a groove.

Fig. 2
figure 2

Transmission spectra: (a) perfect ring, (b)–(c) with θ = 90o

Full size image
Fig. 3
figure 3

Magnetic field intensity distributions of modes M 1, 1.5, 2, 2.5: (a) and (b) for perfect ring, (c)–(f) for L = 100 nm, (g)–(j) for 150 nm, and (k)–(n) for 200 nm, respectively

Full size image

Moreover, though the magnetic field intensity distributions in Fig. 3(a), we can see that the node for M 2 and the antinode for M 1 also have the same region at the top of the RR (i.e., θ  =  0o), where the groove is placed to further investigate the performance. During the FDTD simulations, the parameters are the same as that in Fig. 2. The transmission spectra in Fig. 4 show that four resonance modes of M 1, 1.5, 2, 2.5 are also achieved. Compared to the wavelengths illustrated with red-dotted line, the wavelengths of modes M 1, 1.5, 2.5 are increased by changing the length of the groove, while the one of mode M 2 remains unchanged. The results agree well with the analysis above since the groove stands at the node of M 2 and the antinodes of M 1, 1.5, 2.5. The details of the magnetic field intensity distributions are shown in Fig. 5. It can be clearly seen that there is none of SPP energy in the groove for M 2 (Fig. 5(b), (f), (j)). This is completely different from the results of M 1, 1.5, 2.5 whose magnetic field intensities almost reach maximum in the groove (Fig. 5(a), (c), (d), (e), (g), (h), (i), (k), (l)).

Fig. 4
figure 4

Transmission spectra: (a) perfect ring, (b)–(c) with θ  =  0o

Full size image
Fig. 5
figure 5

Magnetic field intensity distributions of modes M 1, 1.5, 2, 2.5 with θ  =  0o: (a)–(d) for L = 100 nm, (e)–(h) for 150 nm, and (i)–(l): 200 nm, respectively

Full size image

Figure 6 provides the more specific details about the wavelength variations of M 1, 1.5, 2, 2.5 with respect to the length L of the groove. In Fig. 6(a) with θ  =  90o, the linear proportion between the wavelengths of M 1.5, 2.5 and L is further investigated by changing L from 100 to 220 nm with a step of 10 nm, while the ones of M 1, 2 always stays consistent. Besides, in Fig. 6(b) with θ  =  0o, it is also confirmed that the wavelengths of M 1, 1.5, 2.5 increase linearly with L, except for the mode M 2. Therefore, one can flexibly design the wavelengths of the resonance modes by changing the position and the length of the groove.

Fig. 6
figure 6

The wavelength variations of M 1, 1.5, 2, 2.5 with respect to the length of the groove. (a) θ  =  90o, (b) θ  =  0o

Full size image

In the following, the width of the RR and the length of the groove are fixed as 50 and 150 nm, respectively, and the outer radius R is changed to be 210, 220, and 230 nm to find out more characteristics. Obviously, four resonance modes can also be effectively excited due to the influence of the groove, as shown in the transmission spectra in Fig. 7. One can observe that all the wavelengths of the four band gaps have linearly red shift by increasing R. As such, it is concluded that the non-integer modes can be equally excited in different RRs as well, and the wavelengths for all the modes can also be manipulated by the radius. This is another important characteristic to flexibly design the device with preferred performances.

Fig. 7
figure 7

Transmission spectra with different outer radius: (a) θ  =  0o, (b) θ  =  90o

Full size image

Conclusion

Multiple resonance modes have been achieved by using the side-coupled RR system. In addition to the integer resonance modes of those FP resonators, non-integer modes were effectively excited by adding a groove on the RR. The simulation based on FDTD method demonstrated that the position of the groove would significantly affect the wavelengths of the modes. When the groove was placed on the antinodes of the modes, the wavelengths had linearly proportion with the length of groove. Otherwise, the wavelengths were fixed when the groove located on the nodes. Besides, it was investigated that the wavelengths of all the modes could also be manipulated by changing the radius of the RR. One may benefit from this characteristic, since it made the filter design more flexible and the resonance wavelength tunable. This kind of RR filter could find widely applications in the integrated optical circuits and optical system.