1 Introduction

Frost heave, a phenomenon of ground uplift due to soil freezing and swelling, occurs when the ground temperature falls below its freezing point. Frost heave is very common in cold regions, posing a risk to the stability of railways [1, 24], highways [33], pipelines [26], and airports [21] on the frozen ground. The artificial ground freezing method could be adopted as a supporting technique for underground works through water-rich and soft soil layers for its efficiency in preventing water flow and enhancing soil strength [19, 22, 30]. However, potential frost heave may induce deformation to infrastructure above the artificially frozen area. Knowledge of frost susceptibility is essential to estimate the soil behavior under frost heave and to present solution strategies.

When water turns into ice on freezing, its volume expands by about 9%. This water–ice volume expansion induces the in situ frost heave, where water is assumed to freeze in the pores without flowing [13]. The in situ frost heave is minor when the porosity, water saturation, and unfrozen water content are considered. Ice segregation and water migration are other causes of frost heave [15, 37, 43, 44]. During soil freezing, discrete ice lenses form and separate soil particles so that soil expands greatly. Meanwhile, cryogenic suction near the freezing front draws water from the unfrozen zone to continuously feed the growing ice lens. In most cases, ice segregation has the highest contribution to the frost heave. Vapor transfer may play an essential role in frost heave in unsaturated soils [4, 38, 39], where water migration is less significant due to its low hydraulic conductivity.

Quite a few researchers have presented various methods to assess frost susceptibility, theoretically, experimentally, and empirically during the past decades. Many theories have been developed to address the physics of frost heaves, such as the primary heave model [11, 28], secondary heave model [12, 23, 25, 28], segregation potential theory [16, 17], and premelting dynamics [31, 35, 41]. Although interesting, it is not easy for engineers to solve theoretical models that include a group of partial differential equations of water and heat transfer and soil deformation. The frost heave test directly measures frost heave in the laboratory. Such a test is usually conducted on a soil column with unidirectional freezing in one dimension to model the real freezing process of natural ground [3, 27, 36, 45]. However, conducting a frost heave test is complicated and time-consuming, limiting its application to large projects. For practical purposes, engineers have suggested various classification systems for frost susceptibility according to soil properties that could be easily obtained. The classification criterion could be based on the soil particle size [2, 5, 9], plasticity [6, 7, 9, 40], or permeability [32]. Unfortunately, the classification is undoubtedly too empirical to be applied to various soils and environmental conditions.

As mentioned above, water migration is highly associated with frost heave, so the water redistribution in frozen soil may be taken as an indicator of frost susceptibility. Therefore, this study introduced an easy freezing ring test to quantify the water migration during soil freezing. The water redistribution characteristics were analyzed theoretically and compared with the results of direct frost heave tests. Based on the experimental and theoretical results, frost susceptibility was classified by the index of water redistribution. Since the freezing ring test is easier than the traditional frost heave test, it is potentially suitable for large projects that require a great number of tests to be completed.

2 Experimental methods and materials

2.1 Freezing ring test

To prepare soil specimens with moisture content and salt concentration, salt was initially dissolved in distilled water. Subsequently, the solution with the specified concentration was added to dry soil. Herein, sodium chloride (NaCl) is adopted as the salt component owing to its very low eutectic point with soil water (< − 21 °C), ensuring that it stays dissolved even in the frozen soil. In the specimens with salt, the water content is simplified as the ratio of solution mass (including salt and water) to dry soil mass. In the specimens without salt, only water was added to the dry soil. Subsequently, the soil was transferred to a cylindrical mold with a steel ring at the bottom. To shape the sample, the soil in the cylindrical mold was compressed by a steel column into the steel ring, with an inner diameter of 61.8 mm and a height of 20 mm (Fig. 1a). Then, the short cylindrical soil sample and the ring were sandwiched between two pieces of expanded polystyrene (EPS) foam for vertical thermal insulation. After that, the sample with EPS foam was placed in a chest freezer for cooling. During the sample cooling, heat was extracted from the sidewall so that the sample gradually freezes from the outer to the inner zone (Fig. 1b). Cryogenic suction due to freezing drew the water in the inner zone to near the freezing front and turned into ice. As the freezing front moved to the sample center, the total water (ice and water) content increased in the outer zone but decreased in the inner zone. The cooling duration lasted for 6 h to ensure that the sample was completely frozen. Following that, the frozen soil sample was removed from the sample ring. Another cutting ring with a diameter of 50 mm was used to cut the soil sample into two parts: a smaller soil sample with a diameter of 50 mm and a soil layer with an average radius of 28.0 mm (outer diameter of 61.8 mm and inner diameter of 50 mm). Repeating the cutting procedures with different cutting rings whose diameters range from 40 to 10 mm, one can obtain the soil at different radii, ranging from 22.5 to 7.5 mm (Fig. 1c). Consequently, the water content in the cut soil was determined using the oven drying method. In this way, the water content distribution along the radial direction could be obtained.

Fig. 1
figure 1

Procedure of freezing ring test. a Packing soil in the sample ring; b Freezing the soil sample in a chest freezer; c Using cutting rings with diameters from 50 to 10 mm to cut the soil sample into layers with radii ranging from 28.0 mm to 7.5 mm. Φ denotes the diameter of cutting rings in millimeter; R denotes the average radius of the soil layer in millimeter

Full size image

To investigate the temperature field inside the sample, a numerical simulation was conducted. Due to the axisymmetry of the freezing ring test, only half of the geometrical model is needed (Fig. 2a). In the simulation, the difference in the thermal properties between frozen and unfrozen soil is ignored. The phase change is assumed to occur from 0 to − 0.4 °C, and water migration is ignored. The simulated results show that the temperature in the vertical direction varies negligibly in the soil sample (Fig. 2b, c), indicating that the insulating EPS foam makes the heat in the soil only transfer in the radial direction. Although simplified, the simulation provides a schematic of the temperature fields in the freezing sample.

Fig. 2
figure 2

Numerical simulation of temperature distribution in the freezing ring test. a An axisymmetric geometry model for the freezing test. b Simulated isothermal curves in both the soil sample and EPS foam at 0.5 h. c 3-D isothermal surfaces inside the sample at 0.5 h

Full size image

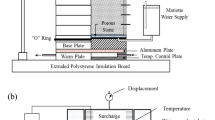
2.2 Frost heave test

The frost heave test was conducted in an axial freezing apparatus (Fig. 3). The soil sample with a diameter of 100 mm and a height of 100 mm was placed in a sample cell which was made of plexiglass. The top and bottom of the sample were touched by two metal plates. Cooling liquid circulated through the metal plates and water baths to control the boundary temperatures for the sample. The sample cell was coated with thermal insulation foam to eliminate the radial heat flux and ensure heat transfers in the axial direction. The top plate was fixed to a loading rod connected to the reaction frame. The bottom place was fixed to another loading rod, which can be driven upward or downward by an actuating motor. The entire testing apparatus was placed in a cooling chamber. During the freezing, the temperature in the cooling chamber was set at 1 °C; the top plate temperature was lower than the soil freezing point; the bottom plate temperature was higher than the soil freezing point. Resistance thermometers spacing 10 mm were inserted into the sample and plates to monitor the temperature. A water source outside the cooling chamber supplies water through a tube connected to the bottom plate. In this way, the soil sample was frozen from top to bottom, and water was drawn through the bottom plate and unfrozen zone to the frozen zone. Due to the frost heave, the soil sample expanded and pushed the bottom plate downward. Each test lasted for about 10 h. After the test, soil slices with a thickness of 10 mm were cut along the sample height. The total water content of these slices was measured using the oven drying method, from which water redistribution could be obtained.

Fig. 3
figure 3

Experimental configuration of frost heave

Full size image

2.3 Testing materials

In this study, three types of soils were selected: a clay obtained from Sanmenxia, Henan Province, China, a silt from Zhengzhou, Henan Province, China, and the China ISO standard sand that pass through 0.5 mm sieve. The particle size distribution curve was determined by sieve analysis for the sand and by the hydrometer method for the silt and clay (Fig. 4). The specific gravity is 2.65, 2.72, and 2.74 for sand, silt, and clay, respectively. The liquid and plastic limits are 36.2 and 19.4, respectively, for clay, and 27.5 and 15.5, respectively, for silt. The boundary temperature, initial water content, and salt concentration are also considered in the tests, as presented in Tables 1 and 2. Besides the tests presented in Table 1, an additional freezing ring test was conducted on the silt sample with a plastic film ring inserted at a radius of 25 mm to stop water migration.

Fig. 4
figure 4

Particle size distribution curves of the tested soils

Full size image
Table 1 Test conditions for freezing ring tests
Full size table
Table 2 Test conditions for frost heave tests
Full size table

3 Experimental results

3.1 Results of freezing ring tests

Figure 5 shows the result of freezing ring tests on silt with an initial water content of 24.9%. The data at the center (r = 0 mm) were excluded because the cut soil in the smallest cutting ring (Φ10 in Fig. 1c) is too small to accurately determine its water content. As the soil with initial water content was fully blended before sample preparation, initial water content is assumed to be distributed uniformly in the entire sample. After freezing, water increased significantly in the outer zone but decreased in the inner zone. The significant water redistribution indicates that water migrates from the inner to the outer zone during freezing. When a plastic film ring was inserted into the soil at r = 25 mm to stop water migration, the water content outside the film ring approximated the initial water content; however, water redistribution still occurred inside the film ring (Fig. 5a). The water migration coincides with the process of heat transfer from the inner to the outer zone. The tests under various boundary temperatures ranging from − 5 °C to − 20 °C show similar water redistribution (Fig. 5b), indicating that the cold boundary temperature is insignificant in the freezing ring tests. Hereinafter, all freezing ring tests were conducted at the boundary temperature of − 20 °C to investigate the impact of soil type, water content, and salt on water migration.

Fig. 5
figure 5

Water redistribution of frozen silt in freezing ring tests with a a plastic film ring inserted at r = 25 mm and b various boundary temperatures. Tc is the boundary temperature (air temperature), and w0 is the initial water content. Each test was conducted twice

Full size image

Figure 6 compares the results of water migration of clay, silt, and sand. Silt has the most significant water redistribution; clay has a weaker water redistribution than silt; sand does not show water redistribution as its water content change is within experimental error. For both clay and silt, a higher initial water content results in higher nonuniformity in the water content. The tendency in water redistribution qualitatively agrees with the frost susceptibility of soils. For a given soil, hydraulic conductivity and water retention capacity are two key properties that control water migration during freezing and consequently frost heave. The hydraulic conductivity controls the water migration in the unfrozen and partially frozen soil. The water retention capacity enables the frozen soil to hold some unfrozen water through which water penetrates into frozen soil. Significant water migration and frost heave only occur if the water pathways are free in both unfrozen and frozen soil. Generally, the soil retention capability negatively correlates with hydraulic conductivity. Sand has high hydraulic conductivity, but the unfrozen water film is too thin to allow water to penetrate into the frozen sand. Clay has a high water retention capability to hold considerable unfrozen water; however, its hydraulic conductivity is very low and resists water migration. Silt has moderate hydraulic conductivity and water retention capacity, inducing the most significant water migration and frost heave. The initial water content affects water migration by changing soil hydraulic conductivity.

Fig. 6
figure 6

Effect of soil type and initial water content on water redistribution. The insert graphs in (a) and (c) zoom in on the water redistribution

Full size image

The effect of salt on water migration was also investigated by adding 0.5 mol/L NaCl solution into the soil (Fig. 7). Although the initial water content is comparable, the nonuniformity in water redistribution is considerably weakened in salt-bearing soils in both clay and silt, indicating that salt resists water migration during freezing. A similar conclusion was made from previous frost heave tests, showing that salt suppresses frost heave [8, 10]. It is well known that salt can depress the soil freezing point by reducing the chemical potential of soil water. An intuitive idea is that the salt-induced freezing point depression reduces cryogenic suction, thus, weakening the water migration and frost heave. In an ideal solution, the freezing point depression coefficient is about 1.86 °C·L/mol. The freezing point of NaCl-bearing soil decreases similar to the ideal dilute solution when the ion molarity is less than 4 mol/L [46]. Thus, the freezing point of the soil containing 0.5 mol/L NaCl (1.0 mol/L ion, including Na+ and Cl−) is 1.86 °C lower than that of salt-free soil. Let us compare the tests on salt-free silt with a boundary temperature of − 5 °C (Fig. 5b) and the NaCl-bearing silt with a boundary temperature of − 20 °C (Fig. 7b). The difference in the boundary temperature is 15 °C, larger than the salt-induced freezing point depression of 1.86 °C. However, water migration in the salt-bearing silt is still much weaker than that in the salt-free silt. The comparison result shows that the salt-induced freezing point depression may not be the true mechanism for restraining water migration and frost heave. The mechanism for the effect of salt on water migration will be discussed in Sect. 4.

Fig. 7
figure 7

Effect of salt on water redistribution

Full size image

3.2 Results of frost heave test

Figure 8 shows the experimental results of frost heave tests. The top temperature gradually decreases to about − 3 °C and − 6 °C for salt-free and salt-bearing soils, respectively. The lower temperature was adopted to compensate for the salt-induced freezing point depression. The bottom temperature was about 3 °C for all tests. Frost heave occurred evidently in the salt-free clay and silt, occurred slightly in the salt-bearing clay, and did not occur in the sand. At the very early stage, the frozen zone may expand, but the unfrozen zone contracts (due to the negative pore water pressure and overburden pressure by the frost heaving force); thus, the frost heave developed quite slowly. Frost heave increases faster after the unfrozen zone is sufficiently compressed. As the temperature tends to be steady, the thermal gradient and freezing rate decrease, decreasing the frost heave rate. Generally, the frost heave rate is higher in silt than in clay, higher in samples with higher initial water content, and higher in samples with lower salt concentration. These experimental results are qualitatively consistent with previous experimental studies [8, 10, 14, 20]. Notably, soil contracted very slightly instead of expanding in the sand test. As the bottom boundary is unfrozen and open to the external water source, the expansion of pore ice squeezes pore water down to outside the sand, limiting the in situ frost heave. Additionally, thermal shrinkage can cause the sand sample to contract when it undergoes cooling.

Fig. 8
figure 8

Evolution of boundary temperature and frost heave

Full size image

The water content along the height of the soil column was measured after the frost heave test (Figs. 9a-c). In salt-free clay, water content increases in the frozen (upper) zone and decreases in the unfrozen (lower) zone. A gradient of w built up in the unfrozen zone, driving water up to feed the growing ice lens (Fig. 9a). The highest water content occurred in the frozen zone near the freezing front, and the lowest water content occurred in the unfrozen zone near the freezing front. In the salt-bearing clay sample, the distribution of water changed slightly relative to the initial water content. In the silt with high initial water content (w0 = 25%), water content increased in the frozen zone and reduced in the unfrozen zone. However, in the silt with low initial water content (w0 = 16%), water content increased in both frozen and unfrozen zones. The increase in water content in the unfrozen silt is caused by the capillary pressure that sucks water from external water sources. Different from the clay situation, water distributes uniformly in the unfrozen zone. The difference in water content distribution between clay and silt is due to the difference between their hydraulic conductivities. Clay has a low hydraulic conductivity so a higher water content gradient is required to drive water to migrate. In contrast, silt has a much higher hydraulic conductivity, so the water content gradient is very low. In the sand, water content increases from top to bottom. Since cryogenic suction is negligible and capillary pressure plays a dominant role in the sand, water was sucked into the unsaturated sand and water content increased from top to bottom to balance the gravitational potential.

Fig. 9
figure 9

Water redistribution of (a–c) and images (d–f) of samples after frost heaving tests. The white bars in (a–c) represent the water content, and the red areas represent the initial water content. The clay sample (d) was upside down when it was photographed

Full size image

Figures 9d–f shows the images of the tested sample. In the clay sample, a network of ice lenses forms in the frozen zone, and the main ice lens occurs near the freezing front (Fig. 9d). In the silt sample, the frozen zone seems to be a whole entity and only one ice lens is visible near the freezing front (Fig. 9e). In the sand sample, no ice lens could be seen (Fig. 9f).

4 Model of radial freezing-induced water redistribution

4.1 Heat and water transfers at freezing front

During radial freezing, the sample center is the symmetric axis, and the freezing front is a contracting circle, as shown in Fig. 10. The inside of the freezing front is unfrozen, while the outside is frozen. Since the sample center is of zero heat flux, the temperature in the unfrozen zone would quickly drop to close to the freezing point. Therefore, shortly after the start of freezing, the latent heat of icing at the freezing front is mainly balanced by the heat flux through the frozen zone, as assumed in the derivation for the Stefan equation (Supporting information in reference [18]):

$$\lambda \frac{{T_{0} - T_{c} }}{{\delta_{f} }} = L{\kern 1pt} \rho {\kern 1pt} {\kern 1pt} \theta_{0} \frac{{{\text{d}}\delta_{f} }}{{{\text{d}}{\kern 1pt} {\kern 1pt} t}}$$
(1)
Fig. 10
figure 10

Schematic of radial freezing

Full size image

where λ is the thermal conductivity; T0 and Tc are the soil freezing point and boundary temperature, respectively; δf is the thickness of the frozen zone (annulus); L is the latent heat released by unit mass of water; ρ is the density of water; θ0 is the initial volumetric water content; t is the time. In Eq. (1), the unfrozen water content and water migration were ignored. Although simplified, it still captures the primary characteristic of energy conservation in radial solidification.

At the initial state, t = 0, and δf = 0. Thus, solving Eq. (1) with the initial condition yields:

$$\delta_{f} = \sqrt {\frac{{2{\kern 1pt} {\kern 1pt} \lambda \left( {T_{0} - T_{c} } \right)t}}{{L{\kern 1pt} {\kern 1pt} \rho {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta_{0} }}}$$
(2)

Eq. (2) is the Stefan equation, which is widely used to estimate the frost depth for ground [18, 34].

The freezing rate, Vf, is defined as the increasing rate of frozen thickness, i.e., Vf = dδf/dt. From Eq. (2), one can easily obtain

$$V_{f} = \frac{{\lambda {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {T_{0} - T_{c} } \right)}}{{\delta_{f} {\kern 1pt} L{\kern 1pt} {\kern 1pt} \rho {\kern 1pt} {\kern 1pt} \theta_{{{\kern 1pt} 0}} }}$$
(3)

According to the Darcy’s law, the volumetric water flux into the frozen zone is given by

$$V_{w} = - \frac{k}{{\rho {\kern 1pt} {\kern 1pt} g}}\nabla p_{w}$$
(4)

where k is the hydraulic conductivity of frozen soil at freezing front; g is the gravitational acceleration; pw is the pore water pressure. The hydraulic conductivity k is highly influenced by the water and ice content. Taylor and Luthin (1978) introduced a resistance factor I to express the soil water diffusivity in the frozen soil. In this study, we assume a similar factor I to relate the hydraulic conductivities between the unfrozen and frozen soil near the freezing front as follows:

$$k = \frac{{k_{0} \left( {{{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }}} \right)^{b} }}{I}$$
(5)

where k0 is the hydraulic conductivity of saturated unfrozen soil; θu is the volumetric water content of unfrozen soil at the freezing front; θs is the saturated water content; b is a parameter that expresses the decay of hydraulic conductivity in unsaturated soil. The resistance factor I express the effect of ice on the depression of hydraulic conductivity in frozen soil.

According to the generalized Clapeyron equation [47], pore water pressure is related to temperature as follows:

$$\eta \left( {T_{m} - T} \right) = \beta p_{i} - p_{w} + cRT$$
(6)

where η (≈ 1.22 MPa/K) and β(≈ 1.09) are constants; Tm(= 273.15 K) is the freezing point of pure ice; pi is the ice pressure; cRT is the osmotic pressure.

Under the condition of zero ice pressure and zero osmotic pressure, Eq. (6) gives

$$\nabla p_{w} = \eta {\kern 1pt} {\kern 1pt} \nabla {\kern 1pt} {\kern 1pt} T = \eta \frac{{T_{c} - T_{0} }}{{\delta_{f} }}$$
(7)

According to Eqs. (4), (5), and (7), the water flux is

$$V_{w} = \frac{{k_{0} \left( {{{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }}} \right)^{b} \eta \left( {T_{0} - T_{c} } \right)}}{{I{\kern 1pt} \rho {\kern 1pt} g{\kern 1pt} {\kern 1pt} \delta_{f} }}$$
(8)

During the radial freezing, the migrated water flux is assumed to freeze in a very narrow zone behind the freezing front. In an infinitesimal duration, Δt, the freezing front contracts, and the volume of frozen zone increases by SVfΔt, where S is the lateral area of the cylinder covered by the freezing front (Fig. 10). The volume of the migrated water is SVwΔt. The migrated water is stored in the expanded frozen zone, increasing water content by D = SVwΔt/SVfΔt = Vw /Vf, at the freezing front. Considering the expression of Vw and Vf ( Eqs. 3 and 8), one could obtain

$$D = \frac{{k_{0} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }}} \right)^{b} \eta L\theta_{0} }}{{I{\kern 1pt} g{\kern 1pt} {\kern 1pt} \lambda }} = D_{0} \left( {{{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }}} \right)^{b}$$
(9a)

where

$$D_{0} = \frac{{k_{0} {\kern 1pt} \eta {\kern 1pt} {\kern 1pt} L{\kern 1pt} {\kern 1pt} \theta_{0} }}{{I{\kern 1pt} g\lambda }}$$
(9b)

Eq. (8) shows that the velocity of water migration increases with the lowing boundary temperature Tc. However, Tc is eliminated in the expression of D (Eq. 9a), indicating that the increase in the water content is independent of the boundary temperature. This is validated by the results of the freezing ring test on silt with various boundary temperatures (Fig. 5b). This is different from the unidirectional freezing test, where the boundary temperature significantly impacts water redistribution and frost heave: the lower the boundary temperature is, the more severe the water migration occurs and frost heave develops [20].

The volumetric water content of the frozen zone at the freezing front, θf, is as follows:

$$\theta_{f} = \theta_{u} + D$$
(10)

4.2 Conservation of water content

Figures 11a–c show the evolution of water content distribution in the frozen and unfrozen zones during the freezing ring test. The origin represents the sample center, and rf denotes the radius of the freezing front. The water in the unfrozen zone is sucked to the freezing front, forming a gradient of water content inside of the freezing front. The characteristic of water content distribution in the unfrozen zone is similar to the results of unidirectional freezing tests on salt-free clays (Fig. 9a). At the early stage of freezing, as the freezing rate is fast, the nonuniformly distributed water content does not have sufficient time to achieve equilibrium, and the gradient of water content is high (Fig. 11a). At a location away from the freezing front, the water content recovers to initial volumetric water content θ0. It means that there is a transitional layer, where water content varies from θu to θ0. The thickness of the transitional layer is denoted by δ. Beyond the transitional layer is the undisturbed zone expressed by r < rf–δ. As freezing continues, the freezing rate slows down and more unfrozen zone is influenced by water migration. Thus, the transitional layer thickens, i.e., δ increases (Fig. 11b). Once the transitional layer extends to the sample center, all unfrozen zone is disturbed and water content decreases (Fig. 11c).

Fig. 11
figure 11

Schematic of water redistribution during soil freezing. (a–c) A gradient of water content characterizes the transitional layer from rf – δ to rf. (a’–c’) The water content in the transitional layer is assumed to be constant

Full size image

For practical purposes, the water distribution in the transitional layer is assumed to be constant (Fig. 11a’–c’). When δ < rf (Fig. 11a’–b’), the water content in the unfrozen zone is as follows:

$$\theta = \left\{ {\begin{array}{*{20}c} {\theta_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r < r_{f} - \delta } \\ \quad {\theta_{u} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{f} - \delta < r \le r_{f} } \\ \end{array} } \right.$$
(11a)

However, when δ ≥ rf (Fig. 11c’), the entire unfrozen zone is disturbed, and the water content is as follows:

$$\theta = \theta_{u} ,\;\;\;\;r < r_{f}$$
(11b)

The thickness of the transitional layer is highly influenced by the freezing rate. During faster freezing, the freezing front moves fast, and water in the inner zone does not have sufficient time to migrate outward. Thus, only a relatively narrow transitional layer is disturbed near the freezing front. Through the first approximation, it is assumed that δ ∝ 1/Vf. From Eq. (3), one can obtain that 1/Vf ∝ δf. Thus, the thickness of the transitional layer can be assumed as

$$\delta = m{\kern 1pt} {\kern 1pt} \delta_{f} = m{\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {R - r_{f} } \right)$$
(12)

where m is the constant of proportionality; R is the radius of the sample; δf = R–rf is the thickness of the frozen zone.

In this study, the water content in the frozen zone refers to the total water content. The volumes of water in the undisturbed zone, transitional layer, and frozen zone are denoted as Qu1, Qu2, and Qf, respectively. Integrating θ in these zones gives

$$Q_{u1} = \theta_{0} \pi (r_{f} - \delta )^{2} l$$
(13a)
$$Q_{u2} = \theta_{u} \pi [r_{f}^{2} - (r_{f} - \delta )^{2} ]{\kern 1pt} {\kern 1pt} l$$
(13b)
$$Q_{f} = \int_{{r_{f} }}^{R} {\theta \cdot 2\pi rl \cdot {\text{d}}r}$$
(13c)

where l is the height of the sample.

Substituting Eq. (12) into Eqs. (13) and taking their differentials yields

$$\frac{{{\text{d}}Q_{u1} }}{\pi l} = \theta_{0} (2A_{1} r_{f} + B_{1} ){\text{d}}r_{f}$$
(14a)
$$\frac{{{\text{d}}Q_{u2} }}{\pi l} = (A_{2} r_{f}^{2} + B_{2} r_{f} + C_{2} ){\text{d}}\theta_{u} + \theta_{u} (2A_{2} r_{f} { + }B_{2} ){\text{d}}r_{f}$$
(14b)
$$\frac{{{\text{d}}Q_{f} }}{\pi l} = - 2r_{f} \theta_{f} {\text{d}}r_{f} = - 2r_{f} [\theta_{u} + D_{0} ({{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }})^{b} ]{\text{d}}r_{f}$$
(14c)

where

$$A_{1} = (1 + m)^{2} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B_{1} = - 2mR(m{ + }1)$$
(15a)
$$A_{2} = - m(m + 2);{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B_{2} = 2mR(m + 1);{\kern 1pt} {\kern 1pt} {\kern 1pt} C_{2} = - m^{2} R^{2}$$
(15b)

In the derivation of Eq. (14c), Eqs. (9a) and (10) are used.

The conservation of water content requires d(Qu1 + Qu2 + Qf) = 0. Thus, uniting Eqs. (14a–c) yields:

$$\frac{{{\text{d}}\theta_{u} }}{{{\text{d}}r_{f} }} = \frac{{2r_{f} [\theta_{u} + D_{0} ({{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }})^{b} ] - \theta_{0} (2A_{1} r_{f} + B_{1} ) - \theta_{u} (2A_{2} r_{f} { + }B_{2} )}}{{A_{2} r_{f}^{2} + B_{2} r_{f} + C_{2} }}$$
(16)

When δ = rf, the transitional layer reaches the center, and the undisturbed zone disappears. In this case, the total volume of water in the unfrozen zone is Qu = πrf2 lθu. Thus, the differential form is

$$\frac{{{\text{d}}Q_{u} }}{\pi l} = r_{f}^{2} {\text{d}}\theta_{u} + 2\theta_{u} r_{f} {\text{d}}{\kern 1pt} r_{f}$$
(17)

The conservation of water content requires d(Qu + Qf) = 0, from which one can obtain

$$\frac{{{\text{d}}\theta_{u} }}{{{\text{d}}r_{f} }} = \frac{{2D_{0} \left( {{{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }}} \right)^{b} }}{{r_{f} }}$$
(18)

Eqs. (16) and (18) can be summarized as follows:

$$\frac{{{\text{d}}\theta_{u} }}{{{\text{d}}r_{f} }} = y\left( {r_{f} ,\theta_{u} } \right)$$
(19a)

where

$$\begin{aligned}&y\left( {r_{f} ,\theta_{u} } \right) \\&= \left\{ {\begin{array}{cc} \frac{{2r_{f} [\theta_{u} + D_{0} ({{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }})^{b} ] - \theta_{0} (2A_{1} r_{f} + B_{1} ) - \theta_{u} (2A_{2} r_{f} { + }B_{2} )}}{{A_{2} r_{f}^{2} + B_{2} r_{f} + C_{2} }},& r_{f} > \delta \\ \frac{{2D_{0} \left( {{{\theta_{u} } \mathord{\left/ {\vphantom {{\theta_{u} } {\theta_{s} }}} \right. \kern-\nulldelimiterspace} {\theta_{s} }}} \right)^{b} }}{{r_{f} }}, &r_{f} \le \delta \\ \end{array} } \right. \end{aligned}$$
(19b)

Eq. (19) implies that the water content tends to negative infinity when rf tends to zero, which is unrealistic. When the water content in the sample center (rf = 0) is too low, the suction becomes extremely high so that it is impossible to attract the water there outward. Therefore, Eq. (19) only applies when the radius does not approach the sample center.

At the initial condition, rf = R, and θu = θ0. However, if rf = R, A2rf2 + A2rf + C2 = 0, and y(rf, θu) would be infinity. To avoid this singularity, a factor ε is introduced to the initial condition:

$$\theta_{u} = \theta_{0} ,{\text{ when }}r_{f} = \varepsilon R$$
(20)

When ε tends to 1, Eq. (20) tends to the real initial condition; however, y(rf, θu) tends to singularity. Thus, a value of slightly less than 1 is reasonable for practical purposes. In this study, ε is set as 0.95.

Eq. (19a) is a nonlinear ordinary differential equation, which can be easily solved using numerical methods. Solving Eq. (19a) with the initial condition Eq. (20), one can obtain the volumetric water content of unfrozen zone at the freezing front θu(rf). Using Eq. (10), we can obtain the volumetric water content of frozen zone at the freezing front θf (rf) = θu(rf) + D. Since the hydraulic conductivity is extremely low in the frozen zone, the water content of frozen zone does not change with time. Thus, the water content at the freezing front θf (rf) gives the water content of the frozen zone at any radius θ (r) when the freezing front is moving (Fig. 11). The gravitational water content and volumetric water content can be converted into each other w(r) = θ(r)ρd /ρ. Consequently, the redistribution of the gravitational water content after freezing is

$$w\left( r \right) = \frac{\rho }{{\rho_{d} }}\left[ {\theta_{u} \left( {r_{f} } \right) + D} \right]$$
(21)

where ρd and ρ are the dry density of soil and water density, respectively.

As mentioned above, when the freezing front tends to the sample center the water content decreases infinitely, which is unrealistic. The water content in the unfrozen zone is hard to migrate if the water content is very low so that the water content in the sample center would not decrease infinitely. In this study, water redistribution was calculated to the least radius of 5 mm.

5 Discussion

5.1 Characteristics of water redistribution

The water redistribution curve for the freezing ring test can be obtained by applying the water redistribution model with parameters presented in Table 3. Figure 12 compares the experimental and modeled water redistribution. Although there is some disagreement, the model captures the main characteristics of water redistribution. In clay samples (Fig. 11a, b), water increases significantly near the boundary. In the intermediate zone, the water content changes slightly. As the freezing propagates to the inner zone, the water content decreases again. As a comparison, in the silt samples (Fig. 11c, d), the water content decreases monotonously from the outer to the inner zone without inflection.

Table 3 Model parameters for radial freezing-induced water redistribution
Full size table
Fig. 12
figure 12

Experimental (points) and modeled (curves) results of water redistribution after radial freezing. In (a) and (c), the points marked by square, circle, and triangle correspond to the curves marked (1), (2), and (3), respectively

Full size image

The effect of salt on the water redistribution curve is modeled by lowering the parameter D0, which describes the abrupt increase in the water content at the freezing front. D0 is mainly determined by the migrated water flux (or water migration velocity) Vw. During freezing, salt can be excluded from the freezing front and accumulates in the unfrozen zone in front of the freezing front, thus, developing a salt concentration gradient in this zone. Due to the salt-induced freezing point depression, a freezing point gradient can also be developed in front of the freezing front: the closer to the freezing front, the lower the freezing point. At the freezing front, soil temperature is equal to the freezing point and the freezing front is in equilibrium. However, when it goes to the unfrozen zone away from the freezing front, both soil temperature and freezing point increase. If freezing point gradient is greater than soil temperature gradient in this unfrozen zone, the soil temperature is lower than the freezing point and the unfrozen zone is supercooled. The phenomenon of soil supercooling induced by salt concentration gradient in unfrozen zone is called constitutional supercooling [29, 42].The constitutional supercooling is an unsteady state, since the soil particles, pore water, and salt, could be engulfed together by the moving freezing front. In this situation, the water migration and ice segregation are highly weakened, thus, reducing D0. Clay has smaller pores than silt; therefore, it is harder for salt to diffuse in clay than in silt. The gradient of salt concentration, the gradient of freezing point, and the constitutional supercooling in clay are greater than in silt. Thus, salt has a more significant impact on the water redistribution in clay than silt (Figs. 11a & c).

The boundary radius is R = 30.9 mm for all samples in the freezing ring test. To model the inner zone surrounded by the plastic film ring at a radius of 25 mm (Fig. 5a), we calculated the water redistribution curve by changing the boundary radius to R = 25 mm (curve 3 in Fig. 12c). Curves (1) and (3) in Fig. 12c were obtained using the same model parameters except for the boundary radius. These two curves show that the water content differs in the outer zone but converges in the inner zone, indicating that the sample size has less impact on the water content in the inner zone. In the test on clay with lower initial water content (Fig. 12b), parameter D0 was reduced from 0.02 to 0.01 due to its higher compactness. The silt sample with lower initial water content has the same soil properties as the sample with higher initial water content; thus, it is modeled with the same D0 (Fig. 12d). As expressed in Eq. (8), the water migration flux is also influenced by the unfrozen water content. Therefore, lower initial water content results in lower water migration and less significant water redistribution.

5.2 Parameter sensitivity

The parameters D0, m, and b represent the water transfer capability, thickness of the transitional layer, and decay of hydraulic conductivity with decreasing water content, respectively. It is helpful to get insight into the water migration characteristics by analyzing the parameter sensitivity. Figure 13 shows the modeled results with variable model parameters D0, m, and b. The higher D0 means higher water transfer capability, resulting in higher nonuniformity of water content (Fig. 13a). The parameter m expresses the expansion rate of the transitional layer at a given freezing rate. It has a significant impact on the shape of the redistribution curve. At a low value of m, the water redistribution curve is relatively flat in the intermediate zone (Fig. 13b). In high-permeability soil, the water migrates easily so that the transitional layer expands fast. In contrast, the transitional layer expands slowly in the low-permeability soil. This coincides with the fact that the relatively flat section occurred in the water redistribution curve of clay samples instead of silt samples (Fig. 12). The parameter b expresses the decay of hydraulic conductivity with desaturation. Figure 13c shows that the variation of b has an insignificant impact on the water redistribution curve in the outer zone. A lower value of b means less decay in the hydraulic conductivity so that water migrates more easily due to cryogenic suction, leading to lower water content in the inner zone.

Fig. 13
figure 13

Sensitivity of water redistribution curve to model parameters. Other parameters used for calculation are ρd = 1.6 g/cm3, w0 = 25%, and saturated water content ws = 25%

Full size image

5.3 Assessing frost susceptibility of soils

Two possible indices can be used to assess frost susceptibility: frost heave amount and frost heave rate. The frost heave amount obtained in laboratory depends on the testing time and usually does not indicate the real frost heave amount in field. Thus, it is not easy to classify frost susceptibility by frost heave amount in a wide range of applications. In contrast, the maximum frost heave rate can easily be determined and is less dependent on the testing time. In this study, we choose the maximum frost heave rate Vh, within 8 h after frost heave initiates, as the index of frost susceptibility. This is similar to the 8-h frost heave rate adopted by ASTM International [3] for assessing frost susceptibility.

The water redistribution curve obtained from the freezing ring test shows the nonuniformity of water content caused by water migration during freezing. Intuitively, the maximum difference in water content between the outermost (r = 28.0) and innermost (r = 7.5) layers, denoted as Δwoi, could be used as the index for water nonuniformity (Fig. 1c). Alternatively, we can choose the increase in water content at the outermost layer relative to the initial water content (denoted as Δwo0) to characterize water migration. To obtain Δwoi, the sample should be cut layer by layer to obtain the innermost layer. In contrast, to obtain Δwo0, the soil needs to be cut only once by the largest cutting ring. Thus, Δwo0 is easier to obtain than Δwoi, and this simplicity may be time-saving in large projects.

Figure 14 shows the variation of water nonuniformity (Δwoi and Δwo0) and maximum frost heave rate (Vh). The qualitative trends are quite similar. Water migration and frost heave are the most severe in silt, lower in clay, and negligible in sand; in both silt and clay, higher initial water content would improve water migration and frost heave, but salt concentration depresses them. Although Δwoi is about twice as much as Δwo0 (Fig. 13a, b), they have almost the same trends. As mentioned before, Δwo0 is easier to measure than Δwoi. Thus, Δwo0 is suggested as the water nonuniformity index to assess frost susceptibility.

Fig. 14
figure 14

Variation of water nonuniformity (a. Δwoi and b. Δwo0) and maximum frost heave rate (c. Vh)

Full size image

The maximum frost heave rate Vh is plotted against Δwo0, as shown in Fig. 15, from which an overall linear relation can be concluded. The correlation between Vh and Δwo0 confirms that the freezing ring test provides an easy way to assess frost susceptibility of soils. The classification of frost susceptibility by the 8-h frost heave rate suggested by ASTM was employed in the classification by Vh in this study. According to the criteria, frost susceptibility is classified into Negligible, Very low, Low, Medium, High, and Very high, depending on Vh (Fig. 16). Additionally, from the relationship between Vh and Δwo0, the classification by Vh can be converted to a classification by Δwo0, shown as the vertical lines in the classification chart. Vh and Δwo0 criteria agree in the light blue zones in the classification chart, showing that the frost susceptibility is High for salt-free silt, Medium for salt-bearing silt, and clay with high initial water content, and Negligible for sand. However, disagreement between Vh and Δwo0 criteria (white zones in the classification chart) occurs in the other clay samples. In the clay with lower initial water content, frost susceptibility is Low according to Vh criteria but Very low according to Δwo0 criteria. In the salt-bearing clay, frost susceptibility is Negligible according to Vh criteria but Very low according to Δwo0 criteria. This disagreement implies the limitation of the freezing ring test in assessing soils that is insensitive to frost heave. This limitation could be overcome by more laboratory tests and field monitoring, from which more sophisticated classification criteria can be developed.

Fig. 15
figure 15

Relationship between maximum frost heave rate and water nonuniformity

Full size image
Fig. 16
figure 16

Classification chart of frost susceptibility. VH, H, M, L, VL, and N denote Very high, High, Medium, Low, Very low, and Negligible, respectively. The data points are the same as those in Fig. 15

Full size image

6 Conclusions

This study conducted a series of freezing ring tests and traditional frost heave tests, considering the effects of soil type, initial water content, and salt concentration. In the freezing ring test, water migration due to cryogenic suction increases the water content in the outer zone but decreases in the inner zone. The water redistribution during freezing ring tests is independent of the boundary temperature. In the unidirectional freezing tests, water migration results in frost heave. Water migration and frost heave are the most significant in silt, lower in clay, and negligible in sand. Higher initial water content would enhance water migration and frost heave, but salt could depress them.

A theoretical model is presented to characterize the water redistribution during freezing ring tests. The model verified that the water redistribution curve is independent of boundary temperature. According to the model, a transitional layer forms in the unfrozen zone, where the water content varies significantly. The transitional layer influences the shape of the water redistribution curve. In clay, the transitional layer is thin due to its low hydraulic water conductivity, causing an inflection on the water redistribution curve. In contrast, the water content varies without inflection in silt. Salt is excluded from the freezing front so that a gradient of salt concentration builds up in the unfrozen zone, inducing the constitutional supercooling and depressing water migration.

Water nonuniformity indices are introduced to express the water migration capability in freezing ring tests. The maximum frost heave rate is adopted to express the frost susceptibility. A good correlation between water nonuniformity and frost heave rate indicates that the freezing ring test is an easy way to assess frost susceptibility of soils. The frost susceptibility can be classified according to the maximum frost heave rate or water nonuniformity. The frost susceptibility is High in salt-free silt, Medium in salt-bearing silt and clay with high initial water content, and Negligible in sand. Disagreement between the classification criterion by water nonuniformity and frost heave rate occurred in the soil with low frost susceptibility.