1 Introduction

Thanks to their low permeability and favourable mechanical properties, claystones are considered as suitable host rocks for deep geological disposal of high-level radioactive waste in Switzerland (Opalinus Clay) and in France (Callovo–Oxfordian claystone—COx). In both countries, extensive researches are carried out in Underground Research Laboratories (URL), for instance the Mont-Terri URL run by the SwissTopo organisation in Switzerland and the Bure laboratory run by Andra, the French Agency for the management of radioactive wastes. To better understand the hydromechanical response in the in-situ tests carried out in these URLs [26] and model the corresponding hydromechanical response using numerical methods [21, 28], it is necessary to further investigate their poroelastic properties to enlarge the existing database about these parameters. Due to their high stiffness and very low permeability (around 10–20 m2), the experimental determination of the poroelastic parameters of claystones is challenging, and literature data are scarce. Poroelastic rock parameters can be determined through drained tests on saturated claystones by using devices with small drainage lengths, like the hollow cylinder device developed by Monfared et al. [36] or small-sized triaxial devices (e.g. dimension of 20 mm in both diameter and height, see Hu et al. [31]). To ensure drained conditions, low enough loading rates have to be applied, while undrained conditions allow faster loading rates [2, 31, 36]. Different testing methods have been developed to measure the permeability of low-permeable geomaterials, like the pulse method [7], the dynamic pressurisation method [39], the transient test [30] or the one-dimensional consolidation test [20, 35]. Following Braun et al. [9], we present in this work the determination of the poroelastic parameters and the intrinsic permeability of the Opalinus Clay through transient experiments, in which fast loading phases are followed by a drainage one.

2 Theoretical framework of poroelasticity and permeability of claystone

2.1 Poroelastic properties under isotropic stress changes

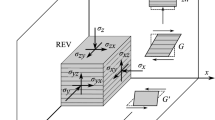
The microstructure of claystones presents apparent bedding planes, such as the COx claystone [16, 17, 34, 44] and the Opalinus Clay [32]. At macro-scale, claystones exhibit a transversely isotropic strain response when submitted to stress changes [3, 19, 45]. The theoretical framework of transversely isotropic poroelasticity has been described, among others, by Cheng [12] and Coussy [14]. According to these authors, the stress–strain relationship can be written in matrix form (Eq. 1), with a coordinate system aligned to the strains ε1 perpendicular to bedding plane and ε2 and ε3 parallel to the bedding plane:

$$\left( {\begin{array}{*{20}l} {{\text{d}}\varepsilon_{1} } \hfill \\ {{\text{d}}\varepsilon_{2} } \hfill \\ {{\text{d}}\varepsilon_{3} } \hfill \\ \end{array} } \right) \, = \left( {\begin{array}{*{20}l} {\frac{1}{{E_{1} }}} \hfill & { - \frac{{\nu_{12} }}{{E_{1} }}} \hfill & { - \frac{{\nu_{12} }}{{E_{1} }}} \hfill \\ { - \frac{{\nu_{12} }}{{E_{1} }}} \hfill & {\frac{1}{{E_{2} }}} \hfill & { - \frac{{\nu_{23} }}{{E_{2} }}} \hfill \\ { - \frac{{\nu_{12} }}{{E_{1} }}} \hfill & { - \frac{{\nu_{23} }}{{E_{2} }}} \hfill & {\frac{1}{{E_{2} }}} \hfill \\ \end{array} } \right) \, \left( {\begin{array}{*{20}l} {{\text{d}}\sigma_{1} - b_{1} {\text{d}}u} \hfill \\ {{\text{d}}\sigma_{2} - b_{2} {\text{d}}u} \hfill \\ {{\text{d}}\sigma_{3} - b_{2} {\text{d}}u} \hfill \\ \end{array} } \right)$$
(1)

where E1 and E2 are the drained Young’s moduli perpendicular and parallel to bedding plane, respectively. The parameters vij are the drained Poisson ratios, with v12 = v13 because of transverse isotropy. Moreover, σ1, σ2 and σ3 denote total stress components, u is the pore pressure and bi are the Biot’s effective stress coefficients.

For an isotropic stress increment (dσ1 = dσ2 = dσ3 = dσ), where dε2 = dε3, the strain changes can be simplified to:

$${\text{d}}\varepsilon_{1} = \frac{{1 - 2\nu_{12} }}{{E_{1} }}{\text{d}}\sigma + \frac{{ - b_{1} + 2\nu_{12} b_{2} }}{{E_{1} }}{\text{d}}u$$
(2)
$${\text{d}}\varepsilon_{2} \, = \, \left( {\frac{{1 - \nu_{23} }}{{E_{2} }} - \frac{{\nu_{12} }}{{E_{1} }}} \right){\text{d}}\sigma + \left( {\frac{{(1 - \nu_{23} )b_{2} }}{{E_{2} }} - \frac{{\nu_{12} b_{1} }}{{E_{1} }}} \right){\text{d}}u$$
(3)

The volumetric strains are calculated through dεv = dε1 + 2dε2:

$${\text{d}}\varepsilon_{v} = \, \left[ {\frac{{1 - 2\nu_{12} }}{{E_{1} }} + 2\left( {\frac{{1 - \nu_{23} }}{{E_{2} }} - \frac{{\nu_{12} }}{{E_{1} }}} \right)} \right]{\text{d}}\sigma + \left[ {\frac{{ - b_{1} + 2\nu_{12} b_{2} }}{{E_{1} }} + 2\left( {\frac{{(1 - \nu_{23} )b_{2} }}{{E_{2} }} - \frac{{\nu_{12} b_{1} }}{{E_{1} }}} \right)} \right]{\text{d}}u$$
(4)

Comparing Eq. (4) with its equivalent form for the case of material isotropy, as shown in Eq. (5), provides the expressions of the drained bulk modulus Kd and the Biot’s skeleton modulus H, which relate volumetric strains with stress and pore pressure changes:

$${\text{d}}\varepsilon_{v} \, = \, \frac{1}{{K_{d} }}{\text{d}}\sigma - \frac{1}{H}{\text{d}}u$$
(5)

As done by Belmokhtar et al. [3] and Braun et al. [9, 10], additional moduli can be defined through Eqs. (6) and (7), which relate the changes of strains perpendicular and parallel to bedding plane with stress and pore pressure changes:

$${\text{d}}\varepsilon_{1} = \frac{1}{{D_{1} }}{\text{d}}\sigma - \frac{1}{{H_{1} }}{\text{d}}u$$
(6)
$${\text{d}}\varepsilon_{2} = \frac{1}{{D_{2} }}{\text{d}}\sigma - \frac{1}{{H_{2} }}{\text{d}}u$$
(7)

The moduli Kd, D1 and D2 can be measured in a drained isotropic compression test, where pore pressure is kept constant (du = 0). Based on the measurements of axial, radial and volumetric strains, one obtains Kd = dσ/dεv, D1 = dσ/dε1 and D2 = dσ/dε2. Analogously, when the total stress is kept constant (dσ = 0) and the pore pressure is changed, one is able to measure the moduli H, H1 and H2 through the relations H = − du/dεv, H1 = − du/dε1 and H2 = -du/dε2.

Using the definition of Terzaghi effective stress increment, i.e. dσd = dσ − du, one get the following alternative expression for the volumetric strain under an isotropic stress increment:

$${\text{d}}\varepsilon_{v} = \, \frac{1}{{K_{{\text{d}}} }}{\text{d}}\sigma_{{\text{d}}} + \frac{1}{{K_{{\text{s}}} }}{\text{d}}u$$
(8)

where Ks is the unjacketed bulk modulus. Comparing Eqs. (5) with Eq. (8), one can infer that 1/H = 1/Kd—1/Ks.

We define undrained conditions for a porous material when the fluid mass in the pores remains constant. In such case, the pore pressure change under isotropic compression can be expressed through du = Bdσ by using the Skempton coefficient B. Volumetric strains and strains perpendicular and parallel to bedding can be described through dεv = dσ/Ku, dε1 = dσ/U1, dε2 = dσ/U2 with the undrained bulk modulus Ku and the moduli U1 and U2 [3, 9, 10]. Undrained conditions, in which the fluid mass has to be kept constant within the specimen, cannot be easily ensured when testing geomaterials, since some fluid mass moves from the specimen to the deformable drainage system during compression [5, 23]. As recalled by Braun et al. [9], no fluid is drained from the sample during a sufficiently fast loading test. Under rapid isotropic compression, the undrained bulk modulus Ku and the moduli U1 and U2 can be determined without any error due to the drainage system. This is not the case in common slower undrained compression tests, in which the measured moduli need to be corrected in order to obtain the correct undrained moduli [3].

Besides experimental evaluation, these undrained poroelastic parameters can be back-calculated when the drained parameters, the sample porosity ϕ and the water bulk modulus Kw are known:

$$B = \frac{{1/K_{{\text{d}}} - 1/K_{{\text{s}}} }}{{1/K_{{\text{d}}} - 1/K_{{\text{s}}} + \phi (1/K_{{\text{w}}} - 1/K_{\phi } )}}$$
$$\frac{1}{{K_{{\text{u}}} }} \, = \, \frac{1}{{K_{{\text{d}}} }} - B\left( {\frac{1}{{K_{{\text{d}}} }} - \frac{1}{{K_{{\text{s}}} }}} \right)$$
(10)

where the modulus Kϕ is the unjacketed pore modulus, which is commonly taken equal to the unjacketed bulk modulus Ks, by considering an ideal porous material in which the pore compressibility equals the grain compressibility [6, 11, 22, 30, 37].

2.2 Back analysis of permeability in a transient consolidation test

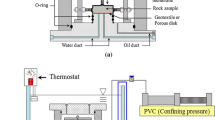
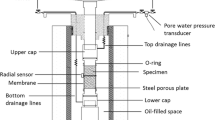
The volumetric strain change with time in a transient consolidation test is used to back calculate the permeability of Opalinus Clay. In isotropic compression cells like those used by Belmokhtar et al. [3] or Braun et al. [9] (Fig. 1), the membrane tightly seals the top and lateral surface of the sample. Consequently, we can assume one-dimensional flow towards the porous disc located at the bottom of the sample during consolidation. The governing equation for the consolidation process under constant isotropic confining pressure can be obtained by using the fluid mass balance in an element, as shown in Eq. (11) [24].

$$\frac{\partial u}{{\partial t}} \, = \, \frac{1}{S}\frac{\partial }{\partial z}\left( {\frac{k}{{\mu_{{\text{w}}} }}\frac{\partial u}{{\partial z}}} \right) \,$$
(11)

where k is the intrinsic permeability, S the storage coefficient, equal to \(\phi (1/K_{{\text{w}}} - 1/K_{\phi } )\) \(+ (1/K_{{\text{d}}} - 1/K_{{\text{s}}} )\), and μw is the water dynamic viscosity. In our test, the z-axis is vertical, equal to zero at the bottom of the specimen and equal to h (where h is the total height of the specimen) at the top.

Note that the permeability k in Eq. (11) corresponds to the permeability perpendicular to bedding, due to the orientation of the specimen. Using Eqs. (5), (8) and (9), and assuming that the permeability and viscosity remain constant over z, Eq. (11) can be rewritten as:

Fig. 1
figure 1

Layout of the experimental device (after Belmokhtar et al. [2] and Braun et al. [9])

Full size image
$$\frac{\partial u}{{\partial t}} \, = \, \frac{kBH}{{\mu_{{\text{w}}} }}\frac{{\partial^{2} u}}{{\partial z^{2} }}$$
(12)

Braun et al. [8] gave a general solution for Eq. (12) for, in the case of our specimen (Fig. 1), controlled pore pressure at the bottom (z = 0) and an impermeable boundary at the top (z = h). When the pore pressure at the specimen bottom changes from ui to uf instantly, the solution of Eq. (12) for the change of pore pressure with time t at the measuring point at a distance of zc from the bottom of sample is given by Eq. (13), which is similar to the Terzaghi–Fröhlich solution of the consolidation equation [40].

$$u(z_{{\text{c}}} ,t) \, = \, \frac{4}{\pi }\left( {u_{i} - u_{f} } \right)\sum\limits_{m = 1,3,5,...}^{m = \infty } \frac{1}{m} \sin \frac{{m\pi z_{{\text{c}}} }}{2h}\exp \left( { - \frac{{m^{2} \pi^{2} }}{4}T_{{\text{v}}} } \right) + u_{{\text{f}}}$$
(13)

where ui is the initial pore pressure. uf is pore pressure at the bottom, which is also the final pore pressure of the sample. \(T_{{\text{v}}} { = }\frac{{C_{{\text{v}}} t}}{{h^{2} }}\) is a dimensionless time factor, in which \(C_{{\text{v}}} { = }\frac{BHk}{{\mu_{f} }}\) is the consolidation coefficient.

The change in volumetric strain at the measuring point with time can then be calculated by using the constitutive Eq. (5), considering dσ = 0, as presented in Eq. (14).

$$\varepsilon_{v} (z_{c} ,t) = \frac{1}{H}\left( {u(z_{c} ,0) - u(z_{c} ,t)} \right)$$
(14)

By adjusting the permeability, the best-fit permeability can be obtained when the mean square error (MSE, Eq. 15) between calculated strain εv and measured strain εvmeas for datapoints n reaches a minimum value.

$${\text{MSE}} = \frac{1}{n}\sum\limits_{1}^{n} {\left( {\varepsilon_{v}^{{{\text{meas}}}} - \varepsilon_{{\text{v}}} } \right)}^{2}$$
(15)

3 Materials and methods

3.1 The Opalinus Clay

The core of Opalinus Clay (approximately 100 cm length and 10 cm diameter) was collected at the Lausen site in Switzerland, at a depth around 35 m. The mean total in-situ stress and pore pressure are estimated as follows: σ = 1.3 MPa and uw = 0.3 MPa, respectively. This results in a Terzaghi effective stress σd = σ − uw = 1.0 MPa. The maximum pre-consolidation stress of the samples is about 18 MPa [27].

Before being shipped, the core was wrapped and sealed in aluminium foil and resin-impregnated into a plastic barrel [2, 27]. Microtomography images taken by the Swiss agency for radioactive waste management Nagra (National Cooperative for the Disposal of Radioactive Waste) revealed the existence of cracks that were carefully avoided through adequately selecting the sampling location within the core. A cylindrical specimen of 38 mm diameter and 11.6 mm height with its axis perpendicular to the bedding plane was air-cored with a diamond coring bit. Both end surfaces were cut planar using a diamond string saw. Specimens were conserved and protected from drying before the test by a tight aluminium foil wrapping and a layer of a 70% paraffin and 30% vaseline oil mixture. The initial suction, natural density and water content of the specimen were measured on cuttings obtained during trimming. The initial suction of the specimen was measured using a WP4C dew point tensiometer (Decagon), providing a value of 16.6 MPa. The volume of the cuttings was measured by hydraulic weighing in hydrocarbon and the water content was determined after drying in an oven at 105 °C for five days, giving w = 4.8%. The porosity ϕ = 0.133 and degree of saturation Sr = 85.1% were calculated considering a solid grain density ρs = 2.71 Mg/m3 [25]. All specimen characteristics are presented in Table 1. The obtained porosity is comparable to the values of 0.12–0.15 obtained by [27] on samples from the same site at 33 m depth.

Table 1 Physical properties of the Opalinus Clay
Full size table

3.2 Experimental device

The isotropic compression cell [3, 9] is shown in Fig. 1. Axial and radial strain gauges glued at mid-height of the sample were used to provide accurate local measurements. In order to get rid of the effects of temperature changes along the gauge and the wires (especially due to room temperature variations outside of the cell), a reference strain gauge with the same wire length as the specimen ones was glued to a block of metal with known thermal and mechanical properties and placed in the cell. The measured strains were corrected by using these data. A constant cell temperature of 25 °C was ensured by a heating belt. The confining pressure and pore water pressure were applied and controlled by pressure volume controllers (PVCs, GDS brand).

3.3 Testing procedure

Before the test, the water duct at the bottom of the cell was dried by flushing it with dry air, to prevent the sample from absorbing water and swelling before being submitted to any external stress. Once the instrumented sample was inserted into the neoprene membrane and installed on the cell pedestal, vacuum was applied using a vacuum pump through the water duct. This also allowed to check whether the membrane was correctly sealed on the specimen. The cell was then filled with silicone oil, closed, and the cell temperature set to a constant 25 °C.

The test programme includes seven steps, as shown in Fig. 2. The resaturation procedure includes Steps 1–3 (Fig. 2a). An external confining stress of 2.5 MPa was applied to the specimen during Step 1. Vacuum was applied through valve 2 to remove any air remaining in the ducts, prior to saturating the sample by injecting a synthetic pore water of the same salinity as that of the Opalinus Clay [38], using the PVC at a pressure of 100 kPa (Step 2). This pressure was chosen small enough to limit any elastic deformation of the sample and to be able to observe the deformations resulting from sample hydration only. Once the deformation stabilised, we increased the confining stress to 4.5 MPa and the pore pressure to 2.0 MPa in Step 3.

Fig. 2
figure 2

Load steps applied during the laboratory test: a Resaturation and loading to initial stress, b Poroelastic and permeability parameter tests (When valve 1 is closed, the pore pressure changes due to undrained conditions are recorded)

Full size image

The hydromechanical tests include Steps 4–7 (Fig. 2b), aimed at determining the poroelastic parameters and the permeability through loading or unloading paths. Following Hart and Wang [29] and Braun et al. [9, 10], a step loading or unloading procedure was applied, as schematically represented in Fig. 3 [9, 10]. The first stage was conducted to instantaneously generate true undrained conditions during fast loading, with negligible amounts of fluid drained from the sample thanks to the very low permeability of the claystone. After an initial fast loading (3 kPa/s), we keep valves 1 and 2 closed and let the pore pressure within the specimen reach equilibrium. Due to undrained conditions, the pore pressure changed during this phase. We suppose an equilibrium when the measured strains stabilise. Then we open valve 1 and let the pore pressure dissipate. The pore pressure distribution within the specimen gradually comes back to 2 MPa.

Fig. 3
figure 3

adopted from Braun et al. [9, 10], shown a with respect to time, b in terms of stress–strain behaviour and c in terms of pore pressure–strain behaviour. Initial fast loading in stage 1 allows one to measure true undrained moduli. Deformations and pore pressure changes obtained from stage 2 also permit to calculate undrained moduli and the Skempton coefficient, while a correction of these parameters is necessary [5, 23]. Strains occurring in stage 3 provide the Biot’s moduli, whereas the total strain changes over all stages provide the drained moduli. The transient strains in stage 3 can be back-analysed to determine the permeability

Multistage loading procedure for measuring various poroelastic properties,

Full size image

Steps 4 to 7 are similar to each other, except for the levels of total stress. In Step 4 we loaded from 4.5 to 5.5 MPa, in Step 5 we unloaded back to 4.5 MPa, in Step 6 we loaded to 7 MPa, and in Step 7 we loaded from 7 to 8 MPa. Note that we assume a linear poroelastic behaviour within each loading step.

4 Experimental results

4.1 Resaturation process

As shown in Fig. 4a (positive strain corresponds to compression), the deformation during compression under 2.5 MPa at constant water content (Step 1) mainly concerns the axial direction perpendicular to the bedding plane, with a final value ε1 = 0.425%. Interestingly, the change in radial strain parallel to bedding is significantly smaller (ε2 = 0.02%). Based on the hypothesis that the volume changes monitored are only due to changes in porosity (i.e. neglecting the compression of the solid phase), the degree of saturation increases from an initial value of 85.1–88.4%.

Fig. 4
figure 4

Measured strain response during the laboratory test: a Resaturation and loading to initial stress, b incremental strain response during resaturation

Full size image

During the subsequent hydration under 2.5 MPa total stress and 100 kPa imposed pore pressure (Step 2), the sample swells (Fig. 4b) with larger increase in axial strain (△ε1 = − 0.31% perpendicular to bedding) compared to the radial one (△ε2 = − 0.185%). This corresponds to an increase in volume of 0.67%, with a ratio Δε1/Δε2 = 1.69. This volume change is a little smaller than the 0.92% expansion obtained by Belmokhtar [2] on a comparable Opalinus Clay sample. The ratio Δε1/Δε2 = 1.69 measured under 2.5 MPa total stress is smaller than the value of 3 obtained by Crisci et al. [15] under free swelling, for an Opalinus Clay sample collected at the Lausen site at a depth of 18 m.

Afterwards, the sample was loaded to a confining stress of 4.5 MPa and a pore pressure of 2.0 MPa (Step 3). The observed strain response is very small (see Fig. 4a) because the effective stress only decreased by 100 kPa. In this step, the elevated pore pressure ensures better saturation [19] due to the dissolution of trapped air.

4.2 Hydromechanical tests

After strain stabilisation in the previous step, the experiments for evaluating poromechanical properties were started. Figure 5 presents the changes in axial, radial and volumetric strain during Steps 4 to 7. During Step 4 (loading from 2.5 to 3.5 MPa effective stress), the axial, radial and volumetric strain increments are equal to 0.067%, 0. 019% and 0.104%, respectively. When unloading from 3.5 to 2.5 MPa effective stress after Step 5, strain increments equal to − 0.092%, − 0. 022% and − 0.134%, respectively, were observed. This shows fairly reversible strains during the stress cycle. Such strains may reasonably be considered as elastic, and suitable for determining the poroelastic parameters. Note also that radial strain increments are significantly smaller than axial ones (ratio Δε1/Δε2 equal to 3.53 and 4.18, respectively), confirming the transversely isotropic response of the Opalinus Clay.

Fig. 5
figure 5

Measured strain response during Steps 4–7

Full size image

4.2.1 Poroelastic parameters

Figure 6 shows a typical experimental result of Step 6, in which undrained loading from 2.5 to 5 MPa was carried out, followed by pore pressure dissipation. The first fast loading stage produces a fully undrained response, and the values U1 = 27.45 GPa, U2 = 46.55 GPa and Ku = 12.62 GPa can be determined using the relation between the incremental stress and incremental strain during this stage (see also Fig. 3). Once the drainage completed, the drained poroelastic parameters Kd, D1 and D2 can be determined from secants, as shown in Fig. 6b (see also Fig. 3). These poroelastic parameters measured for different steps are listed in Table 2. Interestingly, it can be seen that the values of a given parameter obtained from different steps are reasonably close to each other, indicating that the poroelastic behaviour is fairly linear within the investigated effective stress range (4.5–8.0 MPa) and that our measurements are reliable and repeatable. Our experiments were carried out at a stress level at which Corkum and Martin [13] also observed linear elastic deformations in unconfined compression tests. Note that the applied maximum stress is lower than the yield stress of 18 MPa measured by Giger et al. [27] and of 12.8 MPa and 24 MPa determined by Ferrari et al. [20]. The average ratios for D2/D1 and U2/U1 are 3.83 and 1.80, respectively, evidencing the transversely isotropic response of the Opalinus Clay.

Fig. 6
figure 6

Measured stress–strain response in Step 6: a determination of Ku during fast loading, b determination of Kd after full drainage

Full size image
Table 2 Poroelastic parameters measured through different steps (moduli unit: GPa)
Full size table

During each of the Steps 4–7, the pore pressure was recorded in the undrained phase, where the drainage system was closed. The pore pressure is expected to increase/decrease due to undrained loading/unloading, governed by the Skempton coefficient B. Afterwards, under constant stresses, the pore pressure should reach equilibrium. However, because of a leakage at valve 2, the pore pressure along loading paths (i.e. Steps 4, 6 and 7) is observed to decrease slightly with time after having reached a maximum value, while the pore pressure in unloading paths such as Step 5 increases slightly after having reached a minimum value (Fig. 7). At small times, around t ≈ 5 h (Fig. 7), we can evaluate the maximum Bmeas = △umeas/△σc which is the least one affected by the supposedly time-dependent leakage. The values of Bmeas are also shown in Table 2. The Skempton coefficient Bmeas has to be corrected to take into account the elastic properties of the drainage system [3, 5, 23], providing the corrected Skempton coefficient Bcor (Eq. 16). If our measurements are precise and the assumptions of saturated poroelasticity are satisfied, Bcor should be close to B obtained from Eq. (9).

$$B_{{}}^{{{\text{cor}}}} = \frac{{B_{{}}^{{{\text{meas}}}} }}{{1 + \frac{1}{{V(1/K_{{\text{d}}} - 1/K_{{\text{s}}} )}}\left[ {V_{{\text{p}}} /K_{{{\text{dp}}}} - B_{{}}^{{{\text{meas}}}} \left( {\left( {V_{{\text{p}}} (1/K_{{{\text{dp}}}} + \phi_{{\text{p}}} /K_{{\text{w}}} } \right) + V_{{\text{L}}} (1/K_{{\text{w}}} + 1/K_{{\text{L}}} )} \right)} \right]}}$$
(16)
Fig. 7
figure 7

Pore water pressure change under constant external stress after the first fast loading stage for Steps 5 and 6

Full size image

Here, V, Vp and VL denote the volume of the sample, the volume of the porous stone and the water volume in the drainage system, respectively; 1/Kdp is the compressibility of the porous stone; ϕp is the porosity of the porous stone; 1/KL is the compressibility of the ducts and pore pressure transducers connected to the drainage system.

Besides the drained bulk modulus Kd which we measured directly above, Eq. (16) also requires the unjacketed bulk modulus Ks, for which laboratory data are scarce [33]. Belmokhtar et al. [3] obtained, by running an unjacketed test on a specimen of Callovo–Oxfordian claystone, a claystone with comparable characteristics to those of the Opalinus Clay, a value of Ks of 21.7 GPa. In the work of Ferrari et al. [20], the Ks value for Opalinus Clay was calculated based on the mineralogical composition of a sample from the same site and similar depth [27] and on the compressibility of the minerals [1, 41] (see Table 3). The upper bound for Ks is estimated with KsV = 26.3 GPa according to Voigt’s Eq. (17a), and the lower bound is estimated with KsR = 12.1 GPa according to Reuss’s Eq. (17b). The average value of KsH = 19.2 GPa is calculated by using Hill’s Eq. (17c) [43].

$$K_{{{\text{sV}}}} = \sum\limits_{i = 1}^{n} {\nu_{i} K_{si} }$$
(17a)
$$\frac{1}{{K_{{{\text{sR}}}} }} \, = \, \sum\limits_{i = 1}^{n} {\frac{{\nu_{i} }}{{K_{si} }}}$$
(17b)
$$K_{{{\text{sH}}}} = \frac{1}{2}\left( {K_{{{\text{sV}}}} + K_{sR} } \right)$$
(17c)

where vi and Ksi are the volume fraction and the bulk modulus of component i.

Table 3 Mineralogical constituents and their compressibility
Full size table

Ferrari et al. [20] showed that their measurements of Ks were close to the calculated value by Hill’s equation. Ks = 19.2 GPa calculated by using Hill’s equation is also close to the value of 21.7 MPa of Belmokhtar et al. [3] on the Callovo–Oxfordian claystone. Hence, Ks = 19.2 GPa was adopted in this study, together with the other parameters needed in Eq. (16) that are shown in Table 4, including the compressibility of water, porous stone and drainage system adopted from Monfared et al. [36] and Belmokhtar et al. [3]. We obtain a Skempton coefficient B = 0.95 using Eq. (9) and the properties from Table 4. Inserting Bmeas = 0.84 measured in Step 5, together with the values from Table 4, into Eq. (16), we calculate Bcor = 0.96. This value is reasonably close to B = 0.95, confirming measurements are accurate and compatible within the poroelastic framework.

Table 4 Parameters needed in Eq. (16) for the calculation of the Skempton coefficient
Full size table

Compatibility can be also verified by comparing the measured undrained bulk modulus Ku with that indirectly determined by Eq. (10). Using Kd = 0.92 GPa, Ks = 19.2 GPa and B = 0.95, we obtain Ku = 9.63 GPa, a value smaller than that directly obtained by the fast loading method (average value of 13.66 GPa). Similar observations were made by Belmokhtar et al. [4], who stated that the use of total porosity in this calculation tends to underestimate the Skempton coefficient, which leads in consequence to an underestimated Ku through Eq. (10).

Moreover, the Biot coefficient b can be obtained using the relation b = 1 − Kd/Ks and the Biot bulk modulus H through the relation H = Kd/b. All determined parameter values are shown in Table 5. Interestingly, it can be seen that a variation of Ks within the assumed limits has a negligible influence on the calculated values.

Table 5 Calculated volumetric Biot coefficient b and modulus H under isotropic compression
Full size table

4.2.2 Permeability coefficient

As introduced in Sect. 2, after undrained loading in Steps 5 and 6, the drainage valve 1 was opened so that the excess pore water pressure dissipates (Δu), resulting in transient strains which finally reach Δεv = − Δu/H. These transient strains can be simulated using Eq. (14), which allows to back-analyse the permeability. This was done through Eqs. (13) to (15), using the previously determined poroelastic parameters. The evaluated best-fit permeability at 25° C is 1.90 × 10–14 m/s and 1.79 × 10–14 m/s or the intrinsic permeability κ is 1.73 × 10–21 m2 and 1.63 × 10–21 m2 for Step 5 and Step 6, respectively. The comparison of calculated and measured volumetric strains is shown in Fig. 8. It can be seen that the consolidation process can be well predicted using these permeability coefficients, confirming the robustness of the method for determining the hydraulic properties, that were determined for a flow perpendicular to the bedding plane.

Fig. 8
figure 8

Measurement and calculated best-fit of volumetric strain changes during Steps 5 and 6

Full size image

5 Discussion

5.1 Analysis of the anisotropy related to Biot coefficients b i

The anisotropic Biot coefficients b1 and b2 can be calculated by Eqs. (18a) and (18b) [3], in which the average parameter values from Table 2 were adopted.

$$b_{2} = \frac{1}{B} - \frac{1}{B}\left( {\frac{{\nu_{12} }}{{U_{1} }} + \frac{1}{{U_{2} }}} \right)/\left( {\frac{{\nu_{12} }}{{D_{1} }} + \frac{1}{{D_{2} }}} \right)$$
(18a)
$$b_{1} = \frac{1}{B} - \frac{2}{B}\nu_{12} \left( {1 - b_{2} B} \right) - \frac{1}{B}\left( {1 - 2\nu_{12} } \right)\frac{{D_{1} }}{{U_{1} }}$$
(18b)

The Poisson’s ratio v12 was not measured, so we considered values between 0.15 and 0.3. Table 6 shows the computed values for b1 and b2 as a function of v12. It can be seen that b1 is slightly larger than b2, while the variation of v12 has minor influence on b1 and b2, as already observed by Belmokhtar et al. [3]. Recently, Braun et al. [10] also obtained Biot coefficients in the same range, with a small anisotropy detected in the COx claystone. Escoffier [18] found a similar trend with b1 > b2, whereas Vincké et al. [42] found b1 < b2. The significant anisotropy observed in the elastic moduli does not result in a considerable difference in bi.

Table 6 Calculated values of Biot coefficients b1 and b2 as a function of Poisson ratio v12
Full size table

5.2 Comparison of parameters with literature data

Belmokhtar [2] measured the Young’s modulus E1 of Opalinus Clay collected from the same site at the same depth using triaxial tests. In addition, Ferrari et al. [20] measured the deformation modulus Eoed of Opalinus Clay collected from the Mont-Terri URL and the village of Schlattingen at 300 m (OPA-shallow) and 855–891 m depth (OPA-deep), respectively, using oedometric tests (Table 7). Consequently, the drained modulus D1 can be calculated either from E1 using Eq. (19), in which we adopt the measured Poisson’s ratios of Belmokhtar [2], or from Eoed using Eq. (20), in which we assume a Poisson’s ratio of 0.15. A comparison is shown in Table 7, where it can be seen that D1 of about 1.4 GPa measured in this study is close to the calculated one based on triaxial tests by Belmokhtar [2], and a little smaller than D1 calculated based on oedometric tests by Ferrari et al. [20].

$$D_{1} = \frac{{E_{1} }}{{1 - 2\nu_{12} }}$$
(19)
$$E_{1} = \left( {1 - \frac{{2\nu_{12} }}{{1 - v_{23} }}} \right)E_{{{\text{oed}}}}$$
(20)
Table 7 A comparison of D1 measured in this study with calculated values from Belmokhtar [2] and Ferrari et al. [20]
Full size table

The back-analysed values of the consolidation coefficient CV (perpendicular to bedding) (Eq. 13) range from 0.0017 to 0.0020 mm2/s. Giger et al. [27] determined a consolidation coefficient CV (perpendicular to bedding) on samples collected from the same site at similar depth, ranging from 0.0032 to 0.0036mm2/s, which is somewhat higher, but in the same order of magnitude as our values.

5.3 The anisotropy of poroelastic parameters

The anisotropy of the strain response of Opalinus Clay is different during isotropic loading, resaturation, undrained loading and drainage. During saturated isotropic loading, the anisotropy of the drained modulus is the largest, with an average of D2/D1 = 3.8. Under undrained loading, a smaller anisotropy, with an average value of U2/U1 = 1.8, was observed. This is due to the fact that during undrained compression, the liquid phase, which is isotropic in nature, significantly contributes to the strain response. The anisotropy of Biot coefficients is the smallest and the ratio of b1 to b2 is almost equal to 1.0 (ranging from 1.01 to 1.03).

6 Conclusions

The knowledge of the poroelastic parameters of clayey host rocks is essential for the analysis of their hydromechanical response during excavation and long-term geological storage of radioactive waste. However, their determination is challenging, due to the very low permeability of claystones, and rather few data fully addressing their transversely isotropic nature are presently available. Following a methodology proposed by Braun et al. [8], transient experiments were carried out on an Opalinus Clay specimen from Lausen so as to determine several transversely isotropic poroelastic properties, together with the hydraulic conductivity values.

We determined poroelastic properties under stress levels close to the in-situ one, within which the Opalinus Clay was found to behave linearly elastic. The poroelastic parameters Kd and Ku were found to be repeatable under loading and unloading cycles. By adopting a possible range of the unjacketed modulus Ks, using the bulk moduli of the solid phases, the Biot coefficient b and Biot modulus H were calculated and shown to be insensitive to Ks. The Opalinus Clay investigated in this study behaved similarly to clays, with b and B close to 1.0. The elastic moduli showed significant anisotropic characteristics, while negligible anisotropy was detected for the Biot coefficients. Unsurprisingly, these conclusions are in line with some findings on a similar claystone, the Callovo–Oxfordian claystone, by Belmokhtar et al. [3] and Braun et al. [10]. An average intrinsic permeability perpendicular to bedding of 1.68 × 10–21 m2 was back-calculated through two consolidation phases, with similar values after loading and unloading.

Further experiments are required to confirm the repeatability of the measured parameters. Additional experiments on specimens with their axis parallel to the bedding plane could help to cross-check the anisotropic elastic properties and permit to measure the permeability parallel to bedding. Also, possible changes of elastic parameters due to damage or stress dependency need to be investigated further.

The obtained set of parameters allows to better describe the anisotropic response and pore fluid flow in the Opalinus Clay under isotropic stress changes, an important element for the prediction of its poroelastic response in the close field.