An elastoplastic constitutive model for frozen saline coarse sandy soil undergoing particle breakage

Abstract

The mechanical property of frozen saline sandy soil is complicated due to its complex components and sensitivity to salt content and confining pressure. Thus, a series of triaxial compression tests were carried out on sandy samples with different Na₂SO₄ contents under different confining pressures to explore the effects of particle breakage, pressure melting, shear dilation and strain softening or hardening. The test results indicate that the stress–strain curves exhibit strain softening/hardening phenomena when the confining pressures are below or above 6 MPa, respectively. A shear dilation phenomenon was observed in the loading process. With increasing confining pressure, the strength firstly increases and then decreases. By taking into consideration the changes between the grain size distributions before and after triaxial compression tests, a failure strength line incorporating the influences of both particle breakage and pressure melting is proposed. In order to describe the deformation characteristics of frozen saline sandy soil, an elastoplastic incremental constitutive model is established based on the test results. The proposed model considers the plastic compressive, plastic shear and breakage mechanisms by adopting the non-associated flow rule. The breakage mechanism can be reflected by an index related to the initial, current and ultimate grain size distributions. The hardening parameters corresponding to compressive and shear mechanisms consider the influence of particle breakage. Then the effect of particle breakage on both the stress–strain and volumetric strain curves is analyzed. The calculated results fit well with the test results, indicating that the developed constitutive model can well describe the mechanical and deformation features of frozen saline sandy soil under various stress levels and stress paths. In addition, the strain softening/hardening, contraction, high dilation and particle breakage can be well captured.

1 Introduction

Frozen soil, widely distributed on the earth, is composed of solid mineral particles, ice inclusions, liquid water and gaseous inclusions [60]. The mechanical properties of frozen soil are more complicated than those of unfrozen soil due to the existence of ice inclusions, which get even blurry with the addition of salt crystals, i.e., frozen saline soil. With the fast development of artificial ground freezing, engineers have to face the engineering difficulties with the appearance of frozen saline soils [25]. On this circumstance, there is an urgent need to study the constitutive response of frozen saline soil.

The stress–strain relationship of geotechnical materials is considerably complex due to the elasticity, plasticity, viscosity, dilation and nonlinearity features. Numerous models have been developed to describe the mechanical properties of unfrozen soil as well as other solid materials [5, 6, 18, 40, 45, 50, 52,53,54,55, 59, 64]. Some researchers considered that models with one yield surface cannot explain the overall deformation properties and suggested to adopt the double-yield-surface model [33, 34], which was firstly introduced by [47]. Leblanc et al. [29] provided a modified critical state two-surface plasticity model for sand based on a versatile shape function prescribing a family of smooth and convex contours in π-plane. The model adopts a modified multi-axial surface formulation and can be applied to simulate volumetric property as well as stress–strain behavior. As for viscoplastic materials, Voyiadjis et al. [65] developed a double-yield-surface model considering thermodynamic damage and healing process. Yin et al. [80] established a simple double-yield-surface model for clay by referring to the critical state theory. The proposed model can reproduce the main features of clay, and only six material and two state variables need to be determined.

The particle breakage, firstly reported by Terzaghi and Peck [57], commonly occurs when a granular material undergoes compression or shearing under relatively high stress. The soil particle is broken into smaller sizes during loading, leading to the variation of particle grading, reduction of dilatational component as well as degradation of shear strength [83]. The breakage characteristics can be affected by grain size distribution, particle shape, effective stress path, particle hardness, water content and so on [17]. The influence of particle breakage on the mechanical properties of granular materials was considered by previous studies [10, 22, 61, 70, 81]. On the other hand, different modelling methods were developed [12, 20, 48, 66]. According to the definition of relative breakage for compacted crushed aggregates, Einav [13, 14] developed the concept of relative breakage for crushable granular materials from the perspective of thermomechanics. The established theory was derived from the dissipative mechanisms of breakage and plasticity, based on which the constitutive relation was formulated. Both uncoupled and coupled plasticity–breakage yield surfaces were investigated. Daouadji and Hicher [11] analyzed the relationship between grading change and the mechanical properties of granular assembly and pointed out that particle breakage increased the compressibility, in company with the gradual disappearance of dilation for granular materials. The established model reflected the influence of particle breakage by introducing a parameter related to the evolution of grain size distribution. By introducing porosity as a frame-independent internal state variable, Tengattini et al. [56] proposed a constitutive model with the consideration of particle crushing and dilation. The particle crushing was emphasized by the theory of breakage mechanics, while dilation was interpreted through its negative contribution to the overall positive rate of dissipation. With only five parameters to be determined, the proposed model connected the constitutive behavior to index properties which relate to minimum and maximum densities. Based on thermomechanics and micromechanics, Shen et al. [51] developed an elastic–breakage constitutive model of crushable granular materials under the isotropic compression condition. The proposed model can predict the stress dependence of the elastic bulk modulus and the size dependence of the yielding stress. The predicted results agree well with the experimental data.

The influence of particle breakage on the critical state line of soil has been widely investigated. Thus, some soil constitutive models incorporating the change of critical state line to the degree of particle breakage induced by high stresses were developed [15, 67, 72]. Bandini and Coop [1] conducted a series of triaxial tests to examine the effect of particle breakage on the location of critical state line. They found that the particle grading variation caused vertical and rotational movement in the critical state line. However, their work cannot reflect the effect of a rotation of stress on the current particle grading. Kan and Taiebat [21] presented a bounding surface model by incorporating the translation of critical state line under the influence of particle breakage. The model can well capture the key mechanical behaviors of crushable materials under both conventional and complex loading paths. Based on the framework of breakage critical state theory, Xiao et al. [73] developed an elastoplastic constitutive model for rockfill by applying the associated flow rule and isotropic, contractive and distortional hardening rules. The post-peak strain softening, strain hardening and particle breakage characteristics can be well captured. As for frozen saline soil, however, the constitutive relation considering the influence of particle breakage has been rarely studied.

In frozen soil engineering, the constitutive model is very important for mechanical prediction [27]. Both the mechanical properties and constitutive models for frozen soils without salt were extensively investigated [24, 26, 32, 42, 58, 75, 76]. As for frozen saline soil, the presence of fine particles can significantly affect the stress–strain behavior and an increase in salinity can also cause a considerable loss of strength [19]. Zhu et al. [85] formulated an elastic constitutive model for frozen soil considering damage based on micromechanics, which can describe the mechanical properties of frozen soil with different ice contents and temperatures. Based on a series of triaxial compression tests, Lai et al. [25] pointed out that the critical state line of frozen saline sandy soil is curved in p–q plane, and then a double-yield-surface constitutive model was proposed by taking into account the initial anisotropy as well as load-induced anisotropy. The established constitutive model can be applied to describe the mechanical features of geomaterials with straight or curved critical state lines.

In view of the fact that the elastoplastic constitutive model of frozen saline soil describing the effects of both pressure melting of ice and particle breakage has been rarely investigated, the purpose of this study is to develop a phenomenological constitutive model of frozen saline sandy soil emphasizing on these features. Triaxial tests were conducted to reveal the particle breakage characteristics in the process of shearing. Based on the test results, a failure strength line considering the influences of soil particle breakage and ice melting is proposed. Then a constitutive model incorporating the breakage, plastic compressive and plastic shear mechanisms is established by employing the non-associated flow rule. The proposed model is verified by the comparison between simulated and experimental results on relative breakage, stress–strain relation and volumetric deformation.

2 Test conditions and results

2.1 Description of the test

The soil, tested in this paper, was a coarse sandy soil with the grain size composition shown in Table 1. The maximum and minimum void ratios of the tested sand are 0.5650 and 0.3413, respectively. A dry density of 1.85 g/cm³ was used to prepare the samples. The coarse sandy soil was mixed with salt (anhydrous Na₂SO₄ fine particles) to obtain the saline sandy soil with the mass salt content of 0%, 0.5%, 1.5%, 2.5% and 3.5%. The multiple-sieving pluviation method was adopted to obtain relatively homogeneous soil samples. The saline sandy specimens were prepared by split cylinders with the diameter of 61.8 mm and height of 125 mm. The samples were saturated with salt solution which has the same concentration with the saturated sandy samples. Then the saturated samples were put in a container with distilled water to avoid water loss. The specimens together with the container were placed in a refrigerator with the environmental temperature of − 30 °C kept for more than 48 h for a quick freezing to prevent the formation of ice lenses. Afterward, the samples were kept in an incubator for over 24 h at the target temperature of − 6 °C to reach a uniform temperature. Then, the frozen samples were placed into a triaxial pressure cell with hydraulic oil at the temperature of − 6 °C.

Table 1 Parameters of the tested sandy soil (unit:  %)

The confining pressure was increased to the desired values within 30 s. The confining pressures adopted in the test were from 0 to 16 MPa and maintained at a constant value during the triaxial compression test. The axial strain rate of 1.67 × 10⁻⁴ s⁻¹ was chosen during shear process according to the GB/T 50123-1999 [43]. The axial loading was stopped automatically when the axial strain reached up to 20%. After each triaxial compression test, the salt in saline sandy sample was removed by distilled watering for ten times. The desalinated sandy samples were dried at 105 °C for 24 h. Then a sieve analysis was performed on the tested sandy samples to obtain the grain size distribution. Besides, a series of consolidation tests were conducted and the grain size distributions after tests were measured to obtain the breakage parameters.

2.2 Stress–strain and volumetric strain properties of the tested frozen saline sandy soil

The stress–strain curves and volumetric strain curves of frozen saline sandy soil at various confining pressures and salt contents of 0%, 1.5% are shown in Fig. 1. The confining pressure considerably affects the stress–strain behavior. Almost three stages of stress–strain curves can be identified: the initial linear elastic, plastic and softening stages, which is consistent with Yang et al. [77]. The samples exhibit strain softening when the confining pressure is lower than 6 MPa, and there exist peak values of stress–strain curves for axial strain ε_a ≤ 15%. Then the peak values of deviator stress (σ₁–σ₃) are taken as the strength. The strain hardening phenomenon occurs under relatively high confining pressures, and the corresponding values of deviator stress (σ₁–σ₃) at the axial strain of 15% are taken as the strength. As can be seen from the stress–strain curves, the strength firstly increases to a peak value with the increase in confining pressure and then decreases due to the pressure melting and particle crushing under high confining pressures. The strengths of samples with different salt contents at − 6 °C reach the maximum values when the confining pressures are 12–14 MPa. In addition, the strength presents a decreasing tendency with the increase in salt content. The mechanical behavior of frozen saline soil is considerably influenced by the presence of unfrozen water within soil matrix. Generally, the unfrozen water content increases with increasing salinity, leading to a decrease in strength [19].

Fig. 1

Test results of frozen saline sandy soil under various confining pressures

Volumetric strain is defined as the ratio of volume change to the original volume. The volumetric strain is assumed to be positive under compression condition based on the general assumption in geotechnical engineering. From the test results, the confining pressure has a pronounced effect on volumetric strain. The volumes of frozen saline sandy samples reduce with increasing axial strain in the initial stage, and then dilation occurs. However, the dilation features become less obvious with increasing confining pressure. The compression deformation is very small compared with the results from previous studies [25, 26]. This phenomenon may be explained by the fact that most of the voids in the coarse sandy sample are filled by ice, salt crystals and unfrozen water. The potential compression deformation is very limited due to the very few unfilled voids.

2.3 Quantification of particle breakage of frozen saline sandy soil

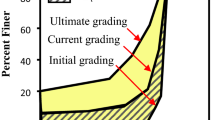
In order to incorporate the particle breakage in a constitutive model, it is essential to identify a suitable parameter to present the amount of particle breakage during loading. Some indices quantifying the particle breakage are based on the increment of fine particles content [39], the increase in particle–surface area [38] and the variation in grain size distribution due to stress changes [23, 30, 36]. Adoption of the parameters considering the influence of grain size distribution can simplify the effects of initial void ratio, particle shape and particle hardness. By assuming that silt and clay particles are unsusceptible to breakage, Hardin [17] proposed the concept of relative breakage based on the integration of the changes in grain size distribution curve for the particle sizes greater than 0.075 mm. The relative particle breakage B_rH can be obtained from the initial cumulative distribution, current cumulative distribution and an arbitrary cutoff value of silt particle size, as shown in Fig. 2a and Eq. (1):

$$B_{\text{rH}} = \frac{{B_{\text{tH}} }}{{B_{\text{pH}} }}$$

(1)

where the parameter B_pH refers to the breakage potential, which can be calculated from the area of ABDA; B_tH refers to the total breakage and underlines the amount of breakage that the soil has undergone, which is equal to the area of ACDA shown in Fig. 2a.

Fig. 2

Definition of relative breakage after Hardin [17] and Einav [13]. d_m and d_M are minimum and maximum diameters of soil particles, respectively

However, the grain size distribution of soils should be limited by an ultimate one, corresponding to very large confining pressure and shear strain, rather than an arbitrary cutoff value of silt particle size. According to three different grain size cumulative distributions: the initial F₀, current F and ultimate F_u, Einav [13, 14] developed the concept of relative breakage after Hardin [17], as shown in Fig. 2b. Meanwhile, he pointed out that the fractional breakage B, donating the breakage of different fractions, can be obtained by measuring the relative breakage B_rE from the experiment.

The expressions of breakage potential B_pE and total breakage B_tE after Einav [13, 14] can be evaluated by integrating the area over logarithmic scale as follows:

$$B_{\text{pE}} = \int_{{d_{\text{m}} }}^{{d_{\text{M}} }} {\left[ {F_{\text{u}} (d) - F_{0} (d)} \right]} \text{d} (\log d)$$

(2a)

$$B_{\text{tE}} = \int_{{d_{\text{m}} }}^{{d_{\text{M}} }} {\left[ {{\it{F}}(d) - F_{0} (d)} \right]} \text{d} (\log d)$$

(2b)

The formulations of F₀, F and F_u can be expressed as:

$$F_{0} (d) = \left( {\frac{d}{{d_{\text{M}} }}} \right)^{{3 - \alpha_{0} }}$$

(3a)

$$F(d) = \left( {\frac{d}{{d_{\text{M}} }}} \right)^{3 - \alpha }$$

(3b)

$$F_{\text{u}} (d) = \left( {\frac{d}{{d_{\text{M}} }}} \right)^{{3 - \alpha_{\text{u}} }}$$

(3c)

where d is the diameter, while d_M is the maximum diameter of soil particles; α₀, α and α_u are the fractal dimensions of initial, current and ultimate gradations, respectively.

Substituting Eqs. (2a, 2b) and (3a, 3c) into Eq. (1) yields:

$$B = B_{\text{rE}} = \frac{{(\alpha - \alpha_{0} )(3 - \alpha_{\text{u}} )}}{{(\alpha_{\text{u}} - \alpha_{0} )(3 - \alpha )}}$$

(4)

According to the initial grain size distribution of the sandy soil, the value of α₀ is chosen as 2.4565. As for the ultimate grain size distribution, a fractal dimension ranging from 2.5 to 2.8 was suggested [49]. By identifying that the grain size distribution of sands evolves with a fractal one, a fractal dimension of 2.57 was employed [10]. According to the experimental results, the grain size distribution of the sandy soil reveals self-similar features and the value of α_u is taken as 2.80.

Figure 3 shows the evolutions of grain size cumulative distributions after triaxial compression test of frozen saline sandy samples under different confining pressures and the temperature of − 6 °C, together with the initial and ultimate distributions. The grain size distribution changes dramatically when the confining pressure is lower than 8 MPa, while the changes weaken gradually as the confining pressure goes up. With the increase in particle size, the probability of defects within a particle increases, so the potential for breakage of a soil particle shows an increasing tendency [17]. The percentage of particles smaller than a given size increases, and the grain size cumulative distribution curves after tests shift upward compared with the initial one as the confining pressure goes up. Increasing the confining stress can cause an increase in soil particle breakage [69, 71]. The grain size cumulative distribution curves are very close when the confining pressure is relatively high, indicating that the amount of particle breakage tends to be nearly stable. Besides, the unfrozen water content increases with increasing confining pressure due to pressure melting of ice, leading to an increase in particle breakage for the particles with diameters larger than 0.075 mm [84].

Fig. 3

Evolutions of grain size cumulative distributions of frozen saline sandy soils

A comparison between Hardin’s breakage index and Einav’s breakage index under various confining pressures is presented in Fig. 4. The two breakage indices exhibit obviously increasing tendency with increasing confining pressure, indicating that considerable particle breakage is identified. The growth rate slows down afterward. However, the index adopted by Hardin [17] is too small to reflect the influence of particle breakage. In addition, it is widely accepted that the grain size distribution tends to be fractal and should be bounded by an ultimate distribution, rather than an arbitrary cutoff value of particle size (0.075 mm). In this paper, the definition of relative breakage after Einav [13, 14], here denoted by B for simplicity, will be employed to incorporate in the constitutive relation.

Fig. 4

Comparison of breakage indices of frozen saline sandy soil based on the definitions after Hardin [17] and Einav [13]

According to the experimental results, the fractal dimension α related to the confining pressure σ_c can be given as:

$$\alpha = m_{0} + n_{\alpha } \log (\sigma_{\text{c}} /p_{\text{a}} )$$

(5)

where m₀ and n_α are material parameters. As for various salt contents, m₀ can be chosen as a constant of 2.36 and the values of n_α are shown in Table 2; p_a is atmospheric pressure with the value of 0.10133 MPa.

Table 2 Values of n_α under various salt contents

From Eqs. (4) and (5), the expression of relative breakage can be given as:

$$B = \frac{{[m_{0} + n_{\alpha } \log (\sigma_{\text{c}} /p_{\text{a}} ) - \alpha_{0} ](3 - \alpha_{\text{u}} )}}{{(\alpha_{\text{u}} - \alpha_{0} )[3 - m_{0} - n_{\alpha } \log (\sigma_{\text{c}} /p_{\text{a}} )]}}$$

(6)

3 Elastoplastic constitutive model for frozen saline sandy soil

The constitutive response of soils can be described by several ways of constructing mathematical models. One is based on the classical theory of elastoplastic solids, developed by applying the thermomechanical theories into the general framework to establish constitutive relation. The thermodynamics theory has been developed widely and applied to study the constitutive relations of different materials [4, 37, 46, 68]. The soil can be regarded as a rate-independent, elastoplastic material, and then the thermomechanical method can be adopted to describe its mechanical properties. The major attraction of thermomechanical approach is that it can satisfy the laws of thermodynamics automatically. The constitutive behaviors of soils, such as elasticity law, yield condition, hardening law and flow rule, can be completely determined by two thermodynamic potentials, i.e., the free energy and dissipation increment functions [7, 9]. Besides, the yield function and plastic potential can be determined simultaneously, rather than being normally given independently in geomechanics.

The relative breakage illustrates the evolution of grain size distribution of soils during loading and can be incorporated in the thermomechanical analysis as an internal variable based on the continuum breakage mechanics (CBM). A new constitutive modelling framework was proposed based on CBM, and the yield function can be directly derived from the rate of breakage and plasticity dissipation mechanisms [14, 56]. The theory combines the breakage and stress–strain behavior of granular materials. For frozen saline sandy soil, the flow mechanism can be regarded as the combination of plastic mechanisms (plastic shear and compressive mechanisms) and breakage mechanism. In the following, a constitutive model considering both the breakage and plastic mechanisms will be developed. The plastic shear and compressive mechanisms are based on the double-yield-surface constitutive model [74] by introducing the parameters related to breakage into the hardening properties to reflect the influence of particle breakage on plastic deformation. The breakage mechanism is described by the free energy potential and dissipation potential related to relative breakage.

In order to develop a new constitutive model, the following basic assumptions are made: (a) The frozen saline coarse sandy soil is supposed to be rate-independent and isotropic; (b) the breakage is only accounted for soil matrix; (c) the breakage of different fractions is assumed to be identical for all of the particle fractions; (d) the average stored energy within grains is related to the particle size, i.e., larger particles store more energy than smaller ones.

3.1 Determination of failure strength line

The failure strength of sands can be regarded as a reference state from which the most important mechanical behaviors are derived [3]. For unfrozen sandy soils under relatively low pressures, the failure strength line (FSL) in p–q plane is a linear one, passing through the origin of the coordinates. With respect to frozen saline sandy soils, the FSL passes through the isotropic tensile point instead of the origin due to the bounding of ice, salt crystal and soil particles at low temperatures. Besides, the FSL of frozen saline sandy soil is bent downward with the increase in hydrostatic pressure, resulting from pressure melting of ice under relatively high pressure. In order to simulate the evolution of FSL for frozen soils, numerous strength criteria have been proposed, including modified Mohr–Coulomb strength criterion [44], polynomial strength criterion [78] and modified hydrostatic pressure strength criterion [31, 82]. Soil particles are inclined to breakage under relatively high pressure. Particle breakage results in the reduction in peak friction angle, indicating the deterioration of soil strength [79]. Results from Xiao et al. [73] also revealed that the slope of CSL in p–q plane decreases with the progressive development of particle breakage.

The FSLs of the frozen saline sandy soils with different salt contents under the temperature of − 6 °C are shown in Fig. 5. It can be found that the strength increases with the increase in confining pressure under relatively low pressures. The samples are liable to deform under low confining pressures, causing the low strength. With the continuous increase in confining pressure, the deformation is limited, resulting in the gradual increase in strength [78]. Then the increasing amplitude slows down and the strength reaches peak values and presents a decreasing trend with a further increase in pressure. Under relatively high pressures, the microcracks expand due to the melting of ice, leading to strength weakening. Besides, particle breakage occurs under large pressure and extensive shear strain, indicating that larger particles are extruded into smaller ones. The interference among particles is reduced as a result of particle breakage, resulting in the strength decrease [35]. In addition, the influence of salt content on strength is obvious when the confining pressure is high. Under a certain pressure, the strength commonly exhibits a decreasing tendency when the salt content varies from 0 to 3.5%. This may be explained by that the amount of unfrozen water increases with increasing salinity, leading to a decrease in strength.

Fig. 5

Experimental results and fitting curves of FSLs of frozen saline sandy soils with various salt contents

Based on the effect of particle breakage and the modified hydrostatic pressure strength criterion [31, 82], the following formula is proposed to describe the failure strength of frozen saline sandy soils with various salt contents in p–q plane:

$$q = \left( {M_{0} - \frac{m}{{p_{\text{a}} }}\left\langle {p - p_{\text{b}} } \right\rangle } \right)p + A_{0} p_{\text{a}} \left[ {1 - \left( {\frac{p}{{A_{1} {p}_{\text{a}} }}} \right)^{n} } \right]\exp \left[ {\left( {\frac{p}{{A_{1} {p}_{\text{a}} }}} \right)^{n} } \right]$$

(7)

where M₀ is the initial slope of FSL, p_b is the critical pressure of particle breakage, m is a constant describing the degree of particle breakage with increasing pressure when p is larger than p_b, A₀p_a is the intercept of FSL in p–q plane, A₁ and n are parameters related to pressure melting of ice. For simplicity, the parameter m is chosen as 0.0018 for different salt contents. < > is the Macaulay symbol, which applies to any scalar variable x:

$$\left\langle x \right\rangle \, = \, x, \, if \, x \ge 0; \, \left\langle x \right\rangle \, = \, 0, \, \quad {\text{if }}x < 0.$$

(8)

As shown in Eq. (7), the FSL turns into the one of modified Cam–Clay model when A₀ and m are both equal to zero. The prediction of FSLs for frozen saline sandy soils with various salt contents is shown in Fig. 5, and the fitting parameters are given in Table 3. The calculated results based on the proposed function of FSLs without considering particle breakage and pressure melting are shown in Fig. 6a, b, respectively. When the hydrostatic pressure is larger than p_b, the influence of particle breakage becomes more and more significant with increasing hydrostatic pressure. The factor of pressure melting has little effect under relatively low pressures, but the influence becomes obvious when the pressure is relatively high, for example higher than 16 MPa.

Table 3 Parameters of the critical strength for saline frozen soils with different salt contents

Fig. 6

Comparisons between test data and calculated FSLs at the salt content of 0%: a considering and not considering particle breakage; b considering and not considering pressure melting

3.2 Fundamental equations of thermodynamics

To develop the current constitutive model, the following stress and strain invariants are used in formulating the stress–strain relationship:

$${\it{p}} = \sigma_{ii} /3 = (\sigma_{11} + \sigma_{22} + \sigma_{33} )/3$$

(9)

$${\it{q}} = \sqrt {\frac{3}{2}s_{ij} s_{ij} }$$

(10)

where s_ij is stress deviator tensor (i = 1, 2, 3, and j = 1, 2, 3) and defined as:

$$s_{ij} = \sigma_{ij} - \sigma_{kk} \delta_{ij} /3$$

(11)

Where σ_ij is stress tensor; δ_ij is the Kronecker delta, δ_ij = 1 if i = j, and δ_ij = 0 if i ≠ j.

The complementary strain invariants are volumetric strain ε_v and shear strain ε_s, defined as:

$$\varepsilon_{\text{v}} = \varepsilon_{ii} = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}$$

(12)

$$\varepsilon_{\text{s}} = \sqrt {\frac{2}{3}e_{\text{ij}} e_{\text{ij}} }$$

(13)

where e_ij is strain deviator tensor and can be expressed as:

$$e_{\text{ij}} = \varepsilon_{\text{ij}} - \varepsilon_{\text{kk}} \delta_{\text{ij}} /3$$

(14)

where ε_ij is strain tensor.

For conventional triaxial tests, the stress and strain invariants are expressed as the following formulae:

$${\it{p}} = (\sigma_{1} + 2\sigma_{3} )/3$$

(15)

$$q = \sigma_{1} - \sigma_{3}$$

(16)

$$\varepsilon_{\text{v}} = \varepsilon_{1} + 2\varepsilon_{3}$$

(17)

$$\varepsilon_{\text{s}} = 2(\varepsilon_{1} - \varepsilon_{3} )/3$$

(18)

The first and second laws of thermodynamics, regarded as the basic energy equations for an isothermal deformation of rate-independent materials, can be written in a local rate form as:

$$\delta W = {\text{d}}\varPsi + \delta \varPhi ,\quad \delta \varPhi \ge 0$$

(19)

where δW is the increment in applied work; ψ and dψ are the Helmholtz free energy and its increment; and δΦ, defined as nonnegative, is a part of the applied work that is dissipated and cannot be recovered. Here, ψ is a state function and has a proper differential, which can be integrated from one state to another, while W and Φ are not state functions and only the increment can be defined. Besides, δΦ is a homogeneous function of degree 1 in the plastic strain increment tensor dε^p_ij and relative breakage increment dB.

The free energy of decoupled material without particle breakage can be regarded as the sum of elastic and plastic components [9] as follows:

$$\varPsi (\varepsilon_{ij}^{e} ,\varepsilon_{ij}^{p} ) = \varPsi^{e} (\varepsilon_{ij}^{e} ) + \varPsi^{p} (\varepsilon_{ij}^{p} )$$

(20)

Referring to the suggested expressions of free energy function [13, 41], the following general form is assumed and employed:

$$\varPsi (\varepsilon_{ij}^{e} ,\varepsilon_{ij}^{p} ) = (1 - \theta B)\left[ {\varPsi_{0}^{e} (\varepsilon_{ij}^{e} ) + \varPsi_{0}^{p} (\varepsilon_{ij}^{p} )} \right]$$

(21)

where $\varPsi_{0}^{e}$ and $\varPsi_{0}^{p}$ are the elastic and plastic components of free energy function for soils without particle breakage; θ is soil grading index, describing how far the ultimate grain size distribution is from the initial one. θ = 1 − J_2u/J₂₀, J_2u and J₂₀ are the second-order moments of grain size distributions, indicating the way in which the grain sizes are distributed about the mean grain size and can be given by:

$$J_{{2{\text{u}}}} = \int_{{d_{\text{m}} }}^{{d_{\text{M}} }} {d^{2} \rho_{\text{u}} } (d)\text{d} d$$

(22)

$$J_{20} = \int_{{d_{\text{m}} }}^{{d_{\text{M}} }} {d^{2} \rho_{0} } (d)\text{d} d$$

(23)

where ρ_u(d) and ρ₀(d) represent the ultimate and initial grain size distributions, respectively.

The total work increment is regarded as the sum of elastic and plastic parts and can be written as:

$$\delta W = \delta W^{\text{e}} + \delta W^{\text{p}} = \sigma_{ij} {\text{d}}\varepsilon_{ij}$$

(24)

$$\delta W^{\text{e}} = \sigma_{ij} {\text{d}}\varepsilon_{ij}^{\text{e}} = (1 - \theta B){\text{d}}\varPsi_{0}^{\text{e}} (\varepsilon_{ij}^{\text{e}} ) = (1 - \theta B)\frac{{\partial \varPsi_{0}^{\text{e}} (\varepsilon_{ij}^{\text{e}} )}}{{\partial \varepsilon_{ij}^{\text{e}} }}{\text{d}}\varepsilon_{ij}^{\text{e}}$$

(25)

$$\delta W^{\text{p}} = \sigma_{ij} {\text{d}}\varepsilon_{ij}^{\text{p}} = (1 - \theta B){\text{d}}\varPsi_{0}^{\text{p}} (\varepsilon_{ij}^{\text{p}} ) + \delta \varPhi = (1 - \theta B)\frac{{\partial \varPsi_{0}^{\text{p}} (\varepsilon_{ij}^{\text{p}} )}}{{\partial \varepsilon_{ij}^{\text{p}} }}{\text{d}}\varepsilon_{ij}^{\text{p}} + \delta \varPhi$$

(26)

From Eqs. (24)–(26), the total stress can be expressed as the sum of shift and dissipative stresses:

$$\sigma_{ij} = \sigma_{ij}^{\text{s} } + \sigma_{ij}^{\text{d} }$$

(27)

$$\sigma_{ij}^{\text{s}} = (1 - \theta B)\frac{{\partial \varPsi_{0}^{\text{p}} (\varepsilon_{ij}^{\text{p}} )}}{{\partial \varepsilon_{ij}^{\text{p}} }}$$

(28)

$$\sigma_{ij}^{\text{d}} = \frac{\partial (\delta \varPhi )}{{\partial {\text{d}}\varepsilon_{ij}^{\text{p}} }}$$

(29)

where σ_ij is the total stress; $\sigma_{ij}^{\text{s}}$ and $\sigma_{ij}^{\text{d}}$ are the shift and dissipative stresses, respectively. The former determines the center of yield surface, while the latter determines the expansion or contraction of yield surface during isotropic hardening or softening [7].

As can be seen from Eqs. (25)–(29), the total increment of plastic work can be regarded as the product of total stress with plastic strain increment, while the plastic dissipation is the result of dissipative stress with plastic strain increment. The plastic work and plastic dissipation are equal when the free energy is only the function of elastic strains.

3.3 Elastic parameters

In classical soil plasticity, the total strain increment dε_ij can be regarded as the sum of elastic and plastic components $\text{d} \varepsilon_{ij}^{\text{e}}$ and $\text{d} \varepsilon_{ij}^{\text{p}}$:

$$\text{d} \varepsilon_{\text{ij}} = \text{d} \varepsilon_{ij}^{\text{e}} + \text{d} \varepsilon_{ij}^{\text{p}}$$

(30)

As for geomaterials, the shear and volumetric strain components are commonly considered. The increments of strain invariants are expressed as:

$$\text{d} \varepsilon_{\text{s}} = \text{d} \varepsilon_{\text{s}}^{\text{e}} + \text{d} \varepsilon_{\text{s}}^{\text{p}}$$

(31)

$$\text{d} \varepsilon_{\text{v}} = \text{d} \varepsilon_{\text{v}}^{\text{e}} + \text{d} \varepsilon_{\text{v}}^{\text{p}}$$

(32)

In order to develop an elastoplastic constitutive model, the elastic parameters should be given firstly. It is noticed that the linear expression is the simplest elastic law possible, with only bulk and shear modulus to be determined. However, some researches indicated that the elastic stiffness of granular materials should be pressure dependent, and the nonlinear elastic relations were developed [16, 63]. In this study, the K–G model is adopted to calculate the elastic component of strain. The elastic shear modulus is obtained from the loading–unloading–reloading triaxial compression tests under constant confining pressure with an axial strain rate of 1.67 × 10⁻⁴ s⁻¹, which is the same as that in the conventional triaxial test as shown in Sect. 2.1. The confining pressures are 1, 3, 6, 10, 12 MPa for each salt content, and totally, 25 tests are needed. The stress–strain curve experiences seven hysteretic loops for each test, from which the elastic shear modulus can be obtained.

The triaxial shear loading–unloading–reloading test curve of the sample with a salt content of 2.5% under confining pressure of 6 MPa is shown in Fig. 7. The dashed line, which is very close to loading–unloading–reloading curve, presents the stress–strain result from the conventional triaxial test under the same test conditions. The elastic shear modulus can be obtained from the slope of hysteretic loop, which is calculated by $G\, = \,{\text{d}}q/\left( {3{\text{d}}\varepsilon_{\text{s}}^{\text{e}} } \right)$. The area of closed hysteretic loop presents the mechanical energy loss during each cycle. The elastic strain accounts for a very small proportion of the total strain compared with the plastic component.

Fig. 7

Triaxial shear loading–unloading–reloading curve of the frozen saline coarse sandy soil

It can be seen from Eq. (25) that the elastic modulus of soils experiencing particle breakage is related to the one of soils without breakage and a linear relation exists between them. Then the elastic shear modulus of frozen saline sandy soils without breakage can be obtained by referring to the results from loading–unloading–reloading test and the relative breakage after loading. Figure 8 represents the results of elastic shear modulus of frozen saline sandy soils with different salt contents without particle breakage under various confining pressures. The elastic shear modulus shows an increasing tendency with the increase in confining pressure for all the samples with various salt contents and tends to be stable afterward. Besides, the salt has an increasingly weakening effect on shear modulus. The following exponential function is proposed to describe the relationship between shear modulus G and confining pressure σ_c:

$$G = G_{0} p_{\text{a}} + m_{\text{g}} p_{\text{a}} \left[ {1 - \exp \left( { - \frac{{\sigma_{\text{c}} /p_{\text{a}} }}{{t_{\text{g}} }}} \right)} \right]$$

(33)

where G₀, m_g and t_g are material parameters of frozen saline sandy soils related to salt content and can be expressed as: G₀ = 96.63S³ − 789.76S² + 1033.54S + 7592.96, m_g = − 195.04S³ + 1507.66S² − 3121.73S + 3969.72, t_g = 10.61S³ − 67.59S² + 101.29S + 39.01, where S is the mass fraction of anhydrous Na₂SO₄. The calculated values of shear modulus by Eq. (33) are shown in Fig. 8. The proposed formula can well describe the variation trend of shear modulus under the influence of confining pressure.

Fig. 8

Relationship between confining pressure and elastic shear modulus of frozen saline coarse sandy soil without breakage at various salt contents

Combination of Eqs. (25) and (33) yields:

$$\frac{{\partial^{2} \varPsi_{0}^{\text{e}} }}{{\partial (\varepsilon_{\text{s}}^{\text{e}} )^{2} }} = 3G_{0} p_{\text{a}} + 3m_{\text{g}} p_{\text{a}} \left[ {1 - \exp \left( { - \frac{{\sigma_{\text{c}} /p_{\text{a}} }}{{t_{\text{g}} }}} \right)} \right]$$

(34)

The relationship between elastic volumetric modulus K and shear modulus G can be given by:

$$K = \frac{2(1 + \upsilon )}{3(1 - 2\upsilon )}G$$

(35)

where υ is Poisson’s ratio of soil and can be derived from the initial slope of ε_v − ε_a curve of triaxial test [2] when negligible particle breakage occurs:

$$\upsilon = \frac{1}{2}\left( {1 - \frac{{\Delta \varepsilon_{\text{v}} }}{{\Delta \varepsilon_{\text{a}} }}} \right)$$

(36)

From Eqs. (33), (35) and (36), the elastic volumetric modulus can be obtained and is shown in Fig. 9. The following expression is employed to describe its relationship with confining pressure:

$$K = m_{\text{k}} p_{\text{a}} \exp (n_{\text{k}} \cdot \sigma_{\text{c}} /p_{\text{a}} )$$

(37)

where m_k and n_k are material parameters which can be regarded as the functions of salt content: m_k = − 454.07S² + 214.69S + 18974.00; n_k = 0.0004S² − 0.0016S + 0.0123.

Fig. 9

Relationship between confining pressure and elastic volumetric modulus of frozen saline sandy soil without breakage at various salt contents

From Eqs. (25) and (37), the following expression can be obtained:

$$\frac{{\partial^{2} \varPsi_{0}^{\text{e}} }}{{\partial (\varepsilon_{\text{v}}^{\text{e}} )^{2} }} = m_{\text{k}} p_{\text{a}} \exp (n_{\text{k}} \cdot \sigma_{\text{c}} /p_{\text{a}} )$$

(38)

By referring to Eqs. (20), (21), (34) and (38), the elastic component of free energy function corresponding to relative breakage is expressed as:

$$\begin{aligned} \varPsi^{\text{e}} & = \frac{3(1 - \theta B)}{2}G_{0} p_{\text{a}} .(\varepsilon_{\text{s}}^{\text{e}} )^{2} + \frac{3(1 - \theta B)}{2}m_{\text{g}} p_{\text{a}} \left[ {1 - \exp \left( { - \frac{{\sigma_{\text{c}} /p_{\text{a}} }}{{t_{\text{g}} }}} \right)} \right](\varepsilon_{\text{s}}^{\text{e}} )^{2} \\ & \quad + \frac{(1 - \theta B)}{2}m_{\text{k}} p_{\text{a}} \exp \left( {n_{\text{k}} .\frac{{\sigma_{\text{c}} }}{{p_{\text{a}} }}} \right)(\varepsilon_{\text{v}}^{\text{e}} )^{2} \\ \end{aligned}$$

(39)

The elastic component of free energy of frozen saline sandy soil experiencing particle breakage depends on both elastic strains and relative breakage. Initially, all energy is stored in the particles when B = 0, and then it is gradually influenced by particle breakage. Smaller particles probabilistically store less energy due to the smaller coordination number. By contrast, larger particles have higher surface area and contact more adjacent particles [13]. Therefore, the free energy shows a decreasing tendency with the progressive development of particle breakage.

3.4 The breakage and plastic mechanisms of frozen saline sandy soil

The constitutive behavior of frozen saline sandy soil is related to two general dissipative mechanisms, i.e., dissipations from breakage and plasticity. Referring to conventional rate-independent plasticity, the breakage dissipation can be seen as a first-order homogeneous function of relative breakage increment. The single-yield-surface model cannot fully describe the mechanical behaviors of geomaterials under complex stress states, and thus, the multiple-yield-surface model is commonly employed. Typically, the plastic compressive and plastic shear mechanisms are considered to account for plastic deformation of soil. The yield surfaces related to plastic volumetric strain and plastic shear strain can be obtained from experiment results based on Eqs. (31) and (32), while the elastic components are calculated by Eqs. (33) and (37).

3.4.1 The particle breakage mechanism of frozen saline sandy soil

In thermodynamic context, the stresses in terms of free energy function, as shown in Eq. (39), may be expressed as:

$$p = \partial \varPsi^{\text{e}} /\partial \varepsilon_{\text{v}}^{\text{e}}$$

(40a)

$$q = \partial \varPsi^{\text{e}} /\partial \varepsilon_{\text{s}}^{\text{e}}$$

(40b)

$$E_{\text{B}} = - \partial \varPsi^{\text{e}} /\partial B$$

(40c)

where E_B, termed as breakage energy, is the energy conjugated to relative breakage with stress units [13]. The breakage energy E_B is a function of elastic stored energy, presenting the total released energy potential of soil from initial grain size distribution to ultimate one.

From Eqs. (39), (40a), (40b) and (40c), the following formula can be obtained:

$$E_{\text{B}} = \frac{\theta }{{2(1 - \theta {\text{B}})^{2} }}\left( {\frac{{p^{2} }}{K} + \frac{{q^{2} }}{3G}} \right)$$

(41)

The dissipation potential related to breakage is comprised of three different parts: increments of relative breakage, plastic volumetric strain and plastic shear strain. By consulting with the constitutive framework proposed by Nguyen and Einav [41] and Tengattini et al. [56], the breakage dissipation increment function under particle breakage mechanism for frozen saline sandy soil is assumed as:

$$\delta \varPhi_{\text{B}} = \sqrt {\delta \varPhi_{B1}^{2} + \delta \varPhi_{B2}^{2} + \delta \varPhi_{B3}^{2} }$$

(42)

where δΦ_B1, δΦ_B2 and δΦ_B3 are homogeneous first-order functions in the increments of relative breakage, plastic volumetric strain and plastic shear strain, respectively.

Considering the first-order homogeneity in the increments of relative breakage and plastic strains, the dissipation rate related to breakage may be expressed as:

$$\begin{aligned} \delta \varPhi_{\text{B}} = \frac{{\partial \delta \varPhi_{\text{B}} }}{{\partial {\text{d}}B}}{\text{d}}B + \frac{{\partial \delta \varPhi_{\text{B}} }}{{\partial {\text{d}}\varepsilon_{\text{v}}^{{p_{\text{B}} }} }}{\text{d}}\varepsilon_{\text{v}}^{{p_{\text{B}} }} + \frac{{\partial \delta \varPhi_{\text{B}} }}{{\partial {\text{d}}\varepsilon_{\text{s}}^{{p_{\text{B}} }} }}{\text{d}}\varepsilon_{\text{s}}^{{p_{\text{B}} }} \\ = E_{\text{B}} {\text{d}}B + p{\text{d}}\varepsilon_{\text{v}}^{{p_{\text{B}} }} + q{\text{d}}\varepsilon_{\text{s}}^{{p_{\text{B}} }} \\ \end{aligned}$$

(43)

The critical pressure under the same relative breakage is much higher than that of the unfrozen soils. In order to describe the hardening properties of frozen saline sandy soil, the three items of dissipation function related to breakage mechanism are given by:

$$\delta \varPhi_{B1} = \frac{{\sqrt {2E_{\text{B}} E_{\text{C}} /\xi } }}{{(1 - B)^{{n_{\text{B}} }} }}{\text{d}}B$$

(44a)

$$\delta \varPhi_{B2} = \frac{p}{{(1 - B)^{{n_{\text{B}} }} }}\sqrt {\frac{{2E_{\text{C}} }}{{\xi E_{\text{B}} }}} {\text{d}}\varepsilon_{\text{v}}^{{p_{\text{B}} }}$$

(44b)

$$\delta \varPhi_{B3} = \left\{ {[M_{0} - \kappa (p)] \cdot p + A_{0} p_{\text{a}} } \right\}{\text{d}}\varepsilon_{\text{s}}^{{p_{\text{B}} }}$$

(44c)

where E_C is an energy constant termed as critical breakage energy, which can denote the critical value of E_B needed to start particle breakage; ξ = λ₁(3 + β₁ · η²)/(3 + β · η²), η = q/p, λ₁ = K/K₁, β = 2/3 · (1 + υ)/(1 − 2υ), β₁ = 2/3 · (1 + υ₁)/(1 − 2υ₁), K = βG, K₁ = β₁G₁, where K₁, G₁ and υ₁ are elastic volumetric modulus, shear modulus and Poisson’s ratio, respectively, when the confining pressure is 1 MPa; $\kappa \left( p \right) = m/p_{\text{a}} \left\langle {p - p_{\text{b}} } \right\rangle$; n_B is regarded as a parameter to reflect the hardening rule of breakage yield surface, which, according to the test results, can be formulated as follows:

$$\begin{aligned} n_{\text{B}} & = - 2.0004 \times 10^{ - 7} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} + 6.1995 \times 10^{ - 5} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} \\ & \quad - 5.7538 \times 10^{ - 3} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} + 0.0778\left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 13.3284 \\ \end{aligned}$$

(45)

The critical breakage energy E_C can be presented in terms of breakage pressure p_cr which corresponds to relative breakage B during isotropic compression test. According to the test results, the relation between p_cr and B is taken in the following form:

$$p_{\text{cr}} = 68.023p_{\text{a}} \exp (4.1711B)$$

(46)

The stresses conjugating to relative breakage, plastic volumetric strain and plastic shear strain can be specified based on Eqs. (43), (44a), (44b) and (44c):

$$E_{\text{B}} = \frac{{\varPhi_{B1} }}{{\sqrt {\varPhi_{B1}^{2} + \varPhi_{B2}^{2} + \varPhi_{B3}^{2} } }}.\frac{{\partial \varPhi_{B1} }}{{\partial {\text{d}}B}}$$

(47a)

$$p = \frac{{\varPhi_{B2} }}{{\sqrt {\varPhi_{B1}^{2} + \varPhi_{B2}^{2} + \varPhi_{B3}^{2} } }}.\frac{{\partial \varPhi_{B2} }}{{\partial {\text{d}}\varepsilon_{v}^{{p_{B} }} }}$$

(47b)

$$q = \frac{{\varPhi_{B3} }}{{\sqrt {\varPhi_{B1}^{2} + \varPhi_{B2}^{2} + \varPhi_{B3}^{2} } }}.\frac{{\partial \varPhi_{B3} }}{{\partial {\text{d}}\varepsilon_{s}^{{p_{B} }} }}$$

(47c)

Based on Eqs. (47a), (47b) and (47c), the breakage yield function is formulated as:

$$f_{\text{B}} = \left( {\frac{{E_{B} }}{{\partial \varPhi_{B1} /\partial {\text{d}}B}}} \right)^{2} + \left( {\frac{p}{{\partial \varPhi_{B2} /\partial {\text{d}}\varepsilon_{v}^{{p_{B} }} }}} \right)^{2} + \frac{{q^{2} }}{{(\partial \varPhi_{B3} /\partial {\text{d}}\varepsilon_{s}^{{p_{B} }} )^{2} }} - 1 = 0$$

(48)

Substituting Eqs. (44a), (44b) and (44c) into Eq. (48) yields:

$$f_{\text{B}} = \frac{{\theta (1 - {\text{B}})^{{2n_{\text{B}} }} }}{{2(1 - \theta {\text{B}})^{2} E_{\text{C}} }}\left( {\frac{{p^{2} }}{{K_{1} }} + \frac{{q^{2} }}{{3G_{1} }}} \right) + \frac{{q^{2} }}{{\left\{ {\left[ {{M}_{0} - \kappa (p)} \right]p + A_{0} {\text{p}}_{\text{a}} } \right\}^{2} }} - 1 = 0$$

(49)

The yield loci for various values of B can be portrayed in the conventional triaxial stress space as shown in Fig. 10. With the progressive development of breakage, the yield surface expands rapidly and much more energy is needed for further breakage. Then by taking q = 0 for breakage yield function, the relationship between critical breakage energy E_C and initial breakage pressure p_cr0 can be obtained when relative breakage is equal to zero:

Fig. 10

Breakage yield surface in p–q plane

$$E_{\text{C}} = \frac{{\theta p_{{{\text{cr}}0}}^{2} }}{{2K_{1} }}$$

(50)

In order to describe the particle breakage properties more accurately, the non-associated flow rule is employed. Thus, the breakage potential function is taken in the following form:

$$g_{\text{B}} = \frac{{M_{1}^{2} \theta (1 - B)^{{2n_{\text{B}} }} }}{{2(1 - \theta B)^{2} E_{\text{C}} }}\left( {\frac{{p^{2} }}{{K_{1} }} + \frac{{q^{2} }}{{3G_{1} }}} \right) + \frac{{q^{2} }}{{\left\{ {[M_{0} - \kappa (p)] \cdot p + A_{0} p_{a} } \right\}^{2} }} + g_{B0} = 0$$

(51)

where M₁ is the material parameter for breakage potential function and g_B0 is the function of relative breakage.

Figure 11 shows the breakage yield locus with relative breakage of 0.25 and the corresponding breakage potential loci with various values of M₁. The value of M₁ is supposed to be 1.10 in this study.

Fig. 11

Breakage yield locus and breakage potential loci for frozen saline coarse sandy soils with various values of M₁ (the dashed lines represent breakage potential loci)

Then the following breakage parameters in p–q plane can be obtained from the breakage yield and potential functions:

$$\frac{{\partial f_{\text{B}} }}{\partial p} = \frac{{\theta (1 - {\it{B}})^{{2n_{\text{B}} }} p}}{{(1 - \theta {\it{B}})^{2} {\it{E}}_{\text{C}} K_{1} }} - \frac{{2{\it{q}}^{2} \left[ {{\it{M}}_{0} - \kappa (p) - p \cdot \frac{\partial \kappa (p)}{\partial p}} \right]}}{{\left\{ {[{\it{M}}_{0} - \kappa (p)] \cdot p + A_{0} p_{\text{a}} } \right\}^{3} }}$$

(52)

$$\frac{{\partial f_{\text{B}} }}{\partial q} = \frac{{\theta (1 - B)^{{2n_{\text{B}} }} q}}{{3(1 - \theta B)^{2} E_{\text{C}} G_{1} }} + \frac{2q}{{\left\{ {[M_{0} - \kappa (p)] \cdot p + A_{0} p_{\text{a}} } \right\}^{2} }}$$

(53)

$$\frac{{\partial f_{\text{B}} }}{\partial B} = \frac{{ - n_{\text{B}} \theta (1 - \theta B)(1 - B)^{{2n_{\text{B}} - 1}} + \theta^{2} (1 - B)^{{2n_{\text{B}} }} }}{{(1 - \theta B)^{3} E_{\text{C}} }}\left( {\frac{{p^{2} }}{{K_{1} }} + \frac{{q^{2} }}{{3G_{1} }}} \right)$$

(54)

$$\frac{{\partial g_{\text{B}} }}{\partial p} = \frac{{M_{1}^{2} \theta (1 - B)^{{2n_{\text{B}} }} p}}{{(1 - \theta B)^{2} E_{\text{C}} K_{1} }} - \frac{{2{\text{q}}^{2} \left[ {M_{0} - \kappa (p) - p \cdot \frac{\partial \kappa (p)}{\partial p}} \right]}}{{\left\{ {[M_{0} - \kappa (p)] \cdot p + A_{0} p_{\text{a}} } \right\}^{3} }}$$

(55)

$$\frac{{\partial g_{\text{B}} }}{\partial q} = \frac{{M_{1}^{2} \theta (1 - B)^{{2n_{\text{B}} }} q}}{{3(1 - \theta B)^{2} E_{\text{C}} G_{1} }} + \frac{2q}{{\left\{ {[M_{0} - \kappa (p)] \cdot p + A_{0} } \right\}^{2} }}$$

(56)

$$\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }} = \frac{{M_{1}^{2} \xi (1 - B)^{{2n_{\text{B}} }} }}{{E_{\text{C}} }}$$

(57)

3.4.2 The plastic compressive mechanism of frozen saline sandy soil

After particle breakage, the soil will develop more deformation under compression due to its larger contractancy properties. The hardening parameter which controls the size of yield surface under plastic compressive mechanism can be improved as a function of relative breakage to reflect the influence of particle crushing on plastic deformation [77]. The commonly adopted method is to incorporate the evolution of grain size distribution into constitutive equations. In this study, the parameters related to particle breakage, employed in the FSL, will be used in the plastic dissipation functions of frozen saline sandy soil. Under plastic compressive mechanism, the plastic dissipation function is assumed as follows according to the results from Collins and Hilder [8]:

$$\delta \varPhi_{\text{v}} = \sqrt {(A_{\text{v}} {\text{d}}\varepsilon_{\text{v}}^{{p_{\text{v}} }} )^{2} + (B_{\text{v}} {\text{d}}\varepsilon_{\text{s}}^{{p_{\text{v}} }} )^{2} }$$

(58)

where A_v and B_v are two parameters that have dimensions of stress. Various constitutive models can be obtained for different types of parameters A_v and B_v. These two parameters are assumed to be expressed by the following forms:

$$A_{\text{v}} = (1 - \vartheta )\chi (p) \cdot p_{0} h_{\text{v}}$$

(59a)

$$B_{\text{v}} = \beta \chi (p) \cdot p_{0} h_{\text{v}}$$

(59b)

where $\vartheta$ and β are two parameters which control the position and shape of yield surface and chosen as 0.3011 and 0.6751, respectively, based on the experimental results; $\chi \left( p \right) = \exp \left( { - m/p_{\text{a}} \left\langle {p - p_{\text{b}} } \right\rangle } \right)$. The plastic work and plastic strains, including volumetric strain and shear strain, can be used as hardening parameters in the constitutive model of soil. In this paper, h_v, as a function of plastic volumetric strain, is the hardening parameter under plastic compressive mechanism.

By differentiating the plastic compressive dissipation function in Eq. (58) with respect to the increments of plastic volumetric strain and plastic shear strain, the dissipative hydrostatic pressure and shear stress are written as:

$$\pi_{\text{v}} = A_{\text{v}}^{2} d\varepsilon_{\text{v}}^{{p_{\text{v}} }} /\delta \varPhi_{\text{v}}$$

(60)

$$\tau_{\text{v}} = B_{\text{v}}^{2} {\text{d}}\varepsilon_{\text{s}}^{{p_{\text{v}} }} /\delta \varPhi_{\text{v}}$$

(61)

Then the following yield function in dissipative stress space is given by eliminating the plastic volumetric strain and shear strain from Eqs. (58), (60) and (61):

$$\left[ {\frac{{\pi_{\text{v}}^{{}} }}{{(1 - \vartheta )\chi (p) \cdot {\it {p}}_{0} h_{\text{v}} }}} \right]^{2} + \left[ {\frac{{\tau_{\text{v}}^{{}} }}{{\beta \chi (p) \cdot {\it{p}}_{0} h_{\text{v}} }}} \right]^{2} = 1$$

(62)

The plastic component of free energy function under compressive mechanism is supposed to be only dependent on plastic volumetric strain. Thus, the shift stress is related to the hydrostatic component:

$$\delta \varphi^{{p_{\text{v}} }} = \vartheta \chi (p){\it {p}}_{0} h_{\text{v}} \cdot \text{d} \varepsilon_{\text{v}}^{{p_{\text{v}} }}$$

(63)

$$\rho_{\text{v}} = \vartheta \chi (p){\it{p}}_{0} h_{\text{v}}$$

(64)

where ρ_v is the isotropic component of shift stress under compressive mechanism.

From Eqs. (62) and (64), the yield function in true stress space is therefore obtained by:

$$f_{\text{v}} = \left[ {\frac{{p - \vartheta \chi (p) \cdot p_{0} h_{\text{v}} }}{{(1 - \vartheta )\chi (p) \cdot p_{0} h_{\text{v}} }}} \right]^{2} + \left[ {\frac{q}{{\beta \chi (p) \cdot p_{0} h_{\text{v}} }}} \right]^{2} - 1 = 0$$

(65)

The yield loci corresponding to Eq. (65) under different plastic volumetric strains are shown in Fig. 12. The solid lines in Fig. 12 represent yield loci that consider the influence of particle breakage. The dashed lines with the same color present yield loci under the same plastic volumetric strain without considering particle breakage. After particle breakage, the compressive yield locus is much closer to the origin, indicating that more plastic deformation will occur under the same stress state.

Fig. 12

Volumetric yield surface of frozen saline coarse sandy soil

By introducing the non-associated flow rule, the following function, which is similar to the yield one, is proposed as plastic potential function under compressive mechanism:

$$g_{\text{v}} = \left[ {\frac{{p - \vartheta \chi (p)p_{0} h_{\text{v}} }}{{(1 - \vartheta )\chi (p) \cdot p_{0} h_{\text{v}} }}} \right]^{2} + \left[ {\frac{q}{{\beta \chi (p) \cdot p_{0} h_{\text{v}} + \alpha p}}} \right]^{2} - 1 = 0$$

(66)

The sketches of plastic potential function with different values of α are shown in Fig. 13, compared with the yield locus when α is equal to zero. The value of α is chosen as − 0.4 in this paper.

Fig. 13

Volumetric plastic potential surface for frozen saline coarse sandy soil

From Eq. (65), the hardening parameter h_v is written as:

$$h_{\text{v}} = \frac{{\vartheta \beta p - \sqrt {T\left( {p,q} \right)} }}{{\beta (2\vartheta - 1)p_{0} \chi (p)}}$$

(67)

where T(p, q) is the function of stress variables, $T\left( {p,q} \right) = \vartheta^{2} \beta^{2} p^{2} + \beta^{2} p^{2} + q^{2} - 4\vartheta q^{2} + 5\vartheta^{2} q^{2} - 2\vartheta \beta^{2} p^{2} - 2\vartheta^{3} q^{2}$.

Based on the test results, the relationship between hardening parameter h_v and plastic volumetric strain $\varepsilon_{\text{v}}^{{p_{\text{v}} }}$ can be given as:

$$h_{\text{v}} = a_{\text{v}} + b_{\text{v}} \ln (c_{\text{v}} + \varepsilon_{\text{v}}^{{p_{\text{v}} }} )$$

(68)

where a_v, b_v and c_v are test parameters that can be obtained by curve fitting:

$$a_{\text{v}} = - 1.5383 \times 10^{ - 7} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} + 1.3982 \times 10^{ - 6} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} + 3.4326 \times 10^{ - 3} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} - 0.0077\left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 66.9545$$

(69a)

$$b_{\text{v}} = 2.5187 \times 10^{ - 7} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} - 1.0827 \times 10^{ - 4} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} + 1.3330 \times 10^{ - 2} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} - 0.3528\left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 13.7675$$

(69b)

$$c_{\text{v}} = 1.2709 \times 10^{ - 9} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} - 4.6018 \times 10^{ - 7} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} + 5.2447 \times 10^{ - 5} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} - 0.0016\left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 0.0137$$

(69c)

Then the parameters related to plastic compressive mechanism are expressed as follows according to Eqs. (65) and (66):

$$\frac{{\partial f_{\text{v}} }}{\partial p} = \frac{{2\left[ {p - \vartheta \chi (p) \cdot p_{0} h_{\text{v}} } \right] \cdot \left[ {\chi (p) - p \cdot \frac{\partial \chi (p)}{\partial p}} \right]}}{{(1 - \vartheta )^{2} p_{0}^{2} h_{\text{v}}^{2} \chi^{3} (p)}} - \frac{{2q^{2} \cdot \frac{\partial \chi (p)}{\partial p}}}{{\beta^{2} p_{0}^{2} h_{\text{v}}^{2} \chi^{3} (p)}}$$

(70)

$$\frac{{\partial f_{\text{v}} }}{\partial q} = \frac{2q}{{\beta^{2} p_{0}^{2} h_{\text{v}}^{2} \chi^{2} (p)}}$$

(71)

$$\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }} = - \frac{{2p\left[ {p - \vartheta \chi (p) \cdot {\text{p}}_{0} h_{\text{v}} } \right]}}{{(1 - \vartheta )^{2} p_{0}^{2} h_{\text{v}}^{3} \chi^{2} (p)}} - \frac{{2q^{2} }}{{\beta^{2} p_{0}^{2} h_{\text{v}}^{3} \chi^{2} (p)}}$$

(72)

$$\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }} = \frac{{b_{\text{v}} }}{{c_{\text{v}} + \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}$$

(73)

$$\frac{{\partial g_{\text{v}} }}{\partial p} = \frac{{2\left[ {p - \vartheta \chi (p) \cdot p_{0} h_{\text{v}} } \right] \cdot \left[ {\chi (p) - p \cdot \frac{\partial \chi (p)}{\partial p}} \right]}}{{(1 - \vartheta )^{2} p_{0}^{2} h_{\text{v}}^{2} \chi^{3} (p)}} - \frac{{2q^{2} \cdot \left[ {\beta p_{0} h_{\text{v}} \frac{\partial \chi (p)}{\partial p} + \alpha } \right]}}{{\left[ {\beta p_{0} h_{\text{v}} \chi (p) + \alpha p} \right]^{3} }}$$

(74)

$$\frac{{\partial g_{\text{v}} }}{\partial q} = \frac{2q}{{\left[ {\beta p_{0} h_{\text{v}} \chi (p) + \alpha p} \right]^{2} }}$$

(75)

3.4.3 The plastic shear mechanism of frozen saline sandy soil

A volumetric yield surface cannot fully explain the deformation characteristics obtained by the tests. Another type of plastic yield surface related to shear sliding should be introduced. For general geomaterials, the yield locus under plastic shear mechanism is most simply regarded as a linear function in p–q plane [62]. However, for frozen soils, a parabolic function is usually recommended and the yield locus can pass through the point corresponding to isotropic tensile strength [25]. Under plastic shear mechanism, from Eq. (58), the dissipation function is assumed as:

$$\delta \varPhi_{\text{s}} = \sqrt {A_{\text{s}} (d\varepsilon_{\text{v}}^{{p_{\text{s}} }} )^{2} + B_{\text{s}} ({\text{d}}\varepsilon_{\text{s}}^{{p_{\text{s}} }} )^{2} }$$

(76)

where A_s and B_s are the functions of stresses and are assumed as:

$${\it{A}}_{\text{s}} = - \frac{{(p - \rho_{\text{s}} )^{2} p_{\text{a}} }}{{p - \rho_{\text{s}} - p_{\text{a}} }}$$

(77a)

$$B_{\text{s}} = \left[ {M_{0} - \kappa (p)} \right] \cdot p_{\text{a}}^{2} h_{\text{s}}$$

(77b)

where h_s presents the plastic shear hardening parameter, which is a function of plastic shear strain; ρ_s is the isotropic component of shift stress under shear mechanism, which is assumed as ρ_s = − A₀p_a.

The shear yield function in dissipative stress space is given by referring to the procedure under plastic compressive mechanism:

$$- \frac{{\pi_{\text{s}}^{2} (p - \rho_{\text{s}} - p_{\text{a}} )}}{{(p - \rho_{\text{s}} )^{2} p_{\text{a}} }} + \frac{{\tau_{\text{s}}^{2} }}{{\left[ {M_{0} - \kappa (p)} \right] \cdot p_{\text{a}}^{2} h_{\text{s}} }} = 1$$

(78)

where π_s and τ_s are dissipative hydrostatic pressure and shear stress under plastic shear mechanism, respectively.

The plastic free energy function is assumed as:

$$\delta \varphi^{{p_{\text{s}} }} = \rho_{\text{s}} \cdot {\text{d}}\varepsilon_{\text{v}}^{{p_{\text{s}} }}$$

(79)

Then the yield function in p–q plane is obtained by:

$$f_{\text{s}} = q^{2} - \left[ {{M}_{0} - \kappa (p)} \right]p_{\text{a}} h_{\text{s}} \cdot (p + A_{0} p_{\text{a}} ) = 0$$

(80)

Figure 14 shows the yield locus described by Eq. (80) with plastic shear strain of 5%. From Fig. 14, it can be seen that the yield surface considering particle breakage and that without considering the influence of breakage are the same before the occurrence of particle crushing. However, with the increase in hydrostatic pressure, the yield locus gradually bends down, indicating that particle crushing considerably affects the shear yield properties of frozen saline sandy soils.

Fig. 14

Shear yield locus of frozen saline coarse sandy soil

By applying the non-associated flow rule, the potential function is then given by Eq. (81) and is shown in Fig. 15:

$$g_{\text{s}} = k_{\text{s}} q^{2} - \left[ {{M}_{0} - \kappa_{\text{s}} (p)} \right]p_{\text{a}} h_{\text{s}} \cdot (p + A_{0} p_{\text{a}} ) = 0$$

(81)

where k_s is a material parameter and here it is 0.6; $\kappa_{\text{s}} = m_{\text{s}} /p_{\text{a}} \left\langle {p - p_{\text{b}} } \right\rangle$, and m_s can be obtained from experimental results:

Fig. 15

Plastic potential surface under shear mechanism

$$m_{s} = - 3.4192 \times 10^{ - 11} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} + 1.3372 \times 10^{ - 8} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} - 1.7268 \times 10^{ - 6} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} + 6.9525 \times 10^{ - 5} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 0.00267$$

(82)

From the test results, the hardening parameter h_s can be regarded as the function of plastic shear strain:

$$h_{\text{s}} = \frac{{\varepsilon_{\text{s}}^{{p_{\text{s}} }} }}{{a_{\text{s}} (\varepsilon_{\text{s}}^{{p_{\text{s}} }} )^{2} + b_{\text{s}} \varepsilon_{\text{s}}^{{p_{\text{s}} }} + c_{\text{s}} }}$$

(83)

where a_s, b_s and c_s are the material parameters and can be identified as:

$$a_{\text{s}} = - 3.0389 \times 10^{ - 8} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} + 1.4015 \times 10^{ - 5} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} - 1.7268 \times 10^{ - 6} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} + 6.9525 \times 10^{ - 5} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 0.00267$$

(84a)

$$b_{\text{s}} = 1.0621 \times 10^{ - 10} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} - 3.3516 \times 10^{ - 8} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} + 3.1768 \times 10^{ - 6} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} + 1.0592 \times 10^{ - 4} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 0.00673$$

(84b)

$$c_{\text{s}} = - 3.6030 \times 10^{ - 12} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{4} + 1.1182 \times 10^{ - 9} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{3} - 9.6043 \times 10^{ - 8} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right)^{2} + 2.4660 \times 10^{ - 6} \left( {\frac{{\sigma_{3} }}{{p_{\text{a}} }}} \right) + 3.7721 \times 10^{ - 5}$$

(84c)

From Eqs. (80) and (81), the parameters related to plastic shear mechanism are expressed as:

$$\frac{{\partial f_{\text{s}} }}{\partial p} = \left[ {\kappa (p) + p\frac{\partial \kappa (p)}{\partial p} + A_{0} p_{\text{a}} \frac{\partial \kappa (p)}{\partial p} - M_{0} } \right]p_{\text{a}} h_{\text{s}}$$

(85)

$$\frac{{\partial f_{\text{s}} }}{\partial q} = 2q$$

(86)

$$\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }} = - \left[ {M_{0} - \kappa (p)} \right](p + A_{0} p_{\text{a}} )p_{\text{a}}$$

(87)

$$\frac{{\partial h_{\text{s}} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }} = \frac{{ - a_{\text{s}} (\varepsilon_{\text{s}}^{{p_{\text{s}} }} )^{2} + c_{\text{s}} }}{{\left[ {a_{\text{s}} (\varepsilon_{\text{s}}^{{p_{\text{s}} }} )^{2} + b_{\text{s}} \varepsilon_{\text{s}}^{{p_{\text{s}} }} + c_{\text{s}} } \right]^{2} }}$$

(88)

$$\frac{{\partial g_{\text{s}} }}{\partial p} = \left[ {\kappa_{\text{s}} (p) + p\frac{{\partial \kappa_{\text{s}} (p)}}{\partial p} + A_{0} p_{\text{a}} \frac{{\partial \kappa_{\text{s}} (p)}}{\partial p} - M_{0} } \right]p_{\text{a}} h_{\text{s}}$$

(89)

$$\frac{{\partial g_{\text{s}} }}{\partial q} = 2k_{\text{s}} q$$

(90)

3.4.4 The elastoplastic incremental constitutive relation of frozen saline sandy soil

In order to describe the deformation mechanism and constitutive behavior of geomaterials, the framework of multi-mechanism elastoplasticity has widely been used [80]. The total plastic strain can be assumed as the product of various mechanisms and divided into additive sub-plastic strains which involve individual mechanism without considering the inter-coupling effect [28]. In this study, three different mechanisms, i.e., breakage, plastic compressive and shear mechanisms, denoted by k = B, v, s, respectively, are considered.

The increments of elastic volumetric strain and shear strain in Eqs. (31) and (32) can be determined by:

$$\text{d} \varepsilon_{\text{v}}^{\text{e}} = \frac{{\text{d} p}}{K}$$

(91a)

$$\text{d} \varepsilon_{\text{s}}^{\text{e}} = \frac{{\text{d} q}}{3G}$$

(91b)

The incremental plastic strain is written as the sum of the ones corresponding to various kinds of mechanisms:

$$\text{d} \varepsilon_{ij}^{p} = \text{d} \varepsilon_{ij}^{{p_{B} }} + \text{d} \varepsilon_{ij}^{{p_{\text{v}} }} + \text{d} \varepsilon_{ij}^{{p_{\text{s}} }}$$

(92)

By employing the non-associated flow rule, the plastic strain increment under each mechanism is determined by:

$$\text{d} \varepsilon_{ij}^{{p_{\text{B}} }} = \text{d} \lambda_{\text{B}} \frac{{\partial g_{\text{B}} }}{{\partial \sigma_{ij} }}$$

(93a)

$$\text{d} \varepsilon_{ij}^{{p_{\text{v}} }} = \text{d} \lambda_{\text{v}} \frac{{\partial g_{\text{v}} }}{{\partial \sigma_{ij} }}$$

(93b)

$$\text{d} \varepsilon_{ij}^{{p_{\text{s}} }} = \text{d} \lambda_{\text{s}} \frac{{\partial g_{\text{s}} }}{{\partial \sigma_{ij} }}$$

(93c)

where dλ_B, dλ_v and dλ_s are positive multipliers related to breakage, plastic compressive and shear mechanisms, respectively.

The consistency conditions, which can determine the multipliers, are given for each mechanism by:

$$\text{d} f_{\text{B}} = \frac{{\partial f_{\text{B}} }}{\partial p}\text{d} p + \frac{{\partial f_{\text{B}} }}{\partial q}\text{d} q + \frac{{\partial f_{\text{B}} }}{\partial B}\text{d} B = 0$$

(94a)

$$\text{d} f_{\text{v}} = \frac{{\partial f_{\text{v}} }}{\partial p}\text{d} p + \frac{{\partial f_{\text{v}} }}{\partial q}\text{d} q + \frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\text{d} \varepsilon_{\text{v}}^{{p_{\text{v}} }} = 0$$

(94b)

$$\text{d} f_{\text{s}} = \frac{{\partial f_{\text{s}} }}{\partial p}\text{d} p + \frac{{\partial f_{\text{s}} }}{\partial q}\text{d} q + \frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{s} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\text{d} \varepsilon_{\text{s}}^{{p_{\text{s}} }} = 0$$

(94c)

From Eqs. (93a), (93b), (93c), (94a), (94b) and (94c), we can obtain:

$$\text{d} \lambda_{\text{B}} = \frac{{ - \left( {\frac{{\displaystyle\partial f_{\text{B}} }}{\displaystyle\partial p}{\text{d}}p + \frac{{\displaystyle\partial f_{\text{B}} }}{\displaystyle\partial q} \cdot {\text{d}}q} \right)}}{{\frac{{\displaystyle\partial f_{\text{B}} }}{\displaystyle\partial B}\frac{{\displaystyle\partial g_{\text{B}} }}{{\displaystyle\partial E_{\text{B}} }}}}$$

(95a)

$$\text{d} \lambda_{\text{v}} = \frac{{ - \left( {\frac{{\displaystyle\partial f_{\text{v}} }}{\displaystyle\displaystyle\partial p} \cdot {\text{d}}p + \frac{{\displaystyle\partial f_{\text{v}} }}{\displaystyle\partial q} \cdot {\text{d}}q} \right)}}{{\frac{{\displaystyle\partial f_{\text{v}} }}{{\displaystyle\partial h_{\text{v}} }}\frac{{\displaystyle\partial h_{\text{v}} }}{{\displaystyle\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\displaystyle\partial g_{\text{v}} }}{\displaystyle\partial p}}}$$

(95b)

$$\text{d} \lambda_{\text{s}} = \frac{{ - \left( {\frac{{\displaystyle\partial f_{\text{s}} }}{\displaystyle\partial p} \cdot {\text{d}}p + \frac{{\displaystyle\partial f_{\text{s}} }}{\displaystyle\partial q} \cdot {\text{d}}q} \right)}}{{\frac{{\displaystyle\partial f_{\text{s}} }}{{\displaystyle\partial h_{\text{s}} }}\frac{{\displaystyle\partial h_{\text{s}} }}{{\displaystyle\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\displaystyle\partial g_{\text{s}} }}{\displaystyle\partial q}}}$$

(95c)

Then the increment of relative breakage can be derived from Eq. (95a):

$${\text{d}}B = {\text{d}}\lambda_{\text{B}} \frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}$$

(96)

The increments of plastic strains under each mechanism are written as:

$$\left\{ \begin{aligned} \text{d} \varepsilon_{\text{v}}^{{p_{\text{B}} }} \hfill \\ \text{d} \varepsilon_{\text{s}}^{{p_{\text{B}} }} \hfill \\ \end{aligned} \right\} = - \left[ {\begin{array}{*{20}c} {\frac{{\frac{{\partial g_{\text{B}} }}{\partial p}\frac{{\partial f_{\text{B}} }}{\partial p}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}}} & {\frac{{\frac{{\partial g_{\text{B}} }}{\partial p}\frac{{\partial f_{\text{B}} }}{\partial q}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}}} \\ {\frac{{\frac{{\partial g_{\text{B}} }}{\partial q}\frac{{\partial f_{\text{B}} }}{\partial p}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}}} & {\frac{{\frac{{\partial g_{\text{B}} }}{\partial q}\frac{{\partial f_{\text{B}} }}{\partial q}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}}} \\ \end{array} } \right]\left\{ \begin{aligned} \text{d} p \hfill \\ \text{d} q \hfill \\ \end{aligned} \right\}$$

(97a)

$$\left\{ \begin{aligned} \text{d} \varepsilon_{\text{v}}^{{p_{\text{v}} }} \hfill \\ \text{d} \varepsilon_{\text{s}}^{{p_{\text{v}} }} \hfill \\ \end{aligned} \right\} = - \left[ {\begin{array}{*{20}c} {\frac{{\frac{{\partial g_{\text{v}} }}{\partial p}\frac{{\partial f_{\text{v}} }}{\partial p}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}}} & {\frac{{\frac{{\partial g_{\text{v}} }}{\partial p}\frac{{\partial f_{\text{v}} }}{\partial q}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}}} \\ {\frac{{\frac{{\partial g_{\text{v}} }}{\partial q}\frac{{\partial f_{\text{v}} }}{\partial p}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}}} & {\frac{{\frac{{\partial g_{\text{v}} }}{\partial q}\frac{{\partial f_{\text{v}} }}{\partial q}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}}} \\ \end{array} } \right]\left\{ \begin{aligned} \text{d} p \hfill \\ \text{d} q \hfill \\ \end{aligned} \right\}$$

(97b)

$$\left\{ \begin{aligned} \text{d} \varepsilon_{\text{v}}^{{p_{\text{s}} }} \hfill \\ \text{d} \varepsilon_{\text{s}}^{{p_{\text{s}} }} \hfill \\ \end{aligned} \right\} = - \left[ {\begin{array}{*{20}c} {\frac{{\frac{{\partial g_{\text{s}} }}{\partial p}\frac{{\partial f_{\text{s}} }}{\partial p}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{s} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}} & {\frac{{\frac{{\partial g_{\text{s}} }}{\partial p}\frac{{\partial f_{\text{s}} }}{\partial q}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{\text{s}} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}} \\ {\frac{{\frac{{\partial g_{\text{s}} }}{\partial q}\frac{{\partial f_{\text{s}} }}{\partial p}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{s} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}} & {\frac{{\frac{{\partial g_{s} }}{\partial q}\frac{{\partial f_{s} }}{\partial q}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{\text{s}} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}} \\ \end{array} } \right]\left\{ \begin{aligned} \text{d} p \hfill \\ \text{d} q \hfill \\ \end{aligned} \right\}$$

(97c)

Based on Eqs. (31), (32), (91a), (91b), (97a), (97b) and (97c), the general formula of elastoplastic incremental constitutive relation is written as:

$$\left\{ \begin{aligned} \text{d} \varepsilon_{\text{v}} \hfill \\ \text{d} \varepsilon_{\text{s}} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } \\ {C_{21} } & {C_{22} } \\ \end{array} } \right]\left\{ \begin{aligned} \text{d} p \hfill \\ \text{d} q \hfill \\ \end{aligned} \right\}$$

(98)

where the elastoplastic compliance matrix can be expressed as follows:

$$C_{11} = \frac{1}{K} - \frac{{\frac{{\partial g_{B} }}{\partial p}\frac{{\partial f_{B} }}{\partial p}}}{{\frac{{\partial f_{B} }}{\partial B}\frac{{\partial g_{B} }}{{\partial E_{B} }}}} - \frac{{\frac{{\partial g_{v} }}{\partial p}\frac{{\partial f_{v} }}{\partial p}}}{{\frac{{\partial f_{v} }}{{\partial h_{v} }}\frac{{\partial h_{v} }}{{\partial \varepsilon_{v}^{{p_{v} }} }}\frac{{\partial g_{v} }}{\partial p}}} - \frac{{\frac{{\partial g_{s} }}{\partial p}\frac{{\partial f_{s} }}{\partial p}}}{{\frac{{\partial f_{s} }}{{\partial h_{s} }}\frac{{\partial h_{s} }}{{\partial \varepsilon_{s}^{{p_{s} }} }}\frac{{\partial g_{s} }}{\partial q}}}$$

(99a)

$$C_{12} = - \frac{{\frac{{\partial g_{\text{B}} }}{\partial p}\frac{{\partial f_{\text{B}} }}{\partial q}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}} - \frac{{\frac{{\partial g_{\text{v}} }}{\partial p}\frac{{\partial f_{\text{v}} }}{\partial q}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}} - \frac{{\frac{{\partial g_{\text{s}} }}{\partial p}\frac{{\partial f_{\text{s}} }}{\partial q}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{\text{s}} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}$$

(99b)

$$C_{21} = - \frac{{\frac{{\partial g_{\text{B}} }}{\partial q}\frac{{\partial f_{\text{B}} }}{\partial p}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}} - \frac{{\frac{{\partial g_{\text{v}} }}{\partial q}\frac{{\partial f_{\text{v}} }}{\partial p}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}} - \frac{{\frac{{\partial g_{\text{s}} }}{\partial q}\frac{{\partial f_{\text{s}} }}{\partial p}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{\text{s}} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}$$

(99c)

$$C_{22} = \frac{1}{3G} - \frac{{\frac{{\partial g_{\text{B}} }}{\partial q}\frac{{\partial f_{\text{B}} }}{\partial q}}}{{\frac{{\partial f_{\text{B}} }}{\partial B}\frac{{\partial g_{\text{B}} }}{{\partial E_{\text{B}} }}}} - \frac{{\frac{{\partial g_{\text{v}} }}{\partial q}\frac{{\partial f_{\text{v}} }}{\partial q}}}{{\frac{{\partial f_{\text{v}} }}{{\partial h_{\text{v}} }}\frac{{\partial h_{\text{v}} }}{{\partial \varepsilon_{\text{v}}^{{p_{\text{v}} }} }}\frac{{\partial g_{\text{v}} }}{\partial p}}} - \frac{{\frac{{\partial g_{\text{s}} }}{\partial q}\frac{{\partial f_{\text{s}} }}{\partial q}}}{{\frac{{\partial f_{\text{s}} }}{{\partial h_{\text{s}} }}\frac{{\partial h_{\text{s}} }}{{\partial \varepsilon_{\text{s}}^{{p_{\text{s}} }} }}\frac{{\partial g_{\text{s}} }}{\partial q}}}$$

(99d)

Until now, the total strain increment can be calculated by substituting Eqs. (52)–(57), (70)–(75), (85)–(90) into Eq. (98), while the increment of relative breakage can be obtained by Eq. (96).

4 Model verification and analyses

The proposed constitutive model is used to simulate the triaxial tests to check its validity. The properties of strain softening/hardening, dilation, pressure melting and particle breakage for frozen saline sandy soils will be captured.

4.1 Parameter determination

In order to obtain the deformation and relative breakage calculated by the proposed model, the parameters need to be determined. There are 5 parameters in shear modulus and volumetric modulus, which are related to salt contents. There are 5 parameters under particle breakage mechanism, which are n_B, E_C, θ, m and p_b. Additionally, 9 parameters need to be determined in the analyses of plastic hardening laws. From a series of conventional triaxial tests, consolidation tests, triaxial shear loading–unloading–reloading tests and sieve analyses, the model parameters can be given, and then the validity of proposed model can be demonstrated. The total model parameters and corresponding determination methods are given in Table 4.

Table 4 Parameters of the proposed model

4.2 Comparison with experimental results

The proposed model can predict the relative breakage under various stress paths. Figure 16 shows the comparisons of relative breakage between calculated and test results at both consolidation and shearing stages of conventional triaxial tests. The simulated relative breakages agree well with the test data, indicating that the proposed model can well capture the crushing properties of frozen saline sandy soils with different salt contents.

Fig. 16

Comparisons of B between simulated results and experimental data under conventional triaxial tests: a, b consolidation stage for samples with the salt contents of 0% and 1.5%, respectively; c, d shearing stage for samples with the salt contents of 0% and 1.5%, respectively

The stress–strain and volumetric strain curves of experimental data and simulated results are shown in Fig. 17. Three different salt contents are adopted to check the validity of the proposed model. It can be seen that the calculated results can well describe the deformation features of the frozen saline sandy soil with different salt contents. Both stress–strain curves and volumetric strain–axial strain curves are very sensitive to confining pressure. The proposed model can reflect strain softening and high dilation properties for samples under relatively low confining pressures, as well as strain hardening and shrinkage characteristics under relatively high confining pressures. In order to check the validity of the non-associated flow rule, a comparison between the simulated results by associated flow rule and non-associated flow rule was performed. The comparison results are shown in Fig. 18. The calculated deviator stress–axial strain curves by associated and non-associated flow rules are very close, and both of them can reproduce the stress–strain curves well. However, as for volumetric strain–axial strain curves, the dilation deformation calculated by the associated flow rule is much larger than the test results. For example, the calculated volumetric strain by associated flow rule is about 5 times as large as the test results when the axial strain is 19.24% under the confining pressure of 14 MPa, which is not appropriate to simulate the constitutive response. Therefore, the non-associated flow rule is adopted in the proposed model.

Fig. 17

Comparisons between the simulated results and experimental data of triaxial compression tests under different confining pressures for samples with various salt contents

Fig. 18

Comparisons between the test data and the calculated results by employing non-associated flow rule and associated flow rule at the salt content of 1.5%

The triaxial compression tests under different stress paths were conducted to examine the capability of the proposed constitutive model in predicting the deformation behaviors of frozen saline sandy soils under complex stress paths. Figure 19 shows the comparison between the experimental data and the calculated results under the stress paths with constant p = 8 MPa and dq/dp = − 31.4. The simulated results are larger than the test data when the axial strain is relatively small, and the gaps are shrinking with increasing axial strain. The calculated and measured strengths are 14.54 MPa and 14.83 MPa under the loading stress path with a constant p, while these two values are 13.10 MPa and 13.67 MPa under the stress path with the constant slope of dq/dp = − 31.4. The errors are 1.96% and 4.17%, respectively, under the two different stress paths. Thus, the proposed model can well predict the strain–strain relation under various loading stress paths.

Fig. 19

Comparison between the calculated values and experimental data for triaxial tests under various loading stress paths

4.3 Effect of particle breakage on the performance of the proposed model

It is well recognized that the deformation and mechanical behaviors of coarse materials depend on the integrity of constituting particles, which is influenced by the degradation of particles during loading. In order to explain the influence of particle breakage on the constitutive response of the proposed model, the stress–strain relationship and volumetric deformation considering particle breakage effect or not are calculated for frozen saline sandy samples under various confining pressures, and the calculated results are illustrated in Fig. 20. It can be seen that the volumetric deformation is almost not influenced by particle breakage under relatively low confining pressures, for example 4 MPa at 0% salt content, while the peak strength and the residual strength with considering particle breakage are a little smaller and larger than those of test results, respectively. The influence of breakage is more obvious with increasing confining pressure. For the samples without considering particle breakage under high confining pressures, for example larger than 8 MPa, the strength shows a considerably increasing trend and the dilation phenomenon is more obvious, indicating a negative contribution of particle breakage to dilation, which conforms to the fact that coarse sands more easily generate shear dilation than fine sands. For the samples with the salt content of 2.5% under the confining pressure of 10 MPa, the calculated results agree well with the test data when particle breakage is considered. However, the calculated strength without considering particle breakage is larger than the test data, and the error between them is about 10.16%. The maximum difference between the calculated volumetric strain without considering particle breakage and the test data can reach 0.31% when the corresponding axial strain is 4.84%, and the relative error between them is about 153%, which is too large to meet the precision requirement of scientific calculation. Thus, the particle breakage can significantly affect the constitutive response.

Fig. 20

Comparisons between the test data and the calculated results by the proposed model considering and not considering particle breakage at different salt contents

5 Conclusions

In this paper, a series of triaxial compression tests were conducted for frozen saline coarse sandy samples with salt contents of 0%, 0.5%, 1.5%, 2.5% and 3.5% by weight under various confining pressures at temperature of − 6 °C. The relative breakage was measured after triaxial tests. Based on the test results, a constitutive model considering particle breakage, plastic compressive and plastic shear mechanisms is established. From this study, the following conclusions can be made:

• (1) A considerable plenty of particle breakage is identified after triaxial compression tests. The relative breakage increases from 0.0847 to 0.3881 when the confining pressure changes from 1 to 14 MPa. The predominant effect of particle breakage is to increase the content of fine particles. The larger particles are not susceptible to breakage due to the larger number of contacts compared with the smaller ones.

• (2) The strength of frozen saline sandy soil increases with increasing confining pressure at first. Then the increasing rate slows down and the strength reaches the peak value, followed by a decreasing trend afterward. A critical strength function in p–q plane is proposed by considering the effects of both particle breakage and pressure melting. The simulated results can well reflect the influence of salt content on the strength compared with experimental data.

• (3) An elastoplastic constitutive model of frozen saline sandy soil is developed under the breakage, plastic compressive and shear mechanisms by employing the non-associated flow rule. Compared with experimental results, the established model can well capture the breakage and deformation characteristics of the samples. The stress–strain relations can be well predicted by the proposed model under different stress paths. Particle breakage exerts a great influence on both the stress–strain behavior and volumetric deformation.