1 Introduction

Besides relative density and effective stress, the mechanical behaviour of granular materials depends on properties of both the aggregate and constituent particles, such as particle size distribution, mineral composition, inter-particle friction, hardness, strength, shape, and angularity. Experimental data indicate that particle irregularity and surface roughness promote looser packing, affect small strain stiffness, peak and critical state friction angles, compressibility, and creep behaviour [4, 7, 13, 17, 18, 29, 40, 49, 59]. Herle and Gudehus [27] have proposed relationships between constitutive parameters and properties of grain assemblies. Quite recently, Park and Santamarina [46] argued that, as particle shape affects the packing density of coarse-grained soils, it should be included in any meaningful soil classification system.

Barrett [8] proposed that the shape of a particle may be described by three potentially independent properties, namely overall form, angularity, and roughness, each referring to a characteristic scale. Overall form carries information on the proportions of the particle at the macro-scale, i.e. on how isometric or elongated the particle is; angularity accounts for local features of the particle at the meso-scale; roughness describes the texture of the particle surface at the micro-scale [15, 28, 39].

Traditionally, in soil mechanics, particle shape is characterised as “angular” or “rounded” following Powers [47], or using reference charts such as that proposed by Krumbein and Sloss [31], in which paradigmatic shapes are arranged in a matrix whose rows and columns correspond to two independent descriptors of sphericity [30] and roundness [55]. These can be quantified by visual comparison of a given particle with the shapes in the matrix, but they are affected by an element of subjectivity and provide at best an indication of particle morphology at the macro- and meso-scale.

Ehrlich and Weinberg [24] and Meloy [38] were among the first to use harmonic analysis of the 2D silhouette of a particle to obtain quantitative information on its shape. More recently, Mollon and Zhao [41, 42] and Zhou and Wang [61] applied spherical harmonic analysis to characterise and reconstruct their morphology in 3D. It has been proposed that higher-order harmonics may monitor grain roughness and surface texture, while lower-order harmonics deal with overall particle shape [12, 61]. Meloy [38] found that a linear relationship exists between the logarithm of the order of high-frequency Fourier coefficients and the logarithm of their amplitude, somehow indicating a self-similar nature of texture.

It has been suggested that natural surfaces may have a multi-scale nature [10], self-similar over a broad range of scales [48], so that a scale-independent parameter, namely the fractal dimension, should carry a signature of the morphology of the outline of the particle. Arasan et al. [5] proposed empirical relationships linking the fractal dimension of a particle’s outline to more conventional morphology descriptors. The results by Orford and Whalley [43], however, indicate that two or possibly more fractal elements emerge from the fractal analysis of the contour of natural grains, reflecting the morphological difference between micro-scale, or textural features, and meso-scale, or structural features.

The aim of this work is to propose a simple and effective method, based on the robust mathematical framework of fractal analysis, to characterise the morphology of soil particles in terms of three new quantitative descriptors that can be associated systematically to the observed mechanical behaviour of aggregates.

2 Background

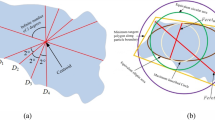
In general, a parameter describing the overall form of the contour of a particle should meet some basic requirements (see e.g. [19]): it should be independent of orientation, non-dimensional and, if possible, bounded between zero and one, corresponding to the two extreme limits of non-compact shapes and extremely compact shapes, such as a circle. Several descriptors of overall form have been used in the literature (see, e.g. [20] for a thorough review). Among others, two-dimensional form descriptors include: e.g. bounding box ratio BBR, or the ratio between the minimum and maximum side of the edge tangent enclosing box; 2D sphericity S, or the ratio between the diameter of the maximum inscribed circle and the diameter of the minimum circumscribed circle; and circularity, or the ratio of the area of the shape to the area of a circle having the same perimeter, C = 4πA/p2. While all these descriptors meet the requirements outlined above, only circularity is a true measure of the compactness of a 2D closed shape, while there are cases in which BBR and S may depend overly on one or two extreme points, or be unaffected by the presence of recesses.

Different quantitative definitions of angularity, describing the local features of the particles boundary at the meso-scale, have been proposed (e.g. [23, 32, 33, 50, 51, 55, 56]). However, they all suffer from ambiguities related to the scale at which angularity should be computed. Along an irregular outline, in fact, the number of recognisable local features increases as the image magnification increases and it is not obvious how to distinguish between structural and textural local features. Wadell [55] identified a “corner” as any portion of the projected outline of a particle which has a radius of curvature, r, less than or equal to the radius of the maximum inscribed circle, Rmax,in, and defined its roundness as the ratio of the two. He defined the overall degree of roundness of a particle as the arithmetic mean of the roundness of individual corners:

$$R = \frac{{\sum {r_{i} } }}{{NR_{\hbox{max} ,in} }},$$
(1)

where N is the total number of corners in the particle’s outline. He recognised the problem of the dependence of the computed value of roundness on the scale of observation, and suggested that roundness should be computed on images of a standard size, somehow supporting the idea that the characteristic scale of local features should be a proportion of the size of the particle. Zheng and Hryciw [60] used locally weighted regression and K-fold cross-validation to eliminate the effect of surface roughness in the assessment of particle roundness by numerical methods based on computational geometry.

Cho et al. [18] proposed to average the values of roundness and 2D sphericity, to obtain another morphological descriptor containing combined information on the macro- and meso-scales, which they called regularity:

$$\rho = \frac{S + R}{2}.$$
(2)

Their experimental results and those from a very large database of published studies on several natural and artificial sands indicate that several mechanical properties such as compressibility, void ratio extent, and small strain stiffness correlate well with particle regularity.

Finally, despite the increasing understanding of the role of roughness on the mechanical behaviour of coarse-grained soils (e.g. [45, 49]), very few well-established procedures exist to characterise the higher order of irregularities and the characteristic scales to which they are associated. The traditional and most direct way to quantify roughness is in terms of the root mean square deviation of a surface or a profile from its average level. This requires high-resolution measurements of the surface, typically obtained by optical interferometry. Moreover, as sand particles are curved, unlike flat-engineered surfaces, the processing procedure must flatten the surface or the contour of the particle, in order to remove the influence of curvature on the computed values of roughness. This may be achieved by some motif extraction method, filtering regular features (such as waviness) from textural features [11, 58] or by discretisation of the surface using best-fit planes of small size [16]. In both cases, however, the results depend on the shape motif parameters or the size of the best-fit planes.

The meaningful characteristic scale associated with textural features may depend on the mechanical parameter under examination; the works by Santamarina and Cascante [49] and Otsubo et al. [45] indicate that textural features at the micron-scale length may dominate the behaviour of contacts in the small strain range, whereas structural features at the nano-scale length, such as those investigated by Yang and Baudet [57] and Yang et al. [58], may be too minute to have an effect on the small strain stiffness even at relatively low confining stress.

As discussed above, many authors have linked the definition of roughness to the fractal dimension of either the outline of the particle [5, 15, 26] or in three-dimensional analyses, of its surface [57, 58]. The value of the fractal dimension is theoretically bound between 1 and 2 in the first case and between 2 and 3 in the second [36], where the lower bounds of the quoted ranges describe a perfectly smooth shape, while the upper bounds correspond to extremely rough shapes.

3 Fractal analysis

3.1 Method

Fractal analysis stems from the observation that the measured length of the contour of many natural irregular closed shapes, p, is a function of the measurement scale, b [35], and that the smaller the measurement scale, the longer the measured length becomes. The approximations with segments of length b of strictly self-similar mathematical curves, such as, e.g. the Koch snowflake [54], have lengths:

$$p = b^{(1 - \alpha )},$$
(3)

where α is the Hausdorff dimension, taking values between 1 and 2. Equation (3) implies that the length of the contour of any truly fractal closed shape diverges to infinity as the measurement scale tends to zero. When dealing with physical objects, indefinite subdivision of space does not make sense, as the minimum measurement scale would be limited at least by the distance at the atomic level, while in practice, well before this is achieved, it is limited by the experimental resolution with which the contour of the particle is defined. However, the plot of the length of the contour of a particle, p, versus measurement scale, b, still carries a signature of the morphology of the particle over the range of experimentally accessible scales. At the upper end of this range, the characteristic dimension of the particle can be conventionally defined as the diameter of the circle having the same area as the particle:

$$D = \sqrt {\frac{4A}{\pi }}.$$
(4)

The input for the fractal analysis is a 2D image of the particle of any resolution, as obtained, e.g. by optical or scanning electron microscopy; it is evident that the higher the resolution of the image, the more the information can be extracted from the analysis. Typically, for natural silica sand, textural features start to emerge at about 1/20 of the characteristic size of the particle, so that, in order to be able to observe them, it should be bmin/D < 0.05, where bmin is the minimum accessible scale of an image of size L and a number of pixels N × N, and it is defined as the ratio between L and N.

In order to obtain quantitative information from images, they were processed by contrast enhancement, binarization, and segmentation. Contrast enhancement increases image sharpness thus facilitating subsequent binarization and segmentation. The method by Otsu [44] was used to obtain the binary version of the original greyscale image, by converting each pixel to either white (foreground) or black (background), based on a threshold value. When the particles were not in contact in the binarized image, they were identified simply by labelling areas composed by all connected foreground pixels. In more complex situations, for instance when processing images containing grains in contact, a watershed algorithm [9] was used for segmentation purposes. Figure 1a shows schematically a binarized particle image after segmentation, in which white pixels correspond to the particle, while black pixels correspond to the background. The contour of the particle can be extracted by subtracting from the binarized image of the particle its 8th-connected eroded, to obtain the external line of 8th-connected pixels (Fig. 1b) in the form of a vector containing their coordinates (xi and yi).

Fig. 1
figure 1

Steps of the method: a thresholding and segmentation of image, b extraction of 8th-connected boundary, c (d), and e measurement of perimeter with segments of fixed length

Full size image

The algorithm, coded in MATLAB [37], computes the length of the contour adopting segments of fixed length (Fig. 1c, d). A point of the contour is chosen as the starting point for the calculation (Fig. 1c), and one end of a segment of length b is fixed to it. A simple “while” loop, which stops when the distance between the starting point and a successive point on the boundary is greater than or equal to b, finds the intersection point between the other end of the segment and the boundary (Fig. 1c). In turn, this intersection point becomes the starting point for the second segment, until the whole contour is covered (Fig. 1d). Since a finite number of points discretise the outline, the exact distance between two subsequent intersection points is not strictly equal to the segment length b, but the maximum error is less than the pixel size. The loop ends when the distance between the intersection point and the initial starting point is less than b (Fig. 1e). The length of the contour is computed as the sum of the distances between all the intersection points. As this length depends on the chosen initial starting point [50], consistently with the definition of the Hausdorff dimension, the procedure is repeated using all the points of the boundary as starting points, and the perimeter of the particle, p, is defined as the minimum computed value of the length of the contour. Finally, the normalised perimeter, p/D, is plotted versus the corresponding normalised stick length, b/D, in a bi-logarithmic plane.

3.2 Three scales of information

Figure 2 shows an example of the results of the fractal analysis applied to a natural grain of Toyoura sand. A SEM photograph of the sand grain at a magnification factor of 300× (Fig. 2a) was obtained from Alshibli [2]. Figure 2b shows the same grain after binarization and segmentation; in this case, careful contrast enhancement was required to avoid altering the contour due to the presence of shadows and overlapping. The characteristic dimension of the particle is D = 185 μm, and the resolution of the image is 960 pixels/mm, or, in other words, one pixel corresponds to bmin = 1.04 μm. After boundary extraction, the perimeter was computed using segments of decreasing length from b = D to b = 0.001D, see Fig. 1c.

Fig. 2
figure 2

Toyoura sand particle: a SEM image; b segmented image; c perimeter at different stick lengths; d log(p/D) versus log(b/D)

Full size image

Figure 2d reports the results of the analysis in terms of log(b/D) versus log(p/D). Starting from b/D = 1 and moving to the left, as b/D decreases, p/D increases rapidly and nonlinearly from its minimum value of 2, corresponding to point (1) in Fig. 2d. For smaller values of b/D, two linear trends can be identified, with slopes − m and − μ, until the computed perimeter saturates and the plot becomes horizontal when the segment length reaches the pixel size, bmin/D = 0.0056.

The larger segment lengths, see, e.g. points (1) to (3) in Fig. 1d, even if providing the least accurate estimate of the actual perimeter of the particle, carry information about its overall proportions at the macro-scale. Intermediate segment lengths, see, e.g. points (3) to (4), recognise the local features of the particle contour at the meso-scale, while small segment lengths, see, e.g. point (5), convey the signature of surface texture, because they can follow the asperities of the contour at the micro-scale, see Fig. 2c.

The results in Fig. 2 are typical of natural sand particles. They confirm the findings by Orford and Whalley [43] on the emergence of two distinct self-similar patterns describing structural and textural features. Moreover, the characteristic scale separating the two, which may be regarded as the maximum size of the micro-asperities, emerges directly from the results and corresponds to the stick length at the point of intersection of the two linear portions of the plot, bm (= 0.028D = 5.4 μm) in Fig. 2d.

The absolute values of the slopes of the two linear portions of the plot relate to the fractal dimension in Eq. (3), and increase with the complexity of the profile [53]. These can be obtained by automatic linear regression in the log(b/D):log(p/D) plane, performing a check on the computed value of the coefficient of determination, R2. Starting from bmin/D, a linear regression is extended to include an increasing number of points, corresponding to larger and larger values of b/D, until R2 remains approximately constant and equal to 1. When R2 decreases by more than 0.02%, the process stops, and starts again with another regression on the remaining data; any linear trend must contain at least five data points. Figure 3 illustrates this procedure for the contour of the Toyoura sand particle of Fig. 2. In this case, the first linear regression ends at a value of b/D = bm/D = 0.028 and the second linear regression at b/D = 0.30, no further linear portions are identified by the algorithm. The computed absolute values of the slopes are m = 0.042 (αm = 1.042) and μ = 0.137 (αμ = 1.137).

Fig. 3
figure 3

Moving linear regression of log(p/D) versus log(b/D) data

Full size image

An important feature of the plot in Fig. 2d is the increase in the dimensionless perimeter above its minimum value of 2 over the range of stick lengths connected to overall shape and structural features (bm/D < b/D < 1):

$$\Delta = \left( {p/D} \right)_{{b_{\text{m}} }} - 2.$$
(5)

For the example in Fig. 2, Δ = 1.55.

Starting from an input binarized image of the grain, with a resolution of 0.5–3 μm/px, the MATLAB algorithm described in this section takes about 20 s on an ordinary PC to extract the boundary, run the fractal analysis of the contour, and recover the slopes of the fractal subsets.

4 Simple shapes

4.1 Structural features: macro- and meso-scale

Fractal analysis was applied first to the contour of simple smooth Euclidean shapes. Figure 4a shows the results obtained for a set of shapes representing a smooth transition from a square to a circle, obtained by rounding off the corners of the square with arcs of increasing radius, from 0.05 to 0.2 of its side. The theoretical normalised perimeters of the circle and the square for an infinitesimal stick length (b/D → 0) are p/D = π (≈ 3.14) and 2 × π0.5 (≈ 3.54), respectively.

Fig. 4
figure 4

Smooth shapes: a family of squares with progressively rounded corners; b family of rectangles of increasing elongation

Full size image

The logarithm of the computed perimeter of the circle rises very rapidly with decreasing logarithm of measurement length, reaching 98% of its asymptotic value at b/D ≈ 0.3; for smaller measurement lengths, the plot is linear and practically horizontal. This is because a smooth circle does not have any structural nor textural features, and therefore, the only linear portion of the plot is characterised by a slope m = μ = 0 (αm = αμ = 1). On the other hand, the corners between the edges of the square act as local features, giving rise to the emergence of a structural fractal subset at intermediate measurement lengths (m ≠ 0, αm > 1), which persists until the computed perimeter reaches about 97% of its theoretical value. The plot then becomes nearly horizontal (μ ≈ 0, αμ ≈ 1), as, again, the figure is smooth. The slope of the “structural” subset is the same for all the rounded squares, m = 0.07, while its extent reduces with increasing radius until it vanishes for the circle. This suggests that the fractal dimension of the structural subset, αm (= 1+m), may depend mainly on the angle existing between the edges while its extent, bm, on the degree of roundness of the corners.

Figure 4b reports the results obtained for a family of rectangles of increasing elongation. As far as the rectangles are concerned, as expected, both the slope and the extent of the structural subset are the same as those obtained for a square, m = 0.07 and bm/D = 0.08, because neither the degree of acuteness, nor their roundness changes with elongation. The computed value of the perimeter at bm/D, always within 97% of the theoretical value, increases significantly with elongation.

4.2 Textural features: micro-scale

Figure 5 shows the results of the fractal analysis of three shapes obtained superimposing to a smooth circle of diameter d an artificial saw-tooth profile consisting of equilateral triangles with decreasing side l = πd/50, πd/100, and πd/200. The characteristic dimensions of the three shapes are D = 1.05d, 1.02d, and 1.01d, respectively. The computed normalised perimeter of the three shapes follows very closely that of the circle, until the measurement length reaches the dimension of the asperity; here, the plot increases abruptly, attaining the theoretical value of the normalised perimeter, p/D = 5.97, 6.12, and 6.20, respectively. Despite some small oscillations, the fractal analysis is able to identify the size of the introduced asperities, although no fractal subset or linear portion of the plot emerges because the particle profile is not self-similar.

Fig. 5
figure 5

Circles with saw-tooth roughness of decreasing size

Full size image

Figure 6g shows the normalised perimeters of four Euclidean approximations of the Koch snowflake [54] at increasing order n = 2–5 (see Fig. 6a–f). The logarithm of the perimeter of each shape increases linearly with the logarithm of decreasing stick length, and then, it becomes constant at a value of b/Dn = Ln/Dn, where Ln represents the length of the side of the order n Euclidean approximation of the Koch snowflake. The slope of all plots is related to the fractal dimension of the Koch snowflake, − mkoch = − 0.262 (αKoch = 1.262). Thus, the fractal analysis of the contour recognises both the complexity of the shape, which in this case is truly scale-independent, (m = μ) and the characteristic scale of the asperities, Ln.

Fig. 6
figure 6

a–f Euclidean approximations of Koch snow flake at increasing order, and g fractal analysis of their contour

Full size image

The increase in the logarithm of the normalised perimeter is linear only if textural features are self-similar; the fact that natural grains present one or more linear subsets indicates that their contour is fractal over characteristic range of scales.

4.3 Morphology descriptors

Based on the results above, we propose that μ, m, and Δ, may be used to describe quantitatively the morphology of a particle at the micro-, meso-, and macro-scale, and that the characteristic length separating the textural and structural features may be taken as the value of bm, representing the maximum size of the micro-asperities.

Because the fractal dimension of a closed shape is theoretically bound between 1 and 2, μ(= αμ − 1) and m(= αm − 1) are automatically bound between 0 and 1, and can be effectively and directly used as morphology descriptors at the micro- and meso-scale. The increase in the dimensionless perimeter above its minimum value of 2 is theoretically the smallest for the circle:

$$\Delta_{\text{circle}} = \left( {p/D} \right)_{{b_{m} }} - 2 \approx \pi - 2 \approx 1.14,$$
(6)

so that a morphology descriptor at the macro-scale, theoretically bound between 0 and 1, can be defined as:

$$M = \frac{{\Delta_{\text{circle}} }}{\Delta }.$$
(7)

To explore the meaning of these quantities and establish their relation with other descriptors adopted in the literature, the fractal analysis was applied to the contour of the paradigmatic shapes included in the chart by Krumbein and Sloss [31] yielding the values of m and M reported in Fig. 7. Each particle in the chart has a dimension of about 10–15 mm, and the resolution of the images is of the order of 3 pixels/mm, far too low to appreciate textural features.

Fig. 7
figure 7

M and m for Krumbein and Sloss chart (1936) particles

Full size image

Figure 8a shows that, both for simple shapes and smooth figures such as those in Krumbein and Sloss [31] chart, descriptor M is a very close measure of circularity, C(= 4πA/p2). For complex shapes, which may be self-similar over a broad range of scales, circularity is not size independent as its definition contains the perimeter of the particle, which increases with decreasing scale of observation. However, because descriptor M is evaluated over the range bm < b < D it accounts only for macro- and meso-features and is therefore effectively independent of the scale of observation.

Fig. 8
figure 8

Relationships between: a descriptor M and circularity C, b descriptor m and regularity ρ

Full size image

Figure 8b shows that for the shapes in Krumbein and Sloss [31] chart, descriptor m correlates very well with ρ, and therefore, it is likely to control all those aspects of the mechanical behaviour that depend on regularity, such as compressibility, void ratio extent, and small strain stiffness.

4.4 Real particles

Figure 9 shows nine SEM photographs of the grains of three natural sands with different morphological features [2].

Fig. 9
figure 9

Natural sand particles: a ASTM sand, b Columbia grout, and c Toyoura sand

Full size image

From a preliminary morphology analysis, conducted using standard charts, ASTM sand grains (Fig. 9a) can be classified as rounded and regular (ρ ≈ 0.9), Columbia grout grains (Fig. 9b) as sub-angular and less regular (ρ ≈ 0.6), and finally Toyoura sand grains (Fig. 9c) as angular and even less regular (ρ ≈ 0.5).

The value of bmin/D is about the same for all three sands. The image of ASTM sand has a lower resolution (380 pixels/mm) than those of Columbia grout and Toyoura sands (960 pixels/mm), but the grain size is larger for ASTM sand, D ~ 850 μm, and smaller for the other two, ranging between 297 and 420 µm, and between 100 µm and 320 µm, respectively.

Figure 9 and Table 1 summarise the results of the fractal analysis of the contour of the nine sand particles, obtained following the procedures outlines in Sect. 3. The results for the three ASTM sand grains (Fig. 9a), at least for b/D ≥ 0.05, overlap with one another and are very close to those obtained for a circle, with very small values of m(≈ 0.02) denoting the absence of structural features. For grains (1) and (3), the almost horizontal linear portion of the plot extends down to bm/D ≈ 0.03, and then, the plot starts to increase linearly (μ ≈ 0.05) as the textural features begin to contribute to the computed value of the normalised perimeter. The extent of the structural subset for grain (2) is more limited. In this case, the textural subset emerges at a value of bm/D ≈ 0.05 with μ ≈ 0.12, almost twice the value computed for the other two grains, which is an index of a textural complexity not easily recognisable by naked eye from the images in Fig. 9a. The three grains have very similar and high values of M = 0.84–0.95, consistent with the isometry of their overall shape, with the highest value associated with grain (3), easily recognised as the most circular in Fig. 9a.

Table 1 Results of fractal analysis of natural sand particles
Full size table

The normalised perimeters of grains (2) and (3) of Columbia grout (Fig. 9b) are very similar. Two clearly identifiable fractal subsets emerge from the fractal analysis of their contour, with m ≈ 0.04 and μ ≈ 0.11, and the same cut-off separating structural and textural features, bm/D = 0.014. For grain (1), only one fractal subset emerges with μ ≈ 0.19 and it is impossible to identify clearly the characteristic scale separating structural from textural effects. In fact, closer inspection of the SEM photographs in Fig. 9b reveals that the contour of grain (1) is characterised by asperities of a larger maximum size than for the other two grains, so that the increase in normalised perimeter due to texture complexity masks in part the effects of structural features. In cases like this, it is difficult to define unambiguously two different linear trends: the descriptor M is computed using a value of normalised perimeter at bm/D = 0.1 corresponding to the end of the linear regression. On average, Columbia grout grains are less circular than ASTM sand, with smaller values of M (≈ 0.75). It must be noted that, for grain (1) the portion of the contour corresponding to the shadowed area in the greyscale image is very irregular, possibly due to inaccuracies in the automatic segmenting procedures that did not recognise distinctly the grain contour. To a certain extent, the same comment applies also to grain (2) of ASTM sand.

Two fractal subsets, characterised by μ ≈ 0.10 and m ≈ 0.05, emerge from the results obtained for all three Toyoura sand grains (Fig. 7c). However, the structural subset for grain (3) extends to smaller scales (bm/D ≈ 0.03) than for grains (1) and (2) (bm/D ≈ 0.07 and 0.08, respectively), denoting a smaller maximum size of textural asperities (bm ≈ 6.7 μm), which would have been difficult to detect by naked eye. Moreover, because grain (3) is more elongated than the other two, its normalised perimeter increases more and has a smaller value of M (≈ 0.6).

The fractal dimensions of the structural and textural subset of the three natural sands given above compare favourably with those reported by Orford and Whalley [43] for carbonate beach grains from the Maldives and pyroclastic particles from the 1980 Eruption of Mount St Helens.

The sand grains in Fig. 9 were chosen intentionally so that two of them would be representative of the typical results for each material, and one would deviate from typical in one or more respects. These deviations may be due to an occasional difference in form, as in the case of the much more elongated grain (3) of Toyoura sand, or by an occasional increase in complexity of the contour, as in the case of grain (2) of ASTM sand, be it true or due to errors in image processing due to the presence of shadows, as partly for grain (1) of Columbia grout. This is an indication of the power of the method, which is very sensitive even to very small variations in the complexity of the contour.

Figure 10 shows nine SEM photographs of grains of a crushed Lightweight Expanded Clay Aggregate (LECA) (see e.g. [14], in the sizes 500–1000 µm or “large” (Fig. 10a), 125–250 µm or “intermediate” (Fig. 10b), and < 63 µm or “fine” (Fig. 10c). The SEM images have a resolution of 340, 686, and 3430 pixels/mm, for large, intermediate, and small grains, respectively.

Fig. 10
figure 10

Crushed LECA in different grain sizes: a 500–1000 μm, b 125–250 μm, and c 63 μm

Full size image

The angularity of crushed LECA particles (Fig. 10) increases from sub-angular to very angular, and their regularity reduces from ρ ≈ 0.5 to ρ ≈ 0.4 with decreasing grain size; due to exposed intra-granular porosity, the particles are visually very rough if compared to natural sand grains.

Fractal analysis permits to appreciate the different morphological characters of the three grain sizes, see Table 2. For all three large grains (Fig. 10a), two fractal subsets emerge from the data, with similar values of m ≈ 0.09–0.13 and μ ≈ 0.15–0.20, and cut-off between structural and textural feature, bm/D ≈ 0.05–0.08. The only significant difference between the three grains is their elongation, which is minimum for grain (2), with the largest value of M ≈ 0.64. On the other hand, both for intermediate (Fig. 10b) and small (Fig. 10c) LECA, only one fractal subset emerges with μ ≈ 0.12–0.15 and it is impossible to identify a characteristic scale separating structural from textural effects. Similar to what happened for grain (1) of Columbia grout, for both “small” and “intermediate” LECA, the increase in normalised perimeter due to texture complexity overlaps with the increase in perimeter due to structural features. It is interesting that the slope of the textural subset is the same for all grain sizes, see Table 2, indicating that the complexity of the contour of fine fragments is the same as that of large grains and that the texture of crushed LECA is self-similar down to a scale of asperities of the order of 0.3 μm. Consistently with what done before, M was computed using the value of normalised perimeter before textural features begin to affect significantly the results, i.e. at bm/D ≈ 0.12–0.29.

Table 2 Results of fractal analysis of crushed LECA particles of decreasing size
Full size table

The high fractal dimension of the textural LECA subset is comparable to those obtained by Orford and Whalley [43] for highly irregular particles with crenellate morphology such as, e.g. carbonate cemented pure quartz sandstones or radiolaria of micro-granular quartz in a matrix of ferruginous quartz.

Figure 11 shows that, for the natural and artificial sand grains considered in this study, the normalised maximum size of microstructural features, bm/D, decreases with increasing equivalent diameter, D. For small particles (D < 100 μm), textural asperities have a characteristic size of between 15 and 30% of the dimension of the particle and, hence, play simultaneously a structural and textural role.

Fig. 11
figure 11

Characteristic dimension of asperities bm/D as a function of particle dimension D

Full size image

5 Discussion

The method discussed above examines the contour of 2D images of particles. This is convenient, because images from very different sources, such as, e.g. SE or optical microscope photographs of particles or of thin sections, are easy to obtain. However, it is necessary to address some issues of meaningfulness of results, resolution, and errors connected with image processing.

The main problem of working with 2D images is that particles tend to lie flat on their major dimensions, introducing a bias in their orientation. This may be overcome by scanning particles allowed to fall under gravity, at a controlled rate, between a laser and a high-speed camera [52], so that an outline of the particle can be recorded at random orientation [3]. However, even in this case, differences have been reported between both the average values and the distribution of computed 2D and 3D morphology descriptors [25]. This is possibly because, when working with 2D images, the outline is evaluated on the projection of the particle, and thus multi-level asperities are flattened in one plane, altering the real particle profile.

In recent years, the development of technology and image processing methods has greatly increased the ability to characterise the microstructure of granular materials in 3D (e.g. [1, 6, 22, 34, 58, 62]). However, full 3D characterisation of particle morphology requires sophisticated computational tools, significant data storage resources, and advanced experimental techniques, such as electron interferometry and X-ray tomography, which are not readily available in the common geotechnical laboratories, with the result that, in practice, charts remain still the most commonly used method of estimating particle shape.

It is evident that the proposed method can be applied to any 2D image, including polar sections of three-dimensional reconstructions of particles obtained by X-ray tomography or advanced optical microscopy, and that the range of experimentally accessible scales depends on the resolution of the input image. SEM images have higher resolutions, of the order of about 1–3 μm/pixel, than images obtained from other sources; basic micro 3D tomography typically reach resolutions of about 10 μm/pixel, while dynamically or statically acquired optical images only of about 20 μm/pixel. Information about surface texture can only be retrieved by high-resolution images, whereas if meso- and macro-scale information is required, it is possible to use also lower-resolution imaging techniques.

As highlighted by the examples discussed above, contrast enhancement, thresholding, and segmentation techniques all play a role in the quality of the obtained results. Although these processes are automatic, they require calibration, which may be time-consuming. This is less critical for thin sections and dynamically acquired images that are usually well in contrast, but externally sourced SEM images and polar sections of 3D reconstructions of particles require careful calibration of the image processing procedures, because of noise, particles contacts, poor contrast, shadows and overlapping. It is very difficult to give general recipes, and each case will have to be considered based on the specific needs.

6 Conclusions

Fractal analysis is a simple, quantitative, and effective method to describe particle shape over the range of experimentally accessible scales. Its application to smooth and artificially roughened simple shapes permitted to define three quantitative non-dimensional descriptors, M, m, and μ, to characterise particle morphology at the macro-, meso-, and micro-scale, respectively.

Descriptor M, or the normalised initial increase in the perimeter ratio (p/D), is a very close measure of circularity; as it accounts only for overall form and structural features, it is effectively independent of the scale of observation. Descriptor m, or the fractal dimension of the structural subset, may be considered as an “irregularity” index at the meso-scale. Descriptor μ, or the fractal dimension of the textural subset, increases with the complexity of the contour, and may be used as a texture index, together with the maximum size of the micro-asperities, which emerges from the results of the fractal analysis.

Application of the method to sand grains of different origins, sizes, angularities, and regularities yielded very convincing results in terms of its ability to identify their key morphological characters. For most grains, the cut-off size of asperities separating textural from structural features emerges clearly from the results as the characteristic length corresponding to the intersection point of the textural and structural subsets. However, there are instances in which only one fractal subset emerges from the data, either because the increase in normalised perimeter due to relatively large micro-asperities masks the structural subset, or because, for very small particles, the particle contour is indeed self-similar over the entire range of accessible scales, as the maximum size of the asperities is comparable to the equivalent dimension of the grain.

Based on the idea that particle morphology is a signature of the formation processes, geologists have used particle shape to identify the geological origin and discriminate between sedimentary environments (e.g. [21, 24, 43]). From the perspective of geotechnical engineering, it will be useful to associate these quantitative morphology descriptors with different aspects of the observed mechanical behaviour, such as, compressibility, stiffness, and strength (e.g. [18, 40]).

It is evident that, as the shape of individual grains of any natural sand is variable, their morphology can only be characterised in terms of average values and standard deviations of the descriptors for statistically representative grain populations.

The method we propose is relatively simple, has low computation effort, and can be applied to 2D images of any resolution, from very low to very high. More information can be extracted as the resolution of the images increases. It is possible that, as suggested by Orford and Whalley [43], using higher-resolution images more than two fractal subsets would emerge.