1 Introduction

Granular flow is a common attribute of various natural phenomena (e.g., debris and rock avalanches, landslides) and industrial processes (e.g., hoppers, chutes and conveyor belts). Study of granular materials poses significant challenges to the scientists as these materials may exhibit solid-like and fluid-like behaviors: They can resist shear stresses like solids and flow like fluids [19, 37, 61]. Various experimental and numerical studies have been conducted to improve the understanding of granular flow behavior. The axisymmetric dynamic collapse of granular columns, an interesting case of granular flow, has been the topic of various experimental studies (e.g., [25, 34]) in the past decade. These simple experiments provided invaluable insights into the dynamic dense granular flow relevant to avalanche events [26].

Lube et al. [34] and Lajeunesse et al. [25] conducted dynamic collapse of axisymmetric cylindrical columns, where inertia plays a role, by instantaneous release of the columns. These cylindrical columns had a wide range of initial aspect ratios a = hi/ri, where hi and ri are the initial height and radius, respectively. It was found that the final deposit morphology (e.g., final height and runout distance) only depends on the initial aspect ratio of the column through a set of simple power-law equations and is insensitive to particle properties (e.g., shape, density and friction) and the amount of released mass [26]. For instance, Lube et al. [34] described different flow regimes based on the initial aspect ratio: (1) For a < 0.74, only particles in the outer region of the column are in motion, while the central region remained unchanged with an undisturbed circular area remaining at the initial height, resulting in a truncated cone-like final deposit; (2) for 0.74 < a < 1.7, the undisturbed circular region gradually erodes, while the final deposit height remains at the initial height and the final deposit forms a sharp cone; and (3) for a > 1.7, the flow begins with a vertical subsiding of the entire top surface, resulting in an abrupt decrease in height, followed by eroding of the top surface and forming of a cone-shaped deposit.

Dynamic collapse of granular columns has also been the focus of various numerical investigations in both continuum and discrete frameworks. In the continuum framework, a multitude of simulation techniques has been used. For example, Chen and Qiu [5], Hurley and Andrade [15] and Szewc [53] used smoothed particle hydrodynamics (SPH) method, while Mast et al. [36] and Zhang et al. [60] used the material point method (MPM) and the particle finite element method (PFEM), respectively. Through implementing appropriate constitutive models and calibration of model parameters (e.g., friction angle and bulk modulus), all of these numerical studies were able to reproduce the experimental observations reasonably well. In the discrete framework, the discrete element method (DEM) has been the method of choice by Lo et al. [33], Girolami et al. [11], Huang et al. [14] and Kermani et al. [24]. In this approach, accurate simulation of experimental results is contingent upon accounting for the effect of non-spherical shape of granular particles by implementing rotational resistance or by using non-spherical particles.

Aside from dynamic collapse, granular materials can undergo quasi-static deformation, as can be observed during active deformation of retaining structures, bridge abutment deformation, pile jacking, etc. In quasi-static granular flow, material particles remain in constant contact through the flow and particle inertia has no effect on the overall flow behavior. Despite the importance of this type of granular deformation in geotechnical engineering, less focus has been placed on conducting experimental and numerical study of this phenomenon. Meriaux [37] conducted the only reported laboratory experiment on the quasi-static collapse of granular columns by slowly moving one of the vertical walls of the rectangular column. Numerical studies on this type of flow are also sparse, including 2D and 3D DEM by Owen et al. [47], 2D PFEM by Zhang et al. [61] and 3D SPH by Kermani and Qiu [22]. It was found that quasi-static collapse generally follows similar patterns as dynamic collapse, and the final deposit profile depends on the initial aspect ratio and is mostly independent of grain size and shape. However, it was noticed that quasi-static collapse leads to a smaller runout distance compared to the dynamic collapse.

To date, there are no reported experimental studies on quasi-static axisymmetric collapse of cylindrical granular columns in the literature due to the difficulty in conducting such tests. However, numerical simulations can provide useful insights into the internal flow mechanisms of quasi-static collapse. The global behavior of dense granular flow (e.g., runout distance) can be modeled as a continuum [8, 9], except in small zones near boundaries such as the sharp tip in the final profile where particle-scale behavior dominates. In this study, the quasi-static axisymmetric collapse of granular columns is modeled in the continuum framework using a 3D SPH model and in the discrete framework using a 3D DEM model. The final deposit profile (e.g., height, runout distance, repose angle), non-deformed region, collapse pattern and energy dissipation for different initial aspect ratios are investigated and compared between the two frameworks. Theoretical analyses for two conceptual cases including a truncated cone-like deposit with a flat surface at the top for small aspect ratios and a cone-like deposit with a tip for large aspect ratios are performed and compared with SPH and DEM results.

2 Numerical implementations

2.1 SPH method

The SPH method is a particle-based Lagrangian mesh-free method proposed by Gingold and Monaghan [10] and Lucy [35] and suitable for a wide range of engineering problems involving large deformation, complex geometries and moving boundaries [30]. In SPH, the computational domain is represented by a series of particles, each possessing various field variables (e.g., mass, velocity, density, pressure and stress). The SPH particles interact only with the neighboring particles that are within their influence domain through a kernel/weighting function Wij. The influence domain that is defined by a smoothing length h describes a zone, outside which the effect of other SPH particles can be considered as zero [30, 31]. The SPH particles follow the continuity and momentum conservation equations [30]. SPH particle approximation of any function f and its derivative for a target particle i is calculated using weighted averaging over the neighboring particles:

$$\left\langle {f\left( {x_{i} } \right)} \right\rangle = \mathop \sum \limits_{j = 1}^{N} f\left( {x_{j} } \right) W_{ij} \frac{{m_{j} }}{{\rho_{j} }}$$
(1)
$$\left\langle {\nabla f\left( {x_{i} } \right)} \right\rangle = \mathop \sum \limits_{j = 1}^{N} \frac{{m_{j} }}{{\rho_{j} }}f\left( {x_{j} } \right)\frac{{\partial W_{ij} }}{{\partial x_{j} }}$$
(2)

where x = position vector; m = particle mass; \(\rho\) = particle density; N = total number of particles within the influence domain of particle i; and j = index for neighboring particles. The widely used cubic spline kernel function introduced by Monaghan and Lattanzio [44] is used in this study.

The continuity and momentum conservation equations are implemented in the SPH formulation as [30]:

$$\frac{{{\text{D}}\rho_{i} }}{{{\text{D}}t}} = \mathop \sum \limits_{j = 1}^{N} m_{j} \left( {v_{i}^{\alpha } - v_{j}^{\alpha } } \right)\frac{{\partial W_{ij} }}{{\partial x_{i}^{\alpha } }}$$
(3)
$$\frac{{{\text{D}}v_{i}^{\alpha } }}{{{\text{D}}t}} = \mathop \sum \limits_{j = 1}^{N} m_{j} \left( {\frac{{\sigma_{i}^{\alpha \beta } }}{{\rho_{i}^{2} }} + \frac{{\sigma_{j}^{\alpha \beta } }}{{\rho_{j}^{2} }}} \right)\frac{{\partial W_{ij} }}{{\partial x_{i}^{\alpha } }} - \mathop \sum \limits_{j = 1}^{N} m_{j}\Pi _{ij} \frac{{\partial W_{ij} }}{{\partial x_{i}^{\alpha } }} + g_{z}$$
(4)

where v = fluid velocity; t = time; gz = acceleration of gravity; \(\Pi _{ij}\) = artificial viscosity term which is used to improve SPH stability [30, 40, 42]; and \(\sigma^{\alpha \beta }\) = total stress tensor consisting of isotropic hydrostatic pressure P and deviatoric shear stress s as:

$$\sigma^{\alpha \beta } = - P\delta^{\alpha \beta } + s^{\alpha \beta }$$
(5)

where \(\delta\) = Kronecker delta and \(\alpha\), \(\beta\) = coordinate directions. The hydrostatic pressure of soil P in the momentum equations is calculated from the standard definition of mean stress as [3]:

$$P = - \frac{{\sigma^{\gamma \gamma } }}{3} = - \frac{{\left( {\sigma^{xx} + \sigma^{yy} + \sigma^{zz} } \right)}}{3}$$
(6)

where \(\sigma^{\gamma \gamma }\) = summation of stress components in x, y, z directions.

2.1.1 Constitutive model

The Drucker–Prager constitutive model with non-associated plastic flow rule based on the work of Bui et al. [3] is used in this study. The yield function f and potential function g are as:

$$f(I_{1} ,J_{2} ) = \sqrt {J_{2} } + \alpha_{\phi } I_{1} - k_{\text{c}}$$
(7)
$$g = \sqrt {J_{2} } + 3\sin \psi I_{1}$$
(8)

where I1 = σxx + σyy + σzz and \(J_{2} = 1/2s^{\alpha \beta } s^{\alpha \beta }\) are the first and second stress tensor invariant; ψ = dilatancy angle; and αϕ, kc are Drucker–Prager constants for 3D conditions and are related to the friction angle ϕ and cohesion c [2, 4, 5] as:

$$\alpha_{\phi } = \frac{2\sin \phi }{\sqrt 3 (3 - \sin \phi )}$$
(9)
$$k_{\text{c}} = \frac{6c\cos \phi }{\sqrt 3 (3 - \sin \phi )}$$
(10)

The stress rate is calculated using elastoplastic stress–strain relationship with non-associated flow rule by Bui et al. [3] as:

$$\dot{\sigma }^{\alpha \beta } = \frac{{{\text{D}}\sigma^{\alpha \beta } }}{{{\text{D}}t}} = 2G\dot{\varepsilon }^{\alpha \beta } + \left( {K - \frac{2G}{3}} \right)\dot{\varepsilon }^{\gamma \gamma } \delta^{\alpha \beta } - \dot{\lambda }\frac{G}{{\sqrt {J_{2} } }}s^{\alpha \beta }$$
(11)

where G = shear modulus; K = bulk modulus; \(\dot{\lambda }\) = plastic multiplier change rate; \(\dot{\varepsilon }^{\gamma \gamma } = \dot{\varepsilon }^{xx} + \dot{\varepsilon }^{yy} + \dot{\varepsilon }^{zz}\) is summation of strain rate tensor in x, y, z directions; and \(\dot{\varepsilon }^{\alpha \beta } = 1/2\left( {\partial v^{\alpha } /\partial x^{\beta } + \partial v^{\beta } /\partial x^{\alpha } } \right)\) is the total strain rate tensor consisting of the elastic strain rate tensor (\(\dot{\varepsilon }_{\text{e}}^{\alpha \beta }\)) and plastic strain rate tensor (\(\dot{\varepsilon }_{\text{p}}^{\alpha \beta }\)):

$$\dot{\varepsilon }_{\text{e}}^{\alpha \beta } = \frac{{\dot{s}^{\alpha \beta } }}{2G} + \frac{{\dot{\sigma }^{\gamma \gamma } \delta^{\alpha \beta } \left( {1 - 2\nu } \right)}}{3E}$$
(12)
$$\dot{\varepsilon }_{\text{p}}^{\alpha \beta } = \frac{{\dot{\lambda }\partial g}}{{\partial \sigma^{\alpha \beta } }}$$
(13)

where E = Young’s modulus and \(\nu\) = Poisson’s ratio.

The plastic multiplier change rate \(\dot{\lambda }\) for non-associated flow rule assuming dilation angle \(\psi = 0^{ \circ }\) is:

$$\dot{\lambda } = \frac{{3\alpha_{\phi } K\dot{\varepsilon }^{\gamma \gamma } }}{G} + \frac{{s^{\alpha \beta } \dot{\varepsilon }^{\alpha \beta } }}{{\sqrt {J_{2} } }}$$
(14)

The simplification of \(\psi = 0^{ \circ }\) is valid when granular materials undergo flow-type failure with large deformation. In this type of granular flow, after some displacement which is small compared to the final runout, critical state is reached, and dilation/contraction becomes zero. Therefore, the flow as a whole may be assumed to have zero plastic volume change.

The final form of stress–strain relationship after considering the contribution from Jaumann stress rate for problems with large deformation, which is the invariant stress rate with respect to rigid body rotation [3, 5, 29], can be calculated as:

$$\begin{aligned} \dot{\sigma }^{\alpha \beta } & = \frac{{{\text{D}}\sigma^{\alpha \beta } }}{{{\text{D}}t}} = 2G\dot{\varepsilon }^{\alpha \beta } + \left( {K - \frac{2G}{3}} \right)\dot{\varepsilon }^{\gamma \gamma } \delta^{\alpha \beta } \\ & \quad - \dot{\lambda }\frac{G}{{\sqrt {J_{2} } }}s^{\alpha \beta } + \sigma^{\alpha \gamma } \dot{\omega }^{\beta \gamma } + \sigma^{\gamma \beta } \dot{\omega }^{\alpha \gamma } \\ \end{aligned}$$
(15)

where \(\dot{\omega }^{\alpha \beta } = 1/2\left( {\partial v^{\alpha } /\partial x^{\beta } - \partial v^{\beta } /\partial x^{\alpha } } \right)\) is the rotation rate tensor.

The SPH differential equations are numerically integrated using the second-order predictor–corrector scheme proposed by Monaghan [41]. The time step is controlled by a combination of criteria including the Courant–Friedrichs–Lewy (CFL) condition and the force and viscous diffusion terms [6, 12, 21, 41]:

$$\Delta t_{1} = \hbox{min} \left( {\sqrt {h/F_{i} } } \right)$$
(16)
$$\Delta t_{2} = \hbox{min} \frac{h}{{c + \mathop {\hbox{max} }\limits_{{}} \left| {\frac{{hv_{ij} x_{ij} }}{{\left| {x_{ij} } \right|^{2} + 0.01h^{2} }}} \right|}}$$
(17)

where F = force per unit mass; \(c = \sqrt {(4G/3\rho) + (K/\rho)}\) is the speed of sound in the material [5, 30]; and \(\Delta t_{2}\) combines the Courant and the viscous time step control [12, 43]. The Courant coefficient is considered as 0.2 here, and the final time step is calculated as:

$$\Delta t = 0.2 \times \hbox{min} \left( {\Delta t_{1} ,\Delta t_{2} } \right)$$
(18)

2.1.2 3D SPH model

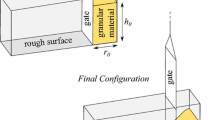
Figure 1 shows a schematic representation of the 3D SPH model used in this study. SPH cylindrical columns have a range of aspect ratios a = hi/ri from 0.55 to 5.5 with a constant radius (ri) of 4.98 cm and variable initial heights (hi). SPH soil particles are initially spaced with a uniform spacing of 5 mm in the domain, which results in 1884 and 17,270 SPH soil particles for a = 0.55 and a = 5.5, respectively. Typical properties of sand: a bulk modulus of 5 MPa, a Poisson ratio of 0.3, a friction angle of 30° and a bulk density of 1540 kg/cm3 corresponding to a specific gravity of 2.65 and a porosity of 0.42, are used.

Fig. 1
figure 1

Schematic representation of a 3D SPH cylindrical column

Full size image

In the developed 3D SPH model, ghost boundary conditions are implemented to model the bottom surface and guarantee no-slip, no-penetration conditions [3, 29, 45, 54]. Ghost particles are defined using the same physical properties and stress values as the corresponding soil particles; however, their velocities are set to be in the opposite direction and normal to the boundary. The cylindrical wall on the other hand is modeled using the dynamic boundary condition. The dynamic boundary particles are treated similar to other soil particles, except that they can be fixed in space or move with a prescribed velocity [6, 12, 50]. In this study, the cylindrical wall particles are assigned a radial velocity of ur which leads to a slow expansion of the column.

2.2 Discrete element method (DEM)

The DEM initially proposed by Cundall and Strack [7] is a widely used numerical method in modeling granular media (e.g., [11, 14, 23, 24, 51, 52, 58, 62]). DEM treats granular materials as an assembly of individual particles, often spheres, within a set of boundary elements known as walls [46]. Motions of DEM particles are calculated through numerical integration of Newton’s equations of motion, and interparticle forces are evaluated using various contact models based on defined contact properties (e.g., stiffness, friction and damping) and overlap between particles. More details of DEM can be found in Itasca [16] and O’Sullivan [46]. Commercial and research DEM code, PFC3D 4.0 (Particle Flow Code in Three Dimensions, [16]), is used in this study.

2.2.1 Contact stiffness

Different contact models are available in PFC3D. The linear contact model has advantages of simplicity and computational efficiency, but is unable to model nonlinear and hysteresis behaviors at contact; the Hertz–Mindlin contact model [39] is capable of capturing nonlinear contact behaviors, but is more computationally expensive. In the linear contact model, the contact stiffness is a constant value, while in the Hertz–Mindlin contact model, the contact stiffness depends on elastic material properties (i.e., shear modulus and Poisson’s ratio), overlap and normal contact forces [16, 39]. In this study, a hybrid approach used by Kermani et al. [24] and similar to Teufelsbauer et al. [56] is applied. In this approach, simulations are conducted using the linear contact model by employing contact stiffness parameters calibrated based on initial simulations with the Hertz–Mindlin contact model for each aspect ratio.

2.2.2 Rotational resistance

In granular flow, the motion of particles should be described by a combination of sliding and rolling, with a more dominant effect of the latter on inclined surfaces [56]. However, DEM spherical particles on their own have no rotational constraint during collapse, which leads to dispersive flow and much longer runout distance [56]. There are different approaches to deal with this problem. One of them is implementing blockiness and elongation to particles to reproduce the angularity and shape of particles [47, 55]. However, shape is a computationally expensive property to model in DEM [57]. Another approach is employing artificial rolling resistance through: (1) implementing resisting moments at particle contacts (e.g., [11, 14, 17, 18, 20, 27, 28, 32, 59, 63, 64]), or (2) directly reducing angular velocities of particles (e.g., [24, 48, 56]). The artificial rotational resistance accounts for energy loss due to the effects of particle shape, hysteretic contact behaviors (e.g., micro-sliding, viscoelasticity and plasticity) and asperities at real contacts [1, 57]. In this study, the angular velocity of spherical particles is reduced by a constant factor of 0.95, which is calibrated against experimental observations of Lube et al. [34] and Lajeunesse et al. [25] and proven to be a simple and efficient approach by Kermani et al. [24]. A higher rotational resistance factor corresponds to less particle rotational constraint and leads to a longer runout distance, a lower final height and a smaller repose angle [24].

2.2.3 3D DEM model

DEM vertical cylindrical columns with an initial constant radius (ri) of 5.68 mm are created by allowing 0.32-mm-diameter spherical particles to freely fall into the column until equilibrium is reached within the specimen. DEM cylindrical columns with aspect ratios of a = 0.55, 1.0 and 2.0 at an initial porosity value of n = 0.42 are generated. These columns consist of 10,000–40,000 particles. Figure 2 shows a schematic representation of the DEM model. The spherical particles are assumed to be made of quartz with a density of 2650 kg/cm3, shear modulus of 29 GPa, Poisson’s ratio of 0.3, particle–particle friction angle of 24° and restitution parameter of 0.75. These DEM samples were previously used in the simulation of dynamic granular collapse by Kermani et al. [24]. The normal kn and tangential ks contact stiffness for particles and walls used in the study for different aspect ratios are presented in Table 1. More details can be found in Kermani et al. [24].

Fig. 2
figure 2

Schematic representation of a 3D DEM cylindrical column

Full size image
Table 1 Equivalent kn and ks for different a
Full size table

It should be noted that the 3D DEM model has smaller dimensions than the 3D SPH model to accommodate a reasonable number of DEM particles for computational efficiency; however, the two models have similar aspect ratios. This treatment is justifiable because the collapses were found to be only dependent on the initial aspect ratio (not initial dimension) [25, 34, 37].

2.3 Quasi-static axisymmetric collapse

To model quasi-static axisymmetric collapse, the cylindrical wall is expanded with a radial velocity of ur, which should satisfy quasi-static criteria. Midi [38] introduced a dimensionless number I as the ratio of the timescale for confining pressure \(T_{\text{p}} = d_{\text{p}} /\sqrt {\rho /p}\) and the timescale for shear deformation \(T_{\gamma } = r_{i} /u\) to characterize the relative importance of inertia and confining pressure:

$$I = \frac{{T_{\text{p}} }}{{T_{\gamma } }} = \frac{{u_{\text{r}} d_{\text{p}} }}{{r_{i} \sqrt {g_{z} h_{i} } }}$$
(19)

where dp = particle size. To satisfy the quasi-static condition, the Midi number should be very small. A parametric study of this investigation reveals that the collapse pattern and final deposit profile are independent of wall velocity as long as the cylindrical wall expands at velocities slow enough to satisfy I < 10−3, which is consistent with experimental observations by Meriaux [37] and numerical findings of Kermani and Qiu [22], Owen et al. [47] and Zhang et al. [61] in simulations of quasi-static collapse of rectangular columns. In this study, the cylindrical walls in the 3D SPH and DEM models are expanded with small radial velocity values to result in small Midi numbers in the range of 10−3–10−5 to reproduce the quasi-static collapse.

3 Results and discussion

The developed 3D SPH and DEM models are used to simulate the axisymmetric quasi-static collapse of cylindrical granular columns. The effects of initial aspect ratio on the final deposit profile (e.g., height, runout distance, repose angle), non-deformed region, collapse patterns and energy dissipation are investigated.

3.1 Collapse pattern

Different collapse patterns are observed depending on the initial aspect ratio. Figures 3, 4, 5, 6, 7 and 8 show the collapse patterns for the 3D SPH columns and 3D DEM columns of various aspect ratios at few different times during the collapse. In order to better illustrate the internal flow during the collapse, the columns are demonstrated using several colored layers. The time is normalized as tn = t/tf, where tf is the final time when the final deposit forms. In this study, the quasi-static collapse is considered to be stopped when: (1) no further contact can be detected between the moving wall and soil particles and (2) the entire deposit comes to a standstill. It should be noted that only granular particles in SPH and DEM simulations are shown in these figures. Here, the collapse patterns for different aspect ratios from SPH and DEM models are compared qualitatively.

Fig. 3
figure 3

Evolution of deposit profile for a cross section of a SPH column with a = 0.55 at: atn = 0; btn = 0.2; and ctn = 1.0

Full size image
Fig. 4
figure 4

Evolution of deposit profile for a cross section of a DEM column with a = 0.55 at: atn = 0; btn = 0.2; and ctn = 1.0

Full size image
Fig. 5
figure 5

Evolution of deposit profile for a cross section of a SPH column with a = 2.0 at: atn = 0; btn = 0.13; ctn = 0.5; and dtn = 1.0

Full size image
Fig. 6
figure 6

Evolution of deposit profile for a cross section of a DEM column with a = 2.0 at: atn = 0; btn = 0.13; ctn = 0.5; and dtn = 1.0

Full size image
Fig. 7
figure 7

Evolution of deposit profile (with horizontally colored layers) for a cross section of a SPH column with a = 5.5 at: atn = 0; btn = 0.14; ctn = 0.57; and dtn = 1.0 (color figure online)

Full size image
Fig. 8
figure 8

Evolution of deposit profile (with vertically colored layers) for a cross section of a SPH column with a = 5.5 at: atn = 0; btn = 0.14; ctn = 0.57; and dtn = 1.0 (color figure online)

Full size image

Figures 3 and 4 show the cross section of the granular deposit for a SPH column and a DEM column, respectively, with a = 0.55 at tn = 0, 0.2 and 1.0. In both figures, granular particles located at the rim of the column slope down toward the moving cylindrical wall, while the central region remains undisturbed, leaving a flat surface at the original height, forming a truncated cone-like deposit.

Figures 5 and 6 show the corresponding plots for SPH and DEM columns, respectively, with a = 2.0 at tn = 0, 0.13, 0.5 and 1.0. For this aspect ratio, the entire granular column subsides initially, retaining a flat surface on top. Later on, the whole deposit slopes toward the moving wall and forms a cone-like deposit with a distinctive tip.

Comparing the SPH and DEM results, it can be noticed that the general collapse trend is quite similar; however, different behaviors can be observed in the regions close to the moving wall and free surface. DEM simulations tend to produce sharper edges for the free surface (e.g., Fig. 3c vs. 4c; Fig. 5d vs. 6d).

As can be noticed in Fig. 6c, DEM particles close to the moving boundaries (i.e., moving wall) are slightly higher than the adjacent internal particles. This is due to a combination of two factors: (1) The lateral spreading of DEM particles close to the moving boundaries is restricted by the boundary and (2) the collapse of the granular column results in internal DEM particles moving underneath the boundary DEM particles. In the 3D DEM model, the wall boundary is frictionless; however, in the 3D SPH model, the cylindrical wall is modeled using the dynamic boundary condition and is frictional. Therefore, this phenomenon is not observed in Fig. 5c. It is worth mentioning that in the dynamic collapse of Lube et al. [34], no upward movement of the granular materials is observed since the particles can flow freely until coming to a standstill.

Figure 7 shows the cross section of the granular deposit for a SPH column with a = 5.5 at tn = 0, 0.14, 0.57 and 1.0. Here, a similar collapse pattern as a = 2.0 is observed. In general, the observed collapse patterns in quasi-static axisymmetric collapse are qualitatively consistent with experimental and numerical observations of dynamic axisymmetric collapse of cylindrical column [5, 24, 25, 34].

The evolution of the shape of colored layers in the deposits indicates that despite significant deformation and distortion, these horizontal layers do not experience mixing during the collapse as shown in Fig. 7. A close observation of the above figures also reveals that all layers spread throughout the collapse, with the upper layer blanketing the entire final deposit. In contrast, Lube et al. [34] reported that in the dynamic collapse, the horizontal colored layers are experiencing varying amounts of spreading due to the difference in the velocity of particles along the free surface, which results in partial blanketing of the deposit by the upper layer.

Additional insights can be gained by observing the deformation patterns of vertical colored layers as shown in Fig. 8 for the same granular deposit for a SPH column with a = 5.5 at tn = 0, 0.14, 0.57 and 1.0. As can be noticed, the entire column subsides in the beginning of the flow with minimal disturbance in the vertical stripes. The gap between the moving wall and the column is initially filled with horizontal spreading of particles in the lower part of the column as shown in Fig. 8b. As the flow continues, particles of the upper part of the column start to spread as shown in Fig. 8c. A very small undisturbed area in the center of the column can be distinguished. Similar trends were reported in 2D DEM simulations of quasi-static collapse of rectangular columns by Owen et al. [47] and dynamic axisymmetric collapse experiments by Lube et al. [34]. In both dynamic and quasi-static collapses, the most distal parts of the deposit consist of particles from the outer vertical layer. However, in dynamic collapse, the middle vertical layer showed significantly more distortion.

3.2 Non-deformed region

After the collapse, an undisturbed region at the center of the deposits can be observed. This non-deformed region is easily recognizable in small aspect ratios; however, it shrinks and becomes less distinguishable as aspect ratios increase. In the experiments of Lube et al. [34], this region was identified through visual inspection of colored granular particles; in SPH simulations, this region is determined by SPH particles with very small accumulative equivalent plastic strains. Figure 9 shows the contour of plastic strains for a SPH column with a = 2.0, where dark blue represents zero accumulative equivalent plastic strain and red indicates the largest plastic strain. Figure 9 shows that the non-deformed region for a = 2.0 is in the form of a cone with a bottom radius of rn.

Fig. 9
figure 9

Accumulative equivalent plastic strain after collapse for a SPH column with a = 2.0: a cross-sectional view and b plan view

Full size image

Figure 10 shows the normalized radius of non-deformed region rn/ri for deposits with different initial aspect ratios for accumulative equivalent plastic strains \(\varepsilon_{{p_{\text{eq}} }}\) = 0.1, 0.15, 0.2, 0.25 and 0.3 which can be considered as negligible compared to the average accumulative equivalent plastic strain. As it can be observed in Fig. 10, for small aspect ratios a < 2.0, rn/ri linearly decreases with aspect ratio, which is consistent with the findings of Lube et al. [34]. Figure 10 also shows that the normalized radius of the non-deformed region in quasi-static collapse remains approximately constant for large aspect ratios and is consistently greater than 0.5, indicating that the radius of the non-deformed region is larger than half of the initial radius.

Fig. 10
figure 10

Normalized radius of regions of various \(\varepsilon_{{p_{\text{eq}} }}\) versus a

Full size image

3.3 Final deposit profile

In the previous section, the evolution of quasi-static collapse of granular columns was qualitatively captured using the developed 3D SPH and DEM models. In order to compare the SPH and DEM results quantitatively, the simulated angle of repose (\(\alpha_{\text{r}}\)), final height (hf) and runout distance (rf) are monitored and compared. The angle of repose is measured as the slope of the surface of the final deposit. Figure 11 shows the final deposit profiles with repose surface (red solid line) for SPH columns with a = 0.55, 2.0 and 5.5. Figure 12 shows the corresponding plots for DEM columns with a = 0.55, 1.0 and 2.0. The simulated angle of repose is measured to be in the range of 25.0° ± 0.5° for the SPH columns and 24.5° ± 1.0° for the DEM columns, which are generally consistent. These simulated angles of repose are smaller than the friction angle used in the SPH simulations (i.e., 30°). Similar deviation is reported in other simulations of quasi-static collapse of rectangular columns (e.g., [47, 61]). Holsapple [13] demonstrated in detail that in both quasi-static and dynamic collapses of granular columns, the failure surface may attain an angle smaller than the friction angle of the material. The tensile instability treatment utilized in the SPH simulations [3] may have also contributed to the deviation.

Fig. 11
figure 11

Repose surface (red solid line) of SPH models with a = : a 0.55; b 2.0 and c 5.5 (color figure online)

Full size image
Fig. 12
figure 12

Repose surface (red solid line) of DEM models with a = : a 0.55; b 1.0; and c 2.0 (color figure online)

Full size image

In order to gain additional insights, the final deposit profiles for two conceptual cases including a truncated cone-like deposit with a flat top (for small aspect ratios) and a cone-like deposit with a distinctive tip at the top (for large aspect ratios) are theoretically calculated. Figure 13 shows the initial column and final deposit profile for these two cases. The normalized final height hf /ri and runout distance (rf − ri)/ri are calculated assuming no volume change during the collapse, which is a valid assumption for flow-type failure with large deformations (see justification for Eq. 14). The initial volume Vi of the granular column and the final volume Vf of the deposit can be calculated, respectively, as:

$$V_{i} = \pi r_{i}^{2} h_{i}$$
(20a)
$$V_{f} = \pi h_{i}^{3} \left[ {\left( {\frac{{r_{f} }}{{h_{i} }}} \right)^{2} - \frac{{r_{f} }}{{\tan \alpha_{\text{r}} h_{i} }} + \frac{1}{{3\tan^{2} \alpha_{\text{r}} }}} \right]\,\,{\text{for}}\,{\text{small}}\,{\text{aspect}}\,{\text{ratios}}$$
(20b)
$$V_{f} = \frac{{\pi r_{f}^{2} h_{f} }}{3}\, {\text{for}}\,{\text{large}}\,{\text{aspect}}\,{\text{ratios}} .$$
(20c)

The normalized final height hf /ri and runout distance (rf − ri)/ri for small aspect ratios:

$$h_{f} = h_{i} \Rightarrow \frac{{h_{f} }}{{r_{i} }} = a$$
(21a)
$$\begin{aligned} r_{f} & = \frac{{r_{i} }}{{2\tan \,\alpha_{\text{r}} }}\left( {a + \sqrt {4\tan^{2} \alpha_{\text{r}} - \frac{{a^{2} }}{3}} } \right) \Rightarrow \\\frac{{r_{f} - r_{i} }}{{r_{i} }} = & \frac{1}{{2\tan \,\alpha_{\text{r}} }}\left( {a + \sqrt {4\tan^{2} \alpha_{\text{r}} - \frac{{a^{2} }}{3}} } \right) - 1 \\ \end{aligned}$$
(21b)

and for large aspect ratios:

$$h_{f} = r_{i} {\sqrt[3]{{3a\tan^{2} \alpha_{\text{r}} }}}\Rightarrow {\frac{{h_{f} }}{{r_{i} }}} = \sqrt[3]{{3\tan^{2} \alpha_{\text{r}} }}a^{{\frac{1}{3}}}$$
(22a)
$$r_{f} = r_{i} \sqrt[3]{{\frac{3a}{{\tan \alpha_{\text{r}} }}}} \Rightarrow \frac{{r_{f} - r_{i} }}{{r_{i} }} = \sqrt[3]{{\frac{3}{{\tan \alpha_{\text{r}} }}}}a^{{\frac{1}{3}}} - 1$$
(22b)

As shown in Fig. 13, the transitional aspect ratio at between the two conceptual cases where the flat surface at the top vanishes can be calculated as:

$$a_{t} = \sqrt 3 \tan \alpha_{\text{r}}$$
(23)

Substituting \(\alpha_{\text{r}} = 25.0^{ \circ }\) into Eq. (23) yields at = 0.81. The transitional aspect ratio was reported to be 0.74 and 1.0 in dynamic axisymmetric collapse of granular column by Lajeunesse et al. [25] and Lube et al. [34], respectively.

Fig. 13
figure 13

Initial column and final deposit for two conceptual cases

Full size image

The normalized final height and runout distance from SPH simulations, DEM simulations and theoretical analyses based on Eqs. (21) and (22) using \(\alpha_{\text{r}} = 25.0^{ \circ }\) are plotted against the aspect ratio a in Fig. 14. As it can be seen, SPH and DEM simulations produce generally consistent results in normalized final height and runout distance, with SPH simulations producing slightly higher values in the normalized final height while DEM simulations producing slightly higher values in the normalized runout distance. Figure 14 also shows that the theoretical analysis based on Eqs. (21) and (22) generally overpredicts the normalized final height and runout distance.

Fig. 14
figure 14

Comparison of SPH simulations, DEM simulations and theoretical analyses: a normalized final height and b normalized runout distance

Full size image

During the analysis of experimental results of dynamic collapse, Lube et al. [34] noticed that the length of the straight line connecting a point on the top outer perimeter of the initial column to the farthest point on the base of the final deposit d = [(rf − ri)2 + h2i]0.5 can be accurately represented by 1.05V1/3ia0.55. Figure 15 shows the normalized value of this length based on third root of the initial volume of granular column \(d/V_{i}^{1/3}\) as a function of the initial aspect ratio from SPH and DEM simulations, and the results from Lube et al. [34] for dynamic collapse. For the two conceptual cases shown in Fig. 13, \(d/V_{i}^{1/3}\) can also be theoretically derived as:

$$\frac{d}{{V_{i}^{1/3} }} = \frac{{\sqrt {[1.07\left( {a + \sqrt {0.87 - a^{2} /3} } \right) - 1]^{2} + a^{2} } }}{{1.46\sqrt[3]{a}}}$$
(24a)

for small aspect ratios and

$$\frac{d}{{V_{i}^{1/3} }} = \frac{{\sqrt {(1.86\sqrt[3]{a} - 1)^{2} + a^{2} } }}{{1.46\sqrt[3]{a}}}$$
(24b)

for large aspect ratios, and these equations are also plotted in Fig. 15. As it can be seen, there is a good agreement among the results of SPH and DEM simulations and the theoretical analyses. In both quasi-static and dynamic collapses, the relationship of \(d/V_{i}^{1/3}\) versus a follows a similar qualitative trend. The theoretical lines for Eqs. (24a) and (24b) can be approximated by a single line of 0.9a0.55 with a coefficient of determination (R2) of 0.99. This line falls below the equation proposed by Lube et al. [34] which can be attributed to smaller runout distance in quasi-static collapse compared to the dynamic collapse.

Fig. 15
figure 15

Comparison of \(d/V_{i}^{1/3}\) versus a from SPH simulations, DEM simulations and theoretical analyses of quasi-static collapse with experimental results of dynamic collapse by Lube et al. [34]

Full size image

3.4 Effect of friction angle and density on deposit morphology

In continuum scale, a series of parametric studies have been conducted on the effect of specific gravity and friction angle on the results of SPH simulations of quasi-static granular collapse. Specific gravity values of 1.00, 2.65 and 5.00 and friction angle values of 20°, 25°, 30° and 35° have been considered in the study. Results of the simulations revealed that bulk density has a negligible effect on final deposit profile, while friction angle plays a significant role. A decrease in friction angle leads to a longer runout distance, a lower final height and a lower repose angle. These results are consistent with the findings of Zhang et al. [61] and Kermani and Qiu [22, 49] and hence are not presented herein.

In addition, a parametric study has been conducted to evaluate the effect of particle density and interparticle friction angle on DEM simulations. Particle density values of 1000, 2650 and 5000 kg/cm3 and particle–particle friction angles of 24° and 30° have been used in the study. Results of simulations demonstrated that final deposit profile is insensitive to these microscale particle properties, which is consistent with the observations of Owen et al. [47].

3.5 Energy dissipation

Energy dissipation is another important quantity in understanding the dynamics of collapse of granular materials. The initial potential energy of the system EPi partially dissipates during the collapse due to dissipative particle–particle interaction (e.g., friction, damping and rotational resistance), resulting in a lower final potential energy EPf at the end of the collapse. As the kinetic energy is zero within the initial column and final deposit (i.e., particles are not in motion), the dissipated energy \(\Delta E\) can be calculated as \(\Delta E = E_{Pi} - E_{Pf}\). For both cases shown in Fig. 13, the initial potential energy is calculated as \(E_{Pi} = \rho g_{z} \pi r_{i}^{2} h_{i}^{2} /2\). EPf and the normalized dissipated energy (\(\Delta E/E_{Pi}\)) can be calculated based on the final deposit profile for small aspect ratios as:

$$E_{Pf} = \rho g_{z} \frac{{\pi h_{i}^{4} }}{4}\left[ {2\left( {\frac{{r_{f} }}{{h_{i} }}} \right)^{2} - \frac{8}{{3\tan \alpha_{r} }}\left( {\frac{{r_{f} }}{{h_{i} }}} \right) + \frac{1}{{\tan^{2} \alpha_{r} }}} \right]$$
(25a)
$$\frac{{\Delta E}}{{E_{Pi} }} = \frac{a}{{6\tan^{2} \alpha_{\text{r}} }}\sqrt {4\tan^{2} \alpha_{\text{r}} - \frac{{a^{2} }}{3}}$$
(25b)

and for large aspect ratios as:

$$E_{Pf} = \rho g_{z} \frac{{\pi r_{i}^{4} }}{4}\sqrt[3]{{3\tan^{2} \alpha_{\text{r}} a^{4/3} }}$$
(26a)
$$\frac{{\Delta E}}{{E_{Pi} }} = 1 - \frac{{\sqrt[3]{{3\tan^{2} \alpha_{\text{r}} }}}}{2}a^{ - 2/3}$$
(26b)

Evolution of potential energy of the granular system can be tracked in SPH and DEM simulations through tracing the height of each particle. Figure 16 shows the normalized dissipated energy \(\Delta E/E_{Pi}\) of the system from SPH and DEM simulations, as well as from the theoretical analysis based on Eqs. (25b) and (26b) using \(\alpha_{\text{r}} = 25.0^{ \circ }\) and at = 0.81 for different aspect ratios. Figure 16 shows that the SPH- and DEM-simulated normalized energy dissipations are in very good agreement and are consistent with the theoretical analyses. The normalized energy dissipation is found to only depend on the initial aspect ratio with separate relationships for low and high aspect ratios, which is consistent with the reported results from 3D dynamic collapse of granular columns by Lajeunesse et al. [25].

Fig. 16
figure 16

Normalized dissipated energy \(\Delta E/E_{Pi}\) versus a

Full size image

3.6 Evolution of heights at the center and moving walls

Figure 17 shows the normalized height h/hi at the deposit center and at the moving walls versus normalized radius r/ri for a = 2.0 from 3D SPH and DEM simulations. As can be noticed, SPH and DEM results are in good agreement during most of the collapse. However, at the final stages of the flow, DEM simulations tend to predict larger values of r/ri (i.e., longer runout) and lower values of h/hi (i.e., shorter deposit height). It should be noted that at the edge of the deposit, where the thickness is very thin, SPH simulations are limited by the SPH particle spacing (i.e., 5 mm) and the method’s continuum-scale nature; hence, DEM simulations may be better suited to capture particle-level behavior in this region.

Fig. 17
figure 17

Evolution of normalized height h/hi for a = 2.0 from SPH and DEM simulations

Full size image

4 Conclusions

In this study, 3D SPH and 3D DEM models are developed to simulate the quasi-static axisymmetric collapse of granular columns. In SPH simulations, the granular materials are modeled as elastoplastic materials undergoing large deformation by using Drucker–Prager constitutive model with a non-associated plastic flow rule. In DEM simulations, to partially account for rotational resistance arising from the combined effects of particle shape and hysteretic contact behavior, particle rotational velocities are reduced by a constant factor at every time step. The developed models are used to investigate the final deposit morphology, collapse pattern, non-deformed region and energy dissipation and to provide insights into the internal flow within the continuum and discrete frameworks. As a result of this study, the following conclusions are reached:

  • SPH and DEM simulations result in quite similar collapse patterns, final deposit morphology and energy dissipation, suggesting that the quasi-static axisymmetric collapse can be modeled using both the continuum and discrete frameworks as long as appropriate constitutive models or contact behaviors are implemented. However, DEM simulations are more capable of capturing particle-level behaviors, such as the sharp edges of the free surface and flow front.

  • Results of SPH and DEM simulations reveal that quasi-static axisymmetric collapse is qualitatively similar to the dynamic axisymmetric collapse: The final profile height, runout distance, collapse pattern and energy dissipation mainly depend on the initial aspect ratio. However, the quasi-static collapse results in shorter runout distances.

  • Monitoring deformation of horizontal colored layers in the initial granular columns reveals that: (1) despite significant deformation and distortion, the granular materials do not experience mixing during quasi-static collapse and (2) the upper layer is blanketing the entire deposit in quasi-static collapse. On the other hand, monitoring deformation of vertical colored layers in the initial granular columns shows that: (1) the most distal part of the deposit is from the outer vertical layer, which is similar to the dynamic collapse and (2) the middle vertical layer shows significantly less distortion than in the dynamic collapse.

  • The final deposit profile (e.g., final height and runout distance) and energy dissipation are theoretically derived for two conceptual cases including a truncated cone-like deposit with a flat surface at the top for small aspect ratios, and a cone-like deposit with a distinctive tip for large aspect ratios, while the slope of the surface in both cases is controlled by the repose angle. The results of the theoretical analysis are in good agreement with SPH and DEM simulations.

  • The non-deformed region at the center of the deposit is determined in SPH simulations by considering particles with a negligible accumulative equivalent plastic strain. The radius of non-deformed region linearly decreases with aspect ratio for a < 2.0, but remains approximately constant for large aspect ratios and is larger than half of the initial radius.