1 Introduction

Natural soils usually experienced a surrounding stress level higher than the current value. This may originate from, e.g., erosion of the surface sedimentary layer, excavation of the covering soils (in open-pit mining) or the changes in groundwater level [6, 7, 12, 19]. Consequently, they have lower void ratio and higher shear strength than the corresponding normally consolidated soils. Some crucial engineering issues are associated with the behavior of these natural stiff clays, e.g., stabilization of excavated slope, settlement of the deep foundation.

The mechanical behavior of overconsolidated clays was investigated by many researchers, both experimentally and theoretically. Some early laboratory works [11, 17] revealed that the strength and pore water pressure (undrained tests) or volumetric deformation drained tests were significantly affected by the consolidation history. Under drained conditions, the heavily overconsolidated soils may show a peak strength and strain softening afterwards. A failure process can also be observed in undrained triaxial tests accompanied by shear localization [4]. Hvorslev [17] used a direct shear box to investigate the shear strength of overconsolidated soils. The failure data for overconsolidated soils can be adequately approximated by a linear relationship in the \(p^{\prime }\)–q stress plane (\(p^{\prime }\) is the effective mean stress and q is the deviatoric stress). This linear relationship was implemented in the constitutive models by several researchers [27, 34, 39].

However, some recent works [1, 10] show that a linear line cannot fit the peak strength of the highly overconsolidated clays accurately, especially at the low stress level. For this reason, curved lines have been used to represent the peak strength on the dry side of the critical state [36, 38]. However, these models for the dry side are relatively complicated, which may limit their application.

Natural stiff clays usually possess some degree of inter-particle bonding and cementation during the deposition history in the geological history. For simplicity, the inter-particle bonding is excluded in this study, and only the overconsolidation related to void ratio is analyzed. In this study, a series of triaxial tests are presented for a silty clay with various consolidation ratios. More attention is paid to the small stress level range, which is comparable, e.g., with the stress state close to the surface of deep excavations. Based on the test results, a nonlinear power law criterion [1] will be used for the basis of the model together with the critical state concept [28, 29].

2 Laboratory investigations

2.1 Material and test procedures

The soil used in this study is a silty clay. It was taken from a highway subsoil in Dresden. The basic physical properties are given in Table 1. The organic content is 2.0 %. The original material was first mixed with water and then sieved through a mesh opening of 0.425 mm to exclude coarse grains from the natural soil. Due to a high initial water content of the slurry, the soil was first exposed to air for a period of time until it reached the desired value (1.5 times the liquid limit).

Table 1 Basic physical properties of the tested silty clay
Full size table

The slurry was poured into a consolidometer (with a diameter of 3.8 cm) and then consolidated to 80 kPa by gradually adding slotted weights on the weight hanger. The duration of each load increment was 2–4 days. After being fully consolidated, the specimens were extruded out from the consolidometer and trimmed into 7.6-cm height. It should be noted that the slurry for the isotropic consolidation test and triaxial test was prepared at the same water content, since the initial water content has a significant influence on the compression and shear strength of the reconstituted clays [15, 16, 32].

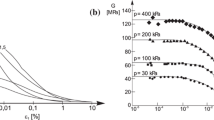
Three types of triaxial tests were conducted: (1) undrained triaxial tests for normally consolidated clay; (2) load-controlled tests in the lightly overconsolidated stress range; (3) mixed-controlled (stress controlled and displacement controlled) tests in the heavily overconsolidated stress range. The predefined stress paths of the second type are shown in Fig. 1 (left). The samples were first isotropically consolidated to 800 kPa and subsequently unloaded to the prescribed cell pressure. The following triaxial stress path is composed by two parts, a conventional drained triaxial stress path \((\frac{\mathrm {d}q}{\mathrm {d}p^{\prime }}=3)\) followed by a stress path with a constant axial force acting on the loading cap (load controlled tests). A decrease of \(p^{\prime }\) was achieved by increasing the back pressure with a given rate. The decrease of q was related to the increase in the cross-sectional area of tested samples.

Fig. 1
figure 1

Schematic figure of the applied stress paths: left type-2, right type-3

Full size image

Figure 1 (right) shows the predefined stress paths of the third type. After being unloaded to the desired cell pressure, linear stress paths with increasing or decreasing \(p^{\prime }\) were followed. In this way, the soil could be tested at a relatively low stress level. These types of tests were performed under mixed-controlled conditions. The samples were compressed along the axial direction with a constant shear velocity (displacement controlled), and the radial pressure was adjusted to meet the predefined stress path (stress controlled). A LabVIEW program was used to keep a constant stress increment ratio (\(\frac{\mathrm {d}q}{\mathrm {d}p^{\prime }}\)) during the tests. The cell pressure decreased (or increased) with an increase in the axial force acting at the loading cap. For more details of the LabVIEW program, see [3, 33]. Similar test program was used by Atkinson [1] to identify the failure points of a heavily overconsolidated soil.

2.2 Test results and analysis

After Butterfield [5], the normal compression line can be expressed as:

$$ \ln v = N^* - \lambda ^{*} \ln \left( p^{\prime }/p_{\mathrm {r}}\right) ,$$
(1)

where \(p_{\mathrm {r}}=1\) kPa is the reference stress, \(N^{*}\) corresponds to the logarithmic value of the specific volume at a reference stress of \(p_{\mathrm {r}}=1\) kPa, and \(\lambda ^*\) is the slope of the normal compression line in a double logarithmic v–\(p^{\prime }\) plane (v being the specific volume). The corresponding swelling line can be represented as:

$$ \ln v = N^* - \lambda ^* \ln \left( p^{\prime }_{\mathrm {c}}/p_{\mathrm {r}}\right) + \kappa ^* \ln \left( p^{\prime }_{\mathrm {c}}{/}p^{\prime }\right) ,$$
(2)

where \(p_{\mathrm {c}}\) is the maximum consolidation pressure and \(\kappa ^*\) is the slope of the swelling line in \(\ln v\)–\(\ln p^{\prime }\) plane.

The experimental stress paths of the second type of triaxial tests are shown in Fig. 2 (three test data are provided with the consolidation pressure of 200 kPa). The stress path can be divided into three possible stages: it initially follows the conventional triaxial stress path to a certain stress state, then the deviatoric stress shows a decrease induced by an increase in the back pressure (the axial force remains constant). Finally, the deviatoric stress decreases and tends toward the critical state line.

Fig. 2
figure 2

Stress paths and the failure points of the triaxial tests: type-2

Full size image

The mobilized friction angle is used to determine the strength of the soil. It is defined as:

$$ \phi _{\mathrm{m}} = \arcsin \left( \frac{\sigma ^{\prime }_1 - \sigma ^{\prime }_3}{\sigma ^{\prime }_1 + \sigma ^{\prime }_3} \right) ,$$
(3)

where \(\sigma ^{\prime }_1\) and \(\sigma ^{\prime }_3\) are the major and minor principal stresses, respectively. The failure points correspond to the maximum mobilized friction angle, and they are plotted in the \(p^{\prime }\)–q plane. Since the samples in Fig. 2 were not heavily overconsolidated, an approximately linear relationship between \(p^{\prime }\) and q can be observed in the tested stress range. This type of failure surface was widely used for overconsolidated soils (e.g., [27, 39]).

Figure 3 shows the stress paths of the four triaxial tests of type-3 (OC-50kPa-1, OC-50kPa-2, and OC-50kPa-3 were preconsolidated at 800 kPa, and OC-50kPa-4 has a preconsolidation pressure of 200 kPa). The failure points are also presented at the state of maximum mobilized friction angle. To included the influence of void ratio, the test data can be normalized by the Hvorslev equivalent pressure \({p^{\prime }_{\mathrm {e}}}^*\) [17] considering:

$${p^{\prime }_{\mathrm{e}}}^*=\exp \left( \frac{N^*-\ln v_\mathrm {f}}{\lambda ^*} \right) ,$$
(4)

where \(v_{\mathrm {f}}=v_\mathrm {0} \exp (-\varepsilon _{\mathrm {vf}})\) is the specific volume at the failure point obtained from the corresponding volumetric strain \(\varepsilon _{\mathrm {vf}}\), and \(v_{0}\) is the initial void ratio of samples. The failure points at the normalized stress plane are shown in Fig. 4. It can be seen that all data follow a unique curve representing a nonlinear relationship between \({p^{\prime }/p^{\prime }_{\mathrm {e}}}^*\) and \({q/p^{\prime }_{\mathrm {e}}}^*.\)

Fig. 3
figure 3

Stress paths and the failure points of the triaxial tests: type-3

Full size image

3 Double logarithmic Hvorslev surface

After Hvorslev [17], the failure envelope of overconsolidated soils can be represented as a straight line. However, this gives satisfactory results only for soils with low and intermediate overconsolidation ratios. Atkinson [1] performed series of triaxial tests on kaolin clay and observed that the linear relationship might overestimate the strength at a low stress level. This is confined by the test results in this study. Atkinson [1] proposed two methods that consider the consolidation history (see also [2]). The simpler one is adopted here—it is a linear relationship in double logarithmic plot between \(\frac{p}{{p^{\prime }_{\mathrm{e}}}^*}\) and \(\frac{q}{{p^{\prime }_{\mathrm{e}}}^*}\),

$$ \frac{q}{M{p^{\prime }_{\mathrm {e}}}^*}= \alpha \left( \frac{p^{\prime }}{{p^{\prime }_{\mathrm {e}}}^*}\right) ^\beta ,$$
(5)

where M is a strength parameter defining the critical state line, \(\alpha \) and \(\beta \) are model parameters which are not independent. Note that the normalization pressure \({p^{\prime }_{\mathrm{e}}}^*\) adopted in this study, see Eq. (4), is different from that used by Atkinson [1].

Fig. 4
figure 4

Normalization of failure points by the Hvorslev equivalent pressure

Full size image

As shown in Fig. 5, the revised Hvorslev surface meets the yield surface of the modified Cam clay model at the critical state, \(q_{\mathrm {cs}} = M p_{\mathrm {cs}}\) (the subscript cs termed as the critical state). Thus, Eq. (5) can be simplified as:

$$\alpha = \left( \frac{p_{\mathrm {cs}}^{\prime }}{{p^{\prime }_{\mathrm {e}}}^*}\right) ^ {(1-\beta )} $$
(6)
Fig. 5
figure 5

Schematic figure for the revised Hvorslev surface within the critical state concept

Full size image

\(p_{\mathrm {cs}}\) being related to \(v_{\mathrm {cs}}\) (specific volume at the critical state) according to the critical state line:

$$ p^{\prime }_{\mathrm {cs}}=\exp \left( \frac{\varGamma -\ln v_{\mathrm {cs}}}{\lambda ^*} \right) ,$$
(7)

where \(\varGamma \) controls the position of the critical state line, corresponding to the logarithmic value of the specific volume at a reference stress of 1 kPa. Note that \(v_{\mathrm {f}}\) in Eq. (4) is the same as \(v_{\mathrm {cs}}\) at the critical state. Combining Eqs. (6), (4), and (7), one obtains:

$$ \alpha = \exp \left( \frac{\left( \varGamma -N^*\right) (1-\beta )}{\lambda ^*} \right) .$$
(8)

In usual elasto-plastic models, the position of the critical state line is sufficiently defined by the yield surface on the wet side, e.g., the following expression holds for the modified Cam clay model:

$$ \varGamma -N^* = -\left( \lambda ^* - \kappa ^*\right) \ln 2 $$
(9)

Using Eq. (2), the Hvorslev equivalent pressure can also be expressed as a function of the preconsolidation pressure \({p^{\prime }_{\mathrm {c}}}\) and the current effective mean stress \(p^{\prime }\):

$$ {p^{\prime }_{\mathrm {e}}}^* = {p^{\prime }_{\mathrm {c}}} ^ {\left( 1 - {\kappa ^*}/{\lambda ^*}\right) } {p^{\prime }}^ {\kappa ^*/{\lambda ^*}} $$
(10)

Substitution of Eqs. (8)–(10) into Eq. (5), one gets the yield surface on the dry side (assuming that the yield surface is consistent with the Hvorslev surface). Logarithmic form is used here for its representation:

$$ \ln \left( \frac{q}{M}\right) - \left[ \beta + \frac{\kappa ^*}{\lambda ^*} (1 - \beta )\right] \ln p^{\prime } = \left( 1 - \frac{\kappa ^*}{\lambda ^*}\right) (1 - \beta ) \ln \left( \frac{p^{\prime }_{\mathrm {c}}}{2} \right) .$$
(11)

It can be seen that the proposed modification of the Hvorslev surface is a rather simple equation compared with some other published models [36, 38]. The peak strength of reconstituted soils results from the interlocking between the soil aggregates [35]. Therefore, in the classical critical state models (e.g., [26, 27]), the zero-tension line is incorporated into the state boundary surface to avoid the “cohesion” effect [30, 31]. In the presented model, the nonlinear parameter \({\beta }\) for the reconstituted soil is calibrated from the real experimental data, which are consistent with the no-tension assumption.

4 Elastoplastic model

4.1 Elastic behavior

Within the framework of elasto-plasticity, the deformations are recoverable within the current yield surface. The elastic volumetric strain increment can be derived from the swelling line in \(\ln p^{\prime }\)–\(\ln v\) relationship:

$$ \hbox {d} \varepsilon ^\mathrm{e}_{\mathrm {v}} = \kappa ^* \frac{\mathrm {d} p^{\prime }}{p^{\prime }} .$$
(12)

The elastic deviatoric strain increment can be expressed as:

$$ \mathrm {d} \varepsilon ^\mathrm{e}_\mathrm {s} = \frac{2(1+\nu )}{9(1-2\nu )} \kappa ^* \frac{\mathrm {d} q}{p^{\prime }} ,$$
(13)

where v is the Poisson’s ratio.

4.2 The yield and plastic potential surfaces

Equation (11) was derived from the modified Cam clay model, in which the effective mean stress at the apex of the ellipse (critical state) is half of the preconsolidation pressure \(p^{\prime }_{\mathrm {c}}\) on the \(p^{\prime }\) axis. A generalization of the modified Cam clay model was proposed by McDowell and Hau [24]:

$$ f_w = q^2 + \frac{M^2}{1-k} \left( \frac{p^{\prime }}{p^{\prime }_{\mathrm {c}}} \right) ^{\frac{2}{k}} {p^{\prime }_{\mathrm {c}}}^2 - \frac{M^2 {p^{\prime }}^2}{1-k}=0;\quad (k \ne 1) ,$$
(14)

where \(f_{\mathrm{w}}\) denotes the definition of the yield surface on the wet side of critical state, and k controls the shape of the yield surface. Obviously, the modified Cam clay model corresponds to \(k=2\) in the generalized model.

The test results from CU triaxial tests on the normally consolidated soil are presented in v–p plot (Fig. 6). The normal compression line and the critical state lines, using three values of k (1.6, 1.8 and 2.0), are also plotted in Fig. 6. It can be seen that the model with \(k=1.8\) fits the data better than the standard modified Cam clay model (k = 2.0).Footnote 1 In the sequel, Eq. (14) with \(k=1.8\) will be used for the yield surface on the wet side of the critical state. Consequently, the location of the critical state line [Eq. (9)] should be adjusted as follows:

$$ \varGamma - N^*= - \left( \lambda ^* - \kappa ^*\right) \ln \xi $$
(15)
$$ \ln \xi= \frac{k}{2k -2} \ln k $$
(16)
Fig. 6
figure 6

Test data (CU tests) of the normally consolidated soil and the critical state lines

Full size image

Considering Eqs. (5), (8), (10), and (15), the Hvorslev surface with Eq. (11) is revised as:

$$\begin{aligned} f_{\mathrm{d}}&= {} \ln \left( \frac{q}{M}\right) - \left[ \beta + \frac{\kappa ^*}{\lambda ^*} (1 - \beta )\right] \ln p^{\prime }\nonumber \\&\quad - \left( 1 - \frac{\kappa ^*}{\lambda ^*}\right) (1 - \beta ) \ln \left( \frac{p^{\prime }_{\mathrm {c}}}{\xi } \right) = 0 \end{aligned}$$
(17)

Herewith, Eqs. (14) and (17) are the yield surfaces on the wet and dry side, respectively.

Regarding the plastic potential function, the disadvantages of the associated flow rule were discussed by Potts and Zdravkovic [27]: (1) it overestimates the shear dilatancy on the dry side; (2) a discontinuity for direction of strain increments arises. A nonassociated flow rule can overcome the above shortcomings [34, 36]. In this study, the associated flow rule was used on the wet side, i.e., \(g_{\mathrm{w}} = f_{\mathrm{w}}\), whereas, on the dry side, the non-associated flow was used. The plastic potential function on the dry side is expressed as:

$$ g_{\mathrm{d}} = q^2 + \frac{M^2}{1-k} \left( \frac{p^{\prime }}{p^{\prime }_{\mathrm {c}}} \right) ^{\frac{2}{k}} {p^{\prime }_{\mathrm {c}}}^2 - \frac{M^2 {p^{\prime }}^2}{1-k}=0;\quad (k \ne 1) $$
(18)

4.3 Hardening parameter

The hardening (softening) behavior is supposed to be isotropic and controlled by the preconsolidation pressure \(p^{\prime }_{\mathrm {c}}\), which corresponds to the intersection between the yield surface (on the wet side) and the \(p^{\prime }\) axis. Hence, \(p^{\prime }_{\mathrm {c}}\) is a function of the plastic volumetric strain \(\varepsilon _\mathrm {v}\):

$$ {\mathrm {d}} p^{\prime }_{\mathrm {c}} = \frac{p^{\prime }_{\mathrm {c}}}{\lambda ^*-\kappa ^*} {\mathrm {d}}\varepsilon _\mathrm {v}^{\mathrm {p}} = \frac{p^{\prime }_{\mathrm {c}}}{\lambda ^*-\kappa ^*} \frac{\partial g}{\partial p^{\prime }} \mathrm {d} \zeta $$
(19)

where \({\mathrm{d}}\zeta \) is the scalar multiplier. Note that a linear relationship is assumed in the double logarithmic plot between specific volume v and effective mean stress \(p^{\prime }\). The hardening (softening) parameter H is expressed as:

$$ H = -\frac{1}{{\mathrm {d}}\zeta } \frac{\partial f_{\mathrm{i}}}{\partial p^{\prime }_{\mathrm{c}}} {\mathrm{d}} p^{\prime }_{\mathrm{c}};\quad (i=w, d) $$
(20)

From Eqs. (14), (17), (19), and (20), it follows:

$$ H = \frac{4 M^2 p^{\prime }_c \left( M^2 {p^{\prime }}^2 -q^2\right) }{k^2 \left( \lambda ^* - \kappa ^*\right) } {\left( \frac{p^{\prime }_c}{p^{\prime }} \right) } ^ {\left( 1 - \frac{2}{k}\right) } $$
(21)

on the wet side of the critical state and

$$ H = \frac{2 (1-\beta ) \left( M^2 {p^{\prime }}^2 -q^2\right) }{\lambda ^* k p^{\prime }} $$
(22)

on the dry side of the critical state. The standard elastoplastic matrix \([D_{\mathrm {ep}}]\) requires the differentiation of the stress components, which can be calculated from Eqs. (14) and (17) and the chain rule.

5 Hypoplastic model

In classical elastoplastic models, the soil behavior is divided into two regimes (elastic and elastoplastic). These models have the following shortcomings: (1) the definition of elastic zone is problematic, especially for clayey soils; (2) in numerical calculations, the relative location of stress state and current yield surface should be checked in each incremental step, which increases its complexity. Hypoplastic model can avoid the mentioned disadvantages. Early hypoplastic models were developed for granular materials (e.g., [9, 13, 18, 37]). In recent years, some hypoplastic models were proposed for fine-grained soils (e.g., [14, 20, 25]).

Mašín [21, 22] proposed a framework which incorporated an asymptotic state boundary surface of an arbitrary predefined shape into a hypoplastic model. In this way, the logarithmic Hvorslev surface in Sect. 3 can be incorporated into the hypoplastic model. Compared with the modified Cam clay model, the hypoplastic Cam clay model [21] can predict (1) a nonlinear response inside the asymptotic state boundary surface (denoted as ASBS in the sequel) with gradually decreasing stiffness and (2) a lower peak strength at the overconsolidated state than the elasto-plastic Cam clay model. However, the strength is still significantly estimated (refer to the model evaluation in the next section). This is the consequence of the predefined shape (ellipse) of the ASBS. In the following, a modification of the hypoplastic Cam clay model is proposed by incorporating the logarithmic Hvorslev surface.

5.1 Basic hypoplastic formulation

The rate formulation of hypoplastic models can be characterized by the following equation [9]:

$$ \mathrm {d}\sigma _{ij} = {\bar{f}}_{\mathrm{s}} \left( L_{ijkl}:{\mathrm {d}}\varepsilon _{kl} + \bar{f}_{\mathrm {d}} N_{ij} \parallel {\mathrm {d}}\varepsilon _{kl} \parallel \right), $$
(23)

where \({\mathrm {d}}\sigma _{ij}\) and \({\mathrm {d}}\varepsilon _{kl}\) are the stress and strain rate tensors, respectively, \({\bar{f}}_{\mathrm{s}}\) is a barotropy factor controlling the influence of mean stress and \(\bar{f}_{\mathrm {d}}\) is a pyknotropy factor, which incorporates the overconsolidation effect, \(L_{ijkl}\) and \(N_{ij}\) are the fourth- and second-order constitutive tensors, respectively.

As shown by Mašín and Herle [23], the asymptotic state boundary surface (ASBS) can be found for any formulation of the hypoplastic models. In the \(p^{\prime }\)–q plane, the ASBS crosses the \(p^{\prime }\) axis at \(p^{\prime }_{\mathrm {c}}\) defined as the size of ASBS. In this study, \(p^{\prime }_{\mathrm {c}}\) is used as the normalization stress: \({\bar{\sigma}}_{ij}=\sigma _{ij}/p^{\prime }_{\mathrm {c}}\). Differentiation of the stress tensor follows:

$$ {\mathrm {d}}\bar{\sigma }_{ij} = \frac{{\mathrm {d}}\sigma _{ij}}{p^{\prime }_{\mathrm {c}}} - \frac{\sigma _{ij}}{p^{\prime 2}_c} {\mathrm {d}}p^{\prime }_{\mathrm {c}} $$
(24)

\(p^{\prime }_{\mathrm{c}}\) can be derived from Eq. (2):

$$ {\mathrm {d}} p^{\prime }_{\mathrm {c}} = \frac{p^{\prime }_{\mathrm {c}}}{\lambda ^*-\kappa ^*} \left( {\mathrm {d}}\varepsilon _v - \kappa ^* \frac{\mathrm {d}p^{\prime }}{p^{\prime }} \right) .$$
(25)

The stress (strain) invariants were used in Eq. (25): \(\varepsilon _v=\varepsilon _{ii}\) and \(p^{\prime }=\sigma _{ii}/3\). Combination of Eqs. (23)–(25) leads to:

$${\mathrm {d}} \bar{\sigma }_{ij} = \frac{\bar{f}_s}{p^{\prime }_{\mathrm {c}}} \left( L_{ijkl}:{\mathrm {d}}\varepsilon _{kl} + \bar{f}_d N_{ij} \parallel {\mathrm {d}}\varepsilon _{kl} \parallel \right) - \frac{\sigma _{ij}}{p^{\prime }_{\mathrm {c}} (\lambda ^*-\kappa ^*)} \left( {\mathrm {d}}\varepsilon _v - \kappa ^* \frac{{\mathrm {d}}p^{\prime }}{p^{\prime }} \right) .$$
(26)

Note that Eq. (26) is different from that derived by Mašín [21], since he used the Hvorslev equivalent pressure [Eq. (4)] as the normalization stress. Analogously to the derivation procedures after Mašín [21], assuming the ASBS changes only in size during asymptotic stretching, i.e., \({\mathrm {d}} \bar{\sigma }_{ij}=0,\) \(N_{ij}\) can be eliminated. Finally, the hypoplastic model can be expressed as:

$$\begin{aligned} \mathrm {d} \sigma _{ij} = \bar{f}_{\rm s} L_{ijkl}:\mathrm {d}\varepsilon _{kl} - \chi \frac{\bar{f}_{\rm d}}{\bar{f}^{\rm A}_{\rm d}} A_{ijkl}: \frac{\mathrm {d} \varepsilon ^{\rm A}_{kl}}{\parallel \mathrm {d}\varepsilon ^{\rm A}_{kl}\parallel } \parallel \varepsilon _{kl} \parallel \end{aligned}$$
(27)

where \(\bar{f^A_{\mathrm {d}}}\) is the value of \(\bar{f}_{\mathrm {d}}\) corresponding to the ASBS, and \({\mathrm {d}}\varepsilon ^A_{kl}\) is the asymptotic strain rate depending on the stress state. The parameters in Eq. (27) follow from:

$$ A_{ijkl}= {} \chi {\bar{f}}_{\mathrm{s}} L_{ijkl} - \frac{\sigma _{ij}}{\lambda ^*-\kappa ^*} \otimes \delta _{kl} $$
(28)
$$ \chi= \frac{\lambda ^*}{\lambda ^*-\kappa ^*} $$
(29)
$$ L_{ijkl}= I_{ijkl} + \frac{\nu }{1-2 \nu } \delta _{ij} \otimes \delta _{kl}, $$
(30)

where \(\otimes \) denotes the tensor product, and \(\delta _{kl}\) is Kronecker’s symbol. If \(\kappa ^*=0\), Eqs. (27)–(29) are identical to Mašín’s hypoplastic Cam clay model. In this case, the size of the ASBS corresponds to the Hvorslev equivalent pressure.

5.2 Incorporation of the logarithmic Hvorslev surface

The pyknotropy factor \({\bar{f}}_{\mathrm {d}}\) in Eq. (27) governs the nonlinear behavior inside the state boundary surface. Similarly to the definition by Mašín [20],

$${\bar{f}}_{\mathrm {d}} = \frac{\xi p^{\prime }}{p^{\prime }_{\mathrm {c}}}, $$
(31)

where \(\xi \) controls the shape of the ASBS on the wet side [see Eq. (14)]. The pyknotropy factor satisfies the following conditions: \(f_d= 0\) for \(p^{\prime } = 0\) and \(f_{\mathrm {d}}= 1\) at the critical state.

In the \(p^{\prime }\)–q plane, the ASBS is divided into two parts: the logarithmic Hvorslev surface [Eq. (17)] on the dry side and the surface of the generalized modified Cam clay model on the wet side [Eq. (14)]. \(\bar{f^A_{\mathrm {d}}}\) (the value of \({\bar{f}}_{\mathrm {d}}\) at the ASBS) can be derived from Eqs. (14), (17), and (31):

$$ \bar{f}^{\mathrm{A}}_\mathrm{d} = \xi \left( \frac{M^2-\eta ^2(1-k)}{M^2}\right)^ {{k}/(2-2k)} $$
(32)

on the wet side, and

$$\bar{f}^{\mathrm{A}}_{\mathrm {d}} = \left( \frac{M}{\eta }\right) ^{{1}/(1-\beta - \kappa ^*(1-\beta )/\lambda ^*)} $$
(33)

on the dry side of the critical state.

The asymptotic strain-rate direction is assumed to be normal to the potential surface g of the elastoplastic model (Sect. 3):

$$\begin{aligned} \frac{{\mathrm {d}} \varepsilon ^A_{kl}}{\parallel {\mathrm {d}}\varepsilon ^A_{kl}\parallel }&= {} \frac{\frac{\partial g}{\partial \sigma _{ij}}}{\parallel \frac{\partial g}{\partial \sigma _{ij}} \parallel }\nonumber \\&= {} \frac{9 k s_{ij}/ p^{\prime } - 2 \left( M^2 - \eta ^2\right) \delta _{ij} }{\parallel 9 k s_{ij}/ p^{\prime } - 2 \left( M^2 - \eta ^2\right) \delta _{ij} \parallel } \end{aligned}$$
(34)

where \(\eta = q/p^{\prime }\) is the stress ratio, and \(s_{ij}=\sigma _{ij}-p^{\prime }\delta _{ij}\) is the deviatoric stress tensor.

The barotropy factor \({\bar{f}}_{\mathrm{s}}\) can be derived from the isotropic form of Eq. (27). Applying algebraic manipulation, one obtains:

$$ {\bar{f}}_{\mathrm{s}} = \frac{3 p^{\prime }}{{\bar{f}}_{\mathrm{d}}/{\bar{f}^{\mathrm{A}}_{\mathrm{d}}} + 1} \left( \frac{{\bar{f}}_{\mathrm{d}}/{\bar{f}^{\mathrm{A}}_{\mathrm{d}}}}{\lambda ^*} + \frac{1}{\kappa ^*} \right) \frac{1-2\nu }{1+\nu } $$
(35)

Equations (27)–(35) give a complete formulation of the hypoplastic model. Note that the value of \({\bar{f}}_{\mathrm{d}}\) at the ASBS is characterized by different equations for the dry [Eq. (33)] and wet side [Eq. (32)].

6 Analysis of the model and its evaluation

6.1 Model parameters

Both proposed models, elastoplastic one and the hypoplastic one, have seven constitutive parameters, i.e., M, \(N^*\), \(\lambda ^*\), \(\kappa ^*\), \(\nu \), k and \(\beta \). Five of them are analog to those in the modified Cam clay model [28]: the strength parameter M can be calculated from the strength data of normally consolidated soils; \(N^*\) and \(\lambda ^*\) define the Normal Compression Line in the \(\ln v\)–\(\ln p\) compression plane, \(\kappa ^*\) is the slope of the swelling line in double logarithmic plot.

The parameter k defines the shape of the SBS for the elasto-plastic model (or ASBS for the hypoplastic model) on the wet side. Its influence will not be investigated in this study, since it was analyzed by McDowell and Hau [24]. The potential surface also depends on k. A new parameter \(\beta \) was introduced to consider the nonlinearity of the SBS (or ASBS) on the dry side in the \(\frac{p}{{p^{\prime }_{\mathrm{e}}}^*}\)–\(\frac{q}{{p^{\prime }_{\mathrm {e}}}^*}\) plane. The Hvorslev surface is affected also by \(\kappa ^*/\lambda ^*\). Figure 7 shows the evolution of the SBS (or ASBS) on the dry side with different values of \(\kappa ^*/\lambda ^*\) and \(\beta \). The following values were employed in the calculations: \(M=1\) and \(k=2\) (both the modified Cam clay model and hypoplastic Cam clay model). In the first case, four different values of \(\kappa ^*/\lambda ^*\) (0.1, 0.3, 0.5, and 1.0) were adopted, and \(\beta =0.7\) was fixed. For the analysis of \(\beta \), \(\kappa ^*/\lambda ^*=0.3\) was fixed, and four different values (0.5, 0.6, 0.7, and 1.0) were considered.

Fig. 7
figure 7

Evolution of the nonlinear Hvorslev surface for different values of \(\kappa ^*/\lambda ^*\) and \(\beta \), respectively

Full size image

It can be seen in Fig. 7 that both factors have significant influence on the SBS (or ASBS). The degree of nonlinearity decreases with the increase of \(\beta \). The value of \(\kappa ^*/\lambda ^*\) determines the location of the critical state in terms of \(\frac{p}{{p^{\prime }_{\mathrm {e}}}^*}\)-\(\frac{q}{{p^{\prime }_{\mathrm {e}}}^*}\) relationship. For \(\kappa ^*/\lambda ^*=1\) or \(\beta =1\), the model corresponds to the yield surface of the Drucker–Prager model [8].

6.2 Analysis of the models

In this section, the proposed elastoplastic and hypoplastic models will be compared with others formulations, including the modified Cam clay model and Mašín’s hypoplastic Cam clay model.Footnote 2 The differences between those models will be analyzed. The material parameters used for the proposed models are presented in Table 2. Poisson’s ratio in both models can be calibrated by trial and error method. To predict comparable stiffness within the semi-elastic regime, the hypoplastic model and elasto-plastic model have different values of Poisson’s ratio depending on their formulations and other model parameters (elastoplastic model, \(\nu =0.2\) and the hypoplastic model, \(\nu =0.3\)).

Table 2 Model parameters of the proposed models
Full size table

Both the modified Cam clay model and Mašín’s hypoplastic Cam clay model have five parameters: M, \(N^*\), \(\lambda ^*\), \(\kappa ^*\), and \(\nu \). Their values also correspond to Table 2. The preconsolidation pressure is assumed to be 500 kPa. Five different overconsolidation ratios (OCR = 10, 5, 2.5, 1.25, 1) are considered in drained conditions. The model predictions are shown in Figs. 8, 9, 10, and 11. The results are represented in four different planes: (1) \(p^{\prime }\)–q, (2) \(\varepsilon _{\mathrm{s}}\)–q, (3) \(p^{\prime }\)–v, and (4) \(p^{\prime }/{p^{\prime }_{\mathrm {e}}}^*\)–\(q/{p^{\prime }_{\mathrm {e}}}^*\).

The peak strengths predicted by the elastoplastic models in the overconsolidation range lie on the initial yield surface. However, the hypoplastic models predict lower values. This effect can be explained as follows: in the elastoplasticity, the size of the initial yield surface remains constant during the elastic deformation and shrinks afterwards due to shear dilatancy. Nevertheless, the size of the ASBS of the hypoplastic model changes with void ratio no mater whether the stress lies inside or on the ASBS. Therefore, the hypoplastic model predicts a lower shear strength than the corresponding elastoplastic model. Still, for the proposed hypoplastic model (Fig. 11), the peak strength is very close to the Hvorslev surface.

Fig. 8
figure 8

Predictions of of drained triaxial tests with different OCR using the modified Cam clay model

Full size image
Fig. 9
figure 9

Predictions of of drained triaxial tests with different OCR using the proposed elastoplastic model

Full size image
Fig. 10
figure 10

Predictions of of drained triaxial tests with different OCR using Mašín’s hypoplastic Cam clay model

Full size image
Fig. 11
figure 11

Predictions of of drained triaxial tests with different OCR using the proposed hypoplastic model

Full size image

6.3 Validation of the model

The calibration of the shape parameter \(\beta \) is shown in Fig. 12. One can notice a reasonable linear relationship between the normalized stress invariants in the double logarithmic plot. Poisson’s ratio v was calibrated by trial and error. The summary of all model parameters calibrated for the soil described in Sect. 2 is given in Table 3. Note that different values of Poisson’s ratio are used for the hypoplastic model (0.20) and the elastoplastic model (0.25).

Fig. 12
figure 12

Calibration of the parameter \(\beta \) of the modified Hvorslev surface (\(\beta =0.75\))

Full size image
Table 3 Model parameters of the tested soil (elastoplastic model and hypoplastic model)
Full size table

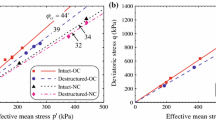
To investigate the influence of the preconsolidation pressure, a triaxial test with \(p^{\prime }_{\mathrm{c}}=200\) kPa was evaluated. From the model parameters in Table 3, one can calculate the nonlinear Hvorslev surfaces at different preconsolidation pressures (Fig. 13). The failure points from the triaxial tests at different \(p^{\prime }_{\mathrm{c}}\) are also shown in this figure. The comparison between the model and the test data reveals a satisfactory performance, although there is a slight difference between the model and the test data at a higher stress level.

Fig. 13
figure 13

Comparison between the strength envelopes from the experimental data and the model predictions

Full size image

Figure 14 shows the stress paths for the normally consolidated Dresden clay in undrained triaxial tests. The experimental data show stress paths with decreasing \(p^{\prime }\) which follow the critical state line afterwards. This behavior reveals the response of a medium dense sand, which may be caused by the considerable content of the silt (70 %) and sand (9 %) in the tested soil. The calculated stress paths of the normally consolidated samples approach the critical state line and stop there.

Fig. 14
figure 14

Laboratory results and numerical simulations using the elastoplastic model (CU triaxial tests on normally consolidated soil)

Full size image

As shown in Fig. 2, a linear Hvorslev line can well represent the failure behavior of the Dresden clay within a slightly overconsolidated state. However, at a low stress level, the failure points deviate substantially from the linear Hvorslev line. Three samples (designated as OC-50kPa-1, OC-50kPa-2, and OC-50kPa-3, respectively) were isotropically consolidated to a mean effective stress of 800 kPa and another 1–200 kPa (designated as OC-50kPa-4, respectively). Afterwards, they were allowed to swell to 50 kPa, resulting in OCR = 16 and 4, respectively. Since the volumetric deformation of test-OC-50kPa-1 in the post-peak regime is not reliable due to a technical problem, only three tests, OC-50kPa-2, OC-50kPa-3, and OC-50kPa-4 are used for the validation of the model.

Figures 15, 16, and 17 (elastoplastic model) and Figs. 18, 19, and 20 (hypoplastic model) show the comparison between the experimental data and the model predictions. The corresponding results of the modified Cam clay model and hypoplastic Cam clay model are also given in these figures for comparisons. The experimental stress paths have constant slopes in \(p^{\prime }\)–q; however, two distinct stages can be distinguished when being normalized by the Hvorslev equivalent pressure \({p^{\prime }_{\mathrm {e}}}^*\). Initially, decreasing \(p^{\prime }/{p^{\prime }_{\mathrm {e}}}^*\) indicates a semi-elastic range, subsequently, after reaching the failure point, the state travels along the revised Hvorslev surface.

From the results in Figs. 15, 16, and 17, it is evident that the proposed model can sufficiently well reproduce the evolution of the deviatoric stress for the three samples with a preconsolidation pressure of 800 kPa. The deviatoric stress increases within the initial yield surface, then it decreases toward the critical state line following the predefined stress path. The model can predict quite well the volumetric behavior. It should be noticed that, the experimental data cannot reach the critical state even after a large shear deformation (axial strain = 20 %). Nevertheless, the critical state can be simulated in the numerical simulations.

Fig. 15
figure 15

Laboratory results and numerical simulations (OC-50kPa-2): elastoplastic models

Full size image
Fig. 16
figure 16

Laboratory results and numerical simulations (OC-50kPa-3): elastoplastic models

Full size image
Fig. 17
figure 17

Laboratory results and numerical simulations (OC-50kPa-4): elastoplastic models

Full size image

It can be seen from Figs. 18, 19, and 20 that the proposed hypoplastic model also provides satisfactory results. Moreover, it predicts smoother stress strain curves than the elastoplastic model. Hypoplastic Cam clay model overestimates the shear strength significantly.

Fig. 18
figure 18

Laboratory results and numerical simulations (OC-50kPa-2): hypoplastic models

Full size image
Fig. 19
figure 19

Laboratory results and numerical simulations (OC-50kPa-3): hypoplastic models

Full size image
Fig. 20
figure 20

Laboratory results and numerical simulations (OC-50kPa-4): hypoplastic models

Full size image

7 Conclusions

The linear Hvorslev surface may overestimate the strength of heavily overconsolidated soils. For this case, a nonlinear Hvorslev surface was formulated for the dry side of the soil behavior. The following conclusions can be drawn from the evaluation of the experimental and model data:

  1. 1.

    The failure points of the tested soil show a nonlinear relationship in \(p^{\prime }\)–q plane on the dry side of the critical state. The nonlinearity increases after being normalized by the Hvorslev equivalent pressure.

  2. 2.

    A new failure surface was formulated based on the critical state concept and the proposal by Atkinson [1]. In this formulation, the stress invariants (\(p^{\prime }\) and q) at the failure points are normalized by the equivalent Hvorslev pressure on the normal consolidation line.

  3. 3.

    The yield surface proposed by McDowell and Hau [24] was used on the wet side of the critical state due to its flexibility. An additional shape parameter k adjusts the location of the Critical State Line and is coupled to the Hvorslev surface.

  4. 4.

    The nonlinear Hvorslev surface was incorporated into the elastoplastic model and the hypoplastic model. Comparisons between the experimental data and the simulations reveal that the proposed model can well represent the stress–strain and volumetric behavior observed in the laboratory. On the contrary, the standard formulations of the elastoplastic and hypoplastic models dramatically overestimate the shear strength in the high overconsolidated range.