Stress-induced anisotropy in granular materials: fabric, stiffness, and permeability

Abstract

The loading of a granular material induces anisotropies of the particle arrangement (fabric) and of the material’s strength, incremental stiffness, and permeability. Thirteen measures of fabric anisotropy are developed, which are arranged in four categories: as preferred orientations of the particle bodies, the particle surfaces, the contact normals, and the void space. Anisotropy of the voids is described through image analysis and with Minkowski tensors. The thirteen measures of anisotropy change during loading, as determined with three-dimensional discrete element simulations of biaxial plane strain compression with constant mean stress. Assemblies with four different particle shapes were simulated. The measures of contact orientation are the most responsive to loading, and they change greatly at small strains, whereas the other measures lag the loading process and continue to change beyond the state of peak stress and even after the deviatoric stress has nearly reached a steady state. The paper implements a methodology for characterizing the incremental stiffness of a granular assembly during biaxial loading, with orthotropic loading increments that preserve the principal axes of the fabric and stiffness tensors. The linear part of the hypoplastic tangential stiffness is monitored with oedometric loading increments. This stiffness increases in the direction of the initial compressive loading but decreases in the direction of extension. Anisotropy of this stiffness is closely correlated with a particular measure of the contact fabric. Permeabilities are measured in three directions with lattice Boltzmann methods at various stages of loading and for assemblies with four particle shapes. Effective permeability is negatively correlated with the directional mean free path and is positively correlated with pore width, indicating that the anisotropy of effective permeability induced by loading is produced by changes in the directional hydraulic radius.

1 Introduction

Granular materials are known to exhibit a marked anisotropy of mechanical and transport characteristics. This anisotropy can be an inherent consequence of the original manner in which the material was assembled or deposited (i.e., the inherent anisotropy that was succinctly described by Arthur and Menzies [6]), but the initial anisotropy is also altered by subsequent loading (stress-induced anisotropy, as in [5, 47, 69]). Anisotropy can be expressed as a mechanical stiffness or strength that depends upon loading direction or as hydraulic, electrical, or thermal conductivities that depend upon the direction of the potential gradient. Although the presence of anisotropy can be directly detected as a preferential, directional arrangement of grains, it can also be subtly present in the contact forces and contact stiffnesses having a predominant orientation. This direction-dependent character is often attributed to the material’s internal fabric, a term that usually connotes one of two meanings. The fabric can be a measurable average of the microscale particle arrangement (such as the Satake contact tensor [58]), or it can be a conceptual phenomenological quantity, often a tensor, that imparts an anisotropic character to a continuum constitutive description of the material (e.g., the fabric tensor of Li and Dafalias [36]). The current work attempts a bridge between these two views of fabric and anisotropy, focusing on stress-induced anisotropy: We identify those physically measurable microscale attributes that are most closely correlated with the bulk stress, stiffness, and permeability. After a brief description of the discrete element (DEM) simulations that form the basis of this study (Sect. 2), we catalog thirteen microscale measures of fabric in Sect. 3, which are reckoned from the biased orientations of the particle bodies and surfaces, of the inter-particle contacts, and of the void space. These measures are quantified for a suite of simulated granular assemblies, each with a different particle shape, which are initially isotropic but undergo stages of biaxial compression that impart an induced anisotropy.

Although fabric anisotropy is an established concept for granular materials, the current work ascertains correlations between specific fabric measures and bulk anisotropies in the stress, stiffness, and permeability. We also consider the associations between the thirteen fabric measures and their relation to particle shape. In Sects. 4 and 5, we characterize the evolution of the mechanical stiffness and the hydraulic conductivity. By considering evolutions of the various fabric measures and the consequent measured behaviors, we determine which of the fabric measures of Sect. 3 are most closely associated with anisotropies in stiffness and permeability.

Stiffness anisotropy can be measured with stress probes [11, 23] or by measuring p-wave speeds in different directions [24, 57]. This anisotropy is known to be induced by several aspects of granular loading. During loading, contacts are depleted in directions of extension, leading to a preponderance of contacts that are oriented in the direction of compression loading [11, 14, 47], and because granular stiffness is largely derived from the stiffnesses of contacts, any directional preponderance of the contacts promotes an anisotropy of stiffness. The most intensely loaded contacts are usually spatially arranged in columnar force chains that are more efficient in bearing stress along their direction of orientation [40, 55]. Among nonspherical elongated particles, the loading history also tends to rotate the particles so that their directions of elongation are perpendicular to the direction of compression—a direction that is favorable to bearing further compression in this direction [45, 47]. A more subtle anisotropy is induced in particles that interact through Hertzian contacts. Loading produces larger contact forces among those contacts that are oriented in the direction of compression, and because the stiffness of a Hertzian contact increases with increasing force, a greater bulk stiffness is induced in the direction of the compression loading [73].

The induced anisotropy is not limited to the mechanical stress–strain relation. The hydraulic properties of the granular assemblies, which depend on both the size and geometrical features of the void space, may also change due to rearrangement of the voids and deformation of the grain network. From a theoretical standpoint, an anisotropy of the permeability tensor means that it has eigenvalues of distinct magnitudes, and there exist three orthogonal principal directions corresponding to these eigenvalues [10, 13]. Wong [75] proposed a simple model that expands the Kozeny–Carman equation to an anisotropic model by simply assuming that the strain and permeability tensors share the same principal directions. This model is supported by experiments on loose and dense sand specimens at low confining pressure. The conclusion is different than the one drawn in [78], which considered triaxial extension tests performed on porous sandstone at confining pressures high enough to produce grain crushing. In this case, the major principal direction of the permeability aligns well with that of the major principal stress due to induced microcracks that were preferentially aligned with the maximum principal stress direction. Sun et al. [66] employed a lattice Boltzmann model to directly compute effective permeabilities both along and orthogonal to a shear band formed during simple shear loading. This numerical experiment suggests that anisotropic effective permeability effects in granular assemblies composed of spherical grains are not strong in the absence of grain crushing. A similar numerical approach will be used in this study.

Flow through porous media depends on the porosity and on the size, shape, and topology of the pore network, which have all received intense interest in recent years [10, 19, 62, 64, 75]. The full characterization of sands and other geomaterials can be accomplished with thin section and with noninvasive tomographic methods analysis [17, 19, 37, 44]. In the former case, three-dimensional microstructures are often statistically reconstructed from one or multiple two-dimensional thin sections [1, 27, 76]. The effective permeability of the microstructures is then calculated by computational fluid dynamics computer models or network models. A drawback of this approach is that the inferred effective permeability may depend on the quality of the pore geometry reconstruction algorithm. Another approach is to directly calculate the effective permeability from a 3D micro-CT image. This method has become increasingly popular in recent years due to the advancement of micro-CT techniques, which both reduce the cost and improve the resolution of micro-CT images. Previous work, such as [4, 19, 63, 64, 74], has found that the estimated permeabilities inferred from lattice Boltzmann and hybrid lattice Boltzmann–finite element methods are consistent with experimental measurements, provided that the computational resolution is sufficient. With both methods, the components of the anisotropic permeability tensor can be calculated from a corresponding inverse problem for a given specimen as shown in [74]. However, to study how evolution of grain kinematics affects the anisotropic permeability, volumetric digital image correlation (DIC) techniques must be used on multiple X-ray tomographic images such that the evolution of the grain fabric and pore geometry is both captured during the experimental test [2, 21]. While this experimental technique can provide invaluable microstructural information at the grain scales, the execution of such a sophisticated experimental campaign that combines volumetric DIC and X-ray tomographic imaging on a deforming specimen is not trivial. As an alternative, Sun et al. [66] applied a region-growing method on a deforming granular assemblies to obtain microstructures from discrete element simulations. The advantage of this approach is that one can study the interconnection between the grain kinematics and hydraulic properties for identical microstructures subjected to different loading paths, without worrying about the difficulty of preparing identical physical specimens in a laboratory setting. This approach has been adopted in this study.

2 DEM simulations

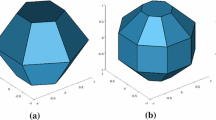
Stress-induced anisotropy was investigated with four initially isotropic DEM assemblies of unbonded smooth particles: one assembly of spheres and three assemblies of oblate ovoid shapes having different aspect ratios. An ovoid is a convex composite solid of revolution with a central torus and two spherical caps, approximating an oblate (flattened) spheroid but allowing rapid contact detection and force resolution (Fig. 1) [31]. The four assemblies were composed of particles having aspect ratios $\alpha$ of 1.0 (spheres), 0.80, 0.625, and 0.50, with sphericity decreasing with lower $\alpha$. The DEM simulations in this study are element tests in which small assemblies of “particles in a box” undergo biaxial plane strain compression. The purpose is to explore the material behavior of a simulated granular element—at both macro- and microscales—rather than to study a larger boundary value problem that would require, perhaps, many millions of particles. Figure 2 shows an initial, unloaded assembly of 6400 ovoid particles with aspect ratio 0.500, representing a small soil element of size $18\times 12\times 12D_{50}$: An assembly is large enough to capture the average material behavior but sufficiently small to suppress mesoscale localization in the form of shear bands. The particles in this image are truncated along the flat periodic boundaries that surround the assembly. The median particle size (by volume) $D_{50}$ was 0.17 mm for all four assemblies, with a size range of 0.075–0.28 mm. For the ovoid particles, these sizes are mid-plane diameters, with the axial height being smaller by factors $\alpha$ of 0.80, 0.625, and 0.50 compared with the mid-plane diameter.

Fig. 1

Ovoid particle, $\alpha =0.50$

Fig. 2

Dense initial assembly of 6400 ovoid particles, $\alpha =0.50$

The open-source OVAL code was used for the simulations [30]. The particles were isotropically compacted into fairly dense arrangements. To construct these arrangements, the 6400 particles were sparsely and randomly arranged within a spatial cell surrounded by periodic boundaries. In the absence of gravity and with a reduced inter-particle friction coefficient ($\mu =0.30$), the assembly was slowly and isotropically compacted by reducing the dimensions in all directions by equal ratios. The initially sparse arrangement with zero stress would eventually “seize” when a loose, yet load-bearing, fabric had formed. A series of fourteen progressively denser assemblies was created by repeatedly assigning random velocities to particles of the previous assembly (simulating a disturbed or vibrated state) and then further reducing the assembly volume until the newer specimen had seized. This compaction procedure, when applied to monodisperse spheres, results in isotropic assemblies with a range of void ratios that compares favorably with the range found with glass ballotini [33]. For the current study, we selected four assemblies having about the same void ratio $e=0.556$ (porosity $n=0.358$): one assembly of spheres and one assembly of each of the three ovoid shapes. After creating these dense assemblies, they were isotropically consolidated to a common mean confinement stress of $p_{{{\rm o}}}=100$ kPa.

During subsequent deviatoric loading, the following properties were assigned to the particles: shear modulus $G=29$ GPa, Poisson ratio $\nu =0.15$, and inter-particle friction coefficient $\mu =0.50$. These values are in the ranges of those measured for quartz grains [42]. Hertz–Mindlin interactions were assumed in computing the normal and tangential forces, and no contact bonding or contact rotational resistance was included in the simulations.

The same slow, quasi-static loading conditions were applied to all four assemblies: biaxial plane strain compression with constant mean stress. To load the assemblies, the larger dimension in the $x_{1}$ direction was reduced at a constant rate (vertical direction in Fig. 2), while maintaining constant width in the $x_{2}$ direction. The width in the $x_{3}$ direction was continually adjusted so that the mean stress p remained 100 kPa. Because of the periodic boundaries, no gravity was applied in the simulations. The containing periodic cell remained rectangular, so that the directions of principal stress remained aligned with the assembly boundaries. Such loading conditions would be expected to produce an orthotropic fabric, with the three principal directions of fabric anisotropy aligned with the principal stress directions.

Fig. 3

Mechanical response during biaxial plane strain compression: a deviatoric stress $\sigma _{11}-\sigma _{33}$, b intermediate deviatoric stress $\sigma _{22}-\sigma _{33}$, c volume change, and d $\pi$-plane stress paths, in which the radial scale is q / p, where $q=\sqrt{3J_{2}}$ with second principal invariant $J_{2}=[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{1}-\sigma _{3})^{2}+(\sigma _{2}-\sigma _{3})^{2}]/6$. Inset plots detail the small-strain behavior

Figure 3a shows the deviatoric stress ratio $(\sigma _{11}-\sigma _{33})/p$ that results from compressive strain $-\varepsilon _{11}$. Strength is seen to increase with decreasing sphericity, and the assembly with the flattest particles ($\alpha =0.50$) had the greatest strength. This trend is consistent with experiments [26, 47] and with other simulations [7, 50, 56]. Evolution of the intermediate principal stress is shown in Fig. 3b. In both Fig. 3a, b, the small-strain behavior is detailed in the smaller inset plots. The volume change, shown in Fig. 3c, follows a less consistent trend. All assemblies began with about the same void ratio, and all assemblies underwent extensive dilation after the strain exceeded 5 %. That is, all assemblies were initially dense relative to the critical state, as all dilated significantly during the deviatoric loading. Although a strain of 60 % was insufficient to bring nonsphere specimens to a critical state of isochoric plastic flow, the least spherical ovoids ($\alpha =0.50$) attained the largest void ratio, followed by the spheres and the ovoids with $\alpha$’s of 0.80 and 0.625. The $\pi$-plane in Fig. 3d shows the evolution of the intermediate principal stress $\sigma _{22}$ during loading with constant p. Although the stress–strain and volume change behavior are quite different for the four particle shapes (Fig. 3a, c), all shapes share nearly the same path of principal stress evolution.

Complete assembly information was collected at numerous strains—as small as 0.002 % and as large as 60 %—during the biaxial compression, so that loading-induced anisotropies of fabric, stiffness, and permeability could be measured. These characteristics are described in Sects. 3, 4, and 5, in which we determine correlations between the different fabric measures and between the fabric and the bulk stiffness and permeability.

3 Evolution of fabric anisotropy

In this section, we catalog several fabric measures and describe their changes induced by biaxial compression loading. The fabric measures are listed in Table 1, which places them in four categories, depending on the object of focus: particles, particle surfaces, contacts between particles, and void space. Many of the measures are either second-order tensors or rendered as matrices, as are appropriate for characterizing anisotropy (as a counterexample, void ratio and density are scalar quantities and are inappropriate for portraying anisotropy). As will be seen, the four categories are not clearly distinct, and some measures are associated with multiple objects.

Table 1 Fabric measures

3.1 Particle bodies

The simplest (and most apparent) measures of fabric anisotropy are those based on the orientations of the particles—information that can be gathered from digitized images of physical specimens, from the geometric data of computer simulations, or by simply disassembling a physical packing of grains. One such measure addresses the orientations of elongated or flat particles. For example, Oda [45] presented histograms of particle orientation as measured from optical micrographs of sheared sand specimens. If the particles are nearly ellipsoidal, then we can identify the three orthogonal directions of an “ith” particle’s principal axes (the unit column vectors ${{\mathbf{q}}}_{1}^{{\rm p},i}$) and the particle’s corresponding widths in these directions (widths $a_{1}^{{\rm p},i}$), where the superscript “p” will denote “particle” information. The information for the single particle can then be collected in a diagonal matrix ${\mathbf{A}}^{{\rm p},i}$ and in a matrix ${\mathbf{J}}^{{\rm p},i}$ comprised of orthogonal column vectors ${\mathbf{q}}_{k}^{{\rm p},i}$:

$${\mathbf{A}}^{{\rm p},i}= {} \left[ \begin{array}{ccc} a_{1}^{{\rm p},i} &{} 0 &{} 0\\ 0 &{} a_{2}^{{\rm p},i} &{} 0\\ 0 &{} 0 &{} a_{3}^{{\rm p},i} \end{array}\right] $$

(1)

$$ {\mathbf{J}}^{{\rm p},i}= {} \left[ {\mathbf{q}}_{1}^{{\rm p},i}, \,{\mathbf{q}}_{2}^{{\rm p},i}, \,{\mathbf{q}}_{3}^{{\rm p},i}\right] $$

(2)

with ${\mathbf{A}}^{{\rm p},i}$ providing the widths and ${\mathbf{J}}^{{\rm p},i}$ providing the orientations. For the ovoid shapes of our simulations, ${\mathbf{q}}_{1}^{{\rm p},i}$ is oriented along a particle’s central axis, and the remaining orthogonal vectors, ${\mathbf{q}}_{2}^{{\rm p},i}$ and ${\mathbf{q}}_{3}^{{\rm p},i}$, are oriented in arbitrary transverse directions. When averaged among all particles in an assembly or image, these quantities can be used to compute a tensor-valued measure of the average particle orientation:

$$ \overline{{\mathbf{J}}}^{{\rm p}}= \left\langle \frac{3}{\text{tr}\left( {\mathbf{A}}^{{\rm p},i}\right) }\, J_{jm}^{{\rm p},i}A_{ml}^{{\rm p},i}J_{kl}^{{\rm p},i}\right\rangle {\mathbf{e}}_{j}\otimes {\mathbf{e}}_{k} $$

(3)

where brackets $\langle \circ \rangle$ designate an average (in this case, of all particles p), and the ${\mathbf{e}}$ are Cartesian basis vectors. Tensor $\overline{{\mathbf{J}}}^{{\rm p}}$ is similar to the orientation tensor of Oda [47] but includes a factor that eliminates the bias of particle size, so that each particle is given an equal weight, regardless of its size. (The factors $3/\text{tr}({\mathbf{A}}^{{\rm p},i})$ can be removed if a size bias is desired.) The factor also normalizes the tensor, so that an assembly of spheres would yield the identity (Kronecker) tensor for $\overline{{\mathbf{J}}}{}^{{\rm p}}$.

The evolution of anisotropy of particle orientations is shown in Fig. 4 for the four assemblies during biaxial plane strain compression. The figure gives the deviatoric difference $\overline{J}_{11}^{{\rm p}}-\overline{J}_{33}^{{\rm p}}$ divided by the mean value of particle orientation tensor $\overline{{\mathbf{J}}}^{{\rm p}}$ (i.e., 1/3 of the trace $\text{tr}(\overline{{\mathbf{J}}}^{{\rm p}})$). The difference is always 0 for sphere assemblies. The ovoid assemblies all begin with a slight anisotropy, but loading results in particles whose wider dimensions are predominantly aligned with the extension direction $x_{3}$, a phenomenon that is widely reported in both 2D [7, 56] and 3D simulations [43, 48] and in physical experiments with sands and assemblies of plastic particles [45, 47]. This tendency is apparent in Fig. 8 for flattened ovoids ($\alpha =0.6262$) at strain $-\varepsilon _{11}=60\,\%$. Figure 4 shows that particle reorientation steadily progresses across the full range of strains, even after the stress condition has nearly reached a steady-state condition (compare with Fig. 3a). With assemblies of the flattest ovoids, a stationary fabric of particle orientation is not yet attained at the largest strain of 60 %. At small strains, very little reorientation occurs, even as the deviatoric stress approaches its peak condition: The ratio $(\overline{J}_{11}^{{\rm p}}-\overline{J}_{33}^{{\rm p}})/(\text{tr}(\overline{{\mathbf{J}}}^{{\rm p}})/3)$ has changed by less than 0.02 % at the strain $-\varepsilon _{11}=0.02$, which is roughly at the peak stress state: Further deformation is required to attain a steady state of fabric. These results show that particle reorientation lags changes in stress during the early stage of loading, but fabric change is more prolonged, and a critical state (steady state) of fabric is not necessarily attained when only the volume and stress are constant.

Fig. 4

Anisotropy of the particle orientations. Compressive loading is in the $x_{1}$ direction

3.2 Particle surfaces

A set of anisotropy measures is associated with the orientations of particle surfaces. The inertia tensor of a particle’s surface is

$$ {\mathbf{I}}^{{\rm s},i}=\int _{\partial S^{i}}{\mathbf{x}} \otimes {\mathbf{x}}\, \text{d}A^{i} $$

(4)

where ${\mathbf{x}}$ is the vector from the centroid of the particle’s surface $\partial S^{i}$ to points on this surface, and ${\mathbf{x}}\otimes {\mathbf{x}}$ is the dyad $x_{i}x_{j}$. Superscript “s” denotes a surface quantity of the particles. The average among all particles is

$$ \overline{{\mathbf{I}}}^{{\rm s}}= \left\langle \frac{3}{\text{tr}\left( {\mathbf{I}}^{{\rm s},i}\right) }\, {\mathbf{I}}^{{\rm s},i}\right\rangle $$

(5)

which has been normalized in a similar manner as $\overline{{\mathbf{J}}}{}^{{\rm p}}$ (Eq. 3).

Kuo et al. [34] introduced an orientation measure by approximating the particle surface area (per unit of volume) of the particles in direction ${\mathbf{n}}$,

$$ S({\mathbf{n}})\approx \frac{S_{{\rm v}}}{4\pi V} \left( 1+\overline{Q}_{ij}^{{\rm s}}n_{i}n_{j}\right) $$

(6)

where $S({\mathbf{n}})$ is a distribution function, $\overline{{\mathbf{Q}}}^{{\rm s}}$ is a surface area tensor, and $S_{{\rm v}}$ is the total surface area of particles in volume V. They used stereological methods proposed by Kanatani [25] to estimate $\overline{{\mathbf{S}}}^{{\rm s}}$ from 2D images along three orthogonal planes. With DEM geometric data, we can directly compute a similar average orientation tensor $\overline{{\mathbf{S}}}^{{\rm s}}$ by integrating the dyads $n_{i}n_{j}$ across the surface of each of the $N_{{\rm p}}$ particles:

$$ \overline{{\mathbf{S}}}^{{\rm s}} =\frac{3}{S_{{\rm v}}} \sum _{i=1}^{N_{{\rm p}}} \int _{\partial S^{i}}{\mathbf{n}}\otimes {\mathbf{n}}\, \text{d}A^{i} $$

(7)

in which $S_{{\rm v}}$ is the total area $\sum \int \, \text{d}A$. In this definition, the tensor is normalized so that $\overline{{\mathbf{S}}}^{{\rm s}}$ is the identity matrix for an assembly of spheres. If we divide by the total mass instead of by $S_{{\rm v}}$, Eq. (7) yields a corresponding measure of specific surface that incorporates its anisotropic character.

Fig. 5

Anisotropy of particle surface orientations during biaxial compression: a orientation $\overline{{\mathbf{I}}}^{{\rm s}}$, b orientation $\overline{{\mathbf{S}}}^{{\rm s}}$, and c correlations between the anisotropies of surface orientation and of particle orientation for ovoids with $\alpha =0.500$

The evolution of $\overline{{\mathbf{I}}}^{{\rm s}}$ and $\overline{{\mathbf{S}}}^{{\rm s}}$ during biaxial compression is shown in Fig. 5a, b for the four shapes. The same trends in both measures are similar to those in the previous Fig. 4 of the particle orientation tensor $\overline{{\mathbf{J}}}^{{\rm p}}$ (correlations are shown in Fig. 5c): (1) The anisotropy of the particle surfaces increases with increasing nonsphericity of the particle shape (smaller $\alpha$), (2) anisotropy grows throughout the range of strains, even after the stress is nearly stable, and (3) fabric change lags stress change at small strains, as the small increase in surface anisotropy contrasts with substantial increases in deviator stress.

3.3 Contacts

The mechanical behavior of granular materials is largely determined by the arrangement and orientations of inter-particle contacts. The Satake fabric tensor $\overline{{\mathbf{F}}}^{{\rm c}}$ is a measure of the average contact (“c”) orientation within a granular medium [47, 58]:

$$ \overline{{\mathbf{F}}}^{{\rm c}}= \left\langle n_{j}^{{\rm c},i}n_{k}^{{\rm c},i}\right\rangle {\mathbf{e}}_{j}\otimes {\mathbf{e}}_{k} $$

(8)

where ${\mathbf{n}}^{{\rm c},i}$ is the unit normal vector of a single “ith” contact, which is averaged for all contacts within the medium. Because force transmission takes place through the contacts, this tensor is commonly associated with stiffness and strength. Radjai [53] found that deviatoric stress is carried primarily through those contacts that bear a larger than mean normal force (also [20, 71]). This observation has led to a variation of the Satake tensor, by averaging the contact orientations among this subset of “strong” contacts:

$$ \overline{{\mathbf{F}}}^{{\text{c}\hbox{-}\text{strong}}}= \left\langle n_{j}^{{\text{c}\hbox{-}\text{strong}},i}n_{k}^{{\text{c}\hbox{-}\text{strong}},i}\right\rangle {\mathbf{e}}_{j}\otimes {\mathbf{e}}_{k} $$

(9)

which has been found to correlate with the deviatoric stress tensor [3, 71].

Another tensor $\overline{{\mathbf{G}}}^{{\rm c}}$ associated with contacting particles is the averaged product of the branch vectors $\mathbf{l}^{{\rm c},i}$ that connect the centers of contacting particles (e.g., [50]):

$$ \overline{{\mathbf{G}}}^{{\rm c}}= \frac{1}{\left( D_{50}\right) ^{2}} \left\langle l_{j}^{{\rm c},i}l_{k}^{{\rm c},i}\right\rangle {\mathbf{e}}_{j}\otimes {\mathbf{e}}_{k} $$

(10)

Magoariec et al. [39] suggested this fabric measure as a possible internal variable for predicting the stress of 2D assemblies of ellipses. The measure reflects both orientation and distance between the particle pairs and admits possible correlations between the orientation and distance [20]. The measure has been normalized so that an assembly of equal-size spheres yields a trace of 1.0. A tensor of strong contacts $\overline{{\mathbf{G}}}^{{\text{c}\hbox{-}\text{strong}}}$ can also be computed, in the manner of Eq. (9).

Stress in a granular medium is the volume average of dyadic products of branch vectors and contact forces $\mathbf{f}^{{\rm c},i}$ among all contacts within an assembly:

$$ \varvec{\sigma }=\frac{1}{V} \sum \mathbf{l}^{{\rm c},i}\otimes \mathbf{f}^{{\rm c},i} $$

(11)

Because differences in the orientations of the contact forces and the contact normals ${\mathbf{n}}^{{\rm c},i}$ are limited by the friction coefficient, the stress is likely related to the average of the dyadic products $\mathbf{l}^{{\rm c},i}\otimes {\mathbf{n}}^{{\rm c},i}$. This observation suggests a third, mixed measure of contact orientation:

$$ \overline{{\mathbf{H}}}^{{\rm c}}= \frac{1}{D_{50}} \left\langle l_{j}^{{\rm c},i}n_{k}^{{\rm c},i}\right\rangle {\mathbf{e}}_{j}\otimes {\mathbf{e}}_{k} $$

(12)

along with its strong-contact counterpart $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$.

Fig. 6

Evolution of contact anisotropies $\overline{{\mathbf{F}}}^{{\rm c}}$, $\overline{{\mathbf{H}}}^{{\rm c}}$, and $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ (Eqs. 8 and 12) expressed as differences of their major and minor principal values. Inset plots detail the small-strain behavior. a Anisotropy of $\overline{{\mathbf{F}}}^{{\rm c}}$, b anisotropy of $\overline{{\mathbf{H}}}^{{\rm c}}$, c anisotropy of $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$, d intermediate anisotropy of $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$

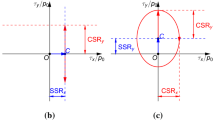
These six measures of contact orientation were investigated with the DEM simulations, with the intent of determining a fabric measure that is most closely associated with deviatoric stress. Some of the results are illustrated in Figs. 6 and 7, and all measures are summarized in Table 2. Figure 6a–c shows the progressions of the normalized deviatoric anisotropies of $\overline{{\mathbf{F}}}^{{\rm c}}$, $\overline{{\mathbf{H}}}^{{\rm c}}$, and $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ across the $x_{1}$–$x_{2}$ directions (e.g., in Fig. 4, we plot the difference $\overline{F}_{11}^{{\rm c}}-\overline{F}_{33}^{{\rm c}}$ divided by the mean $|\overline{{\mathbf{F}}}^{{\rm c}}|=\text{tr}(\overline{{\mathbf{F}}}^{{\rm c}})/3$). As has been widely reported, contact normals become predominantly oriented in the direction of compression, with anisotropy increasing with strain [20, 45, 47, 49, 55]. Kruyt [28] and Oda et al. [47] have shown that the anisotropy of $\overline{{\mathbf{F}}}^{{\rm c}}$ at small strains is primarily the result of contacts being disengaged in the extension direction (also [56]). At larger strains, changes in $\overline{{\mathbf{F}}}^{{\rm c}}$ are also produced by the reorientation of existing contacts [32]. Anisotropy in contact orientation is larger for the less spherical shapes across the full range of strains (see Fig. 6a) [7]. For the sphere assemblies, this anisotropy reaches a peak value at 8–10 % strain, which corresponds to the peak in stress ratio (Fig. 3a). At strains beyond 30 %, the sphere assemblies reach the critical state, in which stress, volume, and contact fabric are stationary, a condition that is also seen in biaxial loading simulations of disks and spheres [28, 50, 77]. With nonspherical particles, more prolonged deformation is required to reach a steady fabric (see Fig. 6a), more evidence of significant fabric rearrangements at large strains and an indication that the steady state of fabric is attained at strains greater than 60 %. For all assemblies at small strains, the rise in the anisotropy among strong contacts, for example $\overline{H}_{11}^{{\text{c}\hbox{-}\text{strong}}}-\overline{H}_{33}^{{\text{c}\hbox{-}\text{strong}}}$ (Fig. 6c), occurs more steeply than that of all contacts, for example $\overline{H}_{11}^{{\rm c}}-\overline{H}_{33}^{{\rm c}}$ (Fig. 6b). In this regard, the strong-contact measures of fabric more closely follow the rise in the stress ratio than do measures that include all contacts.

Table 2 Average correlations between six contact fabric measures and the deviatoric stress during biaxial plane strain compression (see Eq. 13)

For sphere assemblies, the deviatoric part of the fabric tensor $\overline{{\mathbf{F}}}^{{\text{c}\hbox{-}\text{strong}}}$ correlates closely with deviatoric stress, a trend noted in [20, 71]. This trend was not observed with $\overline{{\mathbf{F}}}^{{\text{c}\hbox{-}\text{strong}}}$ for the nonspherical particles, so we searched for a closer stress–fabric correspondence between the other measures of contact fabric. In Table 2, we rank the correlations between deviatoric stress and the deviatoric parts of six contact tensors with respect to their differences $\circ _{11}-\circ _{33}$ and $\circ _{22}-\circ _{33}$ across the full range of strains (0–60 %) and for all four particle shapes. Correlation is measured with Pearson's coefficients “$c_{1}$” and “$c_{2}$,” for example

$$ c_{2}(\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}},\varvec{\sigma })= \frac{\text{cov} ( \overline{H}_{22}^{{\text{c}\hbox{-}\text{strong}}} -\overline{H}_{33}^{{\text{c}\hbox{-}\text{strong}}},\, \sigma _{22}-\sigma _{33})}{\text{std} (\overline{H}_{22}^{{\text{c}\hbox{-}\text{strong}}} -\overline{H}_{33}^{{\text{c}\hbox{-}\text{strong}}}) \,\text{std}(\sigma _{22}-\sigma _{33})} $$

(13)

with the covariance and standard deviations measured across the full range of strains for each particle shape. The complementary correlation $c_{1}$ applies to differences $\circ _{11}-\circ _{33}$. Both correlations are shown in the table. Of the six contact orientation tensors, the mixed-vector orientation $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ is the most closely correlated with the stress tensor $\varvec{\sigma }$. Although $\overline{{\mathbf{F}}}^{{\text{c}\hbox{-}\text{strong}}}$ correlates favorably as small stresses, the correlation is less favorable at stresses beyond 2 % and for nonspherical shapes. The close relationship between $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ and stress is shown in Fig. 7, in which Fig. 7a shows the correspondence of $\overline{H}_{11}^{{\text{c}\hbox{-}\text{strong}}}- \overline{H}_{33}^{{\text{c}\hbox{-}\text{strong}}}$ and $\sigma _{11}-\sigma _{33}$ for the four particle shapes. Although the slope in the figure increases with increasing sphericity of the particles, the relationship for each shape is nearly linear, and even the brief relapses in stress that occur at large strains are accompanied by corresponding decreases in this fabric measure. Figure 7b shows the evolution of stress and of $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ within the $\pi$-plane for ovoids with $\alpha =0.500$. By scaling the path of $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ by a factor of 1.5, the figure reveals a close alignment of the intermediate principal values of stress and those of $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$.

Fig. 7

Correspondence between stress and the mixed-vector contact tensor $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ during biaxial compression: a deviatoric stress versus $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ for four particle shapes during strains of 0–60 %, b $\pi$-plane paths of stress and $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$ for ovoids ($\alpha =0.500$), with the latter tensor scaled by factor 1.5

3.4 Void space

Anisotropy of the void space is known to affect the hydraulic properties of granular, porous materials. The void space can be characterized by size, shape, and connectivity, which can be determined from digitized images or from the geometric descriptions of particles that are immersed in the void space. Experimental techniques, such as X-ray computed tomography (CT) and digital image correlation (DIC), can be used to track the evolution of the grain and void spaces, although the implementation of these methods is far from trivial (e.g., [2]). In this work, we quantify the size and shape of the void space with digitized images extracted from DEM data, whereas void connectivity and Minkowski fabric tensors are directly computed from the DEM geometric data. Together, the two methods are used to characterize the void fabric with a set of scalar, distribution, matrix, and tensor measures (see Table 1, “voids, v”).

The processing of digital images can be performed with discrete morphological methods [61], such as dilation, erosion, opening, and closing. With these methods, an image $X^{{\rm v}}$ is represented as an array of 1’s and 0’s for void and solid space voxels. We digitized the DEM assemblies at several strains during biaxial compression loading. The digital density was such that an average particle was covered by a $20\times 20\times 20$ grid. Figure 8 shows a digital image of an $x_{1}$-$x_{3}$ plane through an ovoid assembly with $\alpha =0.625$. The periodic boundaries are clearly seen along opposite edges of the image. With this image, the $\varepsilon _{11}$ engineering strain is $-0.60$, and dilation has increased the $x_{3}$ dimension to 2.67 times its original width. The original assembly, which was 1.5 times taller in the $x_{1}$ direction (see Fig. 2), now has a width ratio $x_{1}/x_{3}$ of only 0.22. The entire 3D image contains about 60 million voxels.

Fig. 8

Digitized cross section through an ovoid assembly ($\alpha =0.625$) at strain $\varepsilon _{11}=-0.60$. Note that the initial assembly (Fig. 2) was 1.5 times taller (in the $x_{1}$ direction) than its width ($x_{2}$ and $x_{3}$ directions), but the assembly was greatly squashed and broadened by the vertical loading

Fig. 9

Structural templates for characterizing void orientation

Hilpert [22] proposed a method for estimating the cumulative distribution $f^{{\rm v}}$ of pore size $\rho$ from 3D digital images (see also [72]):

$$ f_{\rho }^{{\rm v}}(\rho )= \frac{\text{Vol}\left( \mathcal {O}_{\rho }(X^{{\rm v}})\right) }{\text{Vol}(X^{{\rm v}})} $$

(14)

The void volume in the denominator is a simple counting of the number of void voxels. Quantity $\mathcal {O}_{\rho }(X^{{\rm v}})$ in the numerator is a counting of the morphological opening of $X^{{\rm v}}$ with a sphere-shaped structural template of 1’s having radius $\rho$ [61]. If the template is a single-null voxel (representing radius 0), the opening operation (i.e., an erosion followed by a dilation) leaves the image unchanged, and the quotient is 1.0: 100 % of the void space is larger than size 0. When the template is a digitized ball of radius $\rho$, the quotient is the fraction of void voxels at a distance greater than $\rho$ from the nearest particle.

We generalize the method by applying two other structural templates (Fig. 9). To capture the elongation and direction of the void space, we use a “spar” of length $\ell _{i}$ oriented in direction $x_{i}$: simply a single row of 1’s of length $\ell$ along dimension i (Fig. 9a). This approach yields three cumulative distributions $f_{l_{i}}^{{\rm v}}$ for the uninterrupted “lengths” $l_{i}$ of voids in the three directions, $i=1,2,3$:

$$ f_{\ell _{i}}^{{\rm v}}(\ell _{i})= \frac{\text{Vol}\left( \mathcal {O}_{\ell _{i}}(X^{{\rm v}})\right) }{\text{Vol}(X^{{\rm v}})} $$

(15)

which represents the fraction of void voxels at a distance greater than $\ell _{i}/2$ from the nearest particle surface, as measured in the $x_{i}$ direction. This distribution is related to the mean free path tensor described by Kuo et al. [34], which characterizes the mean separation between particle surfaces from within the void space. They approximated this separation $\lambda$ as a function of the measuring direction ${\mathbf{n}}$:

$$ \lambda ({\mathbf{n}})\approx \overline{\lambda }\left( 1+\lambda _{ij}n_{i}n_{j}\right) $$

(16)

where $\lambda _{ij}$ is the mean free path tensor and $\overline{\lambda }$ is the average separation for all directions and for all points within the void space. Because the median values of the three lengths $l_{i}$ in Eq. (15) represent the median free paths in directions $x_{1}$, $x_{2}$, and $x_{3}$, a matrix $\overline{{\mathbf{L}}}^{{\rm v}}$ can be constructed from these lengths, with the diagonal elements

$$ \overline{L}_{ii}^{{\rm v}}= \frac{3}{\overline{\ell }}\overline{\ell }_{i} $$

(17)

where $\overline{\ell }_{i}$ is the median value of $\ell _{i}$ for which $f_{l_{i}}^{{\rm v}}(\ell _{i})=0.50$, and $\overline{\ell }$ is the trace $\overline{\ell }_{1}+\overline{\ell }_{2}+\overline{\ell }_{3}$. Our neglect of off-diagonal terms in Eq. (17) assumes an orthotropic fabric symmetry aligned in the three coordinate directions.

As a further measure of void orientation, we apply a third structural template to the digitized images: a disk of pixels having radius $r_{i}$ with an axis of revolution in the $x_{i}$ direction (Fig. 9b). This template is used to compute a void distribution of radial “breadths” transverse to the three coordinate directions,

$$ f_{r_{i}}^{{\rm v}}(r_{i})= \frac{\text{Vol}\left( \mathcal {O}_{r_{i}}(X^{{\rm v}})\right) }{\text{Vol}(X^{{\rm v}})} $$

(18)

and the median values $\overline{r}_{i}$ yield a matrix $\overline{{\mathbf{R}}}^{{\rm v}}$ with diagonal elements

$$ \overline{R}_{ii}^{{\rm v}}= \frac{3}{\overline{r}}\overline{r}_{i} $$

(19)

which can be thought to represent median directional hydraulic radii. The denominator $\overline{r}$ is the trace $\overline{r}_{1}+\overline{r}_{2}+\overline{r}_{3}.$

The connectivity of a 3D void space $X^{{\rm v}}$ can be quantified with the Euler–Poincaré characteristic $\chi ^{{\rm v}}(X^{{\rm v}})$ [41]:

$$ \chi ^{{\rm v}}(X^{{\rm v}})= (\text{no.}\,\text{of}\,\text{connected}\,\text{regions,}\,K) +(\text{no.}\,\text{of}\,\text{cavities,}\,C)-(\text{no.}\,\text{of}\,\text{tunnels,}\,G) $$

(20)

where “no.” means “number” If the void space is entirely interconnected (i.e., with no isolated void “bubbles” inside the solid particles), the number of connected regions K is one, which is the case with our DEM assemblies. The cavities C within the interconnected void space are isolated particles or particle clusters that are disconnected from other particles and surrounded by void space. Because gravity will seat each particle against other particles, C is one for sands (i.e., a single connected particle network within the void space $\chi ^{{\rm v}}$). With DEM simulations that proscribe gravity, however, unconnected “rattler” particles can be present and numerous. The number of tunnels in a 3D region (that is, the genus G(X) of the region) is a topological quantity: the maximum number of full cuts that can be made without producing more separated (void) regions. The genus G can be derived by constructing the void connectivity graph in which pore bodies (represented as graph nodes) are connected through restricted passageways (pore throats, represented as graph edges) between particles [17, 22, 35, 54]. This full void graph can be represented as the reduced medial axis (skeleton or deformation retract) of the void space [1, 37, 38, 61]. Genus G (in Eq. 20) of the void space is [1]

$$ G(X^{{\rm v}})= 1+(\text{no.}\,\text{of}\,\text{pore}\,\text{throats})-(\text{no.}\,\text{of}\,\text{pore}\,\text{bodies}) $$

(21)

when $K=1$ and $C=1$, a large positive genus G in Eq. (21) (or a large negative value of $\chi ^{{\rm v}}$ in Eq. 20) indicates many redundant pathways (i.e., pore throats or tunnels) for fluid migration through the void space. Prasad et al. [52] presented a corresponding formula for the genus of the solid phase.

Table 3 Selected Minkowski functionals and tensors for 3D objects X, adapted from Schröder-Turk et al. [59]

Although the Euler–Poincaré characteristic of a sand specimen is usually approximated by performing morphological operations on digitized images [61], DEM simulations permit the direct computation of $\chi$ by applying Minkowski functionals to the geometric descriptions of particle shapes. Minkowski functionals (i.e., Minkowski scalars) arise in integral geometry as four independent scalar values, which include volume and surface area that are associated with a three-dimensional (3D) geometric object and are additive and invariant with respect to translation or rotation of the object. The complete set of Minkowski $\nu$-functionals $W_{\nu }$ of a 3D object X is given in the top part of Table 3, adapted from the summary of Schröder-Turk et al. [59]. The table applies to a region X that is a finite union of convex (but possibly disconnected) objects. In the expressions, $\kappa _{1}$and $\kappa _{2}$ are the principal curvatures of the object’s surface $\partial X$, quantity $(\kappa _{1}+\kappa _{2})/2$ is the mean curvature, and $\kappa _{1}\kappa _{2}$ is the Gaussian curvature. Functional $W_{0}$ is the volume; $W_{1}$ is one-third of the surface area; $W_{2}$ is equal to $2\pi /3$ times the “mean breadth” B(X) of the object; and $W_{3}$ is directly related to the characteristic $\chi$ (see Eq. 20) as

$$ W_{3}=\frac{4\pi }{3}\chi (X) $$

(22)

which is a form of the Gauss–Bonnet formula. Evaluating functionals $W_{2}$ and $W_{3}$ for shapes with sharp edges or corners requires cylindrical or spherical rounding (creating a smooth, differentiable surface) and then finding the integral limit as the radius is reduced to zero.

Functional $W_{3}$ is $4\pi /3$ for a solid ball, and $W_{3}$ is $8\pi /3$ for two disjoint balls ($\chi =1$ and 2, respectively). If two balls are brought into contact, forming a finite contact area, $W_{3}$ is reduced from $8\pi /3$ to $4\pi /3$: The two spherical surfaces have a positive Gaussian curvature $\kappa _{1}\kappa _{2}$ and together contribute $8\pi /3$ to the integral, but the bridge between the two spheres has a negative curvature and contributes $-4\pi /3$. By extension, the Euler–Poincaré characteristic $\chi ^{{\rm s}}$ of an assembly of connected solid particles $X^{{\rm s}}$ is

$$ \begin{aligned}\chi ^{{\rm s}}(X^{{\rm s}})= & {} \frac{3}{4\pi }W_{3}= 1+(\text{no.}\,\text{of}\,\text{particles}) \\&-(\text{no.}\,\text{of}\,\text{contacts}\,\text{between}\,\text{particles}) \end{aligned}$$

(23)

Because the void space and solid space share the same surface $\partial X$ with the same Gaussian curvature, the Euler–Poincaré characteristic of the void space is also

$$ \chi ^{{\rm v}}=\chi ^{{\rm s}} $$

(24)

This approach to quantifying $\chi$ for a DEM assembly (or its void space) involves simply counting the numbers of particles and contacts (as in Eq. 23) and does not require the direct evaluation of surface integrals. The void connectivity is normalized as

$$ \overline{\chi }^{{\rm v}}=\chi ^{{\rm v}}/N^{{\rm p}} $$

(25)

by dividing by the number of particles $N^{{\rm p}}$. Note that $\chi ^{{\rm v}}$ in Eq. (23) is directly related to the degree of structural redundancy of the particle network [29, 70].

Fig. 10

Rectangular blocks used in an example of Minkowski tensors

Beyond Minkowski functionals, Minkowski tensors provide measures of the shape and orientation of the void space. Schröder-Turk et al. [59, 60] identify six rank-two Minkowski tensors that form a complete set of isometry covariant, additive, and continuous functions for three-dimensional poly-convex bodies. Three of the six tensors are given in Table 3. The first two, ${\mathbf{W}}_{1}^{2,0}$ and ${\mathbf{W}}_{1}^{0,2}$, have been applied in the definitions of the surface inertia and surface normal tensors: the $\overline{{\mathbf{I}}}^{{\rm s}}$ and $\overline{{\mathbf{S}}}^{{\rm s}}$ of Eqs. (4), (5), and (7). The final tensor is covariant with respect to translation and rotation; depends solely on the shape, size, and connectivity of a 3D object; and can be directly evaluated from DEM geometric data for either the solid or void regions:

$$ {\mathbf{W}}_{3}^{2,0}(X)= \frac{1}{3}\int _{\partial X}\kappa _{1}\kappa _{2}{\mathbf{x}} \otimes {\mathbf{x}}\, \text{d}A $$

(26)

The meaning of this tensor (and the corresponding functional $W_{3}$) is illustrated with Fig. 10 for the cases of a rectangular block of size $2a_{1}\times 2a_{2}\times 2a_{3}$ and of the block pierced by a square tunnel of size $2a_{1}\times 2b\times 2b$. The sides and edges of the block have zero Gaussian curvature and do not contribute to $W_{3}$ or to ${\mathbf{W}}_{3}^{2,0}$, whose values are derived entirely from the corners. The contribution to $W_{3}$ of a single corner is $\gamma /3$, where $\gamma$ is the Descartes angular deficit of the corner ($\pi /2$ for a square corner). The value of $W_{3}$ for the eight corners of a solid block is $8(\pi /2)/3=4\pi /3$. If the coordinate system is centered within the block, tensor ${\mathbf{W}}_{3}^{2,0}$ is formed from the dyads ${\mathbf{x}}\otimes {\mathbf{x}}$, where vectors ${\mathbf{x}}$ are directed from the center to the corners:

$$ {\mathbf{W}}_{3}^{2,0} (X\,\text{of}\,\text{Fig.}\,\text{10a})=\frac{1}{3}8\frac{\pi }{2} \left[ \begin{array}{ccc} a_{1}^{2} &{} 0 &{} 0\\ 0 &{} a_{2}^{2} &{} 0\\ 0 &{} 0 &{} a_{3}^{2} \end{array}\right] $$

(27)

capturing information of the block’s shape in Fig. 10a. The value of ${\mathbf{W}}_{3}^{2,0}$ for the pierced block (Fig. 10b) equals the expression (27) plus contributions from the eight interior corners. Each of these corners has a negative angular deficit, $-\pi /2$, giving

$$ {\mathbf{W}}_{3}^{2,0}(X\,\text{of}\,\text{Fig.}\,\text{10b})= \frac{4\pi }{3}\left[ \begin{array}{ccc} a_{1}^{2}-b^{2} &{} 0 &{} 0\\ 0 &{} a_{2}^{2}-b^{2} &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right] $$

(28)

A tunnel is seen to modestly reduce the first two diagonal terms, while reducing the third term to zero. Multiple tunnels in the $x_{3}$ direction will make the third term negative, an indicator of multiple pathways (and void anisotropy) in this direction.

The tensor ${\mathbf{W}}_{3}^{2,0}$ of a single object X whose (local) center is offset by vector $\mathbf{t}$ from the origin of a (global) coordinate frame is given by Schröder-Turk et al. (in [59], their Eq. 6):

$$ {\mathbf{W}}_{3}^{2,0}= \breve{{\mathbf{W}}}_{3}^{2,0} +2\cdot \mathbf{t}\otimes \left( \frac{1}{3}\int _{\partial X}\kappa _{1}\kappa _{2} \breve{{\mathbf{x}}}\, \text{d}A\right) +W_{3}\mathbf{t}\otimes \mathbf{t} $$

(29)

which is the parallel–axis relationship for ${\mathbf{W}}_{3}^{2,0}$. In this equation, $\breve{{\mathbf{W}}}_{3}^{2,0}$ and $\breve{{\mathbf{x}}}$ are measured relative to the local center of the object, and the expression in parentheses is the local Minkowski vector $\breve{{\mathbf{W}}}_{3}^{1,0}$, which is equal to zero for spheres, ovoids, and ellipsoids and other objects having orthorhombic symmetry.

For a granular assembly, region X can represent the solid particles, which are joined at their contacts. Combining Eqs. (26) and (29); noting that $W_{3}=4\pi /3$ for a solid particle without holes and that $W_{3}=-4\pi /3$ for a contact bridge; and assuming that $\breve{{\mathbf{W}}}_{3}^{1,0}=0$ for each particle, we have

$$ {\mathbf{W}}_{3}^{2,0}= \sum _{p=1}^{N^{p}}\left( \breve{{\mathbf{W}}}_{3}^{2,0,p} +\frac{4\pi }{3}{\mathbf{x}}^{p}\otimes {\mathbf{x}}^{p}\right) -\sum _{c=1}^{N^{c}}\frac{4\pi }{3}{\mathbf{x}}^{c}\otimes {\mathbf{x}}^{c} $$

(30)

In this expression, contributions are summed from the $N^{p}$ particles and the $N^{c}$ contacts: $\breve{{\mathbf{W}}}_{3}^{2,0,p}$ is the local tensor for particle p, ${\mathbf{x}}^{p}$ is the vector from the assembly’s center to a particle’s center, and ${\mathbf{x}}^{c}$ is the vector from the assembly’s center to a contact. From the example in Fig. 10, we note that the magnitudes of the components of tensor ${\mathbf{W}}_{3}^{2,0}$ depend upon the overall shape and size of the region X as well as on connectivity within the region. During the simulated compression of our box-shaped granular assembly, its overall shape changes from tall to squat (compare Figs. 2 and 8). To compensate for this change in shape, we divide ${\mathbf{W}}_{3}^{2,0}$ by the integral in Eq. (26), as applied to the full assembly’s boundary:

$$ \overline{{\mathbf{W}}}_{3}^{{\rm v},2,0}= ({\mathbf{W}}_{3}^{2,0})^{-1}_{{\rm Eq. 26, boundaries}} \cdot ({\mathbf{W}}_{3}^{2,0})_{{\rm Eq. 30}} $$

(31)

For the rectangular assembly of our simulations, the boundary integral is simply that of a rectangular block, as in Eq. (27). Anisotropies in the void shape and connectivity are measured with this tensor.

Fig. 11

Distribution of void sizes and orientations: a pore size distribution $f^{{\rm v}}_{\rho }$ for ovoid assemblies ($\alpha =0.500$) at strains of 0 and 60 % (Eq. 14), b directed free path distributions $f^{{\rm v}}_{\ell _{i}}$ for sphere assemblies in $x_{1}$ and $x_{3}$ directions at strain 60 % (Eq. 15), c directed free path distributions $f^{{\rm v}}_{\ell _{i}}$ for ovoid assemblies ($\alpha =0.500$) at strain 60 % (Eq. 15), and directed radial breadth distributions $f^{{\rm v}}_{r_{i}}$ for ovoid assemblies ($\alpha =0.500$) at strain 60 % (Eq. 18)

We now apply the various void fabric measures to the DEM simulations of biaxial compression. Distributions of void size and orientation are shown in Fig. 11. The shift in the pore size distributions between the strains $-\varepsilon _{11}=0\,\%$ and 60 % (Fig. 11a) is due to material dilation, causing an increase in void volume. In this figure, void dimensions are normalized by dividing by the median particle size $D_{50}$. Distributions of free path distances directed in the $x_{1}$ and $x_{3}$ directions, $f^{{\rm v}}_{\ell _{1}}(\ell _{1})$ and $f^{{\rm v}}_{\ell _{3}}(\ell _{3})$, are shown in Fig. 11b for the sphere assembly and in Fig. 11c for the ovoid assembly, both at the final strain of 60 %. The void orientation is clearly different for the two types of particles. For spheres at strain 60 %, the voids are slightly longer in the $x_{1}$ direction (i.e., the direction of compressive loading). This observation is consistent with that of Oda and his coworkers [46], who found that columnar voids form between chains of heavily loaded circular disks and that the columns and chains were oriented predominantly in the direction of compression. For the flattest ovoid particles ($\alpha =0.500$), however, the directed free paths are shorter in the direction of compressive loading. As has been seen, elongated particles become oriented with long axes more aligned in the direction of extension (Fig. 4). The voids become elongated in this same direction, as can be discerned in the cross section of Fig. 8 ($\alpha =0.625$). Figure 11d shows the corresponding distribution of the directed radial breadths of the voids for the ovoid assembly at the final strain of 60 %. Comparing Fig. 11c, d, we see that the voids have become elongated in the $x_{1}$ direction while become narrower in the transverse directions.

Fig. 12

Anisotropy of median free path tensor $\overline{{\mathbf{L}}}^{{\rm v}}$ of the voids during biaxial compression. a Anisotropy across directions $x_{1}$–$x_{3}$, b anisotropy across directions $x_{2}$–$x_{3}$

This difference in void shape within assemblies of spheres and within those of flattened shapes is also evident in the evolution of the median free path orientation matrix of Eq. (17) for the four particle shapes (see Fig. 12). Spheres and the most rotund ovoids ($\alpha =0.800$) develop voids that are longer in the $x_{1}$ compression direction ($\overline{L}_{11}^{{\rm v}}-\overline{L}_{33}^{{\rm v}}>0$), whereas the flatter ovoids develop voids that are longer in the extension direction. With these flatter particles, the void elongation continues to change at strains beyond 60 %. Figure 13 shows the corresponding anisotropy of the median radial breadth tensor $\overline{{\mathbf{R}}}^{{\rm v}}$. Comparing Figs. 12 and 13, we see countervailing trends of the two anisotropy measures: As the voids become more elongated in one direction (Fig. 12, as developed with the structural template of Fig. 9a), the voids become narrower in the transverse directions (Fig. 13, as developed with the structural template of Fig. 9b), so that an increase in the anisotropy $\overline{{\mathbf{L}}}^{{\rm v}}$ is accompanied by a counteranisotropy of $\overline{{\mathbf{R}}}^{{\rm v}}$. Although both $\overline{{\mathbf{L}}}^{{\rm v}}$ and $\overline{{\mathbf{R}}}^{{\rm v}}$ are extracted from the void space images, no attempt was made to correlate void ratio with these tensors. All simulations began dense of the critical state, resulting in significant dilation for all assemblies, so that the mean void dimensions (as measured by $f^{{\rm v}}_{\rho }(\rho )$ or the traces of $\overline{{\mathbf{L}}}^{{\rm v}}$ and $\overline{{\mathbf{R}}}^{{\rm v}}$) increased during loading.

Fig. 13

Anisotropy of median radial breadth tensor $\overline{{\mathbf{R}}}^{{\rm v}}$ of the voids during biaxial compression. a Anisotropy across directions $x_{1}$–$x_{3}$, b anisotropy across directions $x_{2}$–$x_{3}$

Fig. 14

Anisotropy of the Minkowski tensor $\overline{{\mathbf{W}}}_{3}^{2,0}$

Void anisotropy is also measured with the normalized Minkowski tensor $\overline{{\mathbf{W}}}_{3}^{{\rm v},2,0}$ (see Eq. 31). Figure 14 shows the deviator of this tensor divided by its trace. The somewhat erratic progression indicates a strong sensitivity of this measure to subtle changes in particle arrangement, and, as such, this measure of void anisotropy is not appropriate unless large numbers of particles can be sampled. The figure indicates that the anisotropy in $\overline{{\mathbf{W}}}_{3}^{{\rm v},2,0}$ increases during loading, following a similar trend as that of the measures $\overline{{\mathbf{J}}}^{{\rm p}}$, $\overline{{\mathbf{I}}}^{{\rm s}}$, and $\overline{{\mathbf{S}}}^{{\rm s}}$ in Figs. 4 and 5.

3.5 Summary of fabric measures

In this section, we have considered thirteen measures of fabric anisotropy and their evolution during biaxial loading. Three (possibly four) of these measures are closely related to particle orientation, and any one of the three would serve as a fabric measure in this regard: the particle orientation tensor ($\overline{{\mathbf{J}}}^{{\rm p}}$) and the two tensors of particle surface orientation ($\overline{{\mathbf{I}}}^{{\rm s}}$ and $\overline{{\mathbf{S}}}^{{\rm s}}$). The Minkowski void tensor $\overline{{\mathbf{W}}}^{{\rm v},2,0}_{3}$ also follows these same trends.

Six measures of contact orientation were also presented, involving contact orientation, branch vector orientation, and mixed contact–branch orientation, and in which we include either all contacts or only the strong-contact subset. Of these measures, the one requiring the most information, the mixed tensor of strong contacts $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$, is most closely correlated with stress evolution. Particle orientation and surface orientation, however, are poorly correlated with the deviatoric stress.

Several measures of void orientation were considered: directional distributions of the free paths $f^{{\rm v}}_{\ell _{i}}(\ell ^{i})$ and transverse radial breadths $f^{{\rm v}}_{r_{i}}(r^{i})$, corresponding orientation matrices $\overline{{\mathbf{L}}}^{{\rm v}}$ of median free paths and $\overline{{\mathbf{R}}}^{{\rm v}}$ of radial breadths, and the average Minkowski tensor $\overline{{\mathbf{W}}}_{3}^{{\rm v},2,0}$. The evolutions of all of these void measures (except for $\overline{{\mathbf{W}}}_{3}^{{\rm v},2,0}$) exhibit trends that are quite different from those of the particle bodies, surfaces, or contacts, in that opposite trends are found in their evolution for the least flattened ($\alpha =1$ and 0.800) and most flattened particles ($\alpha =0.625$ and 0.500, Fig. 12). As for the Minkowski measure $\overline{{\mathbf{W}}}_{3}^{{\rm v},2,0}$, although its calculation requires more extensive information and it holds the promise of capturing both the orientation and the topology of the void space, it results in a more erratic evolution that follows a trend much like that of the simpler measures of particle and surface orientation. These fabric measures will now be investigated in relation to the load-induced anisotropies of stiffness and permeability.

4 Stiffness anisotropy

The strength of granular materials is known to depend on the initial, deposition anisotropy [26, 68], and when loaded in a particular direction, strength can also depend upon the anisotropy that is induced by a previous loading in another direction [5, 24]. The relationship between the current stress and the current fabric has been expressed in so-called stress–force–fabric relations (e.g., those of [7, 9, 20, 49]). Rather than investigating such effects of anisotropy on the stress and on the eventual strength, we focus instead on the incremental stiffness and the influence of previous loading on this stiffness. We began with the same four assemblies, which had a nearly isotropic initial fabric and were confined with an isotropic stress. The monotonic loading in our simulations—biaxial plane strain compression—induced an orthotropic symmetry of the fabric, stress, and stiffness, with principal directions aligned with the coordinate axes.

Elastic solids with orthotropic symmetry exhibit the following compliance relation:

$$\begin{aligned} \left[ \begin{array}{c} \text{d}\varepsilon _{11}\\ \text{d}\varepsilon _{22}\\ \text{d}\varepsilon _{33}\\ \text{d}\varepsilon _{12}\\ \text{d}\varepsilon _{13}\\ \text{d}\varepsilon _{23} \end{array}\right] = \left[ \begin{array}{cccccc} \frac{1}{E_{1}} &{} \frac{-\nu _{12}}{E_{2}} &{} \frac{-\nu _{13}}{E_{3}}\\ \frac{-\nu _{21}}{E_{1}} &{} \frac{1}{E_{2}} &{} \frac{-\nu _{23}}{E_{3}}\\ \frac{-\nu _{31}}{E_{1}} &{} \frac{-\nu _{32}}{E_{2}} &{} \frac{1}{E_{3}}\\ &{} &{} &{} \frac{1}{G_{12}}\\ &{} &{} &{} &{} \frac{1}{G_{13}}\\ &{} &{} &{} &{} &{} \frac{1}{G_{23}} \end{array}\right] \left[ \begin{array}{c} \text{d}\sigma _{11}\\ \text{d}\sigma _{22}\\ \text{d}\sigma _{33}\\ \text{d}\sigma _{12}\\ \text{d}\sigma _{13}\\ \text{d}\sigma _{23} \end{array}\right] \end{aligned}$$

(32)

which involves nine material properties (note $\nu _{12}=\nu _{21}$, $\nu _{13}=\nu _{31}$, $\nu _{23}=\nu _{32}$). With granular materials, however, an initial deviatoric strain of as small as 0.01 % is sufficient to produce plastic deformation, alter the incremental stiffness, and disrupt any previous fabric symmetries [18]. Because of this complexity, which induces nonlinearity, inelasticity, and anisotropy at the very start of loading, we abandon an assumption of uniform linearity and leave aside Eq. (32) in the following. We instead assume a more general behavior that is rate independent and incrementally nonlinear but is positively homogeneous and dependent on the current fabric. The general compliance and stiffness response operators are

$$ \text{d}\varvec{\varepsilon }=\mathbf{f}(\mathcal {S},\text{d}\varvec{\sigma }),\quad \text{d}\varvec{\sigma }=\mathbf{f}^{-1}(\mathcal {S},\text{d}\varvec{\epsilon }) $$

(33)

satisfying

$$ \lambda \, \text{d}\varvec{\varepsilon }= \mathbf{f}(\mathcal {S},\lambda \, \text{d}\varvec{\sigma }), \quad \lambda \, \text{d}\varvec{\sigma }= \mathbf{f}^{-1}(\mathcal {S},\lambda \, \text{d}\varvec{\epsilon }) $$

(34)

for positive scalar $\lambda$ (see Darve [15]). Here $\mathcal {S}$ represents the current state of the material as characterized by its stress, fabric, stress history, etc. The homogeneous tensor response function $\mathbf{f}$ depends upon both the direction and magnitude of the loading increment $\text{d}\varvec{\sigma }$.

To characterize the behavior at a particular state, we followed a program suggested by Darve and Roguiez [16], measuring the multi-directional incremental stiffnesses at various stages of biaxial loading. We applied both loading and unloading increments in three directions to DEM assemblies having a current orthotropic symmetry of fabric that had been induced by the initial monotonic loading of biaxial compression. At various strains during this monotonic loading, we stopped the simulation and applied the six incremental oedometric conditions:

$$ \text{d}\varepsilon _{ii}\ne 0\,\text{with}\,\text{d}\varepsilon _{jj}= \text{d}\varepsilon _{kk}=0,\quad i\ne j\ne k $$

(35)

in which $i=1,2,3$ and with increments $d\varepsilon _{ii}$ that were alternatively positive and negative. For example, after biaxial plane strain compression to a strain of 5 % (i.e., $\varepsilon _{11}=-0.05$), one incremental loading consisted of a small compressive increment $\text{d}\varepsilon _{22}<0$ while maintaining constant normal strains $\varepsilon _{11}$ and $\varepsilon _{33}$ (i.e., constant assembly widths). As a second loading, a small tensile increment $\text{d}\varepsilon _{22}>0$ was applied, also maintaining constant $\varepsilon _{11}$ and $\varepsilon _{33}$. A small increment $\text{d}\varepsilon _{ii}=\pm$0.005 % was used in our simulations. No shearing strains (e.g., $\gamma _{12}$) were applied in our program, so that each of the six loading increments maintained the original principal directions of orthotropic fabric and stress. Throughout the program, fabric and stress changed, but their principal directions would not rotate and the two remained coaxial. That is, if the fabric is characterized by tensor ${\mathbf{a}}$ (perhaps chosen from the list in Table 1), then $({{{\mathbf{a}}}}{:}\varvec{\sigma })^{2}=({\mathbf{a}}{:}{\mathbf{a}})(\varvec{\sigma }{:}\varvec{\sigma })$, $(\dot{{\mathbf{a}}}{:}\varvec{\sigma })^{2}=(\dot{{\mathbf{a}}}{:}\dot{{\mathbf{a}}})(\varvec{\sigma }{:}\varvec{\sigma })$, and $({\mathbf{a}}{:}\dot{\varvec{\sigma }})^{2}=({\mathbf{a}}{:}{\mathbf{a}})({\dot{\varvec{\sigma }}{:}\dot{\varvec{\sigma }}})$, as in [51]. The absence of shearing strains also obviates the need to consider corotational stress rates or increments.

In the study, we exploited a particular advantage of DEM simulations for exploring material behavior: Once a DEM assembly had been created and loaded to some initial strain, the precise configuration $\mathcal {S}$ at that instant (particle positions, contact forces, contact force history, etc.) could be stored and reused with subsequent loading sequences of almost unlimited variety, all beginning from the same stored configuration (e.g., [8, 12]). Following Eq. (35), six incremental tests (three loading and three unloading increments) were begun from the assembly configurations at several strains $\varepsilon _{11}$ during the initial monotonic biaxial loading. Each set of six incremental oedometric (uniaxial compression/extension) tests allows measurement of eighteen material properties for the three cases $i=1,2,3$ with $i\ne j\ne k$:

$$ \text{d}\varepsilon _{ii}>0,\; \text{d}\varepsilon _{jj}=\text{d}\varepsilon _{kk}=0\Rightarrow{\left\{ \begin{array}{ll} O_{i}^{+}= {\partial \sigma _{ii}}/{\partial \varepsilon _{ii}}\\ K_{i}^{j,+}= {\partial \sigma _{jj}}/{\partial \sigma _{ii}}\\ K_{i}^{k,+}= {\partial \sigma _{kk}}/{\partial \sigma _{ii}} \end{array}\right. } $$

(36)

$$ \text{d}\varepsilon _{ii}<0,\; \text{d}\varepsilon _{jj}=\text{d}\varepsilon _{kk}=0\Rightarrow {\left\{ \begin{array}{ll} O_{i}^{-}= {\partial \sigma _{ii}}/{\partial \varepsilon _{ii}}\\ K_{i}^{j,-}= {\partial \sigma _{jj}}/{\partial \sigma _{ii}}\\ K_{i}^{k,-}= {\partial \sigma _{kk}}/{\partial \sigma _{ii}} \end{array}\right. } $$

(37)

where the O and K are generalized oedometric stiffness moduli and lateral pressure coefficients. Darve and Roguiez [16] present an octo-linear hypoplastic framework for orthotropic loadings in which the incremental stress is given as

$$ \left[ \begin{array}{l}\text{d}\sigma _{11}\\ \text{d}\sigma _{22}\\ \text{d}\sigma _{33} \end{array}\right]=\mathbf{C}\left[ \begin{array}{l}\text{d}\varepsilon _{11}\\ \text{d}\varepsilon _{22}\\ \text{d}\varepsilon _{33} \end{array}\right]+{\mathbf{D}}\left[ \begin{array}{l}|\text{d}\varepsilon _{11}|\\ |\text{d}\varepsilon _{22}|\\ |\text{d}\varepsilon _{33}| \end{array}\right] $$

(38)

where matrices $\mathbf{C}$ and ${\mathbf{D}}$ are the incrementally linear and incrementally nonlinear stiffnesses, defined as

$$ \mathbf{C}=\frac{1}{2}\left( {\mathbf{Q}}^{+}+{\mathbf{Q}}^{-}\right) \quad \text{and}\quad {\mathbf{D}}=\frac{1}{2}\left( {\mathbf{Q}}^{+}-{\mathbf{Q}}^{-}\right) $$

(39)

with

$$ {\mathbf{Q}}^{+}= \left[ \begin{array}{lll} O_{1}^{+}&K_{2}^{1+}O_{2}^{+}&K_{3}^{1+}O_{3}^{+}\\ K_{1}^{2+}O_{1}^{+}&O_{2}^{+}&K_{3}^{2+}O_{3}^{+}\\ K_{1}^{3+}O_{1}^{+}&K_{2}^{3+}O_{2}^{+}&O_{3}^{+} \end{array}\right] $$

(40)

and with the ${\mathbf{Q}}^{-}$ matrix defined in a similar way, but with the negative “$-$” moduli and coefficients of Eq. (37).

Fig. 15

Evolution of incremental directional stiffnesses of the sphere assembly. Initial compressive loading is in the $x_{1}$ direction. Inset plots detail the small-strain stiffness.

The additive decomposition in Eq. (38) does not expressly concern elastic and plastic increments: The linear response $\mathbf{C}$ simply gives the average of the loading and unloading stiffnesses, whereas ${\mathbf{D}}$ is its nonlinear hypoplastic complement. We consider stiffness $\mathbf{C}$ as more clearly reflective of the anisotropy of the average bulk stiffness response, as it can identify differences in the average stiffnesses for directions $x_{1}$, $x_{2}$, and $x_{3}$. Figure 15 shows the stiffness evolution for the assembly of spheres when loaded in biaxial compression with constant mean stress. The directional moduli $C_{11}$, $C_{22}$, and $C_{33}$ have been divided by the linear bulk modulus $K_{\mathbf{C}}$ (i.e., the average of the loading and unloading bulk moduli), which is simply equal to the average of the nine terms of matrix $\mathbf{C}$. Although the slope of a conventional stress–strain plot (as in Fig. 3a) is greatly reduced during loading, becoming nearly zero beyond the peak stress state, the linear $C_{ii}$ moduli are seen to change, with $C_{11}$ increasing and $C_{33}$ decreasing, but the assembly also retained stiffness integrity throughout the loading process: The average loading–unloading moduli were altered, but were not fully degraded, by the loading. That is, the granular assembly maintained a load-bearing network of contacts that continued to provide stiffness, even as the stress reached a peak and eventually attained a steady-state, zero-change condition. The figure indicates a developing anisotropy, suggesting that the load-bearing contact network conferred greater stiffness in the direction of compressive loading (stiffness $C_{11}$), while reducing stiffness in the direction of extension (stiffness $C_{33}$). Stiffness evolution $C_{22}$ in the intermediate, zero-strain $x_{2}$ direction follows an intermediate trend.

Fig. 16

Anisotropy in the incremental linear stiffness $C$ of four particle shapes: a deviatoric anisotropy across the $x_{1}$–$x_{3}$ directions and b intermediate deviatoric anisotropy across the $x_{2}$–$x_{3}$ directions. The stiffness deviator is normalized with respect to the average bulk modulus $K_{\mathbf{C}}$. Inset plots detail the small-strain stiffness

The evolution of stiffness anisotropy is more directly measured by the stiffness differences $C_{11}-C_{33}$ and $C_{22}-C_{33}$ (Fig. 16). These measures of stiffness anisotropy are the complements of the stress anisotropies shown in Fig. 3a, b. Although the numerical values of the anisotropies of stiffness and stress do differ, the trends are similar across the primary ($x_{1}$–$x_{3}$) and intermediate ($x_{2}$–$x_{3}$) directions: A rapid rise in stiffness (strength), attaining a peak stiffness (peak strength) at strains of 2–10 %, was followed by a softening (weakening) at larger strains. At large strains, the deviator stress ratios across directions $x_{1}$–$x_{3}$ are in the range 0.8–1.3 for the four particle shapes (Fig. 3a), whereas the stiffness difference ratios are 1.4–2.1 (Fig. 16a). At small strains, shown in the insets of Figs. 3 and 16, both deviatoric stress and stiffness anisotropy increase at the start of loading, although deviatoric stress increases with strain more steeply than stiffness anisotropy. The same trends are apparent across the intermediate directions $x_{2}$–$x_{3}$ (Figs. 3b, 16b).

These similarities of stress and stiffness anisotropies attest to stress and stiffness having a common origin in the mechanical interactions of particles at their contacts. In Sect. 3.3, we found that anisotropy of the mixed-fabric strong-contact tensor, $\overline{{\mathbf{H}}}^{{\text{c}\hbox{-}\text{strong}}}$, correlated most closely with deviatoric stress. However, we found that the mixed-fabric contact tensor among all contacts, $\overline{{\mathbf{H}}}^{{\rm c}}$, most closely correlates with the anisotropy of the incremental stiffness. The evolution of this fabric measure is shown in Fig. 6b. The Pearson coefficient of the stiffness and fabric anisotropies, $C_{11}-C_{33}$ and $\overline{H}^{{\rm c}}_{11}-\overline{H}^{{\rm c}}_{33}$, was an average of 0.985 among the four particle shapes, and the corresponding average correlation for the $x_{2}$–$x_{3}$ anisotropies was 0.981. Nearly the same correlation was found across all particle shapes, and $(C_{11}-C_{33})/K_{\mathbf{C}}$ was consistently about 4.1 times greater than $(\overline{H}^{{\rm c}}_{11}-\overline{H}^{{\rm c}}_{33})/\text{tr}(\overline{H}^{{\rm c}}_{11}-\overline{H}^{{\rm c}}_{33})$ across all strains and all particle shapes. To summarize, stress is most closely associated with the fabric of the most heavily loading contacts (the strong-contact network), whereas stiffness is most closely correlated with the fabric of all contacts. Finally, we note that an assembly’s stiffness is not closely correlated with the orientations of the particle bodies or of the particle surfaces: Plots of $\overline{{\mathbf{J}}}^{{\rm p}}$, $\overline{{\mathbf{I}}}^{{\rm s}}$, and $\overline{{\mathbf{S}}}^{{\rm s}}$ (Figs. 4, 5) are quite different than those of the stiffness in Fig. 16.

5 Effective permeability

The particles that form the solid soil skeleton are often assumed to be impermeable in a timescale important for most engineering applications. For this case, the hydraulic properties of the granular assemblies are dictated by the geometry of the void space among the solid grains. As a result, the effective permeability tensor of a grain assembly is isotropic if and only if the microstructural pore geometry is isotropic. As was seen in Sect. 3.4 for cohesionless granular media, the pore geometry evolves when subjected to external loading. While continuum-based numerical models, such as [65, 67], often employ the size of the void space to predict permeability, the anisotropy of the effective permeability is often neglected. Certainly, this treatment may lead to considerable errors in the hydro-mechanical responses if the eigenvalues of the permeability tensor are significantly different.

In this study, we analyzed the evolution of permeability anisotropy by recording the positions of all grains in the assembly at different strains. As a result, the configuration of the pore space can be reconstructed and subsequently converted into binary images (Fig. 8, also [66]). To measure effective permeability of a fully saturated porous media, one can apply a pore pressure gradient along a basis direction and determine the resultant fluid filtration velocity from pore-scale hydrodynamic simulations. The effective permeability tensor $\mathbf{K}$ is obtained according to Darcy’s law,

$$ k_{ij} = -\frac{\mu ^{v}}{p_{,j}} \frac{1}{V_{\varOmega }} \int _{\varOmega } v_{i}({\mathbf{x}}) \text{d}\varOmega $$

(41)

where $\mu ^{v}$ is the kinematic viscosity of the fluid occupying the spatial domain of the porous medium $\varOmega$. The procedure we used to obtain the components of the effective permeability tensor $k_{ij}$ from Lattice Boltzmann simulation is as follows. First, we assumed that the effective permeability tensor $k_{ij}$ is symmetric and positive definite. We then determined the diagonal components of the effective permeability tensor $k_{ii}$ by three hydrodynamics simulations with imposed pressure gradient on two opposite sides orthogonal to the flow direction and a no-flow boundary condition on the four remaining side faces. Figure 17 shows flow velocity streamlines obtained from lattice Boltzmann simulations performed on two deformed assemblies with grain shapes $\alpha = 0.500$ and 0.800.

After determining the diagonal components of the effective permeability tensor, we replaced the no-slip boundary conditions with slip natural boundary conditions and conducted three additional hydrodynamics simulations, one for each orthogonal axis. Since the effective permeability tensor is assumed to be symmetric and the diagonal components are known, there are three unknown off-diagonal components that remained to be solved. To solve the off-diagonal component, we first expanded Darcy’s law,

$$ v_{1}= \frac{1}{\mu ^{v}} ( k_{11} \partial p / \partial x_{1} + k_{12} \partial p / \partial x_{2} + k_{13} \partial p / \partial x_{3}) $$

(42)

$$ v_{2}= \frac{1}{\mu ^{v}} ( k_{12} \partial p / \partial x_{1} + k_{22} \partial p / \partial x_{2} + k_{23} \partial p / \partial x_{3}) $$

(43)

$$ v_{3}= \frac{1}{\mu ^{v}} ( k_{13} \partial p / \partial x_{1} + k_{32} \partial p / \partial x_{2} + k_{33} \partial p / \partial x_{3})$$

(44)

Putting the known terms on the right sides leads to the system

$$ \left[ \begin{array}{ccc} \partial p / \partial x_{2} &{} \partial p / \partial x_{3} &{} 0 \\ \partial p / \partial x_{1} &{} 0 &{} \partial p / \partial x_{3} \\ 0 &{} \partial p / \partial x_{1} &{} \partial p / \partial x_{2} \end{array}\right] \left[ \begin{array}{c} k_{12} \\ k_{13} \\ k_{23} \end{array}\right] =\left[ \begin{array}{c} -\mu ^{v} v_{1} - k_{11} \partial p / \partial x_{1} \\ -\mu ^{v} v_{2} - k_{22} \partial p / \partial x_{2} \\ -\mu ^{v} v_{3} - k_{33} \partial p / \partial x_{3} \end{array}\right] $$

(45)

By solving the inverse problem described in Eq. (45) with the numerical simulations results from pore-scale simulations, we obtained the remaining off-diagonal components of the effective permeability tensor. In this study, we used the lattice Boltzmann (LB) method to conduct the pore-scale flow simulations. For brevity, we omit description of the lattice Boltzmann method, and interested readers are referred to [63, 64, 66, 74] for details.

Fig. 17

Streamlines from lattice Boltzmann flow simulations performed on assemblies with $\alpha = 0.500$ and 0.800 at 60 % shear strain. a $\alpha =0.500, -\epsilon _{11} = 60\,\%$, b $\alpha =0.800, -\epsilon _{11} = 60\,\%$

Fig. 18

Induced anisotropy of the effective permeability $\mathbf{K}$ for four particle shapes. a Anisotropy across directions $x_{1}$–$x_{3}$, b anisotropy across directions $x_{2}$–$x_{3}$

Figure 18 shows induced anisotropies in the effective permeability tensors $\mathbf{K}$ for the four assemblies during biaxial compression, expressed as differences between diagonal components of the effective permeability tensor, divided by its trace. Differences in the permeabilities of the assemblies of spheres and of the flatter particles are apparent. During early stages of biaxial compression, grain assemblies composed of spheres and the most rotund ovoids have lower permeability in the $x_{1}$ direction (the direction of compressive strain) than in the $x_{3}$ direction (of extension), with $K_{11} - K_{33} \le 0$. Assemblies composed of the flatter ovoids ($\alpha = 0.625$ and 0.500), however, do not exhibit this trend, and compressive strain in the $x_{1}$ direction induces a permeability in this direction, $K_{11}$, that is higher than that in the extensional $x_{3}$ direction, $K_{33}$ (Fig. 18a).

Comparing these trends in the anisotropy of permeability with anisotropies of the various fabric measures, we see little correlation between permeability and the orientations of the particle bodies, of the particles’ surfaces, or of the particles’ contacts. That is, the plots of $\overline{{\mathbf{J}}}^{{\rm p}}$, $\overline{{\mathbf{I}}}^{{\rm s}}$, $\overline{{\mathbf{S}}}^{{\rm s}}$, $\overline{{\mathbf{F}}}^{{\rm c}}$, etc. (Figs. 4, 5, 6) are quite different from those of the permeability in Fig. 18. We do see, however, similarities between the anisotropies of permeability and those of the median free path and the median radial breadth of the void space (see Figs. 12, 13). Anisotropy in the permeability $\mathbf{K}$ is negatively correlated with the median free path matrix $\overline{{\mathbf{L}}}^{{\rm v}}$ and is positively correlated with the median radial breadth matrix $\overline{{\mathbf{R}}}^{{\rm v}}$. These trends are apparent for anisotropies across both the $x_{1}$–$x_{3}$ and $x_{2}$–$x_{3}$ directions. These trends suggest two competing influences on the effective permeability. On the other hand, a larger median free path in a particular direction indicates a reduced tortuosity in this direction, which should increase the directional permeability: a trend that is at variance with the countercorrelated trends in Figs. 12 and 18. A larger median radial breadth in a particular direction is consistent with a larger hydraulic radius for flow in this direction, and anisotropies in the median radial breadth $\overline{{\mathbf{R}}}^{{\rm v}}$ and effective permeability $\mathbf{K}$ should be correlated, which is in accord with the positively correlated trends of Figs. 13 and 18. The numerical experiments indicate that change in the directional hydraulic radii is the more dominant mechanism in influencing the induced anisotropy of the effective permeability. This result is probably attributed to the fact that the void spaces of all four assemblies are highly interconnected and of relatively high porosity.

6 Conclusion

Thirteen measures of fabric are arranged in four categories, depending upon the object of interest: the particle bodies, the particle surfaces, the contacts, and the voids. The orientations of the particle bodies and their surfaces are fairly easy to measure, and their induced anisotropies follow similar trends during monotonic biaxial compression. Anisotropies of these measures increase with loading, but their change lags changes in the bulk stress, and they continue to change even after stress and volume have nearly attained steady values; in particular, nonspherical particles continue to be reoriented at strains greater than 60 %. Although they are easiest to measure, the average orientations of particle bodies and their surfaces are poor predictors of stress, incremental stiffness, and effective permeability. The mechanical response, stress and stiffness, is more closely associated with contact orientation. A mixed tensor, involving both contact and branch vector orientations, is most closely correlated with the stress and stiffness. Stress is closely correlated with the most heavily loaded contacts within an assembly (the strong-contact network), whereas the average orientation of all contacts is most closely correlated with the bulk incremental stiffness. In short, tensor $\overline{{\mathbf{H}}}{}^{{\text{c}\hbox{-}\text{strong}}}$ is the preferred fabric measure for stress, and tensor $\overline{{\mathbf{H}}}{}^{{\rm c}}$ is the preferred fabric measure for incremental stiffness. Two principal measures of pore anisotropy were investigated in regard to the effective permeability: one related to the directional median free path (a countermeasure of tortuosity) and the other related to the directional median radial breadth (a measure of hydraulic radius). The preferred measure for effective permeability is the matrix of the median radial breadths of the void space, $\overline{{\mathbf{R}}}^{{\rm v}}$, as it correlates closely with permeability.