A photogrammetry-based method to measure total and local volume changes of unsaturated soils during triaxial testing

Abstract

Triaxial tests have been widely used to evaluate soil behaviors. In the past few decades, several methods have been developed to measure the volume changes of unsaturated soil specimens during triaxial tests. Literature review indicates that until now it remains a major challenge for researchers to measure the volume changes of unsaturated soil specimens during triaxial testing. This paper presents a non-contact method to measure the total and local volume changes of unsaturated soil specimens using a conventional triaxial test apparatus for saturated soils. The method is simple and cost-effective, requiring only a commercially available digital camera to take images of an unsaturated soil specimen during triaxial testing from which accurate 3D model of the soil specimen is reconstructed. In this proposed method, the photogrammetric technique is utilized to determine the orientations of the camera where the images are taken and the shape and location of the acrylic cell, multiple optical ray tracings are employed to correct the refraction at the air-acrylic cell and acrylic cell–water interfaces, and a least-square optimization technique is applied to estimate the coordinates of any point on the specimen surface. The paper first discusses the theoretical aspects of the proposed method. An image analysis on a caliper was then used to evaluate the accuracy of photogrammetric analysis in the air. A series of isotropic compression tests on a stainless steel cylinder were used to demonstrate the procedure and evaluate the accuracy of the proposed method, while triaxial shearing tests on a saturated sand specimen were used to exam the capacity of the proposed method for measuring the total and localized volume changes during triaxial testing. Results obtained from the validation tests indicate that the accuracy for the photogrammetry in the air is about 10 µm. The average accuracy for single point measurements in the triaxial tests ranges from 0.056 to 0.076 mm with standard deviations varying from 0.033 to 0.061 mm. The accuracy for total volume measurements is better than 0.25 %.

1 Introduction

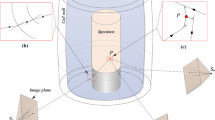
The total and local volume changes of a soil specimen are essential parameters in understanding deformation and strength characteristics of soils. Triaxial tests have been widely used to evaluate constitutive behavior for both saturated and unsaturated soils. A saturated soil is a two-phase system which includes water and soil solids. For triaxial tests on saturated soils, the volume change is usually monitored by pore water volume exchange of the sample. Figure 1a shows a conventional triaxial test apparatus for saturated soils. An unsaturated soil is commonly referred to as a three-phase system which includes water, air, and soil solid. The total volume change of unsaturated specimen is no longer equal to the pore water volume change. As a result, the conventional method to measure the volume change for saturated soil specimens is no longer applicable for unsaturated soils. In the past few decades, many research efforts have been made to develop alternative volume measurement methods for unsaturated soil in triaxial tests. This paper reviews the methods specially developed for volume measurements for unsaturated soils and methods developed for other purposes but can be potentially used for volume measurements for unsaturated soils. It is found that the existing methods have limitations, and it remains a major challenge for researchers to measure the volume change of an unsaturated soil specimen during triaxial testing. A non-contact optical method is therefore developed to measure the total and local volume change of unsaturated soil specimens during triaxial testing by integrating photogrammetry, optical ray tracing, and least-square optimization techniques. This method allows the use of traditional triaxial test apparatus for saturated soils to perform tests for unsaturated soils with minor modifications. Only a commercially available digital camera is needed to take images of an unsaturated soil specimen during triaxial testing from which accurate 3D model of the soil specimen is reconstructed. This paper first discusses the theoretical aspects of the proposed method. Then, results from three validation tests are presented to demonstrate the simplicity and accuracy of the proposed method.

Fig. 1

Typical apparatus for triaxial soil testing: a saturated soils; b double-wall cell for unsaturated soils [2]

2 Literature review

A comprehensive literature search is conducted to review existing methods for the measurements of the volume changes of unsaturated soil specimens. The literature review includes two parts: methods specially designed for measuring volume changes for unsaturated soil specimens; and those developed for strain localization measurements but may potentially be used to measure volume changes. Table 1 summarizes the pros and cons of these methods. Detailed discussions for these methods are presented below.

Table 1 Existing methods for total and local volume changes for unsaturated soils

2.1 Methods specifically developed for measuring volume changes for unsaturated soil specimens

Laloui et al. [22] summarized the existing methods for measuring volume change of unsaturated soil specimens, which can be broadly classified into three categories: (1) measurement of the cell fluid, (2) direct measurement of the air and water volumes, and (3) direct measurement of the soil specimen volume change.

2.1.1 Measurement of the cell fluid

The principle of this method is to deduce unsaturated soil volume changes from volume changes in the confining cell liquid. Although the principle is simple, several problems are often associated with this method, such as immediate expansion of cell wall caused by a pressure increase, Plexiglas creep under constant stress, and possible water leakage. Theoretically speaking, a conventional triaxial cell for saturated soils as shown in Fig. 1a can be used if carefully calibrated. However, the accuracy of the method depends on the quality of the calibration procedure, the volume capacity, and the precision of the measurements. Numerous calibrations are needed since corrections depend on time, stress path, and stress level [21].

Bishop and Donald [2] added an inner cylinder sealed to the outer cell base to minimize the liquid volume (double-wall cell). Mercury was used as the cell fluid between the inner cylinder and the specimen to enhance accuracy. Water was used as the outer liquid, while the mercury was enclosed in an internal jacket with the cell pressure applied to both sides of the jacket. The overall volume change of the soil specimen was then deduced by measuring the rise or fall of the mercury vertical level in the inner cylinder. Josa et al. [18] introduced the automatic monitoring of mercury level via a metal ring floating on its surface. Wheeler [39] designed a double-wall cell to minimize the confining liquid in which an inner cylinder was sealed to both the top and the base of the cell. Equal cell pressures were applied to the inner and outer cells to avoid deformation of the inner cell. Soil volume change was then inferred from the volume leaving or entering the inner cell. Cui and Delage [7] replaced mercury with water for safety reasons and measured water levels via high-precision cathetometer-based readings. Further improvements to the inner cylinder technique have been introduced by Rampino et al. [29]. Ng et al. [27] recorded the differential pressure between the water inside the open-ended inner cell and the water inside a reference tube using a high-accuracy differential pressure transducer (Fig. 1b). The double-wall cell method requires major equipment modifications and is therefore expensive. A double-wall cell testing system typically costs $150,000 and is complex to operate. It cannot eliminate errors from the deformations of the top and the base of the cell. In addition, air bubbles often exist in the inner cell and are difficult to remove. For the acrylic inner cell, water absorption is affected by pressure, temperature, and time, making the calibration of the system very difficult. For small specimens (38 mm in diameter), errors due to this absorption can be significant. Larger specimen, however, requires longer testing time which increases creep. Steel inner cell can be an alternative to solve the problem. However, for this non-transparent inner cell, it is difficult to examine the existence of air bubbles in the cell. The double-wall cell has been extensively used for unsaturated soil testing in the past five decades. A carefully calibrated double-wall cell can measure total volume change to an accuracy of 0.25 % [14].

2.1.2 Direct measurement of the air and water volumes

In this method, volume change of a soil specimen is obtained by measuring the air and water volume changes separately and adding them together [15, 23]. It requires adding an air volume controller filled with air instead of water. To be successful, this method requires the air phase to be continuous. This method is sensitive to small temperature and atmospheric pressure changes. In addition, undetectable air leakage and diffusion through tubes, connections, and high-air-entry disk can also influence the accuracy of the measurements. The errors can be significant for consolidated drained tests, which often takes months to complete. Furthermore, excess pore air pressure can be generated during the test and lead to misleading volume changes. Various improvements were proposed to overcome these limitations. Geiser [15] proposed a mixed air and water controller that allows reduction of air volume to the tubing only to minimize the errors from changes in atmospheric pressure and temperature. Laudahn et al. [23] proposed a method for measuring pore air volume changes in drained tests under atmospheric conditions. GDS Instruments adds a U-tube filled with ethanol to their volume controller for pore air to maintain the pore air always at atmospheric pressure [14]. Although these improvements are available, direct measurement of the air and water volumes is not extensively used by researchers at present.

2.1.3 Direct measurement of the soil specimen volume change

In this method, soil volume change is computed from the direct measurements of axial and radial specimen displacements. This category can be further divided into contact and non-contact methods.

Contact method: The contact method is a commonly used method in which local displacement sensors are directly attached onto the specimen to measure axial/radial deformations during the test (e.g., [5]). Generally, radial displacements are measured at one to three discrete points and assumptions are made as to the shape of the specimens to assess the volumetric strain. This method is generally applicable only for rigid specimens with small deformations. Measurements may become significantly inaccurate in measuring soil volume changes, such as in the case of a shear plane forming across the specimen [22]. It also requires the use of specially designed sensors such as miniature LVDTs [8, 19] and Hall effect transducers [4]. Errors could be raised due to seating, closing of gaps between components, and axial and radial alignment. Generally, less than three measurements can be made due to the limited space inside the cell.

Non-contact method: Romero et al. [33] reported the use of an electro-optical laser scanner to determine the lateral profiles of specimen for radial deformation. It also allowed detection of non-uniformities and localized deformations along the two diametrically opposite sides of the specimen. The technique requires costly modification and sophisticated installation procedures. A triaxial cell needs to be modified by opening a flat window for the laser ray to deal with the refraction from the cell wall and the confining fluid. Hird and Hajj [17] proposed the use of proximity transducers mounted on a rigid tube around the sample to provide an output voltage proportional to the distance of a lightweight conductive target placed on the specimen. Generally, this type of transducer is not waterproof and has to be sealed in housing. Another major drawback is that the target must be aligned with the sensor, which is difficult to satisfy.

2.2 Methods specifically developed for measuring strain localization

Even if a soil element is subject to a homogeneous stress at its boundary, strain localization can occur and propagate into zones of localized shear deformation or shear band because of the inevitable non-uniformity of the mass and stiffness of the material. As a result, the values of stress and strain variables derived from boundary measurements of loads and displacements are only nominal. The only way to understand the localized deformation is to measure the full field of deformation in the specimen [38]. Several methods have been developed to track shear band including X-ray computerized tomography (CT), digital image analysis (DIA) with refraction corrections, and digital image correlation (DIC) (e.g., [10–12, 24, 25, 28, 31, 32, 35, 38]). These methods can potentially be used to measure the total and local volume changes for unsaturated soil specimen during triaxial testing. A brief literature review of these methods in geomaterial studies is presented as follows.

2.2.1 X-ray computed tomography (CT)

X-ray CT is a non-destructive imaging technique to detect the internal structure of an object using an X-ray source. When X-ray beam passes through an object, some photons are either scattered or completely absorbed, resulting in the attenuation of the intensity of beam. The amount of attenuation depends upon the photon energy, the chemical composition, and the density of the object. By interpreting the beam intensity data, information regarding the internal structure of an object can be obtained. The information is presented as two-dimensional cross-sections or stacked to develop 3D renderings of the object for which total and local volume change can be deduced. Roscoe [34] used X-ray radiography to measure two-dimensional (2D) strain fields in sand. From the early 1980s, X-ray tomography was used by Desrues et al. [6, 9, 11] and later by Alshibli et al. [1] to provide valuable 3D information on evolution of void ratio inside a shear band and its relation to critical state. In the past 20 years, using X-ray CT has changed from a pioneering high-tech exotic experimental approach to a still high-tech but well-recognized powerful experimental method. The accuracy could be as high as several microns for small-size soil specimens. The major disadvantage of X-ray CT technique for triaxial soil testing is that it is too expensive. Since the steel and water attenuates the intensity of X-ray beam, conventional triaxial test apparatus cannot be used with X-ray CT for soil testing. A completely different new system such as the one at Washington State University [30] is therefore needed for real-time soil characterizations during shearing with controlled confinement. At present, very few such systems are available in the USA. In addition, suction-controlled triaxial tests for unsaturated soils are often time-consuming (weeks to months/test), which makes its use more expensive. Although possible and having many advantages, it is impractical to use the X-ray CT test to characterize real-time stress–strain behavior for unsaturated soils.

2.2.2 Digital image analysis with refraction correction

Digital image analysis (DIA) is an approach to make measurements using images captured by digital cameras [12, 13, 25, 35]. However, when a photograph is taken for a 3D object using a digital camera, a 2D image is obtained and the depth of the object is lost. In order to make correct measurements, the orientation (including position and shooting direction) of the camera relative to the object are manually controlled in DIA in order to reconstruct its 3D dimensions. In addition, for soil triaxial testing as shown in Fig. 1a, the presence of the confining acrylic chamber and the confining water in the line of vision between the camera and the soil specimen creates an apparent distortion of the specimen which must be accounted for. Parker [28] developed a two-dimensional model to use DIA with 2D refraction corrections to measure soil deformations in a conventional triaxial test cell. Macari et al. [25] proposed a further improvement as shown in Fig. 2. An idealized pinhole camera model is used which is installed “far away” from the soil specimen. To apply the DIA method by Macari et al. [25], system calibrations must be performed first and several implicit requirements must be satisfied: (1) the soil specimen and the confining acrylic chamber are perfectly cylindrical and installed vertically; (2) the digital pinhole camera is placed perfectly at the horizontal direction and its shooting direction exactly passes through the center of the chamber; (3) the soil specimen is installed exactly at the center of the confining chamber and the relative positions of the camera, the chamber, and the soil specimen are accurately known; (4) deformation of acrylic cell wall under water pressure is negligible; and (5) when soil deforms, the deformations occur homogenously along the radial directions. With these assumptions, the Snell’s law [41] is applied twice to determine the positions of the points on the surface of soil specimen. None of these conditions can be met in real conditions as demonstrated in this and the companion papers. The results of the image-based volume measurements depend greatly on how well the model conditions are satisfied throughout the test. Gachet et al. [12] applied the DIA method to determine volume changes of an unsaturated soil from its lateral profiles. Lin and Penumadu [24] used a method similar to Park [28] to analyze a series of combined axial–torsional tests for kaolin clay under undrained conditions. For the measurement points on a specimen surface with spacing of 10 mm, the obtained accuracies of measurement are 0.2 and 0.3 mm in the vertical and circumferential direction, respectively. In addition, the DIA method cannot provide measurements for the whole soil specimen since back view of the soil specimen is blocked by itself.

Fig. 2

2D digital image analysis model with refraction correction (adapted from [25])

2.2.3 Digital image correlation

Digital image correlation (DIC) measures displacements across an object surface based upon the assumption that all soils have their own unique textures in the form of different-colored grains and the light and shadow formed between adjacent grains when illuminated [16, 31, 32, 36, 40]. These textures include numerous small clusters of uniquely colored pixels called subsets and their corresponding gray level variations represent unique mathematical entities that can be tracked during a deformation process. Figure 3 shows fractions of two images for a sand specimen before and after deformation [32]. By best matching the pixel subsets through minimization of an error measure, such as normalized cross correlation [36], subset straining and/or rotations can be captured and measured. The pixel subset matching can be intensively performed so that nearly full-field displacement information can be obtained. Initially, DIC displacements are analyzed incrementally from images taken at short-time steps using a single digital camera at a fixed location. As a result, only 2D analysis can be performed. White et al. [40] presented a DIC method for soil volume measurements which used digital images and particle image velocimetry analysis for measuring soil deformation. Rechenmacher and Medina-Cetina [32] reported use of 3D-DIC to match pixel subset patterns reflected on surfaces of 3D objects in which the 3D object shape is discerned by utilizing two obliquely oriented digital cameras [16, 36]. Based upon the 3D spatial information of the object, 3D displacements between consecutive sets of images are computed using the DIC concepts described above. Results indicated the vertical and horizontal displacements could be measured to an accuracy of ±0.02 mm. The DIC method does not have a component to take the refraction into considerations and therefore cannot directly be used with the conventional triaxial test apparatus for saturated soils to measure the soil volume change. Rechenmacher [31] and Rechenmacher and Medina-Cetina [32] eliminated the refraction effect by carrying out triaxial tests under vacuum confinement without the use of a conventional confining cell. As a result, the confining pressure that can be applied is limited to one atmosphere. The DIC method was only used to measure local volume change (deformation) for a small area of soil specimen and cannot be used to measure displacements for the whole soil specimen.

Fig. 3

Digital image correlation pixel subset matching (Modified from [32])

3 A photogrammetry-based new method

As discussed above, at present, there is no simple and cost-effective method to accurately measure the total and local volume changes for unsaturated soil specimens during triaxial testing. Among all existing methods, image-based methods such as DIC and DIA have the least requirements on testing equipment and appear to be the most cost-effective. With the rapid developments of digital cameras and reduced cost, image-based methods become more and more attractive. However, for measuring volume changes for unsaturated soils during triaxial testing, image-based methods suffer two limitations. First, the relative position of the camera to the object is essential to the reconstruction of 3D models from 2D images. In reality, it is difficult to accurately control the orientation of the camera. Second, the effect of refraction as shown in Fig. 1a is difficult to take into account. Snell’s law is well-established theoretical Eq. [41]. In order to apply the Snell’s law, the shape and location of the acrylic cell relative to the camera position where an image is taken must be accurately determined. However, the acrylic cell as shown in Fig. 1a is deforming during triaxial testing, and its shape and location may change at different cell pressures even if the camera is at a fixed position as proposed by Macari et al. [25].

In order to overcome the aforementioned limitations in digital image measurements, a photogrammetry-based method was developed in this study to reconstruct 3D models of soil specimens. The reconstruction of 3D models utilizes images taken during triaxial testing with conventional triaxial test apparatus for saturated soils with minor modifications. The 3D reconstruction is achieved by integrating photogrammetry [26], optical ray tracing, and least-square optimization. In this proposed method, the camera orientations and the relative shape and location of the acrylic cell are back-calculated from images taken during triaxial testing employing the photogrammetry technique to a high level of accuracy instead of manually controlled and measured.

The procedures of the proposed method are as follows: (1) Attach measurement targets on the acrylic cell, the load frame, and the surface of the membrane (with soil specimen inside) as shown in Fig. 4a. These targets are high-contrast dots with special design which can be identified automatically by software. (2) Take photographs using a calibrated camera around the acrylic cell with soil specimen inside. Figure 4b shows the top view of possible camera positions to reconstruct a full 3D model for a soil specimen during triaxial testing; (3) determine camera orientations and acrylic cell shape and location using the targets posted on the load frame and acrylic cell based upon photogrammetry; and (4) apply optical ray tracing and least-square optimization techniques to determine 3D coordinates of any point on the soil specimen surface as discussed in the later sections.

Fig. 4

System setup and camera positions during photographing for the proposed method: a system setup; b top view of camera positions during photographing

Photographs can be taken at any orientation to obtain best quality and accuracy. Each photograph represents one measurement and as many photographs as possible can be used. The major difference between the proposed method and the DIA is as follows: (1) Camera is carefully calibrated; (2) multiple overlapping images are used instead of using one picture only; (3) an optimization process is performed to get the best accuracy of the result; (4) in order to get the best effects for each point/zone, the camera orientation is arbitrary instead of being manually controlled and positioned; (5) the camera orientation for each photograph and actual shape and position of the confining acrylic chamber is calculated based upon the principle of photogrammetry; (6) full-field 3D deformation instead of a profile or small area of the tested sample can be obtained using the proposed method when compared to the DIA method; and (7) none of the assumptions used in Macari et al. [25] method is needed.

4 Mathematical description of the proposed method

The following sections introduce the founding principles of the proposed method, which can be described in four main steps:

4.1 Step 1: use of photogrammetry to determine camera orientations

Photogrammetry is based upon a pinhole camera model [26] in which the small pinhole and the image plane correspond to perspective center of lens and image sensor of a commercial digital camera as shown in Fig. 5. The light beam from an object point P passes through the pinhole S and forms an image point I’ on the right image plane. In photogrammetry, the image plane in Fig. 5 is depicted at the left to the pinhole, rather than at the right, as it would be the case with the image sensor of an actual camera. This allows one to work with image geometry as found on a right-reading paper print or film dispositive rather than that found on a photographic negative. The new image point is then point I on the left image plane. The fundamental characteristic of the imaging process is that the pinhole S (perspective center of the camera), the image point I, and the object point P all lie on a line in space (called collinearity condition). In image analysis, the upper left corner of an image (point A as shown in Fig. 5) is by default set as the origin of the coordinate system. Two coordinate systems are used, one is the pixel coordinate system in which the coordinates of an image point is defined by pixels (represent the smallest controllable element of a picture), and the other is the physical coordinate system in which the real sizes of the image sensor is used. For a camera image sensor with sizes of F _x and F _y , if it is divided into M columns and N rows of pixels in the x’ and y’ directions, respectively, then the following relationship exists between the physical coordinate system and the pixel coordinate system for the same point I:

$$ \left[ \begin{gathered} x_{I}^{{\prime }} \hfill \\ y_{I}^{{\prime }} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}l} {F_{x} /M} \hfill & 0 \hfill \\ 0 \hfill & {F_{y} /N} \hfill \\ \end{array} } \right]\left[ \begin{gathered} m_{I} \hfill \\ n_{I} \hfill \\ \end{gathered} \right] $$

(1)

where $x_{I}^{{\prime }} ,y_{I}^{{\prime }}$ = coordinates of the image point I in the physical coordinate system of x’Ay’ (mm), $F_{x} ,F_{y}$ = format sizes of the camera image sensor in x and y directions (mm), $m_{I} ,n_{I}$ = coordinates of the image point I the pixel coordinate system mAn (pixel), and $M,N$ = total pixel numbers of the camera image sensor in x′ and y′ directions (pixel).

Fig. 5

Pinhole camera model

In order to facilitate the following discussions, a local 3D coordinate system is often built with origin setting at the pinhole S (i.e., perspective center of the camera lens) as shown in Fig. 5 and lowercase x, y, and z are used to represent the coordinates of any point in this system. The coordinates of the image point I in the local coordinate system can therefore be calculated from the following equations:

$$ \left[ \begin{gathered} x_{I} \hfill \\ y_{I} \hfill \\ z_{I} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}l} {x_{I}^{{\prime }} - P_{x} } \hfill \\ { - y_{I}^{{\prime }} + P_{y} } \hfill \\ { - f} \hfill \\ \end{array} } \right] $$

(2)

where $x_{I}$, $y_{I}$, and $z_{I}$ = x, y, and z coordinates of point I in the local coordinate system (xyz) (mm), subscript “I” indicates the coordinates are associated with point I. f = perpendicular distance between the pinhole and the image plane (equivalent to focus length of the camera) (mm), and $P_{x} ,P_{y}$ = coordinates of point B in the physical coordinate system of x’Ay’ (mm), where point B is the projection of point S on the image plane.

The method proposed in this paper involves analyses of multiple images taken at different orientations as shown in Fig. 4b. As a result, a global coordinate system is also needed so that all images are analyzed in the same coordinate system. For convenience, uppercase X, Y, and Z are used to represent the coordinates of any point in this system as shown in Fig. 6. When the image point I as shown in Fig. 6 is taken, the orientation of the camera can be defined by six parameters: the coordinates of the perspective center of the camera S (X _s , Y _s , Z _s ) and three rotational angles of κ, ω, ϕ of the z’ axis with the X, Y, and Z axes in the global system (representing the shooting directions), then the coordinates of the image point I in the global coordinate system can be calculated as follows:

$$ \left( \begin{gathered} X_{I} \hfill \\ Y_{I} \hfill \\ Z_{I} \hfill \\ \end{gathered} \right) = R\left( {\omega ,\varphi ,\kappa } \right)\left( \begin{gathered} x{}_{I} \hfill \\ y_{I} \hfill \\ z_{I} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} X_{s} \hfill \\ Y_{s} \hfill \\ Z_{s} \hfill \\ \end{gathered} \right) $$

(3)

where R is a rotation matrix defined by the following equation:

$$ R\left( {\omega ,\varphi ,\kappa } \right) = \left( {\begin{array}{*{20}l} {\cos \kappa \,\cos \varphi } \hfill & { - \sin \kappa \,\cos \varphi } \hfill & {\sin \varphi } \hfill \\ {\cos \kappa \,\sin \omega \,\sin \varphi + \sin \kappa \,\cos \omega } \hfill & { - \sin \kappa \,\sin \omega \,\sin \varphi + \cos \kappa \,\cos \omega } \hfill & { - \sin \omega \,\cos \varphi } \hfill \\ { - \cos \kappa \,\cos \omega \,\sin \varphi + \sin \kappa \,\sin \omega } \hfill & {\sin \kappa \,\sin \varphi \,\cos \omega + \cos \kappa \,\sin \omega } \hfill & {\cos \omega \,\cos \varphi } \hfill \\ \end{array} } \right) $$

(4)

X _s , Y _s , Z _s  = coordinates of the pinhole S (perspective center of the camera) in the global system; and κ, ω, ϕ = rotational angles from local coordinate system to the global coordinate system (rotates about z, then y, then x axis).

Fig. 6

Principle of photogrammetry

If a second picture is taken using the same camera at position S ₁ with a different shooting direction and the corresponding image point for the same object point P is I ₁ in the second image, then lines SI, S ₁ I ₁, and SS ₁ have to be on the same plane since I and I ₁ are conjugate image points of the same object point P and the following equation hold true:

$$ \overrightarrow {{SS_{1} }} \cdot \left( {\overrightarrow {SI} \times \overrightarrow {{S_{1} I_{1} }} } \right) = 0 $$

(5)

where

$$\begin{aligned} \overrightarrow {{SS_{1} }} &= \left( \begin{gathered} X_{{S_{1} }} \hfill \\ Y_{{S_{1} }} \hfill \\ Z_{{S_{1} }} \hfill \\ \end{gathered} \right) - \left( \begin{gathered} X_{S} \hfill \\ Y_{S} \hfill \\ Z_{S} \hfill \\ \end{gathered} \right), \overrightarrow {SI} = \left( \begin{gathered} X_{S} \hfill \\ Y_{S} \hfill \\ Z_{S} \hfill \\ \end{gathered} \right) - \left( \begin{gathered} X_{I} \hfill \\ Y_{I} \hfill \\ Z_{I} \hfill \\ \end{gathered} \right) \hbox{and}\,\\ \overrightarrow {{S_{1} I_{1} }} &= \left( \begin{gathered} X_{{S_{1} }} \hfill \\ Y_{{S_{1} }} \hfill \\ Z_{{S_{1} }} \hfill \\ \end{gathered} \right) - \left( \begin{gathered} X_{{I_{1} }} \hfill \\ Y_{{I_{1} }} \hfill \\ Z_{{I_{1} }} \hfill \\ \end{gathered} \right)\end{aligned}$$

subscript “I ₁” indicates the coordinates are associated with point I ₁.

Equation 5 is the coplanarity condition of photogrammetry [26]. In Eq. 5, the camera positions (X _s , Y _s , Z _s ) and shooting directions (κ, ω, ϕ) are unknowns, while the rest are known parameters. Multiple equations can be established for multiple conjugate image points to solve the camera positions and orientations. Once the camera positions and orientations are known, the coordinates of the object point P can also be solved using the collinearity condition since the image points, perspective centers of the camera, and the object point all lie on a line in the space such as line PIS and P I ₁ S ₁ in Fig. 6. This is the principle of photogrammetry. As a non-contact 3D measurement technique, photogrammetry has been used in different fields for more than 160 years and proven to be able to provide measurements with high accuracy [26]. Figure 7 shows an example of camera orientations determined using the photogrammetry. Figure 7a, b shows two images 12 and 13 taken at different orientations. The measurement targets posted on the load frame and wall of the acrylic wall were used to determine the camera orientations for images 12 and 13 which were shown in Fig. 7c. Note that camera stations 12 and 13 were not coplanar.

Fig. 7

Photogrammetric analysis isotropic compression tests on a steel cylinder a image at camera station 12; b image at camera station 13; and c results from the photogrammetric analysis

4.2 Step 2: determine the shape and location of acrylic cell

Figure 7c also shows the relative positions of the measurement targets posted on the surface of the acrylic wall which can be used to determine the shape and location of the acrylic wall in the global coordinate system. The acrylic cell generally has a cylindrical shape. If a local coordinate system is set at the center of the cylinder and the Y’ axis coincides with the center of the cylinder as shown in Fig. 8, then the cylinder has the following mathematical expression:

$$ X^{{{\prime }2}} + Z^{{{\prime }2}} = r^{2} $$

(6)

where r is radius of the cylinder.

Fig. 8

Initial and deformed shapes for the acrylic cell wall

In the triaxial testing, pressure applied to water inside the acrylic cell will cause expansions of the acrylic cell. This is the major reason why a double-cell system is needed for unsaturated soils. In this proposed method, it is suggested that the profile of the deformed acrylic cylinder be quadratic as follows:

$$ X^{{{\prime }2}} + Z^{{{\prime }2}} = AY^{{{\prime }2}} + BY^{{\prime }} + C $$

(7)

or in a matrix form

$$ \left[ {\begin{array}{*{20}c} {X^{{\prime }} } & {Y^{{\prime }} } & {Z^{{\prime }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - A} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ \begin{gathered} X^{{\prime }} \hfill \\ Y^{{\prime }} \hfill \\ Z^{{\prime }} \hfill \\ \end{gathered} \right] - \left[ {\begin{array}{*{20}c} {X^{{\prime }} } & {Y^{{\prime }} } & {Z^{{\prime }} } \\ \end{array} } \right]\left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] - C = 0 $$

(8)

where A, B, and C are parameters describing the expansion of the acrylic cell. When both A and B are zeros, Eq. 7 becomes Eq. 6 which represents a cylindrical shape. In reality, it could be difficult to set the global coordinate system at the center of the acrylic cell with the same coordinate as X′, Y′ and Z′ axes since the acrylic cell keep deforming during the triaxial testing. The following equation is used to transform the acrylic cell from local coordinate system to the global coordinate system:

$$ \left( \begin{gathered} X^{{\prime }} \hfill \\ Y^{{\prime }} \hfill \\ Z^{{\prime }} \hfill \\ \end{gathered} \right) = R_{1} \left( {\omega^{{\prime }} ,\varphi^{{\prime }} ,\kappa^{{\prime }} } \right)\left[ {\left( \begin{gathered} X \hfill \\ Y \hfill \\ Z \hfill \\ \end{gathered} \right) - \left( \begin{gathered} X_{R} \hfill \\ Y_{R} \hfill \\ Z_{R} \hfill \\ \end{gathered} \right)} \right] $$

(9)

where

$$ R_{1} = \left( {\begin{array}{*{20}l} {\cos \varphi^{{\prime }} \,\cos \kappa^{{\prime }} } \hfill & {\cos \omega^{{\prime }} \,\sin \kappa^{{\prime }} + \sin \omega^{{\prime }} \,\sin \varphi^{{\prime }} \,\cos \kappa '} \hfill & {\sin \omega^{{\prime }} \sin \kappa^{{\prime }} - \cos \omega^{{\prime }} \sin \varphi^{{\prime }} \cos \kappa^{{\prime }} } \hfill \\ { - \cos \varphi^{{\prime }} \,\sin \kappa^{{\prime }} } \hfill & {\cos \omega^{{\prime }} \,\cos \kappa^{{\prime }} - \sin \omega^{{\prime }} \,\sin \varphi^{{\prime }} \,\sin \kappa^{{\prime }} } \hfill & {\sin \omega^{{\prime }} \,\cos \kappa^{{\prime }} + \cos \omega^{{\prime }} \,\sin \varphi^{{\prime }} \,\sin \kappa^{{\prime }} } \hfill \\ {\sin \varphi^{{\prime }} } \hfill & { - \sin \omega^{{\prime }} \,\cos \varphi^{{\prime }} } \hfill & {\cos \omega^{{\prime }} \cos \varphi^{{\prime }} } \hfill \\ \end{array} } \right) $$

(10)

X _R , Y _R , and Z _R are the coordinates of the center of the acrylic cell in the global coordinate system. κ’, ω’, ϕ’ are the rotational angles from global coordinate system to the local coordinate system (rotates about x, then y, then z axis).

By inserting Eq. 9 into Eq. 8, the mathematical expression of the acrylic cell in the global coordinate system is obtained as follows:

$$ F(X,Y,Z) = \left[ \begin{gathered} X - X_{R} \hfill \\ Y - Y_{R} \hfill \\ Z - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X - X_{R} \hfill \\ Y - Y_{R} \hfill \\ Z - Z_{R} \hfill \\ \end{gathered} \right] - \left[ \begin{gathered} X - X_{R} \hfill \\ Y - Y_{R} \hfill \\ Z - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] - C = 0 $$

(11)

Equation 11 indicates that in the global coordinate system, nine parameters are needed to describe the shape and location of a deformed acrylic cell: A, B, C, κ’, ω’, ϕ’, X _R , Y _R , and Z _R . As shown in Fig. 7c, 3D global coordinates of measurement targets on the surface of acrylic cell can be obtained using photogrammetry. These data (more than 9 points) can be used to best-fit the shape of the deformed acrylic cell to obtain the nine parameters for the determination of the shape and location of the acrylic cell in the global coordinate system. A least-square method was used for this purpose. The mathematical expression for this process is as follows:

$$ {\text{To}}\,{\text{find}}\,{\text{a}}\,{\text{combination}}\,{\text{of}}\left[ {\begin{array}{*{20}l} A \hfill & B \hfill & C \hfill & {X_{R} } \hfill & {Y_{R} } \hfill & {Z_{R} } \hfill & {\omega^{{\prime }} } \hfill & {\varphi^{{\prime }} } \hfill & {\kappa^{{\prime }} } \hfill \\ \end{array} } \right]{\text{which}}\,{\text{can}} $$

(12)

$$ {\text{Minimize}}\sum\limits_{i = 1}^{n} {\left[ {F(X_{i} ,Y_{i} ,Z_{i} )} \right]^{2} } $$

(13)

where X _i , Y _i , Z _i are coordinates of the ith measurement targets on the surface of the acrylic cell as shown in Fig. 7c.

4.3 Step 3: ray-tracing process

In the previous sections, photogrammetry is used to determine the 3D coordinates of points in the air as shown in Fig. 7c. The objective of this paper is, however, to measure the total and local volume changes of soil specimens inside the acrylic chamber. As shown in Figs. 1a, 2, and 9a, when a light ray passes through the water–acrylic and acrylic–air interfaces, it bends due to refractions. This disturbs the collinearity conditions and the photogrammetry cannot be used directly any more. A ray-tracing technique is used to overcome this limitation.

Fig. 9

Schematic plot of ray-tracing process

It is well known that the path of a light ray is invariant under path reversal. For example, as shown in Fig. 9a, a light ray PC is generated from a source point P on the surface of the soil specimen, bends when traveling through the acrylic cell along line CD, and forms an image point I in the camera with a perspective center of S. Due to the reciprocity of the light ray, one can follow the light ray from the camera perspective center S through the image point I and points D and C back to the light source P. The information needed for the process includes the image itself, camera parameters, camera orientations, shape and location of the acrylic cell, cell wall thickness and refractive indices of the air, acrylic cell, and water. All these information are known and the mathematical expression of the ray-tracing process is as follows:

• a. Find the line of incidence SI or SD

The light ray of incidence SI can be defined by a point S (X _s , Y _s , Z _s ) and a unit direction vector passing points S and I:

$$ \overrightarrow {i} = \left( \begin{gathered} \alpha_{a} \hfill \\ \beta_{a} \hfill \\ \gamma_{a} \hfill \\ \end{gathered} \right) = \frac{{\overrightarrow {SI} }}{{\left| {\overrightarrow {SI} } \right|}} = \frac{1}{{\sqrt {\left( {X_{I} - X_{s} } \right)^{2} + \left( {Y_{I} - Y_{s} } \right)^{2} + \left( {Z_{I} - Z_{s} } \right)^{2} } }}\left( \begin{gathered} X_{I} - X_{s} \hfill \\ Y_{I} - Y_{s} \hfill \\ Z_{I} - Z_{s} \hfill \\ \end{gathered} \right) $$

(14)

The light ray SI intersects with the acrylic cell at point D with global coordinates of (X _D , Y _D , Z _D ). Since point D is on the line SI, one has

$$ \left( \begin{gathered} X_{D} \hfill \\ Y_{D} \hfill \\ Z_{D} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} X_{s} \hfill \\ Y_{s} \hfill \\ Z_{s} \hfill \\ \end{gathered} \right) + d_{1} \vec{i} $$

(15)

where d ₁ is the distance between points S and D. Point D is also on the outer surface of the acrylic cell. Therefore, it satisfies Eq. 11. By inserting Eq. 15 into Eq. 11, a quadratic equation with d ₁ as an unknown variable is obtained.

$$ \left\{ {\left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right] + d_{1} \mathop i\limits^{ \to } } \right\}^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left\{ {\left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right] + d_{1} \vec{i}} \right\} - \left\{ {\left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right] + d_{1} \vec{i}} \right\}^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] - C = 0 $$

(16)

or

$$ ad_{1}^{2} + bd_{1}^{{}} + c = 0 $$

(16a)

where

$$ \begin{aligned} a \, & = \vec{i}^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \vec{i} \\ b \, & = \left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \vec{i} + \vec{i}^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right] - \vec{i}^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] \\ c \, & = \left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right] \, - \, \left[ \begin{gathered} X_{S} - X_{R} \hfill \\ Y_{S} - Y_{R} \hfill \\ Z_{S} - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] - C \\ \end{aligned} $$

Equations 16 or 16a have two roots, representing the distances from point S to the two intersection points with the outer surfaces of the acrylic wall D and D′ as shown in Fig. 9a, respectively. For point D,

$$ d_{1} = \frac{{ - b - \sqrt {b^{2} - 4ac} }}{2a} $$

(17)

The coordinates of point D can then be obtained by inserting Eq. 17 into Eq. 15.

• b. Apply the Snell’s law to find the angle of refraction at point D

The normal of the acrylic cell at point D can be calculated by differentiating Eq. 11 at point D:

$$ \overrightarrow {{N_{1} }} = \left( \begin{gathered} \frac{\partial F}{\partial X} \hfill \\ \frac{\partial F}{\partial Y} \hfill \\ \frac{\partial F}{\partial Z} \hfill \\ \end{gathered} \right) = 2R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X_{D} - X_{R} \hfill \\ Y_{D} - Y_{R} \hfill \\ Z_{D} - Z_{R} \hfill \\ \end{gathered} \right] - R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

(18)

The unit vector of the normal is:

$$ \overrightarrow {{n_{1} }} = \left( \begin{gathered} \alpha_{n1} \hfill \\ \beta_{n1} \hfill \\ \gamma_{n1} \hfill \\ \end{gathered} \right) = \frac{{\overrightarrow {{{\text{N}}_{1} }} }}{{\left| {\overrightarrow {{{\text{N}}_{1} }} } \right|}} $$

(19)

where $\left| {\overrightarrow {{{\text{N}}_{1} }} } \right|$ is the magnitude of the normal vector $\overrightarrow {{{\text{N}}_{1} }}$.

In the three dimensional space, the Snell’s law can also be expressed as follows (see the detailed derivation in the attachment):

$$ \overrightarrow {r}_{1} = \frac{{n_{a} }}{{n_{c} }}\overrightarrow {i} - \left( {\frac{{n_{a} }}{{n_{c} }}\left( {\overrightarrow {i} \cdot \overrightarrow {{n_{1} }} } \right) + \sqrt {1 - \left( {\frac{{n_{a} }}{{n_{c} }}} \right)^{2} \left( {1 - \left( {\overrightarrow {i} \cdot \overrightarrow {n}_{1} } \right)^{2} } \right)} } \right)\overrightarrow {n}_{1} $$

(20)

where r ₁ is the unit vector for the refractive ray DC, n _a and n _c are refractive indices for the air and acrylic cell, respectively.

• c. Find the coordinate of point C at the acrylic cell–water interface

An assumption was made in this paper that the thickness of the acrylic wall is uniform and remains constant under pressure. As a result, the inner surface is expressed as follows:

$$ \left[ \begin{gathered} X - X_{R} \hfill \\ Y - Y_{R} \hfill \\ Z - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X - X_{R} \hfill \\ Y - Y_{R} \hfill \\ Z - Z_{R} \hfill \\ \end{gathered} \right] - \left[ \begin{gathered} X - X_{R} \hfill \\ Y - Y_{R} \hfill \\ Z - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] - \left( {\sqrt C - t} \right)^{2} = 0 $$

(21)

$$ X^{{{\prime }2}} + Z^{{{\prime }2}} = AY^{{{\prime }2}} + BY^{{\prime }} + \left( {\sqrt C - t} \right)^{2} $$

(21a)

where t is the thickness of the acrylic wall. Point C is the intersection point of the light ray with the inner surface. It is on the line DC and the following expression holds:

$$ \left( \begin{gathered} X_{C} \hfill \\ Y_{C} \hfill \\ Z_{C} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} X_{D} \hfill \\ Y_{D} \hfill \\ Z_{D} \hfill \\ \end{gathered} \right) + d_{2} \overrightarrow {{r_{1} }} $$

(22)

where d ₂ is the distance between points C and D. Since point C is on the inner surface of the acrylic cell, it satisfies Eq. 21. By inserting Eq. 22 into Eq. 21, a quadratic equation with d ₂ as an unknown variable is obtained. The equation has two roots, representing the distances from point D to the two intersection points with the inner surfaces of the acrylic wall. For point C, d ₂ can be calculated using Eq. 23 with

$$ d_{2} = \frac{{ - b_{1} - \sqrt {b_{1}^{2} - 4a_{1} c_{1} } }}{{2a_{1} }} $$

(23)

where

$$ \begin{aligned} a_{1} & = \, r_{1}^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \\ b_{1} & = \, \left[ \begin{gathered} X_{D} - X_{R} \hfill \\ Y_{D} - Y_{R} \hfill \\ Z_{D} - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} r_{1} + \, r_{1}^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X_{D} - X_{R} \hfill \\ Y_{D} - Y_{R} \hfill \\ Z_{D} - Z_{R} \hfill \\ \end{gathered} \right] \, - \, r_{1}^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] \\ c_{1} & = \, \left[ \begin{gathered} X_{D} - X_{R} \hfill \\ Y_{D} - Y_{R} \hfill \\ Z_{D} - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X_{D} - X_{R} \hfill \\ Y_{D} - Y_{R} \hfill \\ Z_{D} - Z_{R} \hfill \\ \end{gathered} \right] \, - \, \left[ \begin{gathered} X_{D} - X_{R} \hfill \\ Y_{D} - Y_{R} \hfill \\ Z_{D} - Z_{R} \hfill \\ \end{gathered} \right]^{T} R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] - \left( {\sqrt C - t} \right)^{2} \\ \end{aligned} $$

Coordinates of point C can be calculated using Eq. 22 with known d ₂ .

• d. Apply the Snell’s law a second time to find the angle of refraction at point C

The normal at point C of the inner surface of the acrylic cell can be calculated by differentiating Eq. 21 at point C:

$$ \overrightarrow {{N_{2} }} = \left( \begin{gathered} \frac{\partial F}{\partial X} \hfill \\ \frac{\partial F}{\partial Y} \hfill \\ \frac{\partial F}{\partial Z} \hfill \\ \end{gathered} \right) = 2R_{1}^{T} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - {\mathbf{A}}} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]R_{1} \left[ \begin{gathered} X_{C} - X_{R} \hfill \\ Y_{C} - Y_{R} \hfill \\ Z_{C} - Z_{R} \hfill \\ \end{gathered} \right] - R_{1}^{T} \left[ \begin{gathered} 0 \hfill \\ B \hfill \\ 0 \hfill \\ \end{gathered} \right] $$

(24)

The unit vector of the normal is:

$$ \overrightarrow {{n_{2} }} = \left( \begin{gathered} \alpha_{n2} \hfill \\ \beta_{n2} \hfill \\ \gamma_{n2} \hfill \\ \end{gathered} \right) = \frac{{\overrightarrow {{{\text{N}}_{2} }} }}{{\left| {\overrightarrow {{{\text{N}}_{2} }} } \right|}} $$

(25)

where $\left| {\overrightarrow {{{\text{N}}_{2} }} } \right|$ is the magnitude of the normal vector $\overrightarrow {{{\text{N}}_{2} }}$.

By applying the Snell’s law again with the known incident unit vector u _r and the normal at point C n ₂ , the unit vector for line CP can be found as follows:

$$ \overrightarrow {{r_{2} }} = \left( \begin{gathered} \alpha_{r2} \hfill \\ \beta_{r2} \hfill \\ \gamma_{r2} \hfill \\ \end{gathered} \right) = \frac{{n_{c} }}{{n_{w} }}\overrightarrow {{r_{1} }} - \left( {\frac{{n_{c} }}{{n_{w} }}\left( {\overrightarrow {{r_{1} }} \cdot \overrightarrow {{n_{2} }} } \right) + \sqrt {1 - \left( {\frac{{n_{c} }}{{n_{w} }}} \right)^{2} \left( {1 - \left( {\overrightarrow {{r_{1} }} \cdot \overrightarrow {{n_{2} }} } \right)^{2} } \right)} } \right)\overrightarrow {{n_{2} }} $$

(26)

where r ₂ is the unit vector for the refractive ray CP, n _w is the refractive index for the water.

4.4 Step 4: least-square optimization to calculate coordinates for object point

From Step 1 to Step 3, coordinates of point C and the direction of line CP can be found. The same process can be applied to image points I ₁ , I ₂ ,…, and I _n in multiple images for the same object point P as shown in Fig. 9a. If there is no error, all the re-tracing lines CP, C ₁ P, and C _n P will converge to the same point P and only two re-tracing rays are sufficient to obtain the intersection point P. However, errors unavoidably exist in the measurement and computational processes and it is very likely for lines CP, C ₁ P ₁, and C _n P _n not to intersect in the 3D space as shown in Fig. 9b. A least-square optimization technique is used in this paper to overcome this limitation. It is considered that although the re-tracing ray CP, C ₁ P, and C _n P might not intersect with each other, each ray-tracing line represents an estimate of the light source of the object point P. As a result, the “true” location of point P should be close to those re-tracing rays and has the shortest distances to those re-tracing rays. It is therefore postulated that if the sum of square of a point’s distances to all the re-tracing rays is the minimal, the point is the light source where all the rays are generated. Mathematically, the process to find the “true” location of the object point is to:

$$ {\text{To}}\,{\text{find}}\,{\text{a}}\,{\text{combination}}\,{\text{of}}\,\left[ {X_{P} \, Y_{P} \, Z_{P} } \right]\,{\text{which}}\,{\text{can}}\,{\text{minimize}} $$

(27)

$$ \sum\limits_{i = 1}^{n} {d_{i}^{2} } = \sum\limits_{i = 1}^{n} {\left[ \begin{gathered} X_{P} - X_{{C_{i} }} \hfill \\ Y_{P} - Y_{{C_{i} }} \hfill \\ Z_{P} - Z_{{C_{i} }} \hfill \\ \end{gathered} \right]^{T} \left[ \begin{gathered} X_{P} - X_{{C_{i} }} \hfill \\ Y_{P} - Y_{{C_{i} }} \hfill \\ Z_{P} - Z_{{C_{i} }} \hfill \\ \end{gathered} \right] - \left\{ {\left[ \begin{gathered} X_{P} - X_{{C_{i} }} \hfill \\ Y_{P} - Y_{{C_{i} }} \hfill \\ Z_{P} - Z_{{C_{i} }} \hfill \\ \end{gathered} \right]^{T} \left[ \begin{gathered} \alpha_{r2i} \hfill \\ \beta_{r2i} \hfill \\ \gamma_{r2i} \hfill \\ \end{gathered} \right]} \right\}^{2} \quad (n \ge 3)} $$

(28)

where $X_{{C_{i} }} , { }Y_{{C_{i} }} , { }$and $Z_{{C_{i} }}$ represent the coordinate of the ith point C _i intersecting with the inner surface of the acrylic cell, which are calculated from Eq. 22. $\alpha_{r2i} , \, \beta_{r2i} , \, and \, \gamma_{r2i}$ represent the directional cosines of the refractive ray C _i P as expressed in Eq. 26. At least three tracing rays are needed to use Eq. 28 to estimate the coordinates for one point, which represents three measurements for the same point.

The previous sections discuss how the proposed method is used to calculate the 3D coordinates of one point on the surface of a soil specimen during triaxial testing. The same approach applies to numerous points on the surface of the specimen and a 3D model of the specimen can then be constructed. With the 3D model of the soil specimen, the total volume changes and strain localizations for the whole soil specimen can be calculated, which will be discussed in the following sections.

5 Validation of the proposed method

5.1 Camera calibration and image idealization

A commercially available digital single-lens reflex camera (Nikon D7000) with a 50-mm fixed focal length lens (AF-S Nikkor 50 mm f/1.4G) as shown in Fig. 5a is used to take the photographs needed for the validation tests. The image sensor of the camera as shown in Fig. 5b has a resolution of 16.2 million pixels (4928H:3264V). As discussed in the previous sections, photogrammetry assumes the camera lens is a pinhole. A commercial camera often uses multiple lenses to focus light and its aperture is not a point. Instead of rendering straight lines for light rays, these lenses often slightly bend them either outwards or inwards. Consequently, an image taken for squares with a commercial camera (Fig. 10a) subjects to either barrel (Fig. 10b) or pincushion (Fig. 10c) distortions. In addition, principal distance, principal point, and format size of the image sensor varies even for the same type of camera. The focal length of the lens is also likely to be different from the specifications in the user’s manual. Thus, a camera must be calibrated before being used for extraction of precise and reliable 3D metric information from images.

Fig. 10

Effect of lens distortions

Numerous techniques have been developed for camera calibration since 1950s. The algorithms are generally based on ideal pinhole camera model, with the most popular approach being the well-known self-calibrating bundle adjustment, which has made a high level of performance become commonplace [37]. Some commercial or free software have been developed for camera calibrations and are readily available (e.g., http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/links.html). In this study, a software package called PhotoModeler Scanner from EOS systems Inc. (website: http://www.photomodeler.com/) is used to calibrate the camera used. The calibration is done by taking 12 images of a calibration sheet. The intrinsic (focal length, principal point, distortion parameters) and extrinsic (translation vector and rotation matrix) parameters are then calculated by analyzing the 12 images. Details regarding camera calibration are not elaborated here since it is a well-established technique. Table 2 shows the calibration results for the camera used in this study. As can be seen in Table 2, the 50-mm fixed focal length lens has an actual focal length 53.3864 mm when the camera is treated as an ideal pinhole camera model. The principal point is not exactly at the center of the image sensor before the camera calibration, either.

Table 2 Camera calibration results

The parameters in Table 2 were then used to correct the distorted images (taken by the camera from either barrel or pincushion distortion as shown in Fig. 10b or c) to its “true” shape as shown in Fig. 10a. This process is called “image idealization” in which the following equations were used:

$$ \begin{gathered} x_{c} = x + x\left[ {K_{1} (x^{2} + y^{2} ) + K_{2} (x^{2} + y^{2} )^{2} } \right] + P_{1} \left[ {(x^{2} + y^{2} ) + 2x^{2} } \right] + 2P_{2} xy \hfill \\ y_{c} = y + y\left[ {K_{1} (x^{2} + y^{2} ) + K_{2} (x^{2} + y^{2} )^{2} } \right] + P_{2} \left[ {(x^{2} + y^{2} ) + 2y^{2} } \right] + 2P_{1} xy \hfill \\ \end{gathered} $$

(29)

where $x,y$ = point coordinates in x and y directions in the original images, $x_{c} ,y_{c}$ = coordinates in x and y directions for the same point after image idealization, $K_{1} ,K_{2}$ = radial lens distortion parameters, and $P_{1} ,P_{2}$ = decentering lens distortion parameters.

After image idealizations, the images are ready to be used for the proposed photogrammetry-based method.

5.2 Accuracy of the photogrammetric analysis in the air

The proposed method relies on photogrammetric analyses to accurately determine the camera orientations and locations and shapes of the acrylic cell to correct the effect of refractions. Before evaluating the accuracy of the proposed method, the accuracy of photogrammetric analyses is evaluated. Figure 11 shows the setup of a photogrammetric analysis performed on a Craftsman 150 mm caliper with resolution of 0.05 mm. The caliper is placed on an A4 paper with 432 measurement targets. Six images are taken from different orientations and processed to back-calculate the camera orientations and position of any point of interest on the caliper. The scale for the photogrammetric analysis is established by setting the center-to-center distance between 0 and 150 mm graduates on the main scale to be 150 mm. The scale is then used to measure the distances between the major tick marks on the main scale with an interval of 10 mm. Table 3 lists the analysis results. It can be seen that the errors for the measurements varied from 3 to 30 µm and the average error and average absolute error are −1.4 and 10 µm, respectively. Among the ten measurements, seven of the measurement errors are less than 10 µm. These errors represent the accuracy of the photogrammetric analysis in the air for determination of camera orientations and locations and shapes of the acrylic cell.

Fig. 11

Photogrammetric analyses on a caliper

Table 3 Results from photogrammetric analysis on a caliper

5.3 Equipment, testing materials, and experimental design for triaxial validation tests

The conventional ELE triaxial test apparatus for saturated soils as shown in Fig. 4 is used to validate the proposed method on 3D reconstruction during triaxial testing. Two materials are used: a stainless steel cylinder and saturated sand as shown in Figs. 4 or 7 and 12, respectively.

Fig. 12

Photogrammetric analysis for triaxial shearing tests on a saturated sand specimen. a Image at camera station A; b image at camera station B; and c results from the photogrammetric analysis

5.3.1 Experimental design for isotropic compression tests on the stainless steel cylinder

For the validation tests on the stainless steel cylinder as shown in Figs. 4a or 7a, b, the confining acrylic chamber is 8″ in height, 4″ in outer diameter, and 0.24″ in thickness with a refractive index of 1.491. A total number of 16 measurement targets are posted on the load frame to set up the global coordinate system so that all the measurements can be compared in the same coordinate system as shown in Fig. 4a. A total of 218 measurement targets are posted on the outside surface of the acrylic chamber, which include 2 circles (39 targets/circle) and 8 vertical stripes (12–25 targets/strip). A total of 336 measurement targets (21 targets/circle × 16 circles) are posted on the steel cylinder surface to facilitate the measurements and analysis.

The experimental program includes reconstruction of 3D models of the steel cylinder under following conditions using the proposed method: (1) exposed in air, (2) installed in the triaxial test apparatus with 0, 200, 400, and 600 kPa of confining pressures. The tests are performed in the following way: (1) firmly fix the stainless steel cylinder on the bottom platen of the triaxial test apparatus without the confining chamber (acrylic cell); (2) take photographs from different orientations; (3) carefully install the confining chamber and slowly fill it with water; (4) take photographs from different orientations without applying any confining pressure; (5) increase the confining water pressure to 200 kPa and take photographs from different orientations; and (6) repeat the steps in (5) with the confining water pressures of 400 and 600 kPa, respectively. Figure 4b shows a typical pattern how the photographs are taken. Better measurement accuracy is achieved by the following: (1) taking at least five photographs from different orientations for each area/point of interest, (2) ensuring sufficient overlap between adjacent pictures, and (3) capturing photographs from different view angles. For each test mentioned above, approximately 50 pictures were captured, which took 3–5 min. The images at different confining pressure are then analyzed to reconstruct the 3D model of the steel cylinder.

The modulus of elasticity of stainless steel ranges from 180 to 200 GPa. With the applied maximum confining pressure of 600 kPa in this study, the volumetric strain is less than 1 × 10⁻⁵ and the steel cylinder can be considered as rigid. A rigid specimen provides a good reference for evaluating measurement accuracy for the proposed method. Since photogrammetry is a well-established technique with high level of measurement accuracy, the reconstructed 3D model for Case 1 is used as the “true” result to evaluate the accuracy of the proposed method.

5.3.2 Experimental design for drained tests on saturated sand

Beside isotropic compression tests on the stainless steel cylinder, drained triaxial shearing tests are also performed on a saturated sand specimen to validate the ability of the proposed method for total and local volume change measurements. As shown in Fig. 12a, b, the confining acrylic chamber used in this group of tests is 12″ in height, 6.5″ in outer diameter, and 0.38″ in thickness with a refractive index of 1.491. A total number of 174 measurement targets are posted on the outside surface of the acrylic chamber, including 2 circles (55 targets/circle) and 4 vertical stripes (16 targets/strip).

Oven-dried standard Ottawa fine sand is used to fabricate a specimen with a diameter and height of 71 and 137 mm, respectively. After compaction, the specimen is carefully mounted on the pedestal of the triaxial cell. A suction of 50 kPa is applied to hold the sand specimen in place during sealing. Then, a total of 176 measurement targets (16 targets/circle × 11 circles) are posted on the pre-gridded membrane. To ensure that the volume change of the specimen can be well represented by the movement of those measurement targets, two circles of measurement targets are posted on the top cap and the pedestal. In this way, the entire specimen is covered by the measurement targets. After this, cell chamber is installed and filled with tap water. To shorten the saturation process of the sand specimen, carbon dioxide (CO₂) is used to slowly seep upward from the bottom of the specimen to replace air in sand. Then, de-aired water is allowed to enter the sand specimen from the bottom to top. After this, a back pressure of 400 kPa is applied to dissolve the CO₂ in the sand specimen for several hours. Net confining pressure is maintained to be constant at 35 kPa during this saturation process. When a B value of 0.98 is reached, saturation process is considered to be completed [20]. Then, the chamber and back pressures are simultaneously decreased to 100 and 0 kPa, respectively. Drained triaxial shearing test is performed after this.

For all triaxial shearing tests, a confining pressure of 100 kPa is applied. A vertical displacement rate of 1 mm/min is applied to generate some volume change of the saturated specimen. During loading, drainage valve is kept open to allow water to flow in or out of the specimen. The volume change of the specimen is recorded by monitoring the amount of water flowing in or out of the sand. At every 2 or 3 mm of vertical displacement, load is paused and drainage valve is shut off. Then, the images are captured for future analysis. In this way, there is no volume change on the specimen during image capturing. For each volume measurement by using the proposed method, approximately 25 images around the specimen are taken following the pattern as shown in Fig. 12. The validation test is stopped when a total displacement of 15 mm is reached.

5.4 Presentation of test results

One limitation of the proposed method is that it is computation intensive. A stand-alone computer program called PhotoSoilVolume has been developed to perform the required calculations in the following sections. Figure 13 shows the flowchart for the implementation of the proposed method. For each test, the computations take about 5–10 min.

Fig. 13

Flowchart for the method implementation

5.4.1 Test results on the stainless steel cylinder

• 1. 3D reconstruction of acrylic cell chamber

In the proposed method, measurement targets are posted on the surface of the acrylic cell and photogrammetry is used to determine the camera orientations and to measure the 3D coordinates of these points to define the shapes and positions of the acrylic cell. Figures 7a, b are two of 45 images taken during the isotropic compression test for the steel cylinder with a confining water pressure of 600 kPa. All the images are idealized using Eq. 29 with calibrated camera parameters listed in Table 2. The measurement targets posted on the load frame and the surface of the acrylic cell are used to perform a photogrammetric analysis from which the camera orientations and the coordinates of the measurement points are calculated, while the measurement targets on the specimen surface are influenced by refraction and left for further analyses. Figure 7c shows the photogrammetric analysis results for confining water pressure of 600 kPa. In Fig. 7c, CS represents camera station, while the white dots represent the locations of the measurement targets on the surface of the acrylic cell chamber.

The shape and position of the acrylic cell are described by Eq. (11) with nine parameters: A, B, C, X _R , Y _R , Z _R , κ, ω, and ϕ. Table 4 shows the parameter values obtained by best-fitting the surface measurement points under different cell pressures. In these parameters, κ, ω, and ϕ represent the rotational angles of the acrylic cell relative to the established global system. Since the acrylic cell is axisymmetric, ϕ can always set to be zero and the result is not influenced. As can be seen in Table 4, the acrylic cell is not perfectly vertical compared with the established global system since κ and ω are not zero. They remain relatively constant, indicating the acrylic cell is fairly stable with no rotations during the tests.

Table 4 Parameters for the acrylic cell at different confining pressures

A, B, and C are related to the radius profile of the acrylic cell in the vertical direction and the radii of the acrylic cell at different heights are calculated by the following equation:

$$ r = \sqrt {AY^{2} + BY + C} $$

(30)

where r is of the radius of the acrylic cell and Y is the coordinate in the vertical direction. Figure 14 shows the change of acrylic cell radii in the vertical direction under different cell pressures. It is found that even under zero confining pressure, the acrylic cell is not perfectly cylindrical, which might be plastic deformations caused by previous tests. Figure 14 also indicates the acrylic cell did deform into a barrel shape under applied cell pressures. The maximum change in radius is about 300 µm (from 50.2 to 50.5 mm), which is an order larger than the accuracy of the photogrammetry in air as demonstrated by the photogrammetric analysis on the caliper. The associated change of water volume in the acrylic cell at a confining pressure of 600 kPa is about 2.8 % for a specimen with a diameter of 2 inch and height of 4 inch, which is much larger than the accuracy of 0.25 % achieved by the double-cell triaxial test apparatus. In addition, the test durations in this study are very short (less than 2 h). Most suction-controlled triaxial tests for unsaturated soils are very lengthy and commonly take several weeks or months. As a result, the deformation due to creep could be even bigger. X _R , Y _R , and Z _R represent the coordinates of the center of the barrel-shaped acrylic cell. As can be seen in Table 4, X _R and Z _R values do not change very much, while Y _R value changes slightly due to the expansion of the acrylic cell as shown in Fig. 14. The acrylic cell expands to different shapes and positions at different cell pressures. It is worth noting that for isotropic compression tests at different water pressures, pictures are taken at arbitrary and therefore different positions. Consequently, tests performed on the rigid stainless steel cylinder are “different” tests at different confining pressures.

Fig. 14

Cell radius changes at different confining pressures

• 2. Accuracy for point measurements

Once the camera orientations for each images and the shape and position of the acrylic cell in the global coordinate system are known (e.g., Fig. 7c; Table 4, respectively), multiple ray-tracings are performed to obtain 3D coordinates of any point on the specimen surface using the proposed method. Figure 15a shows the multiple ray-tracing processes used to calculate the 3D coordinates of one point (point 187 as shown in Fig. 7a, b) on the surface of the stainless steel cylinder during triaxial testing using PhotoSoilVolume. A total of seven photos with ID numbers of 12, 13, 14, 29, 30, 35, and 36 (also shown in Fig. 7c), respectively, are used for point 187. Figure 15b shows the enlargement of the seven tracing rays near point 187. They are lines in the 3D space without interception point. The least-square optimization is used to estimate the location of point 187. It is found that the “distances” between these tracing rays and the estimated point of 187 vary from 0.014 to 0.094 mm with an average of 0.049 mm, indicating that the proposed method has a high level of accuracy.

Fig. 15

Ray-tracing process for point 187

The same approach is applied to all the other points and a 3D model of the specimen surface is constructed as shown in Fig. 15a. The results are then compared under the same global coordinate system as shown in Fig. 16a with the results calculated for the steel cylinder when exposed in the air (Test 1) by assuming results for Test 1 (“in air”) are the “true” values. Figure 16a shows the 3D results for all the tests. Figure 16b, c show the comparison of test results for cross-sections 1 and 16, respectively. Due to the limited space, the 2D image for cross-sections 2 and 15 are not presented. No visible difference is found for all the test results. Using the global coordinate system as shown in Fig. 4a, measurement errors are also estimated by calculating the displacement of each point “moving” from its position in Test 1 (exposed in the air) to those obtained from the proposed method in the other tests when the steel cylinder subjected to different confining pressures. It is found that the average errors for 336 targets ranged from 0.056 to 0.076 mm with standard deviations varying from 0.033 to 0.061 mm.

Fig. 16

Comparison of test results under different confining pressures

• 3. Accuracy for the total volume measurements

Different from the DIA and DIC methods, the proposed method can be used to construct a full-field 3D model for the whole specimen instead of a part of the specimen. Once the full-field 3D model for the whole specimen is obtained, the total volume of the soils specimen can be calculated. After the 3D coordinates of points on the specimen surface are obtained as shown in Fig. 15a, a triangular surface mesh is first generated with a hollow cylindrical shape (similar those in Fig. 17). An arbitrary point on the top circular edge is then connected to all the other points on the same circle to form the top surface. The bottom surface is formed in the same way such that an enclosed 3D surface is formed from which the total volume of the specimen is calculated for all the tests. The total volumes of the cylinder vary from 221.525 cm³ (600 kPa) to 221.813 cm³ (200 kPa), while the corresponding “true” value is 222.039 cm³ (measured in air). The errors range from 0.131 to 0.232 %, indicating the accuracy of the proposed method, was high. Analysis of the test results also indicate that many assumptions used in the Macari et al. [25] cannot be satisfied. For example, without calibration, a commercial camera cannot be treated as ideal pinhole camera and it is very difficult to accurately control its position through manual installation. The confining chamber deforms under pressure and the soil specimen is almost impossible to be installed at the center of the chamber.

Fig. 17

Soil deformations at different levels of axial shortening

5.5 Test results on the saturated sand

A series of drained triaxial shearing tests on a saturated sand specimen are used to demonstrate the ability of the proposed method to measure both total volume changes and strain localizations. Figure 17 shows the changes in soil shapes at axial displacements of 0, 2, 4, 6, 8, 10, 12, and 15 mm, respectively, obtained using the proposed method. The soil specimen has approximately a cylindrical shape at the initial stage. There is no obvious change in shape when the axial displacement is 2 mm. With increase in the axial displacement, the soil specimen gradually bulges at the center into a coke bottle shape. The diameter of the specimen at the center is the largest and first narrows toward the two ends and then increases again at the two ends. The shapes are reasonable since the friction between the soil and the loading platens restrains the soil specimen from deforming.

The total volumes of the soil at different axial displacements are calculated using the method discussed previously. The volume changes of the soil specimen are also obtained by direct measurement of the volume of water coming in and out of the soil. It is worth noting that the proposed method measures the absolute volume and volume changes, while the conventional water volume measurements only provide the volume changes relative to the initial conditions. This is beneficial since in the proposed method each measurement is independent of each other. If there is an error in the initial volume measurement, it will not be transferred into later measurements. In order to make valid comparisons, the initial volumes of the soil specimen for the water volume change method are assumed to be the same as the soil volume obtained from the proposed method at confining pressure of 100 kPa with 0 mm of axial displacement, and only the volume changes are compared. Figure 18 shows the comparison of results obtained from the two different methods. As can be seen, both results indicate that the specimen experiences contractions when the axial displacement changes from 0 to 2 mm and dilations for the displacement from 2 to 15 mm, respectively. The difference in volume changes obtained from the two methods is small during the whole process with the average and maximum differences being 0.051 and 0.108 %, respectively. Considering that the accuracy of volume change measurements by directly monitoring water volume changes is about 0.25 % [14], it is concluded that the proposed method can produce results comparable to those obtained from the conventional direct measurement of water volume changes.

Fig. 18

Comparison of volume changes from two different methods

A numerical interpolation technique similar to that in Lin and Penumadu [24] is used to generate a continuous deformation field from the obtained discrete points on the specimen surface. Figure 19 shows the vertical strains developed in the soil specimen at different vertical displacement levels. It can be seen from Fig. 19 that the distribution of vertical displacement and strain is generally uniform until vertical displacement reaches 6 mm. Note from Fig. 17 that the shear band is not visible to the human eye and the specimen still looks relatively uniform. However, the contour plot in Fig. 19 clearly shows that strain localization is fully developed when the vertical displacement is 15 mm.

Fig. 19

Vertical strains at different levels of axial shortening

6 Advantages of the proposed method

There are several advantages in the proposed method over the existing image-based methods. Firstly, the camera is carefully calibrated to satisfy the requirements of the ideal pinhole camera model. Table 2 indicates that if the camera is not calibrated, the error caused by the difference in focal length alone is more than 6 %, not counting the errors caused by distortions. Secondly, the camera orientations for each photograph are calculated based upon the principle of photogrammetry to an accuracy of 10 microns. This eliminates the requirement of accurate control of camera orientations in other image-based method and allows images to be taken at any arbitrary positions. This is advantageous since images are taken at very short distances with the best shooting directions to improve the accuracy of the measurements. In the validation tests, all photos are taken at distance from 590 to 740 mm, while in the method proposed by Macari et al. [25], the camera must be set “far away” from the specimen to make sure the camera is approximately an ideal pinhole camera with shooting direction passing the center of the soil specimen. In addition, it is well known that the magnitudes of distortions at the center of the images are less than that near the borders of the images (as shown in Fig. 10b, c). This proposed method uses points near the center of an image only for the calculation. As a result, higher accuracy can be obtained. Snell’s law is a theoretical equation for refraction correction as long as the incident ray and the normal at the incident point were correct. Thirdly, using photogrammetry technique, shape and location of the used confining chamber (acrylic cell) is accurately determined based on 3D coordinates of the measurement targets posted on cell wall surface. Under different confining pressure levels, movements of the measurement targets on the cell wall surface are well captured which eliminates the error from assuming a fixed chamber location and shape. The mathematical model used for cylindrical- or barrel-shaped objects well represents the shape and location of the test chamber. Fourthly, an optimization process is performed to get the best accuracy of the multiple images. In the proposed method, each image represents a measurement and each image includes many specimen surface points. At least three ray-tracing processes were used to determine the coordinate of any point on the specimen surface. Normally, much more than five images are used to calculate the coordinates for a point. The redundancy can significantly improve the accuracy of the measurements and eliminate any assumptions regarding the specimen deformations.

7 Conclusions

In this paper, a photogrammetry-based method is developed to reconstruct 3D model of a soil specimen during triaxial tests using conventional triaxial test apparatus. It can be used for both saturated and unsaturated soils and both total and local volume changes can be calculated. The key features of the proposed method include: use of photogrammetry to determine camera orientations and location of the acrylic cell, application of ray-tracing technique to accommodate the light bending due to refraction, and implementation of the least-square optimization to estimate the 3D coordinates of points on the specimen surface. The method essentially extends the application of photogrammetry from one optical medium to multiple media. The method is cost-effective since only a commercially available digital camera is needed and minor modification is needed for the conventional triaxial test apparatus for saturated soils.

Results obtained from the validation tests indicate that the accuracy for the photogrammetry in the air is about 10 µm. For preliminary triaxial tests performed in this study, the average accuracy for single point measurements ranges from 0.056 to 0.076 mm with standard deviations varying from 0.033 to 0.061 mm. The accuracy for total volume measurements is better than 0.25 %. Such accuracy is higher than or at least comparable to those from existing methods, indicating the proposed method is sufficiently accurate for triaxial testing for both saturated and unsaturated soils. One limitation of the proposed method could be its intensive computation requirement. However, a computer program called PhotoSoilVolume has been developed to perform the required calculations in a few minutes.

Appendix

1.1 Derivation of the Snell’s law in the 3D space

The scalar form of the Snell’s law is normally expressed as follows [41]:

$$ \frac{{n_{1} }}{{n_{2} }} = \frac{{\sin \theta_{2} }}{{\sin \theta_{1} }} $$

(31)

where $n_{1} \,{\text{and}}\,n_{2}$ = refraction indices for two media, and $\theta_{1} \,{\text{and}}\,\theta_{2}$ = incident and refraction angles with respect to the normal at the refractive boundary.

In the proposed method, incident and refractive rays are often expressed as vectors in 3D space. As a result, it is more convenient to use the vector form of Snell’s law. Its derivations are as follows:$\overrightarrow {i}$ and $\overrightarrow {r}$ are unit directional vectors in space for the incident and refractive rays as shown in the Fig. 20, respectively. $\overrightarrow {n}$ is the surface normal to the refractive boundary at the intersection point and also a unit directional vector pointing to the side of the incident ray. To facilitate the discussion, both $\overrightarrow {i}$ and $\overrightarrow {r}$ are first resolved into two components: one is parallel to n and the other is perpendicular to n.

$$ \overrightarrow {i} = \overrightarrow {{i_{ \bot } }} + \overrightarrow {{i_{\parallel } }} $$

(32)

$$ \overrightarrow {r} = \overrightarrow {{r_{ \bot } }} + \overrightarrow {{r_{\parallel } }} $$

(33)

where subscripts “$\bot$” and “$\parallel$” represents direction parallel to and perpendicular to $\overrightarrow {n}$, respectively.

Fig. 20

Snell’s law

It is worth noting that $\theta_{1} \,{\text{and}}\,\theta_{2}$ are scalars and have ranges from 0 to 90°. Consequently, the following relationships exist:

$$ \overrightarrow {i} \cdot \overrightarrow {n} = - \cos \theta_{1} $$

(34)

$$ \left| {\overrightarrow {{i_{\parallel } }} } \right| = \sin \theta_{1} $$

(35)

$$ \left| {\overrightarrow {{r_{\parallel } }} } \right| = \sin \theta_{2} $$

(36)

Both $\overrightarrow {{i_{ \bot } }} {\text{ and }}\overrightarrow {{r_{ \bot } }}$ are parallel to $\overrightarrow {n}$ but with opposite direction; therefore, they can be expressed as follows:

$$ \overrightarrow {{i_{ \bot } }} = - \cos \theta_{1} \overrightarrow {n} $$

(37)

$$ \overrightarrow {{r_{ \bot } }} = - \cos \theta_{2} \overrightarrow {n} $$

(38)

Combining Eqs. 32 and 36, one has

$$ \overrightarrow {{i_{\parallel } }} = \overrightarrow {i} - \overrightarrow {{i_{ \bot } }} = \overrightarrow {i} + \cos \theta_{1} \overrightarrow {n} $$

(39)

$\overrightarrow {{i_{\parallel } }} {\text{ and }}\overrightarrow {{r_{\parallel } }}$ are also parallel to each other. Therefore,

$$ \overrightarrow {{r_{\parallel } }} = \left| {\overrightarrow {{r_{\parallel } }} } \right|\frac{{\overrightarrow {{i_{\parallel } }} }}{{\left| {\overrightarrow {{i_{\parallel } }} } \right|}} = \sin \theta_{2} \frac{{\overrightarrow {{i_{\parallel } }} }}{{\sin \theta_{1} }} = \frac{{\sin \theta_{2} }}{{\sin \theta_{1} }}\left( {\overrightarrow {i} + \cos \theta_{1} \overrightarrow {n} } \right) $$

(40)

Plugging Eqs. 31 and 34 into Eq. 40, one has

$$ \overrightarrow {{r_{\parallel } }} = \frac{{n_{1} }}{{n_{2} }}\left[ {\overrightarrow {i} - \left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right)\overrightarrow {n} } \right] $$

(41)

Combining Eqs. 31, 34, and 38, one has

$$ \begin{aligned} \overrightarrow {{r_{ \bot } }} & = - \cos \theta_{2} \overrightarrow {n} = - \sqrt {1 - \sin^{2} \theta_{2} } \overrightarrow {n} = - \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}\sin \theta_{1} } \right)^{2} } \overrightarrow {n} = - \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}} \right)^{2} \left( {1 - \cos^{2} \theta_{1} } \right)} \overrightarrow {n} \\ & \quad = - \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}} \right)^{2} \left[ {1 - \left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right)^{2} } \right]} \overrightarrow {n} \\ \end{aligned} $$

(42)

Substituting Eqs. 40 and 41 into Eq. 33 yields:

$$ \overrightarrow {r} = \frac{{n_{1} }}{{n_{2} }}\overrightarrow {i} - \left( {\frac{{n_{1} }}{{n_{2} }}\left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right) + \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}} \right)^{2} \left[ {1 - \left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right)^{2} } \right]} } \right)\overrightarrow {n} $$

(43)

Equation 43 requires four inputs to calculate the unit vector for the refractive ray $\overrightarrow {r}$: $\overrightarrow {i}$, $\overrightarrow {n}$, $n_{1} \,{\text{and}}\,n_{2}$.