Flow rule in a high-cycle accumulation model backed by cyclic test data of 22 sands

Abstract

The flow rule used in the high-cycle accumulation (HCA) model proposed by Niemunis et al. (Comput Geotech 32: 245, 2005) is examined on the basis of the data from approximately 350 drained long-term cyclic triaxial tests (N = 10⁵ cycles) performed on 22 different grain-size distribution curves of a clean quartz sand. In accordance with (Wichtmann et al. in Acta Geotechnica 1: 59, 2006), for all tested materials, the “high-cyclic flow rule (HCFR)”, i.e., the ratio of the volumetric and deviatoric strain accumulation rates $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}/\dot{\varepsilon}_{\rm{q}}^{{\rm acc}}$, was found dependent primarily on the average stress ratio η ^av = q ^av/p ^av and independent of amplitude, soil density and average mean pressure. The experimental HCFR can be fairly well approximated by the flow rule of the modified Cam-clay (MCC) model. Instead of the critical friction angle $\varphi_{\rm{c}}$ which enters the flow rule for monotonic loading, the HCA model uses the MCC flow rule expression with a slightly different parameter $\varphi_{\rm{cc}}$. It should be determined from cyclic tests. $\varphi_{\rm{cc}}$ and $\varphi_{\rm{c}}$ are of similar magnitude but not always identical, because they are calibrated from different types of tests. For a simplified calibration in the absence of cyclic test data, $\varphi_{\rm{cc}}$ may be estimated from the angle of repose $\varphi_{\rm{r}}$ determined from a pluviated cone of sand (Wichtmann et al. in Acta Geotechnica 1: 59, 2006). However, the paper demonstrates that the MCC flow rule with $\varphi_{\rm{r}}$ does not fit well the experimentally observed HCFR in the case of coarse or well-graded sands. For an improved simplified calibration procedure, correlations between $\varphi_{\rm{cc}}$ and parameters of the grain-size distribution curve (d ₅₀,   C _u) have been developed on the basis of the present data set. The approximation of the experimental HCFR by the generalized flow rule equations proposed in (Wichtmann et al. in J Geotech Geoenviron Eng ASCE 136: 728, 2010), considering anisotropy, is also discussed in the paper.

1 Introduction

Based on drained cyclic triaxial tests performed on a medium coarse sand, it has been demonstrated in [8] that the cumulative deformations due to small cycles (strain amplitudes $\varepsilon^{{\rm ampl}} < 10^{-3}$) obey a kind of flow rule, i.e., $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}/ \dot{\varepsilon}_{\rm{q}}^{{\rm acc}}$ = constant for a constant average stress ratio η ^av = q ^av/p ^av, independently of amplitude, polarization, ovality, pressure, void ratio and loading frequency. Only a slight increase in the volumetric portion with increasing number of cycles was reported in [8]. An almost purely volumetric accumulation was observed for cycles applied at isotropic average stresses (η ^av = 0). The cumulative deformations are purely deviatoric at an average stress ratio η ^av = M _cc near the critical stress ratio (η ^av = M _c ≈ 1.25) known from monotonic shear tests. At average stress ratios smaller than critical (η ^av < M _cc), the sand is compacted, while cycles in the over-critical regime (η ^av > M _cc ) lead to cumulative dilatancy.

In the high-cycle accumulation (HCA) model [6], the strain accumulation rate $\dot{\varepsilon}_{ij}^{{\rm acc}}$ is expressed using the HCFR m _ij as its direction:

$$ \dot{\sigma}_{ij}^{{\rm av}} = E_{ijkl} (\dot{\varepsilon}_{kl}^{{\rm av}} - \dot{\varepsilon}_{kl}^{{\rm acc}} - \dot{\varepsilon}_{kl}^{{\rm pl}}) $$

(1)

$$ \dot{\varepsilon}_{kl}^{{\rm acc}} = \dot{\varepsilon}^{{\rm acc}} \, m_{kl} $$

(2)

In this paper, the tensorial components are denoted by subscripts ijkl. In the context of HCA models, the dot over a symbol means the derivative with respect to the number of cycles N (instead of time t), i.e., $\dot{\sqcup}=\partial\sqcup/\partial N$ (for notation, see also Appendix 2). The trend of average effective (Cauchy) stress $\dot{\sigma}_{ij}^{{\rm av}}$ is related to the trend of average strain $\dot{\varepsilon}_{kl}^{{\rm av}}$ by an elastic stiffness E _ijkl . The intensity of accumulation $\dot{\varepsilon}^{{\rm acc}} = \|\dot{\varepsilon}_{kl}^{{\rm acc}}\|$ is described by an empirical function consisting of six multipliers each considering a different influencing parameter (strain amplitude, void ratio, average mean pressure, average stress ratio, cyclic preloading, and changes in polarization). The plastic strain rate $\dot{\varepsilon}_{kl}^{{\rm pl}}$ in Eq. (1) keeps the stress within the Matsuoka–Nakai yield surface. For a detailed explanation of the assumptions and equations of the HCA model, it is referred to [6].

For simplicity, the slight N-dependence of the HCFR observed in [8] is neglected in the HCA model. The η ^av-dependence of m _ij can be sufficiently well described by

$$ m_{ij} = \left[\frac{1}{3} \left(p^{{\rm av}} - \frac{(q^{{\rm av}})^{2}}{M^2 p^{{\rm av}}}\right) \delta_{ij} + \frac{3}{M^{2}} \sigma_{ij}^{*}\right]^{\rightarrow} $$

(3)

of the modified Cam-clay (MCC) model [7, 8] with M = F   M _cc. Generally, F is a complicated function of stress [5]. However, for triaxial conditions F is obtained from

$$ F = \left\{\begin{array}{ll} 1 + M_{\rm{ec}}/3 \quad & \hbox{for}\; \eta^{{\rm av}} \le M_{\rm{ec}}\\ 1 + \eta^{{\rm av}}/3 \quad &\hbox{for} \; M_{\rm{ec}} < \eta^{{\rm av}} < 0\\ 1 \quad &\hbox{for} \; \eta^{{\rm av}} \ge 0 \end{array}\right. $$

(4)

wherein

$$ M_{\rm{cc}} = \frac{6 \sin\varphi_{\rm{cc}}}{3-\sin\varphi_{\rm{cc}}} \quad \hbox{and} \quad M_{\rm{ec}} = - \frac{6 \sin\varphi_{\rm{cc}}}{3+\sin\varphi_{\rm{cc}}}. $$

(5)

The MCC flow rule for monotonic loading uses the internal friction angle in the critical state, $\varphi_{\rm{c}}$, as input parameter. $\varphi_{\rm{c}}$ can be determined from a monotonic test at large shear strains. If the MCC flow rule is applied in the context of the HCA model, $\varphi_{\rm{c}}$ is replaced by the parameter $\varphi_{\rm{cc}}$ which has to be calibrated from cyclic tests. $\varphi_{\rm{cc}}$ and $\varphi_{\rm{c}}$ are of similar magnitude, but not always identical because they are determined from different types of tests. Furthermore, the calibration of $\varphi_{\rm{cc}}$ often concerns stress ratios lower than critical (i.e., η ^av < M _c).

For triaxial conditions, Eq. (3) gives the following ratio of the volumetric and deviatoric strain accumulation rates:

$$ \omega = \frac{\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}}{\dot{\varepsilon}_{\rm{q}}^{{\rm acc}}} = \frac{m_{\rm{v}}}{m_{\rm{q}}} = \frac{M^{2} - (\eta^{{\rm av}})^{2}}{2 \eta^{{\rm av}}} $$

(6)

wherein m _v and m _q are “strain-type” Roscoe invariants of m _ij (see Appendix 2).

A single material parameter ($\varphi_{\rm{cc}}$) is sufficient if the MCC flow rule according to Eqs. (3–5) is used for m _ij in the HCA model. As demonstrated in Sect. 4 $\varphi_{\rm{cc}}$ can be calibrated from the data of drained cyclic triaxial tests performed with different average stress ratios η ^av. However, such calibration may be quite laborious since one needs several high-quality long-term cyclic tests. In order to simplify the calibration procedure, an estimation of $\varphi_{\rm{cc}}$ from the slope angle of a pluviated cone of sand (angle of repose $\varphi_{\rm{r}}$) has been proposed [11]. In the present paper, such simplified calibration of $\varphi_{\rm{cc}}$ is examined on the basis of the data from approximately 350 cyclic triaxial tests performed on 22 clean quartz sands with different grain-size distribution curves.

Furthermore, correlations of $\varphi_{\rm{cc}}$ with parameters of the grain-size distribution curve (mean grain size d ₅₀ and uniformity coefficient C _u = d ₆₀/d ₁₀) are formulated for an estimation of $\varphi_{\rm{cc}}$ when no cyclic test data are available. Similar correlations have been already developed for the parameters appearing in the empirical formula for the intensity of accumulation [9, 12].

A generalized flow rule m _ij has been proposed in [10] considering anisotropy (see equations in Appendix 1). The anisotropic flow rule was required for samples prepared by moist tamping [10]. For samples prepared by air pluviation, an isotropic flow rule is usually sufficient [8, 10]. For triaxial compression and isotropy (anisotropy tensor a _ij  = 0), the generalized flow rule delivers the following strain rate ratio (see Appendix 1):

$$ \omega = \frac{\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}}{\dot{\varepsilon}_{\rm{q}}^{{\rm acc}}} = \frac{1 - \lambda^{-n_{g}}}{\lambda^{-n_{g}}} \quad \hbox{with} $$

(7)

$$ \lambda = -\frac{3}{4 \eta^{{\rm av}} Y_{\rm{c}}} \left[3 \left(3 - \sqrt{(Y_c -9) (Y_c -1)}\right)- Y_{\rm{c}}\right] $$

(8)

$$ Y_{\rm{c}} = \frac{9 - \sin^{2} \varphi_{\rm{ccg}}}{1 - \sin^{2} \varphi_{\rm{ccg}}} $$

(9)

A simplified calibration of the parameters $\varphi_{\rm{ccg}}$ and n _g of the generalized flow rule is discussed in Sect. 5. Again, $\varphi_{\rm{ccg}}$ may be slightly different than $\varphi_{\rm{cc}}$ or $\varphi_{\rm{c}}$.

2 Tested materials and testing procedure

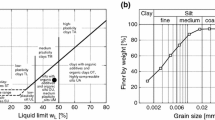
All tests were carried out on specimens of mixed sand. The mean grain size and the uniformity coefficient were systematically varied. The raw material was a natural quartz sand obtained from a sand pit near Dorsten, Germany. It has a subangular grain shape and a specific gravity ρ _s = 2.65 g/cm³. The sand has been sieved into 25 gradations with grain sizes between 0.063 and 16 mm. Afterward, 22 different grain-size distribution curves were mixed from these fractions. 14 of them have a linear shape in the semi-logarithmic scale (Fig. 1a, b). The sands L1 to L7 (Fig. 1a) have the same uniformity coefficient C _u = d ₆₀/d ₁₀ = 1.5, but different mean grain sizes in the range 0.1 mm  ≤ d ₅₀ ≤ 3.5 mm. The materials L4 and L10 to L16 (Fig. 1b) have the same mean grain size d ₅₀ = 0.6 mm, but different uniformity coefficients 1.5 ≤ C _u  ≤ 8.

Fig. 1

Tested grain-size distribution curves

The data from cyclic tests on eight sands with S-shaped grain-size distribution curves (Fig. 1c) are partly documented in [9] and have been re-analyzed for the present investigation. The S-shaped grain-size distribution curves S1 to S6 are rather uniform (1.3 ≤ C _u  ≤ 1.9) having different mean grain sizes in the range 0.15 mm ≤ d ₅₀ ≤ 4.4 mm. The sands S3, S7 and S8 have a similar mean grain size (0.52 mm ≤ d ₅₀ ≤ 0.55 mm) but different uniformity coefficients (1.8 ≤ C _u ≤ 4.5). In [8], the cyclic flow rule has been primarily discussed on the basis of data for sand S3.

The values of mean grain size d ₅₀, uniformity coefficient C _u, curvature index C _c = d ²₃₀ /(d ₁₀ d ₆₀) and minimum and maximum void ratios e _min,  e _max (determined according to DIN 18126) are summarized in Table 1.

Table 1 Index properties (mean grain size d ₅₀, uniformity coefficient $C_{\rm{u}} = d_{60}/d_{10}$, curvature index $C_{\rm{c}} = d_{30}^2/(d_{10} d_{60})$, minimum and maximum void ratios $e_{\min}, \,e_{\max}$) and flow rule parameters for the 22 tested sands

For each sand, four series of drained cyclic tests have been performed. In each series, one parameter (stress amplitude, initial density, average mean pressure, and average stress ratio) was varied, while the other ones were kept constant:

• In the first test series, medium dense samples were consolidated under an average stress of p ^av = 200 kPa and η ^av = 0.75 and subjected to deviatoric stress amplitudes in the range 10 kPa ≤ q ^ampl ≤ 90 kPa.

• In the second series, samples with different initial densities were subjected to a cyclic loading with constant stress amplitude q ^ampl and constant average stress (p ^av = 200 kPa, η ^av = 0.75).

• The average mean pressure p ^av was varied between 50 and 300 kPa in the third test series. The average stress ratio η ^av = 0.75 and the amplitude-pressure-ratio $\zeta = q^{{\rm ampl}}/p^{{\rm av}}$ were the same in all tests on a given material. The samples were medium dense.

• In the fourth test series, the average stress ratio was varied in the range 0.25 ≤ η ^av ≤ 1.25 (with the exception of sand S3 where a larger range −0.88 ≤ η ^av ≤ 1.375 was tested [8]). The experiments were performed on medium dense samples consolidated to p ^av = 200 kPa. For a given material, the stress amplitude q ^ampl was kept constant.

In the test series 2–4, lower amplitude-pressure ratios $\zeta$ were chosen for the finer and more well-graded sands, accommodating the larger strain accumulation rates usually observed for these materials [9].

The test device is described, e.g., in [8]. The samples with a diameter of 10 cm and a height of 20 cm were prepared by air pluviation and tested water-saturated using a back pressure of 200 kPa. The lateral stress σ ₃ was kept constant, while the cyclic axial loading was applied with a pneumatic loading device. Due to its larger deformation, the first irregular cycle was applied with a low frequency of 0.01 Hz in all tests. Afterward, 10⁵ regular cycles were applied with a frequency of 1 Hz. The only exception was the fine sand L1 where lower frequencies of 0.01 or 0.1 Hz were necessary during the regular cycles in order to avoid a build-up of pore water pressure. In that case only 2,000 or 10,000 (regular) cycles were tested. Sands S2, S3, S5 and S8 were tested more extensively than S1, S4, S6, S7 and L1 to L16.

3 Verification of amplitude-, density- and pressure-independence

In general, the test results obtained from the 22 sands confirm the conclusion [8] that the direction of strain accumulation $\dot{\varepsilon}_{q}^{{\rm acc}}/\dot{\varepsilon}_{v}^{{\rm acc}}$ does not significantly depend on amplitude, soil density and average mean pressure p ^av. This is evident from Figs. 2, 3, 4 where the accumulated deviatoric strain $\varepsilon_{\rm{q}}^{{\rm acc}}$ is plotted versus the accumulated volumetric strain $\varepsilon_{\rm{v}}^{{\rm acc}}$. For a given test, the data markers shown in the diagrams of Figs. 2, 3, 4 correspond to different numbers of cycles ($N = 1, 2, 5, 10, 20, 50, \dots, 2 \cdot 10^{4},\, 5 \cdot 10^{4}, \,10^{5}$). The first row of diagrams in Figs. 2, 3, 4 presents data for three of the seven poorly graded sands L1 to L7, while the second row contains data for three of the seven better graded materials L10 to L16. Data for three of the eight S-shaped grain-size distribution curves S1 to S8 are provided in the third row. The strain paths $\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ from tests with different amplitudes (Fig. 2), different initial densities (Fig. 3) and different average mean pressures (Fig. 4) almost coincide. It can thus be concluded that the parameters amplitude, density and average mean pressure need not to be considered in the equations for the cyclic flow rule m _ij . The slight curvature (N-dependence) of the strain paths is disregarded in the HCA model for simplicity.

Fig. 2

$\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ strain paths from tests with different stress amplitudes q ^ampl

Fig. 3

$\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ strain paths from tests with different initial relative densities I _D0 = (e _max − e ₀)/(e _max − e _min)

Fig. 4

$\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ strain paths from tests with different average mean pressures p ^av

4 Stress ratio dependence and calibration of the flow rule parameters from cyclic test data

The increase in the deviatoric portion of the strain accumulation rate with increasing average stress ratio η ^av = q ^av/p ^av is obvious from the $\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ strain paths shown for all tested materials in Fig. 5. The η ^av-dependence is also apparent in Fig. 6 where the cyclic flow rule is depicted by vectors in the p-q-plane. The vectors start at the average stress (p ^av, q ^av) and are inclined by $\varepsilon_{\rm{q}}^{{\rm acc}}/\varepsilon_{\rm{v}}^{{\rm acc}}$ toward the horizontal. The inclination of the vectors grows with increasing average stress ratio. At η ^av = 1.25 the vectors are almost vertical, which means that the accumulation is nearly purely deviatoric ($\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} \approx 0$). This observation agrees well with earlier test series [4, 1, 8]. In Fig. 6, the slight N-dependence of the HCFR appears as a progressive decrease in the inclination of the vectors toward the horizontal.

Fig. 5

$\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ strain paths from tests with different average stress ratios η ^av = q ^av/p ^av. Comparison of the experimental data with the prediction by the MCC flow rule and by the generalized flow rule

Fig. 6

HCFR shown as vectors in the p-q-plane. The vectors start at the average stress ${\varvec{\sigma}}^{{\rm av}}$ of the test and have an inclination of $\varepsilon_{\rm{q}}^{{\rm acc}}/\varepsilon_{\rm{v}}^{{\rm acc}}$ toward the horizontal

The parameter $\varphi_{\rm{cc}}$ entering the MCC flow rule used for m _ij in the HCA model can be calibrated from the cyclic tests performed with different η ^av-values. $\varphi_{\rm{cc}}$ corresponds to the average stress ratio at which the accumulation of volumetric strain vanishes (i.e., $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} = 0$). Usually, this stress ratio is close to η ^av = 1.25. In order to determine $\varphi_{\rm{cc}}$ by interpolation or careful extrapolation, the data of the three tests with η ^av = 0.75, 1.0 and 1.25 have been used for the analysis. The procedure is as follows:

• A curve-fitting of the linear function $\varepsilon_{\rm{q}}^{{\rm acc}} = 1/\bar{\omega} \cdot \varepsilon_{\rm{v}}^{{\rm acc}}$ to the $\varepsilon_{\rm{q}}^{{\rm acc}}$-$\varepsilon_{\rm{v}}^{{\rm acc}}$ data in Fig. 5 delivers an average strain rate ratio $\bar{\omega}$ for each test. For example, for sand L2 $\bar{\omega}$-values of 0.843, 0.379 and 0.027 are obtained for the tests with η ^av = 0.75, 1.0 and 1.25.

• Equation (6) with $\bar{\omega}$ instead of ω is used to calculate M from $\bar{\omega}$ and η ^av. $\varphi_{\rm{cc}}$ is then obtained from Eq. (5) with M = M _cc for triaxial compression. For L2, the M-values for η ^av = 0.75, 1.0 and 1.25 are 1.35, 1.33 and 1.28 and the corresponding $\varphi_{\rm{cc}}$-values are 33.5°, 32.9° and 31.8°. For this sand, all M-values corresponding to $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} = 0$ lie above the largest tested average stress ratio η ^av = 1.25. Therefore, $\varphi_{\rm{cc}}$ has to be calibrated by extrapolation in this case. It should be noted that cyclic tests with η ^av > 1.25 are difficult to perform because the maximum stress during the cycles may lie close to the failure stress, and consequently, an excessive accumulation of deformation may occur.

• There are several possibilities for the choice of the $\varphi_{\rm{cc}}$-value entering the MCC flow rule equations:

  • 1. One could choose the $\varphi_{\rm{cc}}$-value which was determined from the cyclic test performed with the average stress ratio η ^av lying closest to the stress ratio for which zero volumetric strain accumulation ($\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} = 0$) is expected. In the present test series, the $\varphi_{\rm{cc}}$ values from the test with η ^av = 1.25 (e.g., $\varphi_{\rm{cc}} = 31.8^{\circ}$ for sand L2) would be chosen following this approach. The $\varphi_{\rm{cc}}$-values determined in such way are provided for all tested materials in column 7 of Table 1 (“Method 1”).

  • 2. The HCFR measured in the cyclic tests with lower average stress ratios η ^av < 1.25 may be better reproduced by the HCA model with the MCC flow rule if the $\varphi_{\rm{cc}}$ data derived from these tests are also taken into account in the calibration. If data for η ^av = 0.75, 1.0 and 1.25 are available as in the present test series, a mean $\varphi_{\rm{cc}}$-value from these three tests can be set into approach. For all tested materials, the respective $\varphi_{\rm{cc}}$-values are collected in column 8 of Table 1 (“Method 2”, e.g., $\varphi_{\rm{cc}} =(33.5+32.9+31.8)/3 = 32.7^{\circ}$ for L2).

  • 3. If the average strain ratio $\bar{\omega}$ is plotted versus η ^av (see the examples in Fig. 7), Eq. (6) can be fitted to the data. Due to the much larger $\bar{\omega}$ for lower average stress ratios η ^av < 0.75 the curve-fitting should be restricted to the data at η ^av ≥ 0.75. Such curve-fitting is presented as the solid curves in Fig. 7 and results in the $\varphi_{\rm{cc}}$-values given in column 9 of Table 1 (“Method 3”, e.g., $\varphi_{\rm{cc}} = 33.0^{\circ}$ for L2).

The $\varphi_{\rm{cc}}$-values obtained from methods 2 and 3 are very close to each other. With some exceptions (L2, L5, L7, S6), also method 1 delivers $\varphi_{\rm{cc}}$-values of similar magnitude. Consequently, all three methods are more or less equivalent.

Fig. 7

Average strain rate ratio $\bar{\omega} = \varepsilon_{\rm{v}}^{{\rm acc}}/\varepsilon_{\rm{q}}^{{\rm acc}}$ as a function of average stress ratio η ^av

The strain paths predicted by the MCC flow rule, Eq. (6), with the $\varphi_{\rm{cc}}$-values in column 9 of Table 1 have been added as solid lines in the diagrams of Fig. 5. For most tested materials, a good agreement between the predicted and the measured strain paths can be concluded. However, the curvature of some of the experimental paths due to the slight N-dependence is not reproduced.

The calibration of the generalized flow rule for the 22 sands has been undertaken assuming isotropy. Eq. (7) with (8) has been fitted to the $\bar{\omega}$-η ^av data given in Fig. 7 (dashed curves, fitted to data for η ^av ≥ 0.75), delivering Y _c and n _g . The φ _ccg -values calculated from Y _c using Eq. (9) and the parameters n _g have been collected in columns 10 and 11 of Table 1. The ɛ ^acc _q -ɛ ^acc_v strain paths predicted by the generalized flow rule with these parameters are provided as dashed lines in Fig. 5. For most materials, the prediction of both the MCC and the generalized flow rule is similar.

The comparison of experimental and predicted data in Figs. 5 and 7 proves that both the MCC flow rule and the generalized flow rule are suitable for the HCFR of clean quartz sand with various grain-size distribution curves.

5 Simplified calibration procedure

5.1 Estimation of φ _cc from the angle of repose φ _r

For a simplified calibration procedure without cyclic test data, in [8], it has been proposed to estimate φ _cc entering the MCC flow rule from the angle of repose φ _r. For each tested material, φ _r has been obtained from a loosely pluviated cone of sand. The testing procedure is shown in Fig. 8. First, a steel ring was filled with sand in order to guarantee a rough base platen. Then a funnel filled with sand was centrically lifted so that the sand poured out very slowly. The final cone had a base diameter of approximately 60 cm and a maximum height of about 20 cm. Using a depth gauge, the height of the cone was measured in two axes every 2 cm. Four inclination angles of the cone were calculated from this height data (two for each axis). The flattened top of the cone was not included in the analysis. The φ _r value of a test is the mean value of the four inclinations. The φ _r-values given in the last column of Table 1 are mean values from five such tests.

Fig. 8

Determination of the angle of repose $\varphi_{\rm {r}}$ from a loosely pluviated cone of sand

In Fig. 9a, b, the φ _r data are plotted versus the mean grain size d ₅₀ or the uniformity coefficient C _u of the tested material, respectively (cross-symbols). The angle of repose is rather independent of C _u (Fig. 9b). No dependence on mean grain size could be found in the range 0.15 mm ≤ d ₅₀ ≤ 0.6 mm (Fig. 9a). However, φ _r increases in the range of smaller grains (d ₅₀ < 0.15 mm, probably due to electrostatic attraction [2, 3]) and larger grains (d ₅₀ > 0.6  mm). Neglecting the data from the tests on sand L1, the angle of repose can be described by (dashed curves in Fig. 9a, b):

$$ \varphi_{\rm{r}} = 33.2^{\circ} \left[1 + 0.033\, (d_{50}[\hbox{mm}] - 0.6)\right] $$

(10)

Fig. 9

a, b Comparison of the angle of repose $\varphi_{\rm{r}}$ determined from a loosely pluviated cone of sand with the $\varphi_{\rm{cc}}$-values for the MCC flow rule calibrated from the cyclic test data, for different mean grain sizes d ₅₀ and uniformity coefficients C _u. c, d Angles of repose $\varphi_{\rm{r}}$ or $\varphi_{\rm{cc}}$-values calculated from Eq. (11) versus $\varphi_{\rm{cc}}$-values calibrated from the cyclic tests. e–h Parameters n _g and $\varphi_{\rm{ccg}}$ of the generalized flow rule as a function of d ₅₀ and C _u

The $\varphi_{\rm{cc}}$-values entering the MCC flow rule calibrated from the cyclic test data (values from column 9 in Table 1) are also shown in Fig. 9a, b. The sands L1 to L16 and S1 to S8 are distinguished by the black or gray symbols, respectively. Larger discrepancies between the angles of repose and the $\varphi_{\rm{cc}}$-values derived from the cyclic test data are obvious in Fig. 9a, b. For mean grain sizes d ₅₀ > 0.5 mm the angle of repose $\varphi_{\rm{r}}$ is about 2° larger than the $\varphi_{\rm{cc}}$ values from the cyclic tests (Fig. 9a). Furthermore, in the range of uniformity coefficients C _u > 3 significantly larger $\varphi_{\rm{cc}}$-values have been obtained from the cyclic test data compared with the $\varphi_{\rm{r}}$ values from the cone pluviation test. For example, at C _u = 5 and $C_{\rm{u}} = 8\, \varphi_{\rm{r}}$ is about 2° smaller than $\varphi_{\rm{cc}}$.

The dot-dashed curves in Fig. 7 confirm an inaccurate prediction of Eq. (6) with $\varphi_{\rm{c}} = \varphi_{\rm{r}}$ for some of the tested materials. The average stress ratio η ^av corresponding to a pure deviatoric accumulation ($\bar{\omega}$ = 0) is overestimated for d ₅₀ > 0.5 mm and underestimated for C _u > 3. However, for poorly graded fine to medium coarse sands Eq. (6) with $\varphi_{\rm{r}}$ delivers an acceptable prediction of the measured $\bar{\omega}(\eta^{{\rm av}})$ data.

Finally, Fig. 9c corroborates the rather weak correlation between the angle of repose $\varphi_{\rm{r}}$ and the $\varphi_{\rm{cc}}$-values calibrated from the cyclic tests.

It can be concluded that the angle of repose $\varphi_{\rm{r}}$ determined from a loosely pluviated cone of sand can be a suitable estimation for the HCFR parameter $\varphi_{\rm{cc}}$ of poorly graded fine to medium coarse sands. However, the HCFR for coarse or well-graded sands is not well reproduced by Eq. (6) with $\varphi_{\rm{r}}$.

5.2 Correlations between $\varphi_{\rm{cc}}, \varphi_{\rm{ccg}}, n_{\rm{g}}$ and parameters of the grain-size distribution curve

The parabolic shape of the $\varphi_{\rm{cc}}$-d ₅₀-data in Fig. 9a and the increase in $\varphi_{\rm{cc}}$ with C _u in Fig. 9b can be approximated by curve-fitting (solid curves in Fig. 9a, b) as:

$$ \begin{aligned} \varphi_{\rm{cc}} &= \left\{31.5^{\circ} + 0.944 \left[\ln\left(\frac{d_{50}[\hbox{mm}]}{0.6}\right)\right]^{2}\right\} \\ & \quad \cdot \left[1 + 0.088 \ln(C_{\rm{u}}/1.5)\right] \end{aligned} $$

(11)

Fig. 9d confirms a better correlation between the $\varphi_{\rm{cc}}$-values calculated from Eq. (11) and those calibrated from the cyclic tests than in the case of the angle of repose (Fig. 9c). Only the data for sand L10 shows a somewhat larger deviation in Fig. 9d. Therefore, Eq. (11) is recommended for a simplified calibration of the $\varphi_{\rm{cc}}$ parameter entering the MCC flow rule if no cyclic test data is available.

The parameter n _g of the generalized flow rule is only slightly dependent on d ₅₀ and rather independent of C _u (Fig. 9e, f). For a simplified calibration, it can be estimated from (dashed curves in Fig. 9e, f):

$$ n_{\rm{g}} = 0.97 + 0.056 \left[\ln\left(\frac{d_{50}[\hbox{mm}]}{0.6}\right)\right]^{2} $$

(12)

or simply set to 1.0 which is the mean value of all n _g data for the 22 sands. The $\varphi_{\rm{ccg}}$-values used in the generalized flow rule are somewhat larger than the $\varphi_{\rm{cc}}$ values of the MCC flow rule, especially at higher C _u -values (Fig. 9g, h). For a simplified calibration the following correlation between $\varphi_{\rm{ccg}}$ and d ₅₀, C _u can be used (dot-dashed curves in Fig. 9g, h):

$$ \begin{aligned} \varphi_{\rm{ccg}} &= \left\{31.8^{\circ} + 0.906 \left[\ln\left(\frac{d_{50}[\hbox{mm}]}{0.6}\right)\right]^{2}\right\} \\ & \quad \cdot \left[1 + 0.130 \ln(C_{\rm{u}}/1.5)\right] \end{aligned} $$

(13)

6 Summary, conclusions and outlook

The data from approximately 350 drained cyclic triaxial tests performed on 22 specially mixed grain-size distribution curves of a clean quartz sand have been analyzed with respect to the high-cyclic flow rule (HCFR) used in the high-cycle accumulation (HCA) model proposed by Niemunis et al. [6]. The tested materials had mean grain sizes in the range 0.1 mm ≤ d ₅₀ ≤ 4.4 mm and uniformity coefficients 1.5 ≤ C _u ≤ 8.

In general, the conclusions drawn in [8] from tests on a poorly graded medium coarse sand could be confirmed for the various grain-size distribution curves tested in the present study. For all tested materials, the ratio $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}/\dot{\varepsilon}_{\rm{q}}^{{\rm acc}}$ of the volumetric and deviatoric strain accumulation rates was found almost independent of amplitude, soil density and average mean pressure. It depends primarily on the average stress ratio η ^av = q ^av/p ^av. The higher η ^av, the larger is the deviatoric portion of the strain accumulation rate. For stress ratios η ^av ≈ 1.25, the accumulation is almost purely deviatoric, i.e., $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} \approx 0$.

Both, the flow rule of the MCC model for monotonic loading and the generalized flow rule proposed in [10] are suitable to describe the experimentally observed HCFR. Applying the MCC flow rule, the parameter $\varphi_{\rm{cc}}$ calibrated from cyclic tests is used instead of the critical friction angle $\varphi_{\rm{c}}$ determined from monotonic shear tests. $\varphi_{\rm{cc}}$ and $\varphi_{\rm{c}}$ are of similar magnitude but not always identical, because they are calibrated from different types of tests. $\varphi_{\rm{cc}}$ and the parameters $\varphi_{\rm{ccg}}$ and n _g entering the generalized approach have been calibrated from the cyclic test data for all tested materials. The parabolic relationship between $\varphi_{\rm{cc}}$ and mean grain size d ₅₀ takes a minimum at d ₅₀ = 0.6 mm. Furthermore, $\varphi_{\rm{cc}}$ increases with increasing uniformity coefficient C _u. The $\varphi_{\rm{ccg}}$ values used in the generalized flow rule are somewhat larger than the $\varphi_{\rm{cc}}$ values, in particular for uniformity coefficients C _u > 3. The interpolation parameter n _g of the generalized flow rule scatters around 1.0 for all tested materials.

For a simplified calibration of $\varphi_{\rm{cc}}$ in the absence of cyclic test data, the angle of repose $\varphi_{\rm{r}}$ determined from a loosely pluviated cone of sand can be a suitable estimate in the case of poorly graded, fine to medium coarse sands. However, the HCFR of coarse or well-graded sands is not well reproduced by the MCC flow rule with $\varphi_{\rm{r}}$.

For such materials, correlations of $\varphi_{\rm{cc}}, \varphi_{\rm{ccg}}$ and n _g with d ₅₀ and C _u, that have been developed on the basis of the cyclic test data, may give a better approximation of the experimental HCFR. The application of Eqs. (11) and (13) is thus recommended for a simplified calibration procedure.

In future, it is planned to extend these correlations to sands having different grain shapes, surface roughness and mineralogy. Further cyclic testing is necessary for that purpose.

Appendices

Appendix 1: Generalized flow rule

In [10], the direction of accumulation m _ij of the HCA model has been generalized in order to describe (inherent or induced) anisotropy. A second-order structure tensor

$$ a_{ij} = \breve{\sigma}_{ij}^{*}/\breve{p} $$

(14)

has been introduced with $\breve{\sigma}_{ij}$ lying on a stress line for which the flow rule is assumed purely volumetric, i.e., $m_{ij}(a_{ij}) = (\delta_{ij})^{\rightarrow} \cdot \breve{\sigma}_{ij}^{*}$ is the deviatoric part of $\breve{\sigma}_{ij}$ and $\breve{p}$ is the corresponding mean pressure. The isotropic flow rule can be recovered by setting a _ij  = 0. For the critical state, the flow rule is purely deviatoric. For an intermediate stress σ _ij , an interpolation is used. Given a _ij , the stress σ _ij is projected radially onto the deviatoric plane expressed by p = 1. Next, the projected stress σ _ij /p is decomposed as follows (Fig. 10a):

$$ \sigma_{ij}/p = \delta_{ij} + r_{ij} = \delta_{ij} + \sigma_{ij}^{*}/p $$

(15)

The so-called conjugated stress t _ij is found from

$$ t_{ij} = \delta_{ij} + a_{ij} + \lambda(r_{ij} - a_{ij}) $$

(16)

It should lie on the critical surface at p = 1 (Fig. 10b). For that purpose, the scalar multiplier λ must be determined from the condition that the conjugated stress t _ij satisfies

$$ t_{ii} (t^{-1})_{ii} = Y_{\rm{c}} \quad \hbox{or} \quad (t^{-1})_{ii} = -Y_{\rm{c}}/3 $$

(17)

Having found λ, the generalized flow rule is calculated from

$$ m_{ij} = \frac{\delta_{ij} (1 - \lambda^{-n_g}) + \lambda^{-n_g} (t_{ij}^{*})^{\rightarrow}} {\sqrt{(1 - \lambda^{-n_g})^{2} + (\lambda^{-n_{g}})^{2}}} $$

(18)

wherein n _g is an interpolation parameter (a material constant). Linear interpolation is obtained with n _g  = 1.

Fig. 10

Generalized flow rule. a Projection of σ _ij on the deviatoric plane at p = 1. b Definition of conjugated stress t _ij

As an example, the flow rule m _ij for an axisymmetric stress with diagonal components

$$ \sigma_{ij} = \hbox{diag}(\sigma_{1},\sigma_{3},\sigma_{3}) $$

(19)

and for a transversal isotropy

$$ a_{ij} = \hbox{diag}(a, -a/2, -a/2). $$

(20)

is derived. The parameter a and the stress ratio η _iso for which the accumulation is purely volumetric are interrelated via

$$ a = -2/3 \eta_{{\rm iso}}. $$

(21)

Furthermore,

$$ r_{ij} = \hbox{diag}(r, -r/2, -r/2) \quad \hbox{with}\quad r = -2/3 \eta $$

(22)

holds. From two solutions of Eq. (17) ,

$$ \begin{aligned} \lambda_{1|2} &= \frac{1}{2 (a-r)^{2} Y_{\rm{c}}} \left[-9 a + 3 \left(3 r\right.\right. \\ & \pm \left.\left.\sqrt{(a-r)^{2} (Y_{\rm{c}} -9) (Y_{\rm{c}} -1)}\right)\right.\\ & \left.+ (2 a+1) (a-r) Y_{\rm{c}}\right] \end{aligned} $$

(23)

the positive one is chosen as λ. Finally, the strain rate ratio ω is calculated from

$$ \omega = \frac{\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}}{\dot{\varepsilon}_{\rm{q}}^{{\rm acc}}} = \frac{1 - \lambda^{-n_{g}}}{\lambda^{-n_{g}}} \quad \hbox{or} \quad \omega = - \frac{1 - \lambda^{-n_{g}}}{\lambda^{-n_{g}}} $$

(24)

for triaxial compression and extension, respectively. For an isotropic material (η _iso = a = 0) Eq. (23) simplifies to

$$ \lambda_{1|2} = \frac{1}{2 r Y_{\rm{c}}} \left[3 \left(3 \pm \sqrt{(Y_{\rm{c}} -9) (Y_{\rm{c}} -1)}\right)- Y_{\rm{c}}\right] $$

(25)

Appendix 2: Notation

δ _ij :

Kronecker delta (1 for i = j, 0 for i ≠ j)

e :

Void ratio

$\varepsilon_1$ :

Axial strain

$\varepsilon_{3}$ :

Lateral strain

$\varepsilon_v$ :

Volumetric strain ($= \varepsilon_{1} + 2 \varepsilon_{3}$ for triaxial tests)

$\varepsilon_{\rm{q}}$ :

Deviatoric strain ($= 2/3 (\varepsilon_{1} - \varepsilon_{3}$) for triaxial tests)

$\varepsilon^{{\rm ampl}}$ :

Strain amplitude

$\varepsilon^{{\rm acc}}$ :

Residual (accumulated) strain

$\varepsilon_{\rm{v}}^{{\rm acc}}$ :

Accumulated volumetric strain

$\varepsilon_{\rm{q}}^{{\rm acc}}$ :

Accumulated deviatoric strain

$\dot{\varepsilon}^{{\rm acc}}$ :

Intensity of strain accumulation

$\dot{\varepsilon}_{\rm{v}}^{{\rm acc}}$ :

Rate of volumetric strain accumulation

$\dot{\varepsilon}_{\rm{q}}^{{\rm acc}}$ :

Rate of deviatoric strain accumulation

$\varepsilon_{ij}^{{\rm av}}$ :

Average strain tensor

$\dot{\varepsilon}_{ij}^{{\rm av}}$ :

Trend of average strain

$\dot{\varepsilon}_{ij}^{{\rm acc}}$ :

Rate of strain accumulation

$\dot{\varepsilon}_{ij}^{{\rm pl}}$ :

Plastic strain rate

E _ijkl :

“Elastic stiffness” of HCA model

$\varphi_{\rm{c}}$ :

Critical friction angle

$\varphi_{\rm{cc}}$ :

MCC flow rule parameter calibrated from cyclic tests

$\varphi_{\rm{ccg}}$ :

Parameter of generalized flow rule

$\varphi_{\rm{r}}$ :

Angle of repose

F :

Correction factor for M

η :

Stress ratio =q/p

η ^av :

Average stress ratio

I _D :

Relative density

I _D0 :

Initial value of relative density

m _v :

Volumetric part of flow rule (=m _ii )

m _q :

Deviatoric part of flow rule ($=\sqrt{2/3}\|m_{ij}^*\|$)

M :

Critical stress ratio / Stress ratio with $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} = 0$

M _c :

Critical stress ratio for triaxial compression

M _cc :

Stress ratio with $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} = 0$ for triaxial compression

M _ec :

Stress ratio with $\dot{\varepsilon}_{\rm{v}}^{{\rm acc}} = 0$ for triaxial extension

m _ij :

Direction of strain accumulation (high-cyclic flow rule, HCFR)

n _g :

Parameter of generalized flow rule

N :

Number of cycles

p :

Effective mean pressure (=(σ ₁ + 2 σ ₃)/3 in triaxial tests)

p ^av :

Average effective mean pressure

q :

Deviatoric stress (=σ ₁ − σ ₃ in triaxial tests)

q ^ampl :

Deviatoric stress amplitude

σ ₁ :

Effective axial stress

σ ₃ :

Effective lateral stress

σ _ij :

Effective Cauchy stress tensor

σ ^av _ij :

Average effective stress tensor

$\dot{\sigma}_{ij}^{{\rm av}}$ :

Trend of average effective stress

$\breve{\sigma}_{ij}$ :

Stress for which flow rule is purely volumetric

ω :

Strain rate ratio (= $\dot{\varepsilon}_v^{{\rm acc}}/\dot{\varepsilon}_q^{{\rm acc}}$)

$\bar{\omega}$ :

Average strain rate ratio of a test

$\zeta$ :

Amplitude-pressure ratio

$\|\sqcup\|$ :

Norm of $\sqcup$

$\sqcup^{*}$ :

Deviatoric part of $\sqcup$

$\sqcup^{\rightarrow}$ :

Normalization, i.e., $\sqcup/\|\sqcup\|$