1 Introduction

Erosion processes are particularly hazardous phenomena, especially for structures built over soils that can potentially be hydraulically loaded. In a typical erosion process, some of the particles, particularly the small ones, are easily driven out of their resting places by fluid flow. These displacements may compromise the stability of the granular skeleton.

As in many other problems found in engineering, modelling efforts have been mainly based on the continuum approach. Some examples include the modelling of suffusion processes [26] and the onset of fluidization of a portion of the soil [30]. However, there are several details at the micro-scale that are difficult to introduce into models based on the continuum approach. The complex dynamics of the particles being driven by the fluid, including rich phenomena such as the rolling of particles and interlocking [10], is not properly captured by these models. Simulations based on the discrete element method (DEM) have shown that the relative rolling of particles inside the granular skeleton greatly reduces its strength [8] in dry soils. An important question following this reasoning is whether the fluid flow inside the porous medium could also augment this effect and further reduce the soil stability.

Models based on the DEM seems to be suitable to capture all this rich set of details for the solid phase. However, modelling the fluid with a similar approach, for instance with molecular dynamics (MD) [24], is challenging due to the prohibitive computational requirements. A continuous approach for the fluid seems more suitable than the discrete picture to model erosion. DEM has been coupled with several computational fluid dynamics schemes including solutions for the Navier--Stokes (NS) equations by using finite element methods (FEM) [33]. Such models couple the momentum transfer between fluids and particles with a drag force proportional to the difference between the particles and fluid velocities [34]. Usually the constant of proportionality is the drag coefficient which is programmed as a function of the Reynolds numbers formulated from experimental data. Such experiments are conducted with a single spherical particle [22] instead of tightly packed assemblies; therefore, their validity to describe the coupled fluid–grains dynamics within porous media has not been thoroughly explored.

In this paper, a simulation framework focusing on these microscopic effects is presented. The framework is based on the coupling methods published by several authors et al. [5, 6, 22, 18, 1, 13] and the authors of the present paper [7] between the DEM and the lattice Boltzmann method (LBM). The method introduces both linear and angular momentum transfer between the fluid and the particles in contact. Two validation examples are presented to prove that the method is properly defined. The interaction is not assumed to be a particular function of the Reynolds number, which is an advantage over traditional CFD–DEM couplings. Moreover the cubic grid structure of the LBM and the explicit nature of both algorithms make them easily parallelized.

The DEM–LBM framework is then used to study a specific erosion process with a virtual soil made of two distinct particle sizes. The effect of the hydraulic load on each of the soil components can be observed individually, and its outcome can be quantified. Important conclusions about the interaction of the different phases are drawn from the observations, which in turn could potentially be used in the future to formulate better predictive models for the erosion phenomenon.

The paper is structured as follows: Section 2 describes independently the DEM and LBM and then describes the coupling law between the two. Section 3 presents a series of validation examples and compares the results with previous studies. Section 4 illustrates a simulation of a particular case of contact erosion of two granular assemblies of distinct particle sizes, followed by the conclusions of the work in Sec. 5

2 The method

In the following, the DEM, LBM and their coupling implementation details are briefly described. The method is a simplification of the sphero-polyhedra DEM–LBM coupling published by the authors recently [7] applied only to spherical particles in this case. The algorithm is hosted within the Mechsys open source library Footnote 1 which runs in shared memory parallel systems.

2.1 The discrete element method (DEM)

The spherical DEM used for the present study is based on the standard linear dashpot introduced previously in the literature [4]. The discrete elements are free to move inside the domain and a contact is defined when two spheres intersect. Figure 1 shows a pair of DEM spheres in contact. The overlapping length (δ n) is easily checked and this is computationally inexpensive, involving only the calculation of the distance between the centres of the particles. With this definition, a normal force F n between the particles can be defined in the normal direction \(\hat{{\bf n}}\),

$$ {\bf F}_n = K_{\rm n} \delta_{\rm n} {\hat{\bf n}}, $$
(1)

with K n a parameter called the normal stiffness whose value is related to the elastic modulus of the material.

Fig. 1
figure 1

The collision of two DEM particles is detected by the overlapping length δ n, which also defines the normal and tangential forces as explained in the text

Full size image

Particles are also allowed to rotate, and hence at the point of contact x c (which is defined as the middle point of the overlapping length), both particles have a relative velocity that represents the relative displacement of the particle surfaces at that point. This relative velocity is given by,

$$ {\bf v}_{\rm rel} = \boldsymbol{\Upomega}_1 \times ({\bf x}_c - {\bf x}_1) + {\bf v}_1 - \boldsymbol{\Upomega}_2 \times ({\bf x}_c - {\bf x}_2) - {\bf v}_2 $$
(2)

with \({{\varvec{\Upomega}}}_i, {\bf v}_i\) and x i the angular velocity, velocity and centre of the i-th particle. This relative velocity can be decomposed of normal v n and tangential v t components. The tangential component is numerically integrated to obtain the tangential displacement δ t [19]. This displacement is used to determine the tangential force F t along the plane tangential to the overlap between the particles,

$$ {\bf F}_t = K_t \delta_{\rm t} {\hat{\bf t}}, $$
(3)

where \({\hat{\bf t}} = {\bf v}_t/v_t\) and K t is a tangential stiffness. This elastic tangential force represents the effect of static friction in the absence of roughness of the spherical particles. To be physically correct, the tangential force must be bounded by the Coulomb limit [9], and so the correct tangential force is

$$ {\bf F}_t = \min (K_{\rm t} \delta_{\rm t},\mu F_n){\hat{\bf t}}, $$
(4)

which depends on the microscopic friction coefficient μ.

Viscous forces F v are also added to dissipate the energy and simulate inelastic collisions. Such forces are of the form,

$$ {\bf F}_v = G_n m_e v_n{\hat{\bf n}} + G_{t} m_{e} v_{t} {\hat{\bf t}} $$
(5)

which depends on two dissipation constants for the normal G n and tangential G t directions and the effective mass m e of the particle pair.

These forces, and the torques produced by them, are added together to obtain a net force and torque for a given particle. The forces that are described in the following sections, produced by the interaction with the fluid, are also added to the net quantities. Then, the equations of linear motion (Newton’s second law) and for angular motion (Euler’s equations) are numerically integrated by the leap frog method [31].

2.2 The lattice Boltzmann method (LBM)

For the present study, the lattice Boltzmann D3Q15 scheme was used [15]. In this scheme, the space is divided into a cubic domain where each cell has a set of probability distribution functions f i , representing the density of fluid particles going through one of the 15 discrete velocities e i (see Fig. 2). The density ρ and velocity u at each cell position x can be determined by:

$$ \begin{aligned} \rho({\bf x}) &= {\sum\nolimits_{i=0}^{15}} f_i({\bf x}) \\ {\bf u}({\bf x}) &= \frac{\sum_{i=0}^{15} f_i({\bf x}){\bf e}_i}{\rho({\bf x})} \end{aligned} $$
(6)
Fig. 2
figure 2

The LBM cell of the D3Q15 showing the direction of each one of the 15 discrete velocities

Full size image

Each distribution function has an evolution rule derived from the Chapman--Enskog expansion of the Boltzmann equation [27],

$$ f_i({\bf x}+{\bf e}_i \delta t, t+\delta t) = f_i({\bf x},t) + \Upomega_{\rm col}, $$
(7)

where x is the position of the local cell, δ t is the time step and \(\Upomega_{\rm col}\) is a collision operator representing the relaxation processes due to the collision of the fluid particles. For this study, the widely accepted Bhatnagar--Gross--Krook (BGK) model for the collision operator [23] is used, which assumes that the collision processes drive the system into an equilibrium state described by an equilibrium function f eq i ,

$$ \Upomega_{\rm col} = \frac{\delta t}{\tau}\left( f_i^{\rm eq}-f_i \right) $$
(8)

with τ being the characteristic relaxation time. It has been shown that the Navier--Stokes (NS) equations for fluid flow [14] are recovered if,

$$ f_i^{\rm eq} = \omega_i \rho \left( 1 + 3 \frac{{\bf e}_i \cdot {\bf u}}{C^2} + \frac{9({\bf e}_i \cdot {\bf u})^2}{2C^4} -\frac{3u^2}{2C^2} \right) $$
(9)

and the kinetic viscosity of the fluid ν is given by,

$$ \nu = (\tau - 0.5) \frac{\delta_x^2}{3\delta_{\rm t}} $$
(10)

with C = δ x/δ t, a characteristic lattice velocity defined by the grid spacing δ x. Equation 10 imposes a constraint on the choice of τ, which must be greater than 0.5 for the viscosity to be physically correct. It is also known that values close to 0.5 produce unstable numerical behaviour [27] due to the nonlinearity of the NS equations; hence, it is advisable to keep its value close to one.

The LBM is used to represent compressible fluids. There is an equation of state relating the density at a given cell and the pressure p at that cell. For the case of the model described above, such a law is the ideal gas law,

$$ p = \frac{C^2}{3} \rho, $$
(11)

which defines \(C/\sqrt{3}\) as the speed of sound of the simulated fluid. Perfect incompressibility cannot be achieved with this LBM scheme, and the incompressibility limit is taken as the condition where the density fluctuations are small compared with the average density. Compressibility, measured by quantities such as the Mach number, can be tuned by the parameter C as deduced by the equation of state. This will require varying either the time step or the lattice spacing, which may increase the computational requirements for a given simulation, and hence must be done with care.

Body forces, such as the gravity force [20], are simulated by a net force introduced for each cell. The net force F b modifies the velocity used in the calculation of the equilibrium function as follows,

$$ {\bf u}' = {\bf u} + \frac{\delta_t {\bf F}_b}{\rho}. $$
(12)

In the case of gravity, the force is simply F g  = ρ g where g is the gravitational acceleration [3].

2.3 The coupled method

With the LBM and DEM explained separately, the algorithm for their coupling can be explained in detail. The method is an implementation of the one introduced by Owen et al. [22] for spherical particles.

One sphere moving through the lattice representing the fluid will intersect some LBM cells. Inside the spheres, the cells will be fully occupied by the DEM sphere. Outside the DEM sphere, the volume fraction occupied by it will be zero. In the cells comprising the sphere surface, the volume fraction occupied by the DEM particle takes values between 0 and 1. The coupling law must ensure a smooth transition as the sphere invades and vacates the LBM cells during its movement. This coupling law modifies Eq. 7 to account for the volume occupation fraction \(\varepsilon\),

$$ f_{\rm i}({\bf x}+{\bf e}_ i \delta t, t+\delta t) = f_{\rm i}({\bf x},t) + \left(1-B_{\rm n}\right)\left( \frac{\delta t}{\tau}\left( f_{\rm i}^{\rm eq}-f_{\rm i} \right) \right) + B_{\rm n} \Upomega^s_{\rm i}, $$
(13)

where \(\Upomega^s_{\rm i}\) is a collision operator representing the change of momentum due to the collision of the DEM sphere within the LBM cell and B n is a weight coverage function [22] of the form,

$$ B_{\rm n}(\varepsilon) = \frac{\varepsilon_{\rm n}(\tau/\Updelta t - 1/2)}{(1-\varepsilon_{\rm n}) + (\tau/\Updelta t - 1/2)}. $$
(14)

The collision operator between LBM cells and DEM spheres takes the following form [21, 16],

$$ \Upomega^{s}_{\rm i} = \left[f_{\rm i'}({\bf x},t) - f_{i'}^{\rm eq}(\rho, {\bf v}_p)\right] - \left[f_i({\bf x},t) - f^{\rm eq}_i(\rho,{\bf v}_p) \right], $$
(15)

with the symbol i′ denoting the direction directly opposing the e i vector and v p the velocity of the DEM sphere at the cell position (x),

$$ {\bf v}_p = {\varvec{\Upomega}} \times ({\bf x} - {\bf x}_{CM}) + {\bf v}_{CM}, $$
(16)

which depends on the sphere velocity v CM , angular velocity \({\varvec{\Upomega}}\) and position x CM of the sphere’s centre of mass. This is a modification of the commonly used bounce-back condition within cells tagged as solids [27]. In fact if v p  = 0 and \(\varepsilon = 1\), the bounce-back condition is recovered. The forms for B n and \(\Upomega^s_i\) have been deduced empirically from simulations with moving boundaries and have been found to describe accurately the flow effects across cylindrical boundaries [29]. Although other values for B n (as for instance \(B_{\rm n} = \varepsilon_{\rm n}\)) have been tested, this particular form gave the best accuracy. The full discussion on the different forms for B n and \(\Upomega^{s}_{i}\) can be found in [29].

The total force F over a DEM sphere is taken as the addition of the change of momentum given by each of the cells that the sphere covers,

$$ {\bf F} = \frac{\delta_x^3}{\delta_{\rm t}}\sum_{n} B_n \left(\sum_i \Upomega^s_i {\bf e}_i \right). $$
(17)

And the torque T is calculated similarly,

$$ {\bf T}=\frac{\delta_x^3}{\delta_{\rm t}}\sum_n \left[ ({\bf x}_n - {\bf x}_{CM}) \times B_n \left( \sum_i \Upomega^s_i {\bf e}_i \right)\right], $$
(18)

where it is assumed that the units of e i are the same units of the C parameter.

An important implementation issue is the calculation of the volume fraction occupied by the DEM spheres \(\varepsilon\). This issue is extensively discussed in [22] where several schemes, and their strengths and drawbacks, are described. The conclusion is that direct computation of the intersection volume is computationally expensive, and hence impractical for a coupled simulation framework. Several methods are proposed including the numerical integration of the intersection volume.

Herein, an efficient way to calculate \(\varepsilon\) based on the computation of the portion of edges covered by the DEM sphere is illustrated and it will be validated in the following section. In Fig. 3, the algorithm to calculate the volume fraction approximately is shown. The algorithm is based on the length of an edge existing inside the sphere. If an edge is defined as the set of points between the two limits p 0 and p 1, then each of these points p can be described in terms of a parameter s as,

$$ {\bf p} = {\bf p}_0 + s({\bf p}_1 -{\bf p}_0), $$
(19)

with s going from 0 to 1. Finding the length inside the sphere is reduced to finding the intersection points with the sphere surface. This is expressed as the following equation:

$$ \left({\bf p} - {\bf x}_{CM} \right) \cdot \left({\bf p} - {\bf x}_{CM} \right) = R^2, $$
(20)

with R the sphere radius. This equation gives a quadratic polynomial to solve for the parameter s, with two solutions. If the solutions are imaginary then the sphere never intersects the edge. On the other hand, if they are real and both are between 0 and 1, then they represent the limit points of the intersection segment. Finally, if one solution is less than 0 or greater than 1 then it is replaced by the edge limit points p 0 and p 1, accordingly. The intersection length l e is computed for each of the 12 edges. It is then compared with the total edge length to obtain the volume fraction,

$$ \varepsilon = \frac{\sum_{e=1}^{12} l_e}{12 \delta_x}. $$
(21)
Fig. 3
figure 3

The DEM sphere interacting with an LBM cell (cube). The blue lines are the portion of edges covered by the DEM sphere (color figure online)

Full size image

3 Validation

To validate the method, a comparison with the work carried out by Owen et al. [22] is made to measure the drag coefficient of a sphere immersed into the fluid as a function of its Reynolds number Re. The LBM domain is formed by a lattice of 240 × 60 × 60 cells. The lattice size step is δ x = 0.004 m. The DEM sphere is placed at the domain’s centre, and it has a radius of 0.036 m, which is equivalent to 9 LBM cells. The fluid density is taken as ρ = 1,000 kg/m3, the kinematic viscosity ν is 10−4 m2/s and the time step δ t = 1.6 × 10−2 s. Periodic boundary conditions are applied in the three directions, and a constant body acceleration of 7.81 × 10−5 m/s2 is applied to the LBM cells, allowing the drag coefficient to be calculated over a wide range of Reynolds numbers. Figure 4 shows a plane slice plot with the velocity field surrounding the DEM sphere, for a Reynolds number of 30, preventing the formation of eddies behind the sphere.

Fig. 4
figure 4

Cross-sectional contour plot of the fluid velocity field surrounding a DEM sphere for Re = 30. The colourmap is proportional to the fluid velocity (color figure online)

Full size image

To calculate the Reynolds number, the sphere’s diameter D is used as the characteristic length, and the velocity is taken as the average of the velocities of the unoccupied cells v ave,

$$ Re = \frac{v_{\rm ave} D}{\nu}. $$
(22)

The drag coefficient C D is calculated by the reaction force x component, F x over the sphere (Eq. 17) and the average fluid density ρ,

$$ C_{\rm D} = \frac{2F_x}{\rho v_{\rm ave}^2 \pi D^2/4}. $$
(23)

Figure 5 shows the calculated drag coefficient as a function of Re. For comparison, the results from the previous study of Owen et al. [22] are also shown. Additionally, an empirical correlation [32] with experimental data is also presented:

$$ C_D \approx \frac{24}{Re} + \frac{6}{1+\sqrt{Re}} + 0.4 $$
(24)
Fig. 5
figure 5

Sphere drag coefficient C D as a function of the Reynolds number Re

Full size image

As can be seen, the method to calculate the volume fraction \(\varepsilon\) from Eq. 21 gives very similar results to the method used by Owen et al. [22]. It is also relatively easy to implement, requiring few calculations \(\varepsilon\). One point of concern is when the DEM sphere intersects the LBM cell, but not at its edges. In this case, although the real volume fraction is non-zero, Eq. 21 will give \(\varepsilon=0\). This is usually solved by ensuring that the DEM sphere covers a wide range of LBM spheres. In the present case, the radius of the DEM sphere is nine LBM cells, which seems sufficient to reproduce the reported results obtained using similar methods, eliminating this problem.

Another validation for spheres is the simulation of the Magnus effect. The Magnus effect is a lift force applied over a spinning sphere due to the fluid flow asymmetry introduced by the angular velocity. It is an important validation to check the effect the coupling with rotating spheres, which is a problem that is going to be observed during the erosion simulations later on. Figure 6 shows the velocity field disturbed by the spinning sphere. The sphere is spinning in a counter-clockwise direction, dragging the fluid close to it. The net effect is a decrease in the fluid’s velocity at the top portion of the sphere due to this drag and a velocity increase at the bottom. If the system is considered as an inefficient air pump, air will build up at the top causing higher pressure at this point. This pressure gradient pointing downwards generates a force over the spheres in the same direction. The Magnus effect is commonly found in ball sports such as baseball and soccer, where it gives the ball a distinct trajectory. With this force, a lift coefficient can be defined in complete analogy to the drag coefficient,

$$ C_{\rm L} = \frac{2F_{\rm y}}{\rho v_{\rm ave}^2 \pi D^2/4}, $$
(25)
Fig. 6
figure 6

Cross-sectional contour plot of the fluid velocity field surrounding a spinning DEM sphere with an angular velocity ω. The colourmap is proportional to the fluid velocity

Full size image

Hölzer and Sommerfeld [17] conducted a number of simulations on the Magnus effect with a similar LBM scheme, without coupling it with the DEM. A dimensionless variable called the particle’s spin number S Pa is defined for comparison with the results of this previous study,

$$ S_{\rm Pa} = \frac{\omega D}{2 v_{\rm ave}}, $$
(26)

with ω the sphere’s angular velocity.

Simulations varying S Pa were conducted for Re = 30, a value that ensures that eddies do not appear in the simulation. Fig. 7 shows the dependence of the lift coefficient produced by the Magnus effect. It also shows the results obtained by Hölzer and Sommerfeld, and a fairly good match with the results from this study can be seen. For this small Reynolds number range, the dependence on C L on S Pa, and therefore on the angular velocity, appears to be linear.

Fig. 7
figure 7

Sphere lift coefficient C L as a function of the particle’s spin number S Pa

Full size image

4 Simulation of the erosion phenomenon

4.1 DEM stage

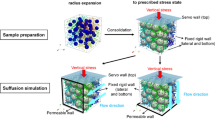
The first stage of the study involves a DEM simulation of the soil skeleton sedimentation until it reaches equilibrium. In order to do this, the larger spheres are placed above the smaller spheres. Both arrays of particles are initially positioned in a hexagonal closed packing, and some spheres are erased randomly to introduce some disorder. There are in total 12,907 small particles with a diameter of 0.4 mm and 30 big particles with a diameter of 3 mm. The spheres are placed inside a rectangular container surrounded by rigid walls of dimensions 2 cm × 2 cm × 4 cm. Table 1 shows the parameters used for the DEM model.

Table 1 Microscopic constants for the DEM stage
Full size table

4.2 Coupled simulation

After equilibrium is reached, the rectangular box is divided into a set of 200 × 200 × 400 LBM cells, producing a lattice spacing constant δ x = 0.1 mm. This spacing is required to ensure that there are enough cells to cover the smallest spheres. By the validation examples presented above, eight LBM cells covering the diameter is enough to obtain accurate results. However, it also poses a problem since 16 million LBM cells occupy roughly 24 GB of memory with double precision variables, which is an amount difficult to find in common desktops. Coarser lattices could be used, but then there may not be enough resolution to properly describe the effect of the LBM fluid on the small particles. Unfortunately, due to this large memory requirement and the time that the simulation takes, it was not possible to consider more DEM particles in the sample. For this reason, more realistic particle size distributions will be impossible to be simulated with the current available computational resources.

Figure 9 shows the DEM sample immersed into the LBM grid. Due to the realistic value taken for the gravity acceleration, the lattice time step is δ t = 1.01 × 10−5 s. Since the normal and tangential stiffnesses are small (very soft particles), this time step is enough to ensure the stability of the DEM method [22]. Also, due to the size of the DEM sample, the maximum deformation given by the weight of all the spheres over the spheres at the bottom is less than 0.001 times the smallest radius, which may be considered negligible. The viscosity of the fluid (Eq. 10) is 1.65 × 10−5 m2/s. Pressure boundary conditions are applied to the bottom and top faces as explained in [12], by controlling the densities at the limit cells using Eq. 11. Periodic boundary conditions are set across the other directions. Gravity is only imposed over the particles, and not over the fluid. Therefore, the driving force of the fluid is not a hydraulic head gradient but a pressure one. The reason for this is the high compressibility of the flow, which will concentrate a high density of fluid at the bottom due to gravity. A solution for this is to take a more realistic equation of state for the fluid, something that is allowed in the LBM as shown in [11], but for the present study, such sophistication was unnecessary. The LBM fluid density is set to an equilibrium value of 1,000 kg/m3. A linear gradient pointing upwards is fixed at the beginning by imposing a gradual increment in density from 0 to 50 kg/m3 at the bottom, which translates to a pressure difference of 1.63 kPa across the total height. This pressure gradient was chosen after observing no significant movement of the particles with smaller values. Lastly, there is a fifth wall perpendicular to the z direction and 2 mm above the lower boundary. The purpose of this wall is to prevent the spheres from coming into contact with the pressure boundary and to leave some space for the pressure of the fluid to build up.

Fig. 8
figure 8

DEM deposition simulation stage. The particles are free to fall by gravity until equilibrium is reached

Full size image
Fig. 9
figure 9

DEM–LBM simulation stage. The transparent colourmap is proportional to the fluids pressure showing a pressure gradient pointing upwards. A buffer of 2 mm between the smallest particles and the lower boundary is left for the pressure to build up unaffected

Full size image

Snapshots of the process at different times are shown in Fig. 10. The red soil in the figure formed by the smaller particles is slowly forced into the void spaces formed by the larger spheres. At the same time, the large particles slowly sink into the gradually emptied lower layers. The effect of the pressure gradient is therefore more significant than gravity for the smaller spheres and less significant for the larger ones. These different effects across distinct particle size ranges are the focus of this study.

Fig. 10
figure 10

Snapshots at different times of the DEM sphero-duck simulation diving into the LBM pool. The video is attached as supplementary material. The transparent colourmap is proportional to the fluids pressure

Full size image

Similar studies have been carried out with physical models [25]. At the laboratory scale, more particles and larger simulation times can be considered, but at the same time, the internal pressure profile and the dynamics of the individual particles are difficult to measure. In the experimental study, the porosity of the soil was measured at different heights by means of the novel spatial time domain reflectometry (Spatial TDR) technique. The reported values for the porosity are close to 0.4 for areas where the soil is not mixed and as low as 0.2 at the points where the smaller spheres are entering the larger voids. In the simulation presented in this paper, measuring the porosity is a matter of adding the volume fraction \(\varepsilon\) (Eq. 21) for cells at a given height and dividing it by the total number of cells for that layer. The results for different simulation times are shown in Fig. 11. Areas where the porosity is equal to 1 are devoid of particles, in particular the buffer of 2 mm above the lower boundary (Fig. 9). Initially, the zones filled with particles have a porosity close to 0.4. As time moves on, and the different spheres start to mix, the porosity at the infiltration zones decays to values close to 0.2, in complete agreement with the experimental studies [25]. Also, the mixing zone is moving upwards over time and getting broader as the larger spheres start to sink.

Fig. 11
figure 11

Porosity ϕ profile as a function of the height

Full size image

After this qualitative match with experimental results, an analysis of the effect of the fluid on the different soil components is carried out. For particles inside of a constant gradient, the net force over a sphere is proportional to the pressure difference between the end points of the sphere and the superficial area. Since the pressure difference is also proportional to the diameter under a constant gradient, the net force is proportional to the cube of the radius. Gravity is also proportional to the cube of the radius, so there is no disparity in the effect of the fluid between the different particle sizes. Therefore, under a constant gradient, the particles should not mix. Following this train of thought, the pressure fluctuation profile is plotted in Fig. 12. The initial linear pressure decay is shown. However, soon after the simulation starts, the pressure profile dramatically changes from the linear configuration to a sigmoid one. Most of the pressure variance is concentrated inside the soil with the smallest particles. Before the particles mix, the porosity of both components is the same, as seen in Fig. 11. Consequently, the abrupt pressure decay in the lower layer must be due to the decreased conductivity. After the mixing starts taking place, the abrupt pressure decay moves to the mixing zone with lower porosity.

Fig. 12
figure 12

Pressure difference with the top boundary \(\Updelta p\) versus height

Full size image

The ratio of solid surface area/pore volume S (a measure of pore tortuosity [28]) is shown in Fig. 13. The tortuosity is greater at the lower layers of small particles. The value of S with the height shows for t = 0 a bimodal distribution separating the contributions from both grain sizes. As the erosion process starts, the value for S (and hence the tortuosity) starts to increase at the mixing zone gradually. As will be shown later on, this increase in tortuosity, and the associated decrease in conductivity, will increase the momentum transfer between the fluid and the particles at this location.

Fig. 13
figure 13

Ratio of solid surface area/pore volume S as a function of the height

Full size image

Figure 14 shows the pressure gradient, calculated numerically, as a function of the height. The gradient is constant at the initial configuration. After 40s, there is a noticeable pressure gradient in the zone occupied by the small particles. However, during and after the 80s mark, the gradient is mostly concentrated in the mixing area with the lowest porosity as seen in Fig. 11. This is an effect that actually increases the mixing process by accelerating the small particles that are filling the large voids at the interface between the two granular samples. The effect on the mean velocity of the small particles can be observed in Fig. 15, in which it is evident that the particles just above the mixing zone are the most mobile ones. In fact, as the process evolves, the velocity of the particles above the mixing zone is the largest, implying that most of the momentum transfer between the fluid and the particles occurs at this point. The fluid average velocity is shown in Fig. 16. It can be seen that it grows in time from being zero initially (t = 0 s) to a maximum value at the zone occupied by the small particles. At the same point that the small particles are accelerated (as seen in Fig. 15), the velocity of the fluid goes suddenly to zero illustrating that at this point full momentum transfer occurs.

Fig. 14
figure 14

Pressure gradient versus height

Full size image
Fig. 15
figure 15

Average velocity of the small particles versus height

Full size image
Fig. 16
figure 16

Average fluid velocity versus height

Full size image

A third effect observed from the simulation is a similar increase in the angular velocity of the particles at the same point that the maximum velocity is found. Figure 17 shows the angular velocity as a function of height. A clear correlation is observed between the behaviours shown in Figs. 15 and 17. It may be concluded then that the fluid is also transferring angular momentum to the small particles. Figure 18 shows the small particles coloured by their velocity. The particles with the highest velocities are surrounding the large particles. Hence, this angular velocity gain further improves the mobility of the particles into the large void spaces by allowing them to roll against the larger particles, effectively reducing friction. This effect is very difficult to reproduce by continuum models, in which the conservation laws considered are usually the conservation of linear momentum and energy. This opens a novel question about the potential effect of the individual particle shapes on the erosion rates in soils with more realistic, which means non-spherical, shapes. Particle shape and interlocking have the secondary effect of hindering particle rotation [8] and, by the observations presented herein, will also force the particles to slide instead of roll against each other. This will produce a greater resistance against mixing. A possible way to study the effect of particle shape using the current model is the introduction of a rolling resistance method [2], and it is the opinion of the authors that this should be the goal of future studies. More sophisticated methods could include the interaction with polyhedral particles introduced by the authors before [7].

Fig. 17
figure 17

Average angular velocity of the small particles versus height

Full size image
Fig. 18
figure 18

Small spheres coloured by their angular velocity (red highest, blue zero). The large spheres are not shown

Full size image

5 Conclusions

A numerical scheme for the simulation of contact erosion is presented coupling the mechanics of a driving fluid with rigid particles representing the solid matrix. The fluid is modelled with the lattice Boltzmann method (LBM), and the solid particles are simulated with the discrete element method (DEM). A coupling scheme is proposed with physically correct momentum transfer at some discrete points around the particles.

The scheme is validated against simulations of the drag coefficient for a broad range of Reynolds numbers and compared with published numerical results and experiments. A second validation is carried out by simulating a spinning sphere inside a flowing fluid. The Magnus effect, by which the spinning sphere suffers a force perpendicular to the average fluid velocity, is calculated as a function of the angular velocity and compared with previous numerical results. These two validation examples show that the proposed approach is physically correct.

After validation, the simulation framework is used to model a simple erosion process inside a soil formed by two distinct particle sizes. Initially, a DEM simulation stage is carried out to prepare the sample. In this stage, both fractions of particle sizes are separated and then allowed to fall by gravity. At the end of this stage, a solid matrix is built with the larger spheres at the top being supported by the smaller ones.

The second stage introduces the fluid with a pressure gradient opposing gravity. A first comparison is done with the results obtained by experiments in previous studies [25] with a set-up resembling the simulated situation. In the experiments, it was observed that each soil component separately has a porosity of approximately 0.4. However, as the simulation evolves, there is a mixing zone in which the small particles start invading the void spaces of the larger ones, with a reduction in the porosity to 0.2, which is in complete agreement with the experimental results.

A micro-mechanical analysis follows in which three different effects are observed. The first effect is an increase in the hydraulic gradient along the space occupied by the small particles. As a consequence, there is a boost to the buoyancy experienced by the smaller particles, which drives them upwards into the layers with larger particles. This boost is caused by the reduced constriction size of the small particles a higher value for the surface area/pore volume ratio S.

The second effect is a sudden reduction in the fluid’s velocity just below the mixing zone. This is followed by an increase, at the mixing zone, in the smaller particle velocities. Therefore, there is a full momentum exchange at the mixing zone between the particles and the fluid, which greatly reduces the hydraulic gradient at this height. It may be said that the significant reduction in porosity forces the fluid to push the spheres up at this height, which produces the particle acceleration reported herein. This effect is also enhanced by a gradual increase in S at this mixing area, building up a higher momentum transfer due to the reduced conductivity.

Finally, the particles are able to roll, an effect which is difficult to model with continuum approaches. In particular, it is observed that the particles roll with higher angular velocities at the mixing zone. This effectively reduces the friction between the smaller and larger particles, which further increases the erosion rate. A relevant question arises as to how the particle shape will affect the erosion rate since a particle’s shape effectively hinders its rotation.

The framework presented herein has revealed important effects present in erosion processes in soil with mixed particle sizes. Although the size of the simulated sample was small, in the future with the advent of ever-growing computational resources, the same model could potentially be used with a realistic number of particles and at field scale. Even now, more situations could be simulated to formulate constitutive models and advance the prediction of erosion and suffusion processes.