The dilatant behaviour of sand–pile interface subjected to loading and stress relief

Abstract

Property and behaviour of sand–pile interface are crucial to shaft resistance of piles. Dilation or contraction of the interface soil induces change in normal stress, which in turn influences the shear stress mobilised at the interface. Although previous studies have demonstrated this mechanism by laboratory tests and numerical simulations, the interface responses are not analysed systematically in terms of soil state (i.e. density and stress level). The objective of this study is to understand and quantify any increase in normal stress of different pile–soil interfaces when they are subjected to loading and stress relief. Distinct element modelling was carried out. Input parameters and modelling procedure were verified by experimental data from laboratory element tests. Parametric simulations of shearbox tests were conducted under the constant normal stiffness, constant normal load and constant volume boundary conditions. Key parameters including initial normal stress ($\sigma_{{{\text{n}}0}}^{\prime }$), initial void ratio (e ₀), normal stiffness constraining the interface and loading–unloading stress history were investigated. It is shown that mobilised stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$) and normal stress increment ($\Updelta \sigma_{\text{n}}^{\prime }$) on a given interface are governed by $\sigma_{{{\text{n}}0}}^{\prime }$ and e ₀. An increase in $\sigma_{{{\text{n}}0}}^{\prime }$ from 100 to 400 kPa leads to a 30 % reduction in $\Updelta \sigma_{\text{n}}^{\prime }$. An increase in e ₀ from 0.18 to 0.30 reduces $\Updelta \sigma_{\text{n}}^{\prime }$ by more than 90 %, and therefore, shaft resistance is much lower for piles in loose sands. A unique relationship between $\Updelta \sigma_{\text{n}}^{\prime }$ and normal stiffness is established for different soil states. It can be applied to assess the shaft resistance of piles in soils with different densities and subjected to loading and stress relief. Fairly good agreement is obtained between the calculated shaft resistance based on the proposed relationship and the measured results in centrifuge model tests.

1 Introduction

Piles are often designed and constructed underneath a deep basement to support superstructure, without considering the effects of stress relief due to basement excavation. The design of these piles is generally based on pile load test carried out at ground surface. Although Zheng et al. [24] carried out finite element analyses of pile capacity in non-dilative soil subjected to stress relief due to excavation, the fundamental shearing mechanisms at pile–soil interface including both dilative and non-dilative characteristics are still not fully understood.

Behaviour of pile–soil interface is controlled mainly by a layer of sand close to the pile (‘shear band’). A conceptual model of the interface is shown in Fig. 1 (after Wernick [22]). The interface soil has tendency to dilate or contract when it is subjected to shearing. Outer soil surrounding the shear band may be considered as an elastic restraining medium [1, 7]. Dilation of the interface soil results in a change in normal stress, which in turn influences the mobilised shear stress of the pile–soil interface. Unit shaft resistance (τ _p) of a pile is given by the following equation:

$$ \tau_{\text{p}} \left( {\Updelta \sigma_{{{\text{n}}0}}^{\prime } } + \sigma_{{{\text{n}}0}}^{\prime } \right)\tan \delta $$

(1)

where $\sigma_{{{\text{n}}0}}^{\prime }$ is the normal effective stress on the pile shaft prior to loading, $\Updelta \sigma_{\text{n}}^{\prime }$ is the change in normal stress due to dilation, and δ is the angle of friction of the interface.

Fig. 1

Conceptual model of a soil–structure interface subjected to shearing (after Wernick [22])

In the literature, shearbox tests under constant normal stiffness (CNS) condition have been carried out to study the shaft resistance of piles [1, 18, 19]. Lehane et al. [14] proposed an approach to estimate the normal displacement of an interface, based on CNS shearbox tests on UWA sand (a standard silica sand typically used in centrifuge tests at the University of Western Australia [14]) with a relative density of 85 % and at normal stress of 40 kPa. Despite these studies, the interface responses are not analysed in terms of the state (i.e. density and stress level) of interface soil. Estimating $\Updelta \sigma_{\text{n}}^{\prime }$ for soils with different densities or subjected to loading and unloading history remains difficult.

The objectives of this study are to investigate shearing mechanisms at pile–soil interface and to explore any contribution of normal stress increase ($\Updelta \sigma_{\text{n}}^{\prime }$) to pile shaft resistance, when a pile is subjected to stress relief due to deep excavation. $\Updelta \sigma_{\text{n}}^{\prime }$ is quantified in terms of the state of interface soil and stiffness constraining the interface (the spring stiffness in Fig. 1). A numerical parametric study using the distinct element modelling (DEM) is presented and discussed. Input parameters and modelling procedure of the DEM study were verified by experimental data from laboratory element tests. Shearbox tests under the CNS condition were simulated. Constant normal load (CNL) and constant volume (CV) conditions are also studied as extreme cases for comparison. The effects of several factors including initial normal stress ($\sigma_{{{\text{n}}0}}^{\prime }$), void ratio of the soil (e ₀), normal stiffness constraining the interface (k _n) and loading and unloading history on a pile–soil interface are investigated. The results are applied to calculate shaft resistance of piles. A comparison is drawn between estimated shaft resistance based on the proposed method in this study and measured data from centrifuge tests presented by Zheng et al. [25].

2 DEM

2.1 Model set-up

A typical DEM model of a shearbox test is shown in Fig. 2. The shearbox is 88 mm in length (L) and 56 mm in height (H). The aspect ratio (L/H) is equal to 1.57, which is typically adopted for shearbox tests [21]. The circular particles have the same diameter (D) of 1 mm. The ratios of box length and height to particle diameter are L/D = 88 and H/D = 56. The simulations were performed using Particle Flow Code in Two Dimensions (PFC^2D) [9].

Fig. 2

A typical DEM model with 5,333 particles

Inter-particle contact is assumed to be linear elastic. Particle sliding occurs when tangential contact force reaches the limit friction, which is controlled by an inter-particle friction angle of 45°. Each particle is idealised as circular. It is well recognised that the use of circular particle leads to excessive rotation as compared to real soil particles [9]. This is why a relatively high inter-particle friction angle of 45° is adopted to predict more realistic results, as suggested by Yimsiri and Soga [23].

Both normal and shear stiffness of each particle were specified as 10⁸ N/m, which is relatively high to minimise particle deformation. This is because soil behaviour (such as dilatant response) is controlled by rearrangement of soil particles rather than deformation of the soil grains. The particle stiffness is a typical value for DEM analyses as used by several researchers [10, 15]. The particle density was 2,650 kg/m³. The coefficient of particle to wall friction was 0.9, which is also relatively high to prevent slippage between bulk material and boundary walls, as suggested by Wang and Gutierrez [21].

Shearbox tests under CNL, CNS and CV conditions were modelled. In each CNS test, normal and shear stiffness of the top wall was specified according to the required normal stiffness (k _n) of each simulation. A stiffness of 10⁹ N/m was specified for other walls. In each CNL test, normal stress applied on the top boundary was constant while the soil sample was free to dilate or contract. In each CV test, the top wall was fixed in vertical direction to achieve a confined condition. Stiffness of each wall was assigned as 10⁹ N/m, which is a typical value for DEM analyses to minimise wall deformation [15].

2.2 Modelling procedures

In each simulation, the number of particles required to fill in the shearbox can be predetermined for a given void ratio. Model sample was generated by filling this number of particles with 60 % reduced size (i.e. 0.6 mm in diameter) into the shearbox by random packing [9]. All particles were then expanded to 1.0 mm in diameter, and the target void ratio of each sample was obtained.

Normal stress was applied on the top and bottom boundaries of a sample through a servo-control mechanism [9], which controls the velocity of each boundary to ensure the normal stress following to a specified value. The movement of each boundary is stopped when the specified normal stress is reached, implying that the state of equilibrium is achieved. During the shearing stage, the lower half of the box was displaced at a speed of 0.05 mm/s, while the upper half was fixed. The shearing speed was low enough to ensure a quasi-static simulation. Each simulation was terminated at a shear displacement of 10 mm.

In order to verify the input parameters and modelling procedure of the DEM study, laboratory shearbox tests were performed. Measured data from the element tests were compared with computed results under CNL boundary condition. Details of the comparison are discussed in appendix.

2.3 Parametric study

Different initial normal stresses ($\sigma_{{{\text{n}}0}}^{\prime }$) of 100, 250, 400 and 1,000 kPa were studied. In order to investigate the effects of density on the interface behaviour, samples with initial void ratios (e ₀) of 0.18, 0.23 and 0.30 were used. Void ratio is derived as the ratio of area of voids to that occupied by particles. Since each particle is represented by a 2D circular disc, void ratio of each sample is set to be quite low as compared to that of a real soil. Samples specified with void ratios of 0.18, 0.23 and 0.30 are intended to simulate real soils in dense, medium-dense and loose states, respectively. The corresponding relative densities of these samples are about 75, 50 and 30 %, based on void ratios of regular packings of 0.10 and 0.35 representing the densest and the loosest states of soil, respectively.

In order to relate the computed results from 2D shearbox simulations with shaft friction of a pile (an axisymmetric problem), cylindrical cavity expansion theory [7] is adopted. The cavity stiffness k _n constraining a pile–soil interface is given by:

$$ k_{\text{n}} = \frac{4G}{{D_{\text{p}} }} $$

(2)

where D _p is pile diameter and G is shear modulus of soil surrounding the interface.

For a given pile diameter (D _p), Eq. (2) is used to calculate k _n, which is equivalent to normal stiffness applied to a 2D shearbox simulated in the DEM analysis. Application of cylindrical cavity expansion theory to shearbox tests under the CNS conditions has been adopted and verified by several researchers [1, 19]. Normal stiffness (k _n) in this study ranges from 1,000 to 10,000 kPa/mm, according to cavity stiffness of soil constraining a pile [14]. Contact stiffness between one particle and a boundary can be easily understood as the change in contact force due to unit displacement (in unit of N/m). For a wall in contact with a number of particles, an average contact stress can be deduced from total contact force and area of the wall. Normal stiffness k _n is used to define the change in contact stress due to unit displacement (in unit of kPa/mm), based on cavity expansion theory (Eq. 2).

The CNL and CV tests can be regarded as special cases of CNS tests with normal stiffness of zero and infinite, respectively. In order to study the effects of stress history on the responses of interface, loading–unloading history was applied in some simulations. Normal stresses of 250 or 400 kPa were applied to the sample and then unloaded to 100 kPa. Shearing stage was simulated subsequently.

3 Interpretation of the DEM study

3.1 Influence of initial normal stress

Figure 3a shows the variations of mobilised stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$) with increasing shear stain (γ) in three simulations under different initial normal stresses ($\sigma_{{{\text{n}}0}}^{\prime }$) of 100, 250 and 400 kPa. The samples have the same initial void ratio (e ₀ = 0.23) and normal stiffness (k _n = 2,000 kPa/mm). Shear strain is calculated as the applied shear displacement normalised by the height (H) of the shearbox. For the sample with $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 kPa, a strain-softening response is observed. The peak stress ratio is about 1.0, which is mobilised at about 1.5 % shear strain. Peak stress ratio of the sample with a higher $\sigma_{{{\text{n}}0}}^{\prime }$ of 250 kPa is about 0.80, mobilised at 2.0–3.5 % shear strain. The sample sheared under $\sigma_{{{\text{n}}0}}^{\prime }$ of 400 kPa shows strain-hardening response. Clearly, a higher normal stress $\sigma_{{{\text{n}}0}}^{\prime }$ leads to a lower peak stress ratio, which is obtained at larger shear strain. The observation is consistent with experimental results reported by Tabucanon et al. [19]. At the final stage, when the applied shear strain is close to 10 %, the computed stress ratio in each case is close to 0.65.

Fig. 3

Effects of initial normal stress $\sigma_{{{\text{n}}0}}^{\prime }$ on a mobilised stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$) and b change in normal stress ($\Updelta \sigma_{\text{n}}^{\prime }$) (e ₀ = 0.23 and k _n = 2,000 kPa/mm)

Figure 3b shows the computed variations of normal stress increment $\Updelta \sigma_{\text{n}}^{\prime }$, with shear strain for the three cases. The sample with $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 kPa shows a slight reduction in normal stress when shear strain is lower than 1.0 %. A clear increase in $\Updelta \sigma_{\text{n}}^{\prime }$ is observed as shear strain increases, due to dilative response of the sample. $\Updelta \sigma_{\text{n}}^{\prime }$ reaches about 180 kPa at a shear strain close to 10 %. It is even higher than the applied initial stress of 100 kPa. The results illustrate that a normal stress change due to dilation can be vital to the behaviour of a pile–soil interface. The sample with $\sigma_{{{\text{n}}0}}^{\prime }$ of 250 kPa shows an increase in normal stress at shear strain larger than 2.0 %. The final magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ is about 150 kPa, which is 17 % lower than that for the sample with $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 kPa. For a given shear strain, the sample with $\sigma_{{{\text{n}}0}}^{\prime }$ of 400 kPa has the lowest $\Updelta \sigma_{\text{n}}^{\prime }$. These observations demonstrate that soil dilation under the CNS condition is suppressed as normal stress increases.

The magnitude of normal expansion at the interface (Δy) for each sample can be obtained from the computed $\Updelta \sigma_{\text{n}}^{\prime }$ and the applied normal stiffness (k _n) by the following equation:

$$ \Updelta y = \Updelta \sigma_{\text{n}}^{\prime } /k_{\text{n}} $$

(3)

Since the three cases shown in Fig. 3b have the same k _n of 2,000 kPa/mm, the pattern of Δy with increasing shear strain in each case is the same as that for $\Updelta \sigma_{\text{n}}^{\prime }$ in Fig. 3b.

3.2 State-dependent interface responses

Since dilation is governed by soil state, the effects of soil density on interface responses are also investigated. Figure 4a shows the mobilised stress ratios ($\tau /\sigma_{\text{n}}^{\prime }$) for samples with e ₀ of 0.18 and 0.30, which were intended to simulate dense and loose sands, respectively. Two different $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 and 1,000 kPa are also considered. Normal stiffness is the same (k _n = 4,000 kPa/mm) for all four cases. For each case with $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 kPa, strain-softening response is observed. Stiffness of the two samples is similar before shear strain reaches about 1 %. The dense sample (e ₀ = 0.18) shows a higher peak stress ratio of about 1.2, mobilised at larger magnitude of shear strain of about 4 %. Peak stress ratio of the loose sample (e ₀ = 0.30) is about 1.1 at 1–2 % shear strain. As expected, computed stress ratio of each sample at $\sigma_{{{\text{n}}0}}^{\prime }$ of 1,000 kPa is much lower, except at final stage when shear strain is about 10 %. Although the dense sample (e ₀ = 0.18) shows slightly strain-softening behaviour, the peak stress ratio is only 0.7. The loose sample (e ₀ = 0.30) shows strain-hardening response during the entire shearing stage.

Fig. 4

Effects of soil state on a mobilised stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$) and b change in normal stress ($\Updelta \sigma_{\text{n}}^{\prime }$) (k _n = 4,000 kPa/mm)

Figure 4b shows the computed $\Updelta \sigma_{\text{n}}^{\prime }$ for the four samples. The dense sample (e ₀ = 0.18) at a low normal stress ($\sigma_{{{\text{n}}0}}^{\prime }$= 100 kPa) shows an increasing $\Updelta \sigma_{\text{n}}^{\prime }$ from the very beginning. The final magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ is about 440 kPa. The loose sample (e ₀ = 0.30) exhibits a reduction in normal stress when shear strain is lower than about 3 %. Although $\Updelta \sigma_{\text{n}}^{\prime }$ gradually increases at larger shear strain, the final magnitude is only 40 kPa, which is less than 10 % of that for the dense sample (e ₀ = 0.18). For the two cases under much higher $\sigma_{{{\text{n}}0}}^{\prime }$ of 1,000 kPa, each sample shows a reduction in normal stress due to shearing, indicating contraction of the interface. Both Fig. 4a, b clearly show that responses of a given interface are governed by the soil state including density (e ₀) and normal stress ($\sigma_{{{\text{n}}0}}^{\prime }$). Both parameters should be considered to quantify shaft resistance of piles.

3.3 Effects of normal stiffness constraining the interface

Dilation of a pile–soil interface is also influenced by normal stiffness constraining the interface [i.e. k _n in Eq. (2)]. Figure 5a shows the mobilised stress ratios ($\tau /\sigma_{\text{n}}^{\prime }$) of three samples with k _n of 2,000, 4,000 and 8,000 kPa/mm. Initial void ratio is 0.18, and normal stress is 100 kPa for each sample. The computed stress ratios are almost identical for the three samples with increasing shear strain up to 10 %. The peak stress ratio is about 1.0, which is mobilised at approximately 1.5 % shear strain. The mobilised stress ratio is independent of the magnitude of normal stiffness (k _n). This is consistent with the observations from laboratory CNS shearbox tests reported by Evgin and Fakharian [3].

Fig. 5

Variations of a stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$), b normal stress increment ($\Updelta \sigma_{\text{n}}^{\prime }$) and c normal displacement (Δy) with shear strain (e ₀ = 0.23 and $\sigma_{{{\text{n}}0}}^{\prime }$ = 100 kPa)

Figure 5b shows the computed $\Updelta \sigma_{\text{n}}^{\prime }$ for the three cases. An increasing normal stress is observed at strain level larger than 1 %. Given the same shear strain, the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ is larger if k _n is higher. This illustrates the effects of confinement on interface responses. Clearly, the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ is larger if a given interface is more constrained by surrounding soil.

Figure 5(c) shows the normal displacements (Δy) for the three samples. Since the applied normal stiffness is different, the patterns of Δy are not same as those of $\Updelta \sigma_{\text{n}}^{\prime }$, as indicated by Eq. (3). The magnitude of Δy is normalised by the diameter (D) of the particles. A positive value of Δy indicates dilation of the interface. The maximum normalised dilation (Δy/D) are 0.09, 0.05 and 0.03, for samples with k _n of 2,000, 4,000 and 8,000 kPa/mm, respectively. It should be noted that although a higher k _n leads to a lower magnitude of Δy, the resulting normal stress $\Updelta \sigma_{\text{n}}^{\prime }$ is actually higher, as previously shown in Fig. 5b. $\Updelta \sigma_{\text{n}}^{\prime }$ is more relevant than Δy to engineering practice, because it is directly related to shear stress of the interface and thus shaft capacity of a pile, as given by Eq. (1).

3.4 Influence of loading–unloading history

Figure 6a shows the mobilised stress ratios ($\tau /\sigma_{\text{n}}^{\prime }$) of three samples to investigate the influence of recent loading and unloading stress history. A normal stress $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 kPa was applied to the first sample. For comparison, normal stresses of 250 and 400 kPa were applied to the other two samples and then unloaded to 100 kPa, prior to shearing stage. It is shown in the figure that the computed stress ratios are almost identical for the three samples with increasing shear strain up to 10 %. The peak stress ratio is about 1.0, which is mobilised at approximately 1.5 % shear strain.

Fig. 6

Influence of loading–unloading stress history on a mobilised stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$) and b change in normal stress ($\Updelta \sigma_{\text{n}}^{\prime }$) (e ₀ = 0.23 and k _n = 2,000 kPa/mm)

Based on the computed results, it can be seen that mobilised stress ratio is not affected by the loading–unloading history. From theoretical point of view, however, the sample subjected to higher normal stress followed by an unloading stage should have a higher density. The peak friction angle of this sample should be higher accordingly, as observed in laboratory shearbox tests under the CNS condition [3]. The similar stress ratios computed from this DEM study may be due to the simplified elastic contact model and circular shape of particles.

Figure 6b shows the computed $\Updelta \sigma_{\text{n}}^{\prime }$ for the three samples without and with loading–unloading history. The sample without unloading history shows a slight reduction in normal stress when shear strain is lower than 1 %, but in general, the computed magnitudes of $\Updelta \sigma_{\text{n}}^{\prime }$ for the three cases are quite close. The loading–unloading stress history has negligible influence on interface responses. But it should be noted that the observation is based on the simplified DEM study.

4 Estimation of $\Updelta \sigma_{\text{n}}^{\prime }$ based on soil state and cavity stiffness

4.1 Maximum increment in normal stress ($\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$)

Results of the DEM study demonstrate that the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ is controlled by the state of interface soil (e ₀ and $\sigma_{{{\text{n}}0}}^{\prime }$) and the cavity stiffness constraining the interface (k _n). In order to quantify the response of a given pile–soil interface, the maximum normal stress increment ($\Updelta \sigma_{\text{n}}^{\prime }$) from each case is further studied. $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ is defined as the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ at a shear displacement of 5 mm, which may reasonably reflect the limiting relative displacement required for a given soil–structure interface. This value has been adopted for the limit of shear displacement to mobilise the strength of piles both in sand [16] and in clay [12, 13]. The 5-mm shear displacement is corresponding to a shear strain of 8.6 %, which is much larger than the strain level for maximum dilation rate in each simulation (between 1 and 4 % shear strain).

Figure 7a shows the computed $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ for medium-dense samples (e ₀ = 0.23). The applied initial normal stresses $\sigma_{{{\text{n}}0}}^{\prime }$ are 100, 250 and 400 kPa. Given the same $\sigma_{{{\text{n}}0}}^{\prime }$, $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ generally increases as k _n increases, as the interface becomes more constrained. The magnitude of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ is limited to an upper value, which is obtained from a corresponding test with fixed boundary, that is, a CV test. As shown in the figure, the upper limit of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ from each CV test is fairly consistent with those from CNS tests under a relative high k _n of 10,000 kPa/mm.

Fig. 7

Dependence of a maximum normal stress increment ($\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$) and b maximum normal displacement (Δy _max) on normal stiffness (k _n)

The maximum normal expansion (Δy _max) corresponding to $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ can be deduced from Eq. (3). The obtained relationship between Δy _max/D and k _n is shown in Fig. 7b. Given the same $\sigma_{{{\text{n}}0}}^{\prime }$, the magnitude of Δy _max decreases with increasing k _n. From Fig. 7a, b, it is clear that a higher $\sigma_{{{\text{n}}0}}^{\prime }$ results in a lower magnitude of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ and a larger Δy _max. Both $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ and Δy _max are also dependent on soil density. A method is proposed for estimating $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ for various soil states in a unified way.

4.2 Relationship between $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ and k _n for various soil densities and stresses

Figure 7a shows that the shapes of each $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$−k _n curve are similar. The magnitude of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ generally increases with increasing k _n until an upper limit is reached. A CV test may be a valid reference for interpreting the $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$−k _n relationship. Therefore, the magnitude of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ is normalised by that obtained from a corresponding CV test ($\Updelta \sigma_{\text{n}}^{\prime * }$). Figure 8a shows the results for samples with different densities and normal stresses. A fairly consistent relationship between normalised $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ and k _n is obtained. The magnitude of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ increases by about 100 % when k _n increases from 1,000 to 10,000 kPa/mm, as dilation of the interface soil is more constrained. An upper limit of $\Updelta \sigma_{\text{n}}^{\prime }$ is reached when k _n is about 10,000 kPa/mm.

Fig. 8

Relationships of a $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$and b Δy _max with normal stiffness (k _n) for soils under various densities and normal stresses

The normalised $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$−k _n relationship is fitted using the following equation:

$$ \left( {\frac{{\Updelta \sigma_{\text{n}}^{\prime } }}{{\Updelta \sigma_{\text{n}}^{\prime * } }}} \right)^{2} + \left( {1 - \frac{{k_{\text{n}} }}{{k_{\text{n}}^{*} }}} \right)^{2} = 1 $$

(4)

where $k_{\text{n}}^{*}$ of 10,000 kPa/mm is a reference normal stiffness to represent CV conditions (see Fig. 7). It should be noted that this value may be only applicable for the simplified DEM study using circular particles with the same diameter. Eq. (4) reasonably represents the computed $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$−k _n relationship for various soil states in a unified way. The upper limit ($\Updelta \sigma_{\text{n}}^{\prime * }$) is required and can be obtained from a CV test. The equation considers the state of interface soil (e ₀ and $\sigma_{{{\text{n}}0}}^{\prime }$) and stiffness constraining a given pile–soil interface. It should be noted that other factors such as shape and size of soil particles may also affect normal stress changes for a given interface.

4.3 Deduced Δy _max based on proposed equation

The maximum normal displacement (Δy _max) in each case can be deduced from the proposed $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$−k _n relationship based on Eqs. (3) and (4). Figure 8b shows the computed Δy _max from the DEM simulations and the deduced Δy _max − k _n curve from Eq. (4). Δy _max is normalised by an upper limit ($\Updelta y_{\hbox{max} }^{*}$), which is obtained from a corresponding CNL test. Both the computed and deduced values of Δy _max are consistent for samples with various densities and initial stresses. For comparison, experimental data from laboratory CNS tests reported in literature [3, 4, 14] are also included in the figure. The normalised Δy _max − k _n relationship is consistent with the measurements reported by various researchers.

Based on laboratory shearbox tests under the CNS condition, Lehane et al. [14] suggested a hyperbolic relationship between Δy _max and k _n:

$$ \frac{{\Updelta y_{\hbox{max} } }}{{\Updelta y_{\hbox{max} }^{*} }} = \frac{1}{{1 + \left( {{{k_{\text{n}} }}/{{k_{\text{nref}} }}} \right)^{0.75} }} $$

(5)

where k _nref of 500 kPa/mm was suggested by Lehane et al. [14]. The two factors (k _nref and the index 0.75) were calibrated based on test results from UWA sand with relative density of 85 % and initial normal stress of 40 kPa. As shown in Fig. 8b, Eq. (5) also gives reasonable dependence of normalised Δy _max on k _n for a variety of soils.

In this study, Eq. (4) is proposed to estimate normal stress change $\Updelta \sigma_{\text{n}}^{\prime }$ for a given interface, based on computed results from the simulated shearbox tests. For engineering practice, $\Updelta \sigma_{\text{n}}^{\prime }$ is directly related to shaft resistance of a pile [as given by Eq. (1)] and is more relevant than Δy. Therefore, the CV simulation tests were carried out to obtain a limiting normal stress increment ($\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$) for a given state of soil. This limit is then used in the proposed relationship by Eq. (4) to obtain $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ for a given pile–soil interface.

5 Application of the DEM results to pile shaft resistance

5.1 Estimation of pile shaft resistance

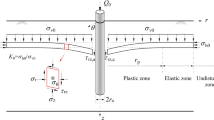
Computed results from the DEM simulations are applied to estimate shaft resistance of piles. The centrifuge tests reported by Zheng et al. [25] provide useful data to illustrate the application of this DEM study. The centrifuge modelling included load tests on 16-mm-diameter (1.6 m in prototype) single piles in dry Toyoura sand with a relative density of about 65 %, at an acceleration of 100 g [25]. Toyoura sand is rather uniform with a uniformity coefficient U (= D ₆₀/D ₁₀) of 1.7 [8]. A granular material with U of less than 10 is regarded as uniformly graded in practice [2]. It should be noted that same size particles are used in the DEM study. The effects of different particle size distributions are not considered. However, as shown in Fig. 8b, the normalised interface expansion (Δy _max/$\Updelta y_{\hbox{max} }^{*}$) for a given pile–soil interface is applicable to various soils reported by different researchers. The interface of each pile in centrifuge tests was made fully rough by bonding sand grains to pile shaft. The measured normalised roughness R _n of the pile interface was 0.21, implying the pile interface is substantially rough [4, 11].

Figure 9a shows the measured unit shaft resistance along three single piles, which modelled conventional pile load test at ground surface [25]. Each pile was 500 mm in length (50 m in prototype), with the upper 200 mm of pile shaft sleeved. Limit shaft resistances of the piles are calculated with and without considering the contribution of $\Updelta \sigma_{\text{n}}^{\prime }$. The results are shown in the figure. For the calculation without considering $\Updelta \sigma_{\text{n}}^{\prime }$, normal stress is estimated as $K_{0} \sigma_{\text{v}}^{\prime }$, where K ₀ is the coefficient of lateral earth pressure and $\sigma_{\text{v}}^{\prime }$ is the vertical effective stress. The friction angle of the interface is assumed the same as the angle of friction at critical state ($\phi_{\text{cv}}^{\prime }$ = 31°) of Toyoura sand [8]. As expected, without considering $\Updelta \sigma_{\text{n}}^{\prime }$, the calculated shaft resistance is in general considerably lower than the measured results. The measured data are a bit scattered because unit shaft resistance is obtained by numerical differentiation from measured axial loads in each pile.

Fig. 9

Comparison between measured and calculated unit shaft resistance of a sleeved piles tested at ground surface and b piles subjected to stress relief due to excavation

On the other hand, the calculation considering $\Updelta \sigma_{\text{n}}^{\prime }$ agrees reasonably well with the measured data. The proposed $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$−k _n relationship in Eq. (4) is used to estimate the contribution of $\Updelta \sigma_{\text{n}}^{\prime }$. The limit value $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ of 208 kPa is taken from the CV test on medium-dense sample with e ₀ of 0.23 and $\sigma_{{{\text{n}}0}}^{\prime }$ of 250 kPa, according to average stress level on the piles in centrifuge tests. k _n is calculated from the equivalent linear shear modulus (G) of the sand and pile diameter (D _p). Very small strain shear modulus (G _max) of Toyoura sand is estimated from Tatsuoka et al. [20]. Degradation of shear modulus with cavity strain (= 2Δy _max/D) is considered by a hyperbolic relationship from Hardin and Drnevich [6]. The value of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ can be calculated for a given depth. As shown in the figure, the calculated result with $\Updelta \sigma_{\text{n}}^{\prime }$ considered generally agrees with the measured shaft resistance of each pile.

Figure 9b shows the measured shaft resistances of three piles tested at the formation level of a 200-mm-deep (20 m in prototype) excavation [25]. Each pile was 300 mm in length and was subjected to stress relief due to excavation. Two calculations are also shown in the figure. For the calculation without considering $\Updelta \sigma_{\text{n}}^{\prime }$, normal stress is estimated as $K_{0}^{OC} \sigma_{\text{v}}^{\prime }$, where $\sigma_{\text{v}}^{\prime }$ is the vertical effective stress after excavation and $K_{0}^{OC}$ is related to the overconsolidation ratio (OCR) [17]: $K_{0}^{OC} = K_{0}^{NC} \cdot {\text{OCR}}^{\sin \phi^{\prime} }$. As expected, the calculated unit shaft resistances are generally lower than the measurements.

For the calculation with $\Updelta \sigma_{\text{n}}^{\prime }$ considered, the proposed $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$– k _n relationship in Eq. (4) is used with $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$of 252 kPa from CV test on sample with e ₀ of 0.23 and $\sigma_{{{\text{n}}0}}^{\prime }$ of 100 kPa. As shown in the figure, the calculated shaft resistance seems to be higher than the measured data at the upper half of each pile, but it is lower than the measurements at the lower half. Although the calculated and measured values do not match perfectly, it is demonstrated that the contribution of $\Updelta \sigma_{\text{n}}^{\prime }$ is critical to pile shaft resistance.

The calculated shaft resistances are integrated along pile shaft to obtain axial load distribution of each pile. The results are shown in Fig. 10a, b, for piles tested without and with stress relief due to excavation, respectively. Measured results from the centrifuge tests are also shown in the figures. The calculated axial loads considering $\Updelta \sigma_{\text{n}}^{\prime }$ show substantial improvement and may be considered as good estimation for the axial load distribution along each pile. The calculated axial loads in Fig. 10b are obtained by numerical integration from unit shaft resistance, which is shown previously in Fig. 9b. The two figures are based on the same set of data, but it seems there is apparent inconsistency between the two. The apparent difference is because numerical integration does not magnify any error calculated in unit shaft resistance at the upper and lower halves of each pile shown in Fig. 9b.

Fig. 10

Comparison between measured and calculated axial loads along a sleeved piles tested at ground surface and b piles subjected to stress relief due to excavation

5.2 Influence of pile diameter on shaft resistance

Given the same state of soil at the interface, the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ is limited when k _n is low, as shown in Fig. 8a. An extreme case is the CNL condition, in which the interface soil is free to dilate, but normal stress on the interface remains constant. Based on Eq. (2), it can be easily deduced that the confined dilation issue becomes insignificant when stiffness of constraining soil is low.

For a pile with large diameter, the contribution of $\Updelta \sigma_{\text{n}}^{\prime }$ is limited due to the inverse relationship of k _n with pile diameter, as illustrated by Eq. (2). Figure 11 shows the deduced relationship between $\Updelta \sigma_{\text{n}}^{\prime }$ and pile diameter (D) from Eq. (4). The values of $\Updelta \sigma_{\text{n}}^{\prime }$ are obtained from medium-dense samples (e ₀ = 0.23). At initial normal stress of 100 kPa, the computed $\Updelta \sigma_{\text{n}}^{\prime }$ decreases from 248 kPa for a 16-mm-diameter model pile to 41 kPa for a pile 1.0 m in diameter. Clearly, the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ for a full-scale pile is much smaller than that for a model pile in centrifuge. Such scale effect for pile shaft resistance has been demonstrated and reported by several researchers [5].

Fig. 11

Dependence of $\Updelta \sigma_{\text{n}}^{\prime }$ on pile diameter

6 Summary and conclusions

The study is to investigate key parameters controlling shaft resistance of a pile subjected to loading or stress relief in dilatant soils. A numerical parametric study using the distinct element modelling (DEM) is presented and discussed. The input parameters and modelling procedure were verified by experimental data from laboratory element tests. DEM shearbox tests were conducted under the constant normal stiffness (CNS), constant normal load (CNL) and constant volume (CV) boundary conditions. Key parameters including initial normal stress, void ratio, normal stiffness constraining the interface and loading–unloading history are investigated. Given the complexity of the problem, the simplified analysis does not consider shape and size of soil particles, which may also affect the normal stress on a given interface. By comparing measured results from centrifuge model tests and the computed results from DEM study, the following conclusions may be drawn:

• 1. Responses of a given pile–soil interface are governed by state of the interface soil including density (e ₀) and normal stress ($\sigma_{{{\text{n}}0}}^{\prime }$). Soil state affects the mobilised stress ratio ($\tau /\sigma_{\text{n}}^{\prime }$), normal stress increment ($\Updelta \sigma_{\text{n}}^{\prime }$) and normal displacement (Δy) of the interface. An increase in $\sigma_{n0}^{\prime }$ from 100 to 400 kPa leads to a 30 % reduction in magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$. An increase in e ₀ from 0.18 to 0.30 reduces $\Updelta \sigma_{\text{n}}^{\prime }$ by more than 90 %, and therefore, shaft resistance is much lower for piles in loose sands.

• 2. Dilation of a pile–soil interface is also influenced by confinement from the constraining soil. Given the same soil state, the magnitude of $\Updelta \sigma_{\text{n}}^{\prime }$ increases by about 100 % when the normal stiffness k _n increases from 1,000 to 10,000 kPa/mm, as the interface is more constrained. An upper limit of $\Updelta \sigma_{\text{n}}^{\prime }$ is reached when k _n is about 10,000 kPa/mm and is close to that obtained from a corresponding CV test.

• 3. A unique elliptical relationship (i.e. Eq. 4) between the normal stress increment and cavity stiffness constraining the interface is established. The magnitude of $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ for a given pile–soil interface can be quantified in terms of state of the interface soil (e ₀, $\sigma_{{{\text{n}}0}}^{\prime }$) and the stiffness constraining the interface (k _n). Normal displacement of a given interface can be deduced.

• 4. The proposed equation for $\Updelta \sigma_{{{\text{n}},\hbox{max} }}^{\prime }$ is applied to estimate the shaft resistance of piles with and without the effects of stress relief due to excavation. The calculated shaft resistances agree reasonably well with the measured results from centrifuge tests.

Appendix: verification of DEM model parameters based on laboratory shearbox tests

Laboratory shearbox tests were performed to verify the input parameters and modelling procedure used in the DEM study. Computed results were compared with measurements from these tests under the CNL boundary conditions. Each laboratory test was performed on Toyoura sand sample, 70 mm diameter and 40 mm thick. Relative density of the sample was 65 %. Constant normal stresses of 100 and 400 kPa were adopted.

Figure 12a compares measured and computed relationships of stress ratio and shear strain. The computed peak stress ratio under normal stress of 100 kPa is 1.0 at a shear strain of about 4 %. Although the peak stress ratio is higher than that measured from laboratory test, the computed results capture the general trend of the experimental data. Considering the simplified model used in the DEM analysis, the computed and measured stress ratios agree fairly well. Figure 12b shows the comparisons of normal displacement from laboratory tests and the DEM study. The consistency between computed and measured results in both figures suggests that the input parameters and modelling procedure of DEM study adopted are reasonable.

Fig. 12

Comparison between computed results from DEM study and measurements from laboratory element tests under CNL condition: a mobilised stress ratio and b normal displacement