1 Introduction

The mechanical behaviour of broken rock is different for unweathered or weathered grains. The degree of geological disintegration, by chemical weathering or by the intensity and the orientation of micro-cracks, has a significant influence on the solid hardness and as a consequence on the evolution of grain abrasion and grain breakage. Furthermore, for rockfills with coarse-grained and uniform particles under stress, the contact forces between particles are much higher than in a well-graded granular material. Thus, grain abrasion caused by the plastification of the contact zones and grain crushing related to the progressive development of micro-cracks are usually more pronounced in coarse-grained rockfills, e.g. [29, 37]. Grain abrasion and grain crushing change the grain size distribution and consequently the limit void ratios of the material. They may also have an influence on the mechanical properties. Depending on the state of weathering the propagation of micro-cracks due to water-induced stress corrosion can be strongly influenced by a change of the moisture content of the grain material. Thus, the mechanical properties of weathered broken rock are different for dry and wet states of the material, e.g. [1, 16, 26, 35, 36]. For weathered rockfill materials the compressibility is higher for a wet than for a dry material as illustrated in Fig. 1. The magnitude of deformation caused by wetting is mainly influenced by the degree of weathering and the chemical reaction with water, the grain size, grain angularity and grain size distribution, the stress level and precompaction. While the stress–strain relations during loading under dry condition or under constant moisture content of granular materials with stable grains may be rate independent, the additional settlement caused by the degradation of the solid hardness is usually a time-dependent process and, under constant load, it is called creep. The present paper considers the case that the time-dependent process of both creep deformation and stress relaxation is initiated by the change of the relative moisture content of the grain material. In this context it is worth mentioning that the moisture content here refers to the water filling the cracks and pores penetrating the surface of the weathered grains. Another effect of partly saturated materials on the mechanical behaviour is related to the inter-particle capillary forces. For coarse-grained rockfills the effect of inter-particle capillary forces on the mechanical behaviour is insignificant and it is neglected in the present paper. For a pre-compressed material under dry conditions (path A–D in Fig. 1), a following wetting under constant pressure leads to an additional compaction (path D–E in Fig. 1b) while wetting under constant volume leads to a stress relaxation (path D–F in Fig. 1c). For mixed boundary conditions both effects can appear simultaneously. Following creep and/or stress relaxation, a continuing loading leads to the stress–volumetric strain curve (path E–C, or path F–C), which follows the curve A–C obtained for an initially wet material, i.e. the memory of the material of the pre-compaction under dry conditions is swept out if the stress–volumetric strain curve obtained for the wet material (path A–C) starts from the same initial density, e.g. [26]. The mechanical properties are also influenced by the initial density of the material as shown for instance in Fig. 2 for triaxial compression tests carried out with weathered broken granite, e.g. [26]. The results obtained for dry and the water-saturated states of the material are different. For the initially loose material (Fig. 2a) the maximum mobilized friction angle is lower and the volume strain is more pronounced than it is observed for the initially dense material (Fig. 2b).

Fig. 1
figure 1

Compression behaviour of weathered broken rock. a Stress–volumetric strain curve in dry and in wet states, b volumetric creep strain as a result of wetting, c stress relaxation as a result of degradation of the solid hardness

Full size image
Fig. 2
figure 2

Evolution of the mobilized friction angle ϕ m and the volume strain ɛ V versus axial strain ɛ22 of dry (solid curve) and water saturated (dashed curve) weathered broken granite under triaxial compression [26]. a Initially loose state of the material, b initially dense state of the material

Full size image

The focus of the present paper is on modelling the essential mechanical properties of weathered and water-sensitive rockfill materials using a continuum approach. In particular, the concept of hypoplasticity is used to take into account the influence of pressure, density, state of weathering and the rate of deformation on the non-linear and inelastic stress strain behaviour. Originally the concept of hypoplasticity was developed to describe the behaviour of sand with stable grains, e.g. [4–6, 17, 28, 32, 42, 45–47]. For the numerical modelling of the evolution of shear strain localization, a non-polar hypoplastic model was extended to a micro-polar model which takes into account particle rotation, couple stresses and the mean grain diameter as a characteristic length, e.g. [9, 10, 12, 23, 39]. Recently, the model has also been extended to clayey soil, e.g. [2, 24, 30, 43]. Hypoplastic models have also been used to solve boundary value problems, e.g. [7, 19, 21, 25, 40, 41]. The present extension to weathered rockfill materials represents another application of the concept of hypoplasticity to the modelling of a particular class of granular materials. In this paper, a moisture-dependent solid hardness is introduced as a key parameter to model the influence of wetting of water-sensitive rockfill materials on the reduction of the resistance to compaction and shearing. Herein, the solid hardness is related to the grain assembly in the sense of a continuum description and does not mean the hardness of an individual grain. The modelling of weathered rockfill materials using a moisture-dependent solid hardness was first proposed by Bauer and Zhu [8]. In [14], the hypoplastic model by Bauer [4] and Gudehus [17] was extended with a moisture-sensitive solid hardness and an additional term for modelling creep and stress relaxation, which was not taken into account in earlier publications [8, 11, 13]. This additional term is a function of the stress, the solid hardness and the rate of the solid hardness. The present version permits the modelling of different creep and stress relaxation intensities for their isotropic and deviatoric parts. In contrast to the visco-hypoplastic relations [20, 27, 33, 44], the magnitude of the stretching rate does not influence the incremental stiffness as long as the solid hardness remains unchanged. The hypoplastic constitutive equation for the evolution of the stress is based on non-linear tensor-valued functions depending on the current void ratio, stress, deformation rate, moisture-dependent solid hardness and rate of degradation of the solid hardness. The model is able to describe inelastic material properties, a pressure-, density- and moisture-dependent incremental stiffness and peak friction angle, strain softening and critical states. As the hypoplastic concept does not need to distinguish between elastic and plastic deformation, the calibration of the constitutive constants is quite easy. General aspects of calibration of hypoplastic models are outlined in more details for instance by [4, 22, 38].

The paper is organized as follows. In Sect. 2, the compression behaviour of an isotropic compressed weathered rockfill material is modelled for dry and wet states. It is shown that a transition from the dry state to the wet state can be captured with a moisture- and time-dependent solid hardness. Moreover, it is also shown that a change of the limit void ratios as a result of the disintegration process of the rockfill material can also be modelled in a consistent manner. For general deformation paths, the degradation of the solid hardness is embedded in the concept of hypoplasticity (Sect. 3). In particular, a hypoplastic model by Bauer [4] and Gudehus [17], which was originally developed for unweathered granular materials, is extended to moisture-sensitive weathered coarse-grained rockfills. In Sect. 4, it is demonstrated that for weathered broken granite under isotropic compression and triaxial compression the model also captures the essential mechanical properties for a transition from dry to water-saturated states.

2 Solid hardness and limit void ratios

2.1 Isotropic compression of dry rockfill material

In the following the isotropic compression behaviour is first discussed for a dry granular material and modelled using a relation between the void ratio e and the mean effective pressure \(p=-(\sigma_{11}+\sigma_{22}+\sigma_{33})/3 \) of the grain skeleton. In particular, the decrease of e with an increase of p is modelled by the following exponential function proposed by Bauer [3]:

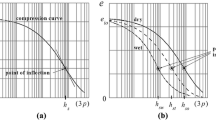
$$ e = e_0\;\hbox{exp}\left[ -\left({\frac{3 p} {h_s}}\right)^{n} \right]. $$
(1)

Herein, the constant e 0 denotes the void ratio for p≈0, h s has the dimension of stress and n is a dimensionless constant. The quantity h s was called granular hardness in some previous publications about hypoplasticity, e.g. [4, 17]. Recently, the term solid hardness was used by Gudehus [20] to express in a more appropriate way the relation to the stiffness of the grain aggregate under isotropic compression, which should be distinguished from the hardness of an individual grain. Experimental investigations show that the quantity h s reflects the isotropic pressure where grain crushing becomes dominant. More precisely, h s represents the isotropic pressure (3p) at which the compression curve in a semi-logarithmic representation shows the point of inflection while the exponent n is related to the inclination of the corresponding tangent (Fig. 3). For high pressures the void ratio in Eq. 1 tends to zero, which can be explained by continuing grain plastification and grain crushing. Equation 1 is consistent within a very wide pressure range with the exception of states p→∞, which are characterized by a phase transition of the material.

Fig. 3
figure 3

Isotropic compression relation according to Eq. 1 in a semi-logarithmic representation

Full size image

2.2 Pressure dependence of the limit void ratios

It is evident that under the same pressure cohesionless granular materials can show different packing densities of the grain assembly so that the void ratio can range between a maximum void ratio e i and a minimum void ratio e d as shown in Fig. 4 in the so-called phase diagram of grain skeletons [18]. The upper bound, e i , can be related to an isotropic compression starting from the loosest skeleton with grain contacts, i.e. for a cohesionless granular material there exists no homogeneous deformation which goes beyond e = e i . In particular, Eq. 1 is used to model the pressure dependence of e i under isotropic compression. The minimum void ratio e d can be achieved by cyclic shearing with very low amplitudes and a nearly fixed mean pressure. Large monotonic shearing leads to a stationary state, which is characterized by a constant stress and constant void ratio. The void ratio in such a limit state, which is called critical void ratio e c , also decreases with the pressure p. The maximum void ratio e i , the minimum void ratio e d and the critical void ratio e c are related to the mean pressure according to [17]:

$$ {\frac{e_i}{e_{i0}}}={\frac{e_d}{e_{d0}}}={\frac{e_c}{e_{c0}}}=\hbox{exp} \left[ -\left({\frac{3 p}{h_s}}\right)^{n} \right] , $$
(2)

where e i0, e d0 and e c0 are the corresponding values for p≈0 as shown in Fig. 4. Although the pressure dependence of the minimum void ratio and the critical void ratio is described in Eq. 2 by functions similar to the one in Eq. 1, it is important to note that only the maximum void ratio e i can be related to an isotropic compression. Thus with the data from an isotropic compression test starting from the initial maximum void ratio e i0 the quantities h s and n can be approximated using Eq. 1 [4]. The quantities for e d0 and e c0 are obtained with conventional index tests [22]. Thus the pressure dependence of the limit void ratios and the critical void ratio according to Eq. 2 is fully determined by the data of a single isotropic compression test and two conventional index tests.

Fig. 4
figure 4

Phase diagram of grain skeletons. Pressure dependence of the maximum void ratio e i , the minimum void ratio e d and the critical void ratio e c according to Eq. 2

Full size image

2.3 Degradation of the solid hardness for wet rockfill material

As illustrated in Fig. 5 the compressibility of weathered rockfill materials is higher for the wet material (dashed curve) than for the dry material (solid curve). The higher compressibility of the wet material can be explained by the degradation of the stiffness of the solid material due to the reaction with water, which leads to grain abrasion and grain breakage and consequently to a rearrangement of particles into a denser state.

Fig. 5
figure 5

Influence of the degradation of the solid hardness on the compression behaviour

Full size image

In order to model the influence of disintegration of the stiffness of a stressed rockfill due to the reaction with water, the constant solid hardness h s in Eq. 1 is replaced by the moisture- and history-dependent state quantity h st . In experiments, e.g. [34], it can be observed that under very low pressures a change of the moisture content does not lead to an additional compaction so that the assumption is made that the void ratio e 0 in Eq. 1 remains unaffected by a change of the moisture content. Then the generalized isotropic compression relation reads:

$$ e= e_0\;\hbox{exp}\left[ -\left({\frac{3 p}{h_{st}}}\right)^{n} \right] , $$
(3)

where the current state of the solid hardness, h st , ranges within h sw  ≤ h st  ≤ h so . Herein, the upper limit h so is the solid hardness before wetting and the lower limit h sw  = h sw (w) is the final degraded quantity depending on the relative moisture content w of the grains. For the sake of simplicity, the exponent n in Eq. 3 is assumed to be independent on a change of the moisture content. Furthermore, it is assumed that the degradation of the solid hardness is irreversible and time dependent, i.e. \(\hbox{d}{h}_{st}/\hbox{d}t=\dot{h}_{st}< 0 \) and h st  = h st (t) is a function of the degradation time t. Thus the time derivative of Eq. 3 yields:

$$ \dot{e}= n e \left({\frac{3 p}{h_{st}}} \right)^n \left[{\frac{\dot{h}_{st}}{h_{st}}} - {\frac{\dot{p}}{p}} \right]. $$
(4)

Herein, \(\dot{e}, \dot{h}_{st}\) and \(\dot{p}\) denote the time derivatives of e, h st and p, respectively. Assuming a constant grain density, the balance equation of mass leads to a relation between the rate of the void rate, \(\dot{e},\) and the volumetric strain rate, \(\dot{\varepsilon}_V,\) i.e. the following relation can be derived:

$$ \dot{e} =(1+e) \dot{\varepsilon}_{v}. $$
(5)

Equation 5 also holds in the case of grain abrasion and grain breakage. Substituting Eq. 5 into Eq. 4 yields for the volumetric strain rate under isotropic compression:

$$ \dot{\varepsilon}_V= {\frac{n e}{1+e}} \left({\frac{3 p}{h_{st}}} \right)^n \left[{\frac{\dot{h}_{st}}{h_{st}}} - {\frac{\dot{p}} {p}} \right]. $$
(6)

For the special case that during degradation of h st the pressure is kept constant, i.e. \(\dot{p}=0,\) Eq. 4 yields for the rate of the void ratio during the process of creep:

$$ \dot{e}=n e \left({\frac{3 p}{h_{st}}} \right)^n {\frac{\dot{h}_{st}}{h_{st}}}, $$
(7)

and Eq. 6 yields for the volumetric strain rate:

$$ \dot{\varepsilon}_V= {\frac{n e}{1+e}} \left({\frac{3 p}{h_{st}}} \right)^n {\frac{\dot{h}_{st}}{h_{st}}}. $$
(8)

Equation 8 indicates that the velocity of compaction, i.e. the volumetric strain rate, is proportional to the velocity of the degradation of the solid hardness and it is also influenced by the pressure level and the current void ratio. The corresponding creep function can be obtained by integration of Eq. 7 or 8. In particular, for the initially dry material with a solid hardness h so pre-compressed up to mean pressure \({p}^{*}\) and void ratio \({e}^{*}\), wetting under \({p}^{*}\)= const. leads to a progressive degradation of the solid hardness accompanied by a reduction of the void ratio according to:

$$ e= e^*\;\hbox{exp}\left[-( h_{so}^n-h_{st}^n ) \left({\frac{3 p^*} {h_{so} h_{st}}}\right)^n \right]. $$
(9)

For the final state, i.e. h st (t→∞) = h sw , the void ratio reaches the value:

$$ e= e^*\;\hbox{exp}\left[-( h_{so}^n-h_{sw}^n ) \left({\frac{3 p^*} {h_{so} h_{sw}}}\right)^n \right]. $$
(10)

Under constant volume, i.e. \(\dot{e}=0,\) Eq. 4 yields for stress relaxation:

$$ \dot{p}= p {\frac{\dot{h}_{st}}{h_{st}}}. $$
(11)

Starting the degradation of the solid hardness from h so and the pre-compaction pressure \({p}^{*}\), the integration of Eq. 11 yields for the process of stress relaxation:

$$ {p}= p^* {\frac{{h}_{st}}{h_{so}}}. $$
(12)

For the final state, i.e. h st (t→∞) = h sw , the relaxated pressure reaches the value:

$$ {p}= p^* {\frac{{h}_{sw}}{h_{so}}}. $$
(13)

It follows from Eq. 13 that the amount of stress relaxation, i.e. \(p^*-p=p^*(1-h_{sw}/h_{so}),\) is proportional to the magnitude of the pre-compression pressure \({p}^{*}\) and it increases with a decrease of the final state of moisture-dependent solid hardness h sw .

If a reaction with water takes place, the process of degradation of the soil hardness is modelled by the following evolution equation:

$$ \dot{h}_{st}= h_{so} \dot{\psi}_t. $$
(14)

Herein, the rate of the solid hardness, \(\dot{h}_{st},\) is proportional to the solid hardness h so for the initial state of the material and scaled by the rate of the disintegration factor ψ t , which is a function of the current state of degradation ψ t and the change of the moisture content w, i.e. \(\dot{\psi}_t= \dot{\psi}_t(\psi_t , w).\) For a more refined modelling, function \(\dot{\psi}_t\) can also be extended with a threshold stress to introduce a minimum stress level at which h so starts to degrade when the moisture content of the material changes. In this paper, the following evolution equation for the disintegration factor ψ t is used:

$$ \dot{\psi}_t=-{\frac{1}{c}} (\psi_t-\psi_w). $$
(15)

Herein, c has the dimension of time and scales the velocity of degradation. The values of the final solid hardness, h sw , and of the disintegration factor, \(\psi_w=h_{sw}/h_{so},\) depend on a given relative moisture content w. In Eq. 15, the rate of disintegration is assumed to be proportional to the difference between ψ t and ψ w . Thus with continued degradation the rate of the disintegration factor decreases and it vanishes when the process of degradation is completed, i.e. for the final state \( \psi_t(t \rightarrow\infty)=\psi_w, \dot{\psi}_t=0 \) and \( \dot{h}_{st}(t \rightarrow\infty)= h_{so} \dot{\psi}_t(t \rightarrow\infty)=0 \) holds. Then the solid hardness h st is equal to h sw . Starting the degradation from t = 0 and ψ t  = 1 for the initial state of the material, the integration of Eq. 14 with respect to Eq. 15 yields:

$$ h_{st}=h_{sw}+(h_{so}-h_{sw})\;\hbox{exp}\left[ -{t}/{c}\right]. $$
(16)

Equation 16 describes an exponential decrease of the solid hardness from the initial value h so to the final value h sw with an increase of the degradation parameter t/c. The constitutive constant c can be calibrated from a creep test or stress relaxation test. Based on the experimental data e and p the (h st −t) diagram can be computed either from Eq. 9 for a creep test or from Eq. 12 for a stress relaxation test. For \(t=0, \dot{h}_{st}(t=0)\) represents the initial inclination of the degradation curve, so that

$$ c=-{\frac{h_{so}-h_{sw}}{\dot{h}_{st}(t=0)}}. $$
(17)

As \(\dot{h}_{st}< 0\) and h so  > h sw , the value of c is positive.

It is obvious that with a degradation of the solid hardness, the pressure-dependent limit void ratios and the critical void ratio are lower for ψ w  < 1 as illustrated by the dashed curves in Fig. 6. In particular for the current solid hardness h st  < h so , Eq. 2 can be rewritten to:

$$ {\frac{e_i}{e_{i0}}}={\frac{e_d} {e_{d0}}}={\frac{e_c}{e_{c0}}}= \hbox{exp}\left[ -\left({\frac{3 p}{h_{st}}}\right)^{n} \right] , $$
(18)
Fig. 6
figure 6

Influence of the degradation of the solid hardness on the limit void ratios. Solid curves are related to h so and ψ t  = 1, dashed curves are related to h st  < h so and ψ t  < 1

Full size image

3 Hypoplastic modelling

For general stress paths, the moisture- and rate-dependent solid hardness and limit void ratios proposed in Sect. 2.3 were embedded in the hypoplastic model by Bauer [4] and Gudehus [17]. In particular for \(\dot{h}_{st}< 0\) the extended constitutive equations read:

$$ \begin{aligned} {\mathop\sigma\limits^{_{{\circ}}}}_{ij} &= f_s \Big[ \hat{a}^2 \dot{\varepsilon}_{ij} + (\hat{\sigma}_{kl} \dot{\varepsilon}_{kl}) \hat{\sigma}_{ij} + f_d \hat{a} ( \hat{\sigma}_{ij} + \hat{\sigma}^*_{ij} ) \sqrt{\dot{\varepsilon}_{kl} \dot{\varepsilon}_{kl}} \Big] \\ &\quad +{\frac{\dot{h}_{st}}{h_{st}}} \left({\frac{1} {3}}\sigma_{kk} \delta_{ij} +\kappa {\sigma}^*_{ij}\right) , \end{aligned} $$
(19)
$$ \dot{h}_{st}= h_{so} \dot{\psi}_t $$
(20)
$$ \dot{\psi}_t=-{\frac{1}{c}} (\psi_t-\psi_w) , $$
(21)
$$ \dot{e} =(1+e) \dot{\varepsilon}_{v}. $$
(22)

Herein, \({\mathop\sigma\limits^{_{{\circ}}}}_{ij}\) is the effective objective stress rate, σ ij the effective Cauchy stress, \({\sigma}^*_{ij} = {\sigma}_{ij} - {\sigma}_{kk}\delta_{ij}/3 \) is the deviatoric part, \(\hat{\sigma}_{ij} = \sigma_{ij}/\sigma_{kk} \) and \( \hat{\sigma}^*_{ij} = \hat{\sigma}_{ij} - \delta_{ij}/3 \) are normalized quantities, δ ij is the Kronecker delta, \(\dot{\varepsilon}_{ij}\) is the strain rate, \(\dot{h}_{st}\) and \(\dot{\psi}_t\) are the rate of solid hardness and the rate of the disintegration factor, respectively, \( \dot{e} \) is the rate of void ratio, and \( \dot{\varepsilon}_{v}=\dot{\varepsilon}_{kk} \) the volumetric strain rate. In contrast to earlier models for weathered rockfill materials, e.g. [15], the present version also takes into account the influence of the deviatoric part of the stress tensor in the last term on the right-hand side of Eq. 19. Herein, the constant κ controls the intensity of the creep velocity or the stress relaxation velocity which can deviate from that of the isotropic part. For κ = 1 the term reduces to \((\dot{h}_{st}/h_{st}) \sigma_{ij} \) and for κ = 0 one obtains the term \((\dot{h}_{st}/h_{st}) \sigma_{kk} \delta_{ij}/3\) wich is the same as proposed in [15].

For states where the degradation of the solid hardness has been completed, i.e. \(\dot{h}_{st}=0\), function \( \hat{a}\) in Eq. 19 is related to critical stress states which can be reached asymptotically under large shearing. Then function \( \hat{a} \) can be represented with respect to the limit condition by Matsuoka and Nakai [31] in the hypoplastic model as shown by Bauer [5]:

$$ \hat{a} = {\frac{\sin \varphi_c}{3 + \sin \varphi_c}} \left[ \sqrt{\frac{8/3 - 3 (\hat{\sigma}^{*}_{kl} \hat{\sigma}^{*}_{kl}) + g \sqrt{3/2} (\hat{\sigma}^{*}_{kl} \hat{\sigma}^{*}_{kl})^{3/2}}{ 1+ g \sqrt{3/2} (\hat{\sigma}^{*}_{kl} \hat{\sigma}^{*}_{kl} )^{1/2}}} + \sqrt{\hat{\sigma}^{*}_{kl} \hat{\sigma}^{*}_{kl}} \right] , $$
(23)

with

$$ g=-\sqrt{6}\;{\frac {\hat{\sigma}_{kl}^{*} \hat{\sigma}_{lm}^{*} \hat{\sigma}_{mk}^{*}}{(\hat{\sigma}_{pq}^{*} \hat{\sigma}_{pq}^{*} )^{3/2} }}. $$

Herein, φ c denotes the intergranular friction angle defined for the critical state under triaxial compression. For critical states, which are defined for \({\mathop\sigma\limits^{_{{\circ}}}}_{ij}=0,\; \dot{\varepsilon}_V=0\) and \(\dot{h}_{st}=0\) under a fixed strain rate \(\dot{\varepsilon},\) factor \(\hat{a}=\hat{a}_c\) and it is equal to the Euclidean norm of the normalized stress deviator as illustrated in Fig. 7. In this context it is worth noting that, for \(\dot{h}_{st}<0\) and a constant \(\dot{\varepsilon}_{ij},\) a simultaneous vanishing of the stress rate and the volume strain rate does not appear, i.e. a critical state cannot be reached during the degradation of the solid hardness. Furthermore, the present model assumes that the stress limit condition, and consequently also the critical friction angle \(\varphi_c,\) remains uneffected by the value of h st . This assumption is made because experimental results showing any clear influence of the critical friction angle on the state of degradation are missing. In contrast to the critical friction angle the influence of the state of the solid hardness on the peak friction angle is well modelled as illustrated for instance in [13].

Fig. 7
figure 7

Trace of the critical stress surface in the π-plane

Full size image

The influence of the mean effective pressure and the current void ratio on the response of the constitutive equation (19) is taken into account with the stiffness factor f s and the density factor f d . In particular, f d represents a relation between the current void ratio e, the critical void ratio e c and the minimum void ratio e d , i.e.

$$ f_d = \left({\frac{e-e_d}{e_c-e_d}} \right)^\alpha, $$
(24)

where α < 0.5 is a constitutive constant. It follows from Eq. 24 that the value of the density factor is: f d  < 1 for e < e c , f d  > 1 for e > e c and f d  = 1 for e = e c . The stiffness factor f s has the dimension of stress and can be decomposed into three parts, e.g. [6]:

$$ f_s=f_e\, f_s^* \,f_b $$
(25)

Herein, f e is the density-dependent part, which represents the ratio of the maximum void ratio e i to the current void ratio as proposed by Bauer [3]:

$$ f_e = \left({\frac{e_{i}}{e}}\right)^{\beta}, $$
(26)

wherein β is a constant. A lower void ratio e means a denser state of the material and consequently a higher value of f e and f s , i.e. the incremental stiffness increases. The meaning of the second part of f s in Eq. 25, i.e. f * s , was firstly discussed by von Wolffersdorff [42] with the empirical relation

$$ f_s^*={\frac{1}{\hat{\sigma}_{kl} \hat{\sigma}_{kl}}}. $$
(27)

f * s takes into account a decrease of the incremental stiffness with an increase of \((\hat{\sigma}_{kl} \hat{\sigma}_{kl}).\) The dependence of the incremental stiffness on the pressure p and the current state of the solid hardness h st is taken into account by factor f b in Eq. 25. As first proposed by Gudehus [17] for the hypoplastic model with a constant h st factor f b can be determined directly by comparing the compression relation (3) for the initial void ratio e 0 = e i0 with the constitutive equation (19). In detail, for the maximum void ratio e = e i , the rate of the pressure p under isotropic compression calculated from Eq. 3, i.e.

$$ \dot{p}= -{\frac{\dot{e}_i}{n e_i}} \left({\frac{h_{st}}{3}}\right)^{n} p^{ (1-n)} + {\frac{\dot{h}_{st}}{h_{st}}} p, $$
(28)

and from Eq 19, i.e.

$$ \dot{p}=-{\frac{1}{3}} f_{ei}\, f_{si}^* \,f_b\, h_i {\frac{\dot{e}_i}{(1+e_i)}} + {\frac{\dot{h}_{st}}{h_{st}}} p,$$
(29)

must coincide, where f ei  = 1, f * si  = 3,

$$ h_i= \hat{a}_i^2 + {\frac{1} {3}}-{\frac{\hat{a}_i}{\sqrt{3}}} \left({\frac{e_{i0}-e_{do}}{e_{c0}-e_{d0}}}\right)^{\alpha} , $$
(30)

and

$$ \hat{a}_i = \sqrt{\frac{8}{3}}\left({\frac{\sin\varphi_c} {3+\sin\varphi_c}}\right). $$
(31)

Thus, factor f b can be obtained as

$$ f_b= {\frac{1+e_i}{n h_i e_i}} \left({\frac{h_{st}}{3}}\right)^{n} p^{ (1-n)}. $$
(32)

With respect to Eqs. 25–27, 30–32, the stiffness factor f s depends on the current void ratio e, the pressure dependent limit void ratio e i , the initial values of the limit void ratios e i0 ,e d0 and e c0, the constants n, φ c , α and β, the normalized stress \(\hat{\sigma}_{kl},\) the moisture-dependent solid hardness h st and the mean effective stress p according to:

$$ f_s = \left({\frac{e_i}{e}} \right)^{\beta} {\frac{(1+e_i)} {n h_i e_i}} \left({\frac{h_{st}}{3}} \right)^n {\frac{p^{ (1-n)}} {(\hat{\sigma}_{kl} \hat{\sigma}_{kl})}}. $$
(33)

In Eqs. 24 and 33, the current void ratio e is related to the pressure and moisture-dependent maximum void ratio e i , minimum void ratio e d and critical void ratio e c according to Eq. 18.

It is obvious that with the consistency condition for the stiffness factor f s the volume strain rate in Eq. 6 is the same as the one obtained from the hypoplastic constitutive equation (19) for monotonic and homogeneous isotropic compressions starting from isotropic stress states, i.e. σ ij  = −p δ ij , and an initial void ratio of e 0 = e i0. During the process of degradation of the solid hardness, both creep and stress relaxation are described by Eq. 19. In particular for \({\mathop\sigma\limits^{_{{\circ}}}}_{ij}=0\) the components \(\dot{\varepsilon}_{ij}\) of the creep strain rate can be computed from the non-linear equation:

$$ \begin{aligned} 0 &= f_s \Big[ \hat{a}^2 \dot{\varepsilon}_{ij} + (\hat{\sigma}_{kl} \dot{\varepsilon}_{kl}) \hat{\sigma}_{ij} + f_d \hat{a} ( \hat{\sigma}_{ij} + \hat{\sigma}^*_{ij} ) \sqrt{\dot{\varepsilon}_{kl} \dot{\varepsilon}_{kl}} \Big] \\ &\quad+{\frac{\dot{h}_{st}}{h_{st}}} \left({\frac{1}{3}}\sigma_{kk} \delta_{ij} +\kappa {\sigma}^*_{ij}\right) , \end{aligned} $$
(34)

and for the condition of a vanishing strain rate, i.e. \(\dot{\varepsilon}_{ij}=0,\) the following relation for the rate of stress relaxation is obtained:

$$ {\mathop\sigma\limits^{_{{\circ}}}}_{ij} = {\frac{\dot{h}_{st}}{h_{st}}} \left({\frac{1}{3}}\sigma_{kk}\delta_{ij} +\kappa {\sigma}^*_{ij}\right). $$
(35)

Another special case is related to states where the degradation of the solid hardness caused by the change of the moisture content has been completed. For such states \(\dot{h}_{st}=0,\) the current moisture-dependent solid hardness is h sw and from Eq. 19 the rate-independent hypoplastic model by Bauer [4] and Gudehus [17] is recovered, i.e.

$$ {\mathop\sigma\limits^{_{{\circ}}}}_{ij} = f_s \Big[ \hat{a}^2 \dot{\varepsilon}_{ij} + (\hat{\sigma}_{kl} \dot{\varepsilon}_{kl}) \hat{\sigma}_{ij} + f_d \hat{a} ( \hat{\sigma}_{ij} + \hat{\sigma}^*_{ij} ) \sqrt{\dot{\varepsilon}_{kl} \dot{\varepsilon}_{kl}} \Big] , $$
(36)

It follows from Eq. 36 that the constitutive parameters φ c , n, e io , e co , e do , α, and β are not influenced by the degradation rate of the solid hardness. Thus, the calibration of these constants as well as h so can be carried out for the dry state of the material, i.e. for ψ = 1, as outlined in more detail for instance by [4, 22]. Only the parameters h sw , κ and c are related to the moisture-dependent granular hardness and to the degradation velocity. The calibration of h sw and c can be carried out based on an isotropic compression test under wet condition as outlined in Sect. 2. Parameter κ also depends on the value of parameter c and can be related to a creep test under triaxial conditions. The hypoplastic model proposed for weathered broken rock materials includes 11 constants. In the present paper, the calibration of the constants is based on experimental data obtained form weathered broken granite with a mean grain diameter of 20 mm under dry and water-saturated conditions. Isotropic and traxial compression tests with a specimen diameter of 800 mm and a specimen height of 800 mm were carried out by Kast [26] at the University of Karlsruhe in Germany. For the calibration some simplifications were assumed because of missing experimental data. In particular, the value of the solid hardness was determined for the dry state and the water-saturated state but not for partly saturated states of the material, κ was set to zero and the value of c was chosen arbitrarily. As the latter only scales the velocity of degradation of the solid hardness during the transition from the dry state to the wet state of the material, the value of c does not influence the final amount of creep deformation and stress relaxation. For the numerical simulations discussed in the next section, the following values were used: φ c  = 42°, h so  = 75 MPa, n = 0.6, e io  = 0.85, e co = 0.39, e do  = 0.2, α = 0.125, β = 1.05, h sw  = 25.5, κ = 0 and c = 12.

4 Comparison of numerical simulations with experiments

For numerical simulations the proposed constitutive model was implemented in the finite element code Abaqus. In the following the results obtained from numerical simulations of homogeneous isotropic and triaxial compression tests are compared with the corresponding experiments by Kast [26]. All simulations are conducted under drained conditions. The degradation of the solid hardness is initiated by saturation of the initially dry specimen. In this context water saturation means the water saturation of the weathered grains and also the water saturation of the void space between the grains. Neglecting the influence of the specific weight of the solid grains and of water, the effective stress is assumed to be equal to the total stress prescribed at the boundary of the specimen.

For isotropic pre-compaction under dry condition a change of the moisture content of the weathered grains initiates a process of degradation of the solid hardness, which is accompanied by creep deformation (Fig. 8). Further numerical simulations show that the amount of creep strain is higher for a higher degradation factor and higher pre-compression, which is also in agreement with experimental observations.

Fig. 8
figure 8

Comparison of the numerical simulation [15] of isotropic compression and creep (solid curve) with the experimental data (dots) reported in [26]

Full size image

Figures 9 and 10 show the numerical results obtained from the simulation of triaxial compression tests under a constant mean pressure of p = 0.8 MPa and the experimental results obtained for weathered broken granite. In particular for the loose material, an initially void ratio of e 0 = 0.418 for the dry state and e 0 = 0.387 for the saturated state is considered. As the initial void ratio is higher than the corresponding pressure-dependent critical one, i.e. for p = 0.8 MPa the critical void ratio e c  = 0.34 for the dry material and e c  = 0.31 for the saturated material, the triaxial compression leads to a further densification for both the dry material (Fig. 9a) and the saturated material (Fig. 9b). The increase of the mobilized friction angle ϕ m with the vertical strain ɛ22 is more pronounced for the dry material than for the saturated one, which is also in agreement with the experiments. In order to study the influence of an initially dense material, the experiments for triaxial compression starting from e = 0.29 for the dry material and e = 0.285 for the saturated solid material are compared with the prediction of the hypoplastic model in Fig. 10a, b. A comparison of Fig. 9 with Fig. 10 shows that the volume–strain behaviour is strongly influenced by the initial density and it differs for the dry and saturated states of the solid material. The additional densification is less pronounced and the maximum mobilized friction angle is higher for the initially dense material. A clear peak state for ϕ m can only be detected for the dry and initially dense material (Fig. 10a). After the peak the value of ϕ m slightly decreases with advanced vertical compression and it is accompanied by dilatancy. For the saturated and initially dense state of the material, the dilatancy is less pronounced.

Fig. 9
figure 9

Triaxial compression under a constant mean pressure starting from an initial void ratio of: a e 0 = 0.418 for the dry state (ψ = 1), b e 0 = 0.387 for the saturated state and ψ = 0.34 (solid curve prediction of the hypoplastic model [15], dots experimental results [26])

Full size image
Fig. 10
figure 10

Triaxial compression under a constant mean pressure starting from an initial void ratio of: a e 0 = 0.29 for the dry state (ψ = 1), b e 0 = 0.285 for the saturated state and ψ = 0.34 (solid curve prediction of the hypoplastic model [15], dots experimental results [26])

Full size image

The behaviour of saturation under a deviatoric stress is shown in Fig. 11. The test starts from the isotropic stress state of p =  0.8 MPa and it can be divided into three parts. In the first part the specimen is dry, i.e. ψ w  = 1, and it is vertically compressed up to the vertical strain of ɛ22 = −1%. Then the specimen is saturated, which leads to creep deformation, i.e. to an increase of the amount of vertical strain ɛ22 and the volumetric strain ɛ V . After the creep phase a continuing vertical compression leads to a further increase of the mobilized friction angle ϕ m and the compaction of the material. Figure 11 shows that the prediction of the numerical model is in good agreement with the experimental results.

Fig. 11
figure 11

Triaxial compression with saturation during the test (solid curve prediction of the hypoplastic model [15], dots experimental results by [26])

Full size image

5 Conclusions

A hypoplastic continuum model has been presented to describe the essential properties of weathered broken rock materials. In particular, an increase of the compressibility and a decrease of the limit void ratios with increasing moisture content of the solid material is modelled in a simplified manner using only a moisture-dependent solid hardness. Creep and stress relaxation are included in the model as predictions of the time-dependent process of degradation of the solid hardness. The comparison of the numerical simulation of an isotropic and a triaxial compression test with the experimental results shows that the model captures the essential properties of weathered rockfill materials for the dry and the water-saturated states of the weathered grains as well as for the transition between these two states.