1 Introduction

For the coming decade, a large number of unmanned lunar lander missions are planned by various nations. For example, NASA plans to create a network of geophysical stations on the lunar surface [21]. The Chinese Space Agency CNSA plans to deliver a rover on the Moon in the frame of the Chang’e 2 mission [14, 30]. Similar lunar surface activities are planned by the Japanese Space Agency JAXA [19], the European Space Agency ESA [8], and India’s Space agency ISRO. Most of these planned activities include drilling on the lunar surface and subsurface sampling. Therefore, it is of high interest to develop small and low power consuming drilling systems, which work well under the lunar environmental conditions.

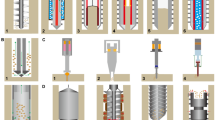
A major problem for any drilling design is to find a proper way to remove the drill debris particles. Figure 1 shows three different concepts for a drilling and sampling system.

Fig. 1
figure 1

Different concepts for drilling and sampling systems

Full size image

The most frequently used method is auger drilling (Fig. 1, left). Here, the way to get rid of the debris is to cut a screw-shaped path along the outer wall of the borestem. As the drill penetrates the material, the cut debris particles move upwards towards the surface along this spiral path. This mechanism works usually well as long as the borehole is not too deep and the ratio of depth to width is not too extreme. If one aims to retrieve drill cores, which remain also mechanically intact for later investigation, a corer (Fig. 1, middle) has to be used. In this case, only the bore debris from a thin cylindrical shell has to be removed; the bulk of the material is contained in the drill core and must be transported upwards and delivered in a storage box for later investigation by an additional retrieval device or by retracting the whole system from time to time. Usually, corers are mechanically complex and heavy, and their operation by a robotic system is also extremely challenging in terms of weight and volume compared to the simpler auger drilling. However, there is another alternative, which we will investigate in this paper, namely a so-called “suction drill” (Fig. 1, right).

With auger drilling, the deeper the drilling proceeds, the more difficult it becomes to remove the debris. This has several reasons:

  • First, there is always a friction between the borestem and the surrounding drillhole wall. This friction force increases linearly with depth even for a homogeneous material, since the “wetted surface” also increases linearly with depth.

  • Second, the overburden pressure of the material (i.e., the weight of the particles present in the spiral cut above the drillbit) also increases linearly with depth.

  • Third, there is another mechanism, which contributes to the friction between drillhole and borestem as the driller proceeds to a larger depth: because the particles form a granular assembly with little mutual cohesion (or better to say adhesion), they can more or less freely slide against each other. The particles residing in larger depth feel the weight of the overlying particles and therefore exert a force also in lateral directions (i.e., against the borestem and the drillhole wall).

The net effect of all these mechanisms is that, for a traditional rotating drill (auger, see Fig. 1, left), the turning moment that must be provided by the driving motor to proceed with the drilling process increases steadily as the drill hole becomes deeper. Even when the drill stem is prolonged step by step, the danger that the system gets stalled at some point rises with increasing depth. This problem is particularly severe when deep and narrow boreholes for subsurface investigations need to be created. Moreover, the process has to take place without direct human interaction and with a limited mass and power budget. This is the typical situation one has to deal with in an unmanned lunar or planetary lander mission.

To circumvent the problem, several alternatives are possible. First, in large drilling stations on Earth, like e.g. those used for subsurface mining or oil extraction, the drillhole can be made wide enough that additional mechanical devices can be installed inside to transport the bore debris out of the hole in regular time intervals. However, such systems are not suitable for robotic space applications, since they are too heavy, too complex, and too power-consuming. For unmanned explorer missions to Moon and Mars, as they are currently planned by the various space agencies noted above, the requirements and constraints for soil sounding with the help of drill holes may be summarized as follows:

  • Weight restriction for a deep drilling device (moderate design goal: 2 m depth) are typically of the order of 10–20 kg.

  • Power restrictions are typically of the order of 10–20 W.

  • Hole diameters should be a few centimeters maximum.

  • In most applications, two basically different types of investigation are desired: (1) in situ measurements in the borehole and (2) collection of the bore debris from different depths, either for analysis aboard the attached lander or for return to Earth.

In Sect. 2 the soil–mechanical and granular properties of the lunar regolith material are reviewed. In Sect. 3 we show a baseline design and discuss possible variants. In Sect. 4 we investigate the basic physics of such an application by formulating the associated hydrodynamic problem and presenting quantitative solutions to demonstrate the feasibility of the suggested approach from the hydrodynamic point of view. Nitrogen gas (N2) is used as the driver gas because of its inert properties. Section 5 gives an estimate of the expected transport capacity for the bore debris particles, and in Sect. 6 the problem of gas diffusion through the surrounding regolith is addressed. Finally, we discuss the advantages and possible disadvantages of the use of the proposed suction drill in a lunar or other planetary environment. The Moon as well as Mars and Venus are possible targets for the application of such a drilling/sampling technique in the foreseeable future. Further interesting objects could be asteroids and comet nuclei, but also terrestrial applications may emerge.

2 Grain sizes and soil–mechanical properties

Most of the presently existing information on the physical and chemical properties of the lunar near surface layers stems from the measurements obtained during the Apollo missions in the 1970s and the preceding unmanned lunar missions. According to this, the lunar surface is not composed of hard bedrock, but rather consists of a several meters thick debris layer, which has formed as a consequence of permanent micrometeorite bombardment (meteoritic gardening) over a period of several billion years. The most detailed information on the properties of the lunar regolith is collected in the Lunar Sourcebook [11]. According to McKay et al. [20], the lunar regolith can be described as a somewhat cohesive, dark gray to light gray soil. It is a “very fine-grained, loose, elastic material derived primarily from mechanical disintegration of basaltic and aorthositic rocks.” Its thickness is typically a few meters in the mare regions and probably 10–20 m in the older highland regions. Additional information on the properties of the lunar regolith can be found in the papers by Costes et al. [7] and Carrier III [2].

A few deep boreholes (the deepest one was 298 cm) were created during the Apollo missions. None of them reached the depth of the bedrock. However, these drillings confirmed that the regolith is in general a rather fine-grained material, which also has some internal cohesion (this property is important for the maintainance of a borehole, of course). According to McKay et al. [20], the mean grain size of the analyzed soil ranges from about 40 μm to about 800 μm, with an average between 60 and 80 μm. Obviously, very rarely, particles with sizes >100 μm exist. There seems to be some variation of the regolith grain size distribution over the lunar surface. However, even the more coarse-grained basaltic soil particles found, for example, at the Luna-24 landing site have still an upper size limit of 0.5 mm. We will consider these findings as a design criterium for the suggested lunar drill.

Further important properties of the lunar regolith that should enter the design considerations for a lunar drill are the soil–mechanical parameters characterizing the material strength and the porosity. Table 1 summarizes typical values in a depth of 1 m and gives the references from which they were retrieved.

Table 1 Representative values for lunar regolith parameters in a depth of 1 m
Full size table

The shear strength of the lunar soil is given by the Mohr–Coulomb law as

$$ \tau=c+\hbox{tan} \varphi $$
(1)

where c is the cohesion between the particles and \(\varphi\) is the angle of internal friction. Both parameters are listed in Table 1. The quoted values are mainly based on measurements with lunar samples returned by the Apollo missions. It should be noted that the value of the compaction strength is much higher. This value would be relevant for other penetration methods like pushing or hammering. Generally, we state that the use of a rotating drillhead and the gentle removal of the debris, as it is proposed in the next section, will cause the smallest possible disturbance of the surrounding soil, both mechanically and thermally.

3 Baseline design

Our baseline design as described in this section is oriented along the drill requirements described in Kömle et al. [16, 17]. The design goal is a drill hole of about 2 m depth, which is deep enough to perform heat flux measurements in the lunar regolith not influenced by surface temperature variations. The diameter of the borehole should be 16 mm, narrow enough to avoid major perturbations of the surrounding ground, and still wide enough to allow insertion of various probes, e.g., thermal conductivity probes, microcameras, etc. The small diameter (as compared to the holes drilled by the astronauts during the Apollo missions) also helps to bring the power and mass budgets down.

The system is aimed to be used for two types of scientific investigations. Its primary purpose is to create a tunnel to allow various analysis instruments (thermal probes, microcameras, etc.) to access the material in different depth layers. Secondly, the drill debris transported to the surface could be collected and chemically analyzed. Concerning the second goal, there is of course the danger that particles from different depths become mixed, which would affect the depth distribution analysis to some extent. Nevertheless, if the recovered particles are to be analyzed as a function of their depth of origin, the system can be made to penetrate the soil stepwise, with sufficient time allocated to flush the drill empty before proceeding to the next section.

A schematics of the suggested design is shown in Fig. 2. A close-up view of the lower part (bore crown and lower part of the suction tube and the borestem) showing also the dimensions of the baseline design is presented in Fig. 3.

Fig. 2
figure 2

The concept of a suction drill device for lunar and planetary surface sampling

Full size image
Fig. 3
figure 3

Suggested dimensions for drillhead and suction tube in our baseline concept for a suction drill

Full size image

Different options could be considered for the shape of the borecrown. In our baseline design, we choose a concave shape for the rotating drill head, which ensures that the drill debris particles move towards the interior of the tube and can therefore be more easily sucked off through the suction tube. Furthermore, this design reduces the impact on the surrounding soil, since the debris is not pressed outwards, but evacuated inwards. A soil morphology very close to the original state is therefore expected to be preserved. Slots in the drillhead with a width of 1 mm assure that only fine-grinded particles enter the inner tube. The borecrown is connected with the driving system by a central rod, and the gas suction tube consists of two concentric tubes positioned symmetrically around the borestem. The outer ring is connected to a gas supply tank, while the inner ring is open to the surface or a collection chamber on the spacecraft. Through this tube, the debris particles are transported towards the surface.

4 Hydrodynamic problem formulation

In the following calculations, we formulate the hydrodynamic problem and try to answer the question, whether or not the use of a gas flow for debris removal is a suitable alternative to traditional methods, in particular, for applications on the Moon, where no gas is available on the surface and the amount needed has to be supplied from a tank mounted on the associated spacecraft.

4.1 Force equilibrium

The first question to be clarified is as follows: given that all debris particles have a radius ≤r p (we assume for simplicity that the particles are spherical)—which vertical gas flux is necessary to lift the particles from the bottom of the borehole and transport them upwards to the surface? To fulfill this condition, the drag force, which the gas stream exerts on the particles, must exceed their weight:

$$ F_{\rm drag} > F_{\rm grav} $$
(2)

The weight of a spherical particle with density \(\varrho_{\rm p}\) and radius r p on the lunar surface is

$$ F_{\rm grav} = g_{\rm moon} \varrho_{\rm p} {\frac{4 \pi r_{\rm p}^{3}}{3}} $$
(3)

where g moon = 1.67 m/s2 = 0.165 g earth is the lunar gravity acceleration and \(\varrho_{\rm p}\) is the mass density of the particle. The drag force acting on a rough spherical particle which interacts with a gas stream of velocity v g can be written as

$$ F_{\rm drag} = {\frac{1}{2}} \varrho_{\rm g} \left(v_{\rm g}-v_{\rm p}\right)^{2}\left(\pi r_{\rm p}^{2}\right)C_{\rm d} $$
(4)

Here v g is the velocity the gas stream and v p the velocity of the dragged particle; \(\varrho_{\rm g}\) is the gas density in the vicinity of the particle and C d is the so-called drag coefficient, whose value depends on the microstructure of the particle surface and usually must be determined experimentally for any particular application. In the case of a rough spherical particle, a value of C d = 0.4 is recommended, which will also be used in our analysis (see [1]).

The relations (2), (3) and (4) imply that a particle resting on solid ground (v p = 0) will be blown away by a vertical gas stream as soon as the kinetic energy density of the gas exceeds a critical value:

$$ {\frac{1}{2}} \varrho_{\rm g} v_{\rm g}^{2} > {\frac{4 \ \varrho_{\rm p} g_{\rm moon} r_{\rm p}}{3 C_{\rm d}}} $$
(5)

\(\varrho_{\rm g}\) can be substituted by the pressure p g and the temperature T g of the moving gas stream by using the ideal gas law

$$ \varrho_{\rm g} = {\frac{m p_{\rm g}}{k T_{\rm g}}} $$
(6)

with the Boltzmann constant k = 1.3806 × 10−23 J/K and (for N2 gas) the molecular mass m = 28 × m proton = 28 × 1.6726 × 10−27 kg.

As soon as the dust particle is entrained into the gas stream, it will quickly accelerate to a constant velocity v p, which depends on the gas parameters ρg and v g and on the cross section and weight of the entrained particle:

$$ v_{\rm p} = v_{\rm g} - \sqrt{{\frac{8 g_{\rm moon}}{3 C_{\rm d}}} {\frac{\varrho_{\rm p}}{\varrho_{\rm g}}} r_{\rm p}} $$
(7)

4.2 Gas outflow through a circular orifice: nonviscous case

To get an idea of how much gas would be needed to operate a suction drill over a reasonably long time, we perform a step-by-step analysis, making use of the formulae given above. To estimate the timescale for the operation of a suction drill with a given amount of gas stored in a tank we calculate the pressure needed to lift a particle of radius r p. For the gas dynamical analysis, we follow largely the formulae that can be found in the classical German textbook on vacuum techniques [28]. The most simple case to be analyzed is the outflow through an orifice or a short tube into vacuum, where the gas viscosity and the gas friction against the tube wall can be neglected. In this case, there is no pressure drop along the outflow tube; the gasdynamical parameters p g, ρg, and T g in the tube are constant and can be calculated from their respective values in the supply tank, p 0, ρ0, and T 0 as follows:

$$ p_{\rm g} = p_{0} \left({\frac{2}{\gamma+1}}\right)^{\frac{\gamma} {\gamma-1}} $$
(8)
$$ \rho_{\rm g} = \rho_{0} \left({\frac{2}{\gamma+1}}\right)^{\frac{1} {\gamma-1}} $$
(9)
$$ T_{\rm g} = T_{0} \left({\frac{2}{\gamma+1}}\right) $$
(10)

Here γ = c p/c V is the ratio of specific heats at constant pressure and constant volume, usually denoted as adiabatic index. In nonviscous flow—as long as the cross section of the tube remains constant—the outflow velocity v g of the gas through the tube into vacuum equals the so-called critical velocity, which is of the order of the sound speed in the gas tank,

$$ c_{0} = \left({\frac{\gamma p_{0}}{\rho_{0}}}\right)^{1/2} $$
(11)

v g is only a function of the gas temperature T 0 in the tank and the adiabatic index γ:

$$ v_{\rm g} = \left({\frac{\gamma k T_{0}}{m}} {\frac{2 \gamma} {\gamma+1}} \right)^{1/2} $$
(12)

With the expressions for \(\varrho_{\rm g}\) and v g given in Eqs. (6) and (12), respectively, the flow velocity of the dust particles entrained in the upward directed gas stream can now be calculated as a function of the pressure in the gas tank p 0 by using Eq. (7). The minimum tank gas pressure necessary to lift particles of radius r p and density ρp is

$$ p_{\rm min,nonvisc} = {\frac{1}{\gamma}} \left({\frac{\gamma+1}{2}} \right)^{{\frac{1}{\gamma-1}}} \left({\frac{8 g_{\rm moon} \varrho_{p} r_{\rm p}}{3 \ C_{\rm d}}} \right) $$
(13)

To evaluate the above formulae, one needs to define some constants and variables. The adiabatic coefficient for N2 gas is γ = 7/5 =  1.4. Concerning the temperatures on the lunar surface, it is clear that there can occur large diurnal variations, from 100 K during lunar night up to 400 K during equatorial noon time. The average surface temperature at the Apollo 15 and 17 landing sites (which is also the temperature in about 1 m depth below the surface) is around 250 K [11, 22]. We will use this value for the following evaluation, not forgetting about the fact that in reality the gas temperature in the supply tank may be significantly different (this depends also on the thermal insolation of the gas tank, which is not considered in this investigation).

Figure 4 shows the levitation velocities of debris particles dragged by a stream of N2 gas as a function of the pressure p 0 in the gas tank. The different curves on the plot represent particle diameters from the millimeter down to the micrometer size range.

Fig. 4
figure 4

Levitation velocities of debris particles dragged by a stream of N2 gas emanating through a short tube from a gas reservoir. The plot shows v p as a function of the pressure p 0 in the gas tank, for particle diameters in the millimeter down to the micrometer size range. The particle density was chosen as 2,900 kg/m3, consistent with the density of the lunar mare basalt analog material JSC-1

Full size image

The total gas mass outflow from a tank containing gas at pressure p 0 through a circular hole of radius R into vacuum is given as

$$ Q_{\rm m}^{*} = \left(\pi R^2\right) p_{0} \left({\frac{m}{kT_{0}}} \right)^{1/2} \left({\frac{2 \gamma} {\gamma+1}} \right)^{1/2} \left({\frac{2}{\gamma+1}} \right)^{{\frac{1} {\gamma-1}}} $$
(14)

This is the case of the so-called “choked flow” for an inviscid gas. Q *m can be considered as the ultimate upper limit for the gas flux through a tube out of a tank.

4.3 Gas outflow through a long tube: viscous case

How does the above result change when the viscosity of the nitrogen gas flowing through the suction tube is included into the calculation? To investigate this question, we apply the formulae given in Wutz [27] and Wutz et al. [28] and make a similar analysis as in the previous section for the nonviscous gas flow. Again, we are only interested in the solution for the choked flow, i.e., the case that the pressure in the second reservoir is zero and the pressure in the tank is at a given value p 0. While for the nonviscous case the gas flux through the tube depends only on the adiabatic index of the gas and on the tube diameter D, in the viscous case the flow rate is also a function of the gas viscosity η and the tube length L. Furthermore, there is a pressure drop over the length of the tube in the direction of the open end.

For the viscosity η of an ideal gas, the so-called Sutherland-formula can be applied [23]:

$$ \eta = \eta_{0} {\frac{T_{\rm ref}+B} {T+B}} \left({\frac{T} {T_{\rm ref}}} \right)^{3/2} $$
(15)

In the case of N2 gas the three constants in Eq. (15) have the following values:

$$ \begin{aligned} T_{\rm ref}&=300.55\ \hbox{K}\\ B&=111\ \hbox{K}\\ \eta_{\rm ref}&=17.81 \times 10^{-6}\ \hbox{Pa s}\\ \end{aligned} $$

where B is Sutherland’s constant for nitrogen gas and ηref is the viscosity at the reference temperature T ref. The temperature dependence of η is plotted in Fig. 5. A value of T = 250 K results in a gas viscosity of η = 1.5403 × 10−5 Pa s.

Fig. 5
figure 5

Dependence of viscosity on temperature for an ideal N2 gas

Full size image

Two different types of gas flow are possible inside the tube: (1) laminar or (2) turbulent. To determine the type of flow and the corresponding gas fluxes is in general a complex problem. However, for long and thin tubes, relatively simple formulae are given by Wutz et al. [28], which we will use for the further analysis.

For laminar flow:

$$ Q_{\rm m} = {\frac{\pi}{16 \eta}} \left({\frac{m}{k T_{0}}} \right) {\frac{R^4}{L}} p_{0}^{2} $$
(16)

For turbulent flow:

$$ Q_{\rm m} = \left({\frac{20 \pi^{2}} {16 \times 3.2}} {\frac{m} {k T_{0}}} \right)^{4/7} \left({\frac{4}{\pi \eta}} \right)^{1/7} 2 R \left({\frac{4 R^{3}} {L}} \right)^{4/7} p_{0}^{4/7} $$
(17)

To decide which of the two formulae have to be applied, Reynolds-number of the flow must be calculated. It can be expressed as

$$ Re = {\frac{2}{\pi \eta R}} Q_{\rm m} $$
(18)

where Q m is the mass flux through a tube with radius R according to the formulae (16) or (17), respectively.

Plotting the Reynolds-number versus the tank pressure p 0 in a “log–log” representation for a given tube geometry (parameters R, L) gives two straight lines with different inclinations and a crossing point, as shown in Fig. 6. The steeper line (left part) is valid on the left side and corresponds to the laminar case, while the flatter line (right side) represents the turbulent case. Using again L = 4 m (two times the assumed operation depth of 2 m) and D = 2R = 5 mm for the dimensions of the tube, we recognize that as long as p 0 < 7 × 103 Pa the gas flow through the tube is laminar. The gas fluxes at pressures p 0 = p min, p 0 = 2 p min, p 0 = 4 p min and p 0 = 8 p min are indicated by asterisk in Figs. 6 and 7. The third (dashed) line in Fig. 7 is the maximum possible flux corresponding to the flow through a short tube or orifice into vacuum.

Fig. 6
figure 6

Reynolds number versus tank pressure for viscous gas outflow through a long tube

Full size image
Fig. 7
figure 7

Gas mass flux versus tank pressure for viscous gas outflow through a long tube

Full size image

Since—in contrast to the nonviscous case calculated in the previous section—there is now a pressure drop along the tube, the gas density also decreases in flow direction and the gas flow speed increases. It reaches Machnumber = 1, i.e., the local sound speed, close to the exit. Referring to the condition (5), which controls the particle lift-off and transport by the gas stream, we now need to determine the gas parameters at the exit \(\varrho_{\rm g}\) and v g. To obtain these values, the pressure p g at the exit is calculated as

$$ p_{\rm g} = p_{0} \left({\frac{2}{\gamma+1}} \right)^{\frac{\gamma} {\gamma-1}} {\frac{Q_{\rm m}} {Q_{\rm m}^{*}}} $$
(19)

where Q *m is the gas flow for the nonviscous case given by Eq. (14) and \(\varrho_{\rm g}\) is obtained from the ideal gas law (6)

From the continuity of the gas flow in the tube, one can now calculate

$$ v_{\rm g} = {\frac{1}{\varrho_{\rm g}}} {\frac{Q_{\rm m}}{\pi R^{2}}} $$
(20)

According to the analysis by Wutz [27] the temperature change of the gas from the tank until the fully developed tube flow is negligible, since in the long tube the Mach number in the flow entrance region is still small (<0.2). Inside the tube, pressure and density decrease in the direction of the flow and the temperature remains approximately constant as long as the tube cross section does not change. Therefore, we can approximately assume a constant T g = T 0 in the whole system.

With the formulae given above it is now again possible to calculate the minimum tank pressure for particle transport against gravity analogous to the formula (13) as

$$ p_{\rm min,visc} = \sqrt{16 \eta {\frac{L}{R^2}} \left({\frac{k T_{0}} {m}}\; {\frac{\gamma+1}{2 \gamma}} \right)^{1/2}\; {\frac{8 \varrho_{\rm p} g_{\rm moon} r_{\rm p}} {3 C_{\rm d}}}} $$
(21)

Furthermore, the reduction of the gas mass flow caused by a tube of length L and radius R in comparison to the maximum outflow at a given tank pressure can be calculated. In Table 2 (columns 1 and 2) Q m/Q *m is listed for tank pressures from p min,visc up to 8 p min,visc. The minimum tank pressure is calculated by formula (21) for a particle radius r p = 1 mm. The calculated numbers indicate that the outflow from the tank is quite strongly inhibited by the long suction tube.

Table 2 Normalized gas flows and Knudsen numbers for different tank pressures
Full size table

Table 3 shows how the ratio p min,visc/p min,nonvisc depends on the size of the debris particles. This ratio is about 102 for millimeter-sized particles, but increases to 103 for micrometer-sized particles. Again, the difference between the minimum pressures in the viscous and nonviscous case reflects the flow resistance caused by the long tube.

Table 3 Minimum tank pressures for particle levitation in the viscous and the nonviscous case for different particle sizes
Full size table

4.4 Knudsen numbers

The Knudsen number is defined as the ratio of the mean free path of gas molecules to a characteristic macroscopic length scale. In the case of gas flow through a tube, this length scale is the tube diameter D = 2R.

In terms of gas pressure and temperature, the Knudsen number can be written as

$$ Kn = {\frac{\bar{s}}{D}} = {\frac{k T_{\rm g}}{\sqrt{2} \pi\sigma^{2} p_{\rm{g}}D}}$$
(22)

where σ = 3.1 × 10−10 m is the diameter of the N2 molecule, and \(\bar{s}\) is the mean free path of the molecules in the gas.

Small Knudsen numbers (Kn < 10−2) characterize the collisional (hydrodynamic) flow regime, while flows with Kn > 0.5 correspond to the so-called free molecular regime. The range in-between is denoted as the transitional of Knudsen regime. All formulae given above are only strictly valid as long as the flow is in the collisional regime. In Table 2 (columns 3 and 4) the Knudsen numbers for a tube with D = 2R =  5 mm are listed for the gas pressures near the tank and near the exit, respectively. Tank and exit pressures are calculated for particle sizes of D p = 2r p = 1 mm. As can be seen, Knudsen numbers are clearly in the collisional regime near the inlet, but may move to the transitional regime close to the exit. Since the overall accuracy of the formulae given by Wutz is around 20%, we think that the hydrodynamic formulae are still applicable, although not with high accuracy. Certainly, for the a detailed design, corrections associated with the gas rarefaction close to the tube exit may be necessary.

4.5 Influence of dust loading on the gas stream

A point not yet covered in this study is the influence of the dust loading on the gas flow itself. A simple way to include this influence without dealing with the full dust/gas interaction problem is to use a variable adiabatic index. As shown by Wallis [26] and reviewed in Kieffer [15], the effect of mass loading on the gas flow can be simulated by introducing a modified

$$ \gamma_{\rm mix} = {\frac{c_{\rm p} + \beta c_{\rm s}} {c_{\rm V} + \beta c_{\rm s}}} $$
(23)

instead of the regular γ of the driver gas, where β is the mass ratio of solids to vapour in the flow and c s is the heat capacity of the solid phase (in our case the debris particles). With these modifications, the behavior of a gas–particle system will obey the laws of fluid dynamics as developed for perfect gases.

4.6 Operation timescale for given amount of gas

If M is the mass of stored gas in kilograms, a rough estimate of the time needed to empty the gas tank by outflow through a long tube into vacuum is given by

$$ t = {\frac{M}{Q_{\rm m}}} $$
(24)

Figure 8 shows the results for our baseline scenario (L = 4 m, D = 5 mm) with particle diameters from 1 mm down to 1 μm. The tank pressure is assumed to be four times the equilibrium pressure for particle levitation.

Fig. 8
figure 8

Timescale for viscous gas flow from the storage tank through a 4 m long and 5 mm diameter tube into vacuum for an ideal N2 gas

Full size image

According to Fig. 8 an operation time of the order of 100 h is possible to transport particles of 1 mm diameter continuously out of the borehole, when the tank contains about 5–6 kg of N2 gas. We think this would be quite reasonable for a lunar mission scenario. If the particles can be milled to smaller sizes, correspondingly smaller gas fluxes are necessary and the operation time would increase dramatically.

5 Transport capacity of a suction drill

To estimate the transport capacity of a suction drill we consider the following scenario:

  • Drill hole depth: L h = 2 m

  • Drill hole diameter: D h = 16 mm ⇒ radius R h =  8 mm

The bulk density of the regolith layer to be drilled is chosen as \(\varrho_{\rm p} = 1,825\,\hbox{kg}/\hbox{m}^3,\) a typical value for the lunar regolith in 1 m depth (see Table 1). Now assume a realistic penetration velocity of the drill; in our example we choose v drill =  20 mm/min = 3.33 × 10−4 m/s. This translates into the time needed to excavate a 2 m deep hole of t h = L h/v h = 6,000 s = 100 min. With these figures, the volume of the drillhole is V h = πR 2h L h = 4.02 × 10−4 m3 and the excavated mass is M h = ρp V h = 0.74 kg.

The volume excavated per second with this penetration speed is then V hs = (π R 2h )v h = 6.70 × 10−8 m3/s, while the volume of one debris particle with radius r p = 0.5 × 10−3 m is \(V_{\rm p} ={{4 \pi r_{p}^{3}}/3} =5.24 {\times}10^{-10}\,\hbox{m}^{3}.\) This gives (assuming that all particles produced by the drilling process have the maximum size of 1 mm diameter, which is the worst case) a particle production rate of

$$ {\frac{{\rm d}n_{p}}{{\rm d}t}} = {\frac{V_{\rm hs}}{V_{\rm p}}} = 128 \; \hbox{particles/s} $$
(25)

Now we can easily check if the gas fluxes calculated in the previous section for viscous gas flow through the tube are large enough to remove the bore debris continuously, so that no material accumulates at the bottom of the borehole. According to this model, for a particle with D p = 1 mm and a gas pressure p 0 = 4 p min = 3,152 Pa (see Table 3) the equilibrium particle speed would be v p > 250 m/s.

Keeping in mind the uncertainties of the model (for example, things like the acceleration phase of the particles are not considered and and there may be other effects that could play a role), we make a very pessimistic assumption on v p, namely v p = 1 m/s. With this speed, a single particle would cross a distance of 2D p = 4r p = 2 × 10−3 m within a time period of \({\delta}t ={{2 D_{\rm p}}/{v_{\rm p}}} =2 {\times}10^{-3}\)  s.

Assume now that every δt seconds a particle is entrained into the gas stream and transported upwards along the borehole (which is again a worst case scenario!), the time needed to remove the 128 debris particles produced within 1 s would be

$$ t_{\rm blow} = {\frac{{\rm d}n_{\rm p}}{{\rm d}t}} \delta t = 0.25 \hbox{s} < 1\hbox{s} $$
(26)

Thus, the result of the above analysis is that, even with the worst case assumptions used, the bore debris could be removed by the gas stream and no accumulation of particles at the bottom of the borehole would occur.

6 Gas escape via the regolith

To make the suction drill work properly, it will be necessary to penetrate the regolith to a certain (shallow) depth before the gas is turned on. Otherwise, a crater may form instead of a slender hole, because the uppermost 10–15 cm of the regolith are particularly porous and soft. Before turning the gas on for debris removal, the drillhead should form a plug in the soil, so that the bulk of the gas flows back through the central tube and does not escape via the open pores in the regolith or along the boundary layer.

To investigate whether or not gas escape through the pores of the surrounding regolith could pose a problem for the operation of the suction drill, we have run a numerical simulation using a Comsol Multiphysics model [4]. The geometry and the dimensions of this model are roughly those of the borehead and suction tube shown in Fig. 3. The borecrown is inserted into the regolith to a depth of 4 cm. The model is 2D-axisymmetric. Through the outer concentric tube, the gas flows from the tank to the bottom of the borehole. From there, it can escape in two ways: either it flows back through the central tube towards the surface, or it diffuses into the surrounding regolith. Mathematically, the problem of viscous gas flow in a porous medium under the action of a pressure gradient ∇p can (in a simplified form) be described by Darcy’s law, which gives the flow field \(\vec{v}\) as (see, e.g., [24]):

$$ \vec{v} = -{\frac{\kappa}{\eta}} \nabla p $$
(27)

where κ denotes the permeability of the porous medium and η is the viscosity of the gas. In a stationary situation and using the ideal gas law (Eq. 6) to substitute density by pressure, one obtains the following transport equation for the gas flowing through the medium:

$$ \nabla \cdot \left(-{\frac{\kappa}{\eta}} {\frac{m p}{k T}} \nabla p \right) = 0 $$
(28)

To solve the problem, first the material parameters appropriate for the lunar regolith have to be specified. For the gas viscosity, we use Eq. (15) with T = 250 K. The gas permeability of the regolith is more difficult to specify, since no in situ data exist. Carrier III et al. [3] quote a value of (1–7) × 1012 m2. This value was derived from lab tests with the exhaust gases of the Surveyor lunar landers, and it was found to be consistent with the expected values for fine-grained regolith-like granular material [5]. In the following model calculation, we have used the upper limit κ = 7 × 1012 m2. To calculate the gas in the tubes and in the regolith numerically, we attribute a large, but finite permeability also to the domains inside the gas flow tubes. In the example shown, the permeability in the flow tubes is assumed to be a factor 10,000 higher that the permeability in the surrounding regolith. As pressure boundary conditions at the inlet and outlet of the tube we have taken values derived from Tables 2 and 3 in the previous chapter, which were found to be high enough to lift millimeter-sized particles (p inlet = 416 Pa, p outlet = 89 Pa). Figures 9 and 10 show the components of the flow field obtained from the calculation. They clearly indicate that the bulk of the gas stream returns to the surface through the inner concentric ring. Diffusion velocities of the gas into the surrounding regolith are very low, of the order of mm/s to cm/s only, while in our example the inflow and outflow of the gas through the tubes takes place with speeds around 40 m/s. Thus, we can conclude that taking into account what we know about the permeability of the regolith gas loss into the pores is not expected to pose a serious problem for the operation of the suction drill. The situation should even improve as the borehole becomes deeper and deeper, because then it becomes exceedingly more difficult for the gas to escape through the regolith towards the surface.

Fig. 9
figure 9

Gas flow velocities in the tubes and the regolith calculated by applying Darcy’s law: z-component

Full size image
Fig. 10
figure 10

Gas flow velocities in the tubes and the regolith calculated by applying Darcy’s law: r-component

Full size image

7 Contamination issues

The drilling method proposed here differs from classical drilling techniques in the utilization of a carrier gas, in our case molecular nitrogen. It is therefore worthwhile to consider some issues concerning the contamination or alteration of the sample material by using such a process. For applications on targets as the Moon, mainly forward contamination from Earth towards the target by extralunar equipment is to be considered.

The COSPAR Planetary Protection Policy [6] refers to contamination as “the exchange of organic-constituent or biological material between Earth and the target planet or moon ....”. However, to conserve the originality of a sample or an environment to be inspected, also chemical and physical contamination can be of interest. It must be assured that the process does not alter the sample to a point that the scientific measurements taken become unrepresentative.

It is therefore of interest when one considers the drilling process by gas suction to review the (potential) scientific measurements that such a mission should fulfill, and then to evaluate the influence of such a process on the measurements.

The scientific objectives for the two application examples considered here, Moon and Mars, differ significantly: while the determination of elemental abundances and geochemistry are predominant for in situ selenology, for Mars it is mainly exobiology; thus, the search for traces of life and its by-products is the important point here. However, since on Mars there is a planetary atmosphere, which can in principle be compressed and used as a driver gas for a suction drill, the problem of contamination by an extraplanetary gas source is not posed there. Therefore, in the following, we will concentrate on potential problems associated with a lunar application.

The Moon will be the target of several missions in the future, on the one hand as “test-bed” for technologies that are needed to extend human exploration towards the planet Mars, and on the other hand in the scientific interest to identify potential elements for In Situ Resource Utilization (ISRU), to understand the magmatic and thermal history of the Moon and the processes that formed our celestial neighbor [10]. While many of such measurements can be done from the orbit, in situ ground-checks will ultimately be necessary to verify the models that were built by using orbital data and to collect data that cannot be measured from orbit (such as Helium 3 abundance and some physical soil characteristics).

7.1 Chemical contaminations

In terms of geochemical measurements, future exploration attempts will be most likely based on the research for in situ resources. Such elements include oxygen, hydrogen, helium, and water for life support and energy production. Furthermore, some metals, silicon, glass, and some raw isotopes might be of interest for mining activities in the lunar soil [18]. For the suction drill concept especially the gases are of interest, since it must be assured that the chemical composition of the soil is not altered by the introduction of process gases. Oxygen, hydrogen, and helium may therefore cause problems, since those might falsify the measurements taken in situ. Several works state the potential abundance of these elements as follows:

  • Oxygen: 43.4 wt%,

  • Hydrogen: 50 ppm [11, 18],

  • Helium: 3 ppm and

  • Helium-3: 0.02 ppm [13].

The choice of the carrier gas is therefore critical. We consider molecular nitrogen as the appropriate choice for the following reasons:

  • Nitrogen is a highly inert gas due to its strong triple bonds, not reacting with the abovementioned elements under the conditions that reign on lunar applications (the Haber–Bosch Process, which is the reaction of Dinitrogen and Hydrogen, requires above 150 atm and above 450 °C [9]).

  • Nitrogen does not show up in the list of the elements of interest for ISRU and its introduction into the soil sample would therefore not alter the measurements of those elements of interest.

Although highly purified Nitrogen can be used for this process, the gas will nevertheless contain impurities that need to be considered for the sample analysis. Ultra High Purity Nitrogen (99.999% min) is commercially available but comes with the following impurities: 3 ppm H2O, 5 ppm O2 and 1 ppm CH4 (see [12]). These elements must be considered for the measurement of hydrogen and water abundances, although their amount is very small.

7.2 Physical modifications

Virtually, every technique of deep layer sample retrieving will modify the morphology and physical characteristics of the soil to some extent. Parameters, such as the density of the soil, largely determine the thermal characteristics and thus should be conserved in its original state as far as possible. The proposed process here has the advantage that the surrounding soil is expected to be less altered than with other sampling means, since the drill debris is transported inside the drilling tube to the surface and not on its perimeter like with an auger. Thin-walled coring devices such as those used during the Apollo missions (11) also lead to a compression of the soil inside and outside the tube, since the sample needs to be “squeezed” into the corer for retrieval. In the case of a suction device, the debris particles are removed before such pressures appear. Nevertheless, the usage of a gas to evacuate the drill debris might bring problems whose extent must be evaluated during prototype tests.

7.3 Biological contaminations

Biological contamination is a less critical issue for lunar exploration. Equipment that is sent to the Moon must be free from terrestrial life forms to assure the preservation of the lunar environment. In the case of the suction drill, this means that, not only the mechanical equipment has to be cleaned from bacteria by careful sterilization, but also the gas that is used for the debris transport.

8 Conclusions and outlook

The results presented in the previous sections indicate that, even in the case of a body with practically absent surface gas pressure, a suction drill may be a suitable alternative to traditional drilling devices. This is particularly interesting for the Moon, which will see a couple of lander and rover missions in the next decade. We think that the proposed drilling/sampling device might be suitable both for mobile stations (rovers), for example the Chinese Chang-Er mission, and for stationary surface stations, which are planned to be distributed on the lunar surface by NASA in the next decade, as well as for the planned European, Japanese, and Indian missions.

Of course in the case of the Moon, which has no own atmosphere, the amount of gas needed to operate the drill must be included in the weight budget. However, as we have demonstrated in this paper, the requirements are minor, and for most missions, it should be possible to include this resource, since cold gas tanks are usually anyway needed for lander and surface operations.

In the case of Mars or Venus, the problem of resources is not posed. Since Mars has a (although thin) CO2 atmosphere, the atmosphere provides an unlimited gas resource, as already noted by Zacny et al. [29]. In this case, one would rather need a gas compressor instead of a gas tank, which provides the necessary reservoir pressure to blow the debris out of the borehole. Venus has a very dense atmosphere with a surface pressure of about 90 bar, which could be used instead of a gas tank to operate a suction drill.

Based on the results of this first feasibility study, the next steps to validate the concept of a lunar suction drill are planned as follows:

  • Experimental verification of the predicted dust transport capacity: for this purpose lunar analog sample material milled to a defined grain size has to be prepared and filled into a predrilled borehole. This assembly is then placed in a vacuum chamber and combined with a simple gas suction system, which can be operated at different pressures. Such a test will provide the necessary information on the entrainment of the debris particles into the gas stream in dependence of tube geometry and tank pressure.

  • Prototype design and manufacture: the data from such experiments, together with the theoretical treatment presented in this paper, will provide the necessary information to build a first prototype of the suction drill and to test its performance in a laboratory environment.