1 Introduction

Hard overconsolidated clays are, in general, anisotropic materials. If ground displacements due to tunnelling and other excavations in this type of soil formations are to be realistically predicted, then anisotropic behaviour description must be included in the soil model used. The aim of the work described in this paper is to investigate the influence of initial plastic anisotropy on the ground displacements induced by the excavation of a tunnel. There is also elastic anisotropy and strain induced plastic anisotropy, but those were left out in this study. Plastic anisotropy may be due to the soil sedimentation and consolidation process followed by unloading (overconsolidation) and also, in the case of structured soils, the fabric/structure that are the result of other processes, with only the first being considered in this case. The bounding surface model for structured soils proposed by Kavvadas and Belokas [14] is used here and implemented into the finite difference explicit code FLAC. This model incorporates capabilities to simulate soil destructuring, initial and induced anisotropy, cyclic loading and small strain response. These are important features occurring in natural overconsolidated soils. Other models have been formulated for structured soils, such as that of Kavvadas and Amorosi [13], and that of Rouainia and Muir Wood [19], but this one is improved in three aspects. The first aspect is the shape of the bounding surface, which, in this model, is a distorted ellipsoid aligned with the normal consolidation line. There is a large body of experimental evidence supporting such a shape [6, 8,21]. The shape of a distorted or rotated ellipsoid for the bounding surface has also been used in several models [1, 2, 11, 9, 10, 22, 16]. The second aspect is the use of the material constants of the destructured soil (intrinsic soil properties [3]). The term “material constants” used here designates the constants of the material model. The third aspect is the non associated flow rule.

Anisotropy has been considered in the numerical analysis of tunnelling in overconsolidated clays with elastoplastic models, for instance, by Einav and Puzrin [7], and Ng and Lee [17]. In the former, while the authors state that they are using a hyperelastic model that is anisotropic, in reality, the model is isotropic as are any models whose strain energy density function is solely dependent on invariants of the strain tensor. As the plastic part of the model is a hyperplastic version of the modified Critical State Model, the analysis presented is entirely isotropic. The advantage being attributed to the hyperelastic model used consists in the curved undrained stress paths produced. This is only an advantage if the model has a large elastic domain, which is not the case with the two surface model used in this work that is also capable of producing such undrained paths inside the bounding surface. The model used in this work assumes that the variation of shear stiffness with shear strains is due to the plastic mechanism. In the work of Ng and Lee [17], the authors use a conventional elastic perfectly plastic soil model with linear transversely anisotropic elasticity so that only elastic anisotropy is considered. Anisotropy of shear strength is not taken into account. Elastic anisotropy is expected to be dominant only for very small strains. In the present work, it was decided to take the opposite approach with emphasis placed on plastic anisotropic behaviour while elasticity is maintained isotropic. Available experimental evidence [4], while confirming some anisotropy of elastic (small-strain) stiffness, also shows that it is not very significant.

2 Model description

In the description of the model that follows all stresses are effective. The stress and strain rate tensors are decomposed into isotropic and deviatoric parts: \({\varvec{\upsigma}} = p{{\mathbf{I}}}+{{\mathbf{s}}},{\dot {\varvec{\upvarepsilon}}} = \left({\dot{\varepsilon_{v}} /3} \right)\,{{\mathbf{I}}} + {\dot{\bf e}},\) with the stress and strain rate invariants defined as \(p={\hbox{tr}}\,{\varvec{\upsigma}}/3, q = \sqrt {3/2\,\,{{\mathbf{s}}}:{{\mathbf{s}}}}, {\dot{\varepsilon}}_{V} = {\rm tr}\,{\dot{\varvec{\upvarepsilon}}}\) and \(\dot \varepsilon_{q} = \sqrt {2/3\,\,{\dot{\bf e}}:{\dot{\bf e}}}.\)

2.1 Elastic part

In order to represent the small strain elastic response, a hypoelastic model, with a non-linear dependence of the tangent moduli relative to the mean stress, was adopted. The incremental model is defined by the following variable tangent moduli:

$${\rm d}{\varvec{\upsigma}} = B\,{\rm d}\varepsilon _{V} \,{{\mathbf{I}}} + 2\,G\,{\rm d}{{\mathbf{e}}}\quad \hbox{where} \,\,B = B_{0} \left({{p \mathord{\left/{\vphantom {p {p_{r}}}} \right.} {p_{r}}}} \right)^{m} \quad \hbox{and} \quad G = G_{0} \left({{p \mathord{\left/ {\vphantom {p {p_{r}}}} \right.} {p_{r}}}} \right)^{m} .$$
(1)

This model has three material constants: the tangent bulk modulus for p =  p r , B 0, the tangent shear modulus for p = p r , G 0, and an exponent, m, which defines the variation of the tangent moduli with p. This hypoelastic model is well established and has been widely applied [19, 15, 18].

An undesirable property of the hypoelastic models is the non-compliance with the laws of thermodynamics. This may lead to a situation, unacceptable from a physical viewpoint, where energy is generated in closed stress or strain loops. This drawback is not expected to be important in the assumed circumstances of the present study, where cyclic loading conditions are not present. However, it has the advantage of a greater simplicity of the model and its numerical implementation.

Einav and Puzrin [7], compare the results given by a hypoelastic model, such as the one used in this work, with those given by a hyperelastic model, when applied to the numerical simulation of a tunnel excavation in overconsolidated clay. The plastic part is a conventional hardening plasticity model. In this context, because there is a large elastic domain, it is advantageous to use the hyperelastic model that is able to reproduce curved undrained stress paths inside the yield surface, while the hypoelastic model would only give vertical stress paths in (p, q) space. In contrast, the bounding surface model used here only has a very small elastic domain (the “bubble”) and plastic strains occur inside the bounding surface. The model is thus able to reproduce the shear stiffness reduction that takes place with increasing shear strains, even in the small strain range, together with the correctly curved undrained stress paths. The hyperelastic model, in order to preserve its energy conservation properties, should be implemented as a total (not incremental) stress–strain relation, with the implication that initial strains corresponding to desired initial stresses should be given. Also, this elastic model is isotropic but could easily be extended into the anisotropic (transversely isotropic or orthotropic) range.

2.2 Plastic part

The plastic part of the model describes the irreversible and highly nonlinear behaviour observed for strains higher than 10−4. The model adopted is the one described in Kavvadas and Belokas [14]. It is a generalisation of the modified cam-clay model (MCC), with continuous plasticity, following the general bounding surface formulation of Dafalias [5]. The bounding surface is a sheared ellipsoid, which makes the plastic behaviour anisotropic. The model includes a mechanism to simulate the strain induced destructuring, which is a relevant aspect of natural soils. The plastic model may actually be combined with different elastic models. The different surfaces that make up the model are represented in Fig. 1.

Fig. 1
figure 1

2D representation of the model’s surfaces

Full size image

The most exterior surface, the bounding surface, which is the structure strength envelope (SSE), represents the material with its structure intact, and is defined by the function:

$${F}\left({\varvec{\upsigma}},{\varvec{\upsigma}}_{K} ,\alpha \right) = \frac{1}{{c^{2}}}\left({{{\mathbf{s}}} - \frac{p} {{p_{K}}}{{\mathbf{s}}}_{K}} \right):\left({{{\mathbf{s}}} - \frac{p} {{p_{K}}}{{\mathbf{s}}}_{K}} \right) + (p - p_{K})^{2} - \alpha^{2} = 0$$
(2)

that, in geometrical terms, describes a sheared ellipsoid of revolution, whose position and alignment is given by the tensor \({\varvec{\upsigma}}_{K} = {{\mathbf{s}}}_{K} + p_{K}{{\mathbf{I}}}.\) The length of the surface in the p axis direction is 2α. The semi-axis ratio of the ellipsoid depends on the constant c. When \({\varvec{\upsigma}}_{K} = \alpha \,{{\mathbf{I}}}\) and \(c = \sqrt {2/3} \,M,\) the MCC model’s ellipsoid, which is isotropic, is obtained. The interior bubble, that bounds the elastic domain, is the plastic yield envelope (PYE). It is defined, in stress space by the following function:

$$f\left({{\varvec{\upsigma}},{\varvec{\upsigma}}_{K} ,{\varvec{\upsigma}}_{L} ,\alpha} \right) = \frac{1} {{c^{2}}}\left({{{\mathbf{s}}} - {{\mathbf{s}}}_{L} - \frac{{p - p_{L}}} {{p_{K}}}{{\mathbf{s}}}_{K}} \right):\left({{{\mathbf{s}}} - {{\mathbf{s}}}_{L} - \frac{{p - p_{L}}}{{p_{K}}}{{\mathbf{s}}}_{K}} \right) + (p - p_{L})^{2} - (\xi \,\alpha)^{2} = 0$$
(3)

This PYE bubble is homothetic to the SSE, shrunk by a scale factor ξ ≪ 1 and translated \({\varvec{\upsigma}}_{L}-{\varvec{\upsigma}}_{K}\) in relation to \({\varvec{\upsigma}}_{K}\). The PYE, f = 0, is obtained from the SSE substituting \({\varvec{\upsigma}}\) by \({\varvec{\upsigma}}-{\varvec{\upsigma}}_{L}+{\varvec{\upsigma}}_{K}\) and α by ξα, in F = 0. The tensor \({\varvec{\upsigma}}_{L}\) is the centre of the bubble (PYE).

In order to simulate the destructuring process, the existence of a surface, also homothetic to the SSE and representing the intrinsic behaviour of the material (without structure), is assumed. With increasing plastic strains, the SSE will tend to this intrinsic structure strength envelope (ISSE). It also assumed that this surface has the same orientation of the SSE, only with a smaller dimension, α*. That is, the following relation holds

$${\varvec{\upeta}}_{K}^{*} = \left({{1 \mathord{\left/{\vphantom {1 {p_{K}^{*}}}} \right. } {p_{K}^{*}}}} \right){{\mathbf{s}}}_{K}^{*} = \left({{1 \mathord{\left/ {\vphantom {1 {p_{K}}}} \right. } {p_{K}}}} \right){{\mathbf{s}}}_{K} = {\varvec{\upeta}}_{K}$$
(4)

where the mean stress normalised deviatoric tensor \({\varvec{\upeta}}_{K} \) determines the SSE orientation in stress space.

There is also the phase transformation envelope (PTE), which separates the dilatant region (exterior of PTE) from the contractant region (interior of PTE). The PTE has the shape of a cone with apex in the origin of stress space, and is defined by the function

$$ \hbox{h}({\varvec{\upsigma}}) = {1\mathord{\left/{\vphantom {1 {k^{2}}}} \right. } {k^{2}}}\left({{\mathbf{s}}} - p\,{\hat{\varvec{\xi}}} \right):\left({{\mathbf{s}}} - p\,{\hat{\varvec{\xi}}} \right) - p^{2} = 0, $$
(5)

with the deviatoric tensor \({\hat{\varvec{\xi}}}\) fixing the alignment of the cone’s axis and k it’s opening. The PTE is fixed in stress space. For \({\hat{\varvec{\xi}}} = 0\) and k = c the critical state surface of the MCC model with circular deviatoric cross-section is recovered. This model incorporates isotropic hardening, controlled by the internal variable α. The evolution of α is given by

$${\dot{\alpha}} = \alpha^{*} \left[ {{{\left({1 + e} \right)} \mathord{\left/ {\vphantom {{\left({1 + e} \right)} {\left({\lambda^{*} - \kappa ^{*}} \right)}}} \right.} {\left({\lambda^{*} - \kappa^{*}} \right)}}} \right]{\dot{\varepsilon}}_{V}^{p} - (\alpha - \alpha^{*})(A_{V} {\dot{\varepsilon}} _{V}^{p} + A_{q} \dot \varepsilon_{q}^{p})$$
(6)

with \( A_{V} = \zeta_{V}\,\exp (-\eta_{V} \,\varepsilon_{V}^{p})\) and \(A_{q} = \theta_{q} + \zeta_{q} \,\exp (- \eta_{q} \,\varepsilon_{q}^{p}),\) in which ζ v , ζ q , η v , η q  and  θ q are material constants controlling the material’s destructuring due to both volumetric and deviatoric strains. λ* and κ* are, respectively, the slope of the normal and elastic isotropic compression lines in (ln p′,v) space. α*, which defines the length of the ISSE, is obtained from \(\alpha^{*} = \frac{1}{2}\left[ {p^{*} + \alpha \left({1 - {{p_{K}} \mathord{\left/ {\vphantom {{p_{K}} \alpha}} \right.} \alpha}} \right)} \right],\) where \(p^{*} = \exp \left[ {{{\left({N_{n} - v} \right)} \mathord{\left/ {\vphantom {{\left({N_{n} - v} \right)} {\lambda^{*}}}} \right.} {\lambda^{*}}}} \right]\) and

$$N_{n} = N_{\rm iso} - (N_{\rm iso} - \Upgamma)\left[ {{{\left({\frac{{{{\mathbf{s}}}_{K} :{{\mathbf{s}}}_{K}}} {{p_{K}^{2}}}} \right)} \mathord{\left/ {\vphantom {{\left({\frac{{{{\mathbf{s}}}_{K} :{{\mathbf{s}}}_{K}}}{{p_{K}^{2}}}} \right)} {\left({\frac{{{{\mathbf{s}}}:{{\mathbf{s}}}}}{{p_{K}^{2}}}} \right)_{\rm cs}}}} \right.} {\left({\frac{{{{\mathbf{s}}}:{{\mathbf{s}}}}} {{p_{K}^{2}}}} \right)_{\rm cs}}}} \right]^{n}.$$

The term inside square brackets raised to the power n, is a scalar measure of the deviatoric stress level of the centre of the SSE (its value is 1 on the PTE and 0 on the isotropic axis). The original description of the model [1] does not provide an expression for this. A possible realization is as follows: the stress point (p K , s cs) lies on the PTE and has the same mean stress and the same deviatoric direction of the current centre of the SSE. The deviatoric part is given by s cs = λPT s K , such that h(λPT s K ) = 0. Solving for the scalar multiplier,

$$ \begin{aligned} \lambda_{\rm PT} &= \frac{{\left|{p_{K}} \right|}} {{{{\mathbf{s}}}_{K} :{{\mathbf{s}}}_{K}}}\times \left[ { \hbox{sgn} \left({p_{K}} \right){{\mathbf{s}}}_{K} :{\hat \xi} + \sqrt {\left({{{\mathbf{s}}}_{K} :{\hat \xi}} \right)^{2} - {{\mathbf{s}}}_{K} :{{\mathbf{s}}}_{K} \left({{\hat \xi }:{\hat \xi -}k^{2}} \right)}} \right]\hbox{and}\\ N_{n} &= N_{\rm iso} - (N_{\rm iso} - \Upgamma)\lambda_{PT}^{- 2n} , \end{aligned} $$
(7)

where N iso is the specific volume for p = 1 kPa on the isotropic compression line and Γ is the equivalent for the critical state line. N n is the specific volume at p = 1 kPa for different values of the ratio q/p. n is a material constant assuming values between 2 and 3. The subscript “cs” refers to the critical state (on the PTE). The material is completely destructured when α = α*, with the hardening depending solely on the plastic volumetric strain increment. The ISSE will then coincide with the SSE.

Besides isotropic hardening, the model includes also anisotropic hardening, both kinematic and distortional, of the bubble and the SSE. The anisotropic component of SSE’s hardening is determined by the tensor \({\varvec{\upsigma}}_{K},\) the evolution laws of which are:

  1. (a)

    if F < 0, the stress state is inside the SSE and \({\dot{\varvec{ \upsigma}}}_{K} = \left({{{\dot \alpha} \mathord{\left/{\vphantom {{\dot \alpha} \alpha}} \right.} \alpha}} \right){\varvec{\upsigma}}_{K}, \)

  2. (b)

    if F = 0, the stress state is on the SSE and \({\dot{\varvec{\upsigma}}}_{K} = \frac{\dot{\alpha}}{\alpha}\left[ {\varvec{\upsigma}}_{K} + \psi \left({\mathbf{s}} - \chi \frac{p}{p_{K}}{\mathbf{s}}_{K} \right) \right].\)

There is only anisotropic hardening of the SSE when the stress point (and the bubble) reaches it. The anisotropic hardening stabilises when \({\varvec{\upeta}} =\chi \,{\varvec{\upeta}}_{K}.\) The principal stress axes of the anisotropy tensor \({\varvec{\upsigma}}_{K}\) rotate towards the principal stress axes. Thus, there are two more material constants, ψ and χ. The higher the value of ψ, the faster anisotropy evolution takes place. The kinematic hardening of the bubble (PYE), determined by the evolution of the tensor \({\varvec{\upsigma}}_{L} ,\) only takes place when f = 0. There are two distinct situations:

  1. (a)

    if F = 0, the bubble and the SSE are in contact and \({\varvec{\upsigma}}_{L} = (1 - \xi) {\varvec{\upsigma}} - \xi {\varvec{\upsigma}}_{K}, \)

  2. (b)

    if F < 0, the bubble must move in the direction joining the stress state to the conjugate point, \({\varvec{\upsigma}}^{\prime},\) which is the point located on the bounding surface (SSE), F = 0, where the normal has the same direction of the normal at the current stress point, \({\varvec{\upsigma}},\) on the PYE. This implies that

    $${\dot{\varvec{\upsigma}}}_{L} = \frac{\dot{\alpha}}{\alpha} {\varvec{\upsigma}}_{L} + {\dot {\mu}}\, {\varvec{\upbeta}}\,\,\hbox{with} \quad {\varvec{\upbeta}} = \frac{1}{\xi}({\varvec{\upsigma}} - {\varvec{\upsigma}}_{L}) - ({\varvec{\upsigma}} - {\varvec{\upsigma}}_{K}) $$
    (8)

The movement of the bubble inside the SSE must be in the direction of the conjugate point (Fig. 2) so that intersection of both surfaces is avoided when the stress point attains the bounding surface, with F = 0. \(\dot{\mu}\) is a hardening factor found by invoking the consistency condition relative to the PYE, that is, the requirement that the stress point must remain on the PYE, with f = 0, while plastic deformation is occurring, with the implication that \({\dot{f}}= 0.\) The kinematic hardening factor thus obtained is given by

$${\dot{\mu}} = \left(\frac{\partial{f}} {\partial {\varvec{\upsigma}}}:{\varvec{\upbeta}}\right)^{- 1} \left\{\frac{\partial{f}}{\partial {\varvec{\upsigma}}}:{\dot{\varvec{\upsigma}}} - 2\frac{\dot{\alpha}}{\alpha} \left[\frac{1}{c^{2}}\left({{\mathbf{s}} - \frac{p - p_{L}}{p_{K}}{\mathbf{s}}_{K} - {{\mathbf{s}}}_{L}} \right):\left({{{\mathbf{s}}} - \frac{p}{p_{K}}}{{\mathbf{s}}}_{K} \right)+(p - p_{L})p\right]\right\}$$
(9)

The flow rule, defining the magnitude and direction of the plastic strain rate is \( {\dot{\varvec{\upvarepsilon}}}^{p} = \dot{\gamma} _{f} \,{{\mathbf{P}}}_{f}, \) where the tensor \({{\mathbf{P}}}_{f},\) imposing the plastic strain rate direction, assumes the following form:

$${{\mathbf{P}}}_{f} = - \frac{\bar{\lambda}_{1}} {\alpha}\,\hbox{h} ({\varvec{\upsigma}})\,{{\mathbf{I}}} + \frac{1}{c^{2}}\,{{\mathbf{s}}},$$
(10)

with the constant \(\bar{\lambda}_{1}\) responsible for the magnitude of the volumetric strains. Its value also determines the slope in the (p,q) plane of the stress path due to anisotropic (K 0) consolidation. This flow rule in non-associated. For the destructured material (α = α*), the critical state is attained when the stress is simultaneously on the SSE, \({f}({\varvec{\upsigma}}) =0,\) and on the PTE, \(\hbox{h}({\varvec{\upsigma}})=0.\) Under these conditions, the flow rule dictates that the volumetric plastic strain rate, \(\dot{\varepsilon}_{V}^{p} = 0,\) which implies that \(\dot{\alpha} = 0,\) and thus, conditions of perfect plasticity (no hardening) are met. The plastic multiplier \(\dot{\gamma}_{f}\) prescribes the plastic strain rate magnitude and is defined as

$$\dot{\gamma}_{f} = \frac{1} {H_{f}}\frac{\partial{f}} {\partial {\varvec{\upsigma}}}:{\dot{\varvec{\upsigma}}}$$
(11)

or in a strain-controlled process, invoking the elastic law and the flow rule, it becomes

$$\dot{\gamma}_{f} =\frac{\partial{f}} {\partial {\varvec{\upsigma}}}:{{\mathbf{D}}}: {\dot{\varvec{\upvarepsilon}}}\left({H_{f} + \frac{\partial{f}} {\partial {\varvec{\upsigma}}}:{{\mathbf{D}}}:{{\mathbf{P}}}_{f}} \right)^{- 1} $$
(12)

One of the main features of the bounding surface models is that the plastic modulus on the bubble, H f , is interpolated from the plastic modulus, H′′, which is computed on the image point, \({{\varvec{\upsigma}}^{\prime \prime}}\) (Fig. 2). The image point is located at the intersection of the line joining the origin of stress space, 0, to the current stress point, \({\varvec{\upsigma}},\) with the SSE, where F = 0. The value λ such that \(F({\lambda}{\varvec{\upsigma}}) =0\) must be computed, so that \({{\varvec{\upsigma}}^{\prime \prime}} = \lambda {\varvec{\upsigma}}.\) There are two solutions to this quadratic equation that correspond to the two intersection points of the line with the ellipsoid defined by  F = 0. The desired solution is the positive root given by

$$\lambda = {{\left({- B + \sqrt {B^{2} - 4\,A\,C}} \right)} \mathord{\left/{\vphantom {{\left({- B + \sqrt {B^{2} - 4\,A\,C}} \right)} {\left({2\,A} \right)}}} \right.} {\left({2\,A} \right)}} $$
(13)

where \(A = \frac{1}{{c^{2} }}{\left( {{\bf{s}} - \frac{p}{{p_{K} }}{\bf{s}}_{K} } \right)}:{\left( {{\bf{s}} - \frac{p}{{p_{K} }}{\bf{s}}_{K} } \right)} + p^{2} ,\;B = - 2pp_{K} \;{\text{and}}\;C = p^{2}_{K} - \alpha ^{2}\) The plastic modulus at the current stress state, H f , on the bubble (f = 0), may be obtained from the plastic modulus H″ on the image point by means of the following interpolation function

$$H_{f} = H^{\prime \prime}+ \left|{H^{\prime \prime}} \right | \left[ {\left({1 - {\delta \mathord{\left/{\vphantom {\delta {\delta_{0}}}} \right.} {\delta_{0}}}} \right)^{- \gamma} - 1} \right]$$
(14)

where δ is the normalised distance between \({\varvec{\upsigma}}\) and the conjugate point \({\varvec{\upsigma}}^{\prime}\) defined as

$$\delta = \frac{\partial{f}} {\partial {\varvec{\upsigma}}}:{\varvec{\upbeta}}\left({2\alpha \left\| \frac{\partial{f}}{\partial {\varvec{\upsigma}}} \right\|} \right)^{- 1} $$
(15)

with \({\beta} = {{\varvec{\upsigma}}^{\prime}} - {\varvec{\upsigma}}.\) δ0 is made equal to δ each time there is a transition from elastic to elastoplastic behaviour, when δ/δ0 = 1 and H f = ∞. When the stress point is on the \(\hbox{SSE},\; { {\varvec{\upsigma}} = {\varvec{\upsigma}}^{\prime} = {\varvec{\upsigma}}^{\prime \prime}}, \delta=0\; \hbox{and} \; H_{f} = H^{\prime \prime}.\)

Finally, the expression for the plastic modulus on the image point H″, obtained by imposing the consistency condition on the bounding surface (the requirement that the image point must remain on the SSE, \({\dot{{f}}} = 0)\) is H″ = 2ξR T, with

$$T = \left({p^{\prime \prime}- p_{K}} \right)p^{\prime \prime}+ \frac{1}{{c^{2}}}\left({{{\mathbf{s^{\prime \prime}}}} - \frac{{p^{\prime \prime}}}{{p_{K}}}{{\mathbf{s}}}_{K}} \right):\left[ {{{\mathbf{s^{\prime \prime}}}} - \frac{{p^{\prime \prime}}} {{p_{K}}}{{\mathbf{s}}}_{K} + \frac{{p^{\prime \prime}}}{{p_{K}}}\psi \left({{{\mathbf{s^{\prime \prime}}}} - \chi \frac{{p^{\prime\prime}}} {{p_{K}}}{{\mathbf{s}}}_{K}} \right)} \right]$$
(16)

and

$$ R = \frac{1}{\alpha}\left\{{\alpha^{*} \left({\frac{{1 + e}} {{\lambda^{*} - \kappa^{*}}}} \right)\hbox{tr} \,{{\mathbf{P}}}_{f} - \left({\alpha - \alpha^{*}} \right)\left[ {A_{V} \,\hbox{tr} \,{{\mathbf{P}}}_{f} + A_{q}\, \hbox{sgn}\left({\dot \gamma_{f}} \right)\sqrt {\frac{2}{3}} \left\|{\hbox{dev} \,{{\mathbf{P}}}_{f}} \right\|} \right]} \right\}.$$
(17)
Fig. 2
figure 2

Conjugate and image points on the bounding surface

Full size image

3 Numerical implementation

The model described above was programmed in the explicit finite difference code FLAC [12], which is widely used for geotechnical applications. In this way the model can be applied to relevant geotechnical engineering problems such as tunnel construction. Because of the explicit nature of the global solution algorithm used in FLAC, very expensive implicit stress update algorithms for the model should be avoided. In an explicit code, very small time steps (usually corresponding to very small strain increments) must be used anyway, so the stress update algorithm should have a computational cost as low as possible. Hence, an explicit Euler integration scheme, with optional subincrementation, was used.

The point of transition from elastic to plastic behaviour on a given strain increment was found assuming a straight incremental stress path. The solution is the positive root of the following quadratic equation:

$${f} \left({ {\varvec{\upsigma}} + \lambda_{Y} \Updelta {\varvec{\upsigma}} } \right) = A_{\rm I} \lambda_{Y}^{2} + A_{\rm II} \lambda_{Y} + A_{\rm III} = 0 $$
(18)

where \(A_{I} = \left({{1 \mathord{\left/{\vphantom {1 {c^{2}}}} \right.} {c^{2}}}} \right)\left[ {\Updelta {{\mathbf{s}}}:\left({\Updelta {{\mathbf{s}}} - 2\left({{{\Updelta p} \mathord{\left/{\vphantom {{\Updelta p} {p_{K}}}} \right.} {p_{K}}}} \right){{\mathbf{s}}}_{K}} \right) + \left({{{\Updelta p} \mathord{\left/{\vphantom {{\Updelta p} {p_{K}}}} \right.} {p_{K}}}} \right)^{2} {{\mathbf{s}}}_{K} :{{\mathbf{s}}}_{K}} \right] + \Updelta p^{2} ,\)

$$A_{\rm II} = 2\left[ {\frac{1}{{c^{2}}}\left({\Updelta {{\mathbf{s}}} - \frac{{\Updelta p}} {{p_{K}}}{{\mathbf{s}}}_{K}} \right):\left({{{\mathbf{s}}} - {{\mathbf{s}}}_{L} - \frac{{p - p_{L}}}{{p_{K}}}{{\mathbf{s}}}_{K}} \right) + \Updelta p\left({p - p_{L}} \right)} \right]\quad \hbox{and} \quad A_{\rm III} = {f} \left({\varvec{\upsigma}} \right).$$

To prevent the stress point drifting away from the bubble, which invariably happens when using explicit integration, the stress point is projected onto the bubble’s surface in the direction of the its centre, after the plastic correction. The correction is as follows:

$${\varvec{\upsigma}}^{\rm corr} = (1 - \lambda_{C}){\varvec{\upsigma}}_{L} + \lambda_{C} {\varvec{\upsigma}}, \, \hbox{with}\, \lambda _{C} = \left({\sqrt {1 + {{{f} \left({\varvec{\upsigma}} \right)} \mathord{\left/{\vphantom {{{f} \left({\varvec{\upsigma}} \right)} {\left({\xi \,\alpha} \right)^{2}}}} \right.} {\left({\xi\alpha} \right)^{2}}}}} \right)^{- 1}$$
(19)

Results of the model obtained with the stress update procedure described above were successfully verified against known results of the MCC model. It was also verified to converge with decreasing step size. Before being used in a boundary value problem (tunnel excavation), the model was also successfully applied in the reproduction of anisotropic (oedometric) consolidation and conventional drained and undrained triaxial compression tests (with assumed homogeneous strains).

4 Overconsolidation and initial anisotropy

The soil consolidation process takes place under zero lateral strain conditions and is eventually followed by unloading, which might be due to erosion of overlying strata. This is the overconsolidation process, oedometric loading followed by partial unloading. The overconsolidation process is closely linked to the initial anisotropy of the soil. In fact, it can be said that the soil’s initial or inherent anisotropy is the anisotropy induced by the overconsolidation process. The soil structure (or fabric) may also affect the soil’s anisotropy, but, being a distinct aspect from overconsolidation, it will not be addressed here.

The axisymmetric stress paths associated with the overconsolidation process, which will result in the initial stresses, are illustrated in Fig. 3. During the consolidation process the soil follows the straight path from 0 to A. This path is associated with normally consolidated states and the earth pressure coefficient, K nc0 , is constant along the path. It is then followed by the curved unloading path from A to B. This path is tangent to the elastic unloading line at A, the slope of which depends on the Poisson’s ratio, ν, for isotropic elasticity. The stress states on the unloading line are overconsolidated and the coefficient of earth pressure, K oc0 , is variable and increases with increasing unloading. The unloading process is limited (becomes tangent to at the origin) by the zero vertical tension line, K 0 = ∞, because soil, unless it is structured, cannot withstand tensile effective stresses.

Fig. 3
figure 3

Consolidation and unloading stress paths (zero lateral strain)

Full size image

There is experimental evidence that the normal consolidation process distorts the yield surface such that its axis tends to become aligned with the normal consolidation line in stress space [6, 8, 21]. It is mainly this distortion of the yield surface that is responsible for the plastic anisotropic behaviour.

If the stress \(({\varvec{\upsigma}})\) and anisotropy \(({\varvec{\upsigma}}_{K})\) tensors are axisymmetric (two principal values are equal) and share the same principal axes, the PYE and the SSE can be simplified to:

$${f} = \left({{2\mathord{\left/ {\vphantom {2 {3c^{2}}}} \right.} {3c^{2}}}} \right)\left[ {q - q_{L} - \left({p - p_{L}} \right)\left({{{q_{K}} \mathord{\left/ {\vphantom {{q_{K}} {p_{K}}}} \right.} {p_{K}}}} \right)} \right]^{2} + \left({p - p_{L}} \right)^{2} - (\xi \alpha)^{2} = 0$$
(20)

and

$${F} = \frac{2}{3c^{2}}\left({q - p\frac{{q_{K}}} {{p_{K}}}} \right)^{2} + \left({p - p_{K}} \right)^{2} - \alpha^{2} = 0$$
(21)

with

$$q_{\left(\bullet \right)} = \sigma_{1}^{\left(\bullet \right)} - \sigma_{3}^{\left(\bullet \right)}\, \hbox{and}\,\sigma _{2}^{\left(\bullet \right)} = \sigma_{3}^{\left(\bullet \right)} $$

Under these conditions, the SSE and the bubble can be represented as ellipses in the (p, q) plane. This property is used in the next two simulations to illustrate some of the main characteristics of this model’s anisotropic hardening. The first example concerns an initially anisotropic material (q K  ≠ 0) that undergoes isotropic compression (see Fig. 4). The initial SSE is aligned with a stress path having a slope corresponding to K 0 = 0.5. The initial anisotropy is gradually erased and the material becomes isotropic.

Fig. 4
figure 4

Initially anisotropic soil under an isotropic strain path

Full size image

The initial anisotropy of the soil can be related to the value of K 0 assuming that it was consolidated under a zero strain condition in the plane of symmetry (horizontal). The SSE ellipse is then aligned with a line with slope \(\eta_{0} = {{q_{0}} \mathord{\left/ {\vphantom {{q_{0}} {p_{0}}}} \right.} {p_{0}}} = {{3(1 - K_{0})} \mathord{\left/{\vphantom {{3(1 - K_{0})} {\left({1 + 2K_{0}} \right)}}} \right.} {\left({1 + 2K_{0}} \right)}}.\) If p K = α, the anisotropy tensor deviatoric component in the direction of the applied strain is \(s_{1}^{K} = {{2\alpha (1 - K_{0})} \mathord{\left/{\vphantom {{2\alpha (1 - K_{0})} {\left({1 + 2K_{0}} \right)}}} \right.} {\left({1 + 2K_{0}} \right)}}\) and in the plane of symmetry is \(s_{3}^{K} = s_{2}^{K} = - {s_{1}^{K}}/2.\) The value of K 0 must be lower than one. Values of K 0 higher than one, meaning η0 < 0, are only possible if there is unloading, in which case the anisotropy direction would not adjust, or if triaxial compression under extension conditions occurs (ɛ1 = 0 and ɛ3 = ɛ2 > 0).

A different situation occurs when an initially isotropic material is submitted to K 0 consolidation. Here the SSE is gradually sheared until it aligns itself with the K 0 consolidation line (only if χ = 1). This process is shown in Fig. 5. The stress path followed by the material defines the anisotropy (induced anisotropy). The normal consolidation followed by unloading stress paths, together with the sequence of yield and bounding surfaces given by the bubble model, is shown in Fig. 6.

Fig. 5
figure 5

Initially isotropic soil under K 0 consolidation

Full size image
Fig. 6
figure 6

Normal consolidation and unloading with bubble model

Full size image

5 Tunnel construction

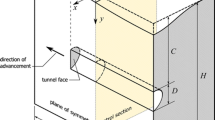
In this section, the effect of the initial stresses and initial plastic soil anisotropy in the displacements surrounding an idealized scenario of a tunnel excavation is analysed. The tunnel has a circular cross-section with a diameter of 10 m and its crown is 20 m below the ground surface. The ground where the tunnel is excavated is an overconsolidated hard clay. The soil is saturated and the water table is at the ground surface. The numerical analyses are made with the program FLAC [12], under plane strain and undrained conditions. Due to symmetry conditions only half the tunnel is considered. The soil model used is the one described above. The finite difference structured (regular) mesh has 800 elements with a larger number of smaller elements concentrated around the tunnel opening. Each element has 4 nodes and is the result of the superposition of the two possible arrangements of two triangular sub-zones. This is done to avoid element locking under isochoric plastic deformation. The relaxation of the tunnel boundary forces takes place in 10,000 increments and a final equilibrium state is considered to have been achieved when the relative force residual is less than 10−7.

Some of the material constants used are taken from Kavvadas and Amorosi [13], who used a model sharing many features with the current one, for Vallericca clay. The latter is a stiff, overconsolidated, medium plasticity and activity, natural Plio-Pleistocene marine clay with about 30% calcium carbonate content. The material parameters used are B 0 = 12,500 kPa, G 0 = 9,375 kPa, p r  = 100 kPa, m = 1, λ* = 0.118, κ* = 0.012, n = 2, N iso = 2.15, Γ = 2.08, v 0 = 1.363, c = 0.85, ξ = 0.08, k = 0.85, p K  = α = 500 kPa, χ = 1, ψ = 0, γ = 10, \(\bar \lambda_{1}=0.22 \) and \({\hat{\varvec{\xi}}}=0.\) In these simulations, induced anisotropy is not modelled so ψ = 0. Because destructuring is not considered in the analysis the associated material constants \((\zeta_{v},\zeta_{q} ,\, \eta_{v}, \, \eta_{q}, \, \hbox{and} \, \theta_{q})\) are zero. The same material constants apply to all analyses.

The soil is assumed to have a constant (with depth) pre-consolidation mean effective stress p max = 1,000 kPa. This corresponds to a maximum effective vertical stress

$$\sigma_{\hbox{v}}^{\rm max} = {{\left({3p_{\rm max}} \right)} \mathord{\left/{\vphantom {{\left({3p_{\rm max}} \right)} {\left({1 + 2K_{0}^{nc}} \right)}}} \right.} {\left({1 + 2K_{0}^{nc}} \right)}},$$
(22)

with the normally consolidated coefficient of earth pressure given by the well known empirical formula

$$K_{0}^{\rm nc} = 1 - \sin \phi_{\rm cs}, $$
(23)

where ϕcs is the friction angle at the critical state. The value of c = k = 0.85 corresponds to ϕcs = 26.3°, which gives K nc0 = 0.56. The value of K nc0 then determines the components of the deviatoric tensor s K , which is responsible for the anisotropy, as described above. The material constant \({\bar{\lambda}}_{1} \) was then adjusted such that the model produces a normal consolidation stress path with the desired slope. The value of 0.22 was obtained.

The assumption of a constant pre-consolidation pressure results in an overconsolidation ratio (OCR = ratio of the maximum effective vertical stress to the current one) increasing with the proximity to the ground surface. The overconsolidated coefficient of earth pressure can be obtained from the empirical formula [20]

$$K_{0}^{\rm oc} = K_{0}^{\rm nc} \,OCR^{w}$$
(24)

with w = 0.4 for this type of soil. The empirical formula with w = 0.66 agrees well with the unloading response of the bubble model. As the OCR varies with depth so does the coefficient of earth pressure and this variation depends on the assumed value of w.

Two cases are considered: one where the excavation of the tunnel takes place without support and another where a linear elastic sprayed concrete lining (E = 4.8 MPa and ν = 0.2), 0.25 m thick, is applied after 50% stress relief. For the first case two distinct initial stress situations are analysed: one for the empirically suggested exponent value of w = 0.4, and the other for value consistent with the soil model, w = 0.66. For the second case, with the lining, only the value w = 0.4 is used. For both cases, and in order to evaluate the effect of the initial plastic anisotropy, an isotropic instance, with the bounding surface having the same isotropic length, but aligned with the isotropic axis, with s K  = 0, is also computed.

5.1 Excavation without lining and w = 0.4

The horizontal displacements for the excavation without lining are presented for a vertical line located 6 m from the tunnel’s axis in Fig. 7. The initial stress field is computed from the empirical formula for the overconsolidated earth pressure coefficient with exponent w = 0.4, which is rather different from the one obtained from the bubble model.

Fig. 7
figure 7

Horizontal displacements along vertical line (w = 0.4)

Full size image

For comparison purposes the response considering only the nonlinear elastic part of the soil model is also presented. Negative displacements are in the direction of the tunnel’s axis. The zero value in the vertical distance axis is aligned with the tunnel’s axis.

The horizontal displacements in the isotropic case are higher and the curve is narrower than in the anisotropic one. In Fig. 8, the vertical displacements along a horizontal line located 6 m above the tunnel’s axis are shown. Negative displacements are settlements. The zero value in the horizontal distance axis is aligned with the tunnel’s axis.

Fig. 8
figure 8

Vertical displacements along horizontal line (w = 0.4)

Full size image

The maximum settlements are similar for both anisotropic and isotropic cases but, contrary to what occurs with the horizontal displacements, the anisotropic distribution curve is narrower. The excess displacement values obtained in the elastoplastic analyses relative to the elastic one is the product of the plastic strain mechanisms of the bubble model.

In Fig. 9, the isostatics for isotropic and anisotropic instances are superposed. The isostatics are curves that are tangent at every point to the principal stress vectors. It can be seen that the principal stresses directions are not coincident.

Fig. 9
figure 9

Isostatics for isotropic (dashed line) and anisotropic cases (w = 0.4)

Full size image

5.2 Excavation without lining and w = 0.66

Here the difference from the previous case resides in the initial stress field that results from the application of the earth pressure coefficient empirical formula for overconsolidated soils with exponent w = 0.66. This would agree with the initial stress field obtained if the bubble model were used to model the normal consolidation and unloading processes.

In contrast to the previous case the horizontal displacement magnitudes are higher in the anisotropic situation than in the isotropic one (see Fig. 10). Also in contrast to the previous case, the anisotropic vertical displacements are greater than the isotropic ones (see Fig. 11). As in the previous case the anisotropic curve is narrower. The initial stresses have a great influence on the displacements and affect the plastic anisotropy effect. In this case, they are entirely consistent with the model but not necessarily more realistic than the case with w = 0.4.

Fig. 10
figure 10

Horizontal displacements along vertical line (w = 0.66)

Full size image
Fig. 11
figure 11

Vertical displacements along horizontal line (w = 0.66)

Full size image

Near the ground surface, the horizontal displacements take place in the direction away from the tunnel. This is in contradiction with what is usually observed and does not occur for w = 0.4. With the proximity to the ground surface, the OCR values become very large and, accordingly, the empirical expression predicts very large values of K 0. These values will eventually cause the initial stresses close to the ground surface to be outside the PTE, in the softening and dilatant region. The load transfer from the tunnel excavation will tend to increase the horizontal stresses, even if it is very small, causing the soil to fail in extension with softening and dilatancy. This effect will be more pronounced, the higher the value of w is. In order to avoid this, the value for K 0, should probably be limited so that the initial stresses are not outside the PTE. Also, in most tunnel excavations, the water table is below the ground surface, creating an unsaturated region near the surface, which in the case of clay soils, is associated with large capillary suctions. This would considerably change the soil behaviour near the ground surface. An unsaturated soil model would be needed to correctly model this effect.

In Fig. 12, the deviatoric plastic strain contours for 1% strain are shown for the isotropic and anisotropic cases, as well as both values of w. The anisotropic and isotropic cases are represented, respectively on the right and left sides of the tunnel. The value w = 0.4 is associated with a thicker line than the value w = 0.66. In the anisotropic case, the plastic region develops in the vertical direction, both below the invert and above the crown, with a larger extension in the case of w = 0.66. In contrast, the isotropic version’s plastic region develops more in the horizontal direction, w = 0.4, or uniformly all around, w = 0.66.

Fig. 12
figure 12

Contours of deviatoric plastic strain (1%). Right side anisotropy. Left side isotropy. Thick line: w = 0.4. Thin line: w = 0.66

Full size image

In all cases there is a marked pore pressure reduction around the opening due to dilatancy which, under undrained conditions, is associated with an increase in the mean effective stress and shear strength.

Because plastic anisotropy is mainly anisotropy of strength, but also with influence on the direction of the plastic strains, the influence of the initial stress state, i.e. where it is located relative to the bounding surface, on the model response is considerable. Thus, great care should be applied when defining the initial stress field such that it is realistic and consistent with the models’ internal variables initial values.

The use of a pre-consolidation mean effective stress varying with depth might improve the realism of the analysis, being more consistent with an overconsolidated formation.

5.3 Excavation with lining

In the case of the excavation with lining, only the initial stress field obtained with w = 0.4 is considered. In terms of horizontal displacements, there is not much difference between the anisotropic and isotropic instances, with the magnitude being a bit smaller in the former and the curve being a bit narrower in the latter (see Figure 13).

Fig. 13
figure 13

Horizontal displacements along vertical line on lined tunnel (w = 0.4)

Full size image

There is a more pronounced difference in terms of the vertical displacements with the anisotropic magnitude being greater and its curve narrower (see Fig. 14). The differences between the anisotropic and isotropic cases are smaller in the lined excavation case because the elastic strains are a greater proportion of the total strains.

Fig. 14
figure 14

Vertical displacements along horizontal line on lined tunnel (w = 0.4)

Full size image

6 Conclusions

A model for structured overconsolidated soils with initial and induced anisotropy was successfully implemented in the explicit finite difference code FLAC. The influence of the initial stresses and the initial plastic soil anisotropy in the ground displacements around a shallow tunnel were analysed under plane strain conditions. Some of the material constants used in the analysis were taken from Vallericca clay [13]: a stiff, overconsolidated marine clay with medium plasticity and activity. The destructuration process was not taken into account in the analyses. A constant value of the preconsolidation mean effective stress with depth was used, resulting in an OCR increase with the proximity to the ground surface. The overconsolidated coefficient of earth pressure can be obtained by an empirical correlation [20], in which the OCR is affected by an exponent w. The value of w = 0.66 was found to be in close agreement with the response given by the bubble model, however the value w = 0.4 is usually suggested for this type of ground. These two values, which determine the initial stress conditions, were taken into account in the tunnel’s numerical analysis. No lining was applied in this first series of analyses. In a second series of analyses, a sprayed concrete lining was placed after a 50% stress relief resulting from the excavation. In this case only the overconsolidation exponent value w = 0.4 was considered. An isotropic nonlinear elastic calculation was also performed for all the analysed cases.

In the case of smaller initial horizontal stresses (w = 0.4), the consideration of initial plastic anisotropy produced smaller ground displacements. Maximum horizontal displacements are characteristically 25% smaller and maximum settlements are typically 10% smaller than the corresponding results obtained under the assumption of initial plastic isotropy, see Figs. 7 and 8.

In the case of larger initial horizontal stresses (w = 0.66), the consideration of initial plastic anisotropy produced larger ground displacements. Maximum horizontal displacements are characteristically 10% larger and maximum settlements are typically 75% larger than the corresponding results obtained under the assumption of initial plastic isotropy, see Figs. 10 and 11.

From the results of the analyses performed, it is clear that both initial stresses and soil anisotropy have a considerable influence on the ground displacements induced by tunnel excavation. There is a non-trivial interaction between the stress anisotropy, expressed by the K 0 value, and the strength anisotropy of the soil.

It was shown that, for the same initial stresses, the anisotropic response is considerably different from the isotropic one. Because the former is in better agreement with experimentally observed clay behaviour [5, 8, 21], it should be used in order to obtain more realistic ground displacements.

The plastic regions obtained under conditions of strength anisotropy develop in the vertical direction, both above the crown and below the invert. The isotropic plastic regions develop horizontally or evenly around the tunnel. In the w = 0.4 scenario, the value of K 0 is approximately equal to 1 at the level of the tunnel. In the w = 0.66 scenario, the value of K 0 at the tunnel’s level is between 1.5 and 2.

In all cases a marked pore pressure reduction around the opening due to dilatancy, associated with an increase in the mean effective stress and shear strength, is predicted.

The assumed initial stress field has a great influence on the results, both for isotropic and anisotropic soil response. Its choice is thus critical to achieve realistic predictions. In order to avoid a state of incipient failure close to the ground surface, the value of K 0 should only be marginally outside the critical state surface (PTE), if at all.

The importance of the subject requires further analyses involving case studies of monitored tunnel excavations in hard clays together with more experimental research into the capabilities of the model to reproduce real overconsolidated soil behaviour, including work on identification of material model’s constants. The simultaneous influence of elastic and plastic anisotropy should also be assessed in future works. Extension from plane strain conditions to full 3D analyses should also be considered.