1 Introduction

The study of unsaturated soils has a long but somewhat uneven history. The role of suction on the behaviour of unsaturated soils was early recognized (e.g. [15]) and in the late 1950s and 1960s, there was intense experimental work (e.g. [5, 6]) where, generally, laboratory results were interpreted in terms of newly defined effective stresses for unsaturated soils. This period was followed by a relative lull in the fundamental study of the mechanical behaviour of unsaturated soils reinforced perhaps by the relative failure of the proposed effective stress expressions for this type of soils [35]. During that period, unsaturated soils tended to be lumped together with other materials in soil categories variously described as “difficult soils”, “regional soils”, “special soils” or other similar names.

To set the study of unsaturated soils on a proper course, it was essential to realize that any soil could be unsaturated and, therefore, there could be no reason why a fundamental approach, already successful in the case of saturated soils, could not be applied also to this type of materials. As a matter of principle, there is nothing special in an unsaturated soil apart from the simple fact that some part of the pore space is occupied by air (or other non-wetting fluids). Instead of considering unsaturated soils as a separate class of materials, there should be a seamless continuity with the by now well-established understanding of saturated soil behaviour. Important steps in this direction were given by the separate consideration of two stress variables in the definition of state surfaces [47], an idea already anticipated in [6, 12]. The use of state surfaces and the theoretical and experimental justification of using two independent stress variables were further reinforced by the work of Fredlund and Morgenstern [19] and Fredlund and Rajardho [20]. More comprehensive evidence on relevant stress variables has been provided by Tarantino et al. [61].

Since at least the 1980s, there has been a new explosion of interest on unsaturated soils resulting in a large amount of theoretical developments, laboratory investigations, methods of suction control and measurement, and, to a lesser extent, field applications. A fundamental tool to organize the observations obtained from this systematic research is the development of suitable constitutive laws capable of reproducing, to a satisfactory extent, the most important features of the mechanical behaviour of unsaturated soils. Overcoming the limitations of the state surface approach, elastoplasticity has proved a very successful framework for developing constitutive laws appropriate for unsaturated soils. Those laws lie at the core of general theoretical coupled formulations devised for this type of materials that include mechanical deformation, gas flow, liquid flow and, often, thermal aspects (e.g. [23, 40, 49, 62]). In this paper, a summary review of developments of elastoplastic models for unsaturated soils is presented. Inevitably, more attention is given to the advances with which the authors have been associated. For space reasons, the theoretical frameworks and numerical algorithms through which the models are applied to the analysis of engineering problems are not examined. A number of those issues have been reviewed and discussed in [55, 56].

2 Basic elastoplastic models

2.1 Elastoplastic models using net stresses

One of the first elastoplastic models designed explicitly for describing the mechanical behaviour of unsaturated soils was presented in [3] and, in a more summary form, in [28]. The model was formulated adopting net stresses (σ ij  − u aδ ij ) and suction (s = u a − u w) as fundamental variables. σ ij are total stresses, u a the air pressure, u w the water pressure and δ ij Kroneckers’s delta. The suction defined as u a − u w can be called capillary suction. Other measures of suction could in fact be adopted, but a full consideration of this possibility is outside the scope of this paper (see, for instance [29]). The model, with some slight modifications, came to be known as the Barcelona Basic Model (BBM) and can perhaps be summarized by Fig. 1, where a three-dimensional yield surface in p–q–s space is depicted. p is the mean net stress and q is (σ1 − σ3). Under saturated conditions (s = 0), the yield surface corresponds to the Modified Cam Clay (MCC) ellipse and the size of the elastic domain increases as suction increases. The rate of increase, represented by the loading-collapse (LC) curve is one of the fundamental characteristics of the model.

Fig. 1
figure 1

Three-dimensional representation of the yield surface in the BBM

Full size image

One of the main objectives of the development of this model was to try to insert unsaturated soil mechanics into the mainstream of current and past developments in saturated soil mechanics. This aim guided many of the choices adopted in the definition of the model and explains the rough simplicity of many of its features. It was intended that the model could be used to make qualitative predictions by simple hand manipulation in the same way that the conceptual critical state framework is often used. This implied the adoption of net stresses as one of the basic stress variables. If other stress variables are used, it is quite difficult to follow conventional laboratory stress paths in an effective manner. Indeed, the first use of the concepts underlying the BBM model was presented in [2], before the mathematical formulation was fully developed. The need for a clear connection with saturated soil mechanics led to the adoption of the MCC as the reference model in such a way that the BBM constitutive law becomes the classic MCC model when s becomes zero (i.e. on reaching saturation). In fact many other elastoplastic-saturated models could have been used, as the unsaturated formulation is general.

Further examples of the very simplistic assumptions adopted in the model are the use of straight lines for the void ratio–ln p relationships (implying a continuous increase of the collapse strains upon wetting) or the linear increase of apparent cohesion with suction. Simplicity also implies that only a limited number of additional parameters are required. In spite of this lack of complexity, the model can describe a large number of typical features of the mechanical behaviour of unsaturated soils in a natural unforced way [2, 3]. Some examples are the variation of wetting-induced swelling or collapse strains depending on the magnitude of applied stresses, the reversal of volumetric strains observed sometimes during wetting-induced collapse, the increase of shear strength with suction, the stress path independency associated with wetting paths and the opposite when the stress path involves drying or the apparent increase of preconsolidation stress with suction.

Other models were quickly developed that, while keeping the same core of basic assumptions, sought to improve some of the shortcomings of the original BBM. Thus, Josa et al. [38] used non-linear relationships for the variation of void ratio with ln p so that collapse strains did not increase indefinitely but they went through a maximum before reducing to zero at high stresses. Wheeler and Sivakumar [67] used model functions more closely based on experimental results and Cui et al. [16] adopted a saturated yield function typical of anisotropically consolidated soils.

2.2 Elastoplastic models using alternative stress variables

The choice of appropriate stress variables for unsaturated soils has often been an intensively debated issue, often in connection with the possibility of defining a single effective stress measure. As pointed out in Jommi [36]: “in fact, no single stress variable has ever been found which, substituted for effective stress, allows for a description of all the aspects of the mechanical behaviour of a given soil in the unsaturated range”. A second variable is generally required to represent the stabilizing influence of suction on intergranular forces and the volumetric effects of its removal or weakening, by wetting.

As summarized by Gens [26], the two stress variables used by most (though not all) unsaturated constitutive models can be expressed as

$$ (\sigma _{{ij}} - u_{{\text{a}}} \delta _{{ij}} ) + \mu _{1} (s, \ldots )\delta _{{ij}}\;{\text{;}}\;\mu _{2} (s, \ldots )$$
(1)

where μ1 and μ2 are functions of suction s and, sometimes, of other variables as well. The authors advocate the use of the term constitutive stress, σ c, for the first stress variable in order to emphasize the fact that it is not the only stress variable required to describe the full unsaturated soil behaviour. Although tensor functions could be used, most constitutive models assume that μ1 and μ2 are scalars.

Depending on the expression for μ1, three main classes of models can be distinguished: (1) μ1 = 0, (2) μ1(s) function of suction but not of degree of saturation and (3) μ1(s, S r) dependent on suction and degree of saturation (S r).

The first case corresponds to the use of net stresses, as in the models discussed in the previous section. Although it is the simplest and most practical choice in terms of stress path representation, it poses difficulties when trying to incorporate hydraulic hysteresis effects. In addition, this class of models requires an explicit variation of apparent cohesion with suction. This gives more flexibility to the model at the cost of additional assumptions. This type of formulation may encounter difficulties in the transition between unsaturated and saturated states although they can be overcome by applying special techniques [63].

In the second case, the definition of constitutive stress includes explicitly the suction but not the degree of saturation [24, 41, 46, 48, 50, 51]. The increase of strength with suction is implicit in the definition of constitutive stress and it does not require an additional specific relationship. Stress path representation is now less simple. Transition between unsaturated and saturated states is again not straightforward, even when the desaturation suction (or air-entry value) is adopted as baseline. Hydraulic hysteresis effects are not easily reproduced either.

In contrast, no special difficulties arise in unsaturated–saturated transition when, in the third case, the constitutive stress includes a dependency on stress and degree of saturation [7, 36, 37, 57, 59, 66]. Hydraulic hysteresis effects are also naturally incorporated and the strength increase with suction results directly from the definition of the constitutive stress. Naturally, the representation of stress paths is now more complex and it becomes impossible if, as it is often the case, data on water content is not available or unreliable. In any case, all constitutive models reviewed share the same core of assumptions: (1) use of two independent stress variables, (2) formulation of some type of LC yield surface, and (3) use of a saturated model as a limiting case.

The classic Bishop’s equation for effective stress is an instance of the third type of constitutive stress:

$$ (\sigma _{{ij}} )_{{\text{c}}} = \sigma _{{ij}} - u_{{\text{a}}} \delta _{{ij}} + \chi (S_{{\text{r}}} )(u_{{\text{a}}} - u_{{\text{w}}} )\delta _{{ij}} . $$
(2)

A popular form of the above equation results when χ is considered equal to degree of saturation, S r. Then,

$$\begin{aligned} (\sigma _{{ij}} )_{{\text{c}}} & = \sigma _{{ij}} - u_{{\text{a}}} \delta _{{ij}} + S_{{\text{r}}} (u_{{\text{a}}} - u_{{\text{w}}} )\delta _{{ij}}\\ & = \sigma _{{ij}} - (1 - S_{{\text{r}}} )u_{{\text{a}}} \delta _{{ij}} - S_{{\text{r}}} u_{{\text{w}}} \delta _{{ij}} . \\ \end{aligned} $$
(3)

Expression 3, often called Bishop’s stress, has been found to represent the average stress acting on the solid phase by Hassanizadeh and Gray [31] from the entropy inequality exploited via the Coleman-Noll procedure, by Lewis and Schrefler [43] using volume averaging, and by Hutter et al. [34] on the bases of mixture theory. However, this apparent coincidence between different approaches does not imply necessarily that this stress variable must be used in the definition of constitutive models.

In this context, the contribution of Houlsby [32] has provided much needed clarification of this issue. Houlsby [32] showed that, under reasonably general conditions, the rate of work input (W) per unit volume of unsaturated soil is (the work dissipated by flow of fluids has not been included):

$$ \ifmmode\expandafter\dot\else\expandafter\.\fi{W} \equiv u_{{\text{a}}} n(1 - S_{{\text{r}}} )\ifmmode\expandafter\dot\else\expandafter\.\fi{\rho }_{{\text{a}}} /\rho _{{\text{a}}} - (u_{{\text{a}}} - u_{{\text{w}}} )n\ifmmode\expandafter\dot\else\expandafter\.\fi{S}_{{\text{r}}} + {\left[ {\sigma _{{ij}} - {\left( {S_{{\text{r}}} u_{{\text{w}}} + (1 - S_{{\text{r}}} )u_{{\text{a}}} } \right)}\delta _{{ij}} } \right]}\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }_{{ij}} $$
(4)

where ρa is the air density, n, the porosity and ε ij the strains. Neglecting the term for air compressibility, Eq. 4 indicates that the average solid stress of Eq. 3 is work-conjugate with the soil skeleton strain whereas the suction, s, is work conjugate with the strain-like variable \( - n\ifmmode\expandafter\dot\else\expandafter\.\fi{S}_{{\text{r}}} . \) It is equally valid to select as basic stress variable the quantity ns (called modified suction in [66]), with minus the variation of degree of saturation, \( - \ifmmode\expandafter\dot\else\expandafter\.\fi{S}_{{\text{r}}} , \) as the work conjugate variable.

However, the above decomposition of the work input rate expression is not the only possible one. Rearranging Eq. 4, the following expression, in which net stresses explicitly appear, can be obtained:

$$ \ifmmode\expandafter\dot\else\expandafter\.\fi{W} \equiv u_{{\text{a}}} n(1 - S_{{\text{r}}} )\ifmmode\expandafter\dot\else\expandafter\.\fi{\rho }_{{\text{a}}} /\rho _{{\text{a}}} - (u_{{\text{a}}} - u_{{\text{w}}} )(\ifmmode\expandafter\dot\else\expandafter\.\fi{v}_{{\text{w}}} /v) + [\sigma _{{ij}} - u_{{\text{a}}} \delta _{{ij}} ]\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }_{{ij}} $$
(5)

where net stresses are work-conjugate with soil skeleton strains and \( - \ifmmode\expandafter\dot\else\expandafter\.\fi{v}_{{\text{w}}} {\text{/}}v \) is the work-conjugate variable of the suction. v is the specific volume (1 + e) and v w is equal to (1 + S r e), e is the void ratio. From this point of view, Bishop stresses and net stresses stand on an equal footing and the matter of adopting one or the other must be decided using criteria of convenience. It should be pointed out, however, that only the choice of Bishop stress and modified suction results in work-conjugate strain increments that are integrable [32, 66].

As indicated above, the stress variables chosen to represent the independent effects of suction, μ2(s,...), are invariably scalars. However, the main effect of suction (at least in granular materials) is the generation of capillary interparticle forces normal to the contacts. It would be reasonable to expect, as pointed out by Li [44], that the stress variable should incorporate some kind of fabric measure of the soil, a variable that no longer would be a scalar. Unfortunately, the practical applicability of this idea is difficult due to the complexity of determining the soil fabric and its variation as the soil deforms.

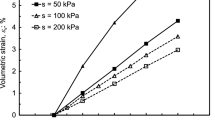
On a simpler level, Gallipoli et al. [22] have introduced a new scalar variable, ξ, that is a rough measure of the intergranular bonding due to water menisci. In this way, the independent effect of capillary forces between particles can be readily accounted for. Therefore, variable ξ takes the role of μ2 and is defined as ξ = f(u a  − u w)(1 − S r) where f(u a  − u w) represents the variation of the interparticle force with suction and (1 − S r) accounts for the number of water menisci per unit volume of the solid fraction. Analysing experimental results, it has been found that the excess of void ratio of an unsaturated soil over the stable saturated void ratio is a unique function of the new variable ξ (Fig. 2). On this basis, and using Bishop’s stress as constitutive stress variable, an elastoplastic constitutive model can be developed capable of accounting for many features of unsaturated soil behaviour in a rather economical way [22].

Fig. 2
figure 2

Normal compression lines at constant suction in terms of average skeleton stress or Bishop’s stress. a Data from Sharma [54]. b Data from Sivakumar [58]. Excess of void ratio of an unsaturated soil over the stable saturated void ratio as a function of the bonding variable ξ. c Data from Sharma [54]. d Data from Sivakumar [22, 58]. Average skeleton stress corresponds to Bishop’s stress

Full size image

3 Coupled hydraulic models

A glaring omission of the BBM and other early formulations was the lack of a specific model to describe the variation of water content or degree of saturation due to changes of stresses and/or suction. If the mechanical model is defined in terms of net stresses, the consequences are limited as there is no direct coupling between hydraulic and mechanical model. Thus in the BBM, hydraulic behaviour was simply defined in terms of a state surface. However, when degree of saturation or other hydraulic parameters enter the definition of the constitutive model, the hydraulic-mechanical coupling must be carefully considered. In this context, Houslby’s expressions, 4 or 5, linking mechanical and hydraulic variables, are especially relevant.

The issue of the hydraulic component of the constitutive model was first addressed by Wheeler [65] and Dangla et al. [17]. Probably, the first full attempt to couple hydraulic behaviour with a mechanical model for unsaturated soil was presented by Vaunat et al. [64]. They described a constitutive law that addresses the irreversible behaviour of unsaturated soils upon wetting and drying, with particular attention to the phenomenon of hydraulic hysteresis, i.e. the fact that the relationship between degree of saturation (or other hydraulic parameters) and suction is different when the soil is wetted from that obtained when drying the same soil. The model is built on the BBM, but incorporates two additional yield surfaces derived from hydraulic hysteresis. One yield surface defines the plastic changes in the water content during drying (suction increase, SI) and the other during wetting (suction decrease, SD). These two yield surfaces are coupled as the movement of one will cause the movement of the other, but not coupled with the load-collapse (LC) yield surface. By incorporating the SI and SD yield surfaces with hydraulic hysteresis, this model is able to predict the irreversible change of degree of saturation during cyclic wetting and drying.

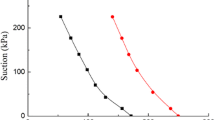
More recently, Wheeler et al. [66], based on Buisson and Wheeler [10], presented an elastoplastic constitutive model that also fully couples hydraulic hysteresis (Fig. 3a) with the mechanical behaviour of the unsaturated soil. For stress variables, they adopted Bishop’s stress and modified suction, s* = ns. According to Eq. 4, the work-conjugate variables are strains and degree of saturation. Wheeler et al. [66] suggested that, using those variables, the LC yield surface can be simplified to a vertical straight line and the SI and SD yield surfaces, arising from hydraulic hysteresis, can be simplified to horizontal straight lines (Fig. 3b). The three yield surfaces are fully coupled with one another, as the movement of one will cause movement of the other two. The model is able to predict, for an unsaturated soil, a number of irreversible behaviour features in an economical way.

Fig. 3
figure 3

a Model for hysteretic water retention behaviour. b Load collapse (LC), suction increase (SI) and suction decrease (SD) yield curves for isotropic stress states [66]

Full size image

A model of the same type has been recently presented by Sheng et al. [57] showing that it can be cast in the thermodynamic framework proposed by Collins and Houlsby [14]. In this case the stress variables are Bishop’s stress and suction, not modified suction. Although the use of modified suction provides some advantage in thermodynamical considerations, there is no essential difference between the two stress quantities as the porosity n plays a role similar to a scaling parameter. The hysteretic water retention model is presented in Fig. 4a; it is composed of a wetting and a drying curve with scanning curves spanning the two. No dependency on void ratio is introduced. The two main water retention curves correspond to the SI and SD yield surfaces that together with the LC yield curve constitute the mechanical part of the model (Fig. 4b). In this particular model, the yield surfaces are not coupled but move independently of each other.

Fig. 4
figure 4

a Hysteretic hydraulic behaviour under constant void ratio. b SI, SD and LC yield surfaces in three-dimensional space [57]

Full size image

Accepting the hypotheses that led to expression 4, and neglecting the air compressibility term, the plastic component of the work input rate is

$$ {\text{d}}W^{{\text{p}}} = ({\varvec{\upsigma}}_{ij} )_{{\text{c}}} {\text{d}}{\varepsilon}_{ij}^{{\text{p}}} + ns{\text{d}}S^{{\text{p}}}_{{\text{r}}} $$
(6)

where (σ ij )c is the constitutive (Bishop) stress.

For uncoupled materials, where the elastic modulus is independent of the plastic strains, the plastic work increment can be decomposed into two components [13]:

$$ {\text{d}}W^{{\text{p}}} = {\text{d}}\psi _{2} + {\text{d}}\phi $$
(7)

where ψ2 is the part of the Helmholtz free energy that depends on plastic strains only and dφ is the dissipation increment. The basic thermodynamical requirements on any constitutive model are that (1) the dissipation dφ is strictly positive for any non-zero plastic strain, and (2) that the free energy dψ2 yields zero when integrated over a closed loop of plastic strain.

In terms of triaxial stress states, the plastic work increment can be expressed as

$$ {\text{d}}W^{{\text{p}}} = p_{{\text{c}}} {\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} + q{\text{d}}\varepsilon ^{{\text{p}}}_{\gamma } + ns{\text{d}}S^{{\text{p}}}_{{\text{r}}} $$
(8)

where p c is the mean constitutive stress, i.e. the mean Bishop’s stress in this case.

The last term of the equation is only relevant to yielding in the SI or SD yield surfaces, as the movement of the LC yield surface does not contribute to S pr . Therefore,

$$ {\text{d}}W^{{\text{p}}} = p_{{\text{c}}} {\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} + q{\text{d}}\varepsilon ^{{\text{p}}}_{\gamma } + (ns_{{\text{I}}}{\text{d}}S^{{\text{p}}}_{{\text{r}}}\;{\text{or}}\;ns_{{\text{D}}}{\text{d}}S^{{\text{p}}}_{{\text{r}}}).$$
(9)

In Eq. 9, the third and fourth terms will occur when the SI or SD yield curves are engaged, respectively. Since both s I and s D are known function of the plastic increment of the degree of saturation and n is independent of dS pr , the last two terms of the equation above are integrable and give zero when integrated around a closed loop of S pr . Therefore, these two terms belong to the free energy dψ2.

To find the first two terms in Eq. 8, it is assumed that plastic volumetric and plastic deviator strains are caused only by yielding at the LC yield surface. This is a strong restriction on the role of the SI and SD surfaces. Then

$$ {\text{d}}W^{{\text{p}}} = {\left( {\frac{1} {2}p_{{\text{c}}} {\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} + (ns_{{\text{I}}} {\text{d}}S^{{\text{p}}}_{{\text{r}}}\;{\text{or}}\;ns_{{\text{D}}} {\text{d}}S^{{\text{p}}}_{{\text{r}}}}) \right)}+ {\left( {\frac{1} {2}p_{{\text{c}}} \frac{{({\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} )^{2} + \frac{{M^{2} }} {\zeta }({\text{d}}\varepsilon ^{{\text{p}}}_{\gamma } )^{2} }} {{{\sqrt {({\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} )^{2} + \frac{{M^{2} }} {\zeta }({\text{d}}\varepsilon ^{{\text{p}}}_{\gamma } )^{2} } }}}} \right)}$$
(10)

where M and ζ are model parameters. The terms of the first brackets are all integrable and give zero in a closed loop. Therefore, they are the contribution of the plastic strain work from the free energy and hence correspond to dψ2. The term in the second set of brackets is not integrable because it involves the plastic shear strain. This term thus corresponds to the dissipation function dφ.

$$ {\text{d}}\psi _{{\text{2}}} = \frac{1} {2}p_{{\text{c}}} {\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} +(ns_{{\text{I}}} {\text{d}}S^{{\text{p}}}_{{\text{r}}}\;{\text{or}}\;ns_{{\text{D}}} {\text{d}}S^{{\text{p}}}_{{\text{r}}})$$
(11)
$$ {\text{d}}\phi = \frac{1} {2}p_{{\text{c}}} \frac{{({\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} )^{2} + \frac{{M^{2} }} {\zeta }({\text{d}}\varepsilon ^{{\text{p}}}_{\gamma } )^{2} }} {{{\sqrt {({\text{d}}\varepsilon ^{{\text{p}}}_{{\text{v}}} )^{2} + \frac{{M^{2} }} {\zeta }({\text{d}}\varepsilon ^{{\text{p}}}_{\gamma } )^{2} } }}} \ge 0. $$
(12)

The dissipation function 12 is obviously strictly positive whenever the plastic strains are non-zero, as required. It can also be shown that the dissipation function above is a homogeneous function of degree 1 in the plastic strain increments. Equations 11 and 12 indicate that the plastic yielding at the SI and SD yield surfaces does not contribute to the plastic dissipation, but only to the plastic work. This means that all plastic work associated with a plastic increment of degree of saturation is stored and can be recovered during a reversed plastic increment of saturation. This plastic work is very much the same as the “locked-in elastic energy” due to the shift or back stress [13]. Obviously, analogous analyses are required concerning other constitutive models. Recently, Tamagnini and Pastor [60] have examined a generalized plasticity model in terms of a similar thermodynamic framework.

4 Double structure model for expansive soils

There has been a steady trend to incorporate into the constitutive laws for unsaturated soils additional features for representing the effects of new variables. For instance, models have been proposed that include the effect of cementation [1, 42], temperature [25, 33] or chemical variables [21, 45]. However, perhaps the area of more intense development has been that of expansive clays.

These materials have been traditionally studied because of foundation problems associated with cycles of wetting and drying. However, there has been significant additional interest due to the fact that expansive clays are now widely used as the basic material for constructing waste-isolation barriers. It is generally acknowledged that most of the basic elastoplastic models mentioned above cannot easily accommodate the behaviour of highly expansive soils. The predicted behaviour inside the yield locus is elastic and, therefore, predicted strains will be small and, often, largely reversible. Instead, the swelling behaviour of expansive clays gives rise to large strains that are strongly stress-path dependent.

A clear instance of this are the results of a series of swelling tests followed by compression stages performed in an oedometer and presented in Fig. 5. It can be observed that strains during swelling are large and very sensitive to the magnitude of applied stress. Subsequent compression curves only cluster together at larger stresses, so there is a significant region in which strains are strongly stress path dependent. This is just an example of the path dependent and irreversible behaviour generally associated with the generation of large strains in expansive clays. Many other instances have been reported (e.g. [8, 9, 11]).

Fig. 5
figure 5

Wetting and compression tests on compacted samples of El Arahal [39]

Full size image

Because the source of expansive clay behaviour lies in the physicochemical phenomena occurring in the vicinity of the clay particle, there is some merit in trying to incorporate explicitly this microstructural level in the model [27]. The formulation developed contains now two structural levels: a microstructure where the interactions at particle level occur and a macrostructure that accounts for the overall fabric arrangement of the material comprising aggregates and macropores.

The microstructure is modelled by an adequate physicochemical model (diffuse double layer theory, for instance) and the resulting strains are assumed to be largely reversible. The macrostructure is governed by a conventional elastoplastic model for unsaturated soil, generally the BBM. It appears reasonable to assume that the macrostructure does not influence the behaviour of the microstructure but the reverse is not true, microstructural deformation may cause strains in the macrostructure that may be irrecoverable. The model is summarized in Fig. 6a. The LC curve corresponds to the macrostructural model and the two yield surfaces (SI and SD) represent the loci of the points from which irreversible strains on the macrostructure start to occur. The SI and SD lines are also called neutral lines because no microstructural strains are generated when the stress path moves along them. Although they share the same names, the SI and SD yield loci of the double structure model are conceptually different from the SI and SD yield loci associated with hydraulic hysteresis discussed in the previous section. The magnitude of the effect of microstructure on macrostructure is controlled by interaction functions (Fig. 6b) and it depends on the normalized distance to the macrostructural yield locus (LC). As shown in Fig. 6b, each branch is associated with a specific interaction mechanism. The distance to the LC curve can be considered a measure of density of the macrostructure. Is a soil state lies on or near the LC, the macrostructure is collapsible and, therefore, loose. The packing of the macrostructure becomes denser as the soil states moves away from the LC. The shapes of the interaction functions reflect the varying response of the macrostructural to microstructural strain for the different soil states.

Fig. 6
figure 6

a Schematic representation of the double structure model in the isotropic plane. b Interaction function linking microstructural and macrostructural strains

Full size image

As for the BBM, the first application towards explaining the main features of behaviour of expansive soils was performed without resorting to a specific mathematical formulation [27]. Therefore, net stresses and suction were the selected stress variables. In this case, however, it is necessary to define carefully the type of suction to be used. Whereas in the macrostructure the matric (or capillary) suction is the relevant one, total suction (i.e. matric plus osmotic suction) may be required when dealing with the microstructure.

The double structure model thus defined is able to account for the large strains and many irreversibility and stress path dependency features of expansive clay deformation [27]. It is sometimes claimed that irreversible phenomena of expansive clays arise as a consequence of hydraulic hysteresis. It is unlikely to be the case. Hydraulic hysteresis is largely a geometric phenomena associated with the pore shapes and pore entrance sizes whereas irreversibility in expansive clays arises mainly from fabric disruption. An added advantage of keeping track of two structural levels and, hence, two pore structures is that important parameters such as permeability can be related to the macrostructural pore sizes since the contribution of the microstructural pores to overall water flow is negligible. This possibility has proved very valuable in the analysis of hydration of engineered barriers for radioactive waste disposal [52].

A first mathematical expression of this conceptual model was presented in Alonso et al. [4] but, recently, a more convenient formulation based on generalized plasticity concepts has been developed [53] while keeping the same basic features and assumptions. The generalized stress–strain relationships are derived within a framework of multi-dissipative materials that provides a consistent and formal approach when several sources of energy dissipation exist. The generalized plasticity approach (Fig. 7) has some significant advantages:

  • No clear evidence exists concerning the shapes of the internal yield surfaces corresponding to the interaction mechanisms between the two structural levels. Their experimental determination is not likely to be easy either.

  • The effect of drying/wetting cycles on the behaviour of expansive soils is a matter of great practical importance. Generalized plasticity is especially well adapted to deal with this type of generalized cyclic loading.

  • It is a formulation well suited for implementation in numerical codes in a simple, robust and structured manner.

There are additional advantages to the explicit consideration of two structural levels in the development of the constitutive model. For instance, time dependent behaviour arises in a natural way if transient hydraulic non-equilibrium between macrostructure and microstructure is considered, a very plausible scenario.

Fig. 7
figure 7

a Definition of microstructural loading and unloading in the generalized plasticity model. The line of separation is called neutral line. b Mapping of the current soil state onto the main yield locus in the generalized plasticity model [53]

Full size image

The double structure approach is especially useful when trying to incorporate the effects of chemical variables on the mechanical behaviour of expansive clays. Because of their large proportion of active clay minerals, those materials are especially susceptible to changes in the geochemical environment. Since chemical variables affect mainly the behaviour of the water-particle system, it is only necessary to modify the microstructural model to take into account the effects of the new chemical variables. The chemical effects on the macrostructure are accounted for by the existing interaction model. A constitutive model that uses the double structure framework and accounts for the separate effects of changes in solute concentration and cation exchange has recently been developed [30].

5 Concluding remarks

The advances in constitutive modelling of unsaturated soils in the last two decades have been numerous and wide-ranging and it is still an area of very active research at present. Indeed unsaturated soil approaches have proved to be quite general, and are being extended to a number of different materials, e.g. chalk partially saturated with oil and water [18]. Reviewing recent developments, it is possible to identify a number of significant features:

  • All constitutive models require two independent stress measures as basic variables. Increasingly, the main stress variable includes degree of saturation and suction.

  • Incorporation of thermodynamic considerations is becoming more frequent, with an increasing trend towards formulating constitutive models within a consistent thermodynamic framework. Those considerations also tend to influence the choice of basic stress and strain variables.

  • Increasing attention is paid to the incorporation of micromechanical information into the models. It has proved very useful to capture important features of expansive soil behaviour. So far, the incorporation has been performed in a conceptual and approximate manner, but more refined approaches are to be expected in the future.

  • Enhanced behaviour frameworks are introduced to account for the effects of an increasing number of non-mechanical (thermal, chemical) variables on the stress–strain behaviour of unsaturated soils. Sometimes, the use of a double structure approach provides a convenient platform for the incorporation of those new variables into constitutive laws.

Those developments are driven, on the one hand, by the goal of achieving consistent formulations on sound thermodynamical bases and, on the other hand, by the need to provide effective answers to increasingly complex civil and environmental engineering problems.