1 Introduction

Compaction bands are localized, planar zones of compressed material that form normal to the most compressive stress. Compaction bands were found by Mollema and Antonellini [19] in a porous sandstone from the Navajo Formation. More recently, Sternlof and Pollard [27] documented field observations of compaction bands in the Jurassic Aztec sandstone of southeastern Nevada. Such bands have been observed also in the laboratory [20, 21, 30], in high porosity rocks that failed by cataclastic flow, as well as in polycarbonate honeycombs [22], steal foams [23] and plaster [18]. Within these bands in high porosity sandstones, microstructural observations in laboratory samples revealed intragranular cracks—recent field observations of Sternlof et al. [28] show almost no cracking—that extend across the grains and result in comminution and pore collapse [1]. These field and laboratory results suggest that compaction bands are probably a common feature in high porosity rocks.

The evolution of compaction bands has been observed to take several forms: once initiated a compaction band may widen to accommodate the cumulative strain (diffuse bands) [1, 21], or alternatively further compaction is accommodated by the initiation of additional bands that remain relatively narrow (discrete bands); alternating bands of compacted and uncompacted material [1, 16, 30]. There is little understanding so far for the origins of these different morphologies although Baud et al. [1] have pointed out some of the key microstructural attributes that are favorable for the development of compaction localization in the form of discrete bands. The relationship of the laboratory compaction bands to those observed in the field has not, also, been fully established. Microscopic differences regarding the amount of the grain-scale fracturing indicates that further study is needed to determine the exact relationship.

Because the material within the compaction bands is more dense, it has lower permeability than the surrounding material [8, 29]. Hence, compaction bands constitute barriers to fluid flow, adversely affecting the injection and extraction of fluids for storage or energy production. The presence of compaction bands affects the overall mechanical strength of the formation as well. The grain breakage and microstructural weakening within the compaction bands could lead to breakout phenomena causing increased sand production [5–7]. Permeability reduction and increased sand production are of economic significance in the oil industry.

Systematic studies [1, 30] have demonstrated that compaction localization is associated with stress states in the transitional regime from brittle faulting to cataclastic flow where two different damage mechanisms are active (axial microcracks that grow and coalesce, and pores that collapse while grains are crushed). In the cataclastic flow, it is known that application of nonhydrostatic stresses causes the pore space in a high porosity rock to compact (shear-enhanced compaction) and permeability to decrease. In the brittle regime, contradictory observations in sandstones were reported. Nevertheless, Zhu and Wong [31] observed that permeability in four different sandstones with porosity above 15% consistently decreased with increasing stress. The current understanding of the effect of stress on permeability in porous rock is not quite comprehensive. Experimental studies [9, 24, 31] revealed that permeability in sandstones is very sensitive to loading path through the interplay of hydrostatic and deviatoric loadings. On the other hand, Somerton et al. [26] concluded that in coal, permeability is affected primarily by the mean effective stress and that the nonhydrostatic stress has negligible influence.

Since the pioneering work of Rudnicki and Rice [25], the onset of localized deformation has been interpreted as instability in the constitutive description of the deforming homogeneous material. To date, most of the modeling efforts for the prediction of compaction bands have focused on two invariant constitutive descriptions of the homogeneous deformation. Rudnicki and Rice [25], Olsson [20] and Issen and Rudnicki [11, 12] adopted a simple constitutive framework whereby the yield envelope and inelastic volumetric change can be characterized by the pressure sensitivity parameter and the dilatancy factor, respectively. Their results are roughly consistent with the conditions under which compaction bands form. Recently, Issen [10] proposed a two-yield surface model to capture the combined effect of the two different damage mechanisms active in the transitional regime from brittle faulting to cataclastic flow, where compaction bands form, in which the shear yield surface and cap meet at a vertex. The bifurcation analysis for this model is elaborate, but analytical results are available for some special cases. The results obtained have extended the range of parameters over which compaction bands form. However, laboratory and numerical work suggest that the third stress invariant may play a significant effect on the description of the mechanical response of geomaterials [2–4, 14, 15, 17]. Nevertheless, bifurcation analysis applies only to the onset of localization and further analyses are required to elucidate the development of the localized failure.

The present study identifies the development of compaction bands in a sedimentary limestone, namely the Tuffeau de Maastricht calcarenite. The experimental results are presented in Sect. 2. Section 3 revisits the general localization theory of deformation bands. Section 3 also presents the formulation and calibration of an elastoplastic constitutive model developed by Kim and Lade [14, 15, 17] on the basis of the experimental observations of the mechanical behavior of the tested rock. The developed model is used in Sect. 4 for back analysis of the experimental results. Conclusions concerning the permeability evolution and its dependence on the stress states and formation of compaction bands are drawn in Sect. 5. In the last Sect. 6 follows an overall discussion of the study. In matters of terminology, compactive stresses and strains are taken positive.

2 Experimental procedure and mechanical data

The tested rock, the Tuffeau de Maastricht calcarenite, is a high-porosity outcrop yellowish-white porous sedimentary limestone. The Tuffeau is a siliceous limestone formed from the erosion of other rocks by marine sedimentation 90 million years ago. The word “Tuffeau” comes from the Latin tofus meaning spongy stone.

All tests were conducted on right circular cylinders (approximately 38 mm in diameter and 76 mm in height, that is a height-to-diameter ratio of 2:1), under triaxial and K-constant compression. Cores were drilled in the same direction (perpendicular to the bedding of the rock) to eliminate the possibility of lithological variations and anisotropy influencing the results. The tolerance of the samples was within the International Society for Rock Mechanics (ISRM) requirements. Thin nitrile sleeves were used to separate the dry samples from the confining fluid while for the saturated samples FluoroEthylene-Propylene (FEP) teflon sleeves were used. Axial deformations were measured using linear variable differential transformer (LVDTs), while radial ones were measured in two orthogonal directions using cantilever jigs. The samples were tested at room temperature inside a pressure vessel. Both the axial force and the confining pressure were applied by servo-controlled hydraulic systems.

In tests performed for permeability measurements, the samples were saturated with purified kerosene. Each steel piston used had two fluid ports delivering the fluid to a centered hole in the piston front face. Sintered steel disks were placed at the end faces of the saturated samples to distribute the fluid over the cross section. Volumetric flow rates were recorded by the fluid delivery pumps (Quizix SP-5200), while a differential pressure transducer recorded the pressure drop across the sample.

A set of mechanical data for Tuffeau de Maastricht calcarenite is shown in Fig. 1. The axial stress is plotted against the axial strain for specimens tested in conventional triaxial experiments with confining pressures as indicated in the figure. The samples deformed uniaxially and at confining pressure 0.5 MPa are representative of the brittle faulting regime. The axial stress attained a peak, beyond which the stress progressively dropped (strain softening). The peak stress shows a positive correlation with mean stress (Fig. 2). At 0.5 MPa confining pressure the volumetric strain increased, but near the peak stress it reversed to a decrease (Fig. 3). Visual inspection of the tested samples confirmed the development of shear localization.

Fig. 1
figure 1

Axial stress versus axial strain curves obtained from conventional triaxial experiments performed at confining pressures as indicated in the figure

Full size image
Fig. 2
figure 2

Failure envelope of the tested rock. In “□”, data from tests not presented in this figure

Full size image
Fig. 3
figure 3

Mean stress versus volumetric strain curves for a set of conventional triaxial tests performed at confining pressures as indicated in the figure

Full size image

In the “transitional” regime between brittle faulting and cataclastic flow (deformation at confining stresses 2, 2.5, 4, 4.5 and 5 MPa) the volumetric strain increased in all experiments monotonically with ongoing deformation (Fig. 3). A peak in the differential stress and strain softening (negative slope in the axial stress vs. axial strain curve) are evident at the deformation behavior of the samples tested at 2, 2.5, 4 and 5 MPa confining pressure. CT scans and microscopic observations confirmed the formation of compaction bands and development of several conjugate shear bands of high angle in the samples tested at 4.5 and 5 MPa confining pressure. The CT scan of the sample tested at 4.5 MPa confining pressure revealed the formation inside the sample of fractures (dark areas) that were not visible in the outer surface (Fig. 4). The fractures were generated in high angles (almost normal some of them) to the plug axis that is the direction of the most compressive stress. The whole specimen was first impregnated by blue-stained epoxy and then petrographic thin sections (30 mm thick) were taken and examined by transmitted light microscopy. The thin section presented in Fig. 5 was located to a part of the plug where an open fracture had been observed in the CT image and demonstrates the presence of released grains in the fractures. In another thin section (Fig. 6) crushed grains close to a fracture and some micro cracks oriented orthogonal to the fracture can be seen. The CT scan of the sample tested at 5 MPa confining pressure (Fig. 7) reveals also fractures oriented in high angles to the most compressive stress. In both samples grain packing is evident across the fractures (Fig. 8). Grain breakage and packing along the fractures but not in the large fragments in between them suggest that localization occurred in the loading phase. In the unloading phase (elastic phase), due to stress release, fractures emerged inside the localization zones since the grain bonds were broken and fragments were not attached to each other by cement (released grains). The orientation of some of the fractures (normal to the most compressive stress) suggests the formation of compaction bands.

Fig. 4
figure 4

CT-scan of a sample tested triaxially at 4.5 MPa confining pressure

Full size image
Fig. 5
figure 5

Thin section photo of the sample tested at 4.5 MPa confining pressure showing released grains in fracture. A 0.5 mm scale bar is shown

Full size image
Fig. 6
figure 6

Thin section photo of the sample tested at 4.5 MPa confining pressure showing crushed grains close to a fracture. Some micro cracks (upper arrows) are oriented orthogonal to the fracture (horizontal, just above the photo). A 50 μm scale bar is shown

Full size image
Fig. 7
figure 7

CT-scan of a sample tested triaxially at 5 MPa confining pressure

Full size image
Fig. 8
figure 8

Thin section photo of the sample tested at 5 MPa confining pressure showing possible denser grain packing close to large fragments that are not compressed. A 0.5 mm scale bar is shown

Full size image

Additional insight is gained by examining the effects of the hydrostatic and deviatoric stresses on volumetric strain (Fig. 3). There is a point in the hydrostat denoted P* which corresponds to the onset of grain crushing and pore collapse. Deviations from the hydrostat imply that additional volumetric strain change is induced by the deviatoric stresses. In the transitional regime between brittle faulting and cataclastic flow, beyond the stress levels, denoted by C* in Fig. 3, that correspond approximately to the first local peak stresses, deviatoric stresses provide a significant contribution to the compactive volumetric strain (shear-enhanced compaction). In contrast, in the brittle faulting regime deviatoric stresses induced the volumetric strain to decrease (shear-enhanced dilation). The mean stress–volumetric strain curves describing the experiments at 2 and 2.5 MPa have the qualitative descriptions of the others in the transitional type of failure. That is, before the peak stress was attained, the volumetric strain increased somewhat relative to the hydrostat, but then a pronounced increase occurred post-peak.

3 Formulation of deformation bands

In this section we revisit the general localization theory of deformation bands and calibrate the elastoplastic model developed by Lade and Kim to the experimental data.

3.1 General analysis of deformation bands

We assume an elastoplastic material with a yield function F and a plastic potential function Q. If plastic volumetric strain v p is used as the only parameter to keep track of the history of inelastic deformation, then the yield condition can be written as

$$F(\sigma_{ij},k)=0, $$
(1)

where k := k(v p) is a function of the plastic volumetric strain v p induced by the stresses σ ij (i,j = 1,2,3).

When the stress state is on the yield surface, the inelastic strain increments dε p ij (i,j = 1,2,3) are assumed to be normal to the plastic potential Q, thus are assumed to be expressed by the following relation:

$$ {\rm d}\epsilon_{ij}^{\rm p} = {\rm d}\lambda_{\rm p} \frac{\partial Q}{\partial\sigma_{ij}},$$
(2)

where dλp is a non-negative factor of proportionality and ∂ denotes partial differentiation with respect to the indicated variable. Then, the rate constitutive equation takes the form:

$${\rm d}\sigma_{ij} = C_{ijkl}^{\rm e} \left({\rm d}\epsilon_{kl} - {\rm d}\lambda_{\rm p} \frac{\partial Q}{\partial\sigma_{ij}}\right),$$
(3)

where with isotropy in the elastic response, the elasticity tensor reads:

$$C_{ijkl}^{\rm e}=\frac{E}{2(1+\nu)}\left(-\frac{2\nu}{1+\nu} \delta_{ij} \delta_{kl} + \delta_{ik} \delta_{jl}+\delta_{il}\delta_{jk}\right).$$
(4)

E and ν denote Young’s modulus and Poisson ratio, respectively, and δ ij is the Kronecker’s delta.

Because v p changes with inelastic deformation, so that the stress state remains on the yield surface, the following consistency condition must be satisfied:

$$ {\rm d}F = \frac{\partial F}{\partial \sigma_{ij}} {\rm d}\sigma_{ij} + \frac{\partial F}{\partial k} \frac{{\rm d}k}{{\rm d}v_{\rm p}} {\rm d}v_{\rm p}. $$
(5)

Substituting

$$ {\rm d}v_{\rm p} = {\rm d}\epsilon_1^{\rm p} + {\rm d}\epsilon_2^{\rm p}+{\rm d}\epsilon_3^{\rm p}={\rm d}\lambda_{\rm p}\sum\limits_{i= 1}^3 \frac{\partial Q}{\partial \sigma_{i}}, $$
(6)

where σ i (i = 1,2,3) denote the principal stresses and dε p i (i = 1,...,3) denote the principal plastic strain increments, into (5), solving for dλp and substituting the result into (5) yields the following expression for the stress increments:

$$ {\rm d}\sigma_{ij} = C_{ijkl}^{\rm ep} {\rm d}\epsilon_{kl},$$
(7)

where the elastoplastic constitutive operator C ep ijkl is given by

$$ C_{ijkl}^{\rm ep} = C_{ijkl}^{\rm e} - \frac{C_{ijmn}^{\rm e} {f}_{{mn}} {f}_{pq} C_{pqkl}^{\rm e}} {{f}_{rs} C_{rstu}^{\rm e} {f}_{tu}+H}, \quad f_{ij}=\frac{\partial {F}}{\sigma_{ij}} $$
(8)

and

$$ H = -\frac{\partial F}{\partial k} \frac{{\rm d}k}{{\rm d}v_{\rm p}} \sum\limits_{i=1}^3 \frac{\partial Q}{\partial \sigma_{i}}, $$
(9)

is the plastic hardening modulus.

The loading criterion for a given strain increment reads:

$$\left\{\begin{array}{*{20}l} {f_{ij}} C_{ijkl}^{\rm e}{\rm d} \epsilon_{kl}> 0, & \hbox{plastic loading;}\\ {f_{ij}} C_{ijkl}^{\rm e}{\rm d} \epsilon_{kl}=0, & \hbox{neutral loading;}\\ {f_{ij}} C_{ijkl}^{\rm e}{\rm d} \epsilon_{kl}< 0, & \hbox{elastic unloading.}\\ \end{array}\right.$$
(10)

Rudnicki and Rice [25] showed that localized deformation in a planar zone with unit normal n is a bifurcation from homogeneous deformation if a non trivial solution exists to the following eigenvalue problem:

$$ \left\{ n_iC_{ijkl}^{\rm ep}n_l\right\}m_k=0,$$
(11)

A non-trivial solution for the m k is possible only when

$$ det \left\{n_iC_{ijkl}^{\rm ep}n_l\right\} = 0.$$
(12)

n i C ep ijkl n l is the acoustic tensor and m its eigenvector. The localization condition is the result of the requirements that the traction rates be continuous across the band boundary and that the velocity field be continuous at the instant of band localization. The nature of the deformation band at localization depends on the inner product (n,m) of the vectors n and m:

$$\left\{\begin{array}{*{20}l} ({\mathbf{n}},{\mathbf{m}}) = -1, & \hbox{pure dilation band;}\\ -1 < ({\mathbf{n}}, {\mathbf{m}}) < 0, & \hbox{dilatant shear band;}\\ ({\mathbf{n}}, {\mathbf{m}}) = 0, & \hbox{pure shear band;}\\ 0 < ({\mathbf{n}}, {\mathbf{m}}) < 1, & \hbox{compactive shear band;}\\ ({\mathbf{n}}, {\mathbf{m}}) = 1, & \hbox{pure compaction band.}\\ \end{array}\right.$$
(13)

3.2 Constitutive model developed by Lade and Kim

Kim and Lade [14, 15, 17] developed a single hardening constitutive model for frictional materials. The model incorporates all three stress invariants and it was validated by the authors for sand and plain concrete. It consists of twelve parameters that are to be calibrated from at least a hydrostatic, a uniaxial and a conventional triaxial experiment in the brittle faulting regime. The restricted number of tests necessary for the calibration of the model is of importance, since the number of in situ cores available for testing is often restricted as well. It should be noted however that the presence of the third invariant is not necessary for the simulation of the experiments performed.

In Table 1 values of Young’s modulus E and Poisson ratio ν obtained from unloading–reloading cycles performed at different conventional triaxial experiments are given. The averaged values, together with the parameters of model that are calibrated below, are used in order to calculate the elastoplastic tensor C ep ijkl of Sect. 3.1.

Table 1 Determination of Young’s modulus E and Poisson ratio ν for Tuffeau de Maastricht rock from unloading–reloading cycles in conventional triaxial experiments at confining pressures as indicated in the table
Full size table

3.2.1 Plastic potential function

The plastic potential function is expressed as a function of the three stress invariants I 1, I 2 and I 3 in the following form:

$$Q = \left(c_0 - \frac{I_1^2}{I_2} + c_3 \frac{I_1^3}{I_3} \right) I_1^\mu,$$
(14)

where the subscript “1” denotes the direction of the most compressive stress.

The parameter c 0 controls the intersection with the hydrostatic axis, the parameter c 3 acts as a weighting factor between the triangular shape (from the I 3 term) and the circular shape (from the I 2 term), and the exponent μ determines the curvature of the meridians. A constant stress a (tensile strength) must be added to stresses before substituting them to the invariants. a is a cohesion like parameter. If a uniaxial extension test is not available then a can be approximated reasonably well from the compressive strength σc, using the relation

$$ a = -0.22 \sigma_{\rm c}^{0.75},$$
(15)

which holds for sedimentary rocks [13]. The above relation yields a = 0.5142 MPa for the tested Tuffeau. In what follows we will keep the notation used for the stresses and for the stress invariants to denote the translated stresses and translated stress invariants, respectively.

Determination of the parameters c 3, c 0, μ

In Kim and Lade [14], it was shown for various frictional materials that c 3 decreases as the rigidity of the materials increase, and the cross-section of the plastic potential surface changes from a triangular to a rounded shape. The effect of material rigidity was also observed in the characteristics of the failure surfaces. Thus the curvature of failure surface meridians increases with increasing rigidity. This curvature is modeled by the parameter m in the failure criterion (Sect. 3.2.2). The relation between c 3 and m for frictional materials can be expressed as a power function

$$c_3 = 0.00155\,m^{-1.27}, $$
(16)

giving c 3 = 0.0007, since m = 1.853 (Sect. 3.2.2).

By defining now

$$ \nu_{\rm p} = -\frac{{\rm d}\epsilon_3^{\rm p}}{{\rm d}\epsilon_1^{\rm p}}, $$
(17)

and substituting the plastic strain increments using the plastic flow rule, under triaxial compression conditions, we obtain

$$c_3 \frac{I_1^3}{I_3} - \frac{I_1^2}{I_2} = \frac{1}{\mu} \left\{\frac{1}{1 + \nu_{\rm p}} \left[ \frac{I_1^3}{I_2^2} \left( \sigma_1 + \sigma_3 + 2\sigma_1 \nu_{\rm p} \right) + c_3 \frac{I_1^4}{I_3^2} \left( \sigma_1 \sigma_3 + \sigma_3^2\nu_{\rm p} \right)\right] - 3c_3 \frac{I_1^3}{I_3} + 2 \frac{I_1^2}{I_2} \right\} - c_0,$$
(18)

or

$$ f_1 = \frac{1}{\mu} f_2-c_0. $$
(19)

Then the parameters μ, and c 0 can be determined by linear regression from several data points (Fig. 9). For the tested rock μ = 4.32 and c 0 = −2.96. Notice that the condition of irreversibility, that is plastic work should be positive whenever a change in plastic strain occurs [15], is satisfied since

$$\mu > 0, $$
(20)
$$c_0 > -(27c_3 + 3). $$
(21)
Fig. 9
figure 9

Determination of the parameters μ and c 0 by linear regression from several data points

Full size image

The plastic potential surface for Tuffeau de Maastricht has the shape of an asymmetric cigar in the principal stress space (Fig. 10). The surface is continuous throughout the stress space except at the intersection with the hydrostatic axis behind the origin of the space.

Fig. 10
figure 10

Plastic potential surface for Tuffeau de Maastricht calcarenite in principal stress space

Full size image

3.2.2 Failure criterion (peak-stress criterion)

\(F_f= \left({I_1^3}/{I_3} - 27\right)I_1^m = \eta.\) The above criterion was proposed by Kim and Lade [13] based on data for different types of rock. The constant parameters m and η can be determined by plotting \(({I_1^3}/{I_3} - 27)\) versus \(({1}/{I_1})\) at failure in a log–log diagram and locating the best fitting straight line. The intercept of this line with \(({1}/{I_1} ) = 1\) is the value of η = 1127.716, and m = 1.853 is the slope of the line (Fig. 11).

Fig. 11
figure 11

Failure envelope for Tuffeau de Maastricht rock in a diagram of the first and second principal stresses

Full size image

3.2.3 Yield criterion and hardening/softening law

The proposed isotropic yield function is expressed as follows:

$$F = f \left(\sigma_{i}\right) - k\left(v_{\rm p}\right), $$
(22)

in which

$$f (\sigma_i) = \left(c_3 \frac{I_1^3}{I_3} - \frac{I_1^2}{I_3} \right) I_1^h {\rm e}^q,$$
(23)

and k(v p) keeps track of the history of inelastic deformation based solely in the plastic volumetric strain v p. The parameter c 3 was determined in the plastic potential function. Parameters h (constant) and q (variable) control the meridional curvature of the yield surface.

The yield surface together with the compactive yield cap have the shape of an asymmetric tear drop with a smoothly rounded triangular cross section as shown in Fig. 12.

Fig. 12
figure 12

Yield envelope for Tuffeau de Maastricht calcarenite in principal stress space

Full size image

Parameter determination for yield criterion

Consider two stress points A and B on the same plastic volumetric strain contour (plastic volumetric strain contours coincide with yield surfaces). We suppose that q, which is variable, is 1 at the failure point B and 0 at the point A which lies on the hydrostatic axis. Then \(F(\sigma_i)_{{\rm at A}} = F(\sigma_i)_{{\rm at B}}\) or

$$h = \frac{{\ln (a)\text{e}}}{{\ln (I_{{1A}} /I_{{1B}} )}},\quad a = (27c_{3} + 3)^{{ - 1}} {\left( {c_{3} \frac{{I^{3}_{{1B}} }}{{I_{{3B}} }} - \frac{{I^{2}_{{1B}} }}{{I_{{2B}} }}} \right)}$$
(24)

In Table 2 the values of h, in the conventional triaxial experiments at confining pressures that correspond in the brittle faulting regime and in the transition regime between brittle faulting and cataclastic flow, are given.

Table 2 Determination of the parameter h for Tuffeau de Maastricht rock
Full size table

The parameter q is a function of stress level such that

$$\left\{\begin{array}{*{20}l}q=0, & \hbox{during hydrostatic compression;}\\0< q< 1, & \hbox{during hardening;}\\q=1, & \hbox{at failure stresses.}\\\end{array}\right.$$
(25)

The dependence of q on the stress level in the hardening regime will be investigated in the sequel. We have to keep in mind though, that q = 0 during hydrostatic compression in order to calibrate the parameters of the hardening law that follows.

Hardening law \(k := f^\prime (v_{p})\)

The translated hydrostatic pressure may be modeled by a quadratic function of the plastic volumetric strain, up to a value v inp chosen for the best fitting possible, but otherwise arbitrary:

$$I_1 = Kv_{\rm p}^2+Lv_{\rm p}+W, $$
(26)

where the parameters K, L and W are all constants. Then, the parameters of the quadratic function (K, L and W) update so that

$$K(v_{\rm p}^{\rm in})^2 + Lv_{\rm p}^{\rm in} + W = \left(K(v_{\rm p}^{\rm in})^2+ Lv_{\rm p}^{\rm in}+W\right)_{\rm updated}, $$
(27)
$$ 2Kv_{\rm p}^{\rm in} + LW = \left(2Kv_{\rm p}^{\rm in} + L\right)_{\rm updated}, $$
(28)
$$ \left(-\frac{L}{2K} \right)_{\rm updated} = v_{\rm p}^{*}. $$
(29)

(27) and (28) yield that the curve which simulates the translated hydrostatic pressure is C 1 differentiable (Fig. 13), while due to (29) the transition from hardening to softening occurs when the plastic volumetric strain takes the value v *p (see also Softening law).

Fig. 13
figure 13

Simulation of the translated hydrostatic principal stress I 1 as a function of plastic volumetric strain

Full size image

The plastic volumetric strain contour at v *p approximates the compactive failure cap, that is the curve defined by the stress states C* (Table 3).

Table 3 Values of v p on the compactive failure cap for different triaxial compression tests
Full size table

So for a hydrostatic compression test (q = 0, q defined in the yield criterion)

$$f (\sigma_i) = f'(v_{\rm p}) \Rightarrow f'(v_{\rm p}) = (27c_3+3)(Kv_{\rm p}^2+Lv_{\rm p}+W)^h.$$
(30)

Variation of q

The stress level \(S = {F_f}/ {\eta} \) varies from 0 on the hydrostatic axis to 1 at the failure surface. S is a hyperbolic function of

$$q = {\rm ln}\left(\frac{f^\prime(v_{\rm p})}{b}\right), \quad b={\left(c_3 \frac{I_1^3}{I_3} - \frac{I_1^2}{I_3} \right)I_1^h} $$
(31)

that is \(S\,=\,{q}/{(\beta+\gamma q)}\) where β and γ are constant parameters. Since the curve passes through (1,1) we obtain

$$q = \frac{\beta S}{1 - (1-\beta)S}.$$
(32)

Figure 14 presents the variation of q with respect to the stress level for the tested Tuffeau. β was found to be approximately 0.7.

Fig. 14
figure 14

Variation of q as a function of the stress state S

Full size image

Softening law \(k := f^{\prime\prime}(v_{\rm p})=A{\rm e}^{-Bv_{\rm p}}\)

Softening may begin anywhere along the monotonically increasing hardening curve and is initiated when q = 1, which in turn occurs when S = 1. Softening may also occur when the plastic volumetric strain takes the value v *p of the plastic volumetric strain contour that approximates the failure cap, that is in the case of Tuffeau de Maastricht rock the value 0.0115 strain (Table 3). This value must be equal to \(v_{\rm p}^{*} = -{L}/{2K}\) for which the hardening modulus H = (27c 3 + 3)h(Kv 2p  + Lv p+W)h-1(2Kv p+L) becomes zero and softening begins.

Determination of the parameters A and B

The slope of the softening curve is set equal to one-tenth the negative slope of the hardening curve at the peak point. This assumption enables us to calculate both parameters

$$A = (f')_{\rm peak} {\rm e}^{B(v_{\rm p})_{\rm peak}},$$
(33)
$$B = \frac{1}{10} \left(\frac{{\rm d}f''}{{\rm d}v_{\rm p}}\right)_{\rm hard, peak} \frac{1}{(f')_{\rm peak}}.$$
(34)

The values of all the parameters that are needed for the calculation of the elastoplastic tensor C ep ijkl of the tested rock are listed in Table 4.

Table 4 Parameters needed for the calculation of the elastoplastic tensor C ep ijkl of Tuffeau de Maastricht rock
Full size table

4 Back test analysis

The back analysis of the triaxial tests used for the calibration of the elastoplastic model follows. Because of the non-linear constitutive model, the simulation of the tests is performed incrementally using numerically Euler forward integration.

Fig. 15
figure 15

Experimental data and numerical simulation of a hydrostatic test

Full size image

Figure 15 shows the numerical simulation in comparison with the experimental data of a hydrostatic test up to point P* that corresponds to the onset of grain crushing and pore collapse. In the uniaxial compressive test the numerical data is roughly consistent with the experimental data, and the reason is that in the calibration as customary the uniaxial test was not taken into account (Fig. 16).

Fig. 16
figure 16

Experimental data and numerical simulation of a uniaxial test. The two left curves represent the radial strains (experimental and simulated)

Full size image

The comparison of the numerical simulation of the conventional triaxial experiment at 0.5 MPa confining pressure with the experimental data (Fig. 17), together with the back analysis of the other tests below, shows that the model of Lade and Kim does capture the behavior of Tuffeau rock.

Fig. 17
figure 17

Experimental data and numerical simulation of a conventional triaxial test at 0.5 MPa confining pressure. The two left curves represent the radial strains (experimental and simulated)

Full size image

The bifurcation analysis for this test predicts a localization of the homogeneous deformation in an dilatant (almost isochoric) shear band (0 < (n, m) = O(10−2)) in the softening regime. The angle between the plane of localization and the most compressive stress is approximately 0.241π. In the next figure (Fig. 18) the back analysis of a conventional triaxial test with 2 MPa confining pressure is presented. The predicted localization band that forms in the softening regime, is in this case a compactive shear band ((n, m) < 0) with the aforementioned angle being approximately 0.345π. The same angle between the plane of the predicted localization band and the most compressive stress in the conventional triaxial experiment at 2.5 MPa confining pressure is 0.342π approximately (Fig. 19). The onset of the predicted compactive shear band occurs again post-peak. The above tests were representatives of the brittle faulting regime and the transitional regime between brittle faulting and cataclastic flow. In the conventional triaxial experiments that follow with confinements in the cataclastic flow regime, namely at 4, 4.5 and 5 MPa confining pressures, the model predicts pure compaction bands ((n, m) ≃  −1) pre-peak. The comparison of the experimental data with the numerical simulation as well as the predicted onsets of the pure compaction bands are given in Figs. 20, 21 and 22 for the tests at confining pressures 4, 4.5 and 5 MPa, respectively. Again only the deviatoric part of the tests is considered.

Fig. 18
figure 18

Experimental data and numerical simulation of a conventional triaxial test at 2 MPa confining pressure. The two left curves represent the radial strains (experimental and simulated)

Full size image
Fig. 19
figure 19

Experimental data and numerical simulation of a conventional triaxial test at 2.5 MPa confining pressure. The two left curves represent the radial strains (experimental and simulated)

Full size image
Fig. 20
figure 20

Experimental data and numerical simulation of a conventional triaxial test at 4 MPa confining pressure. The two left curves represent the radial strains (experimental and simulated)

Full size image
Fig. 21
figure 21

Experimental data and numerical simulation of a conventional triaxial test at 4.5 MPa confining pressure. The two left curves represent the radial strains (experimental and simulated)

Full size image
Fig. 22
figure 22

Experimental data and numerical simulation of a conventional triaxial test at 5 MPa confining pressure. The two left curves represent the radial strains (experimental and simulated)

Full size image

5 Permeability reduction

There was an appreciable scatter in permeability between different samples. Instead of presenting the normalized data from all the experiments performed, we prefer to show the primary data of those samples with comparable permeabilities.

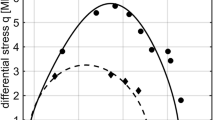
In Fig. 23 the axial stress as a function of the axial strain at conventional triaxial experiments performed at 4, 4.5 and 5 MPa effective pressures and a K-constant experiment for K = 0.7 (the ratio σ2/σ1 is equal to 0.7, where σ2 = σ3 and σ i (i = 1,...,3) are the principal stresses), are shown. The tests were drained with the pore pressure kept constant at 2 MPa. The stress–strain curves of the conventional triaxial experiments in Fig. 18 are similar to those of the samples that were subjected to loading at corresponding confining pressures. However, there is a difference in the strength, due to the presence of kerosene used to saturate the samples and to creep since at 0.5 MPa effective mean stress some preliminary permeability measurements had to be recorded. This difference is approximately 13.6% of the strength of the dry samples. All the above experiments are performed at effective pressures that correspond to the cataclastic flow regime. Permeability consistently decreases with increasing strain, independently of whether the sample showed hardening or softening. The mechanical data presented in Sect. 2 indicate that with the onset of shear-enhanced compaction C* (a threshold in differential stress) coupling of the deviatoric and hydrostatic stresses induce considerable volumetric strain increase. The critical stress levels C* mark the onset of significant reduction in permeability as well. Before the onset of shear-enhanced compaction permeability is primarily controlled by the effective mean stress, independent of the deviatoric stresses. With the onset of shear-enhanced compaction, however, the nonhydrostatic loading exerts dominant control over permeability (Fig. 24).

Fig. 23
figure 23

Axial effective stress versus axial strain curves obtained from conventional triaxial and a K-constant experiments performed for testing permeability evolution

Full size image
Fig. 24
figure 24

Permeability plotted against mean effective stress for conventional triaxial experiments in the cataclastic flow regime

Full size image

Minor differences can be seen between the hydrostatic and triaxial experiments when permeability is plotted as a function of volumetric strain (overall positive correlation).

6 Concluding remarks

The mechanical behavior of Tuffeau de Maastricht calcarenite was studied. Dry conventional triaxial and hydrostatic experiments were performed. The data obtained was used to calibrate the parameters of the single hardening elastoplastic model developed by Kim and Lade. The numerical results were in good agreement with the experimental ones. The tested samples were CT scanned and petrographic thin sections were taken based on these CT scans, in an effort to identify the presence of deformation bands.

The model predicts dilatant shear bands in the brittle faulting regime in accordance with the experimental observation, while in the transitional regime between brittle faulting and cataclastic flow predicts compactive shear bands and almost pure compaction bands. The localization points in the cases of dilatant shear bands and compactive shear bands occur post-peak (after the peak in the stress–strain curve is attained). Almost pure compaction bands are predicted before the onset of shear-enhanced compaction (that is the first local peak). The localization points in all test back analysis are very close to the first local peaks where deformation bands are assumed to form with the exception of the test back analysis of the triaxial experiment performed at 5 MPa confining pressure, where the onset of the compaction band is predicted quite pre-peak.

Conventional triaxial and K-constant experiments were also performed to elucidate the stress dependence of permeability. The effective mean stresses were sufficiently high that the sample failed by cataclastic flow. The critical stress levels C* (onsets of shear-enhanced compaction) mark the onset of considerable permeability reduction due to the coupling effect of the deviatoric and hydrostatic stresses. Before the onset of shear-enhanced compaction, permeability is primarily controlled by the effective mean stress, independent of the deviatoric stresses.