Introduction

The vegetation found in natural rivers can significantly change the flow field characteristics due to vegetative drag forces, thereby affecting the transport of pollutants and sediment. Based on the impact of the substance transport on the flow, the substances in the vegetated flow can be divided into two groups: passive scalar (inorganic pollutant) and active scalar (sand). In general, the mixing process of pollutant transport in the flow mainly includes molecular diffusion, turbulent diffusion, and shear-flow dispersion (Huai et al. 2018). Molecular diffusion is defined as the mass diffusion caused by Brownian motion (the movement of molecules). Turbulent diffusion, however, is defined as material migration resulting from the random motion of the vortex in the flow. Shear-flow dispersion is the additional material diffusion owing to the inhomogeneous distribution of the time-averaged velocity, i.e., the velocity gradient. In natural rivers, dispersion plays a dominant role in the material transport process, with much larger rates than molecular diffusion and turbulent diffusion (Taylor 1953). Since the ratio of the width to depth is usually high, the mixing time of pollutants in vertical and transverse directions is relatively short. The uneven distribution of the velocity in the vertical direction exerts a comparatively minor effect on the dispersion, and therefore, it is concluded that the dispersion is mainly caused by the longitudinal velocity non-uniformity in the lateral direction (Fischer 1967), termed the longitudinal dispersion coefficient. The longitudinal dispersion coefficient is generally used to represent the parameters of the mixing rate of pollutants in water quality modeling, and it has significant research value and thus deserves further study (Hui et al. 2010; Nepf et al. 1997; Patil et al. 2009).

The longitudinal dispersion coefficient is calculated by solving the convection–diffusion equations in certain cases, such as laminar flow and turbulent flow in a circular tube and laminar flow in an elliptical tube and an open channel. However, there is no complete analytical solution that predicts the longitudinal dispersion coefficient in natural rivers, since in these rivers, various unpredicted factors, such as dead zone and vegetation, are involved (Huai et al. 2012; Lees et al. 2000). At present, the longitudinal dispersion coefficient in the open-channel flow with emergent vegetation can be calculated by inserting the coefficient into the convection–diffusion equation to obtain the specific concentration distribution of the particle. Previous researchers optimized the longitudinal dispersion coefficient of the empirical formula by extending the N-zone model to establish the 3-zone model or by applying the Fourier transform to simplify the calculation method (Huai et al. 2018; Kashefipour and Falconer 2002; Wang and Huai 2016; Zeng and Huai 2014). Lightbody and Nepf (2006) estimated the longitudinal dispersion coefficient in rivers with emergent marsh using measured data collected from field experiments and focused on the influence of the velocity inhomogeneity along the stem height on the longitudinal dispersion coefficient. Nepf et al. (2007) also discovered that the decrease of velocity profile near the vegetation canopy had a great influence on the longitudinal dispersion coefficient. Perucca et al. (2009) adopted the triple integral equation to predict the longitudinal dispersion coefficient in the channel where the floodplain is covered by vegetation. Compared to the longitudinal dispersion coefficient in the channel without vegetation, the vegetation in the floodplain was found to have an obvious effect on the longitudinal dispersion coefficient, as high as 70–100%. Shucksmith et al. (2010) investigated the relationship between the longitudinal dispersion coefficient and \(H{u}^{*}\)(where \(H\) is the water depth and \({u}^{*}\) denotes the friction velocity) in the channel with submerged or non-submerged vegetation using experimental data. Murphy et al. (2007) divided the submerged vegetated flow into vegetated layer and non-vegetated layer along the water depth and then developed the N-zone model to estimate the longitudinal dispersion coefficient. Additionally, Huai et al. (2018) also adopted the partition model to produce a three-zone model with two zones in the vegetation area and another in the main channel in the transverse direction. In their studies, the longitudinal dispersion coefficient inside the vegetation region is neglected, where the velocity gradient is pretty small. However, some preconditions must be met before neglecting the longitudinal dispersion coefficient inside the vegetation region.

In addition, numerical simulation methods, such as the random displacement method (RDM), large eddy simulation (LES), and machine learning models (Naa et al. 2021; Noori et al. 2021), have been widely adopted for determining the longitudinal dispersion coefficient in the vegetated flow in accordance with previous studies. Liu et al. (2018) used RDM to analyze the longitudinal dispersion in the open channel covered by floating vegetation. In RDM, the movement of each particle indicates the material transport in the flow. The RDM model has the advantages of intuitively and clearly connecting the microscopic movement of small particles with the macroscopic transport process and also no need to solve the complex convection–diffusion equation. RDM is computationally efficient, and the steep gradient of the tracer concentration has no effect on RDM, so it avoids artificial dispersion. In the study of longitudinal dispersion coefficient, the RDM is often regarded as more accurate.

This study adopts RDM to investigate the longitudinal transport process in the open channel, which is partially covered by emergent vegetation. Using the experimental data on flow velocity and Reynolds stress, the profile of the transverse turbulent diffusion coefficient in the lateral direction was constructed, which can be integrated into the RDM to calculate the longitudinal dispersion coefficient. The simulation results were verified by using the previously measured longitudinal dispersion coefficient based on the measured concentration curve, indicating that the analytical model was feasible and effective in predicting this coefficient in the open channel partially covered by emergent vegetation.

The following is the structure of the paper. The “Random displacement model and longitudinal dispersion in the channel without vegetation” section primarily demonstrates the basic principle of the Random displacement model and applies it to open channels without vegetation. The “Four-zone model in the partially emergent vegetated flow” section presents a four-zone model of partially emergent vegetated flow, including the longitudinal velocity and turbulent diffusion coefficient. The “Random displacement model and longitudinal dispersion in the channel without vegetation” and “Four-zone model in the partially emergent vegetated flow” sections are the “Material and Method” sections. The RDM can be used to calculate the longitudinal dispersion coefficient in the partially vegetated channel after knowing the longitudinal velocity and turbulent diffusion coefficient in each sub-region. Therefore, the “Results: Comparison of the longitudinal dispersion coefficient in the flow with emergent vegetation” section compares RDM simulation results to experimental results from previous studies, which can be renamed the “Results” section. The “Discussion” section discusses the parameter in the RDM model in order to determine the model's applicability. The “Conclusion” section concludes with a summary of the paper.

Material and method

Random displacement model and longitudinal dispersion in the channel without vegetation

Based on Fick’s laws of diffusion and sectional velocity distribution, the random displacement model (RDM) was used to predict the contact behavior of numerous independently moving discrete particles, track the positions of these particles to simulate the mass transport of fluid flow, and then reflect the fluid characteristics of mass transport. RDM is a Lagrangian method, which overcomes the limitations of the Eulerian method with the numerical discretization for high-concentration gradients and the need to cover the whole region. In addition, RDM provides an important bridge that connects the characteristics of microscopic particles and macroscopic transport. Previous researchers have mainly applied the RDM model for pollutant transport, escape of spores from the crop, and displacement through a porous medium with irregular distribution and molecular diffusion (Angstmann et al. 2015; Follett et al. 2016; Guillon et al. 2014; Liang and Wu 2014). This study aims to apply this model to predict the material transport in the partially vegetated flow and also predict the longitudinal dispersion coefficient.

Gardiner (1985) demonstrated that the change in the position of a particle is mainly caused by deterministic force (the first term on the right side of Eq. (1)) and random turbulent transport (second term on the right side of Eq. (1)). At each time step, the position of the particle is determined by the velocity and the turbulent diffusion coefficient. The position of the particle in three directions is determined as below:

$$\Delta x=\left(\frac{\partial {E}_{x}}{\partial x}+u\right)\Delta t+\sqrt{2{E}_{x}\Delta t}{R}_{1}$$
(1)
$$\Delta y=\left(\frac{\partial {E}_{y}}{\partial y}+v\right)\Delta t+\sqrt{2{E}_{y}\Delta t}{R}_{2}$$
(2)
$$\Delta z=\left(\frac{\partial {E}_{z}}{\partial z}+w\right)\Delta t+\sqrt{2{E}_{z}\Delta t}{R}_{3}$$
(3)

where \({E}_{x}\), \({E}_{y},\) and \({E}_{z}\) represent the turbulent diffusion coefficients in the longitudinal, transverse, and vertical directions, respectively. \(u\), \(v,\) and \(w\) indicate the velocities in the longitudinal, transverse, and vertical directions, respectively. \({R}_{1}\), \({R}_{2},\) and \({R}_{3}\) represent independent random variables in the standard normal (Gaussian) distribution.

Assuming that all variables in the vertical direction are constant in a shallow channel, a two-dimensional flow is simulated. The particles are uniformly released and distributed within a certain cross-section in the open channel partially covered by the emergent vegetation, and then, the positions of discrete particles along the flow are tracked. As the longitudinal turbulent diffusion is low in comparison with the longitudinal convection and the transverse and vertical velocities are close to 0, Eqs. (1–3) can be further simplified as follows:

$$\Delta x=u\Delta t$$
(4)
$$\Delta y=\frac{\partial {E}_{y}}{\partial y}\Delta t+\sqrt{2{E}_{y}\Delta t}{R}_{2}$$
(5)

To make the scale of the transverse movement of particles induced by the random diffusion smaller than that induced by the convective effect at each time step (Wilson and Yee 2007), the time step \(\Delta t\) needs to be limited and is calculated as follows:

$$\Delta t<min\left(\frac{0.05h}{{\left(\frac{\partial {E}_{y}}{\partial y}\right)}_{max}},\frac{{\left(0.05h\right)}^{2}}{{\left({E}_{y}\right)}_{max}}\right)$$
(6)

To prevent particles from wandering away from the computational region, corresponding boundary conditions must be imposed. Both sides of the channel can be considered as reflection boundaries and calculated using the expressions as follows:

$${y}_{new}=-{y}_{old}, {y}_{old}<0$$
(7)
$${y}_{new}= 2B-{y}_{old}, {y}_{old}>B$$
(8)

Based on these equations, the positions for each particle at each time step can be obtained. The longitudinal dispersion coefficient, \({k}_{x}\), can be determined in accordance with the position statistics of the entire particles and calculated as follows:

$${D}_{L}=\frac{{\sigma }_{x}^{2}\left({t}_{2}\right)-{\sigma }_{x}^{2}\left({t}_{1}\right)}{2\left({t}_{2}-{t}_{1}\right)}$$
(9)

where \({t}_{2}\) and \({t}_{1}\) represent the time points after the release of particles. \({\sigma }_{x}^{2}\left({t}_{2}\right)\) and \({\sigma }_{x}^{2}\left({t}_{1}\right)\) are the variances of positions of all particles at the time points of \({t}_{2}\) and \({t}_{1}\), respectively. For the open channel, the velocity profile is logarithmic and presented as follows:

$$u\left(z\right)=\frac{{u}_{*}}{\kappa }ln\left(\frac{30z}{{k}_{s}}\right)$$
(10)

where \({u}_{*}\left(=\sqrt{gSh}\right)\) is the friction velocity; \(\kappa \left(= 0.41\right)\) is the Karman coefficient; and \({k}_{s}\) is the roughness height. The turbulent diffusion coefficient \({E}_{z}\) is expressed as follows (Yang and Choi 2010):

$${E}_{z}=\kappa h{u}_{*}\left(1-\frac{z}{h}\right)\frac{z}{h}$$
(11)

where \(h\) refers to the water depth. The analytical model for the prediction of \({k}_{x}\) in the open channel is shown as follows (Wang and Huai 2016):

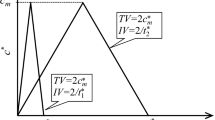
$${D}_{L}= 0.0798{\left(\frac{B}{h}\right)}^{0.6239}{\left(\frac{U}{{u}_{*}}\right)}^{2}h{u}_{*}$$
(12)

where \(U\) indicates the cross-sectional average velocity. Additionally, in the analytical model, \(h=1m\), \(B= 0.1 m,\mathrm{and}\) \({u}_{*}= 0.01\mathrm{m}/\mathrm{s}\). In the simulation model, the time step \(\Delta t\) is 0.05 s, the number of the particles is 10,000, and \({k}_{s}= 0.01 \mathrm{m}\). The particle distribution along the \(x\)-axis at different time points is shown in Fig. 1. The histograms in Fig. 1b at a certain time point follow the standard Gaussian distribution, verifying the feasibility of RDM in this study. In addition, \({k}_{x}\) in Eqs. (9) and (12) is approximately same (Fig. 2), indicating that the RDM method has a certain level of applicability and accuracy for the prediction of LDC.

Fig. 1
figure 1

Particles distributions across the water depth (a) and histograms of particle size distributions (b) at different time points

Full size image
Fig. 2
figure 2

Comparison between \({D}_{L}\) in the RDM model and in the analytical method

Full size image

Four-zone model in the partially emergent vegetated flow

This study aims to explore the steady uniform flow in the open channel, which can be partially covered by emergent vegetation (Fig. 3a), as mangroves are commonly found near coastlines. The experimental data were acquired by Zhang et al. (2021a) and Huai et al. (2018), who conducted the experiment in a straight open channel with 20 m long and 1 m wide. The vegetation zone of 8 m in length is located in the middle of the channel and close to the side wall (see Fig. 3b, c). The layout of the emergent vegetation proposed by Zhang et al. (2021a) in the open channel is asymmetric, with vegetation width \({B}_{v}\)= 0.5 m (Fig. 3b). The vegetation layout proposed by Zhang et al. (2021a) consists of four solid floats with a diameter of 2 cm and four hollow floats with a diameter of 4 cm, which are connected alternately by a thin rope. Moreover, the vertical projection of this flexible vegetation changes with the water depth, indicating that the vegetation is emergent. Huai et al. (2018) adopted a symmetrical arrangement, and the 0.25-m-wide vegetation zone was set on both sides of the flume (Fig. 3c). The vegetation was simulated by cylindrical rigid rods with a diameter of 7 mm. Both of the vegetation types considered in this study were arranged in a parallel manner. Detailed information about the experiment is presented in Table 1, in which \(B\) indicates the channel width and \({B}_{v}\) denotes the width of the vegetation zone; H and h represent the water depth and vegetation height, respectively; \(a\) denotes the vegetation frontal area per unit water volume.

Fig. 3
figure 3

3D view of natural river channel with floodplain vegetation; planform of the open channel (b and c), (b) Asymmetrical arrangement of the model proposed by Zhang et al. (2021a), c symmetrical arrangement of the model proposed by Huai et al. (2018). \(B\) Represents the width of the channel; \({B}_{v}\) represents the width of the vegetation region

Full size image
Table 1 Experimental conditions for six different cases. B is the width of the channel; \({B}_{v}\) represents the width of the vegetation region; \(H\) represents the total water depth; \(h\) is the height of the submerged vegetation; \(a\) represents the projected frontal area of the vegetation per unit volume
Full size table

Due to the impact of vegetation resistance, the flow velocity in the vegetation zone is low and significantly different from that in the main channel zone. The velocity difference generates the shear vortices, i.e., the Kelvin–Helmholtz vortex near the interface between two zones (Fig. 4). These shear vortices with certain length scales penetrate into the vegetation and main channel zones, promoting the exchange of momentum and mass between these two zones. Since the Reynolds stress decreased rapidly from its maximum value at the interface to a certain value in the vegetation zone, the corresponding length is the penetration length (\({\delta }_{I}\)) of shear vortices (White and Nepf 2007; Zhang et al. 2021a). The penetration length (\({\delta }_{O}\)) of shear vortices in the main channel corresponds to the distance at which the Reynolds stress decreases gradually from its peak value to zero. Therefore, \({\delta }_{O}>{\delta }_{I}\) (White and Nepf 2008). According to the flow characteristics in the open channel partially covered with emergent vegetation, the cross-sectional zone can be reasonably categorized into four zones (Fig. 4), namely, the steady-state zone in the vegetation zone (I), the inner zone of shear layer vortex (II), the outer zone of shear layer vortex (III), and the steady-state zone in the main channel (IV). In the shear layer vortex (zones II and III), the flow structure is complex, and flow velocity changes in the transverse direction. In the steady-state zones (zones I and IV), the velocity is nearly uniform, with the average values of \({U}_{1}\) and \({U}_{4}\), respectively. In this paper, the RDM model is used to deduce the cross-sectional concentration flux in the partially vegetated channel, and it is necessary to understand the distribution of velocity and the transverse turbulent diffusion coefficient in the cross-section.

Fig. 4
figure 4

Four sub-zones and the transverse distribution of the depth-averaged velocity; green area represents the vegetation zone, and blue area represents the main channel

Full size image

Longitudinal velocity profiles in all zones

Some researchers have proposed analytical solutions for the transverse distribution of flow velocity in the vegetated channel (Chen et al. 2010; Liu et al. 2013). These analytical solutions are generally needed to calibrate the values of coefficients according to experimental data, which are difficult to be directly used to predict the velocity distribution. However, based on the shear vortex, White and Nepf (2008) developed an analytical model, which did not need the calibration of secondary flow coefficients and had high accuracy in predicting the velocity. Therefore, this analytical model was improved according to the actual situation considered here.

  1. (1)

    In the steady-state zone in the vegetation zone (zone I), the velocity distribution is more uniform, and the drag force of vegetation is much greater than the friction of the channel bed. We can calculate the velocity (\({U}_{1}\)) by using the balance between the vegetation drag force and pressure gradient from the water surface, shown as follows:

$${U}_{1}=\sqrt{\frac{2gs}{{C}_{D}mD}}$$
(13)

where \({C}_{D}\) indicates the drag coefficient of the vegetation; \(m\) refers to the number of vegetation stems per unit bed area; \(D\) represents vegetation diameter; \(s\) signifies the channel slope, and \(g\) indicates the acceleration of gravity. The dimension of length is denoted by the letter \(L\) and the dimension of time is denoted by the letter \(T\). The unit of \(g\) is \(\frac{L}{{T}^{2}}\); the unit of \(s\) and \({C}_{D}\) is 1; the unit of \(m\) is \({L}^{-2}\); the unit of \(D\) is \(L\). Hence, the unit of Eq. (13) is \({\left(\frac{\frac{L}{{T}^{2}}*1}{1*{L}^{-2}*L}\right)}^{0.5}={\left(\frac{\frac{L}{{T}^{2}}}{{L}^{-1}}\right)}^{0.5}={\left(\frac{{L}^{2}}{{T}^{2}}\right)}^{0.5}=\frac{L}{T}\), which is same as the dimension of velocity \({U}_{1}\).

  1. (2)

    In the steady-state zone (zone IV) in the main channel, the velocity distribution is also uniform, and velocity (\({U}_{4}\)) results from the balance between the pressure gradient and resistance of the channel bed, shown as follows:

    $${U}_{4}=\sqrt{\frac{2ghs}{{C}_{f}}}$$
    (14)

where \({C}_{f}\) indicates the resistance coefficient for the bed channel.

  1. (3)

    In the inner layer of the shear layer vortex (zone II), the velocity distribution follows an S-shaped curve that approximates the hyperbolic tangent and is expressed as follows (White and Nepf 2008):

    $${U}_{2}={U}_{s}\left(tanh\left(\left(y-{y}_{0}\right)/{\delta }_{I}\right)+1\right)+{U}_{1}$$
    (15)

where \({y}_{0}\) is defined at the interface between the vegetation and the main channel zones. \({U}_{s}\) is the slip velocity and calculated by the formula \({U}_{s}={U}_{y0}-{U}_{1}\), where \({U}_{y0}\) is the velocity at \({y}_{0}\). The penetration length is calculated by \({\delta }_{I}= 0.14{ \left({C}_{D}nD\right)}^{-1}\) (Zhang et al. 2021a, b), where \(n\) represents the number of vegetation stems per unit area.

  1. (4)

    In the outer layer of the shear layer vortex (zone III), the velocity distribution is identical to a parabolic velocity profile of the boundary layer (White and Nepf 2008; Zhang et al. 2021b) and expressed as follows:

    $${U}_{3}= 3{U}_{4}{tanh}^{2}\left[\sqrt{\frac{3}{4\left(\frac{{U}_{ym}}{{U}_{4}}+2\right)}}\left(y-{y}_{m}\right)/{\delta }_{O}+{tanh}^{-1}{\left(1+\frac{\frac{{U}_{ym}}{{U}_{4}}-1}{3}\right)}^{0.5}\right]-2{U}_{4}$$
    (16)

where \({y}_{m}\) is the matching point at which the velocity gradients in zones II and III are consistent. \({U}_{ym}\) is the matching velocity at the position of \({y}_{m}\). \({U}_{ym}\) and \({\delta }_{O}\) can be solved iteratively (in Eqs. (40) and (42), respectively, (White and Nepf 2008)). Once \({U}_{ym}\) and \({\delta }_{O}\) are obtained, \({y}_{m}\) and \({U}_{s}\) can be calculated as follows:

$${U}_{s}=\frac{{\delta }_{I}}{{\delta }_{O}}\frac{{U}_{4}-{U}_{1}}{\left(1-{tanh}^{2}\left(1.89exp\left(-4.03{\delta }_{I}/{\delta }_{O}\right)\right)\right)+\left(1+tanh\left(1.89exp\left(-4.03{\delta }_{I}/{\delta }_{O}\right)\right)\right)\frac{{\delta }_{I}}{{\delta }_{O}}}$$
(17)
$${y}_{m}={\delta }_{I}\left({tanh}^{-1}\left(\frac{{U}_{ym}-{U}_{1}}{{U}_{s}}\right)\right)+{y}_{0}$$
(18)

According to the velocity expressions in the corresponding zones, the transverse distribution of velocity in the open channel partially covered by emergent vegetation can be calculated (Fig. 5a) and then applied to the RDM model. Note that the boundary condition is “no-slip condition” which denotes that the velocity and the turbulent diffusion coefficient are zero at the side walls of the channel, namely, \({\left.U\right|}_{y=0, B}=0\) and \({\left.{E}_{y}\right|}_{y=0, B}=0\).

Fig. 5
figure 5

The four-zone velocity and the turbulent diffusion coefficient in the improved model

Full size image

Turbulent diffusion coefficient profiles in all zones

Concerning the steady uniform flow in the open channel without vegetation, the transverse profile of the turbulent diffusion coefficient is considered to be uniform (Liu et al. 2018). In the open channel, which is partially covered by the vegetation, the shear vortex formed near the interface causes the frequent exchange of momentum and mass between the zones, and the transverse turbulent diffusion coefficient is relatively large and not uniform. The formula previously used for the calculation of the transverse turbulent diffusion coefficient in the open channel is no longer applicable for the vegetated flow. However, there have been no reliable results of the research on the profile of the transverse turbulent diffusion coefficient in the partially vegetated flow. Therefore, this study adopts the concept of partition for transverse turbulent diffusion coefficients and applies relevant models to predict these coefficients in four subzones.

In the steady-state zone in the vegetation zone (zone I) and the steady-state zone in the main channel (zone IV), the distributions of velocity and Reynolds stress are uniform, and the transverse turbulent diffusion coefficient is considered constant. In zone I, the flow structure is similar to that in the open channel, fully covered with emergent vegetation. The transverse turbulent diffusion coefficient is related to velocity, vegetation diameter, and vegetation density. Nepf (2004) evaluated the transverse turbulent diffusion coefficient in the vegetated flow by theoretical and experimental methods and proposed the following formula:

$${E}_{y1}=A\sqrt[3]{{C}_{D}aD}{U}_{1}D$$
(19)

where \(A\) is the empirical coefficient. Additionally, in the open-channel flow with emergent vegetation, the turbulent diffusion coefficient is anisotropic, and its value is \(A\)= 0.8.

In zone IV, the lateral distribution of the velocity is logarithmic, which is similar to the vertical distribution of velocity in the open channel without vegetation. This is due to the fact that the sidewall of the channel acts as the channel bed in the open channel. Near the interface between zones III and IV (Huai et al. 2019), the Reynolds stress is 0, suggesting that the effect of emergent vegetation on the flow velocity can be offset by the influence of the channel sidewall. Therefore, the transverse turbulent diffusion coefficient at the interface between the two zones can be considered as 0. Furthermore, this interface can be considered as a free water surface. The form of the transverse turbulent diffusion coefficient shows consistency with that of the vertical turbulent diffusion coefficient in the open channel, shown as follows:

$${E}_{y4}=\kappa \left({B}_{m}-{\delta }_{O}\right){u}_{*}\left(1-\frac{y}{{B}_{m}-{\delta }_{O}}\right)\frac{y}{{B}_{m}-{\delta }_{O}}$$
(20)

Regarding the transverse turbulent diffusion coefficient of the shear vortex in zones II and III, one theory suggests that the vertical turbulent diffusion coefficient can be proportional to the shear vortex scale and the rotational velocity of the vortex can be used as a reference (Ghisalberti and Nepf 2005). Therefore, we can assume that the transverse turbulent diffusion coefficient can be mainly affected by the shear vortex size (\({\delta }_{I}+{\delta }_{O}\)) and velocity difference (\(\Delta U={U}_{4}-{U}_{1}\)) between the main channel and the vegetation zone. In the shear vortex, the magnitude and range of the turbulent diffusion coefficient are relatively large due to the severe disturbance of the flow structure caused by vegetation. The transverse turbulent diffusion coefficient increases approximately linearly and reaches its peak value around the interface between the vegetation zone and the main channel, followed by an approximately linear decrease. Its maximum value is calculated as follows:

$${E}_{max}= 0.032\Delta U\left({\delta }_{I}+{\delta }_{O}\right)$$
(21)

Based on this analysis, the distribution of the transverse turbulent diffusion coefficient can be obtained (Fig. 5b) and applied to the RDM model to predict the longitudinal dispersion coefficient in the flow partially covered by emergent vegetation.

Effect of the number of particles and simulation time

Understanding the complex distributions of longitudinal velocity and the turbulent diffusion coefficient in the lateral direction, the RDM model can be employed for the open-channel flows with emergent vegetation to predict the longitudinal dispersion coefficient. Initially, all particles are released instantaneously and evenly distributed across the cross-section, similar to the phenomenon occurring in laboratory experiments. The number of particles should be determined first. The simulation results are not reliable enough when the number of particles is low. The larger the number of particles calculated in the RDM model, the more accurate the results of the simulation, while the computational efficiency will be reduced. Therefore, the threshold of the particles number, which is not only adequately to be simulated, but also the calculation efficiency is satisfied, needs to be confirmed. In case 2, 5000, 10,000, 20,000, and 50,000 particles are adopted to investigate the influence of the number of particles in the RDM model. The simulation time was 1000 s, and the time step \(\Delta t\) was set to 0.05 s. Figure 6 shows the development of the instantaneous longitudinal dispersion coefficient (\({D}_{L}\)) with time (\(t\)). As expected, the accuracy of the simulation is positively correlated with the number of particles. Figure 6 demonstrates that the larger the number of particles, the more stable the longitudinal dispersion coefficient. \({D}_{L}\) fluctuates greatly when the number of particles is 5000, for which the shortest time is taken compared with other conditions. When the numbers of the particles are 10,000, 20,000, and 50,000 (Liang and Wu 2014; Liu et al. 2018), the difference of \({D}_{L}\) is less than 10%, which is considered narrow and can be ignored. The difference in \({D}_{L}\) with 5000 and 10,000 particles is greater than 10%, while it is 7% with 10,000 and 20,000 particles and 4% with 20,000 and 50,000 particles, indicating that the simulation results tend to be more stable as the particle number increases. In order to maximize computational efficiency, the particle number is set to 10,000 in all cases, which is sufficient to produce reliable and stable simulation results.

Fig. 6
figure 6

The impact of the number of particles on the longitudinal dispersion coefficients for case 2

Full size image

Results: comparison of the longitudinal dispersion coefficient in the flow with emergent vegetation

According to the experimental conditions imposed in the studies conducted by Zhang et al. (2021a) and Huai et al. (2018), the RDM model was used to calculate the theoretical longitudinal dispersion coefficient (\({D}_{L(predicted)}\)). To validate the RDM predictions, the measured longitudinal dispersion coefficients from Zhang et al. (2021a) and Huai et al. (2018) were used. They measured the Rhodamine concentration in the partially vegetated channel using two fluorescence detectors (Rhodamine Probes, YSI Springs, OH). The two probes were positioned in two locations: one near the leading edge of the vegetation and one far away from the leading edge, where the flow was fully developed. The routing procedure calculated the measured longitudinal dispersion coefficient, DL(measured), based on the two concentration curves for the time dependence. More information about the experiments can be found in Zhang et al. (2021a) and Huai et al. (2018). In the RDM simulation, a total of 10,000 particles are released instantaneously and evenly across the cross-section. The time step \((\Delta t)\) is set at 0.05 s. As stated in the “Material and method” section, independent random variables (\({R}_{1}\), \({R}_{2},\) and \({R}_{3}\)) are generated from a standard Gaussian distribution. Therefore, the simulation for each case is repeated three times, with the final result reported as the average of the three repeated simulations. In Fig. 7, hollow circles represent the individual simulation result under each flow condition, and solid circles represent the average value of the three individual simulation results. A narrow difference exists among the individual simulation values, demonstrating that the simulation result is stable. As shown in Table 2 and Fig. 7, the theoretical dispersion coefficient values from RDM are compared to the measured ones obtained from the routing procedure, with an average relative error of 7.9%. The average relative error between measured and theoretical longitudinal dispersion coefficient values is less than those reported by Zhang et al. (2021a) and Huai et al. (2018), indicating that the RDM model is more reliable and better at predicting longitudinal dispersion coefficients in partially vegetated channel flow.

Fig. 7
figure 7

Comparison of measured and predicted values of the longitudinal dispersion coefficient for each case (\({D}_{L}\))

Full size image
Table 2 Comparison between the measured and the predicted \({D}_{L}\) and Fickian time scales for each experimental case; \({t}_{m}\) represents the actual Fickian time; \({t}_{tc}\) represents the theoretical Fickian time; \(\widetilde{t}={t}_{m}/{ t}_{tc}\) represents the average value of the dimensionless time scale
Full size table

Discussion

Fickian time scales

As demonstrated in Eq. (9), the longitudinal dispersion coefficient gradually increases since the release of tracers and reaches its steady value after a certain period of time. Therefore, Fickian time (\(t)\) is defined as a time scale required for predicting the longitudinal dispersion coefficient to obtain the constant value. The Fickian time scale is theoretically calculated as follows (Maier 2002):

$${t}_{tc}=\frac{{B}^{3}}{{\int }_{0}^{B}{E}_{y}dy}$$
(22)

where \({E}_{y}\) denotes the transverse turbulent diffusion coefficient. The theoretical values of the Fickian time scales for each case are presented in Table 2. Previous studies have shown that the ratio of the measured and the theoretical Fickian time scales is considered to be a dimensionless time scale ratio, which is represented by \(\widetilde{t}\) (Liang and Wu 2014; Wu and Chen 2014) and calculated as follows:

$$\widetilde{t}=\frac{{t}_{m}}{{t}_{tc}}$$
(23)

where \({t}_{m}\) is the measured Fickian time scale. The dimensionless time scale \(\widetilde{t}\) is represented by the uniform mixing of independent particles in the whole cross-section, i.e., when the longitudinal dispersion coefficient can reach an asymptotic value (Maier 2002). Wang et al. (2017) suggested that the time scale for the transverse distribution to approach uniformity is \(\widetilde{t}= 0.5\) in a laminar open-channel flow. Gill and Sankarasubramanian (1970) demonstrated that the longitudinal dispersion coefficient could increase with time as well as reach the asymptotic value at \(\widetilde{t}= 0.1-0.2\). However, the average value for the cases 1–3 is 0.1, which is basically close to the one obtained by Gill and Sankarasubramanian (1970) and smaller in comparison with that in the laminar open-channel flow. The average value for the cases 4–6 is 0.4, which is slightly smaller than that in the laminar open-channel flow. The average value for cases 1–3 is smaller than that for cases 4–6, indicating that the flexible vegetation (Zhang et al. 2021a) is more conducive to the transverse mixing of flow than the rigid vegetation (Huai et al. 2018).

For cases 1–3, the Fickian time (\({t}_{m}\)) gradually decreased with increasing water depth (Fig. 8). The reasonable explanation of this phenomenon is that the more serious the effect of disturbance in the flexible emergent vegetation on the flow with increasing water depth, the stronger the mass transport at the cross-section. It indicates that the strong mass transport at the specific cross-section corresponds to the small Fickian time scale. For cases 4–6, the relationship between \({t}_{m}\) and water depth was not obvious (Fig. 8). Although the disturbance in the rigid vegetation became more serious with increasing water depth, the transverse mass transport at the cross-section was not large enough. Therefore, it would take a longer time for the longitudinal dispersion coefficient to reach its steady-state value, i.e., \({t}_{m}\) may increase with increasing water depth, as observed for the case 5.

Fig. 8
figure 8

Fickian time for all cases: a measured ones, b theoretical ones

Full size image

Sensitivity analysis

In this paper, the RDM model could be applied in the partially vegetated channel to predict the longitudinal dispersion coefficient. However, before using RDM, we need to determine some key parameters, such as water depth, vegetation density, vegetation diameter, vegetation height, channel bed slope, the width of the vegetation zone, friction velocity along the vegetation interface, widths of the four sub-zones, velocities in the main channel and vegetation zone, etc., among which, all parameters except the last two can be obtained accurately from the experiments carried out by Zhang et al. (2021a) and Huai et al. (2018). Therefore, these parameters are held constants for each experimental case, and there is no need to include them in the sensitivity analysis. In addition, the remaining parameters, namely the widths of the four sub-zones and the velocities in the main channel and the vegetation zone, can be further simplified into three parameters, including the width of the vegetation zone (zone I, \({y}_{1}\)), the width of the shear layer (\({\delta }_{O}+{\delta }_{I}\)), and the velocity difference (\(\Delta U={U}_{4}-{U}_{1}\)). The selection and inclusion of these three parameters may lead to the major uncertainty in the simulation results. Thus, we conducted the sensitivity analysis for these parameters to determine their effects on the simulation results. During the sensitivity analysis, the uncertainty of these parameters both increased and decreased by 10% to evaluate their impact on the longitudinal dispersion coefficient.

The flow patterns in zone I were similar to those in the dead zone and not disturbed by the shear layer, where the velocity and diffusion were low (Harvey et al. 2005). Figure 9 presents the results of the sensitivity analysis of \({y}_{1}\), indicating that the longitudinal dispersion coefficients increased by 12.7% when \({y}_{1}\) increased by 10%. On the one hand, \({y}_{1}\) increased, indicating that the minimum velocity occupies greater channel width. To keep the flow rate unchanged, the velocity outside zone I tends to increase. Thus, the velocity gradient becomes larger, eventually resulting in an increase in the longitudinal dispersion coefficient in the open channel. On the other hand, the maximum and minimum values of the transverse turbulent diffusion coefficient remain unchanged with increasing \({y}_{1}\). The gradient for the transverse turbulent diffusion coefficient in zone II near the interface was steeper, which would result in a decrease in the cross-sectional average value of the turbulent diffusion coefficient. For the open-channel flow, the longitudinal dispersion coefficient and the turbulent diffusion coefficient were inversely correlated. Furthermore, with the increase in \({y}_{1},\) the longitudinal dispersion coefficient eventually increased, which is verified in Fig. 9. Conversely, when \({y}_{1}\) decreased by 10%, the longitudinal dispersion coefficient decreased by 10.1%.

Fig. 9
figure 9

Sensitivity analysis of the width of zone I, \({y}_{1}\)

Full size image

When the width of the shear layer (\({\delta }_{o}+{\delta }_{I}\)) near the interface increases, the velocity gradient across the cross-section will also increase to a certain extent on the basis of the constant flow rate. Additionally, the transverse turbulent diffusion coefficient will increase correspondingly. These are the two reasons for a decrease in the longitudinal dispersion coefficient. Therefore, the increase in \({\delta }_{o}+{\delta }_{I}\) would lead to the decrease in the longitudinal dispersion coefficient, as shown in Fig. 10.

Fig. 10
figure 10

Sensitivity analysis of the width of the shear layer, \({\delta }_{o}+{\delta }_{I}\)

Full size image

The velocity difference \(\Delta U\) in Eq. (21) has a positive linear relationship with the transverse turbulent diffusion coefficient. According to Fig. 5b, the maximum turbulent diffusion coefficient near the interface region increased with increasing \(\Delta U\), indicating the increase in the diffusion coefficient across the shear layer. As mentioned, the longitudinal dispersion coefficient has an inverse correlation with the turbulent diffusion coefficient. Therefore, a larger value of \(\Delta U\) corresponds to a smaller longitudinal dispersion coefficient, as observed in Fig. 11.

Fig. 11
figure 11

Sensitivity analysis of the velocity difference \(\Delta U\)

Full size image

The results of sensitivity analysis are presented in detail in Table 3, which shows that the three parameters have a certain influence on the longitudinal dispersion coefficient. To be specific, both \({\delta }_{o}+{\delta }_{I}\) and \(\Delta U\) have negative impacts on the longitudinal dispersion coefficient, but \({y}_{1}\) has a positive impact. \(\Delta U\) has the least strong effect, while \({y}_{1}\) has the greatest influence on the predicted longitudinal dispersion coefficient.

Table 3 Results of the sensitivity analysis
Full size table

Conclusion

To conclude, this study improved the random displacement model, aiming to investigate the longitudinal dispersion coefficient in the open channel partially covered by emergent vegetation. Based on the structure of the shear vortex at the interface between the emergent vegetation zone and the non-vegetation zone, the flow field was divided into four sub-zones in the lateral direction. Then, the transverse distribution models were developed to predict the longitudinal velocity and the transverse turbulent diffusion coefficient in these four sub-zones. Due to the complex flow structure in the shear vortex, the magnitude and range of variation of the transverse turbulent diffusion coefficient were larger in these sub-zones than in the remaining sub-zones, with an increase to its maximum value, followed by a linear decrease. In sub-zone I, the distribution of the turbulent diffusion coefficient was approximately parabolic, similar to that in the open channel. In sub-zone IV, however, the turbulent diffusion coefficient remained constant. In addition, the analytical longitudinal dispersion coefficient from the random displacement model was verified using previous experimental data, demonstrating that the improved RDM can effectively simulate the particle positions in the open channel partially covered by the emergent vegetation. The research on pollutant diffusion has contributed to research studies focusing on the longitudinal dispersion coefficient as the core. This study can provide a theoretical basis for the transport and diffusion of pollutants in the vegetated flow with a complex flow structure, which is of great importance for the sustainable development of river ecological environment and the optimization of the planning and design of the river course.