Introduction

Water safety is fundamental for sustainable earth life (Krishna et al. 2020; Ighalo and Adeniyi 2020). Access to clean water is essential for human beings to stay healthy and avoid illnesses caused by water contamination. Currently, approximately 1 billion people do not have access to safe drinking water (Ekere et al. 2019). According to the World Health Organization (WHO), water-borne diseases cause approximately 2.2 million fatalities each year in developing countries (Olukanni et al. 2014). Water purification treatment and sustainable strategies for water resources have become critical issues because of the scarcity of water usage as a result of water pollution (Wang et al. 2019). The WHO projected that purified drinking water treatment would be available to 5.2 billion people (Ravindra et al. 2019). Nitrogen and phosphorous are two major factors that contribute to water eutrophication caused by a large amount of inorganic nutrient pollution (Yang et al. 2008; Zhu et al. 2011; Zhao et al. 2012). Thus, increased attention has been drawn to elevated nutrient status and eutrophication by seeking water pollutant removal measurements (Sierp et al. 2009; Wu et al. 2011).

Researchers have greatly focused on wastewater treatment, particularly on pollutant removal metrics. Several studies have been conducted on the reduction of pollutants through the design and construction of sustainable ecosystems to maintain the human–nature balance (Mistch et al., 1992), which can remove pollutants at a low cost, such as the construction of artificial wetlands or the facilitation of floating islands (Li et al. 2010; Mietto et al. 2013; Borne 2014). Different types of hydrophytes have been used in numerous wastewater treatment technologies because aquatic vegetation regulates the structure of water bodies and assimilates nutrients for microbial organic decomposition; meanwhile, the competition for living space and nutrients by hydrophytes within water bodies limits algal growth (Li et al. 2010). Aquatic vegetation’s roots would trap and uptake the contaminant, allowing biofilms to attach to the root system (Headley and Tanner 2012; Machado Xavier et al. 2018; Wang et al. 2020a). Plant absorption of the mineralized nutrient could lead to water purification and governance through microbial decomposition. As an improvement to the ecological floating bed, it employs a mechanism composed of vegetation roots and other microbial carrier packing to achieve efficient water treatment (Wu et al. 2016). Accordingly, the contaminant removal effect of the artificial filter system can be regarded as a reacting boundary. In wastewater purification and environmental risk assessments, the reacting boundary is considered to discuss the solute transport process in an impermeable tube (Paul and Mazumder 2011). The homogeneous and heterogeneous reactions of two parallel plates to dispersion have been discussed (Soundalgekar and Gupta 1975). The shape of the contaminant cloud would change, and the centroid of the contaminant cloud would shift with the change of the boundary absorption intensity (Das et al. 2021). However, the effects of two boundary absorption intensities on pollutant removal within water bodies have not been thoroughly studied. The total removal capacity of the two absorption boundaries within water bodies need further discussion, taking into account the ratio variations of two boundary absorption intensities.

The critical factor for water purification is to reveal how the contaminant cloud expands within water flows. Taylor (1953) first named the dispersivity in Poiseuille flow within a tube to determine the mechanism of the contaminant transport process; then, a series of researches, including numerical simulation, laboratory experiments, field measurements, and analytical analysis, has been carried out to study the solid particle within water flows (Alinejad et al. 2013; Alinejad and Esfahani 2014, 2016; Peiravi and Alinejad 2021; Araban et al. 2022; Moafi Madani et al. 2022; Fischer et al, 1975, 1976; Lightbody and Nepf 2006; Nepf 2012; Liu and Masliyah 2005; Wang and Zhang 2020; Wang and Cirpka 2021). Many studies have focused on the feature of mean concentration distribution over cross-sections using the 1D dispersion model, and the standard Gaussian distribution of the contaminant concentration distribution in the longitudinal direction has been achieved to describe the contaminant transport in water flows (Barton 1983; Zeng et al. 2011). However, the contaminant transport within water flows can be affected by the nonuniform transverse velocity structure and lateral diffusion (Huai et al. 2019; Wang et al. 2020a, b), resulting in non-uniformity of the concentration distribution in the transverse direction (Nepf 1999; Serra et al. 2004; Nepf 2012). Significant skewness can be observed in the mean concentration distribution at the initial timescale due to the heterogeneous transverse diffusion at the beginning of the dispersion process (Jiang et al. 2017; Wang and Huai 2018). The mean concentration distribution over cross-sections cannot exactly predict the environmental dispersion mechanism due to the complicated pollutant transport process; the 2D analysis of environmental dispersion within water has drawn increasing attention because it can capture the characteristic of spatial contaminant cloud expansion (Barik and Dalal 2018; Guo et al. 2018; Guo et al. 2019). Furthermore, the design of constructed wetland for water treatment pays close attention to the contaminant absorption capacity within water bodies because boundary absorption intensity variations can lead to the heterogeneity of contaminant concentration distributions, especially in the transverse direction, and the expansion of contaminant cloud would be reduced (Sankarasubramanian and Gill 1973; Wang and Chen 2017; Smith 1983; Guo et al. 2019; Wang et al. 2020a). Therefore, spatial concentration distribution should be prioritized in environmental dispersion studies, particularly in boundary absorption water treatment research. The typical first-order reaction model has been widely employed to study the contaminant removal with absorption boundary in water bodies (Dentz and Carrera 2007; Rao et al. 2016; Barik and Dalal 2018; Machado Xavier et al. 2018; Liu et al. 2018; Wang and Huai, 2018). However, few studies have investigated the effect of two absorption boundaries on the contaminant transport process; accordingly, the expansion of the contaminant cloud becomes complicated. Dispersion heterogeneity also significantly exists in the transverse direction due to the diffusion-like process with lateral diffusion and nonuniformity of velocity profile in the lateral direction (Wu et al. 2011; Chen 2013). To explore the mechanism of cloud expansion and the centroid shifting process in the transverse direction, the irreversible reaction model is adopted to illustrate the absorption effect at two river banks in this work. Das et al. (2021) proved that the centroid of the contaminant cloud would shift in the transverse direction with the changes of absorption intensities at two boundaries, moreover, impacting factors of environmental dispersion need to be discussed, furthermore, in order to explore the key to cloud shift in the transverse direction, the ratio of two boundary absorption intensities is especially discussed to illustrate the difference between two boundary absorption intensities in this work for extending the analysis of environmental dispersion through two irreversible boundaries.

The analytical methods for environmental dispersion have been widely extended to explore the 2D spatial environmental dispersion. Many studies have employed different methods to achieve an asymptotic analytical solution of the mean cross-sectional concentration distributions (Aris 1956; Zeng et al. 2011). The pollutant transport process can be significantly affected by the different boundary effects, such as bed absorption. Accordingly, there is a significant variation in the local concentration distribution from the mean concentration distribution, and the mean concentration over cross-sections cannot precisely predict the contaminant transport process (Wu et al. 2015; Wang and Chen 2016, 2017; Wang et al. 2020b). Mei et al. (1996) multiscale perturbation theory has been expanded to allow the investigation of accurate 2D concentration distributions (Barik and Dalal 2018; Wang et al. 2020a). Taking into consideration the two irreversible absorption boundaries at riverbanks in this work, the spatial environmental dispersion process, particularly the transverse dispersion within water bodies between two bank-absorption boundaries, requires further investigation. The feature of the contaminant cloud expansion, such as the contaminant centroid position shift, requires further investigation with the consideration of two bank absorption boundaries. The multiscale perturbation theory has been extended to study the contaminant transport process and feature of pollutant cloud expansion to investigate the details of spatial concentration distributions within two irreversible boundaries at two riverbanks. The projections of this work are as follows: (I) achieving an analytical solution of the 2D concentration distribution with the ratio of two boundary-absorption intensities on the basis of the multiscale theory; (II) discussing the contaminant removal capacity with different ratios of two bank absorption intensities; (III) predicting the position of the transverse maximum concentration distribution under the effect of two irreversible boundaries with different absorption capacities and determining the relation between the maximum concentration distribution in the transverse direction and the ratio of two bank-absorption capacities.

Methods

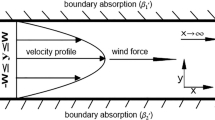
This work considers an instantaneous release of pollutants under the premise of two irreversible first-order absorption boundary conditions at two river banks. The sketch of a river with two irreversible absorption banks is shown in Fig. 1. In order to explore the spatial concentration distribution in the open channel caused by the difference between two absorption intensities at two boundaries, the Multi-scale method (Mei et al. 1996) was first adopted by Das et al.  (2021) in the open channel to study the environmental dispersion with two irreversible boundaries, for taking crest position analysis and avoiding the negative range in the transverse direction, instead of being at the centre in Das et al.'s work (2021), the origin of the coordinate system is put at the right bank to keep the range of channel width from zero to W in this work.

Fig. 1
figure 1

Sketch for the river with two irreversible absorption banks

Full size image

The governing equation of contaminant transport can be written as follows:

$$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}=D\frac{\partial^2C}{\partial {x}^2}+D\frac{\partial^2C}{\partial {y}^2}$$
(1)

where C is the concentration (kg m−3), t is time (s), u is flow velocity (ms−1), and D is dispersivity (m2 s−1).

The initial concentration distribution is illustrated as follows:

$$C\left(x,y,0\right)=\frac{Q}{W}\delta (x)$$
(2)

where δ(x) is the Dirac delta function.

The upstream and downstream concentrations can be expressed as follows:

$${\left.C\left(x,y,t\right)\right|}_{x=\pm \infty }=0$$
(3)

According to the different absorption intensities at the two banks, the boundary conditions are given as follows:

$$D{\left.\frac{\partial C\left(x,W,t\right)}{\partial y}\right|}_{y=0}={\left.{\beta}_0C\left(x,W,t\right)\right|}_{y=0}$$
(4)
$$D{\left.\frac{\partial C\left(x,W,t\right)}{\partial y}\right|}_{y=W}={\left.-{\beta}_1C\left(x,W,t\right)\right|}_{y=W}.$$
(5)

The contaminant transport process is studied in a nondimensional coordinate system to simplify the governing equation and deduction of the solving process.

$${x}^{\prime }=\frac{x}{L},\kern0.5em {y}^{\prime }=\frac{y}{W},\kern0.5em {\displaystyle \begin{array}{ccc}\tau =\frac{Dt}{W^2},& \varepsilon =\frac{W}{L},& \begin{array}{ccc} Pe=\frac{\left\langle u\right\rangle W}{D},& \psi =\frac{u}{\left\langle u\right\rangle }=6{y}^{\prime }-6y^{{\prime}2}& \begin{array}{cc}{C}^{\prime }=C/\frac{Q}{W}& {\beta_i}^{\prime }=\frac{\beta_iL}{D}\end{array}\end{array}\end{array}}$$
(6)

where L is the length scale of the contaminant cloud, and W is the width of the river. Pe is the Peclet number.

$$\left\langle u\right\rangle ={\int}_0^1 udy$$
(7)

The governing equation can be written as follows using these non-dimensional parameters:

$$\frac{\partial {C}^{\prime }}{\partial \tau }+\varepsilon P\mathrm{e}\psi \frac{\partial {C}^{\prime }}{\partial {x}^{\prime }}={\varepsilon}^2\frac{\partial^2{C}^{\prime }}{\partial x^{{\prime}2}}+\frac{\partial^2{C}^{\prime }}{\partial y^{{\prime}2}}$$
(8)

The upstream and downstream conditions are expressed as follows:

$${\left.{C}^{\prime}\left({x}^{\prime },{y}^{\prime },\tau \right)\right|}_{x^\prime =\pm \infty }=0$$
(9)

The boundary conditions at two banks are

$${\left.\frac{\partial {C}^{\prime }}{\partial {y}^{\prime }}\right|}_{y\prime =0}={{\varepsilon \beta}_0}^{\prime }{C}^{\prime}\left({x}^{\prime },0,\tau \right),$$
(10)
$${\left.\frac{\partial {C}^{\prime }}{\partial {y}^{\prime }}\right|}_{y\prime =1}=-{{\varepsilon \beta}_1}^{\prime }{C}^{\prime}\left({x}^{\prime },1,\tau \right),$$
(11)

Based on the three timescales (τ0, τ1, τ2), the concentration expansion can be written as follows:

$${C}^{\prime }=C^{\prime}_0+\varepsilon C^{\prime}_1+{\varepsilon}^2C^{\prime}_2+O\left({\varepsilon}^3\right),$$
(12)

The governing equation and boundary conditions can be rewritten by substituting the multiscale time deviation and concentration expansion:

$${\displaystyle \begin{array}{cc}\begin{array}{l}\left(\frac{\partial C^{\prime}_0}{\partial {\tau}_0}-\frac{\partial^2C^{\prime}_0}{\partial y{\prime}^2}\right)+\varepsilon \left(\frac{\partial C^{\prime}_1}{\partial {\tau}_0}+\frac{\partial C^{\prime}_0}{\partial {\tau}_1}+ Pe\psi \frac{\partial C^{\prime}_0}{\partial {x}^{\prime }}-\frac{\partial^2C^{\prime}_1}{\partial y{\prime}^2}\right)\\ {}+{\varepsilon}^2\left(\frac{\partial C^{\prime}_1}{\partial {\tau}_0}+\frac{\partial C^{\prime}_1}{\partial {\tau}_1}+\frac{\partial C^{\prime}_0}{\partial {\tau}_2}+ Pe\psi \frac{\partial C^{\prime}_1}{\partial {x}^{\prime }}-\frac{\partial^2C^{\prime}_0}{\partial x{\prime}^2}-\frac{\partial^2C^{\prime}_2}{\partial y{\prime}^2}\right)+\dots =0\end{array}&, 0<{y}^{\prime }<1\end{array}}$$
(13)
$${\displaystyle \begin{array}{cc}\frac{\partial C^{\prime}_0}{\partial {y}^{\prime }}+\varepsilon \left(\frac{\partial C^{\prime}_1}{\partial {y}^{\prime }}-{\beta}_0^{\prime }C^{\prime}_0\right)\Big)+{\varepsilon}^2\left(\frac{\partial C^{\prime}_2}{\partial {y}^{\prime }}-{\beta}_0^{\prime }C^{\prime}_1\right)=0,& {y}^{\prime }=0\end{array}},$$
(14)
$${\displaystyle \begin{array}{cc}\frac{\partial C^{\prime}_0}{\partial {y}^{\prime }}+\varepsilon \left(\frac{\partial C^{\prime}_1}{\partial {y}^{\prime }}+{\beta}_1^{\prime }C^{\prime}_0\right)+{\varepsilon}^2\left(\frac{\partial C^{\prime}_2}{\partial {y}^{\prime }}+{\beta}_1^{\prime }C^{\prime}_1\right)=0,& {y}^{\prime }=1\end{array}}$$
(15)

Then, C′1 can be achieved through the comparison of O (1) terms within Eqs. (13)–(15):

$${\displaystyle \begin{array}{cc}\frac{\partial C^{\prime}_0}{\partial {\tau}_0}=\frac{\partial^2C^{\prime}_0}{\partial y{\prime}^2},& 0<{y}^{\prime }<1,\end{array}}$$
(16)
$$\frac{\partial C^{\prime}_0}{\partial {y}^{\prime }}{\left|{}_{y\prime =0}=\frac{\partial C^{\prime}_0}{\partial {y}^{\prime }}\right|}_{y\prime =1}=0$$
(17)

Variable C′1 can be achieved through the comparison of O (ε) terms

$${\displaystyle \begin{array}{cc}\frac{\partial C^{\prime}_1}{\partial {\tau}_0}+\frac{\partial C^{\prime}_0}{\partial {\tau}_1}+ Pe\psi \frac{\partial C^{\prime}_0}{\partial {x}^{\prime }}=\frac{\partial^2C^{\prime}_1}{\partial y{\prime}^2},& 0<{y}^{\prime }<1,\end{array}}$$
(18)
$${\left.\frac{\partial C^{\prime}_1}{\partial {y}^{\prime }}\right|}_{y\prime =0}={\beta_0}^{\prime }C^{\prime}_0,$$
(19)
$${\left.\frac{\partial C^{\prime}_1}{\partial {y}^{\prime }}\right|}_{y\prime =1}=-{\beta_1}^{\prime }C^{\prime}_0,$$
(20)

The assumption of C′1 can be written as follows:

$$C^{\prime}_1= PeA\left({y}^{\prime}\right)\frac{\partial C^{\prime}_0}{\partial {x}^{\prime }}+\left({\beta_1}^{\prime }+{\beta_1}^{\prime}\right)B\left({y}^{\prime}\right)C^{\prime}_0$$
(21)

Comparing the coefficient terms yields:

$${\displaystyle \begin{array}{cc}\frac{d^2A}{dy{\prime}^2}=\psi -\left\langle \psi \right\rangle, & 0<{y}^{\prime }<1,\end{array}}$$
(22)
$${\displaystyle \begin{array}{cc}\frac{d^2B}{dy{\prime}^2}=-1,& 0<{y}^{\prime }<1\end{array}}$$
(23)

The boundary conditions can be obtained as:

$${\left.\frac{dA}{dy^{\prime }}\right|}_{y\prime =0}={\left.\frac{dA}{dy^{\prime }}\right|}_{y\prime =1}=0,$$
(24)
$$\left\langle A\right\rangle =0$$
(25)

In order to discuss the efforts made by two boundary-absorption intensities’ difference, the ratio (r) of absorption intensity at left bank and absorption intensity at right bank is adopted to illustrate the difference between two boundary absorption intensities.

The boundary condition of B can be obtained with the ratio of two boundary absorption intensities:

$${\left.\frac{dB}{dy^{\prime }}\right|}_{y\prime =0}=\frac{1}{1+r},$$
(26)
$${\left.\frac{dB}{dy^{\prime }}\right|}_{y\prime =1}=-\frac{r}{1+r},$$
(27)
$$\left\langle B\right\rangle =0,$$
(28)

where r = β1′/β0′.

On the basis of second-order term (O(ε2)), Eqs. (15)–(17) become

$${\displaystyle \begin{array}{cc}\frac{\partial C^{\prime}_1}{\partial {\tau}_0}+\frac{\partial C^{\prime}_1}{\partial {\tau}_1}+\frac{\partial C^{\prime}_0}{\partial {\tau}_2}+ Pe\psi \frac{\partial C^{\prime}_1}{\partial {x}^{\prime }}=\frac{\partial^2C^{\prime}_0}{\partial x{\prime}^2}+\frac{\partial^2C^{\prime}_2}{\partial y{\prime}^2},& 0<{y}^{\prime }<1\end{array}}$$
(29)
$${\left.\frac{\partial C^{\prime}_2}{\partial {y}^{\prime }}\right|}_{y\prime =0}={\beta_0}^{\prime }C^{\prime}_1(0),$$
(30)
$${\left.\frac{\partial C^{\prime}_2}{\partial {y}^{\prime }}\right|}_{y\prime =1}=-{\beta_1}^{\prime }C^{\prime}_1(1)$$
(31)

The concentration derivation according to τ0 can be neglected because timescale τ0 is much larger than τ1 and τ2. The equation can be transformed into

$$\frac{\partial C^{\prime}_0}{\partial {\tau}_2}+\frac{\partial C^{\prime}_1}{\partial {\tau}_1}+ Pe\psi \frac{\partial C^{\prime}_1}{\partial {x}^{\prime }}=\frac{\partial^2C^{\prime}_0}{\partial x{\prime}^2}+\frac{\partial^2C^{\prime}_2}{\partial y{\prime}^2}$$
(32)

We obtain the following expression with the averaging operation in the transverse direction:

$$\frac{\partial C^{\prime}_0}{\partial {\tau}_2}+\frac{\partial \left\langle C^{\prime}_1\right\rangle }{\partial {\tau}_1}+ Pe\left\langle \psi \frac{\partial C^{\prime}_1}{\partial {x}^{\prime }}\right\rangle =\frac{\partial^2C^{\prime}_0}{\partial x{\prime}^2}-{\beta_1}^{\prime }C^{\prime}_1(1)-{\beta_0}^{\prime }C^{\prime}_1(0)$$
(33)

With two new dimensionless variables βi∗(≥0) = εβi′ and \(\eta =\frac{x^{\prime }}{\varepsilon }- Pe\left[\left\langle \psi \right\rangle +\left({\beta_0}^{\ast }+{\beta_1}^{\ast}\right)\left\langle \psi B\right\rangle +{\beta_1}^{\ast }A(1)+{\beta_0}^{\ast }A(0)\right]\tau\), the C′0 can be solved through deduction as:

$$C{\prime}_0=\frac{1}{\sqrt{4\pi {D}_c\tau }}\mathit{\exp}\left(-\frac{\eta^2}{4{D}_c\tau }-\left({\beta_0}^{\ast }+{\beta_1}^{\ast}\right)\left({\beta_0}^{\ast }B(0)+{\beta_1}^{\ast }B(1)+1\right)\tau \right)$$
(34)

Subtracting (33) from (32) yields the following equation:

$$\frac{\partial C^{\prime}_1}{\partial {\tau}_1}+ Pe\psi \frac{\partial C^{\prime}_1}{\partial {x}^{\prime }}- Pe\left\langle \psi \frac{\partial C^{\prime}_1}{\partial {x}^{\prime }}\right\rangle =\frac{\partial^2C^{\prime}_2}{\partial y{\prime}^2}+\left({\beta_1}^{\prime }C^{\prime}_1(1)+{\beta_0}^{\prime }C^{\prime}_1(0)\right)$$
(35)

Based on C′0 and C′1, the assumption of C′2 can be written as follows:

$$C^{\prime}_2={Pe}^2X\left({y}^{\prime}\right)\frac{\partial^2C^{\prime}_0}{\partial x^{{\prime}2}}+\left({\beta_0}^{\prime }+{\beta_1}^{\prime}\right) PeY\left({y}^{\prime}\right)\frac{\partial C^{\prime}_0}{\partial {x}^{\prime }}+{\left({\beta_0}^{\prime }+{\beta_1}^{\prime}\right)}^2Z\left({y}^{\prime}\right)C^{\prime}_0$$
(36)

Terms X, Y, and Z can be illustrated as follows:

$$\frac{d^2X}{dy^{{\prime}2}}=\psi A-\left\langle \psi \right\rangle A-\left\langle \psi A\right\rangle,$$
(37)
$${\left.\frac{dX}{dy^{\prime }}\right|}_{y\prime =0}={\left.\frac{dX}{dy^{\prime }}\right|}_{y\prime =1}=0,$$
(38)
$$\left\langle X\right\rangle =0,$$
(39)
$$\frac{d^2Y}{dy^{{\prime}2}}=\psi B-\left\langle \psi \right\rangle B-\left\langle \psi B\right\rangle -A-\left[\frac{{\beta_1}^{\prime }}{{\beta_0}^{\prime }+{\beta_1}^{\prime }}A(1)+\frac{{\beta_0}^{\prime }}{{\beta_0}^{\prime }+{\beta_1}^{\prime }}A(0)\right],$$
(40)
$${\left.\frac{dY}{dy^{\prime }}\right|}_{y\prime =0}=\frac{1}{1+r}A(0),$$
(41)
$${\left.\frac{dY}{dy^{\prime }}\right|}_{y\prime =1}=-\frac{r}{1+r}A(1),$$
(42)

where r = β1′/β0′ = β1∗/β0∗.

$$\left\langle Y\right\rangle =0$$
(43)
$$\frac{d^2Z}{dy^{{\prime}^2}}=-B-\left(\frac{{\beta_0}^{\prime }}{{\beta_0}^{\prime }+{\beta_1}^{\prime }}B(0)+\frac{{\beta_1}^{\prime }}{{\beta_0}^{\prime }+{\beta_1}^{\prime }}B(1)\right)$$
(44)
$${\left.\frac{dZ}{dz^{\prime }}\right|}_{z^\prime =0}=\frac{1}{1+r}B(0)$$
(45)
$${\left.\frac{dZ}{dz^{\prime }}\right|}_{z^\prime =1}=-\frac{r}{1+r}B(1)$$
(46)
$$\left\langle Z\right\rangle =0$$
(47)

The solution of the 2D concentration distribution with the ratio of two boundary absorption intensities is obtained as follows:

$${\displaystyle \begin{array}{c}{C}{\hbox{'}}=C^{\prime}_0+\varepsilon C^{\prime}_1+{\varepsilon}^2C^{\prime}_2\\ {}=\left(1+\left({\beta_0}^{\ast }+{\beta_1}^{\ast}\right)B+{\left({\beta_0}^{\ast }+{\beta_1}^{\ast}\right)}^2Z\right)C^{\prime}_0+\left( PeA+\left(+{\beta_0}^{\ast }+{\beta_1}^{\ast}\right) PeY\right)\frac{\partial C^{\prime}_0}{\partial \eta }+P{e}^2X\frac{\partial^2C^{\prime}_0}{\partial {\eta}^2}\end{array}}$$
(48)

where

$${\displaystyle \begin{array}{l}\begin{array}{l}\begin{array}{l}Z\left({y}^{\prime}\right)=\frac{1}{24}y^{{\prime}4}-\frac{1}{6\left(1+r\right)}y^{{\prime}3}+\frac{4-r+{r}^2}{12{\left(1+r\right)}^2}y{\prime}^2-\frac{2-r}{6{\left(1+r\right)}^2}{y}^{\prime }+\frac{7-r-2{r}^2}{72{\left(1+r\right)}^2}-\frac{1}{120},\\ {}B\left({y}^{\prime}\right)=-\frac{1}{2}y^{{\prime}2}+\frac{1}{1+r}{y}^{\prime }-\frac{1}{2\left(1+r\right)}+\frac{1}{6},\\ {}X\left({y}^{\prime}\right)=\frac{3}{56}y^{{\prime}8}-\frac{3}{14}y^{{\prime}7}+\frac{19}{60}y^{{\prime}6}-\frac{1}{5}y^{{\prime}5}+\frac{1}{30}y^{{\prime}4}+\frac{1}{60}y^{{\prime}3}-\frac{1}{168}y^{{\prime}2}+\frac{1}{12600},\end{array}\\ {}Y\left({y}^{\prime}\right)=\frac{7}{60}y^{{\prime}6}-\frac{5+2r}{10\left(1+r\right)}y^{{\prime}5}+\frac{3}{4\left(1+r\right)}y{\prime}^4-\frac{3-r}{6\left(1+r\right)}y^{{\prime}3}-\frac{17-13r}{120\left(1+r\right)}y^{{\prime}2}+\frac{1}{60\left(1+r\right)}{y}^{\prime }+\frac{6-r}{120\left(1+r\right)}-\frac{1}{60},\end{array}\\ {}Z\left({y}^{\prime}\right)=\frac{1}{24}y^{{\prime}4}-\frac{1}{6\left(1+r\right)}y^{{\prime}3}+\frac{4-r+{r}^2}{12{\left(1+r\right)}^2}y^{{\prime}2}-\frac{2-r}{6{\left(1+r\right)}^2}{y}^{\prime }+\frac{7-r-2{r}^2}{72{\left(1+r\right)}^2}-\frac{1}{120}\end{array}}$$

Results and discussion

Verification of results

The numerical simulation experiments are provided to compare with the analytical solution for validation and verify the analytical solution of the contaminant distribution. The numerical solutions are carried out by Fluent software by using the finite volume method. The mean concentration distributions over the cross-section at three time points with β0 = β1 = 0 are illustrated. The numerical simulation experiments by Fluent based on the governing equation and boundary equations are given by Eqs. (1)-(5) Fig. 2

Fig. 2
figure 2

Comparation between analytical solutions and numerical solutions

Full size image

Analysis of spatial concentration distribution

The effect of two bank-absorption intensities on environmental dispersion can be reflected by the 2D spatial contaminant cloud expanding process. The 2D spatial concentration distribution under the effect of two bank-absorption intensities is thoroughly discussed to study the effect of two bank-absorption intensities by presenting the concentration distributions in the longitudinal and transverse directions. The spatial contaminant clouds are also illustrated to present the contaminant transport process.

Longitudinal concentration distribution

To discuss the feature of the longitudinal concentration distribution, the mean concentration over cross-sections and the longitudinal concentration distributions at three characteristic layers are chosen to present the trait of longitudinal concentration distributions considering the two bank-absorption boundaries. As shown in Fig. 3a significant deviation exists between the longitudinal concentration distributions and the mean concentration distribution in the open channel due to the bank absorption intensity variation at two sides. Given a certain total absorption intensity (β0 *  + β1 *  = 0.5) within the open channel flow, the longitudinal concentration distributions at the top and bottom layers evidently deviate from the mean concentration distribution with a larger difference (r = 12) between two bank-absorption intensities than that with a smaller ratio (r = 4) of two absorption intensities. In addition, the less discrepancy of the absorption strength between two banks results in a lower longitudinal concentration distribution, indicating that the capacity of contaminant absorption would be affected by the ratio of two bank-absorption strengths.

Fig. 3
figure 3

Longitudinal concentration distributions at feature layers

Full size image

Transverse concentration distribution

Given that the bank-absorption intensity at two banks affects the expansion of contaminant cloud, the transverse concentration distributions are illustrated in Fig. 4 to clarify the effects of two bank-absorption discrepancies on environmental dispersion. The transverse concentration distribution flattens with the increase in the overall bank absorption intensity, indicating that the total solute quantity shrinks under the bank absorption. The curve presents a symmetric central layer (z’=0.5H) with the same bank-absorption intensities at both sides. The transverse concentration distribution peak deviates with the change of the ratio of two bank-bank absorption intensities. The transverse concentration distribution is symmetric concerning the central layer when absorption intensities are the same at both river banks. In addition, the ratio of two bank-absorption intensities influences the total capacity within the flows, as shown in Fig. 4, under the same absorption strength. The crest value of the concentration distribution attains the minimum with no discrepancy between the two bank-absorption strengths (β0 : β1 = 1). The maximum of the transverse concentration distributions increases with the increase in the difference between two bank-absorption intensities, demonstrating that the absorption capacity within flows would be weakened as the two bank-absorption capacities greatly vary.

Fig. 4
figure 4

Transverse concentration distributions with different bank-absorption intensities

Full size image

Position of maximum transverse concentration distribution

The transverse concentration distribution is significantly changed with the variation of the two bank-absorption intensities, indicating that the centroid of the contaminant cloud skews with different two bank-absorption intensities. Meanwhile, the position of the crest concentration distribution also drifts with the change in absorption intensity at two river banks. Thus, the position of the transverse concentration distributions with different two bank-absorption intensities is studied, as shown in Fig. 5. The analytical solutions of the crest concentration distribution with different two bank-absorption intensities are represented by the dots. The crest position distribution is symmetric according to the center point (β0 * /(β0 *  + β1*) =0.5, P=0.5), and these solutions can be treated as a linear fitting. The fitting equation for the crest of the transverse concentration distribution is provided as follows:

$$P=0.82\frac{\beta_0^\ast }{\beta_0^\ast +{\beta}_1^\ast }+0.09.$$
Fig. 5
figure 5

Crest of transverse concentration distributions with ratios of two bank-absorption strengths

Full size image

As shown in Fig. 5, the position of the maximum concentration distribution increases with the increment of difference between two absorption intensities at two river banks, and the correlation coefficients are all above 0.99, indicating a good match between the crest position obtained by fitting equation and that achieved by analytical method.

The given model for illustrating the shift of crest position (\(P=0.82\frac{\beta_0^\ast }{\beta_0^\ast +{\beta}_1^\ast }+0.09\)) presents a good match with these results under different total absorption intensities and time points, the correlation coefficients are all above 0.9 as shown in Table 1.

Table 1 Correlation Coefficients with different total absorption intensities at various time points
Full size table

Residual mass with different ratios of the two bank-absorption capacities

This work aims to study the effect on the total absorption capacity within the open channel by two bank-absorption discrepancies, as shown in Fig. 6 and Table 2. The residual mass increases with the enlargement of the two bank-absorption at the same time point, indicating the deferment of the total absorption process within the open channel caused by the two bank-absorption discrepancies. Accordingly, the best capacity of the total absorption occurs at two banks with the same absorption intensity. This work provides instructions on the design of constructed wetlands to achieve the best absorption effect with irreversible absorption boundary conditions on two river banks.

Fig. 6
figure 6

Residue mass of contaminant with different ratios of two bank-absorption intensities

Full size image
Table 2 Residual mass under different conditions
Full size table

2D concentration distribution

2D concentration distributions are given to express the effect of two bank-absorption intensities on the contaminant cloud characteristics. With the same total bank-absorption intensities, the centroid of the contaminant cloud drifts with the changes of the two bank-absorption ratios, as illustrated in Fig. 6. Meanwhile, the crest point of the concentration distribution also deviates from the center to the side with less absorption capacity. The skewness of the contaminant cloud shape becomes more evident with the increment of two bank-absorption discrepancies. The high-concentration area significantly expands, indicating that the total absorption capacity would be restrained due to the discrepancy between the two bank absorption intensities. In addition, the larger total bank-absorption capacity results in a contaminant cloud with a lower concentration distribution. However, the shapes of the contaminant clouds are similar with the same ratio of two bank-absorption intensities, manifesting the similar feature of the environmental dispersion process, indicating that the bank-absorption discrepancy and the total absorption capacity can make sense on the contaminant cloud feature and dispersion period as illustrated in Fig. 7

Fig. 7
figure 7

Two dimensional concentration distributions

Full size image

Conclusion

The exact analytical solution of the 2D concentration distribution according to the absorption intensity ratio between two river banks is achieved in this work. To express the effect of the two bank-absorption intensities on contaminant transport, the longitudinal concentration distribution, transverse concentration distribution, and 2D spatial concentration distribution have been illustrated to indicate the efforts on environmental dispersion by two bank-absorption intensities. In addition, the crest position of the concentration distribution in the transverse direction has been fitted to a linear equation.

The longitudinal concentration distributions in this work have been discussed by choosing three characteristic layers, namely, the top, center, and bottom layers. The result shows that the two bank-absorption discrepancies would result in the deviations of the longitudinal concentration distributions at three feature layers from the cross-sectional mean concentration distributions. The deviation indicates the heterogeneity of contaminant spatial distribution within the flows under the two bank-absorption discrepancies. In addition, the discrepancy can also affect the contaminant absorption capacity within the open channel.

The transverse concentration distributions can directly illustrate the efforts on environmental dispersion made by two bank-absorption intensities. The discrepancy of the two bank-absorption intensities would result in an increment in contaminant concentration distribution in the transverse direction, indicating that the discrepancy of two bank-absorption intensities can cause the inhibition of contaminant transport. With a certain total absorption capacity, the spatial concentration distributions turns more heterogeneous as the ratio deviates from 1 gradually, and the transverse concentration distribution appears to be symmetric to the center (0.5W) when the ratios of absorption intensities at two stream-banks are in accord with β0 : β1 = β1 : β0. In addition, the crest position of the concentration distribution changes with different ratios of the two bank-absorption intensities.

The spatial concentration distribution has been created to explain the efforts on 2D concentration distributions by two bank-absorption intensities, with the same absorption intensity in total. The high concentration area expands with the increase in concentration discrepancy, indicating the increment of the remaining contaminant quantity. The expansion of the contaminant cloud deviates with the increment of two bank-absorption discrepancies, manifesting the heterogeneous distribution in the transverse direction led by two bank absorption effects.

The crest position of the transverse concentration distributions has been illustrated with a variation of the two bank-absorption intensities to discuss the feature of concentration distributions. The results have been fitted to a linear distribution of crest position of the transverse concentration distribution with the ratio of two bank-absorption intensities. The given model for illustrating the shift of crest position (\(P=0.82\frac{\beta_0^\ast }{\beta_0^\ast +{\beta}_1^\ast }+0.09\)) presents a good match with these results under different total absorption intensities and time points, the correlation coefficients are all above 0.9. The solution of the exact position of crest concentration distribution in the transverse direction is achieved in this work to illustrate the contaminant cloud expansion feature and predict the intake area for safe water use.

The residual mass of the contaminant within the open channel is discussed to approve the deferment caused by two bank-absorption discrepancies. The result depicts the increment in residue mass with the discrepancy in two bank-absorption intensities, providing instructions for the artificial wetland construction to achieve the best absorption capacity with irreversible boundary conditions at two banks. Under a certain total absorption intensity within the open channels at the same time points, the residual mass would be larger with the greater deviation of absorption-intensity ratios from 1, and the difference between the residual mass with the certain total absorption intensity (β0 * + β1 *  = 1) but different absorption intensity ratio (1 and 20) at two banks can even go 84%, indicating the deviation of boundary-absorption intensities at two streambanks would give a negative impact on the process of contaminant absorption within open channels through two absorbing stream-boundaries.