Introduction

Recently, most of countries have great concern about how to maximize energy efficiency due to not only their official duty to reduce carbon dioxide emission but also disappointing return on investment to renewable energy business. According to the International Energy Agency’s report of the G8 Summit in 2008, operating efficiency of coal-fired power plants should be enhanced above 40 % in order to reduce the amount of carbon dioxide emission and the volume of coal consumption [1]. If the temperature of main steam in coal-fired power plant increases by 20 °C, thermal efficiency will also increase up to about 1 %. However, inherent creep property of metallic materials is the principal barrier which prevents enhancement of operating efficiency. In general, metallic materials at above a half of their melting temperature show significant creep deformation which cannot be explained by mechanical properties at room temperature. In any facilities or mechanical components operated at high temperature, therefore, creep deformation must be taken into account critically. Thanks to many great senior researchers, experiment methods and microscopic analyses on creep issues have been well studied, and especially uniaxial creep test, suggested by ASTM E139-11 [2], has been used to obtain creep properties of metallic material universally. However, as uniaxial creep test needs bulk of materials, this test cannot be applied to in-service facilities or components.

To overcome this limitation, Small Punch Creep Test (SPCT) has been alternatively suggested to evaluate creep properties of in-service material [3, 4]. Since SPCT just needs a thin sheet of material (10 × 10 × 0.5 mm), it is well fitted to determine creep properties of in-service components at high temperature. In addition, SPCT has an advantage in test time because rupture in SPCT happens very quickly compared to the conventional uniaxial creep test. Various studies on SPCT have been carried out during several decades. Chakrabarty has suggested an analytical solution through membrane stretching theory [5]. Yang and Wang have provided a relationship between creep strain and punch displacement [6]. Chen has investigated non-dimensional analysis to obtain creep properties of material [7]. Hyde has developed general strain analysis using membrane stretching theory and finite element method [8]. Also, the European Committee for Standardization has carried out a Code of Practice for SPCT [9].

Components of SPCT can be divided into three; a small sheet specimen, two dies to fix specimen, and punch ball under constant load. SPCT results show similar features, but definitely not the same, to uniaxial creep test results, that is, uniaxial creep test generates strain and stress data, whereas SPCT results have displacement and load data. Until nowadays, lots of researchers have studied on how to interpret SPCT results in order to compare with uniaxial creep test results [9–12]. Not only 2-dimensional or 3-dimensional finite element models [13–16] have been developed to obtain local strain and stress data but also microscopic analysis [17, 18] on specimen has validated creep phenomenon within SPCT specimen. From these diverse studies, certain empirical equations about stress and strain of SPCT have been derived [9], and stress distribution on SPCT specimen in the process of experiment is revealed by finite element analysis [19]. Also, many studies on boundary conditions, factors, and parameters affecting SPCT results have been carried out [6, 13, 17].

In this paper, a direct methodology with Chakrabarty’s membrane stretching theory is applied to SPCT results in order to derive equivalent strain and strain rate. Especially, we focus on the thinnest point in SPCT specimen and obtain equivalent strain and strain rate data at the thinnest point. There are several previous researches to support our proposal. Park [17] investigated thickness decrease of every position on the specimen right before failure and compared it with finite element analysis result. It suggested that the thinnest point on a specimen is a dominant position to cause total failure of SPCT with the highest stress concentration. Several studies also provide that rupture occurs near the thinnest point of the specimen and its location does not change during the test, and therefore investigation of the thinnest point was carried out in order to obtain creep properties through finite element analysis [7, 16, 17]. Moreover, Lee’s observation of fracture surface shows microscopic evidence such as growth and coalescence of crack at the thinnest point and occurrence of intergranular fracture caused by intergranular cavity crack at that point [18]. Lee’s study not only provides fracture mechanism on SPCT specimen, but also explains why the thinnest point is important in order to obtain creep property from SPCT. In order to validate the proposed methodology, uniaxial creep test results and SPCT results using STS 316L stainless steel under the test temperature of 650 °C [20, 21] which is operation condition in power plants are cited. SPCT results of STS 316L stainless steel are converted into strain and strain rate data using this direct methodology. With converted data, the Monkman-Grant model [22], which is a method to predict material’s creep life, is investigated by uniaxial creep test and SPCT. Finally, comparison of the Monkman-Grant models provides a good correlation between uniaxial creep test and this direct methodology using SPCT results.

Methods

Chakrabarty’s Membrane Stretching Model

Chakrabarty’s study provides not only general analytic solution of plastic deformation but also peculiar solution of stretching forming over hemispherical punch heads [5, 23]. Figure 1 shows a spherical pressure vessel in a spherical coordinate and represents the stress state of an infinitesimal element and Fig. 2 shows a schematic of Chakrabarty’s membrane stretching model in 2-dimensional cross section view including z-axis in Fig. 1.

Fig. 1
figure 1

Spherical coordinate for hemispherical pressured vessel

Full size image
Fig. 2
figure 2

A schematic of Chakrabarty’s membrane stretching model in SPCT

Full size image

In Fig. 1, the spherical pressure vessel forms a surface of revolution with respect to z-axis and the element, which has a thickness, T, is defined by spherical coordinate system. Radial direction component is R, circumferential direction is θ and meridional direction is ϕ. The stress state of the element is also represented by spherical coordinate system and the component of the stress state shows radial stress, p, in radial direction, circumferential stress, σ θ , in θ direction and meridional stress, σ ϕ , in ϕ direction. Basically, when the element is located apart from r, which is a vertical distance from z-axis, the circumferential and meridional radii of curvature are formulated like:

$$ {\rho}_{\theta }=r\ \mathrm{cosec}\ \phi, {\rho}_{\phi }=\frac{\partial r}{\partial \phi } \sec \phi $$
(1)

ρ θ is the circumferential radius of curvature and ρ ϕ is the meridional radius of curvature. And due to exact spherical shape, ρ θ and ρ ϕ should be defined like:

$$ {\rho}_{\theta }={\rho}_{\phi }=R $$
(2)

Using these geometric constraints, the equations of meridional and radial equilibrium with no friction condition are expressed by:

$$ \begin{array}{ll}\frac{\partial }{\partial r}\left(T{\sigma}_{\phi}\right)=\frac{T}{r}\left({\sigma}_{\theta }-{\sigma}_{\phi}\right),\hfill & p=\frac{T}{R}\left({\sigma}_{\theta }+{\sigma}_{\phi}\right)\hfill \end{array} $$
(3)

More details for derivation of these two equilibrium equations are shown in Appendix. Because the element experiences only three normal stresses without shear stress, that state is principal stress state. Therefore, each current stress direction means the principal direction of stress for that element. And a material is postulated to experience ideally plastic deformation with a constant yield stress in accordance with Levy-Mises flow rule, in which elastic deformation is neglected because it is relatively very small. Poisson’s ratio of material is set to be 0.5 in incompressible condition and the principal direction of stress is then assumed to be equal to that of strain increment. Therefore, incompressible condition can be expressed such that

$$ {\varepsilon}_{kk}={J}_1=3{\varepsilon}_m={\varepsilon}_{11}+{\varepsilon}_{22}+{\varepsilon}_{33}={\varepsilon}_{\theta }+{\varepsilon}_{\phi }+{\varepsilon}_T=0 $$
(4)
$$ {\varepsilon}_{ij}^{\prime }={\varepsilon}_{ij}-{\varepsilon}_m{\delta}_{ij}={\varepsilon}_{ij} $$
(5)

In this case, the first plastic strain invariant, J 1, is 0 and thus, the deviatoric strain tensor, ε ′ ij , is equal to the plastic strain tensor, ε ij , because the mean strain, ε m , is also 0. ε θ means the circumferential strain, ε ϕ means the meridional strain and ε T means the radial strain which is direction of thickness. Each strain term means the principal strain as well. If r 0 is initial position of the element which is located apart from r, each strain value is formulated like:

$$ \begin{array}{lll}{\varepsilon}_{\theta }= \ln \left(\frac{r}{r_0}\right),\hfill & {\varepsilon}_{\phi }= \ln \left(\frac{\partial r}{\partial {r}_0} \sec \phi \right),\hfill & {\varepsilon}_T= \ln \left(\frac{T}{T_0}\right)\hfill \end{array} $$
(6)

Where T 0 is the initial thickness of the element, more details on derivation of each strain component are shown in Appendix. Biaxial tension on the element provides σ θ  = σ ϕ and therefore, ε θ is also equal to ε ϕ . From this relationship, the von-Mises equivalent strain, ε q , is represented as:

$$ {\varepsilon}_q=\sqrt{\frac{2}{3}{\varepsilon}_{ij}^{\prime }{\varepsilon}_{ij}^{\prime }}=\sqrt{\frac{2}{3}{\varepsilon}_{ij}{\varepsilon}_{ij}}=\sqrt{\frac{2}{3}\left({\varepsilon_{\theta}}^2+{\varepsilon_{\phi}}^2+{\varepsilon_T}^2\right)}=\left|{\varepsilon}_T\right|= ln\left(\frac{T_0}{T}\right) $$
(7)

The von-Mises equivalent strain can be obtained directly by measuring the thickness of a specimen.

The Monkman-Grant Model

The Monkman-Grant model, a method to predict the creep life of metallic material, is composed of the creep failure time t f , minimum strain rate \( {\dot{\varepsilon}}_{min} \), and constants m and C such that

$$ {t}_f{{\dot{\varepsilon}}_{min}}^m=C $$
(8)

Depending on metals, the constant m varies between 0.8 and 0.95, while the constant C varies between 3 and 20 when t f has unit of hour and \( {\dot{\varepsilon}}_{min} \) has unit of percent over hour respectively [22]. It is also reported that the constant m depends on the microstructure of material such as grain size [24]. In general, equation (8) is used after it is converted into logarithmic scale. After conversion, it is plotted as a straight linear graph, which has m slope. Using this linear graph, we can expect long term creep life using linear approximation. In this paper, the Monkman-Grant models of uniaxial creep test and SPCT are examined and compared to each other. The results of SPCT mostly have a shorter rupture time rather than those of uniaxial creep test in the Monkman-Grant model.

Material and Experimental Procedure

Uniaxial creep test and SPCT for STS 316L stainless steel have been carried out at 650 °C by Im [20] and Kim [21]. STS 316L stainless steel, which is an austenite type stainless steel, is widely used in fossil and atomic power plant because it is representative steel including good heat-resistant property. Specific compositions of STS 316L stainless steel are shown in Table 1.

Table 1 Chemical compositions of STS 316L [21]
Full size table

A uniaxial creep test needs round bar shaped specimen with the gage section diameter of 6 mm and gage length of 30 mm as shown in Fig. 3(a). This specimen is initially placed inside a thermal chamber for heating. Once it reaches to a test temperature, a uniaxial creep test begins with a constant load in the air condition. Displacement is recorded by a linear variable differential transformer (LVDT) which has the capacity to measure the change of 1 μm.

Fig. 3
figure 3

Types of creep test specimen: (a) Uniaxial creep test (b) SPCT

Full size image

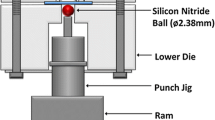
In contrast, as shown in Fig. 3(b), SPCT needs a very thin sheet specimen (10 × 10 × 0.5 mm), which is much smaller than a typical uniaxial creep specimen. Better comparison between uniaxial creep specimen and SPCT specimen is depicted in Fig. 4. One uniaxial creep specimen requires material for more than two hundreds of SPCT specimens. This SPCT specimen is placed between the upper and the lower die with argon gas condition, and a punch ball is loaded on the specimen. Punch displacement is also measured by an LVDT. Both 2-D and 3-D Schematics of an SPCT tester are shown in Fig. 5. R is a radius of punch ball (1.2 mm), a is an inner radius of lower die (2 mm), b is a fillet radius (0.2 mm) of lower die, and T 0 is a thickness of specimen (0.5 mm). As shown in Fig. 5(a), each central vertical axis of punch, punch ball and specimen should coincide with one another in order to avoid anisotropic effect. In other words, punch ball should convey force through the exact center point of specimen and then eventually penetrate it. Therefore, the initial thickness of specimen has to be uniform in order to prevent deviation of force direction. Also, the surface of specimen must be flawless. This is the reason why SPCT is normally performed in argon gas condition to prevent oxidation. The upper and the lower die also play an important role in preventing slip between specimen and punch ball. Without appropriate force transmission, membrane stretching theory cannot be applied to SPCT. Thus, each test should accompany all the above requirements.

Fig. 4
figure 4

Comparison between uniaxial creep specimen and SPCT specimen

Full size image
Fig. 5
figure 5

Schematics of SPCT: (a) 2-D model (b) 3-D model

Full size image

Experimental Results

Table 2 lists various mechanical properties of STS 316L stainless steel at room temperature and 650 °C, respectively. Its creep properties at 650 °C such as minimum creep strain rate \( {\dot{\varepsilon}}_{min} \), failure time t f , and total strain to failure ε f are also provided in Table 3. Here, \( {\dot{\varepsilon}}_{min} \) is obtained by taking derivative of creep strain with respect to time. Figure 6 represents SPCT curves of STS 316L stainless steel at 650 °C. When we use different punch balls, one is Al 2 O 3 and the other is Si 3 N 4. Kim et al. investigated effect of friction of two different punch balls and showed that the difference of friction coefficient affects minimum punch displacement rate ḣ min and failure time t f as shown in Fig. 6 [21]. They also determined the friction coefficients of Al 2 O 3 and Si 3 N 4 against STS 316L stainless steel as 0.4 and 0.5, respectively. To be specific, the bigger friction coefficient is, the longer t f and the smaller ḣ min even in same experiment condition. Although ḣ min and t f vary depending on the type of punch ball, we can observe, in both cases, very typical creep behaviors consisting of initial rise, steady state increase, and rupture with necking. In the next section, these two different SPCT results are used to validate equivalent strain analysis, and the effect of friction coefficient of punch ball is discussed when creep life expectation is carried out.

Table 2 Mechanical properties of STS 316L at room temperature and 650 °C [20]
Full size table
Table 3 Creep properties of STS 316L at 650 °C [20]
Full size table
Fig. 6
figure 6

SPCT curves of STS 316L stainless steel at 650 °C (a) Al 2 O 3 punch ball (b) Si 3 N 4 punch ball [21]

Full size image

Equivalent Strain Analysis

In SPCT, transition from bending to membrane stretching is elucidated both theoretically and experimentally. Chakrabarty provided an analytic solution on bending deformation as well as membrane stretching deformation, which suggested that membrane stretching deformation is dominant when punch displacement exceeds the initial thickness of specimen [25]. Mao also showed that punch displacement at transition from bending to membrane stretching is about 0.8 mm for 10 × 10 × 0.5 mm specimen [26]. Therefore, the equivalent strain relationship in Chakrabarty’s membrane stretching theory is applied in this context in order to obtain strain data.

The equivalent strain in equation (7) can be derived from the direct investigation of thickness change in an SPCT specimen. Mao investigated thickness change at the local necking and crack initiation position using seven different materials [26]. As shown in Fig. 7, each small punch test is stopped to measure the thickness at the thinnest point, and this process is repeated until fracture.

Fig. 7
figure 7

Measurement of thickness at the thinnest point [26]

Full size image

From this investigation, Mao suggested an empirical equation of thickness T as a function of punch displacement h and thickness T such that

$$ \frac{T}{T_0}={e}^{-1.2{\left(\frac{h}{2}\right)}^{1.5}} $$
(9)

Note that this is only valid when experimental conditions such as specimen type, punch ball size, and inner diameter of lower die are identical to Mao’s experiment. He also reported that loading capacity of the specimen is deteriorated by significant decrease of thickness and the circumferential crack propagation.

Substituting equation (9) into equation (7) yields the equivalent strain with respect to the punch displacement [26].

$$ {\varepsilon}_q=1.2{\left(\frac{h}{2}\right)}^{1.5} $$
(10)

Since we now obtain the equivalent strain directly from small punch test result by using equation (10), no more finite element analysis is required to investigate stress and strain equivalent to uniaxial test results.

This direct analytical solution to small punch test can be also applied to SPCT because the main fracture occurs near the thinnest point and thickness change versus the punch displacement shows the similar trend in both tests although test condition and microscopic deformation mechanism are not exactly the same. Under this assumption, substitution of the displacement results of SPCT in Fig. 6 into equation (10) yields the conversion of punch displacement into the equivalent strain ε q . The equivalent strain rate \( \dot{\varepsilon_q} \) can be also obtained simply by taking time derivative of the equivalent strain ε q . Especially, MATLAB, commercial software, is used to acquire a time derivative between two consecutive data points. In summary, the proposed method enables us to investigate creep properties directly from SPCT without any aid of finite element simulation and reference data from uniaxial creep test as shown in Fig. 8 which is derived by applying 421.83 N with Al 2 O 3 punch ball.

Fig. 8
figure 8

Equivalent strain and strain rate curves. (a) 100 % raw data, (b) sampling by 50 %, (c) sampling by 25 %

Full size image

Note that there are lots of noises in Fig. 8(a) because creep test usually takes long time and produces a plethora of data. In contrast, equivalent strain ε q and rate \( \dot{\varepsilon_q} \) curves in Fig. 8(b) and (c) look more stabilized by data filtering. Due to this reason, data filtering in creep test is generally allowed to procure constant minimum equivalent strain rate \( {\dot{\varepsilon}}_{q,\ min} \) [12]. The minimum equivalent strain rate \( {\dot{\varepsilon}}_{q,\ min} \) and the corresponding failure time t f for all SPCT results are listed in Tables 4 and 5. Both tables show a similar trend to the standard uniaxial creep test such that the minimum equivalent strain rate \( {\dot{\varepsilon}}_{q,\ min} \) is inversely proportional to failure time t f . Besides, we can quantitatively elucidate the friction effect of punch ball which not only affects the minimum punch displacement rate ḣ min but also the minimum equivalent strain rate \( {\dot{\varepsilon}}_{q,\ min} \). The bigger friction coefficient of Si 3 N 4 punch ball in Table 5 causes the smaller minimum equivalent strain rate \( {\dot{\varepsilon}}_{q,\ min} \) compared to the case of Al 2 O 3 punch ball in Table 4 under the same loading condition. These results suggest that friction effect between punch ball and specimen should be also considered as an important factor in SPCT.

Table 4 Equivalent strain analysis results for SPCT using Al 2 O 3 punch ball
Full size table
Table 5 Equivalent strain analysis results for SPCT using Si 3 N 4 punch ball
Full size table

This information is indispensable to creep life evaluation with the Monkman-Grant model which will be discussed in the next section. Also, all equivalent strain ε q and rate \( \dot{\varepsilon_q} \) curves for SPCT results in Fig. 6 are additionally provided in Appendix.

Discussion

The Monkman-Grant model in equation (8) is applied to the equivalent strain analysis results in order to evaluate creep life expectation. The minimum strain rate \( {\dot{\varepsilon}}_{min} \) and failure time t f in Table 3 can be utilized to construct the Monkman-Grant model for the uniaxial creep test. Likewise, the Monkman-Grant models for SPCT are composed by the minimum equivalent strain rate \( {\dot{\varepsilon}}_{q, min} \) and failure time t f obtained from Figs. 12 and 13 in Appendix.

Figure 9 shows three Monkman-Grant models, one is for the uniaxial creep test and the others for SPCT. Their parameters are summarized in Table 6. Since these three Monkman-Grant models show a strong correlation to one another, direct solution from the equivalent strain concept using the membrane stretching theory has a strong potential for a novel and unique interpretation without any additional endeavor such as uniaxial creep test and finite element analysis. Distribution of SPCT and uniaxial creep test results in Fig. 9 also explains another advantage of SPCT which needs shorter test time than uniaxial creep test. This is because SPCT has faster minimum strain rate and shorter failure time compared to uniaxial creep test. In addition, as shown in Table 6, two representative punch balls do not affect the Monkman-Grant model significantly although punch ball’s friction should be considered in equivalent strain analysis. Therefore, one can predict creep life directly from SPCT regardless of punch ball type.

Fig. 9
figure 9

Comparison of the Monkman-Grant models of STS 316L stainless steel for uniaxial creep test and SPCT with different punch balls at 650 °C

Full size image
Table 6 Parameters for the Monkman-Grant model of each test type
Full size table

In summary, Fig. 10 illustrates a direct procedure to obtain strain and strain rate only using SPCT. This flow chart provides a standard manual of SPCT for creep life estimation. An SPCT is carried out at elevated temperature using 10 × 10 × 0.5 mm specimen, and several interrupts are needed to measure thickness T at the thinnest point during the test. The thickness change is applied to the equivalent strain in Eq. (7), and then the equivalent strain rate \( \dot{\varepsilon_q} \) is derived with respect to time t. As a result, the minimum equivalent strain rate \( {\dot{\varepsilon}}_{q, min} \) and failure time t f are obtained. Finally, the Monkman-Grant model can be drawn like Fig. 9.

Fig. 10
figure 10

A flowchart of creep life prediction using SPCT

Full size image

Conclusion

In this paper, Chakrabarty’s membrane stretching theory is applied to obtain the equivalent strain from SPCT result. From this equivalent strain analysis, SPCT data, which is punch displacement and time, can be converted into strain and time. In order to compare results of SPCT with uniaxial creep test, creep properties and SPCT results of STS 316L stainless steel are referred in this investigation. This comparison uses the Monkman-Grant model for uniaxial creep test and SPCT at same test temperature. Conclusions for this research are drawn.

  1. (1)

    Chakrabarty’s membrane stretching theory provides the equivalent strain data at the thinnest point even in the SPCT specimen. This can be obtained from investigation of thickness change at the thinnest point in the specimen and provides creep curve for SPCT.

  2. (2)

    The Monkman-Grant model of SPCT result, which is obtained from the equivalent strain analysis, shows an excellent agreement with that of uniaxial creep test. Dispersion in the Monkman-Grant model of SPCT indicates faster minimum strain rate and shorter failure time than the uniaxial creep test and suggests SPCT can be substituted for uniaxial creep test.

  3. (3)

    The Monkman-Grant models of SPCT from different punch balls, which are Al 2 O 3 and Si 3 N 4, show a similar trend with each other. This means that effect of punch ball is not critical in the Monkman-Grant model of SPCT.

  4. (4)

    In this paper, an empirical relation which is thickness change along punch displacement is used to apply the equivalent strain analysis. But, because this empirical relation is derived for small punch test not for “small punch creep test”, thickness measurement at the thinnest point of SPCT is, in the future, needed for more concrete validation of the direct solution.