Introduction

The use of aluminium alloys has been widespread in the automotive, aircraft and aerospace industries during the last decades. However the inability to make highly resistant welds by conventional methods has been a hindrance to the use of such alloys. The Welding Institute (TWI, Cambridge, UK) developed a solution to this problem in 1991 through the invention of a new welding process: friction stir welding (FSW) [1]. Friction stir welding, which in fact is a hot extrusion process, uses a spinning tool consisting of a pin with a shoulder for consolidation, a backing plate, and lateral constraint to maintain the weld specimen position during the joining process. After joining is complete, a heterogeneous microstructure is produced between the weld nugget and the heat affected zones which impacts the local properties of the weld. Since these variations affect the overall behaviour of the weld joint, it is important to obtain accurate values for the elastic and plastic properties within the weld. Moreover, due to the wide range of applications of the FSW process, strain-rate dependence of these properties is of interest.

Several methods have been used to characterize the mechanical properties of various types of welds, such as global tensile specimens [2, 3], ball indentation [4–6], micro-specimens [7–9] or macro specimens cut in different areas of the weld [10–14]. However, these methods require specialized equipment, a great deal of time to perform the characterization, and tend to lack in spatial resolution. Lockwood and Reynolds [15] employed Digital Image Correlation (DIC) [16] to obtain extensive data with high spatial resolution during mechanical tests of welded specimens. DIC is a non intrusive method for displacement field measurements during tests. With this method it is possible to measure local deformation with a spatial resolution around 0.1 mm2 on an area of 30×10 mm2, gathering a wealth of information regarding the gradient of mechanical properties within the weld. This kind of characterisation has already been performed in previous studies [15, 17, 18]. However, these techniques consisted of choosing a few areas considered homogeneous and identifying properties over those regions. The problem is that even if some areas have been subjected to the same kind of thermo-mechanical transformation during the welded process and present similar types of grain structure, the properties continue to evolve within each area of the weld.

The aim of this study is to realize a more local identification of the elasto-plastic parameters of an Al 5456 FSW weld, focusing on the description of the evolution of the plastic properties throughout the weld while it is subject to deformation at different strain-rates. DIC was used for full-field deformation measurement, and then mechanical parameters have been identified using inverse methods. With the development of DIC over the past decades, several methodologies have been proposed to perform efficient identification of the mechanical parameters from full field measurements. One of the most commonly used consists in building up a finite element model of the experiment. Then, experimental and simulated data are compared through a cost function, and the identification of the mechanical parameters is completed through minimization of this function [19–23]. A disadvantage of the FEM-based iterative inverse procedure is that it is time-consuming. For example, a recent study [24] indicates that it takes 2.5 to 3 h of computation to identify one visco-elastic parameter (Johnson–Cook model). The same author reported 6 to 23 h for respectively 3 and 5 parameters in quasi-static elasto-plasticity [20]. In a attempt to have a more time-efficient method with equivalent accuracy, the investigators selected the Virtual Fields Method [25].

The Virtual Fields Method was introduced in the early 1990’s in order to solve inverse problems in materials constitutive parameter identification with the aid of full-field measurements. Since, it has been successfully applied to the identification of constitutive parameters for homogeneous material in elasticity [26–28], elasto-plasticity [29, 30] and visco-plasticity [31]. The method has also been used for heterogeneous materials (welds) in quasi-static loading and elasto-plastic material response [32]. However, during this previous study, the authors opted to focus on individual areas of the FSW joint, treating each one as an independent, homogeneous material. It is believed that the evolution of the plastic properties of the weld follow a more continuous evolution. In order to get a more accurate description of this evolution, it is necessary to carry out a more local identification. This is one of the developments of this work, along with the study of the influence of the strain-rate on the plastic properties of the weld.

Experiments and Specimens

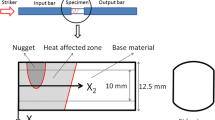
FSW was performed on a 12.7 mm thick Al5456 plate specimen, welded at a rotationnial speed of 480 rpm and welding speed of 3.4 mm.s − 1. The length of the welded area, including the extrusion zone and the heat affected zones, was approximately 38 mm. Transverse tensile specimens have been extracted by cutting across the weld (Fig. 1). Specimen dimensions were 12.7×165×3.8 mm3 with the weld situated in its center. Before performing tensile loading the specimens were coated with a thin layer of white paint, and an airbrush was used to randomly spray black dots on top of it to create a high contrast speckle pattern [16]. The field of view of the camera was 38 mm along the X 2-direction (centered in the middle of the weld) and encompassed the entire specimen width in the X 1-direction (Fig. 1). After surface preparation, the specimen was placed in hydraulic friction grips and the experiment was performed on a MTS machine. The camera used for the image recording depended on the displacement rate. For the low speed quasi-static tests a Q-ICAM CCD camera with a 55 mm Nikon lens was used (Table 1). For higher strain-rates a Phantom v7.1 camera with a 200 mm Nikon lens was used (Table 2). The cameras were positioned on a tripod 1.5 meter from the specimen, the lens direction was normal to the observed surface and the specimen was lit by a goose neck fibre optic light. The choice of a cold light is critical here. Previous experiments carried out with regular lights showed a drastic increase in noise level (standard deviation: 3,000 μstrain). This was mainly due to the air in front of the camera being heated, as discussed in previous articles [33, 34]. The quantification of the noise level was performed by carrying out DIC on two static images and calculating the standard deviation of the resulting displacement and strain fields. It is worth noting that the resolution is higher for the tests at higher speeds while a smaller subset is used. Generally, high speed cameras would induce a higher noise level. However, there is no drastic difference between the resolution of the Q-ICAM and the Phantom v7.1 cameras. In this case, the reduction of noise is mainly due to the use of a better speckle pattern in the tests at higher speeds.

Fig. 1
figure 1

Representation of FSW weld with the field of view shaded in grey with a thickness of 3.8 mm along the X 3 direction

Full size image
Table 1 Low speed test parameters (0.01 mm/s)
Full size table
Table 2 High speed test parameters (0.16 s − 1 and 0.63 s − 1)
Full size table

A displacement ramp of 0.01 mm.s − 1 was applied to the specimen for a nominal strain-rate of 83 μs − 1 and data was collected every 4 seconds. Faster tests have been run at a nominal strain rate of 0.15 and 0.63 s − 1 for respective imaging speeds of 1,000 and 2,000 fps. A maximum loading of 14 kN, for an average axial strain of 8 % is experienced by the specimen during the test (Fig. 17).

All images were processed using the 2D-DIC software VIC-2D [35]. Here the correlation was not incremental, so the initial reference image was kept for all correlation steps. VIC-2D was also used to compute the strain fields by analytical differentiation of a least square quadratic fit over a 5×5 window of the displacement fields.

Virtual Fields Method

The Virtual Fields Method makes use of the Principle of Virtual Work which, in the case of quasi-static deformation, can be written as in equation (1). The convention of summation over repeated indices is used here (equation (2)).

$$ -{\kern-3pt} \int{\kern-6pt}\int{\kern-6pt} \int_{V}\sigma_{ij}\varepsilon_{ij}^{*}\, dV {\kern-2pt}+{\kern-4pt} \int{\kern-6pt} \int_{S_{V}}T_{i}u^{*}_{i}\, dS {\kern-1pt}+{\kern-4pt} \int{\kern-6pt}\int{\kern-6pt} \int_{V}f_{i}u^{*}_{i}\, dV {\kern-2pt} ={\kern-1pt} 0 \label{eq:VWP} $$
(1)
$$ (i,j) = (1,2,3) \label{eq:conv} $$
(2)
$$ T_{i} = \sigma_{ij}n_{j}~{\rm over}~S_{V} \label{eq:T} $$
(3)

where:

V :

is the volume over which the equilibrium is written

S V :

is the boundary surface of V

σ ij :

is the stress tensor

\(u^{*}_{i}\) :

is the virtual displacement field

\(\varepsilon^{*}_{ij}\) :

is the virtual strain tensor deriving from \(u^{*}_{i}\)

f i :

is the volume force vector

T i :

is the imposed traction vector over the boundary S V

Volume forces are neglected in comparison to the load and the internal forces. Finally the Principle of Virtual Work writes:

$$ -\int{\kern-6pt}\int{\kern-6pt}\int_{V}\sigma_{ij}\varepsilon_{ij}^{*}\, dV + \int{\kern-6pt}\int_{S_{V}}T_{i}u^{*}_{i}\, dS = 0 \label{eq:VWP2} $$
(4)

Virtual Fields Method in Elasticity

In elasticity, assuming that the material is isotropic, Young’s modulus and Poisson’s ratio can be identified by using two different virtual fields. The two following fields were used in this work:

$$ \left\{ \begin{array}{lll} u_{1}^{*(1)} & = & 0 \\[6pt] u_{2}^{*(1)} & = & x_{2} \end{array} \right. \label{eq:VFelast1} $$
(5)
$$ \left\{ \begin{array}{lll} u_{1}^{*(2)} & = & x_{2}(x_{2}-L)x_{1}\\[6pt] u_{2}^{*(2)} & = & 0 \end{array} \right. \label{eq:VFelast2} $$
(6)

where L is the length of the field of view (Fig. 1). It is assumed that the specimen is in a plane-stress state, so the first integral can be factorised by the thickness e with S the area of interest. By using equations (5) and (6) into equation (4) the Principle of Virtual Work can be written as a set of equations.

$$ \left\{ \begin{array}{lll} {\kern-12pt}&-&e\dfrac{E}{1-\nu^{2}}\displaystyle\int{\kern-6pt}\int_{S}\varepsilon_{22}\, dS - e\dfrac{\nu E}{1- \nu^{2}}\int \int_{S}\varepsilon_{11}\, dS \\[13pt] &&{\kern12pt}+ \displaystyle\int{\kern-6pt}\int_{S_{V}}x_{2}T_{2}\, dS = 0 \\[13pt] {\kern-12pt} &-&e\dfrac{E}{1-\nu^{2}}\displaystyle\int{\kern-6pt}\int_{S}x_{2}(x_{2}-L)\varepsilon_{11}\, dS \\[13pt] && {\kern12pt}- e\dfrac{\nu E}{1-\nu^{2}}\displaystyle\int{\kern-6pt}\int_{S}x_{2}(x_{2}-L)\varepsilon_{22}\, dS \\[13pt] {\kern-12pt} &-&e\dfrac{E}{2(1+\nu)} \displaystyle\int{\kern-6pt}\int_{S}(2x_{2}-L)x_{1}\varepsilon_{12}\, dS \\[13pt] &&{\kern12pt}+ \displaystyle\int{\kern-6pt}\int_{S_{V}}x_{2}(x_{2}-L)x_{1}T_{1}\, dS = 0 \end{array} \right. \label{eq:PVWelast1} $$
(7)

In the case of uniaxial loading, the integration of T 2 over the cross-section of the specimen is equal to F, the value of the external loading measured during the test, and the boundaries of the area of interest are of coordinates x 2 = 0 and x 2 = L. T 1 being unknown, the second field has been chosen in order to nullify the second integral. It results the following values for the traction vector integrals (equation(8)).

$$ \left\{ \begin{array}{lll} \displaystyle\int{\kern-6pt}\int_{S_{V}}x_{2}T_{2}\, dx_{1}dx_{3} = L\int{\kern-6pt}\int_{S_{V}}T_{2}\, dx_{1}dx_{3} = FL \\[13pt] \displaystyle\int{\kern-6pt}\int_{S_{V}}x_{2}(x_{2}-L)x_{1}T_{1}\, dx_{1}dx_{3} = 0 \end{array} \right. \label{ext} $$
(8)

Full-field measurement has been performed on the surface of the specimen during the experiment. In order to carry out the identification of the elastic parameters, the integrals over the surface are approximated as discrete sums (see for instance equation (9)) with w the width of the specimen, N the number of measurement points over this area, and the bar indicates spatial averaging over the field of view. It leads to a new formulation of equation (7) reported in equation (10).

$$ \displaystyle\int{\kern-6pt}\int_{S}\varepsilon_{ij}\, dS \simeq \frac{Lw}{N}\sum\limits_{k=1}^{N}\varepsilon_{ij}^{k} = Lw\overline{\varepsilon}_{ij} \label{eq:discrete} $$
(9)
$$ \left\{ \begin{array}{l} -e\left(\dfrac{E}{1-\nu^{2}}\overline{\varepsilon}_{22} - \dfrac{\nu E}{1-\nu^{2}}\overline{\varepsilon}_{11}\right) + FL = 0\\[13pt] -\dfrac{E}{1-\nu^{2}}\overline{x_{2}(x_{2}-L)\varepsilon}_{11} - \dfrac{\nu E}{1-\nu^{2}} \overline{x_{2}(x_{2}-L)\varepsilon}_{22} \\[13pt] \dfrac{E}{2(1-\nu)}\overline{(2x_{2}-L)\varepsilon}_{12} = 0 \end{array} \right. \label{eq:PVWelast2} $$
(10)

Then equation (10) can be solved by inversion of the linear system.

Virtual Fields Method in Plasticity

In plasticity, a simple linear isotropic hardening model is used, as defined in [36]. This means that the model only involves the yield stress (σ y ) and the hardening slope (H) (equation (11)).

$$ \sigma = f(\varepsilon,E,\nu,\sigma_{y},H,t) \label{eq:Plastlaw} $$
(11)

Due to the non-linearity of the stress-strain relationship in plasticity, it is not possible to extract the mechanical parameters from the first integral, and carry out the identification as it has been done in elasticity. This problem has been solved by Grédiac and Pierron [30]. Here, the identification has been carried out by constructing a cost function dependent of the plastic parameters (equation (12)). This function is the sum of the quadratic difference of the principle of virtual work over time. Then the plastic parameters have been identified by minimization of the cost function (Fig. 2).

$$\begin{array}{lll} \Phi(\sigma_{y},H) &=& \sum\limits_{t=t_{0}}^{t_{f}}\left[-e\displaystyle\int{\kern-6pt}\int_{S}{\sigma_{ij}(\varepsilon,E,\nu,\sigma_{y},H,t)\varepsilon_{ij}^{*}}\,dS \right.\\[3pt] && \left.+ \int{\kern-6pt}\int_{S_{V}}T_{i}(t)u^{*}_{i}\, dS\right]^2 \label{eq:VFMplast2} \end{array} $$
(12)

Moreover, the stress-strain relationship being non-linear, each step of the experiment provides an independent equation. Therefore, a single virtual field is sufficient to obtain a well determined system [30]. In theory, only two sets of data should be sufficient to carry out the identification of σ y and H. However, due to the measurement noise and the approximation of linear isotropic hardening, more sets of data need to be used to obtain an accurate identification of the plastic parameters.

Fig. 2
figure 2

Flowchart of the identification of plastic parameters using the VFM

Full size image

In order to calculate the value of Φ(σ y ,H), the stress field is computed at each step of the experiment using the method proposed by Sutton et al. [36]. This is an iterative method based on the radial return. However, with this method, the noise is an issue in the plastic region despite its low level. If the strain local increment between two images is negative because of the noise, the associated stress will be calculated as if the material was unloading and therefore, going back to the elastic region. Due to the difference of one order of magnitude between hardening and Young’s moduli, it greatly amplifies the effect of the noise in the stress field. This is why the strain field has been smoothed over time, using an iterative least square convolution method [37]. The smoothing was performed over 17 consecutive images with a second order polynomial function. Figure 3 shows that the smoothing process has a small influence over the strain field, the noise level being low (130 μstrain). Nevertheless, on Fig. 4, it can be seen that it has a strong impact on the computed stress in the plastic area.

Fig. 3
figure 3

Smoothing over time of the average value of ε 22 in one elementary slice at the centre of the weld

Full size image
Fig. 4
figure 4

Influence on the smoothing on σ 22 calculation

Full size image

Application of the Virtual Fields Method to Heterogeneous Materials

Moving to heterogeneous materials presents another issue. Knowing that the mechanical parameters are not constant throughout the weld, it is not possible to carry out the identification on the whole specimen as it is done for homogeneous materials.

It has been shown by Sutton et al. [32] that the elastic properties remain constant within the weld. Therefore, the identification of Young’s modulus and Poisson’s ratio was performed on the whole specimen which is considered as a homogeneous material.

For the plastic parameters the identification was performed on elementary slices over the whole width, the length of each slice being that of one data point, denoted L 2 (Fig. 5). As a first approximation, it is assumed that the weld is homogeneous through the width (X 1 direction). A specific virtual field was used for this identification (equation (13)). It is important to notice that the origin of the axis is moving, depending on the slice over which the identification is carried out (Fig. 5).

$$ \left\{ \begin{array}{lll} x_{2}<0 & u_{1}^{*}=0 & u_{2}^{*}=0 \\[6pt] 0<x_{2}<L_{2} & u_{1}^{*}=0 & u_{2}^{*}=x_{2} \\[6pt] x_{2}>L_{2} & u_{1}^{*}=0 & u_{2}^{*}=L_{2} \end{array} \right. \label{eq:Fields_hete} $$
(13)

Then by replacing equation (13) in the cost function (equation (12)) it leads to the following equation:

$$ \Phi(\sigma_{y},H) = \sum\limits_{\rm time}{[-ewL_{2}\overline{\sigma}_{11}(\varepsilon,E,\nu,\sigma_{y},H,t) + F(t)L_{2}]^2} \label{eq:VFMhete} $$
(14)

The minimisation of the cost function is based on the Nelder–Mead simplex method [38]. Knowing that it is a minimisation process, it is necessary to input starting values for the identified parameters. Those could have an impact on the result of the identification process. Therefore, in order to ensure the uniqueness of the results, the identification process has been carried out with a wide range of starting parameters. As it is shown in Fig. 6, the cost function is well conditioned and has a unique minimum which corresponds to the identified parameters, at least over a range of “reasonable” values for σ y and H. Also, Fig. 6 shows that the cost function is significantly more sensitive to σ y than H.

Fig. 5
figure 5

Representation of the area of interest on the FSW weld

Full size image
Fig. 6
figure 6

Illustration of the unique minimum value of the cost function for the identification of the plastic parameters during the 83 μs − 1 experiment at −11 mm from the centre of the weld

Full size image

Results

Elastic Parameters

Given the amount of images and data provided by DIC, the identification of the elastic parameters was performed using 24 to 33 images. The results, mean values of the identification over these images, are shown in Table 3. The reference values (as given by the supplier) of these parameters have been added in order to give a reference to the results obtained. A steady identification of these parameters around 72 GPa and 0.32 has been obtained for both low and high strain-rate experiments.

Table 3 Mean elastic parameters identified by the VFM, ± indicates the standard deviation
Full size table

Plastic Parameters

All the areas of the weld do not yield at the same time. It leads to a slight increase in computation time but allows a more steady identification of the evolution of the yield stress throughout the weld. The number of images used ranges from 300 (quasi-static test) to 97 (0.15 s − 1 test), depending on the imaging speed and the duration of the test. To carry out the minimization process, initial values are necessary. However, it has been showed that the cost function is well conditioned and admits a unique minimum over a range of reasonable values. Therefore, the choice of these starting point does not have any impact over the identified values. In order to reduce the computation time, starting values close to the base material’s were chosen: 255 MPa for the yield stress [39] and 1 GPa for the hardening modulus. For a test at nominal strain-rate of 0.63 s − 1, the identification has been carried out on 53 vertical slices, considered as homogeneous material, each one the length of one data point, over 136 images, which makes a total of 106 parameters identified in 460 seconds (Processor: Intel dual core 2×2.8 GHz, Memory: 1.5 GB).

The results concerning the yield stress are presented in Fig. 7. It is interesting to note that the profile of the yield stress in the weld presents an asymmetry between the advancing side (0 < x 2) and the retreating side (x 2 > 0), while the hardening properties (Fig. 8) have a more symmetrical distribution. On the other hand, it exhibits an evolution on a much wider scale than the yield stress. These results are consistent with the values obtained by Fonda et al. [40] for the same material at a nominal strain rate of 290 μs − 1 (Fig. 9).

Fig. 7
figure 7

Identification of the yield stress throughout the weld

Full size image
Fig. 8
figure 8

Identification of the hardening through the weld

Full size image
Fig. 9
figure 9

Identification of the yield stress (red curve) by Fonda et al. [40], with the advancing side on the left and the center of the weld corresponding to the 3rd specimen. A good correlation between these values and the one obtained in Fig. 7 for the 83 μs − 1 experiment can be observed

Full size image

Also, the reference value of the yield stress for the base material (255 MPa [39]) is not yet reached at the edges of the area of interest. It is likely that the field of view is too small, with the material throughout the field of view affected by the FSW process.

Then, in order to ensure the validity of the identified parameters, the load has been reconstructed from the strain values over a slice using the identified parameters to check that it is matching the load measured during the experiment (Figs. 10 and 11). Also, local stress-strain curves are represented on Fig. 12 with the representation of the linear hardening model, in order to check for the quality of the model. It is clear from these figures that the model suitably represents the material response from the test.

Fig. 10
figure 10

Load and reconstructed load versus strain at 10 mm from the center of the weld on the advancing side of the specimen for a nominal strain-rate of 0.15 s − 1

Full size image
Fig. 11
figure 11

Load and reconstructed load versus strain at the center of the weld for a nominal strain-rate of 0.15 s − 1

Full size image
Fig. 12
figure 12

Local stress-strain curve for a nominal strain-rate of 83 μs − 1

Full size image

Moreover, two tests have been carried out for higher strain-rates to explore the repeatability of the process (Figs. 13, 14, 15, 16). Similar values of plastic parameters have been identified on both experiments at a given strain rate, with a maximum coefficient of variation of 1.3 % for the identification of the yield stress. As shown in Fig. 17, the strain-rate localises in the centre of the weld when this area enters plasticity, with values one order of magnitude higher than for the base material. Therefore, the identified yield stress values reported in Fig. 7 correspond to different strain-rates at the different locations. Furthermore, the strain-rate evolves during the experiment at each section of the weld (Fig. 17). In order to properly identify a strain rate dependence, one would have to parametrize the yield stress to be a function of strain rate and include the associated parameters within the identification loop, in the same spirit as in [31]. However, to retain the spatial resolution of the identified parameters, it will be necessary to combine the data from different tests at gradually increasing strain rates. This is a significant step ahead from the procedure used in [32] and will require additional developments.

Fig. 13
figure 13

Identification of the yield stress for two tests for a nominal strain-rate of 0.63 s − 1

Full size image
Fig. 14
figure 14

Identification of the hardening modulus for two tests for a nominal strain-rate of 0.63 s − 1

Full size image
Fig. 15
figure 15

Identification of the yield stress for two tests at a nominal strain-rate of 0.15 s − 1

Full size image
Fig. 16
figure 16

Identification of the hardening modulus for two tests at a nominal strain-rate of 0.15 s − 1

Full size image
Fig. 17
figure 17

Evolution of the localisation of the strain-rate during the experiment at a nominal strain-rate of 0.63 s − 1

Full size image

Conclusion

In this study a new method for the identification of the heterogeneous elasto-plastic parameters of welds has been proposed. It offers a significant improvement in the spatial resolution and enables the determination of plastic parameters over local areas. The repeatability of the experiment has been evaluated over different tests with a coefficient of variation under 1.3 % for the identification of the yield stress. Moreover, the influence of the strain-rate over the plastic properties of the weld has been investigated. Results show that the yield stress and hardening modulus undergo a significant change even at low strain-rate (10 s − 1). According to the authors knowledge, there are no studies reported in the literature for these strain rates, making it difficult to independently evaluate our results. Further experiments would be needed to fully understand the influence of the strain-rate in this range. Finally, it would be interesting to move to higher strain-rates to identify the influence of the dynamic effect on the plastic properties of the weld. This is currently underway and will be reported in the near future.