Assessment of Non-Adiabatic Behaviour in Thermoelastic Stress Analysis of Small Scale Components

Abstract

The classical thermoelastic equation and the generalized heat conduction equation are developed to deal with a non-adiabatic response in thermoelastic stress analysis. A FE simulation procedure is set up to solve the heat conduction equation over a range of loading frequencies. A small disc (20 mm diameter) loaded under three-point diametric compression is used to examine the effect of in-plane heat conduction. As the disc has regions of zero, moderate and high stress gradients it is an ideal component for this analysis. A regime is developed that provides a basis for an assessment of the nature of the response and allows a minimum loading frequency to be identified so that adiabatic behaviour is obtained. This validity of this approach is demonstrated on steel disc of 20 mm diameter. A special loading device has been designed to obtain the three-point loading and a recently introduced Instron Electropuls test machine is used to achieve the high levels of cyclic loading required for the adiabatic conditions.

Introduction

Thermoelastic stress analysis (TSA) is a well-established full-field, non-contacting experimental stress analysis technique. Its basis is the measurement of the small temperature change that occurs in solids when they are subjected to a stress change [1]. For a linear elastic, isotropic, homogeneous material the standard treatment assumes that the temperature change occurs isentropically and hence the temperature change ∆T is directly related to the stresses in the component, as follows [1]:

$$ \Delta T = \frac{{\alpha T_0 }}{{\rho C_p }}\Delta \sigma_I $$

(1)

where ρ is the material density, C _p is the specific heat at constant pressure, α is the coefficient of linear thermal expansion, T ₀ is the specimen absolute temperature and Δσ _I is the change in the sum of principal stresses.

Typically a highly sensitive infrared detector array is used to obtain the small temperature change so that the detector output can be directly related to the change in the sum of the principal stresses on the surface of the specimen [1]. In the development of the classical thermoelastic relationship given by equation (1), adiabatic conditions are assumed and therefore only reversible conversions between mechanical energy and thermal energy are considered. In practice, pseudo adiabatic conditions are achieved by the application of cyclic stress to give the stress change given in equation (1). The frequency of the applied stress is such that heat transfer is minimised to within an area equal to the measurement region observed by a single detector in infrared detector array. However, some heat diffusion (an irreversible process) is unavoidable in components that contain stress gradients. The likelihood of non-adiabatic behaviour is increased in materials with a high thermal conductivity, i.e. most engineering metals. For small scale components, such as MEMS, electronic circuitry and medical devices, the stress gradients are steep as the stresses can vary greatly over small areas. In situations where heat transfer is significant then the thermoelastic temperature change must also include the effects of heat conduction.

Non-adiabatic behaviour in TSA has been analysed using several numerical approaches. Dunn [2] used a finite difference technique to solve the two-dimensional heat conduction equation, where the heat input term (heat generated in the body) was calculated from the stress field obtained from the FE model. Sathon and Dulieu-Barton [3] used a FE technique to quantify the solutions of a simple two dimensional model of a bar with a through slot, where non-adiabatic behaviour was observed over various load frequencies and slot dimensions. Another recent study of the non-adiabatic effect has been carried out by Inoue and Kishimoto [4]. The Boundary Element Method (BEM) was used in their study, which showed that under non-adiabatic conditions, heat diffusion effects lead to an underestimation of stress concentration.

The aim of the present work is to examine more closely the boundaries of the adiabatic response in the context of small scale specimens. The basis of the assessment is the phase of the thermoelastic response and its relationship with the thermal diffusion length and the geometry of the test specimen. To this end it was decided to concentrate on in-plane conduction only and select a specimen that has large in-plane stress gradient in comparison to the through thickness gradient. The classical thermoelastic equation and the generalised heat conduction equation for thermoelasticity are developed to deal with a non-adiabatic response in thermoelastic stress analysis. A FE simulation procedure is developed to solve the heat conduction equation over a range of loading frequencies which is confirmed by an experimental validation.

Theory

The entropy change that occurs as a material is deformed under the application of a load leads to development of the classical thermoelastic equation [5]. The change in temperature, ΔT, caused by a change in the strain invariant, ∆ε _I , of the material can be obtained from the energy balance equation which may be described by the following expression:

$$ Q = \rho C_{\varepsilon } \Delta T + \frac{{T_0 E\alpha }}{{1 - 2\nu }}\Delta \varepsilon_I $$

(2)

where C _ε is the specific heat at constant strain, E is Young’s modulus and ν is Poisson’s ratio.

The law of heat conduction that provides the rate of heat absorbed by an element without an internal heat source can be expressed as:

$$ \frac{dQ}{dt} = k\nabla^2 T $$

(3)

where, k is the thermal conductivity.

By differentiating equation (2) with respect to time and combining with equation (3), the generalised heat conduction equation for the thermoelastic effect without an internal heat source is obtained as follows:

$$ k\nabla^2 T = \rho C_{\varepsilon } \frac{{\partial T}}{{\partial t}} + \frac{{\alpha T_0 E}}{{1 - 2\nu }}\frac{{\partial \varepsilon_I }}{{\partial t}} $$

(4)

It can be seen that equation (4) is in the form of a heat diffusion equation containing an effective heat source (second term on the right hand side) caused by the thermal mechanical interaction, i.e. the thermoelastic effect. Equation (4) can be rewritten in terms of C _p and σ _I , as follows

$$ \frac{{\partial T}}{{\partial t}} = - \frac{1}{{\rho C_p }}\left[ {\alpha T_0 \frac{{\partial \sigma_I }}{{\partial t}} - k\nabla^2 T} \right] $$

(5)

An examination of equation (5) shows that the heat transfer is dependent on three quantities: (i) temperature gradient (∇ ² T term), (ii) material thermal conductivity (k term) and (iii) loading frequency (∂σ _I /∂t term). As the heat generated is a function of the stress induced temperature change, ∂T/∂t, the temperature gradient, (∇² T, is a function of the stress gradient. If the stress gradient, and hence the temperature gradient, is zero adiabatic conditions are obtained, if the thermal conductivity is zero adiabatic conditions are obtained and if both of these quantities are finite then pseudo adiabatic conditions are obtained by reducing the measurement time increment, i.e. increasing the loading frequency. Equation (5) can be solved analytically for certain problems such as a plate subjected to pure bending vibration [6]. However, for most cases, it is more practical to use numerical techniques to obtain the solutions in terms of the temperature change.

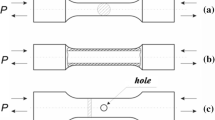
To develop a means of assessing non-adiabatic behaviour in TSA, a finite element approach was devised [7] that described the behaviour defined in equation (5) (see next section). To assess the validity of such an approach it was decided that a test specimen was required where a theoretical stress solution was available. Therefore, a disc under three-point symmetrical diametric compression [see Fig. 1(a)] was used to examine the effect of in-plane heat conduction. This specimen was chosen over the more conventional ‘Brazilian disc’ as it has three regions of different stress gradient, one of which is close to zero. The sum of principal stresses along the loaded diameter of the disc is available [8]:

$$ \sigma_x + \sigma_y = - \frac{6P}{{\pi dt}}\left[ \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right.\frac{{d^3 + 8y^3 }}{{d^3 - 8y^3 }}\left. \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right] $$

(6)

where P is the applied load, d is diameter of the disc, t is thickness and y is a Cartesian coordinate with its origin at the centre of the disc defined in Fig. 1(a).

Fig. 1

Disc under three-point diametric compression. (a) Disc geometry, (b) Stresses distribution along loading diameter

Figure 1(b) shows the normalised distribution of the sum of principal stresses along a loaded diameter, i.e.:

$$ \left[ {\frac{{\pi dt}}{6P}} \right]\,\sigma_x + \sigma_y = - \frac{{1 - 8\frac{y}{{d^3 }}^3 }}{{1 + 8\frac{{y^3 }}{{d^3 }}}} $$

(7)

Equation (7) shows that at the loading point, where y = d/2, the stresses are infinite. This is shown clearly in the plot of Fig. 1(b) where the stress sum decreases rapidly as y/d = −0.5 is approached. It should be noted that in an actual material this infinite condition is not achieved as the material will yield. However, this theoretical plot is useful as three different ‘regions’ of stress distribution can be observed. Firstly from the loaded point until y/d > −0.40 there is a region of high stress gradient. In a test this may not be as steep as the infinite condition will not be achieved; however the stress gradient will still be relatively large. From −0.25 ≤ y/d ≤ 0.2 there is a practically zero stress gradient, for y/d > 0.20 there is a moderate gradient stress. As the stress gradient drives the non-adiabatic behaviour this specimen makes an excellent basis for validation and observation of the affects on non-adiabatic behaviour in the three regions of stress gradient. It should be considered that the local plasticity that occurs as a result of the material yielding at the loading point may introduce a further heating source in the experimental work; this will be discussed later in the paper.

Simulation Procedure

To model the non-adiabatic effects of heat diffusion, a finite element model of the thermoelastic coupling was created by linking the mechanical and the thermal tools of ANSYS software. The FE analysis was divided into two steps. Firstly, a standard FE structural stress analysis was performed to determine the sum of the principal stresses resulting from the applied load range, using linear elements. Then, the heat generation rate was calculated by determining ΔT from the linear model and inputting into to a thermal harmonic model. A schematic representation of this procedure is presented in Fig. 2.

Fig. 2

Flow chart showing the routine for simulating the thermoelastic response

In the structural stress analysis, the simulation process starts with geometrical modelling and discretisation. A static analysis is carried out based on the loads, boundary conditions and mechanical material properties defined for the problem. The next step is to process the solution so that the sum of the principal stresses is calculated at each node in the model. Then the thermal harmonic analysis can be carried out using an identical model to that in the structural analysis. The heat generation rate $\dot{q}$, is calculated at each node and loading frequency, ω, using the following relationship:

$$ \dot{q} = - \alpha T\omega \frac{{\sigma_I }}{2}\sin \left( {\omega t - \left. {\frac{\pi }{2}} \right)} \right. $$

(8)

It is important that the FE mesh is the same in both steps in the procedure so that all stress data from the individual nodes can be input automatically into the thermal analysis routine. The post processing of the thermal analysis extracts the magnitude and phase of each node in the model. After finishing this step the results are written into a data file and the next loop is started, i.e. the ΔT corresponding to the next loading frequency is defined and another solution is obtained. Therefore, the number of loops for thermal analysis depends on the number of loading frequencies required. Essentially at each loading frequency the FE simulation is solving for the stress terms and integrating over the time equivalent for the period of the loading cycle.

A model of a mild steel circular disc with 20 mm in diameter was developed to validate the simulation procedure against the theory. Shell elements were chosen because these are essentially 2D elements. The solution given in equation (6) is assuming 2D conditions, although the thickness of the disk is included, it is assumed that the stress is uniform through the thickness of the disc. The element type used in the thermal model was a SHELL57, 3-D 4-node thermal element. The SHELL57 element was used as it allows only in-plane conduction and constrains the conduction in the plane of the disc. Therefore a SHELL63, a 4 node shell element, had to be used to create the structural model. The element size was about 0.2 mm × 0.2 mm and the model had 29298 degrees of freedom. (3D elements have been used for more complex geometries [7].) The model was subjected to three symmetrically spaced peripheral point loads; to avoid the singularity at the point load the stress was taken to be the average of the elements surrounding the point load node.

The simulated thermoelastic response is shown in Fig. 3, giving contour plots of both temperature and phase at loading frequencies of 2 Hz, 20 Hz, 50 Hz and 100 Hz. To examine the trend of the non-adiabatic effects more closely in the thermoelastic response, the solutions along a loaded diameter for loading frequencies from 2 Hz to 1,000 Hz are given in Fig. 4. The theoretical static stress solution obtained from equation (6) and input into equation (1) to give ΔT is also included in Fig. 4(a). The excellent agreement between the analytical solution and the FE solution at the higher loading frequencies validated the model and hence it was not necessary to carry out any convergence studies.

Fig. 3

Contour plots ∆T and phase at loading frequencies. (a) 2 Hz, (b) 20 Hz, (c) 50 Hz, (d) 100 Hz

Fig. 4

∆T and phase of nodes along loaded diameter from FEA. (a) ∆T data, (b) Phase data

It can be observed from Figs. 3 and 4 that loading frequency and stress gradient are the important parameters when considering non-adiabatic behaviour in a material. The attenuation of ΔT occurs at the high stress gradient region in the disc, especially near the loading point, which is caused by the very high stress gradients in this region. Likewise the corresponding phase response shows large departures from uniformity at the edge of the disc and that as the frequency increases the phase becomes more uniform giving a value of zero. It can be seen in Fig. 4(a) that only with a loading frequency of 1,000 Hz is the theoretical solution given by equation (6) obtained; this is particularly noticeable in the region of high stress gradient. The phase in the high stress gradient region shows large departures from the in-phase condition and as the frequency decreases the out of phase region increases and is shown clearly in the phase contour plots in Fig. 3. A similar trend is seen in the moderate stress gradient region but is not as evident in the phase contour plots. Only in the zero stress gradient region it can be seen that ΔT is constant at all loading frequencies and ΔT is in phase at all loading frequencies.

Specimen and Loading Jig

The test specimen was a mild steel circular disc of diameter 20 mm by 4 mm thick. To apply the three-point loading a test rig was designed as illustrated in Fig. 5. The rig consists of a rectangular mild steel plate, 4 mm thick with a large circular hole centred on the horizontal centre line, and a slot from the hole to the edge of the plate. The slot imparted a degree of flexibility to the plate so that under the action of two opposed forces [see Fig. 5(a)] the slot tended to close and the hole to contract. The loading forces acted through pins positioned in a pair of parallel opposed grooves machined across the outer edge of the plate. To obtain a purely radial load and to reduce the effects of friction the disc is loaded via three pins mounted in three equi-spaced machined grooves along the circumference of the large circular hole. It is important that friction is minimised as a frictional loading may change the stress field. This is illustrated in [8] where a three point load was imparted to a disc by loading against the flat platens of a vee-block. Also friction may cause localised heating and this will increase the temperature (T ₀ ) locally and change the thermoelastic response (see equation (1)). The rig was positioned in the loading machine with the disc within and a compressive cyclic load applied. The disc was coated with matt black paint prior to testing.

Fig. 5

Disc in radial loading jig. (a) Geometry of jig, (b) FE model

It was recognised that the loading provided by the rig would not provide the ideal point load condition shown in Fig. 1. The pins would spread the load over an area and the infinite stress predicted by equation (6) would not occur. The singularity occurring as a result of the point has been accounted for in the original FEA model, so it could be said that the model is better modelling reality. Nevertheless it was decided a second FE model was required that included the test rig and the pins thereby directly simulating the load imparted to the disc through the pins from the test rig loading. The model is shown in Fig. 5(b). The element type used in this model was the same as that used previously. The disc was modelled in an identical fashion to that used previously. For consistency shell elements were used to model both the pins and rig. In both cases the elements were 0.2 mm × 0.2 mm. As linear elements were used and therefore the local plasticity at the contact could not be modelled, the contact between the pins and disc and the pins and the rig is point to point over a single node and the nodal stress was determined by taking the mean value of the stress from the two adjacent elements in the pin and the two adjacent elements in the disc. This was considered to be a better approach than attempting to estimate the extent of deformation of the pins or the disk. The degrees of freedom in each pin were 294 and in the rig were 38,802. The friction between pins and disc was not considered in the model. This model is used for comparison with the experimental data in the analysis of the results.

The FEA showed that a load of 250 N ± 150 N [applied to the rig as shown in Fig. 5(a)] would produce about 180 MPa maximum principal stress sum in the disc, which was considered sufficient to produce a noise free thermoelastic signal. This low load is difficult to achieve at high frequency on standard servo-hydraulic test machines. Therefore an Instron Electropuls electro-dynamic test machine was used, which allowed very accurate loads to be applied over a range of frequencies from 0–100 Hz.

Themoelastic Analysis

In the above it has been shown that for a simple small specimen non-adiabatic behaviour strongly affects the thermoelastic response and that a loading frequency in excess of 50 Hz is required to obtain an adiabatic response. A Stress Photonics DeltaTherm system was used to collect the TSA data. The detector receives infra-red radiation associated with temperature variation caused by the thermoelastic effect on the specimen and the thermoelastic data is obtained in terms of magnitude and phase. To obtain ΔT from the DeltaTherm system, the magnitude of the signal was used because this is independent of the phase setting. The system software includes temperature calibration file that allows the data to be presented in terms of ΔT. Figures 6 and 7 show ΔT and phase contours of the disc at frequencies of 2 Hz, 20 Hz, 50 Hz and 100 Hz respectively, as well as the FE results for the comparison. In terms of distribution and shape of the contours ΔT and phase, the agreement between the experiment and the FEA is very good. Practically three-fold symmetry is developed in the ΔT experimental results given in Fig. 6 but the response from the two contact points to the left of the disc is greater than the single contact point to the right. This is also echoed in the FEA and is clear in the plots for 50 and 100 Hz. As this is apparent in the numerical and experimental data it cannot be due to friction between roller and disc as friction is not modelled in the FEA. Therefore the slight lack in three-fold symmetry must be an artefact of the rig design. However, it is considered that the experimental set-up is such that meaningful results can be obtained even if there is deficiency in the load applied by the jig that prevents full three-fold symmetry from being developed. An inspection of the ΔT values obtained from the centre of the disc at each loading frequency shows excellent correspondence with the FEA. However the ΔT values obtained at the loading points at the two lower frequencies are much greater than that given by the FEA. Here this could be accounted for by heating (caused by either local plasticity or friction) between the roller and the disc which is dissipated at higher frequencies.

Fig. 6

Contour plots of ∆T: TSA (left) and FEA (right). (a) 2 Hz, (b) 20 Hz, (c) 50 Hz, (d) 100 Hz

Fig. 7

Contour plots of phase: TSA (left) and FEA (right). (a) 2 Hz, (b) 20 Hz, (c) 50 Hz, (d) 100 Hz

Figure 7 shows that with increasing frequency, the phase contour becomes more uniform, which means that an adiabatic response was obtained by increasing the frequency to 100 Hz. However the briefest inspections of Fig. 7 shows there are significant differences between the experimental and numerical data. In general the phase data at the centre of the disc corresponds with that of the FEA which is very encouraging. However at the edges and the contact points there is significant difference between the two data sets. Unfortunately it proved impossible to get the scales on the two data sets to appear the same and this makes the data somewhat difficult to interpret. In Fig. 7(a) the negative phase is apparent at the edges of the experimental data and in general a similar trend is observed in both data sets. In Fig. 7(b) the areas of negative phase that are localised to the edge of the disc in the numerical work spreads much deeper into the disc. The triangular pattern this causes is evident also in 6b and appears to be a dynamic effect that is less evident at 50 Hz and practically non existent at 100 Hz. It is important to note that the natural frequency of the disc is 14.4 Hz according to the FEA and this goes some way to explain the triangular pattern evident in Figs. 6(b) and 7(b). The experimental data shown in Figs. 7(c) and d show that the experimental phase data is practically uniform at 50 Hz and 100 Hz levels.

To enable a more straight forward comparison ΔT and the corresponding phase response averages along the three loaded diameters for all load frequencies are plotted and shown in Figs. 8 and 9 respectively. To compare the results of TSA and FEA techniques in detail, data from FE model are also shown in the figures. It can be seen that the agreement between the two techniques is very good, confirming the validity of the FE simulation. Quantitatively, there is a small discrepancy of the ΔT values between two techniques at the loading point. In Fig. 8(b), (c) and (d) the experimental value is less than the FEA solution, probably as a result of material yield which is not accounted for in the linear elastic FE model. In Fig. 8(a) at the lowest loading frequency the general agreement is not as good as the loading point is approached and this could be accounted for by heat generation caused by friction and the local plasticity (not included in the FE thermal model) not being dissipated as effectively at the lower frequency.

Fig. 8

∆T comparison between FEA and TSA. (a) 2 Hz, (b) 20 Hz, (c) 50 Hz, (d) 100 Hz

Fig. 9

Phase data comparisons between FEA and TSA. (a) 2 Hz, (b) 20 Hz, (c) 50 Hz, (d) 100 Hz

In terms of phase, it is evident that, phase data from TSA is rather noisy and large fluctuations are observed for the higher frequencies. Nevertheless, the trend of each curve in the phase plot corresponds well with the FEA, i.e. (1) a sharp change in phase near the loading point and at the free edge corresponds with the large stress gradient, (2) zero degree phase occurs in the central part of the disc which indicates a uniform stress region, and (3) the largest phase shift is observed at the two ends of the disc diameter at the lowest loading frequency and the smallest phase shift is observed at the highest loading frequency.

The DeltaTherm system processes the data using a digital Fast Fourier Transform (FFT) [9]. It functions in a practically identical manner to the analogue type lock-in analyser and determines the magnitude and phase from the sampled signal. This is done by correlating the sampled signal with the reference signal. The resulting processed signal is the signal that is in-phase with the reference signal. The process also removes any input caused by background radiation, i.e. the in-phase signal is derived using only the input at the reference frequency of the applied load. The other output obtained from the correlation is the signal which shifted by 90 degrees from the reference signal.

The phase image provides the phase angle of each data point relative to a reference datum. This datum is set by the operator by adjusting the phase setting on the system and is not necessarily set at 0 or 180 degrees. In this work the datum has been shifted to zero for comparison purposes. In areas where the in-phase response is small there will be a greater contribution of noise to the signal. This effect is illustrated clearly in Fig. 9 [with exception Fig. 9(c)] where the scatter is much higher regions where the measured response is small and the noise in the in-phase and out-of phase response large. Clearly it would be beneficial to reduce the effect of noise and establish a more accurate means of determining the phase angle.

Non-Adiabatic Response Analysis

Notwithstanding the noise that is evident in the measured phase data it is evident from the work in the previous section that phase changes are a good indicator for assessing the boundary of the adiabatic response. It was decided to develop a model that includes the phase of the response, the material properties of the specimen, the loading frequency and a geometrical factor. FE simulations were carried out on discs with diameters of 8 mm, 20 mm and 100 mm (to give different stress gradients) and loading frequencies of 2 Hz, 10 Hz, 20 Hz, 50 Hz,100 Hz and 1,000 Hz. Phase data was obtained from three locations close to the free end (i.e. where there is a moderate stress gradient), at the centre of the disc (i.e. where there is a zero stress gradient) and 0.01 mm from loading point (i.e. where there is a high stress gradient). In each case the phase data was plotted against the thermal diffusion length, $\gamma = \sqrt {\frac{k}{{\rho C_p \pi f}}}$, (f is the loading frequency), divided by the radius of the disc (i.e. γ/r). The plot of the phase data obtained from FE simulations against γ/r is shown in Fig. 10(a), (b) and (c).

Fig. 10

Relationship between phase and parameter γ/r from FEA. (a) Data from free edge, (b) Data from centre of disc, (c) Data adjacent to loading point

In Fig. 10 the origin of the curves represents fully adiabatic behaviour, i.e. at high loading frequencies. As the quantity γ/r increases, the non-adiabatic behaviour is also increasing. In Fig. 10(a) it can be seen that there are two clear regions in the data γ/r < 0.02 (turning point) where an adiabatic response is obtained and γ/r > 0.02. Accepting that the non-adiabatic response is as a result of the stress gradient at the loading points then the turning point could indicate when the loading frequency is sufficient to eliminate non-adiabatic behaviour caused by the stress gradient. For the disc of diameter 100 mm and the least stress gradient all of the data occurs in the γ/r < 0.02 region indicating that even at 2 Hz the response is adiabatic. However, for the smaller discs (8 mm and 20 mm in diameter) the plot indicates that the frequency must be nearly 100 Hz to obtain adiabatic conditions in this region. The phase data are zero in Fig. 10(b) and as expected indicates that adiabatic behaviour occurs in the centre of the disc regardless of geometry or loading frequency, clearly demonstrating that no heat transfer can take place in a region of zero stress gradient. Figure 10(c) is similar to Fig. 10(a). From the analysis above a minimum loading frequency can now be identified so that adiabatic behaviour can be ensured during experimental work. In the case of the 20 mm disc from Fig. 10(a) and (c) it can be seen that this must be greater than 50 Hz.

To confirm if a similar trend is obtained experimentally Fig. 11 shows a plot of the experimental data obtained for the disc with 20 mm diameter subjected to frequencies of 2 Hz, 5 Hz, 10 Hz, 20 Hz, 30 Hz, 40 Hz, 50 Hz, 60 Hz, 70 Hz, 80 Hz and 100 Hz. For comparison the FEA data is presented at the same frequencies in Fig. 11. It can be seen that the data shows the identical trends. For the 20 mm disc, the FEA phase data of 100 Hz falls into the region γ/r < 0.02, i.e. totally adiabatic conditions should occur at least 100 Hz, which is validated by the TSA data. However, the magnitude of the phase change in the experimental data is slightly greater than that given by the FEA, especially at the lower frequencies.

Fig. 11

Phase response from TSA and compared with those from FEA

Stress Analysis

To obtain quantitative stress values from the thermoelastic output it is necessary to determine the calibrator factor, A. A number of techniques have been described [10] for the calibration of isotropic materials. The calibration method involves relating the measured thermoelastic signal to a known stress distribution produced in a sample specimen by a known applied load. Therefore, a mild steel circular disc of diameter 20 mm by 4 mm thick loaded in two-point diametric compression (the Brazilian disc) was tested using a load of 125 N ± 100 N and the frequencies from 2–100 Hz.

The analytical stress solution for the Brazilian disc is well known [11] and the surface stress sum along its vertical diameter can be expressed as follows:

$$ \Delta \sigma_I = \frac{4P}{{\pi dt}}(\frac{{4y^2 + d^2 }}{{4y^2 - d^2 }}) $$

(9)

Combining this with the well known relationship between Δσ _I and the thermoelastic signal, S, (∆σ _I = AS where A is a calibration factor) gives the following relationship:

$$ S = \frac{4P}{{A\pi dt}}(\frac{{4y^2 - d^2 }}{{4y^2 + d^2 }}) $$

(10)

This expression provides a linear relationship between S and A so that if thermoelastic data is taken along the vertical diameter of the disc, S can be plotted against the bracketed term in equation (10). Knowing the applied load, thickness and diameter of the disc allows the calibration constant to be derived from the gradient of the plot. Figure 12(a) shows a signal plot along the vertical diameter of the disc loaded at 100 Hz. The linearised version of this is shown in Fig. 12(b), which allowed the calibration constant to be determined as 0.038 MPa/U.

Fig. 12

Calibration using Brazilian disc. (a) Signal along the vertical diameter, (b) S~$\frac{{d^2 - 4y^2 }}{{4y^2 + d^2 }}$

The derived calibration constant was then used to calibrate the thermoelastic signal data obtained in the experimental work to obtain the stress distribution of the three-point loaded disc. Figure 13 plots the principal stress sum along loaded diameter obtained at all the loading frequencies used in the experimental work; the plot also contains the stress solution derived from the FEA. It can be seen that the stress obtained from the test correlates practically exactly with the FEA results. With decreasing frequency the measured stress reduced significantly especially adjacent to the loading point. It is shown that to obtain accurate stress data from TSA it is important that adiabatic conditions are achieved throughout the specimen.

Fig. 13

Stress values from the thermoelastic output compared with FEA

Conclusions

• (1) The well-known classical thermoelastic equation and the generalized heat conduction equation for thermoelasticity are developed to deal with a non-adiabatic response in thermoelastic stress analysis.

• (2) An FE simulation procedure has been developed to simulate the thermoelastic effect under non-adiabatic conditions. This validity of this approach is demonstrated experimentally using a mild steel disc of 20 mm diameter under three-point diametric loading. The ΔT values derived from the FE and the TSA show an excellent correspondence.

• (3) The phase data obtained experimentally from the disc contained large scatter, however it was concluded that a modelling approach based on the phase of the thermoelastic response, and its relationship with the thermal diffusion length and the geometry of the test specimen, could be used to derive loading frequencies where adiabatic behaviour was obtained.

• (4) The technique for identifying the limits of adiabatic behaviour was validated in two ways (i) by showing that the trends in experimentally derived phase were similar to those in the model and (ii) by stress calibrating the thermoelastic data from the three-point loaded disc and showing that only at a loading frequencies of 50 Hz and 100 Hz there was a good correspondence with the theory.