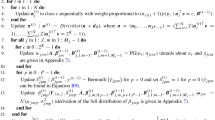An Exploratory Diagnostic Model for Ordinal Responses with Binary Attributes: Identifiability and Estimation

Abstract

Diagnostic models (DMs) provide researchers and practitioners with tools to classify respondents into substantively relevant classes. DMs are widely applied to binary response data; however, binary response models are not applicable to the wealth of ordinal data collected by educational, psychological, and behavioral researchers. Prior research developed confirmatory ordinal DMs that require expert knowledge to specify the underlying structure. This paper introduces an exploratory DM for ordinal data. In particular, we present an exploratory ordinal DM, which uses a cumulative probit link along with Bayesian variable selection techniques to uncover the latent structure. Furthermore, we discuss new identifiability conditions for structured multinomial mixture models with binary attributes. We provide evidence of accurate parameter recovery in a Monte Carlo simulation study across moderate to large sample sizes. We apply the model to twelve items from the public-use, Early Childhood Longitudinal Study, Kindergarten Class of 1998–1999 approaches to learning and self-description questionnaire and report evidence to support a three-attribute solution with eight classes to describe the latent structure underlying the teacher and parent ratings. In short, the developed methodology contributes to the development of ordinal DMs and broadens their applicability to address theoretical and substantive issues more generally across the social sciences.

1 Introduction

Latent structure models (e.g., see von Davier, 2009), which are also referred to as restricted latent class models or diagnostic models (DMs) in measurement and psychometric research, are frequently used to classify respondents into substantively relevant classes. DMs assume that observed binary (e.g., correct/incorrect on educational test items) or ordinal (e.g., rating scales or partial credit) responses relate to a collection of discrete latent variables or attributes. DMs are popular methods for providing a fine-grained classification in terms of substantively important latent attributes, such as educational skills or psychological states.

Prior research developed both confirmatory (e.g., see de la Torre, 2011; Henson, Templin, & Willse, 2009; von Davier, 2008) and exploratory (e.g., see Y. Chen, Liu, Xu, & Ying, 2015; Y. Chen, Culpepper, Chen, & Douglas, 2018; Culpepper, 2019; Culpepper & Chen, 2018; Xu, 2017; Xu & Shang, 2018) DMs for binary data. Binary DMs are used in educational research to classify students into skill-based attribute profiles using tests of fraction-subtraction (de la Torre & Douglas, 2004, 2008; DeCarlo, 2011), spatial rotation (Culpepper, 2015), and geometric sequences (Shute, Hansen, & Almond, 2008). Recent applications also used binary DMs to model learning (Y. Chen, Culpepper, Wang, & Douglas, 2018; Kaya & Leite, 2017; Li, Cohen, Bottge, & Templin, 2016; Madison & Bradshaw, 2018; Wang, Yang, Culpepper, & Douglas, 2017) and detect skill acquisition (Ye, Fellouris, Culpepper, & Douglas, 2016). Additional research applied binary DMs to items measuring pathological gambling (Templin & Henson, 2006) and social anxiety (Y. Chen et al., 2015).

DMs are widely applied to binary response data; however, binary response models are not applicable to the wealth of ordinal data collected by educational, psychological, and behavioral researchers. For instance, large-scale testing programs, such as the National Assessment of Educational Progress, include ordinal response variables to evaluate students’ performance on essays or constructed response tasks. In these cases, students may receive partial credit in the form of an ordinal score rather than a binary correct or incorrect. Furthermore, there is a longstanding tradition in the social sciences for researchers to measure constructs with ordinal responses. For instance, large-scale assessment background questionnaires include items with rating scales to measure individual differences in opportunity to learn, educational aspirations, and academic experiences. Each of the aforementioned constructs provides a context for students’ dispositions and learning environment, and fine-grained classifications with a general DM could provide educators and practitioners with information to identify students in need of interventions or to describe patterns or profiles of human development as measured by rating scales. Clearly, research on ordinal DMs provides opportunities to advance diagnostic research in education and, more generally, in the social sciences.

In this study, we offer a general, exploratory DM for ordinal response data to broaden the applicability of these methods in the social sciences. Specifically, prior research developed ordinal DMs (J. Chen & de la Torre, 2013, 2018; Haberman, von Davier, & Lee, 2008; Karelitz, 2004; R. Liu & Jiang, 2018; Ma & de la Torre, 2016, 2019, Templin, 2004; von Davier, 2008) and this paper offers three contributions to the literature. First, we discuss identifiability of structured mixture models for multivariate multinomial response data. Fang, Liu, and Ying (2019) established sufficient conditions for the identifiability of a structured multinomial mixture model for polytomous attributes. We consider the case for binary attributes and show less stringent restrictions are needed to establish sufficient conditions for identifiability than for the polytomous attribute case. Second, we propose a fully exploratory ordinal diagnostic model for uncovering the latent structure and inferring the underlying latent processes. The introduction of an exploratory diagnostic model for ordinal data is an important contribution given current ordinal DMs are confirmatory models that are dependent upon correct specification of the latent structure with expert knowledge or substantive theory. As demonstrated in research on binary DMs (e.g., see Henson & Templin, 2007; Rupp & Templin, 2008), misspecification likely leads to inaccurate classifications and biased parameter estimates. Our model extends the confirmatory general ordinal model of J. Chen and de la Torre (2018) to the exploratory setting. Specifically, our model uses a cumulative probit link function and a fully saturated model with main effects and higher-order interactions involving the latent binary attributes. In order to uncover the underlying structure, we adapt Bayesian model selection tools as described for binary DMs (Culpepper, 2019) to infer the relationship between attributes and observed ordinal responses. Third, we present a Bayesian formulation that provides a convenient approach for imposing monotonicity restrictions on the item response functions (IRFs), so that higher attribute levels are associated with non-decreasing observed response probabilities. It is important to note that enforcing monotonicity conditions is not a requirement for identifying model parameters. Instead, monotonicity of latent class response probabilities may improve interpretation of the exploratory solution.

The remainder of this paper includes four sections. The first section introduces the unstructured mixture model for multivariate multinomial response data and presents new results concerning the identifiability of model parameters. The second section introduces a structured mixture model for ordinal data and presents a Bayesian formulation. Moreover, we review issues related to monotonicity conditions and the coding of attributes. The third section reports results from a Monte Carlo simulation study regarding the recovery of model parameters. We provide evidence of accurate parameter recovery for sample sizes as small as 500 observations. The fourth section presents an application of the exploratory ordinal DM to twelve items of the public-use, Early Childhood Longitudinal Study, Kindergarten (ECLS-K) Class of 1998–1999 approaches to learning and self-description (ALS) questionnaire with $n=13{,}354$ complete observations. We discuss the implications of the study, offer future research directions, and provide concluding remarks in the final section. We direct readers to the “Appendix” for a description of the Gibbs sampling algorithm and full conditional distributions.

2 Mixture Models for Multinomial Response Data

The purpose of this section is to discuss a mixture model for multinomial response data. We first outline a model and then discuss the identifiability of model parameters.

2.1 Mixture of Multinomial Response Data

Let $Y_j$ for $j=1,\ldots ,J$ be a random ordinal response with a realization $y_j\in \left\{ 0,\ldots ,M_j-1\right\}$ where $M_j\ge 2$ denotes the number of response options. The random J-vector is denoted by ${\varvec{Y}}=(Y_1,\ldots , Y_J)^\top$, and the observed vector of responses is ${\varvec{y}}= (y_{1},\ldots ,y_{J})^\top$. The support for ${\varvec{Y}}$ is defined as ${\varvec{y}}\in \times _{j=1}^J \left\{ 0,\ldots ,M_j-1\right\}$, which implies there are $\prod _{j=1}^JM_j$ observed response patterns.

The purpose of exploratory ordinal DMs is to uncover a latent structure involving fewer attribute profile patterns to describe the $\prod _{j=1}^JM_j$ observed response patterns. We introduce a collection of K binary attributes to provide a more parsimonious representation of the $\prod _{j=1}^JM_j$ observed patterns using $2^K$ latent profile patterns. We refer to the K-vector of latent binary attributes as ${\varvec{\alpha }}=(\alpha _1,\ldots ,\alpha _K)\in \left\{ 0,1\right\} ^K$.

Unstructured latent class models are important models in psychometric research (e.g., see Fang et al. 2019; Green, 1951; Hojtink & Molenaar, 1997; McDonald, 1962; Proctor, 1970; Rost, 1988). For multinomial data, the unstructured model includes a $M_j$-vector of category response probabilities for each class and item. To simplify notation, we use the integer representation of the ordinal attributes to refer to the latent classes. That is, let ${\varvec{v}}=(2^{K-1},2^{K-2},\ldots ,1)^\top$ and note that ${\varvec{\alpha }}^\top {\varvec{v}}$ is a bijection that maps the attribute profiles to integers $c\in \left\{ 0,\ldots ,2^K-1\right\}$. Let the probability of observing a response of m on item j for members with the latent attribute profile of class c is $\theta _{jcm}=P(Y_j=m|{\varvec{\alpha }}^\top {\varvec{v}}=c)$ and define the vector of response probabilities for class c as ${\varvec{\theta }}_{jc}=(\theta _{jc0},\ldots ,\theta _{jc,M_j-1})^\top$. The model for $Y_j$ given membership in class c is a multinomial probability mass function defined as,

$$\begin{aligned} p(y_j|{\varvec{\alpha }}^\top {\varvec{v}}=c,{\varvec{\theta }}_{jc})=\sum _{m=0}^{M_j-1}\theta _{jcm}\,\mathcal I(y_j=m) \end{aligned}$$

(1)

where ${\mathcal {I}}(\cdot )$ is the indicator function. Let ${\varvec{\pi }}$ be a $2^K$ vector of structural latent class probabilities where element c is defined as $P({\varvec{\alpha }}^\top {\varvec{v}}=c)=\pi _c$. Furthermore, let ${\varvec{\Theta }}\in \mathrm{I\!R}^{M_1\times \cdots \times M_J\times 2^K}$ denote the response probabilities for all items and latent classes. We assume the responses in the J-vector ${\varvec{Y}}$ are independent given ${\varvec{\alpha }}$, which implies the distribution of ${\varvec{Y}}$ given the item and structural parameters is,

$$\begin{aligned} p({\varvec{y}}|{\varvec{\Theta }},{\varvec{\pi }}) = \sum _{c=0}^{2^K-1}\pi _c \prod _{j=1}^J p(y_j|{\varvec{\alpha }}^\top {\varvec{v}}=c,{\varvec{\theta }}_{jc}). \end{aligned}$$

(2)

Let ${\varvec{Y}}_i=(Y_{i1},\ldots ,Y_{iJ})^\top$ be a random J-vector of ordinal responses for individual i and define the realized values as ${\varvec{y}}_i=(y_{i1},\ldots ,y_{iJ})^\top$. Let the random $n\times J$ matrix of mixed ordinal responses be $\mathbf{Y }=({\varvec{Y}}_1,\ldots ,{\varvec{Y}}_n)^\top$. The likelihood of observing a sample of $i=1,\ldots ,n$ independent observations is,

$$\begin{aligned} p({\varvec{y}}_1,\ldots ,{\varvec{y}}_n|{\varvec{\Theta }},{\varvec{\pi }})=\prod _{i=1}^n p({\varvec{y}}_i|{\varvec{\Theta }},{\varvec{\pi }}). \end{aligned}$$

(3)

An equivalent approach for describing the model in Eq. (3) is to instead consider the implied marginal probabilities for all response patterns (e.g., see Allman, Matias, & Rhodes, 2009; J. Liu, Xu, & Ying, 2013). The distribution of $\mathbf{Y }$ for class c and all response patterns is defined by the $\left( \prod _{j=1}^J M_j\right)$-vector,

$$\begin{aligned} {\mathbb {P}}_{c}=\bigotimes _{j=1}^J {\varvec{\theta }}_{jc}. \end{aligned}$$

(4)

which is a Kronecker product of all item response probabilities for class c. Let $\mathbf{T }=({\mathbb {P}}_0,\ldots ,{\mathbb {P}}_{2^K-1})$ be a $\left( \prod _{j=1}^J M_j\right) \times 2^K$ matrix denoting the model probabilities for all item response patterns and latent classes. The implied marginal probability for the model is a finite mixture of the $2^K$ classes,

$$\begin{aligned} {\mathbb {P}} = \mathbf{T } {\varvec{\pi }}=\sum _{c=0}^{2^K-1}\pi _c\mathbb P_{c}. \end{aligned}$$

(5)

2.2 Identifiability Conditions for Binary Attributes and Multinomial Responses

This subsection discusses conditions for identifying mixtures of multinomial response data. We first introduce a few definitions, examples and prior results and then present an identifiability Theorem for structured multinomial mixture models with binary attributes.

Definition 1

(Identifiability) The model parameters $(\varvec{\Theta },{\varvec{\pi }})\in \Omega$ are identifiable if $p({\varvec{y}}_1,\ldots ,{\varvec{y}}_n|{\varvec{\Theta }},{\varvec{\pi }})=p({\varvec{y}}_1,\ldots ,{\varvec{y}}_n|{\varvec{\Theta }}',{\varvec{\pi }}')$ implies $\varvec{\Theta }=\varvec{\Theta }'$ and ${\varvec{\pi }}={\varvec{\pi }}'$.

Remark 1

Definition 1 is the classic notion of likelihood identifiability where each unique combination of parameter values corresponds to a different value of the likelihood function.

Definition 2

(Kruskal Rank) For a matrix $\mathbf{T }$, the Kruskal rank of $\mathbf{T }$, i.e., ${{\,\mathrm{rank}\,}}_K(\mathbf{T })$, is the largest number I such that every set of I columns of $\mathbf{T }$ are independent.

Remark 2

Note that ${{\,\mathrm{rank}\,}}_K (\mathbf{T })\le {{\,\mathrm{rank}\,}}(\mathbf{T })$. If $\mathbf{T }$ is of full column rank then ${{\,\mathrm{rank}\,}}_K (\mathbf{T })= {{\,\mathrm{rank}\,}}(\mathbf{T })$ (Allman et al., 2009).

Definition 3

(Three-way array) Let $\mathbf{T }=[\mathbf{T }_1,\mathbf{T }_2,\mathbf{T }_3]$ be a three-way array where each of the matrices has R columns and the (i, j, k) element is defined as $t_{ijk}=\sum _{r=1}^R t_{1ir}t_{2jr}t_{3kr}$ with $\mathbf{T }$ defined as

$$\begin{aligned} \mathbf{T }=[\mathbf{T }_1,\mathbf{T }_2,\mathbf{T }_3]=\sum _{r=1}^R \varvec{t}_{1r}\otimes \varvec{t}_{2r}\otimes \varvec{t}_{3r} \end{aligned}$$

(6)

where $\varvec{t}_{ir}$ is column r of $\mathbf{T }_i$ for $i=1,2,3$.

Example 1

(Latent class models as a three-way array) We can write the model in Eq. (5) as a three-way array by letting $\mathbf{T }_i$ for $i=1,2,3$ be matrices for three sets of non-overlapping items. Specifically, let ${\mathbb {J}}_i$ for $i=1,2,3$ denote three mutually exclusive and exhaustive sets of items. The distribution of responses for $j\in {\mathbb {J}}_i$ for class c is

$$\begin{aligned} {\mathbb {P}}_{ic}=\bigotimes _{j\in {\mathbb {J}}_i} {\varvec{\theta }}_{jc} \end{aligned}$$

(7)

where ${\mathbb {P}}_{ic}$ is a vector of length $\prod _{j\in \mathbb J_i} M_j$. Consequently, $\mathbf{T }_i=({\mathbb {P}}_{i0},\ldots ,\mathbb P_{i,2^K-1})$ and $R=2^K$ given each $\mathbf{T }_i$ is a $(\prod _{j\in {\mathbb {J}}_i}M_j)\times 2^K$ matrix of latent class response pattern probabilities for the items in ${\mathbb {J}}_i$. The three-way array representation of Eq. (5) is,

$$\begin{aligned} \mathbf{T }=[\mathbf{T }_1,\mathbf{T }_2,\mathbf T _3]=\sum _{c=0}^{2^K-1}\pi _c {\mathbb {P}}_{1c} \otimes \mathbb P_{2c}\otimes {\mathbb {P}}_{3c}. \end{aligned}$$

(8)

Theorem 1

(Allman et al., 2009). Consider the three-way array representation of a multinomial mixture model with $i=1,\ldots ,r$ classes. Suppose all entries of ${\varvec{\pi }}$ are positive. Then, if

$$\begin{aligned} {{\,\mathrm{rank}\,}}_K(\mathbf{T }_1)+{{\,\mathrm{rank}\,}}_K(\mathbf{T }_2)+{{\,\mathrm{rank}\,}}_K(\mathbf{T }_3)\ge 2r+2 \end{aligned}$$

the parameters of the model are uniquely identifiable, up to label swapping.

Remark 3

Note Allman et al.’s  (2009) result is based upon Kruskal’s (1976, 1977) theorem concerning the uniqueness of three-way arrays. Similar to Y. Chen, Culpepper, and Liang (2018) and Fang et al.  (2019), we use Kruskal’s (1976, 1977) result to establish an identifiability condition for multinomial response data with binary attributes.

Definition 4

(The$\mathbf{Q }$matrix) Let $\mathbf{Q }=(\varvec{q}_1,\ldots ,\varvec{q}_J)^\top$ be a $J\times K$ binary matrix where $q_{jk}$ is the (j, k) element of $\mathbf{Q }$ and $q_{jk}=1$ if attribute k is required for item j and $q_{jk}=0$ otherwise.

Remark 4

The $\mathbf{Q }$ matrix imposes structure on the response probabilities $\varvec{\Theta }$. For instance, items with $\varvec{q}_j=\varvec{e}_k$ are referred to as simple structure items that load only on attribute k. Simple structure items include only two distinct vectors of responses probabilities; ${\varvec{\theta }}_{j1}=(\theta _{j10},\ldots ,\theta _{j1,M_j-1})^\top$ for $\alpha _k=1$ and ${\varvec{\theta }}_{j0}=(\theta _{j00},\ldots ,\theta _{j0,M_j-1})^\top$ for $\alpha _k=0$. In contrast, items with complex structure that load onto two or more attributes include more than two vectors of response probabilities. Readers are directed to J. Chen and de la Torre (2018) for a discussion of the relation between $\mathbf{Q }$ and various reduced ordinal DMs.

Theorem 2

$\varvec{\Theta }$ and ${\varvec{\pi }}$ are identifiable, up to label swapping, if ${\varvec{\pi }}$ is positive, each item has distinct item response functions for at least two latent classes, and conditions (C1) and (C2) are satisfied:

• (C1) The rows of $\mathbf Q$ can be permuted to the form, $\mathbf{Q }^\top =[\mathbf{I }_K,\mathbf{I }_K,(\mathbf{Q }\,')^\top ]^\top$ where $\mathbf{I }_K$ is a K-dimensional identity matrix and $\mathbf{Q }\,'$ is a $(J-2K)\times K$ matrix.

• (C2) For any two latent classes c and $c'$, there exists at least one item in $\mathbf{Q }\,'$, in which ${\varvec{\theta }}_{jc}\ne {\varvec{\theta }}_{jc'}$.

Proof

We show the bound in Theorem 1 is achieved. Let $\mathbf{Q }$ be defined as in (C1) and let $\mathbb J_1=\{1,\ldots ,K\}$, ${\mathbb {J}}_2=\{K+1,\ldots ,2K\}$, and $\mathbb J_3=\{2K+1,\ldots ,J\}$. Fang et al.  (2019) showed for the polytomous attribute case that the simple structure assumption and distinct latent class IRFs implies $\mathbf{T }_1$ and $\mathbf T _2$ are full column rank, which for the binary attribute case indicates ${{\,\mathrm{rank}\,}}_K(\mathbf{T }_1)={{\,\mathrm{rank}\,}}_K(\mathbf{T }_2)=2^K$. That is, simple structure for items in $\mathbf{T }_1$ and $\mathbf{T }_2$ implies that

$$\begin{aligned} \mathbf{T }_{1}=\bigotimes _{j=1}^{K} {\mathbf {p}}_j,\; \mathbf T _{2}=\bigotimes _{j=K+1}^{2K} {\mathbf {p}}_j \end{aligned}$$

(9)

where ${\mathbf {p}}_j=({\varvec{\theta }}_{j0},{\varvec{\theta }}_{j1})$ is a $M_j\times 2$ matrix of response probabilities. The assumption of distinct probabilities (i.e., ${\varvec{\theta }}_{j0}\ne {\varvec{\theta }}_{j1}$) implies ${{\,\mathrm{rank}\,}}({\mathbf {p}}_j)=2$ for all $j\in \{1,\ldots ,2K\}$ and properties of Kronecker products imply ${{\,\mathrm{rank}\,}}(\mathbf T _1)=\prod _{j=1}^K{{\,\mathrm{rank}\,}}(\mathbf{p }_j)=2^K$ and, similarly, ${{\,\mathrm{rank}\,}}(\mathbf{T }_2)=2^K$.

We next establish that the ${{\,\mathrm{rank}\,}}_K(\mathbf{T }_3)\ge 2$ for the binary attribute case. In other words, it must be shown that every pair of the $2^K$ columns of $\mathbf{T }_3$ are independent. A proof by contradiction proceeds by assuming columns c and $c'$ are dependent. That is, columns c and $c'$ of $\mathbf{T }_3$ are ${\mathbb {P}}_{3c}$ and ${\mathbb {P}}_{3c'}$, respectively, and are dependent if there exists nonzero $u_c$ and $u_{c'}$ such that $u_c{\mathbb {P}}_{3c}+u_{c'}{\mathbb {P}}_{3c'}=\varvec{0}$ for all response patterns for items in ${\mathbb {J}}_3$. However, if (C2) is satisfied there exists an item $j\in \{2K+1,\ldots ,J\}$ such that ${\varvec{\theta }}_{jc}\ne {\varvec{\theta }}_{jc'}$. There is at least one response pattern ${\varvec{y}}_{3(j)}\in \times _{j'\in \mathbb J_3{\setminus } j } \{0,\ldots , M_{j'}-1\}$ with a nonzero probability for items in ${\mathbb {J}}_3$ that excludes item j. Let the value of the distribution function for ${\varvec{y}}_{3(j)}$ be $p_{3c(j)}$ for class c and $p_{3c'(j)}$ for class $c'$. The $M_j$ elements of ${\mathbb {P}}_{3c}$ and ${\mathbb {P}}_{3c'}$ corresponding to the distribution of ${\varvec{y}}_{3(j)}$ and values of $y_j=0,\ldots ,M_j-1$ equals $p_{3c(j)}{\varvec{\theta }}_{jc}$ and $p_{3c'(j)}{\varvec{\theta }}_{jc'}$, respectively. If ${\mathbb {P}}_{3c}$ and ${\mathbb {P}}_{3c'}$ are dependent then $u_c p_{3c(j)}{\varvec{\theta }}_{jc}+u_{c'} p_{3c'(j)}{\varvec{\theta }}_{jc'}=\varvec{0}$ for nonzero $u_c$ and $u_{c'}$. However, ${\varvec{\theta }}_{jc}$ and ${\varvec{\theta }}_{jc'}$ are distinct (i.e., independent) and the equality is only achieved if $u_c=u_{c'}=0$. c and $c'$ were chosen arbitrarily, so ${{\,\mathrm{rank}\,}}_K(\mathbf{T }_3)\ge 2$. $\square$

Remark 5

Fang et al.  (2019) showed that multinomial mixture models with polytomous attributes are identified if $\mathbf{Q }$ include three $\mathbf{I }_K$ matrices for three non-overlapping sets of items. The requirement of three $\mathbf{I }_K$ matrices in $\mathbf{Q }$ is restrictive and Fang et al.  (2019) note their sufficient conditions could be relaxed if “additional constraints on parameters are assumed” (p. 25). Theorem 2 shows that the sufficient condition can be reduced to two $\mathbf{I }_K$ matrices if attributes are binary and additional items exist in $\mathbf{Q }'$ that distinguish all of the classes.

3 A General Diagnostic Model (GDM) for Ordinal Data

We next discuss two issues related to the GDM for ordinal data. First, we present a structured mixture modeling framework, which uses a cumulative link function for ordinal responses, and discusses monotonicity conditions. Second, we present a fully Bayesian formulation and discuss posterior inference.

3.1 Structured Mixture Model with a Cumulative Link Function

The model in Eq. (3) may include many parameters for each item for even modest values of K. Consequently, some degree of regularization of the model parameters may improve estimation. There is not a clear approach for regularizing the latent class response probabilities as parameterized in Eq. (3). In this subsection, we describe a reparameterization of $\varvec{\Theta }$ that enables the application of Bayesian variable selection techniques.

One strategy for modeling ordinal responses is to use a cumulative link function (e.g., see Albert & Chib, 1993) for an unstructured mixture model (e.g., see Bao & Hanson, 2015; DeYoreo, Reiter, & Hillygus, 2017; Kottas, Müller, & Quintana, 2005). Specifically, we can rewrite the latent class probabilities for items j$(\theta _{jc0},\ldots ,\theta _{jc,M_j-1})$ using a cumulative link function $\Psi (\cdot )$ and $M_j-1$ thresholds, $(\tau _{jc1},\ldots ,\tau _{jc,M_j-1})$ where $\tau _{jc0}<\tau _{jc1}<\cdots<\tau _{jc,M_j-1}<\tau _{jcM_j}$ with the endpoints defined as $\tau _{jc0}=-\infty$ and $\tau _{jcM_j}=\infty$. Furthermore, a commonly used parameterization fixes $\tau _{jc1}=0$ and incorporates a latent class mean parameter for item j, $\mu _{jc}$. Therefore, the cumulative probability of a response at level m or less using a cumulative link function is,

$$\begin{aligned} P(Y_j\le m\left| {\varvec{\alpha }}'{\varvec{v}}=c,\tau _{jc,m+1},\mu _{jc}\right. )=\sum _{m'=0}^m \theta _{jcm'}=\Psi \left( \tau _{jc,m+1}-\mu _{jc}\right) \end{aligned}$$

(10)

where $\Psi (\cdot )$ is a generic cumulative link function. Accordingly, the probability of response m by members of class c to item j is $\theta _{jcm} = \Psi \left( \tau _{jc,m+1}-\mu _{jc}\right) -\Psi \left( \tau _{jcm}-\mu _{jc}\right)$ where $\Psi \left( \tau _{jc0}-\mu _{jc}\right) =0$ and $\Psi \left( \tau _{jcM_j}-\mu _{jc}\right) =1$.

Prior studies estimated the $2^K$$\mu _{jc}$’s in an unstructured fashion (e.g., see DeYoreo et al., 2017; DeYoreo & Kottas, 2018; Kottas et al., 2005). In contrast, we reparameterize and impose structure on the latent class mean parameters in Eq. (10) by defining $\mu _{jc}=\varvec{a}_c^\top \varvec{\beta }_j$ where $\varvec{\beta }_j$ is a P-vector of parameters for item j and $\varvec{a}_c$ is a design vector for class c that uniquely maps ${\varvec{\alpha }}^\top {\varvec{v}}$ to a set of P dummy coded variables (the coding for $\varvec{a}_c$ is discussed in the next subsection). Our reparameterized model for the cumulative conditional probability of a response at level m or less is,

$$\begin{aligned} P(Y_j\le m\left| {\varvec{\alpha }}^\top {\varvec{v}}=c,\varvec{\beta }_j,\tau _{jc0},\ldots ,\tau _{jcm}\right. )=\sum _{m'=0}^m \theta _{jcm'}=\Psi \left( \tau _{jc,m+1}-\varvec{a}_c^\top \varvec{\beta }_j\right) . \end{aligned}$$

(11)

Note the model in Eq. (11) implies that the conditional probability an observed response equals m is $\theta _{jcm} = \Psi \left( \tau _{jc,m+1}-\varvec{a}_c^\top \varvec{\beta }_j \right) -\Psi \left( \tau _{jcm}-\varvec{a}_c^\top \varvec{\beta }_j\right)$ and the conditional probability mass function for item j under the reparameterized model is,

$$\begin{aligned} p(y_j\left| {\varvec{\alpha }}^\top {\varvec{v}}=c,\varvec{\beta }_j,\tau _0,\ldots ,\tau _M\right. )=\sum _{m=0}^{M_j-1}\left[ \Psi \left( \tau _{m+1}-\varvec{a}_c^\top \varvec{\beta }_j\right) -\Psi \left( \tau _{m}-\varvec{a}_c^\top \varvec{\beta }_j\right) \right] {\mathcal {I}}(y_j=m). \end{aligned}$$

(12)

Let $\mathbf{B }=\left( \varvec{\beta }_1,\ldots ,\varvec{\beta }_J\right) ^\top$ be a $J\times 2^K$ matrix of regression parameters. Furthermore, let $\varvec{\tau }_j$ denote the $M_j-1$ thresholds for item j and let $\mathbf{T }=\left( \varvec{\tau }_1,\ldots ,\varvec{\tau }_J\right) ^\top$ denote the thresholds for all J items. Note that we refer to the reparameterized likelihood function for a sample of n independent observations as $p(\mathbf{Y }|\mathbf{B },\mathbf{T },{\varvec{\pi }})$.

3.1.1 Coding Attribute Profiles

We next discuss how to code attribute profile c as the vector of latent predictors, $\varvec{a}_c$, in the cumulative link function. The most general exploratory model is referred to as a saturated model, which includes all main- and higher-order interaction effects terms of the attribute levels. Accordingly, the saturated model includes all effects and the number of design predictors and coefficients is $P=2^K$. Researchers can in principle estimate exploratory models with fewer parameters (i.e., $P<2^K$) to estimate more restricted models, but the discussion that follows considers the saturated model.

Table 1 Example design matrix for K = 3 by attribute profile, ${\varvec{\alpha }}$.

Table 1 presents an example design matrix for the saturated model with K = 3. In this case, the design vector for an arbitrary ${\varvec{\alpha }}$ is $\varvec{a}=(1, \alpha _{3}, \alpha _{2}, \alpha _{2}\alpha _{3}, \alpha _{1}, \alpha _{1}\alpha _{3}, \alpha _{1}\alpha _{2}, \alpha _{1}\alpha _{2}\alpha _{3} )$. In the saturated model with $K=3$ the main effects are $\alpha _1$, $\alpha _2$, and $\alpha _3$, the two-way interactions are $\alpha _1\alpha _2$, $\alpha _1\alpha _3$, and $\alpha _2\alpha _3$, the three-way interaction is $\alpha _1\alpha _2\alpha _3$. The second column of Table 1 presents the $2^K$ = 8 latent classes, and columns three to ten show the elements of the design vectors $\varvec{a}_c$ for each c. For instance, latent class ${\varvec{\alpha }}_3=(0,1,1)^\top$ corresponds with the design vector $\varvec{a}_3=(1,1,1,1,0,0,0,0)^\top$. Finally, Table 1 shows that the first element of $\varvec{a}_c$ is a one for the intercept, which indicates the reference group is the class with ${\varvec{\alpha }}=(0,0,0)^\top$.

It is worth mentioning another reason for studying the design matrix. Specifically, as shown in the first column of Table 1 we order the elements of $\varvec{a}$ according to the integer representation of the binary profile, ${\varvec{\alpha }}$. Table 1 demonstrates a simple coefficient labeling strategy in the second row of Table 1, which includes attribute profile labels in the order of the integer representation. Table 1 shows that the labels in the second row provide an alternative way to refer to effects denoted by the products of the a’s. We see that the alternative main effect labels in Table 1 all have two zeros included. For instance, the main effect for $\alpha _1$ corresponds to the label “100.” In contrast, the labels for the two-way interaction effects include one zero. For instance, an alternative label for the interaction involving attributes one and three (i.e., $\alpha _1\alpha _3$) is “101.” Furthermore, we see that the intercept label is “000” and the label for the interaction among the highest attribute levels (i.e., the coefficient for $\alpha _{1}\alpha _{2}\alpha _{3}$) is “111.” For a general value of K, this labeling scheme implies that the intercept label has K zeros, the labels for main effects include $K-1$ zeros, two-way interaction labels have $K-2$ zeros, and K-way interaction labels are without any zeros.

3.1.2 Monotonicity Conditions

We next discuss monotonicity conditions for the latent class IRFs. Specifically, the monotonicity condition we consider is

$$\begin{aligned} P(Y_j \ge m|{\varvec{\alpha }},\varvec{\beta }_j) \ge P(Y_j \ge m|{\varvec{\alpha }}',\varvec{\beta }_j),\; \text {if } {\varvec{\alpha }}\ge {\varvec{\alpha }}' . \end{aligned}$$

(13)

The condition in Eq. (13) states that the probability of responding m or greater on item j for members with attribute profile ${\varvec{\alpha }}$ is greater for all classes that are element-wise smaller than ${\varvec{\alpha }}$. It is important to note that the condition in Eq. (13) is satisfied for the ordinal GDM if $\mu _{jc}\ge \mu _{jc'}$ for ${\varvec{\alpha }}_c\ge {\varvec{\alpha }}_{c'}$. Consequently, the monotonicity conditions in Eq. (13) can be translated into a lower-bound condition for each coefficient (e.g., see Y. Chen, Culpepper, & Liang, 2018). We let $L_{jp}$ denote the lower bound for $\beta _{jp}$.

3.2 Bayesian Model

This subsection outlines a Bayesian formulation for the ordinal latent class model using a cumulative probit link function. We first discuss the model formulation and then discuss posterior inference.

3.2.1 Model Formulation and Priors

We use a data augmentation strategy as found in Bayesian item response theory models (e.g., see Albert 1992; Béguin & Glas, 2001; Culpepper, 2016) for the probit cumulative link function. That is, we introduce a deterministic relationship between the random ordinal response $Y_{ij}$ and a continuous augmented latent variable $Y_{ij}^*$ so that $Y_{ij}=m$ whenever $\tau _{jm}<Y_{ij}^*<\tau _{j,m+1}$. Next, we assume the augmented variable $Y_{ij}^*$ is conditionally normally distributed as $Y_{ij}^*\left| {\varvec{\alpha }}_i,\varvec{\beta }_j\right. \sim {\mathcal {N}}(\varvec{a}_i^\top \varvec{\beta }_j,1)$.

We consider a categorical prior for ${\varvec{\alpha }}_i$ (e.g., see Culpepper, 2015) conditioned upon the latent class structural probabilities ${\varvec{\pi }}$, which is the $2^K$ vector of class probabilities. The conditional probability that ${\varvec{\alpha }}_i$ has the attribute configuration of class c given ${\varvec{\pi }}$ is,

$$\begin{aligned} P\left( {\varvec{\alpha }}_i^\top {\varvec{v}}=c|{\varvec{\pi }}\right) = \sum _{c'=0}^{2^K-1} \pi _{c'}{\mathcal {I}}({\varvec{\alpha }}_i^\top {\varvec{v}}=c). \end{aligned}$$

(14)

Note that we specify conjugate ${\varvec{\pi }}\sim \text {Dirichlet}(\varvec{n}_0)$ prior for the structural parameters and implement a uniform prior with $\varvec{n}_0=\varvec{1}_{2^K}^\top$.

We employ the stochastic search variable selection prior specification for $\mathbf{B }$ as described in Culpepper (2019). The prior for $\mathbf{B }$ is conditioned on $\mathbf{Q }$. The prior for $\varvec{\beta }_{j}$ given $\varvec{q}_j$ is,

$$\begin{aligned} p\left( \varvec{\beta }_{j}|\varvec{q}_j\right)&\propto \prod _{p=0}^{2^K-1} v_p^{-1/2}\exp \left( -\frac{1}{2}\beta _{jp}^2/v_p \right) \mathcal I\left( \beta _{jp}>L_{jp}\right) \end{aligned}$$

(15)

$$\begin{aligned} v_p&={\tilde{q}}_{jp}/c_1 + (1-{\tilde{q}}_{jp})/c_0. \end{aligned}$$

(16)

Note as discussed in Culpepper (2019) $\tilde{\varvec{q}}_j$ is a $2^K$ vector that includes all possible products of the elements of $\varvec{q}_j$. For instance, for $K=2$, $\varvec{q}_j=(q_{j1},q_{j2})^\top$ and $\tilde{{\varvec{q}}}_j = (1,q_{j2},q_{j1},q_{j1}q_{j2})^\top$. The precision for $\beta _{jp}$ is $c_1$ when ${\tilde{q}}_{jp}=1$ and $c_0$ for ${\tilde{q}}_{jp}=0$. The SSVS approach uses fixed values for the constants $c_0$ and $c_1$. Specifically, $c_0$ is set to a large value (e.g., we set $c_0$ = 500 in this paper) to reflect a smaller variance for $\beta _{jp}$ and a distribution that is more concentrated near zero. In contrast, $c_1$ is fixed as a smaller value (e.g., we set $c_1=1$) to depict a prior distribution for $\beta _{jp}$ that is consistent with an active coefficient.

Under the SSVS formulation, the elements of $\mathbf{Q }$ denote the “activeness” of the coefficients. We assume the elements of $\mathbf{Q }$ are independently distributed given a hyper parameter $\omega$. Specifically, the prior is $q_{jk}|\omega \sim \text {Bernoulli}(\omega )$. Furthermore, $\omega \sim \text {Beta}(a,b)$ is a Beta prior for $\omega$ and we set $a=b=1$ to employ a uniform prior for $\omega$ in the simulation study and application.

Prior research notes the difficulty associated with estimating the thresholds in mixture models for ordinal data (e.g., see Bao & Hanson, 2015; DeYoreo et al., 2017; DeYoreo & Kottas, 2018; Kottas et al., 2005) and instead recommend treating the thresholds as fixed rather than random. We investigated this issue and conducted several Monte Carlo simulation studies to assess parameter recovery when thresholds are treated as random. In particular, we sampled thresholds using the Metropolis–Hastings approach of Cowles (1996). The results from these numerical experiments supported prior research regarding the difficulty with estimating model parameters when thresholds are random. Accordingly, we follow the recommendation of prior researchers and fix the thresholds. In particular, we fix the thresholds as $(\tau _{jc1},\ldots ,\tau _{jc,M_j-1})= \left( 0,2,\ldots ,2(M_j-2)\right)$. Fixing the thresholds has the added benefit of computational speed by avoiding Metropolis–Hastings updates for thresholds (e.g., see Cowles, 1996).

3.2.2 Posterior Inference

The posterior distribution of interest is,

$$\begin{aligned} p\left( \mathbf{Y }^*,\mathbf{A },\mathbf{B },{\varvec{\pi }},\mathbf Q ,\omega |\mathbf{Y }\right) \propto p\left( \mathbf{Y }|\mathbf Y ^*\right) p\left( \mathbf{Y }^*|\mathbf{A },\mathbf B \right) p(\mathbf{A }|{\varvec{\pi }}) p(\mathbf{B }|\mathbf{Q })p(\mathbf Q |\omega )p({\varvec{\pi }})p(\omega ) \end{aligned}$$

(17)

where $\mathbf{Y }^*$ is an $n\times J$ random matrix of augmented data and $\mathbf{A }=({\varvec{\alpha }}_1,\ldots ,{\varvec{\alpha }}_n)$ refers to the latent attributes. We use a Gibbs sampling algorithm to approximate the posterior distribution (see the “Appendix” for additional details).

4 Monte Carlo Simulation Study

4.1 Overview

This section presents results from a Monte Carlo simulation study to evaluate the accuracy of parameter recovery for different sample sizes. The population model parameters were defined by the values estimated in the application (e.g., see the values for $\mathbf{B }$ and ${\varvec{\pi }}$ in Table 5) to ensure the simulated parameters are consistent with applied data. Accordingly, the simulation used $J = 12$, $M_j=4$, and $K = 3$. We considered four sample sizes of $n = 500$, 1000, 1500, and 2000 and generated 100 replications per condition for a total of 400 simulated datasets. For each replication of the simulation study, we executed a single chain of length 100,000 with a burnin of 20,000 iterations. Additionally, the SSVS parameters were defined as $c_1=1$ and $c_0=500$.

We measure parameter recovery by computing the expected absolute deviation (EAD) of the estimates from the population values. In particular, we assess the accuracy of item parameter estimates by comparing the estimated and population cumulative IRFs (i.e., see Eq. 11). That is, the estimated cumulative IRF for class c is,

$$\begin{aligned} {\hat{F}}_{jcm} = \sum _{m'=0}^m {\hat{\theta }}_{jcm'} \end{aligned}$$

(18)

where ${\hat{\theta }}_{jcm'}$ is defined using a probit link and the posterior mean for ${\varvec{\beta }}_j$. We estimate the expected absolute deviation between the item j across T scans of the posterior using

$$\begin{aligned} EAD(F_{jcm}) = \frac{1}{T}\sum _{t=1}^T \left| {\hat{F}}_{jcm} - F_{jcm}\right| . \end{aligned}$$

(19)

For $K=3$ there are eight parameters for each item, so to simplify the presentation of results we compute an overall average expected absolute deviation for item j and response level m as,

$$\begin{aligned} EAD(F_{jm}) = \frac{1}{2^K}\sum _{c=0}^{2^K-1}EAD(F_{jcm}). \end{aligned}$$

(20)

We report EAD for all items and sample sizes for $m=0,1,2$ (note the $m=3$ case is excluded because $F_{jc3}=1$).

We also assess accuracy in the estimation of the latent class structural probabilities, ${\varvec{\pi }}$. That is we estimate ${\varvec{\pi }}$ by computing the posterior mean and then compute the EAD for each element.

Table 2 Summary of Monte Carlo simulation study average expected absolute deviation for the cumulative item response functions by response level $m=0,1,2$ and $n=500, 1000, 1500, 2000$.

Table 3 Summary of Monte Carlo simulation study expected absolute deviation for the latent class structural probabilities ${\varvec{\pi }}$ by $n=500, 1000, 1500, 2000$.

4.2 Results

The Monte Carlo simulation results provide evidence that the developed algorithm accurately recovers the item and structural parameters across all sample sizes. Table 2 reports the average EAD for all items by response levels $m=0,1,2$ and sample sizes of $n=500, 1000, 1500, 2000$. The results in Table 2 show that average EAD for the cumulative IRFs is less than 0.038, 0.027, 0.023, and 0.021 for sample sizes of $n=500, 1000, 1500, 2000$, respectively. Furthermore, Table 3 reports the expected absolute deviation of the estimate ${\varvec{\pi }}$ and shows that the latent class probabilities are accurately recovered.

We also recorded the run-time for the developed algorithm. We found evidence that Markov chains with 100,000 iterations required, on average, 146.6 s, 276.0 s, 417.3 s, and 639.4 s for sample sizes of 500, 1000, 1500, and 2000 on a cluster with 2.50 GHz processors.

5 Application: Approaches to Learning and Self-Description (ALS) Questionnaire

We next report results from an application of the ordinal DM to the public-use ALS data file, which was collected through the Early Childhood Longitudinal Study, Kindergarten Class of 1998-1999 (ECLS-K; Tourangeau et al., 2015). The public-use ALS dataset included student ratings by parents and teachers on the approaches to learning scale. The dataset includes responses from teachers and parents for a total of 21,409 students of which 13,354 were complete records for the variables studied.

The ALS questionnaire includes twelve items with $M_j$ = 4 response categories and scale anchor labels of “0 = never” and “3 = very often.” Table 4 reports the item stems and category proportions for parent (i.e., items 1–6) and teacher (i.e., items 7–12) responses. Table 4 shows that proportionally fewer students received a rating of “never” by parents or teachers. The items also demonstrated variability in response proportions. For instance, over 80% of parents responded in the highest two categories for items two (“Show interest in a variety of things?”), five (“Eager to learn new things?”), and six (“Creative in work or in play?”). In contrast, Table 4 shows that teachers tended to report ratings of “1,” “2,” and “3” more uniformly than parents.

Table 4 Approaches to learning and self-description item stems and category proportions for a random sample of n = 13,354 kindergarten students.

5.1 Results

We estimated an exploratory ordinal DM solution using $K=3$ to demonstrate the model and interpret parameter estimates. Note that we ran a single chain of length 100,000 with a burnin of 20,000 iterations. The algorithm required 3087 s to complete 100,000 iterations on a laptop with a 2.20 GHz processor. We implemented the model with the SSVS scale parameters equal to $c_1=1$ and $c_0=500$.

Table 5 Approaches to learning and self-description element-wise means for $\mathbf{Q }$, $\mathbf B$, and ${\varvec{\pi }}$ for a random sample of n = 13,359 kindergarten students from the early childhood longitudinal study (ECLS-K) class of 1998–1999.

Table 5 reports ALS model parameter estimates for $\mathbf{Q }$, $\mathbf{B }$, and ${\varvec{\pi }}$. Specifically, we constructed $\overline{\mathbf{Q }}$ with the posterior element-wise means (i.e., ${\bar{q}}_{jk}=\frac{1}{T}\sum _{t=1}^T q_{jk}^{(t)}$ where t indexes values in the Markov chain). The results in Table 5 provide evidence of a dense structure for $\mathbf{Q }$ given the absence of simple structure items. The estimated $\mathbf{Q }$ matrix suggests that the latent structure for items is associated with whether ratings were recorded by parents or teachers. In fact, the teacher responses about students approaches to learning (i.e., items seven through twelve) relate to attributes two and three, whereas there are some items where the parent ratings load onto all three attributes.

The values of the coefficients provide insight about how changes in attribute levels relate to observed responses. For instance, consider the coefficients for item twelve (“Pays attention well”). Item 12 relates to the main effects and interaction between attributes two and three. Additionally, the main effects for attributes two and three relate to responses on all but items two and four. There is evidence of several higher-order interaction effects. For instance, $\alpha _2\alpha _3$ relates to item nine and $\alpha _1\alpha _2$ relates to item three. There is also some evidence of disjunctive relationships as indicated by negative interaction effects. In fact, there is evidence of a negative three-way interactions for items one and three.

The IRFs provide another perspective for interpreting the relationship between the attributes and items. For instance, consider the impact of the first attribute on item one by comparing the IRFs for members of classes “000” and “100.” Students classified as possessing attribute profile “000” received ratings of (0, 1, 2, 3) from theirs parents with probabilities of (0.09, 0.65, 0.26, 0.00). In contrast, the probabilities for the students in the “100” class had response probabilities of (0.00, 0.19, 0.68, 0.13). A change of $\alpha _1$ from zero to one increases the chance students receive parent ratings of a “2.”

Fig. 1

Counter-clock-plots depicting the estimated item response functions by latent class ${\varvec{\alpha }}$ (x-axis) and item (y-axis) for the ALS data with $M_j=4$ for $j=1,\ldots ,12$ and $K=3$.

Figure 1 presents counter-clock-plots to illustrate the category response probabilities by latent class and item. That is, the “clock” for a given ${\varvec{\alpha }}$ and item presents the probabilities of observed responses of 0, 1, 2, and 3 in four quadrants in a counter-clockwise order. For instance, Fig. 1 shows that the probability members of classes “011” and “111” of reporting a “3” is nearly one for items eight, nine, eleven, and twelve. Figure 1 also illustrates how increases in latent levels relate to changes in response probabilities. For instance, the probability of reporting a “2” or “3” on items seven through twelve increases as $\alpha _3$ changes from 0 to 1.

The last row of Table 5 reports the posterior mean of the latent class structural parameter, ${\varvec{\pi }}$. The values of the estimated ${\varvec{\pi }}$ suggest that the largest three classes were “101,” “011,” and “010” with class probabilities of ${\hat{\pi }}_5 = 0.19$, ${\hat{\pi }}_{3} = 0.18$, and ${\hat{\pi }}_2 = 0.15$, respectively. In contrast, the three smallest classes were “000,” “100,” and “110” with probabilities equal to ${\hat{\pi }}_0$ = 0.07, ${\hat{\pi }}_4 = 0.07$, and ${\hat{\pi }}_6 = 0.08$.

5.2 Model Fit

The previous subsection reported results for a model with two attributes to demonstrate the model in an application. This subsection discusses model fit to understand how well the estimated model describes the observed data.

Fig. 2

Plot of observed total scores and posterior predictive probabilities (PPPs). Note Boxplots are marginal distributions. The dashed, horizontal lines indicate posterior probabilities of 0.025 and 0.975. In the plot, 2.31% of students had total score PPPs less than 0.025 or greater than 0.975.

We report posterior predictive probabilities (e.g., see Sinharay, Johnson, & Stern, 2006) to evaluate the fit of the model with K = 3. In particular, we assess model fit by assessing how well the model reproduced students’ total scores. That is, we used the samples from the posterior to simulate ordinal responses from the model and computed a distribution for each student’s total score to calculate the proportion of times total scores generated in the posterior distribution exceeded the observed values. Figure 2 plots the observed total scores against each student’s posterior predictive probability (PPP). Figure 2 shows that 50% of students’ PPPs equal values between 0.249 and 0.610, which provides some support that the model describes students’ total scores. Furthermore, additional evidence of model fit is illustrated by the fact that the PPPs for most students fell between cutoffs of 0.025 and 0.975. The horizontal lines in Fig. 2 separate observations that were less accurately predicted by the model (i.e., PPPs below 0.025 or above 0.975). In fact, 2.31% of students had extreme PPPs outside of the 0.025 and 0.975 range and could be considered less accurately predicted by the model.

6 Discussion

Ordinal DMs are necessary for providing a fine-grained classification on substantively relevant attributes. Ordinal DMs are applicable to address research questions in numerous settings with examples including partial credit responses in education and ratings in survey research. We next discuss the implications of the study, review limitations, offer future research directions, and provide concluding remarks.

We presented a new exploratory diagnostic model for ordinal data that improves upon existing research. Our model used a cumulative probit link along with Bayesian variable selection techniques to infer the relationship between a collection of binary attributes and observed ordinal responses. A potential advantage of the proposed method is that a priori knowledge about the latent structure is not needed and our model provides researchers with a framework for inferring the latent structure to inform substantive theory development. It is worth mentioning that although we considered an exploratory approach in this paper the developed framework could be implemented in a confirmatory fashion. That is, the methods could be used in a confirmatory setting by fixing the elements of $\mathbf{Q }$ to indicate which item parameters are active versus inactive. Furthermore, researchers with partial knowledge about the underlying structure could also fix some $q_{jk}$ and estimate others.

The utility of the proposed framework will likely be judged by the insights the methodology offers applied researchers. Accordingly, our application to the ALS items serves as an example of the type of novel inferences that are available with ordinal DMs. In particular, we uncovered evidence that a three-attribute solution with eight classes describes teacher and parent responses to the twelve public-use ALS items. The results offered evidence that the latent structure was associated with whether the ratings were from teachers or parents. Additionally, we found evidence that the relationship between observed responses and latent attributes was characterized by main effects and higher-order interactions. We also found that some of the parent item responses loaded on all three attributes. The uncovered structure may suggest that there is a common attribute underlying the approaches to learning and self-description items that both teachers and parents consider in responses about their students. Teacher ratings related to the common attribute and as well as attribute three. One inference could be that the first attribute (which related only to parent ratings) captured learning behaviors that are observed in informal settings outside of schools, whereas the third attribute characterized student feature found in formal academic settings. Future research should apply the developed ordinal DM to additional ALS items to assess the extent to which the uncovered attributes more generally capture the latent structure.

Another contribution relates to the establishment of weaker sufficient conditions for model identifiability. We followed Fang et al.’s (2019) recommendation to relax their sufficient conditions for polytomous response DMs with polytomous attributes. Specifically, Theorem 2 shows that a sufficient condition for identifying ordinal DM parameters with binary attributes is that the $\mathbf{Q }$ matrix must include simple structure for two items and the latent classes must be distinguished by a least one of the remaining items. It is important to note that we did not explicitly enforce the identifiability conditions when analyzing the ALS items. The algorithm could be restricted to stochastically searching the space of identified $\mathbf{Q }$ matrices (e.g., see Y. Chen, Culpepper, Chen, & Douglas, 2018). We used the ALS model parameters as to generate data in the Monte Carlo simulation study. The Monte Carlo results provided evidence that, although the estimated $\mathbf{Q }$ was not strictly identified, the algorithm was successful in recovering model parameters. One implication is that future research may be able to establish even weaker identifiability conditions for ordinal DMs with binary attributes than required by Theorem 2.

There are several additional issues for researchers to consider when applying ordinal DMs. First, researchers may need to reverse-code variables when applying the monotonicity constraints. That is, the monotonicity constraints assume that higher latent attribute levels relate to higher observed responses. A negatively-worded item would need to be reverse-coded to ensure a clear interpretation of the attributes. Alternatively, the identifiability conditions require restrictions on $\mathbf{Q }$ and the distinctness of some probabilities, so estimation with reverse-coded items could proceed without monotonicity restrictions.

Second, we considered an unstructured model for the latent class probabilities ${\varvec{\pi }}$. There may be instances where the latent class structure can be approximated with a higher-order factor model (Culpepper & Chen, 2018; de la Torre & Douglas, 2004; Henson et al., 2009) or an underlying multivariate normal distribution with a vector of thresholds and a polychoric correlation matrix (Y. Chen & Culpepper, 2018; Henson et al., 2009; Templin, Henson, Templin, & Roussos, 2008). Future research could establish guidelines for selecting competing structures for ${\varvec{\pi }}$.

Third, in our application of the ordinal DM to the ALS data we analyzed the subset of complete cases, which implies that we implicitly assumed incomplete data were ignorable and missing at random. Future research should investigate the plausibility of the ignorability assumption with the restricted-use data and consider modeling the missing data mechanism if the assumption is untenable.

Lastly, the Monte Carlo simulation study was limited to one set of population parameters derived from applied data. Additional applications of the ordinal DM are needed to identify a distribution of parameter values that can be expected in practice. Subsequent Monte Carlo simulation studies are needed to evaluate parameter recovery for an expanded set of population parameter values.

In conclusion, advancing ordinal DMs is critical for establishing tools that yield fine-grained classification of respondents into substantively meaningful latent clusters. The developed methodology contributes to research on ordinal DMs. We provided an exploratory methodology that broadens the applicability of ordinal DMs to social science research and allows researchers to refine substantive theory about the latent structure underlying ordinal response data.

Appendix: Gibbs Sampling Algorithm and Full Conditional Distributions

This section discusses the full conditional distributions used to approximate the posterior distribution of the ordinal diagnostic model parameters with Gibbs sampling. For iteration $t=1,\ldots , T$ we sample:

• 1. For $i=1,\ldots ,n$,

  • (a) ${\varvec{\alpha }}_i^{(t)}$ from the multinomial full conditional distribution ${\varvec{\alpha }}_i^{(t)}|{\varvec{Y}}_i,\mathbf B ^{(t-1)},{\varvec{\alpha }}_1^{(t)},\ldots ,{\varvec{\alpha }}_{i-1}^{(t)},{\varvec{\alpha }}_{i+1}^{(t-1)},\ldots ,{\varvec{\alpha }}_{n}^{(t-1)}$ where the conditional probability ${\varvec{\alpha }}_i^{(t)}$ is classified as profile c is,

    $$\begin{aligned} P({\varvec{\alpha }}_i^{(t)\top }{\varvec{v}}&=c|{\varvec{Y}}_i,\mathbf B ^{(t-1)},{\varvec{\alpha }}_1^{(t)},\ldots ,{\varvec{\alpha }}_{i-1}^{(t)},{\varvec{\alpha }}_{i+1}^{(t-1)},\ldots ,{\varvec{\alpha }}_{n}^{(t-1)})\nonumber \\&=\frac{(n_{ci}+n_{c0})\prod _{j=1}^J \theta _{jc,y_{ij}}^{(t-1)} }{\sum _{c=0}^{2^K-1} (n_{ci}+n_{c0}) \prod _{j=1}^J \theta _{jc,y_{ij}}^{(t-1)} } \end{aligned}$$

    (A1)

    where $\theta _{jc,y_{ij}}^{(t-1)}=\Phi \left( \tau _{jc,y_{ij}+1}-{\varvec{a}}_c^\top {\varvec{\beta }}_j^{(t-1)}\right) -\Phi \left( \tau _{jc,y_{ij}}-{\varvec{a}}_c^\top {\varvec{\beta }}_j^{(t-1)}\right)$. Notice that we integrate ${\varvec{\pi }}$ from the prior distribution $p(\mathbf A ,{\varvec{\pi }})=p({\varvec{\alpha }}_1,\ldots ,{\varvec{\alpha }}_n|{\varvec{\pi }})p({\varvec{\pi }})$ and instead use the conditional prior distribution $p({\varvec{\alpha }}_i|{\varvec{\alpha }}_1^{(t)},\ldots ,{\varvec{\alpha }}_{i-1}^{(t)},{\varvec{\alpha }}_{i+1}^{(t-1)},\ldots ,{\varvec{\alpha }}_{n}^{(t-1)})$ which implies the usual $\pi _c$ (e.g., see Equation 7 of Culpepper, 2019) is replaced with $n_{ci}+n_{c0}$ where $n_{ci}$ is the number of respondents other than i that are classified in class c (e.g., see Jain & Neal, 2004) and $n_{c0}$ is the prior Dirichlet parameter (note $n_{c0}=1$ for a uniform prior).

  • (b) For $j=1,\ldots ,J$ update the latent augmented data from the full conditional distribution

    $$\begin{aligned} Y_{ij}^{*(t)}|Y_{ij},{\varvec{\alpha }}_i^{(t)},{\varvec{\beta }}_j^{(t-1)}\sim \mathcal N({\varvec{a}}_i^{(t)\top }{\varvec{\beta }}_j^{(t-1)},1) \mathcal I(\tau _{jc,y_{ij}}<Y_{ij}^{*(t)}<\tau _{jc,y_{ij}+1}) \end{aligned}$$

    (A2)

    where $\tau _{jc,y_{ij}}$ and $\tau _{jc,y_{ij}+1}$ are lower and upper thresholds for the observed value of $Y_{ij}$ for class c and item j. Recall we follow previously discussed strategies and fix the thresholds as ${\varvec{\tau }}_j=(0,2,\ldots , 2(M_j-2))^\top$.

• 2. Update the latent class probabilities (i.e., the mixing weights) as ${\varvec{\pi }}^{(t)}|\mathbf{A }^{(t)}$ from the Dirichlet full conditional distribution (e.g., see Culpepper, 2015).

• 3. For $j=1,\ldots ,J$,

  • (a) For $k=1,\ldots ,K$ sample $q_{jk}^{(t)}$ from the Bernoulli full conditional distribution $q_{jk}^{(t)}|{\varvec{\beta }}_j^{(t-1)}, q_{j1}^{(t)},\ldots ,q_{j,k-1}^{(t)},q_{j,k+1}^{(t-1)},\ldots ,q_{jK}^{(t-1)},\omega ^{(t-1)}$ (e.g., see Culpepper, 2019).

  • (b) For $p=1,\ldots ,P$ sample $\beta _{jp}^{(t)}$ from the truncated normal full conditional distribution $\beta _{jp}^{(t)}|Y_{1j}^{*(t)},\ldots ,Y_{nj}^{*(t)},\mathbf A ^{(t)},\beta _{j1}^{(t)},\ldots ,\beta _{j,p-1}^{(t)},\beta _{j,p+1}^{(t-1)},\ldots ,,\beta _{j,P+1}^{(t-1)}, {\varvec{q}}_j^{(t)}$ (e.g., see Culpepper, 2019).

• 4. Sample $\omega ^{(t)}$ from the Beta full conditional distribution $\omega ^{(t)}|\mathbf{Q }^{(t)}$ (e.g., see Culpepper, 2019).