Bayes Factor Covariance Testing in Item Response Models

Abstract

Two marginal one-parameter item response theory models are introduced, by integrating out the latent variable or random item parameter. It is shown that both marginal response models are multivariate (probit) models with a compound symmetry covariance structure. Several common hypotheses concerning the underlying covariance structure are evaluated using (fractional) Bayes factor tests. The support for a unidimensional factor (i.e., assumption of local independence) and differential item functioning are evaluated by testing the covariance components. The posterior distribution of common covariance components is obtained in closed form by transforming latent responses with an orthogonal (Helmert) matrix. This posterior distribution is defined as a shifted-inverse-gamma, thereby introducing a default prior and a balanced prior distribution. Based on that, an MCMC algorithm is described to estimate all model parameters and to compute (fractional) Bayes factor tests. Simulation studies are used to show that the (fractional) Bayes factor tests have good properties for testing the underlying covariance structure of binary response data. The method is illustrated with two real data studies.

1 Introduction

In the one-parameter item response theory (IRT) model, the natural heterogeneity in item responses is modeled through a latent variable and item parameters. This latent variable, also referred to as a random effect (e.g., van der Linden & Hambleton, 1997; Skrondal & Rabe-Hesketh, 2004), represents a person’s effect on the probability of a correct response. Conditional on the latent variable, person’s responses are assumed to be conditionally independently distributed, which is known as the assumption of local or conditional independence. By integrating out the latent variables the item responses can be modeled jointly with a structured covariance matrix. In this paper, a new Bayesian framework is proposed for estimating and testing covariance structures that are induced by latent variables or random item parameters in IRT models.

A marginal item response model is considered, where the latent variable is integrated out. Under this marginal item response model, (fractional) Bayes factor (BF) tests are proposed to make inferences about the dependency structure of item response data. The BF tests can be used to investigate whether a (unidimensional) latent variable can explain the correlation between responses or whether assumptions of local independence hold. The test results can also be used in model building to justify any conditional independence assumptions. For instance, it can provide evidence for a multidimensional scale or verify a testlet (Wainer et al., 2007) or a random item effect structure (e.g., Verhagen & Fox, 2013a). More generally, the proposed method results in a default quantification of the relative evidence in the data between (marginal) IRT models with different covariance structures, without needing subjective proper priors. To the best of our knowledge, there is no method that can do this. The proposed (fractional) BF tests can quantify evidence in favor of a null hypothesis, representing, for instance, the assumption of local independence or (full) measurement invariance. The test method is consistent and will select the true covariance structure with probability one, when the sample size goes to infinity. Furthermore, the method is based on observed data and does not depend on large-sample theory. The quantification of the relative data evidence between two possible IRT models is accurate for any sample size. The description of the method is limited to one-parameter IRT models, but a generalization of the method to more complex IRT models is treated in the discussion.

A new approach is presented to define (fractional) BF tests to investigate the dependency structure of the item response data. Latent responses of the marginal IRT model are transformed in order to obtain the posterior distribution of the covariance parameter in closed form. An orthogonal (Helmert) transformation matrix is used to partition the total sum of squares of the latent responses into between and within-group sum of squares (e.g., Lancaster, 1965). The posterior distribution of the covariance parameter will be referred to as a shifted-inverse-gamma distribution, due to its resemblance with the inverse-gamma distribution. As a result, the resulting low-dimensional integrals, for calculating BFs, are efficiently computed using MCMC. It is shown that the proposed BF methods can also be used to test for random item effects (De Jong et al., 2007; De Boeck, 2008; Fox, 2010; Verhagen & Fox, 2013a, b). In a marginal modeling framework, item responses from group members are more strongly correlated than those from different groups, and this item covariance structure can be directly modeled and tested using the proposed method.

For estimating the parameters, a non-informative improper prior for the covariance parameter is proposed. The BFs can be sensitive to the choice of priors (Kass & Raftery, 1995; Sinharay & Stern, 2002). Therefore, a parameterization is required, which supports the specification of default priors for testing the covariance structure. For the marginal IRT model two default priors are proposed for testing the covariance structure: a fractional Bayes factor (FBF) in combination with an improper (non-informative) reference prior, and a proper balanced prior with a shifted-inverse-gamma distribution, which provides equal weight to positive and negative covariances. The FBF approach of O’Hagan (1995) is used to avoid the dependency of the Bayes factor (BF) on unknown constants due to using an improper prior. The FBF methods are evaluated using simulation studies. It is shown that the proposed methods have good properties for testing the underlying covariance structure of dichotomous item response data. Furthermore, in comparison with the Mantel–Haenszel (MH) test, it is shown that the BF tests have much more power to detect a dependence between item pairs.

In contrast to the proposed marginal approach, estimating the latent variable and making inferences about latent variable variance can be challenging. A random effects variance of zero is often of specific interest, but this point lies on the boundary of the parameter space. Classical test procedures such as the likelihood ratio test can break down (Pauler et al., 1999). In the Bayesian framework, the computation of a marginal likelihood can involve high-dimensional integrals, since a latent variable is assigned to each subject. The integrals are usually not available in closed form, and approximations are required. Laplace integrations and Taylor series approximations are commonly used, but these methods are computationally demanding and lack accuracy (Kass & Raftery, 1995). The Bayesian information criterion (BIC) can be used, but it may fail when the parameter lies on the boundary of the parameter space (Pauler et al., 1999; Hsiao, 1997). It is also not clear how to define the penalty term of the BIC (Spiegelhalter et al., 2002). The BIC is an approximation to the Bayes factor, which is equal to the ratio of marginal distributions of the data for two hypothesis. Saville & Herring (2009) proposed a low-dimensional approximation to the Bayes factor using a Laplace approximation, but they considered a re-parameterization of the linear mixed effect model. This avoids testing parameters on the boundary of the parameter space, but requires the specification of (default) priors for a different parameterization of the model, and it remains an approximation to the Bayes factor test. For the BIC, a normal approximation of the likelihood function is considered, which is typically skewed for covariance parameters, and this approximation is expected to be inaccurate for small sample sizes. The proposed fractional Bayes factor (FBF) tests on the other hand are exact, and no prior information is needed.

Furthermore, Bayesian estimation (MCMC) methods have been proposed to test a latent variable variance (Albert & Chib, 1997; Cai & Dunson, 2006; Kinney & Dunson, 2008; Sinharay & Stern, 2002). They are computationally intensive and rely on subjective prior choices, which specify the degree of support for a random effect. For example, Cai & Dunson (2006) proposed selection-type mixture priors, where a positive probability is assigned to a zero variance of the random effects or to parameters in a decomposition of the random effects covariance. Subsequently, MCMC methods are used to obtain posterior samples from different models, where the mixture prior arranges movements between models. Although multiple models can be compared, the method is generally time-consuming and can lack accuracy in high dimensions. The proposed FBF tests on the other hand are easy to compute, and again (arbitrary) prior specification of the existence of random effects is not needed.

The paper is organized as follows: A marginal IRT model is introduced using a latent response variable. In a similar way, a marginal IRT model with random item effects is introduced. Then, a Helmert transformation of the latent responses is described to define the posterior distribution of the covariance parameter. An MCMC method is described to estimate the model parameters. Subsequently, FBF tests are proposed to test the underlying covariance structure, where different simulation studies are represented to show the good performance of the proposed tests. Two real data studies are given to illustrate the (fractional) BF methods. Finally, a discussion of the results is given.

2 Marginal IRT

Two marginal IRT models are considered. First, the one-parameter IRT model is marginalized with respect to the latent variable using the normal population distribution, which leads to a marginal ability model. This marginal model is used to test the data support for a unidimensional factor structure. Second, the one-parameter IRT model with random difficulty parameters is marginalized with respect to the random item difficulties. This marginal model is referred to as the marginal random difficulty model, which is used to test measurement invariance.

2.1 A Marginal Ability Model

Consider the one-parameter IRT model for dichotomous observations $y_{ij}$, where i refers to respondent $i (i=1,\ldots ,n)$ and j to item $j (j=1,\ldots ,p)$. The probability of a correct response is given by

$$\begin{aligned} P\left( Y_{ij} = 1 \mid \theta _{i}, b_j \right)= & {} \Phi \left( \theta _{i} - b_j\right) . \end{aligned}$$

(1)

Furthermore, the ability parameters are assumed to be normally distributed according to $\theta _{i} \sim \mathcal {N}\left( \mu _{\theta },\tau \right)$. The difficulty parameters also follow a normal distribution given by $b_j \sim \mathcal {N}(\mu _{b},\omega _b^2)$.

The difficulty parameters can be identified, when the $\mu _{\theta }$ equals zero or when the sum of the difficulty parameters is restricted to zero. The $\mu _{\theta }$ is included to explain all model components and to avoid a description of the marginal model under a specific identification restriction. In the simulation study and real data studies, the $\mu _{\theta }$ equals zero to identify the model.

According to the one-parameter IRT model in Equation (1), consider a latent response variable, which is normally distributed and positively (negatively) truncated when the corresponding response equals one (zero). A latent response variable can be defined for the marginal response model by plugging in the population distribution for the ability parameter and merging the error terms in the equation for the latent response variable. To see this, consider the one-parameter IRT model for the latent response and integrate over the population distribution of the ability parameter. It follows that

$$\begin{aligned} Z_{ij}= & {} \theta _{i} - b_j + e_{ij}, \nonumber \\= & {} \mu _{\theta } + e_{\theta _i} - b_j + e_{ij} \nonumber \\= & {} \mu _{\theta } - b_j + \tilde{e}_{ij}, \end{aligned}$$

(2)

where $e_{ij}\sim \mathcal {N}(0,1)$ and $e_{\theta _i}\sim \mathcal {N}(0,\tau )$. The error, $e_{ij}$, in the latent response distribution and the error, $e_{\theta _i}$, of the population distribution of ability are conditionally independently distributed. Therefore, the sum of the error terms, $\tilde{e}_{ij}$, is normally distributed with mean zero and variance $1+\tau$.

The latent responses of person i are no longer independently distributed, since the conditional independence assumption no longer holds for the marginal IRT model, represented in Equation (2). The implied dependency structure, after integrating out the latent variable, follows by considering the covariance between two latent responses, say of person i to item j and of person k to item l. It follows that

$$\begin{aligned} { Cov}\left( Z_{ij},Z_{kl}\right)= & {} { Cov}\left( \mu _{\theta }-b_j + e_{\theta _i} + e_{ij},\mu _{\theta } - b_l + e_{\theta _k} + e_{kl}\right) \nonumber \\= & {} { Cov}\left( e_{\theta _i} + e_{ij},e_{\theta _k} + e_{kl}\right) \nonumber \\= & {} { Cov}\left( e_{\theta _i},e_{\theta _k}\right) + { Cov}\left( e_{ij},e_{kl}\right) \nonumber \\= & {} \left\{ \begin{array}{ll} \tau + 1 &{}\quad \text { if }\,\, i=k,j=l \\ \tau &{} \quad \text { if }\,\, i=k,j\ne l \\ 0 &{} \quad \text { if }\,\, i\ne k. \end{array} \right. \end{aligned}$$

This dependency structure is known as compound symmetry (CS), representing a common covariance between latent responses of each person and a common variance component across item responses.

In a slightly different way, it can be shown directly that after marginalization, a multivariate probit model is obtained. Therefore, consider the IRT model defined in Equation (1) and integrate out the latent variable,

$$\begin{aligned} P\left( Y_{ij}= 1 \mid b_j, \mu _{\theta },\tau \right)= & {} E_{\theta }\left[ \Phi \left( \theta _{i} - b_j \right) \right] \nonumber \\= & {} E_{\theta }\left[ P\left( Z_{ij} \le \theta _{i} - b_j \mid \theta _{i}\right) \right] \nonumber \\= & {} P\left( Z_{ij} + e_{\theta _i} \le \mu _{\theta } - b_j \right) \nonumber \\= & {} \Phi \left( \frac{\mu _{\theta }-b_j}{\sqrt{1+\tau }} \right) , \end{aligned}$$

(3)

where the random error term $e_{\theta _i}$ represents the random difference between the person’s ability, $\theta _i$, and the population average level of ability, $\mu _{\theta }$, which is normally distributed with mean zero and variance $\tau$.

It follows that a latent response variable can be defined for the marginal response model, represented by the marginal success probability given in Equation (3). Let $\varvec{\Sigma }$ be the covariance matrix of the latent responses, which has a compound symmetry (CS) structure. Each latent response vector $\mathbf {z}_i$ is truncated multivariate normally distributed, where the vector lies in the set

$$\begin{aligned} \Omega \left( \mathbf {y}_i \right) = \{\mathbf {z}_i : z_{ij} \le 0\quad \text { if }\,\,y_{ij}= 0,z_{ij} \ge 0 \quad \text { if }\,\, y_{ij}=1 \}. \end{aligned}$$

(4)

The distribution of each response vector $\mathbf {y}_i$ can be expressed as a multivariate probit model. It follows that the marginal response model can be expressed as

$$\begin{aligned} P\left( \mathbf {Y}_{i}=\varvec{y}_{i} \mid \mathbf {b},\mu _{\theta },\varvec{\Sigma } \right) = \int _{\Omega \left( y_{ip} \right) } \ldots \int _{\Omega \left( y_{i1} \right) } \Phi _p\left( \varvec{z}_{i} \mid \varvec{b}, \mu _{\theta }, \varvec{\Sigma }\right) { d}\varvec{z}_{i}. \end{aligned}$$

Albert & Chib (1993), Chib & Greenberg (1998), and Edwards & Allenby (2003) developed a framework for estimation through data augmentation. In a more general data augmentation approach Hoff (2009, chap. 12) showed the estimation of the Gaussian copula model for ordinal data.

2.2 A Marginal Random Item Effect Model

In large-scale surveys, items are often not invariant and may show differential item functioning. Item response models with random item parameters have been developed to account for the random variation in item functioning across clusters (e.g., countries, schools). Following the work of De Jong et al. (2007), De Boeck (2008), Fox (2010), and Verhagen & Fox (2013a, b), in a conditional IRT modeling approach, the random item parameters are considered to be random (item) effects. This random item effect modeling approach has the advantage that items are allowed to be non-invariant and that anchor items are not needed to identify the scale of the latent variable while accounting for group-specific differences in the latent variable.

Verhagen & Fox (2013a) developed BFs to test the hypothesis of invariant items using the random item effect IRT model. They used an encompassing prior modeling approach (Klugkist & Hoijtink, 2007). The prior for the restricted measurement invariant model is constructed by restricting the encompassing prior, representing measurement variance, to the specification of measurement invariance. In this conditional approach, the objective is to evaluate whether the variance parameter, representing the variability in item functioning, equals zero. This parameter value is on the boundary of the parameter space. Therefore, the (item effect) variance parameter is not identified under the measurement invariance hypothesis. By using a null hypothesis representing approximate measurement invariance, the variance parameter is also defined under the null hypothesis.

In a marginal modeling approach, the random item effect variance is represented by the covariance of latent responses of the same cluster (e.g., country and region) to an item. When this covariance parameter is equal to zero, the item responses are not clustered, and the item does not function differently over clusters. A covariance value of zero is not on the boundary of the parameter space, which makes it possible to test differential item functioning given a non-informative prior for the covariance parameter. Furthermore, the random item effect IRT model assumes a population of clusters, and the observed data stem from sampled clusters. In the marginal IRT model, the selection of clusters is not explicitly modeled, only the implied dependency structure.

Let observation $y_{ijg}$ refer to the response of respondent i in cluster g to item j. According to a random item effect IRT model, the conditional success probability is given by

$$\begin{aligned} P\left( Y_{ijg}=1 \mid \theta _{i}, \tilde{b}_{jg} \right)= & {} \Phi \left( \theta _i - \tilde{b}_{jg} \right) , \end{aligned}$$

where the effect of a nesting of respondents in clusters is ignored. The random difficulty parameter $\tilde{b}_{jg}$ is assumed to be normally distributed with mean $b_j$ and variance $\sigma _{b_j}$. Consider the random item effect IRT model for the latent responses, which is marginalized by integrating out the random difficulty parameter. It follows that

$$\begin{aligned} Z_{ijg}= & {} \theta _i - \tilde{b}_{jg} + e_{ijg} \nonumber \\= & {} \theta _i - b_{j} + \epsilon _{b_{jg}} + e_{ijg} \nonumber \\= & {} \theta _i - b_{j} + \tilde{e}_{ijg}, \end{aligned}$$

(5)

where $e_{ijg}\sim \mathcal {N}(0,1)$ and the sum of the error terms is again normally distributed, $\tilde{e}_{ijg} \sim \mathcal {N}(0,1+\sigma _{b_j})$, since both error terms in the sum are independently distributed. In relation to the marginal ability model, the difficulty parameters can be identified by restricting the $\mu _{\theta }$ or the sum of the difficulty parameters to zero. When estimating the model parameters, the $\mu _{\theta }$ is restricted to zero.

The implied dependency structure by integrating out the random difficulty parameter follows by considering two responses to the same item j; that is,

$$\begin{aligned} { Cov}\left( Z_{ijg},Z_{kjl}\right)= & {} { Cov}\left( \theta _i - b_{j} + \epsilon _{b_{jg}} + e_{ijg},\theta _k - b_{j} + \epsilon _{b_{jl}} + e_{kjl}\right) \nonumber \\= & {} { Cov}\left( \epsilon _{b_{jg}} + e_{ijg},\epsilon _{b_{jl}} + e_{kjl}\right) \nonumber \\= & {} { Cov}\left( \epsilon _{b_{jg}},\epsilon _{b_{jl}}\right) + { Cov}\left( e_{ijg},e_{kjl}\right) \nonumber \\= & {} \left\{ \begin{array}{ll} \sigma _{b_j} + 1 &{}\quad \text { if }\,\, g=l, i=k \\ \sigma _{b_j} &{} \quad \text { if }\,\, g=l, i\ne k \\ 0 &{} \quad \text { if }\,\, g\ne l. \end{array} \right. \end{aligned}$$

Within each cluster g, a common covariance between responses to the same item is specified, which can be recognized as a CS covariance structure.

The marginal probability of success is equal to the expected conditional success probability, and it follows that

$$\begin{aligned} P\left( Y_{ijg}=1 \mid \theta _i, b_j, \sigma _{b_j}\right)= & {} E\left( \Phi \left( \theta _i - \tilde{b}_{jg} \right) \right) \nonumber \\= & {} E\left( P\left( Z_{ijg} \le \theta _i - \tilde{b}_{jg} \mid \tilde{b}_{jg} \right) \right) \nonumber \\= & {} P\left( Z_{ijg} + \epsilon _{b_{jg}} \le \theta _i - b_{j} \right) \nonumber \\= & {} \Phi \left( \frac{\theta _i - b_{j}}{\sqrt{1+\sigma _{b_{j}}}} \right) . \end{aligned}$$

(6)

The marginal IRT model, represented by Equation (6), is again a normal ogive IRT model. It follows that each vector of latent continuous responses to item j of cluster g is multivariate normally distributed with mean $\varvec{\theta }_g-b_{j}$ and a CS covariance matrix with non-diagonal elements equal to $\sigma _{b_j}$ and diagonal elements $1 + \sigma _{b_j}$. Subsequently, the distribution of $\mathbf {y}_{jg}$ can be expressed as a multivariate probit while taking into account the region of support similar to Equation (4).

3 Posterior Distribution of the CS Parameter

To make inferences about the dependency structure under the marginal IRT model, interest is focused on the covariance parameter. As shown in Equation (2) and Equation (5), the marginal IRT model for the latent responses can be represented as a multivariate probit with a CS covariance structure. The object is to define a prior and posterior distribution for the covariance parameter and to define a (fractional) BF test for evaluating the dependency structure. It will be shown that after an orthogonal transformation of the latent responses, the posterior distribution of the covariance parameter can be obtained in closed form.

To explain the methodology, consider multivariate normally distributed random variable $\mathbf {z}_i=(z_{i1},\ldots ,z_{ip})^t \sim \mathcal {N}\left( \mu \mathbf 1 _p,\varvec{\Sigma }\right)$ for $i=1,\ldots ,n$. It is assumed that the covariance matrix has a compound symmetry structure and is represented by $\varvec{\Sigma }=\sigma ^2 \mathbf {I}_p + \tau \mathbf {J}_p$, which equals

$$\begin{aligned} \mathbf {\varvec{\Sigma }} = \left[ \begin{array}{ccccc} \sigma ^2+\tau &{} \tau &{} \cdots &{} \tau \\ \tau &{} \sigma ^2+\tau &{} \cdots &{} \tau \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \tau &{} \tau &{} \cdots &{} \sigma ^2 + \tau \\ \end{array} \right] . \end{aligned}$$

(7)

An orthogonal matrix, represented by $\mathbf {H}$, can be used to partition the sum of squares of a vector of p observations, $\mathbf {z}$, into components of sums of squares. The total sum of squares remains the same after an orthogonal transformation, since $\mathbf {z}^t\mathbf {z} = \mathbf {z}^t \mathbf {H}^t \mathbf {H}\mathbf {z}=\mathbf {z}^t \mathbf {I}\mathbf {z}$. In “Appendix A,” the properties of the orthogonal Helmert matrix are shown, which will be used to derive the posterior of the CS parameters.

When applying the Helmert transformation, $\tilde{\mathbf {z}}_i = \mathbf {H}\mathbf {z}_i$, the first component of the Helmert transformed random variables, $\tilde{\mathbf {z}}_i$, is normally distributed with mean $\sqrt{p}\mu$ and variance $\sigma ^2 + p\tau$. The remaining components are independently normally distributed with mean zero and variance $\sigma ^2$. This is shown in “Appendix B.”

Consider n repeated observations on a p-variate random variable, which are stored in a matrix $\mathbf {z}=(\mathbf {z}_1,\ldots ,\mathbf {z}_n)$ of dimension p by n. Each column of $\mathbf {z}$ is assumed to be p-variate distributed with mean $\mu$ and variance $\varvec{\Sigma }$. Let $\tilde{\mathbf {z}}$ denote the Helmert transformed representation of $\mathbf {z}$, which follows from $\tilde{\mathbf {z}}=\mathbf {H}\mathbf {z}$. From “Appendix B” follows that the conditional distribution of the first row of $\tilde{\mathbf {z}}, \tilde{\mathbf {z}}_{1} = (\tilde{z}_{11},\ldots ,\tilde{z}_{n1})=(\sqrt{p}\bar{z}_{1}, \ldots ,\sqrt{p}\bar{z}_{n})$ is given by

$$\begin{aligned} p\left( \tilde{\mathbf {z}}_{1} \mid \mu ,\sigma ^2,\tau \right) = p^{-n/2}\left( 2\pi (\sigma ^2/p+ \tau )\right) ^{-n/2}\exp \left( \frac{-S^2_B/2}{(\sigma ^2/p + \tau )} \right) , \end{aligned}$$

(8)

where $S_B^2=\sum _{i=1}^n\left( \overline{z}_i - \mu \right) ^2$ is the between-group sum of squares.

From the expression in Equation (8), it follows that the term $\sigma ^2/p + \tau$ is restricted to be positive. As a result, $\tau$ is greater than $-\sigma ^2/p$ (with $\sigma ^2/p$ restricted to be positive) and the covariance parameter is restricted to the interval $\tau \in \left( -\sigma ^2/p,\infty \right)$. Thus, when considering the IRT model in Equation (1), the ability parameter is assumed to be normally distributed with variance $\tau >0$. This causes the observations in the response patterns of each individual to be positively correlated. When integrating out the ability parameter, a marginal model is obtained (Equation (2)), where $\tau$ has become a covariance parameter in the compound symmetry covariance matrix (Equation (7)). In this alternative representation, it is possible to loosen the restriction on $\tau$, from $\tau > 0$ to $\tau > -\sigma ^2/p$. However, only when $\tau >0$, the IRT model and the marginal IRT model are equivalent; when $\tau =0$ or $-\sigma ^2/p<\tau <0$, the item responses are not nested within individuals (i.e., the data do not have a multilevel structure).

Hence, three different covariance structures can be identified depending on the sign of the covariance parameter. When $\tau >0$, there is a common positive covariance between the observations of each p-variate random variable $\mathbf {z}_i$, and this covariance structure can be described by a latent variable with a variance of $\tau$. When $\tau =0$, the observations of each p-variate random variable $\mathbf {z}_i$ are independently distributed with variance $\sigma ^2$. When introducing a latent variable, its variance would be equal to zero, since the observations are independently distributed.

When the covariance parameter is negative, $-\sigma ^2/p<\tau <0$, the mean response-pattern scores, $\overline{z}_i$, show even less variation than the variation in mean scores of patterns with independently generated responses, which corresponds to the situation with $\tau =0$. This means that in the distribution of $\mathbf {z}_i$ in Equation (8), the between-group sum of squares, $S_B^2$, representing the sample heterogeneity among response patterns, would be even lower than the one for $\tau =0$, when there is no heterogeneity across response patterns. A negative correlation between responses implies that those observations do not share any common information, which would be necessary to measure a latent variable. In scale analysis, the negative covariance between responses cannot lead to the measurement of a latent variable, since the latent variable always implies a positive covariance between responses. The marginal model, after integrating out the latent variable, represents a wider parameter space for $\tau$, including a negative support. This property proves to be beneficial for constructing conditionally conjugate priors for $\tau$, and for evaluating hypotheses on $\tau$, which will be discussed below.

3.1 Marginal Ability Model

Given the model in Equation (2), interest is focused on the posterior distribution of the covariance parameter $\tau$. This posterior can be analytically derived given the Helmert transformed observations.

A non-informative reference prior for $\tau$ can be derived according to Jeffreys’ rule, which states that the prior is chosen proportional to the square root of Fisher’s information measure. In the multivariate probit model, $\sigma ^2=1$ to identify the model. Using the likelihood for $\tau$ in Equation (8), it can be shown that the information measure is equal to

$$\begin{aligned} E\left( \frac{d \log p\left( \tilde{\mathbf {z}}_{1} \mid \mu , \tau \right) }{d \tau }\right) ^2 \propto \left( p^{-1}+\tau \right) ^{-2}, \end{aligned}$$

where the expectation is taken with respect to the distribution $p\left( \tilde{\mathbf {z}}_{1} \mid \mu , \tau \right)$.

It follows that the non-informative reference prior is given by

$$\begin{aligned} p\left( \tau \right) \propto \left( p^{-1} + \tau \right) ^{-1}. \end{aligned}$$

(9)

Box & Tiao (1973, chap. 5) also considered this prior for the variance parameter of a random effect and considered extensions to describe a multiparameter prior.

Given the prior in Equation (9), the posterior distribution of parameter $\tau$ can be expressed as

$$\begin{aligned} p\left( \tau \mid \tilde{\mathbf {z}}_1,\mu \right)= & {} c \left( p^{-1}+ \tau \right) ^{-(n/2+1)}\exp \left( \frac{-S^2_B/2}{p^{-1} + \tau } \right) , \end{aligned}$$

(10)

where $S^2_B = \sum _i \left( \overline{z}_{i} - \left( \mu _{\theta }-\overline{b}\right) \right) ^2$ and $\overline{b}=\sum _j b_j/p$. The kernel of the posterior resembles the inverse-gamma distribution, but the $\tau$ is shifted downward by 1 / p. The normalizing constant can be computed using the kernel representation of the inverse-gamma distribution while taking into account that $\tau +1/p > 0$,

$$\begin{aligned} c^{-1}= & {} \int _{\tau =-1/p}^{\infty } \left( p^{-1}+ \tau \right) ^{-(n/2+1)}\exp \left( \frac{-S^2_B/2}{p^{-1} + \tau } \right) d\tau \\= & {} \int _{\lambda =0}^{\infty } \lambda ^{-(n/2+1)}\exp \left( \frac{-S^2_B/2}{\lambda } \right) d \lambda \\= & {} \frac{\Gamma (n/2)}{(S^2_B/2)^{n/2}}. \end{aligned}$$

The posterior of $\tau$ will be referred to as a shifted-inverse-gamma distribution, due to its resemblance with the inverse-gamma distribution except for the shift operation. The shifted-inverse-gamma density can be expressed as

$$\begin{aligned} p\left( \tau ; \alpha ,\beta ,\gamma \right)= & {} \frac{\beta ^{\alpha }}{\Gamma (\alpha )}\left( \tau +\gamma \right) ^{(-\alpha -1)}\exp \left( \frac{-\beta }{\tau +\gamma } \right) , \end{aligned}$$

(11)

with shape parameter $\alpha$, scale parameter $\beta$, and location (shift) parameter $\gamma$. The density function is defined over the support $\tau > -\gamma$ with $\gamma >0$. The density function will also be referred to as $\text{ shifted- }\mathcal {IG}\left( \alpha ,\beta ,\gamma \right)$.

As a result, the posterior distribution of $\tau$ given $\tilde{\mathbf {z}}_1$ in Equation (10) can be stated as a shifted-$\mathcal {IG}\left( \frac{n}{2},\frac{S_B^2}{2},\frac{1}{p}\right)$. If $\tau$ has a shifted-inverse-gamma distribution, then $1/(\tau +\gamma )$ has a gamma distribution. This relationship can be used to express the cumulative distribution function (CDF) of the shifted-inverse-gamma in terms of the CDF of the gamma distribution and, subsequently, as an incomplete gamma function.

The CDF of the shifted-$\mathcal {IG}\left( \alpha =\frac{n}{2},\beta =\frac{S_B^2}{2},\gamma =\frac{1}{p}\right)$ can be expressed as

$$\begin{aligned} P\left( \tau \le x \mid \alpha ,\beta ,\gamma \right)= & {} \frac{\beta ^{\alpha }}{\Gamma (\alpha )}\int _{-\gamma }^{x}\left( \tau +\gamma \right) ^{-\alpha -1}e^{-\beta /(\tau +\gamma )}d\tau \nonumber \\= & {} \frac{\beta ^{\alpha }}{\Gamma (\alpha )}\int _{0}^{x+\gamma }t^{-\alpha -1}e^{-\beta /t}dt (t = \gamma +\tau )\nonumber \\= & {} \frac{\beta ^{\alpha }}{\Gamma (\alpha )}\int _{\frac{1}{x+\gamma }}^{\infty } v^{\alpha -1}e^{-\beta v}dv (v = 1/t) \nonumber \\= & {} \frac{\phi \left( \alpha ,\beta /(x+\gamma )\right) }{\Gamma (\alpha )}, \end{aligned}$$

(12)

where $\phi \left( \alpha ,\beta /(x+\gamma ) \right)$ denotes the upper incomplete gamma function with parameters $\alpha$ and lower integration bound $\beta /(x+\gamma )$.

Furthermore, in Equation (12) the CDF of the shifted-inverse-gamma is expressed in terms of the CDF of the gamma distribution, since $v=1/(\tau + \gamma )$ is gamma distributed with shape parameter $\alpha$ and rate parameter $\beta$. To make this more explicit, let $G(\alpha ,\beta )$ denote the CDF of the gamma distribution with shape parameter $\alpha$ and rate parameter $\beta$. Let $v=(\tau +\gamma )^{-1}$ be gamma distributed. Then, from Equation (12) follows that

$$\begin{aligned} P\left( \tau \le x \mid \alpha ,\beta ,\gamma \right)= & {} P\left( v \ge \frac{1}{x+\gamma } \mid \alpha ,\beta ,\gamma \right) \nonumber \\= & {} 1 - \frac{\beta ^{\alpha }}{\Gamma (\alpha )}\int _{0}^{\frac{1}{x+\gamma }} v^{\alpha -1} e^{-\beta v} dv \nonumber \\= & {} 1 - G\left( \frac{1}{x+\gamma };\alpha ,\beta \right) . \end{aligned}$$

(13)

Thus, the CDF of the shifted-$\mathcal {IG}\left( \frac{n}{2},\frac{S_B^2}{2},\frac{1}{p}\right)$, represented by $F\left( \tau ; \frac{n}{2},\frac{S_B^2}{2},\frac{1}{p}\right)$, can be expressed by the CDF of the gamma distribution represented by $G\left( \frac{1}{\tau +p^{-1}}; \frac{n}{2},\frac{S_B^2}{2}\right)$, where $\frac{S_B^2}{2}$ is the rate parameter.

3.1.1 A Balanced Prior Approach

Besides the improper prior defined in Equation (9), a balanced (proper) prior is defined, which has the key property that the prior probability of a negative effect is equal to the prior probability of a positive effect, i.e., $P\left( \tau <0 \mid H_u\right) =P\left( \tau > 0 \mid H_u\right) =.5$ where $H_u:\tau \ne 0$. The balanced prior originally dates back to Jeffreys (1961). The use of a balanced prior is recommended when testing hypotheses with inequality constraints, such as one-sided tests (e.g., Mulder et al., 2010).

Here, a balanced prior is proposed for testing the covariance parameter $\tau$. Let $p(\tau ; \alpha ,\beta _0,\gamma )$ be a shifted-inverse-gamma balanced prior with shape parameter $\alpha =1/2$ and shift parameter $\gamma =p^{-1}$. The scale parameter $\beta _0$ can be derived from the balanced informative property of the prior. It follows that

$$\begin{aligned} P\left( \tau \le 0 \mid \beta _0, \gamma \right)= & {} \frac{1}{\Gamma \left( \frac{1}{2}\right) } \int _{\frac{\beta _0}{\gamma }}^{\infty } v^{\frac{1}{2}-1}\exp (-v)dv \\= & {} \frac{2}{\sqrt{2\pi }}\int _{\left( \frac{2\beta _0}{\gamma }\right) ^{\frac{1}{2}}}^{\infty } \exp \left( -\frac{w^2}{2}\right) dw (v = w^2/2) \\= & {} 2\left( 1-\Phi \left( \frac{2\beta _0}{\gamma }\right) ^{\frac{1}{2}}\right) = \frac{1}{2}. \end{aligned}$$

The prior’s shape parameter $\beta _0$ can be solved from the last equation, and $\beta _0=\frac{\Phi ^{-1}\left( \frac{3}{4}\right) ^{2}}{2p}$, where $\Phi ^{-1}(.)$ is the inverse of the cumulative normal distribution function.

3.2 Marginal Random Difficulty Model

Consider the truncated multivariate distribution of $\mathbf {z}_{jg} \sim N\left( \varvec{\theta }_{g} - b_{j},\varvec{\Sigma }\right)$, where $\varvec{\theta }_{g}=(\theta _{1g},\ldots ,\theta _{mg})^t$, according to the model in Equation (6). Here, the posterior distribution of the covariance parameter $\sigma _{b_j}$ is of specific interest. It follows that each vector of latent continuous responses to item j of cluster g is multivariate normally distributed with mean $\varvec{\theta }_g-b_{j}$ and a CS covariance matrix, $\varvec{\Sigma }$ with non-diagonal elements equal to $\sigma _{b_j}$ and diagonal elements $1 + \sigma _{b_j}$. Subsequently, the distribution of $\mathbf {z}_{jg}$ can be expressed as a multivariate probit model while taking into account the region of support similar to Equation (4).

Let $\tilde{\mathbf {z}}_{j1}$ represent the first component of the Helmert transformed latent response data, $\mathbf {H}\,\mathbf {z}_{jg}$ $\left( g=1,\ldots ,G\right)$. This Helmert transformed latent response vector contains the information about the covariance parameter $\sigma _{b_j}$, and the conditional distribution of $\tilde{\mathbf {z}}_{j1}$ is represented by

$$\begin{aligned} p\left( \tilde{\mathbf {z}}_{j1} \mid \varvec{\theta }, b_j, \sigma _{b_j} \right)\propto & {} (1/m + \sigma _{b_j})^{-G/2}\exp \left( \frac{-S^2_B}{2(1/m + \sigma _{b_j})} \right) , \end{aligned}$$

(14)

where $S_B^2=\sum _{g=1}^{G} \left( \overline{z}_{jg} - \mu _g \right) ^2$ is the between-group sum of squares, with $\mu _g=\overline{\theta }_g - b_j$, with $\sigma _{b_j} > -1/m$, where m is the common cluster size and $\overline{\theta }_g$ the average score in group g. The posterior distribution for $\sigma _{b_j}$ is a $\text{ shifted- }\mathcal {IG}\left( G/2,S^2_B/2,1/m \right)$, when using a non-informative reference prior.

4 MCMC Method

Given the latent response data, the population parameters and the item parameters can be directly sampled from their full conditional distributions using results from the multivariate normal model. However, the covariance matrix has a specific structure, and it is not correct to use an inverse-Wishart distribution as a prior, which assumes an unrestricted covariance matrix. Azevedo et al. (2016) developed a general MCMC algorithm to sample from a multivariate normal distribution with a restricted covariance matrix. In this approach, a non-informative prior is specified for the unrestricted covariance matrix, and priors are not directly specified for the parameters of the restricted covariance matrix. In the present approach, a non-informative reference prior for $\tau$ is specified while taking into account the CS structure of the covariance matrix.

Consider the marginal ability model, Equation (2), where the augmented data are multivariate normally distributed, $\mathbf {z}_i \sim N(\mu _{\theta } - \mathbf {b},\varvec{\Sigma })$. Then, the conditional distribution of the augmented data $\mathbf {z}$ can be simplified, since the inverse of the CS matrix can be obtained in closed form (Fox, 2010, pp. 151–152). Let $\mathbf {z}_{i,-j}$ denote the vector of augmented responses of subject i excluding the jth response. Furthermore, for covariance matrix $\varvec{\Sigma } = \mathbf {I}_p + \tau \mathbf {J}_p$, let $\varvec{\Sigma }_{j,-j} = \tau \mathbf {1}^t_{p-1}$ denote the jth row of the covariance matrix excluding the jth value, and let $\varvec{\Sigma }_{-j,-j} = \mathbf {I}_{p-1} + \tau \mathbf {J}_{p-1}$ denote the covariance matrix excluding row j and column j. The conditional distribution of $z_{ij}$ given $\mathbf {z}_{i,-j}$ is normal with mean

$$\begin{aligned} E\left( z_{ij} \mid \varvec{\Sigma }, \mathbf {z}_{i,-j},\mu _{\theta },\mathbf {b}\right)= & {} \mu _{\theta } - b_j +\varvec{\Sigma }_{j,-j} \varvec{\Sigma }^{-1}_{-j,-j}\left( \mathbf {z}_{i,-j}- \varvec{\mu }_{-j}\right) \nonumber \\= & {} \mu _{\theta } - b_j +\tau \varvec{1}^t_{p-1}\left( \tau \mathbf {J}_{p-1}+\mathbf {I}_{p-1}\right) ^{-1} \left( \mathbf {z}_{i,-j} - \varvec{\mu }_{-j}\right) \nonumber \\= & {} \mu _{\theta } - b_j +\frac{\tau }{1+(p-1)\tau }\varvec{1}^t_{p-1}\left( \mathbf {z}_{i,-j}- \varvec{\mu }_{-j}\right) , \end{aligned}$$

(15)

where $\varvec{\mu }_{-j} =\mu _{\theta }-\mathbf {b}_{-j}$, and variance

$$\begin{aligned} { Var}\left( z_{ij} \mid \varvec{\Sigma },\mathbf {z}_{i,-j}\right)= & {} \Sigma _{j,j} - \varvec{\Sigma }_{j,-j}\varvec{\Sigma }^{-1}_{-j,-j}\varvec{\Sigma }_{-j,j} \nonumber \\= & {} \frac{1+p\tau }{1+(p-1)\tau }. \end{aligned}$$

(16)

When conditioning on the information that $\mathbf {z}\in \varvec{\Omega }(\varvec{y})$, Equation (4), the components of variable $\mathbf {z}_i$ are independently (truncated) normally distributed with each mean and variance given in Equation (15) and (16), respectively.

Given the latent response data, $\mathbf {z}$, the remaining parameters can be sampled directly from their full conditionals. The conditional posterior distribution of each item parameter j is normally distributed with mean

$$\begin{aligned} E\left( b_j\mid \mathbf {z}_j,\tau ,\mu _b,\omega _b^2\right)= & {} \left( \frac{n}{\tau +1} + \frac{1}{\omega ^2_b}\right) ^{-1}\left( \frac{n\left( -\overline{z}_j+\mu _{\theta }\right) }{\tau +1} + \frac{\mu _b}{\omega ^2_b}\right) \end{aligned}$$

(17)

and variance

$$\begin{aligned} { Var}\left( b_j\mid \mathbf {z}_j,\tau ,\mu _b,\omega _b^2\right)= & {} \left( \frac{n}{\tau +1} + \frac{1}{\omega ^2_b}\right) ^{-1}. \end{aligned}$$

(18)

According to the identification constraint, hyperprior parameter $\mu _{\theta }$ is restricted to 0. The $\mu _b$ and $\omega ^2_b$ are given a normal-inverse-gamma prior, and the posterior distributions are given by, respectively,

$$\begin{aligned} \mu _b \mid \omega ^2_{b},\mathbf {b}\sim & {} \mathcal {N}\left( \frac{p_0}{p+p_0}\mu _{0}+\frac{p}{p+p_0}\overline{b},\frac{\omega ^2_b}{p+p_0}\right) \end{aligned}$$

(19)

$$\begin{aligned} \omega ^2_{b} \mid \mathbf {b}\sim & {} \mathcal {IG}\left( g_1 +\frac{p}{2},g_2+\frac{SS}{2}\right) , \end{aligned}$$

(20)

where scale parameter $SS=\sum _j\left( b_j-\overline{b} \right) ^2 + \frac{p\,p_0}{p+p_0}\left( \overline{b} -\mu _{0} \right) ^2$ and $\overline{b}=\sum _j b_j/p$.

Let $\tilde{\mathbf {z}}_{1}$ denote the first components of the Helmert transformed representation of the augmented variable $\mathbf {z}$. The between-group sum of squares can be expressed in terms of the Helmert transformed data and the latent response data $\mathbf {z}$ (“Appendix A”). It follows that

$$\begin{aligned} pS^2_B= & {} \sum _i \left( \tilde{z}_{i1} - \sqrt{p}(\mu _{\theta }-\overline{b}) \right) ^2 \nonumber \\= & {} p\sum _i \left( \overline{z}_i - (\mu _{\theta }-\overline{b}) \right) ^2, \end{aligned}$$

(21)

where $\overline{b}=\sum _j b_j/p$. The posterior distribution of $\tau$ is a shifted-$\mathcal {IG}(n/2,S_B^2/2,1/p)$ according to Equation (10). Values can be sampled from the shifted-$\mathcal {IG}$ using a variable transformation. At MCMC iteration l, sample $\lambda ^{(l)}=\tau +1/p$ from the inverse-gamma distribution, $\mathcal {IG}(n/2,S_B^2/2)$, to obtain a draw $\tau ^{(l)}=\lambda ^{(l)} - 1/p$.

For the marginal random item effect model, the distribution of the transformed latent response data is given in Equation (14). Values can be drawn from the posterior distribution of $\sigma _{b_j}$, which is a shifted-$\mathcal {IG}$. At MCMC iteration l, sample $\sigma ^{(l)}=\sigma _{b_j} + 1/m$ from the inverse-gamma distribution, $\mathcal {IG}(G/2,S_B^2/2)$, to obtain a draw $\sigma _{b_j}^{(l)}=\sigma ^{(l)} - 1/m$.

5 Fractional Bayes

To evaluate the assumption of local independence, the implied covariance structure is evaluated under the marginal ability model, as given by Equation (3). Several hypotheses will be of specific interest. The hypothesis $H_0: \tau =0$ assumes that the response observations of a person are uncorrelated. Under this null hypothesis, there is no latent variable which explains the correlation between responses. The hypothesis $H_1: \tau < 0$ states that the covariance between responses is less than zero. It is theoretically possible that the responses of a pattern show less correlation than expected under a random assignment of responses to response patterns. The unrestricted hypothesis $H_2 : \tau > 0$ states that there is a common positive covariance between a subject’s responses, which implies that a unidimensional latent variable can explain the correlation between responses. Finally, let $H_u : \tau \ne 0$ define the unrestricted hypothesis for $\tau$.

To determine which hypothesis is mostly supported by the data, the marginal distribution of the data under each hypothesis needs to be computed. This marginal distribution of the data represents the support of the data for the hypothesis.

For hypothesis $H_t$ $(t \in 0,1,2 \text { or }u)$, the marginal distribution of the response pattern of person i is represented by

$$\begin{aligned} p\left( \mathbf {y}_i \mid H_t\right)= & {} \int _{\mathbf {z}_i \in \Omega (\mathbf {y}_i)} p\left( \mathbf {z}_i \mid H_t\right) d \mathbf {z}_i\\= & {} \int _{\mathbf {z}_i \in \Omega (\mathbf {y}_i)} \int _{\tau \in H_t} p\left( \mathbf {z}_i \mid \tau , H_t\right) p(\tau \mid H_t)d\tau d \mathbf {z}_i, \end{aligned}$$

where $p(\tau \mid H_0)$ has a point mass at $\tau =0$. The $\Omega (\mathbf {y}_i)$ defines the set for each latent response vector $\mathbf {z}_i$, according to Equation (4).

When considering the improper prior for $\tau$, Equation (9), the marginal distribution of the data is proportional to a unknown normalizing constant. If improper priors are specified under both hypotheses, the ratio of marginal distributions will depend on the ratio of two unknown normalizing constants.

To avoid the dependency of the BF on unknown constants, the fractional Bayes factor approach of O’Hagan (1995) is followed. The marginal distribution of the data under the hypothesis will be normalized using a minimal information sample. Therefore, the marginal distribution is divided by the marginal distribution taken to the power of s, where s denotes the minimal (likelihood) information to deal with the improper prior. It follows that

$$\begin{aligned} m_0\left( \mathbf {y},s \right)= & {} \frac{\int _{\mathbf {z} \in \Omega (\mathbf {y})} \int _{\tau \in H_0} p\left( \mathbf {z} \mid \tau , H_0\right) p(\tau \mid H_0)d\tau d \mathbf {z}}{\int _{\mathbf {z} \in \Omega (\mathbf {y})} \int _{\tau \in H_0} p\left( \mathbf {z} \mid \tau , H_0\right) ^{s}p(\tau \mid H_0)d\tau d \mathbf {z}}, \end{aligned}$$

and subsequently, the FBF can be defined as

$$\begin{aligned} B_{0u}^F = \frac{m_0(\mathbf {y},s)}{m_u(\mathbf {y},s)} =\frac{\int _{\mathbf {z} \in \Omega (\mathbf {y})} m_0(\mathbf {z},s)d \mathbf {z}}{\int _{\mathbf {z} \in \Omega (\mathbf {y})} m_u(\mathbf {z},s)d \mathbf {z}} , \end{aligned}$$

(22)

where $m_u(\mathbf {y},s)$ is the normalized marginal distribution of the data under hypothesis $H_u:$ $\tau \ne 0$.

The marginal distribution under the unconstrained hypothesis can be obtained using the Helmert transformation such that $(\tilde{\mathbf {z}}_{2},\ldots ,\tilde{\mathbf {z}}_{p})$ are independently normally distributed and $\tau$ given $\tilde{\mathbf {z}}_{1}$ is shifted-inverse-gamma distributed. Let $s=1/n$ to deal with the improper prior for $\tau$; subsequently, the denominator in the $BF^F_{0u}$ can be expressed as

$$\begin{aligned} m_u(\mathbf {z},s=n^{-1})= & {} \frac{p\left( \tilde{\mathbf {z}}_{2},\ldots ,\tilde{\mathbf {z}}_{p} \mid \mathbf {b} \right) \int _{\tau \in H_u} p\left( \tilde{\mathbf {z}}_{1}\mid \tau , \mathbf {b}, H_u\right) p(\tau )d\tau }{\int _{\tau \in H_u}p\left( \tilde{\mathbf {z}}_{1}\mid \tau , \mathbf {b}, H_u\right) ^{1/n}p(\tau )d\tau } \\= & {} (2\pi )^{\frac{-n(p-1)}{2}}\exp \left( -S^2_W/2\right) \frac{\int _{\tau \in H_u} p\left( \tilde{\mathbf {z}}_{1}\mid \tau , \mathbf {b}, H_u\right) p(\tau )d\tau }{\int _{\tau \in H_u}p\left( \tilde{\mathbf {z}}_{1}\mid \tau , \mathbf {b}, H_u\right) ^{1/n}p(\tau )d\tau } \\= & {} (2\pi )^{\frac{-(np-1)}{2}}\exp \left( -S^2_W/2\right) \frac{\Gamma (n/2) \left( p\left( S^2_B/2\right) \right) ^{-n/2}}{\Gamma (1/2)\left( p\left( S^2_B/2n\right) \right) ^{-1/2}}, \end{aligned}$$

where $S^2_W=\sum _{i=1}^{n}\sum _{j=1}^{p} \left( z_{ij}-\overline{z}_i\right) ^2$.

Both integrals were solved using the fact that the kernel of the posterior distribution of $\tau$ resembles the inverse-gamma distribution. The numerator of the FBF in Equation (22) can be obtained directly. It follows that

$$\begin{aligned} m_0(\mathbf {z},s=n^{-1})= & {} \frac{p\left( \tilde{\mathbf {z}}_{2},\ldots ,\tilde{\mathbf {z}}_{p} \mid \mathbf {b}, \right) p\left( \tilde{\mathbf {z}}_{1}\mid \tau , \mathbf {b}, H_0\right) }{p\left( \tilde{\mathbf {z}}_{1}\mid \tau , \mathbf {b}, H_0\right) ^{1/n}} \\= & {} \frac{(2\pi )^{\frac{-np}{2}}\exp \left( -\frac{1}{2}\left( S^2_W + p S^2_B\right) \right) }{(2\pi )^{\frac{-1}{2}}\exp \left( -p S^2_B/2n\right) } \\= & {} (2\pi )^{\frac{-(np-1)}{2}}\exp \left( -\frac{1}{2}\left( S^2_W + p S^2_B\left( 1-\frac{1}{n}\right) \right) \right) , \end{aligned}$$

which represents the marginal distribution of the data for $\tau =0$. The minimum information sample of $s=n^{-1}$ is used to define a normalizing constant for the improper prior for $\tau$.

The FBF defined in Equation (22) can be expressed as,

$$\begin{aligned} B_{0u}^F = \frac{m_0(\mathbf {y},s)}{m_u(\mathbf {y},s)} = \frac{\Gamma \left( \frac{1}{2}\right) }{\Gamma \left( \frac{n}{2}\right) }\int _{\mathbf {z} \in \Omega (\mathbf {y})} \frac{\exp \left( -\frac{1}{2}\left( pS^2_B\left( 1-\frac{1}{n}\right) \right) \right) }{ \left( p\left( S^2_B/2\right) \right) )^{-n/2}\left( p\left( S^2_B/(2n)\right) \right) ^{1/2}}d \mathbf {z}, \end{aligned}$$

(23)

where the integrand can be evaluated as a closed expression in the MCMC algorithm for the marginal ability model.

In the same way, the FBF to evaluate hypothesis $H_2: \tau >0$ to $H_u: \tau \ne 0$ can be derived. The terms of the unrestricted marginal distribution of the data cancel out, and the FBF can be expressed in terms of the CDF of the shifted-inverse-gamma distribution, and according to Equation (13), also in terms of the CDF of the gamma distribution. Subsequently, the $B^F_{2u}$ equals

$$\begin{aligned} B^F_{2u} = \frac{m_2(\mathbf {y},s)}{m_u(\mathbf {y},s)}= & {} \int _{\mathbf {z} \in \Omega (\mathbf {y})}\frac{1-F\left( n/2,S^2_B/2,1/p \right) }{1-F\left( 1/2,S^2_B/2n,1/p \right) } d \mathbf {z}. \end{aligned}$$

The restriction of $\tau < 0$ referred to as hypothesis $H_1$ compared to $H_u$ leads to a comparable FBF. In this case, a ratio of cumulative probabilities is evaluated of $\tau$ assigned to the interval $\left( -1/p,0\right)$,

$$\begin{aligned} B^F_{1u} = \frac{m_1(\mathbf {y},s)}{m_u(\mathbf {y},s)}= & {} \int _{\mathbf {z} \in \Omega (\mathbf {y})}\frac{F\left( n/2,S^2_B/2,1/p \right) }{F\left( 1/2,S^2_B/2n,1/p \right) } d \mathbf {z}. \end{aligned}$$

The ratio of both FBFs can be used to evaluate the hypothesis $H_1:\tau < 0$ to $H_2: \tau > 0$, which equals

$$\begin{aligned} B^F_{12} = \frac{m_1(\mathbf {y},s)}{m_2(\mathbf {y},s)}= & {} \int _{\mathbf {z} \in \Omega (\mathbf {y})} \frac{F\left( n/2,S^2_B/2,1/p \right) }{F\left( 1/2,S^2_B/2n,1/p \right) }\left[ \frac{1-F\left( 1/2,S^2_B/2n,1/p \right) }{1-F\left( n/2,S^2_B/2,1/p \right) }\right] d \mathbf {z}. \end{aligned}$$

Note that it would also be possible to compute the ratio of posterior probabilities of $\tau <0$ to $\tau >0$, but this would assume that $\tau \ne 0$. In this case, the multiple hypothesis testing problem is considered to evaluate $\tau =0$ versus $\tau <0$, and versus $\tau >0$.

6 Simulation Studies

First, a parameter recovery study is given, which shows that the parameters of the marginal IRT model can be accurately estimated under different conditions. Second, results are reported of simulation studies in which the performance of the (fractional) BF tests for different prior specifications and different sample sizes was investigated. Third, a comparison is made between the FBFs and the Mantel–Haenszel statistic to identify a dependence between item pairs.

6.1 Parameter Recovery

A total of 100 data sets were simulated to evaluate the performance of the MCMC algorithm for estimating the marginal IRT model parameters. We considered 100 and 1000 subjects responding to 10 and 15 items. The marginal model with the (improper) reference prior (9) and the balanced prior for $\tau$ was considered. For each data set, difficulty parameters were sampled from a normal distribution with a mean of 0 and a standard deviation of .1 and 1 for the sample of 100 and 1000 subjects, respectively. For the sample size of 100, the standard deviation was specified to be smaller in order to avoid bias in the posterior mean estimates of the difficulty parameter due to shrinkage.

The latent response data were assumed to be multivariate normally distributed with a common covariance parameter $\tau$ equal to .1 and .5, and a compound symmetry covariance structure, according to Equation (7), where $\sigma ^2=1$ to identify the variance of the scale. The $\mu _{\theta }$ was fixed to 0 to identify the mean of the scale. Dichotomous response data were generated according to the marginal IRT model defined in Equation (3). A normal-inverse-gamma prior was specified for the hyperprior parameters $\mu _{b}$ and $\omega _b^2$, and values were drawn from the posterior distributions specified in Equation (19) with $\mu _0=0$ and $p_0=1$, and Equation (20) with $g_1=1/2$ and $g_2=1/2$, respectively. This hyperprior specification ensured that the posterior mean and variance of the item difficulty parameter were almost completely determined by the data (see Equations (17) and (18)).

The MCMC algorithm was ran for 5000 iterations, and a burn-in period of 1000 iterations was used. Trace plots of MCMC iterations showed a very rapid convergence and efficient mixing of the chains. Furthermore, convergence and autocorrelations plots and diagnostics were used to investigate the convergence of the chains using the R package coda (Plummer et al., 2006). They did not show any irregularities.

For each condition, 100 data sets were simulated and the average parameter estimates over the 100 data sets are shown in Table 1. For each data set the posterior means (Mean) and the posterior standard deviation (SD) were calculated. The average bias, denoted as Bias(b), and the average mean squared error, denoted as MSE(b), were computed for the difficulty parameter estimates.

Table 1 Simulated and re-estimated marginal item response model parameters (100 replications).

For 100 persons, under the balanced prior, the covariance estimates are slightly smaller to those under the reference prior, since more weight is given to negative covariance values under the balanced prior.

For 100 persons, the sampling variability is large, but the covariance estimates were significantly different from zero, when considering the 95% highest posterior density intervals. When increasing the sample size, from 10 to 15 items and/or from 100 to 1000 persons, the accuracy of the estimates improved. The estimated posterior standard deviations were smaller, and the mean estimates closer to the true values.

Fig. 1

Posterior density estimates of the covariance parameter $\tau$ for different data samples, and for $n=1000$ and $p=10$, MCMC trace plots for the reference (empty circles) and balanced priors.

Fig. 2

BF and FBF test results on $\tau$ averaged over 50 replications, for two priors and $n=100$ and $p=5$.

The prior parameters of the difficulty parameters were accurately estimated, for the different conditions. The item difficulty estimates were not of interest, and for each replicated data set a different set of item difficulty parameters was used. The accuracy of the covariance estimates was shown given the normal population distribution for the difficulty parameters. The average bias of the difficulty estimates is close to zero, and the average MSE mainly represents the variance in estimates due to measurement error.

In Fig. 1, the upper plot shows the posterior density estimates of $\tau$ for three different conditions ($n=100, p=5$; $n=100,\,p=10$; and $n=1000,\,p=5$), where the true covariance value equals .1. It can be seen that the posterior density curves for the balanced prior are more shifted toward zero for $n=100$. Under both priors, the posterior density estimates are more sharply peaked when increasing the number of items and/or the number of persons. The lower boundary value of the parameter space of $\tau$ equals $-1/5$ for the 5-item test, and $-1/10$ for the 10-item test, respectively. It shows that $\tau =0$ is no longer a boundary value in the marginal model.

The lower plot in Fig. 1 shows the rapid convergence of the first thousand MCMC iterates under both priors (plotted empty circles correspond to the reference prior), for $n=1000$ and $p=10$ and $\tau =.1$ the true covariance value. The trace plots show the stable behavior of the chains, where the chains move quickly through the parameter space.

6.2 Performance BF Tests

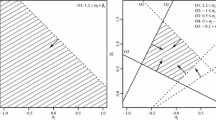
The characteristics of the BF tests for $\tau$ were evaluated. The computation of the BF tests requires draws from the posterior distributions and does not require parameter estimates. Therefore, it was possible to consider the performance of the BF tests for a (relatively) small data set, which was smaller than in the parameter recovery study. Two conditions were considered: 100 persons and a 5-item test and 1000 persons and a 10-item test, for which the results are shown in Figs. 2 and 3, respectively.

In Fig. 2, the four subplots show the true covariances value of $\tau$ on the x-axis. On the y-axis, the logarithms of the estimated FBF using the reference prior and of the estimated BF using the balanced prior are shown. In Fig. 2, each plotted test result is an average over 50 simulated data sets. For the BF and FBF results, an estimated smoothing spline is drawn in each subplot to illustrate the trend. Although the results are affected by the sampling variability, in most cases they lead to correct decisions for both priors.

The subplots do not show a clear difference between both priors. However, when testing inequality constraint $\tau <0$ ($\tau >0$) against the unconstrained hypothesis and the log FBF converged to 0, the BF with the balanced prior showed $\log (2)$ points more evidence for $\tau <0$ ($\tau > 0$) if the inequality constraint is supported by the data. The FBF did not show a distinction between the unconstrained and constrained hypothesis, where the BF based on the balanced prior showed a clear preference for the less complex constrained hypothesis. A similar behavior was also observed for the FBF and a balanced prior approach in the case of testing a mean parameter (Mulder, 2014).

In Fig. 3, the results of the behavior of the tests are given for $n=1000$ and 10 items averaged over 50 simulated data sets. The decrease in sampling variability led to much more accurate test results, but the trends of both tests are similar to the ones shown in Fig. 2. Both estimated test results led to accurate decisions, although the BF based on the balanced prior showed $\log (2)$ to more weight of evidence for the constrained hypothesis in those areas.

Fig. 3

BF and FBF test results on $\tau$ averaged over 50 replications, for two priors and $n=1000$ and $p=10$.

6.3 Mantel–Haenszel for Test Dimensionality

When latent variables, $\theta _i$, underlie the item responses, then for each response pattern, the conditional covariance between item pairs is assumed to be zero. So, for item responses $Y_{ij}$ and $Y_{il}$, the conditional covariance is zero given the latent variable $\theta _i$,

$$\begin{aligned} { Cov}\left( Y_{ij},Y_{il}\mid \theta _i \right)= & {} 0. \end{aligned}$$

(24)

Stout et al. (1996) considered the item-pair conditional covariances to assess the test dimensionality. However, the covariance was conditioned on the number-correct score instead of $\theta _i$ and estimated by a maximum likelihood estimator. Furthermore, an asymptotic normal distribution of the statistic was used to quantify the extremeness of a statistic value. Sinharay et al. (2006) used the Mantel–Haenszel (MH) statistic as a discrepancy measure in a posterior predictive check to evaluate whether the item-pair’s conditional covariance is positive given a rest score r (i.e., the number-correct score excluding the two items).

In this simulation study, the performance of the proposed FBFs is compared to that of the MH statistic in detecting a violation of unidimensionality by evaluating the conditional covariance. Response data were simulated under a two-dimensional one-parameter item response model, where one latent variable, $\varvec{\theta }_1$, underlay all item responses and a second latent variable was only related to the first two items. The object was to identify the presence of the second latent variable by evaluating the conditional covariance of the responses to the first two items given the general latent variable $\varvec{\theta }_1$.

When integrating out the second latent variable in the two-dimensional item response model, a (marginal) unidimensional item response model with a CS covariance matrix, and covariance parameter $\tau$, is obtained. The conditional covariance in Equation (24) is tested by evaluating the covariance parameter $\tau$, which represents the correlation implied by the second latent variable. When local independence holds, a second latent variable is not supported by the data and $\tau =0$, representing no additional correlation between the responses. When $\tau >0$, a violation of local independence is identified due to the presence of a second latent variable.

Let $n_{jj',r}$ denote the number of correct responses to item j and item $j'$ for those with a rest score r denoted as $n_r$. Then, the MH statistic is given by,

$$\begin{aligned} { MH}\left( \mathbf {y}\right)= & {} \frac{\sum _r n_{11,r}n_{00,r}/n_r}{\sum _r n_{10,r}n_{01,r}/n_r}. \end{aligned}$$

(25)

A posterior predictive p-value can be computed by evaluating the extremeness of the MH statistic for the observed data under the model, which is given by

$$\begin{aligned} p_0\left( \mathbf {y}\right)= & {} P\left( { MH}\left( \mathbf {y}^{(rep)}\right) > { MH}\left( \mathbf {y}\right) \mid \mathbf {y} \right) , \end{aligned}$$

where $\mathbf {y}^{(rep)}$ are the replicated data under the unidimensional item response model, assuming local independence between item pairs given the general latent variable $\varvec{\theta }_1$. The sampling distribution of the MH statistic is not needed, since the extremeness of the observed MH value is evaluated using replicated data.

The proposed FBFs, using the reference prior, under the marginal ability model given $\varvec{\theta }_1$, were used to evaluate the conditional covariance. Therefore, the ratio of the marginal distribution of the data under the assumption of unidimensionality $(\tau =0)$ to the marginal distribution of the data under a violation of unidimensionality was computed. In that case $\tau >0$, local independence did not hold and a positive conditional covariance represented the presence of a second latent variable.

For 500 persons, a response pattern of 10 items was simulated, where the item difficulties and latent variable $\varvec{\theta }_1$ were generated from a standard normal distribution. For the second latent variable, data were simulated for different item-pair dependencies, where $\tau$ ranged from 0 (i.e., local independence) to .5. Given the mean structure under the assumption of local independence, the FBFs only required the responses to the first two items. The MH statistic required a rest score, which was computed as the number correct on the remaining 8 items. Each posterior predictive p-value was computed using 10,000 replications, and 500 data replications were used for each level of $\tau$.

In Table 2, the estimated FBFs across 500 data replications are given for $H_0$ $(\tau =0)$ versus $H_2$ $(\tau > 0)$. When local independence was simulated, the average FBF resulted in strong support for the null hypothesis, with 13.5 times more evidence for the null relative to the alternative. The median of the computed p-values is reported. The (median) posterior predictive p-value of .52 showed no evidence to reject the null hypothesis, and the estimated average MH statistic was not extreme (around 1.82). Note despite the similar conclusion, the advantage of the FBF is that it provides a quantification of the relative evidence in the data that only one latent variable underlies the item responses. The posterior predictive p-value, and p-values in general, cannot be used for this purpose.

For data simulated with $\tau =.1$ for the items 1 and 2, around $9\%$ of the total factor variance was contributed by the second latent variable. The FBF showed approximately 33 times more evidence for hypothesis $H_2$ $(\tau > 0)$, while the p-value of the MH statistic did not identify any significant additional correlation in the data. It can be seen that the FBF detected each violation of item-pair dependence. The MH statistic detected a violation of local independence, given a significance level of .05, when $\tau \ge .4$ and more than 28% of the latent variable variance stemmed from the second latent variable.

It can be concluded that the results of the FBF led to correct decisions for all conditions and showed much more power than the MH statistic, which also required additional item responses to determine a rest score.

Table 2 MH statistic versus the FBF to detect violations of local independence.

Table 3 TerraNova test on five main content areas: covariance estimates and log BF tests under the balanced and reference prior.

Fig. 4

(Iterative) EAP estimates of $\tau$ for each TerraNova content domain under the conditional (one-factor) and marginalized IRT model.

7 Multidimensionality of a TerraNova Test

The TerraNova data, originally used by Yao (2010) and Sinharay (2013), were used to illustrate the (fractional) BF test procedure to verify a multidimensional factor structure. From 3953 examinees responses are available on five main content areas referred to as Language (LG), Mathematics (MT), Reading (RD), Science (SC), and Social Studies (SS). The number of items for each content domain is given in Table 3.

The marginal IRT model, represented in Equation (3), was fitted for each domain to estimate the covariance structure. Therefore, the MCMC algorithm was ran for 2000 iterations, and parameter estimates were computed using a burn-in period of 1000 iterations. In each MCMC iteration, the EAP estimates of the covariance parameter $\tau$ were computed for each domain. In Fig. 4, under the label “Marginal Model,” the upper five lines show the change in EAP estimates. Each plotted line of EAP estimates shows a fast convergence to a stable outcome across MCMC iterations.

In Table 3, under the label “Marginal,” the posterior mean estimate of $\tau$ is given for each domain. The covariance estimates show that the item responses are correlated within each domain with the smallest covariance among responses to Science items and the highest to Reading items. The BF tests under both priors showed much evidence in favor of a positive covariance for each domain. Beside differences in item difficulties across domains, the estimated covariances also differ and range from .255 to .497. Therefore, it was not likely that one common factor would explain all covariances, including covariances among each person’s responses from different domains.

To evaluate the multidimensionality of each domain, a general factor was measured using all content domain items with the one-parameter IRT model. Then, for each domain, it was investigated whether there was still a positive covariance among responses given the general factor. Therefore, this general factor was included in the mean term of the marginal IRT model of Equation (3). The MCMC algorithm was ran for 2000 iterations to estimate the conditional covariance structure of item responses within each content domain given the general factor. The trace plots of the estimated EAPs of each covariance parameter are given in Fig. 4. The lowest five lines correspond to the conditional covariance estimates, and it can be seen that the EAP estimates converge quickly and show not much variability between domains.

In Table 3, for each content domain, the conditional covariance estimates are given under the label “Conditional.” The covariance estimates are much smaller than those estimated under the marginal model, which shows that the general factor explains most of the covariances among each person’s responses to all domain items. In each domain, a small (conditional) covariance effect was estimated, which provided support for a second factor variable. The (fractional) BF tests were used to estimate the amount of support in favor of the hypothesis of a positive conditional covariance. From Table 3 follows that for all domains there was evidence for a second factor, since sufficient support was given to the hypothesis of a positive conditional covariance.

This procedure could be extended to measure support for a third factor, and so forth. However, in this case the estimated conditional covariance estimates were already very small. When conditioning on the two measured factors, it is highly unlikely that there would be any common covariation left among each person’s responses.

8 Testing Differential Item Functioning in PISA

The Mathematics data from the Programme of International Student Assessment (PISA 2003) were analyzed to investigate differential item functioning. In Fox (2010, Chapter 7.6), different random item effect models were used to model and identify differential item functioning of 8 Mathematics items of booklet 1 over 40 countries given responses of 9796 students. Here, a subset of 10 countries were considered to illustrate the performance of the BF tests to evaluate hypotheses about differential item functioning. This subset was a balanced sample, where a total of 250 students were selected from each country. The proposed (fractional) BF tests required a balanced design per item, although not necessarily balanced over items. Otherwise, the shift parameter in the conditional distribution of the transformed latent response data given $\sigma _{b_j}$, Equation (14), would vary over countries leading to a complex mixture distribution.

In the marginal IRT model, represented in Equation (6), the covariance components, $\sigma _{b_j}$, were used to model differential item functioning. A different covariance component was specified for each item using the non-informative reference prior. An item did not show differential item functioning, when the covariance component was not significantly greater than zero.

The clustering of students in countries was modeled using a random intercept population model for student ability. The identification rule of the random item effect model was not needed (which would restrict the average difficulty of the eight items to be equal across countries), since country-specific item parameters were not parameterized. The average level of ability was fixed to zero to identify the mean of the latent scale.

The MCMC algorithm was run for 5000 iterations, and a burn-in period of 1000 iterations was used. The estimated average item difficulty was $-.57$, and the variation in difficulty across items .41. The item difficulty estimates and standard deviations are shown in Table 4.

Table 4 PISA 2003: testing for cross-national item variation using log BF tests under the balanced and reference priors.

Fig. 5

PISA 2003: posterior densities of the covariance parameters representing differential item functioning of 8 Mathematics items.

For each item, a positive correlation between responses of the same country was estimated given the international item difficulty estimate while also accounting for differences in country means. The estimated standard deviations of the covariance estimates were relatively large, but the posterior densities of the covariance parameters were positively skewed. Each covariance parameter was conditionally shifted-inverse-gamma distributed, with the shift parameter equal to the inverse of the country’s sample size. Therefore, the shift was relatively small and hardly influenced the shape of the posterior distribution. The posterior densities are plotted in Fig. 5. It can be seen that items 2 and 7 show the strongest correlations between country-clustered responses while conditioning on cross-national differences in latent means and the (international) item difficulty estimates. Item 3 showed the smallest correlation between country’s responses.

In order to check the measurement invariance assumptions, a formal testing procedure was applied. For this reason, the (fractional) BF tests were computed using the balanced prior and using the reference prior. The test results showed support for cross-national item variation for all 8 items. The FBF test with the reference prior showed less evidence in favor of differential item functioning compared to the BF test with the balanced prior. For both tests the strength of evidence increased in favor of the hypothesis $\sigma _{b_j} > 0$, when the covariance estimate was located further away from zero.

9 Discussion

A Bayes factor approach to test the covariance structure of dichotomous item response data has been proposed. In a marginal IRT modeling framework, the evaluation of the covariance structure does not involve testing on the boundary of the parameter space. A simple procedure has been proposed, where the multivariate normally distributed latent item responses are transformed using the Helmert matrix. It has been shown that the first Helmert transformed component contains the information about the covariance component of the CS covariance structure. As a result, the posterior distribution of the covariance component is a shifted-inverse-gamma given the Helmert transformed responses.

The Helmert transformed item responses are independently distributed such that a closed form representation of the marginal likelihood can be obtained. For the latent response data, it facilitates the construction of closed form expressions of (fractional) BFs for evaluating hypotheses about the covariance component. A conjugate reference prior and an innovative balanced prior were proposed, which provide equal weight to positive and negative covariance values. Simulation studies showed good behavior of the BFs to make decisions about the covariance structure, when testing conditional independence and when testing measurement invariance. Efficient procedures have been proposed to implement the methodology in a Bayesian IRT modeling framework.

The Helmert method cannot be directly applied to more complex IRT models. For instance, when including a discrimination parameter in the item response model, then the Helmert transformation does not lead to a closed form expression of the posterior distribution for the covariance parameter. Consider the one-parameter model for latent responses in Equation (2) and extend this model with a discrimination parameter. For normally distributed ability parameters with mean $\mu _{\theta }$ and variance $\tau$, it follows that

$$\begin{aligned} Z_{ij}= & {} a_j \theta _i - b_j + e_{ij} \\= & {} a_j\left( \mu _{\theta } + \epsilon _{\theta _i} \right) - b_j + e_{ij} \\= & {} a_j\mu _{\theta } - b_j + a_j\epsilon _{\theta _i} + e_{ij}. \end{aligned}$$

It can be seen that the discrimination parameter is included in the covariance matrix of the errors due to the component $a_j\epsilon _{\theta _i}$. To make this more explicit, the covariance matrix of the latent responses of subject i is given by

$$\begin{aligned} { Var}\left( \mathbf {Z}_{i}\right)= & {} \mathbf {I}_p + \tau \mathbf {a}\mathbf {a}^t, \end{aligned}$$

where $\mathbf {a}$ is the vector of discrimination parameters. This covariance matrix does not have a compound symmetry structure. Subsequently, a Helmert transformation of the $\mathbf {z}_i$ will not reveal within and between-group sum of squares, where the between-group sum of squares contains all data information about $\tau$. However, the posterior distribution of $\tau$ under the one-parameter model can serve as a proposal distribution (i.e., importance sampling function) to sample the covariance parameter under the two-parameter and more complex item response models through a sampling importance resampling method. Then, the (fractional) Bayes factor could also be computed via importance sampling. This is in line with Perrakisa et al. (2014), who advocated the use of marginal posterior distributions as an importance sampling function to estimate the marginal likelihood of the data. The derived posterior distributions under the one-parameter response model will serve as importance sampling functions to obtain MCMC samples from more complex response models, and this will be a topic for future research.

For relatively small sample sizes the different priors did not influence the behavior of the BF, and both priors lead to similar conclusions. This makes for instance the procedure also suitable for analyzing data retrieved from a pilot study. The dimensionality of the underlying factor structure can be tested, and tests might identify inconsistencies in relationships between items. Subsequently, the instrument could be appropriately adjusted before collecting more data. The presented procedure extends the work of random effects selection in generalized linear mixed models. For balanced response data, under a marginal modeling approach the posterior distribution of the clustering effect can be derived through a Helmert transformation of the (latent) response data. This Helmert transformation also enables the construction and computation of the marginal likelihood of the data. Instead of an orthogonal transformation of the response data, specific decompositions of the covariance matrix has been considered to make inferences about the covariance structure or covariance pattern (e.g., Daniels & Pourahmadi, 2002; Cai & Dunson, 2006). The procedures are applicable to more general covariance structures, but are computationally intensive and often require specific priors.

The presented method can be extended to other types of categorical data (e.g., ordinal, nominal), since a data augmentation scheme can be used to generate latent continuous response data (Fox, 2010). The generalization to more nested and non-nested clustering effects is also interesting. In that case, the objective is to define orthogonal transformations to partition the total sum of squares such that each component is a sufficient statistic for one of the covariance components. This would provide support to a very efficient evaluation of complex covariance structures of categorical response data.

Appendices

Appendix A: (Orthogonal) Helmert Transformation Matrix

An orthogonal matrix $\mathbf {H}$ has the property that $\mathbf {H}^t\mathbf {H} = \mathbf {H}\mathbf {H}^t=\mathbf {I}$, where the rows of $\mathbf {H}$ are mutually orthogonal and each row has a unit norm. A particular $(p\times p)$ orthogonal matrix is the Helmert matrix, where the first row has elements $p^{-\frac{1}{2}}$, and all zeroes of the triangle above the main diagonal and below the first row. The remaining elements below the main diagonal are positive, where row j $(j=2,\ldots ,p)$ has elements $\left[ \frac{1}{\sqrt{j(j+1)}} \mathbf {1}^t_j,\frac{-j}{\sqrt{j(j+1)}},\mathbf {0}\right]$. Lancaster (1965) referred to it as Helmertian in the strict sense and showed various properties of Helmert matrices (see also, Searle, 1971, pp. 31–33). Subsequently, the Helmert matrix of order p is given by

$$\begin{aligned} \mathbf {H} = \left[ \begin{array}{cccccc} \frac{1}{\sqrt{p}} &{} \frac{1}{\sqrt{p}} &{} \frac{1}{\sqrt{p}} &{} \cdots &{} \frac{1}{\sqrt{p}}\\ \frac{1}{\sqrt{2}} &{} -\frac{1}{\sqrt{2}} &{} 0 &{} \cdots &{} 0\\ \frac{1}{\sqrt{6}} &{} \frac{1}{\sqrt{6}} &{} -\frac{2}{\sqrt{6}} &{} \ddots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} 0 \\ \frac{1}{\sqrt{p(p-1)}} &{} \frac{1}{\sqrt{p(p-1)}} &{} \frac{1}{\sqrt{p(p-1)}} &{} \cdots &{} -\frac{p-1}{\sqrt{p(p-1)}} \end{array} \right] . \end{aligned}$$

(26)

Appendix B: Helmert Transformed Normal Random Variables

Consider a multivariate normally distributed random variable $\mathbf {z}_i=(z_{i1},\ldots ,z_{ip})^t \sim \mathcal {N}\left( \mu \mathbf 1 _p,\varvec{\Sigma }\right)$, where the covariance matrix has a compound symmetry structure represented by $\varvec{\Sigma }=\sigma ^2 \mathbf {I}_p + \tau \mathbf {J}_p$. The $\mathbf {z}_i$ are transformed using Helmert, and the transformed variable is given by $\tilde{\mathbf {z}}_i=\mathbf {H}\mathbf {z}_i$. The components of the transformed variable $\tilde{\mathbf {z}}_i$ are independently normally distributed. The first component of the Helmert transformed variable, $\tilde{z}_{i1}$, is normally distributed with mean and variance equal to,

$$\begin{aligned} E\left( \tilde{z}_{i1}\right)= & {} E\left( \sqrt{p}\bar{z}_i\right) = \sqrt{p}E\left( \sum {z}_{ij}/p\right) = \sqrt{p}\mu \\ { Var}\left( \tilde{z}_{i1}\right)= & {} { Var}\left( \sqrt{p}\bar{z}_i\right) = p { Var}\left( \bar{z}_i\right) = { Var}\left( \sum _{j=1}^{p} z_{ij}\right) /p \\= & {} \left[ \sum _{j=1}^p \left( \sigma ^2+\tau \right) + \sum _{k=1}^p\sum _{j\ne k} \tau \right] /p \\= & {} \left[ p(\sigma ^2+\tau ) + p(p-1)\tau \right] /p = \sigma ^2 + p\tau , \end{aligned}$$

respectively.

Consider a sample $\mathbf {z} = \left( \mathbf {z}^t_{1},\ldots ,\mathbf {z}^t_{n}\right) ^t$, where the components are identically and independently multivariate normally distributed. Subsequently, let $\lambda = \sigma ^2 + p\tau$, the probability density function of the first Helmert transformed component, $\tilde{\mathbf {z}}_{1}$, is given by

$$\begin{aligned} p\left( \tilde{\mathbf {z}}_{1} \mid \mu , \lambda \right)= & {} \left( 2\pi \lambda \right) ^{-n/2}\exp \left( \frac{-\sum _i \left( \tilde{z}_{i1} - \mu \sqrt{p}\right) ^2/2}{\lambda } \right) \\= & {} \left( 2\pi \lambda \right) ^{-n/2}\exp \left( \frac{-p\sum _i\left( \overline{z}_i - \mu \right) ^2/2}{\lambda } \right) \\= & {} \left( 2\pi \lambda \right) ^{-n/2} \exp \left( \frac{-p S^2_B/2}{\lambda } \right) , \end{aligned}$$

where $S^2_B = \sum _i\left( \overline{z}_i - \mu \right) ^2$. The probability density function of the $\tilde{\mathbf {z}}_{1}$ can be expressed as the density of $\overline{\mathbf {z}}_i$ given $\sigma ^2$ and $\tau$. It follows that

$$\begin{aligned} p\left( \overline{z}_1,\ldots ,\overline{z}_n \mid \sigma ^2,\tau ,\mu \right)= & {} \left( 2\pi (\sigma ^2 + p\tau )\right) ^{-n/2}\exp \left( \frac{-pS^2_B/2}{\sigma ^2 + p\tau } \right) \\= & {} (2\pi p)^{-n/2}\left( \sigma ^2/p + \tau )\right) ^{-n/2}\exp \left( \frac{-S^2_B/2}{\sigma ^2/p + \tau } \right) , \end{aligned}$$

where $\tau > \sigma ^2/p$, since $\lambda = \sigma ^2 + p\tau > 0$ when considering $\sigma ^2$ a constant.

The remaining $n(p-1)$ components $\left( \tilde{\mathbf {z}}_{2},\ldots ,\tilde{\mathbf {z}}_{p}\right)$ are distributed according to

$$\begin{aligned} p\left( \tilde{\mathbf {z}}_{2},\ldots ,\tilde{\mathbf {z}}_{p} \mid \mu ,\sigma ^2 \right)= & {} \left( 2\pi \sigma ^2\right) ^{-n(p-1)/2} \exp \left( \frac{-\sum _{i=1}^n\sum _{j=2}^p \tilde{z}_{ij}^2}{2\sigma ^2} \right) \\= & {} \left( 2\pi \sigma ^2\right) ^{-n(p-1)/2} \exp \left( \frac{-S^2_W}{2\sigma ^2} \right) \end{aligned}$$

where $S^2_W = \sum _{i=1}^{n}\sum _{j=2}^{p}\tilde{z}_{ij}^2 = \sum _{i=1}^{n}\sum _{j=1}^{p}\left( z_{ij} -\overline{z}_i\right) ^2$.