1 Introduction

One of the mainstream response models used in adaptive testing is the three-parameter logistic (3PL) model. The model explains the probability of a correct response U i =1 by a test taker with ability \(\theta \in\mathbb{R}\) on items i=1,…,I as

$$ \Pr \{U_{i}=1\}=p_{i}(\theta )=c_{i}+(1-c_{i}) \frac{\exp [a_{i}(\theta -b_{i})]}{1+\exp [a_{i}(\theta -b_{i})]}, $$
(1)

where \(b_{i}\in\mathbb{R}\) can be interpreted as the difficulty parameters of item i, a i ∈(0,∞] as a parameter for its discriminating power, and c i ∈[0,1] represents the height of the lower asymptote required to deal with the effects of random guessing. For notational convenience, we collect the parameters for item i in a vector η i =(a i ,b i ,c i ).

The origin of the question of what sample of test takers to choose when estimating the parameters η i for new items in a testing program can be traced back to Wingersky and Lord’s (1984) study of the effects of the distribution of the test takers’ abilities on the standard errors of the item-parameter estimates. One of their discoveries was that a uniform ability distribution offered substantially better standard errors than a bell-shaped distribution.

The same problem was analyzed more formally by Berger (1991, 1992, 1994), Berger and van der Linden (1991), Jones and Jin (1994), Stocking (1990), and van der Linden (1988, 1994) from the perspective of statistical optimal design theory. A typical optimal-design formulation of the problem of estimating the item parameters η i consists of the definition of a design space with ability points θ=(θ 1,θ 2,…,θ D ) and a vector of integer-valued weights w=(w 1,w 2,…,w D ), \(\sum\nolimits_{d}w_{d}=N\), where N is the intended sample size, which together define the sample of test takers. The focus, of course, is on the derivation of a design (θ,w) that gives the best estimates of η i .

The solution to the problem is less straightforward than, for instance, for the well-studied problem of estimating a slope parameter in univariate linear regression for four different reasons. Firstly, item calibration for the model in (1) involves the estimation of multiple parameters per item, and the design has to be optimized facing contradictory demands for each parameter. For instance, intuitively, a difficulty parameter is estimated best by a sample with maximum weight on the design point matching its true value, whereas the estimation of the guessing parameter seems to require maximum weights at the lower design points. A fruitful area of optimal design theory, however, deals with the definition of criteria of optimality for the simultaneous estimation of multiple parameters. Most of the criteria are based on the asymptotic covariance matrix for the parameters that are estimated. A well-established example is minimization of the determinant of the covariance matrix or, equivalently, maximization of the determinant of the Fisher information matrix. The criterion leads to solutions referred to as D-optimal. The criterion is easy to interpret, is known to have favorable properties, such as invariance of the optimal design under linear transformation of the parameters (for a proof, see Fedorov 1972, Section 2.2), and has been the main criterion addressed in the optimal item calibration design literature reviewed below. However, other so-called alphabetic optimality criteria (A-optimality, E-optimality, etc.) may occasionally be more relevant; for a review of several of them, we refer to Berger and Wong (2009) and Silvey (1980). The optimal design procedure presented in this paper is based on the posterior expected contribution of the test takers to the observed information matrix for the item parameters. The procedure allows for an easy plug-in of a Bayesian version of any of these optimality criteria.

Secondly, we typically calibrate multiple items at the same time, but a sample that is optimal for one item is likely to be off target for the others. The only way to prevent complicated compromises between multiple items is through an incomplete sampling design with different samples assigned to different items. Fortunately, the adaptive design presented in this paper allows us to do so without any extra organizational efforts.

Thirdly, although it is interesting to known what the optimal design (θ,w) would be for a given set of item parameters for theoretical reasons, it is generally impossible to select individual test takers with ability parameters equal to the design points. A case in point is the D-optimal design for the item parameters in the 2PL model, that is, the response model in (1) with c i =0. If the ability parameters were known, the design problem would be equivalent to the one for logistic regression of U i on θ. The univariate logistic regression model is known to have a D-optimal design consisting of equal weights at design points θ=b i ±1.542/a i (that is, at the two ability levels corresponding to the response probabilities of 0.176 and 0.824 for the item); see, e.g., Abdelbasit and Plankett (1983). However, to actually use this result, we would need to select different test takers from a large stock of subjects with known abilities for each individual item—a condition that does not seem very realistic.

Fourthly and lastly, because IRT models are nonlinear in the item parameters, optimal design solutions based on the Fisher information matrix are dependent on the unknown values of the parameters that are estimated. That is, we must actually know the true values of these parameters to be able to estimate them optimally.

Solutions at true parameter values are known as locally optimal solutions. How to approximate them when designing a calibration sample design is a challenge. One approach is to provide an initial guess of the values of the item parameters and optimize the design at the guessed values. Obviously, this type of solution can never be better than the initial guess. An alternative version of the approach is to introduce an a priori distribution for the item parameters and optimize the expected design given the distribution. The alternative is more sophisticated in that, in addition to point estimates of the parameters, it forces us to specify our uncertainty about these estimates as well. The method is further improved when the prior distribution can be derived from empirical information, for instance, when a new field-test item is drawn from a larger family of items with a distribution of parameters known from earlier calibration.

More sophisticated solutions, however, are based on a sequential (Berger 1992, 1994; Jones & Jin, 1994; Chang & Lu, 2010) or minimax approach (Berger, King, & Wong, 2000). A sequential approach begins with an initial estimate of the item parameters, \(\widehat{\boldsymbol {\eta }}_{i}^{(0)}\), and the design (θ (0),w (0)) optimal at the estimate. The design is used to collect the responses from w (0) test takers with abilities at θ (0), which are used to calculate both an improved estimate \(\widehat{\boldsymbol {\eta }}_{i}^{(1)}\) and design (θ (1),w (1)). The procedure is repeated until the item-parameter estimates are sufficiently accurate according to the chosen criterion of optimality. Sequential D-optimal designs were introduced by Wynn (1970). For an application for the 2PL model that capitalizes on the earlier analogy with logistic regression, see Berger (1992).

A minimax approach is conservative in that it tries to minimize the consequences of the worst possible outcome. It does so by specifying a region of interest for the parameter values and optimizing the design for the most unfavorable values in the region. For instance, the minimax D-optimal design for item calibration for the 2PL model by Berger et al. (2000) is obtained by maximizing the minimum value of the determinant of the information matrix for the item parameters over the region of interest across all possible designs.

We are aware of three earlier publications in the psychometric literature that refer to adaptive testing as an important element of the design of an item-calibration sample but differ essentially from the design presented in this paper. Jones and Jin (1994) assumed online adaptive testing but only to choose test takers with estimated ability levels to populate a periodically updated D-optimal design for the estimation of the item parameters. The question where these test takers should come from was barely addressed. Chang and Lu (2010) were more explicit in this respect and assumed alternating stages with (i) adaptive testing to build up a stock of test takers with estimated abilities (ii) sequential administration of a set of field-test items to a sample from these test takers to update the item-parameter estimates. However, the expectation that earlier test takers are willing to return to take an extra item each time a sequential design happens to assign one to them seems rather optimistic. Makransky and Glas (2010) studied the problem of item calibration for the case of a new adaptive testing program without any previously calibrated items. Their main concern was to find strategies for the inclusion of items in adaptive tests that simultaneously guarantee fair scoring of the test takers and quick calibration of the test items. Their study did not involve any optimization with respect to one of the optimal design criterion, though.

The design proposed in this paper is an optimal Bayesian design for item calibration that is adaptive in a double sense: It assumes both adaptive testing of test takers from an existing pool of calibrated items and adaptive assignment of field-test items to the test takers. The design can be implemented in real time; more specifically, it does not assume any return of earlier test takers for later item calibration. The feature is achieved by reversing the type of adaptation assumed in the literature reviewed above. Rather than adaptively assigning test takers with estimated abilities to individual field-test items, the current design uses both the adaptively obtained posterior distributions of the test takers’ abilities and the sequentially updated posterior distributions of the field-test parameters to optimally assign the field-test items to the test takers.

In addition, the proposed design is innovative in a few other ways. First, because it does not capitalize on the earlier equivalence of the 2PL model with known θs and logistic regression, it is presented directly for the more popular 3PL model. However, without any major adjustments, the same design can be used for any of the other mainstream response models as well. Second, the design does not need a correction for bias due to measurement error in the predictor (errors-in-variables problem) inherent in the frequentist approach to logistic regression, such as one of the proposals in Stefanski and Carroll (1985) used by Jones and Jin (1994) or the improvement by Chang and Lu (2010). Instead, in a Bayesian fashion, all remaining error in the θ estimates after adaptive testing is integrated out when calculating the posterior expected information matrix for the parameters of the field-test items on which their assignment is based. Finally, the design is implemented using alternating runs of MCMC sampling from the posterior distributions of the θs of the test takers and the field-test parameters η i while reusing samples from earlier posterior distributions for all other parameters. As our empirical study shows, this use of MCMC sampling requires computation times short enough for application to adaptive testing.

Finally, Jones and Jin (1994) suggested a complication for sequential item calibration due to the dependence of the later design updates on response data. The same issue is a key point in the development of the design in Chang and Lu (2010). These concerns about dependence remind us of identical concerns about possible violations of the assumption of local independence in the early adaptive testing literature due to the fact that the selection of later items always depends on the previous responses by the same test taker. However, we believe treatment of the issue from the perspective of missing-data theory has settled it. The dependence of design variables on earlier response variables is not the same thing as dependence between response variables. For a more detailed discussion, see Mislevy and Chang (2000).

2 Adaptive Testing

In adaptive testing, ability parameter θ is estimated in real time, with an update of the estimate after each new response. The next item administered to the test taker is selected to be statistically optimal at the current update. A key element of the optimal design for item calibration presented in this paper is Bayesian updating of the θ estimates.

Let i=1,…,I denote the items in the pool from which the test is administered. The items in the test are denoted as k=1,…,K. Hence, the item in the pool administered as the kth item in the test can be denoted as i k . We focus on the selection of an arbitrary item k. The responses to the previous k−1 items for the test taker are collected in the vector \(\mathbf{u}_{i_{k-1}}=(u_{i_{1}},\ldots,u_{i_{k-1}})\). Let g(η i ) be the posterior density of the parameters of item i in the operational pool. In practice, the operational items are typically calibrated with enough precision to treat them as known. But, for generality, we assume a full posterior distribution for each item; the case of negligible calibration error can be represented by posterior distributions degenerated at their point estimates. In addition, we use g(θ j ) to denote the prior density of θ for test taker j. Observe that we avoid the restriction of a common prior for all test takers; the option of individual priors allows us to use different starting positions for different test takers based on relevant collateral information (e.g., earlier scores or response times on the same test).

The marginal posterior distribution of θ after k−1 items is equal to

$$\begin{aligned} & g(\theta _{j}\mid \mathbf{u}_{i_{k-1}}) \\ & = \frac{g(\theta _{j})\int \cdots\int\prod_{l=1}^{k-1}g(\boldsymbol {\eta }_{i_{l}}) p(\theta _{j};\boldsymbol {\eta }_{i_{l}})^{u_{i_{l}}}[1-p(\theta _{j};\boldsymbol {\eta }_{i_{l}})]^{1-u_{i_{l}}} \,d\boldsymbol {\eta }_{i_{1}}\ldots d\boldsymbol {\eta }_{i_{k-1}}}{\int g(\theta _{j}) [\int \cdots\int \prod_{l=1}^{k-1}g(\boldsymbol {\eta }_{i_{l}})p(\theta _{j};\boldsymbol {\eta }_{i_{l}})^{u_{i_{l}}} [1-p(\theta _{j};\boldsymbol {\eta }_{i_{l}})]^{1-u_{i_{j}}} \,d\boldsymbol {\eta }_{i}\ldots d\boldsymbol {\eta }_{i_{k-1}}] \,d\theta _{j}}, \end{aligned}$$
(2)

where p(θ j ;η i ) is the response probability in (1).

In the current context, we are only interested in the full posterior distributions \(g(\theta _{j}\mid \mathbf{u}_{i_{k-1}})\) as they evolve during the test, not in any point estimates derived from them. Also, the way in which the posterior distributions are used for item selection during adaptive testing is currently not of interest; the proposed calibration procedure works for any type of item selection. For a review of the available criteria, see van der Linden and Pashley (2010).

3 Calibration Design

Suppose that, in addition to the operational pool of items i=1,…,I for the adaptive test, we have a set of candidate items f=1,…,F that are to be field tested and calibrated for future use. To guarantee field testing under realistic conditions, the items are inserted into the test without revealing to the test takers whether the items they see are operational or not. From a statistical point of view, it is best to assign field-test items to the very last positions in the test, an assignment that would enable us to profit maximally from the information available in the test taker’s posterior distribution of θ during adaptive testing. On the other hand, permanent use of this rule might make the field-test items immediately recognizable, and hence increase the likelihood of less serious behavior.

A practical solution is to assign a few field-test items surreptitiously to positions close to the end of the test. For instance, when three items are to be assigned to a test with 25 operational items, we could randomly assign them to three out of the last six positions in a test of 28 items. However, the question of which positions to assign field-test items to is not addressed in this paper; its answer is likely to be determined by practical considerations. Rather, the subject of this research is how to assign field-test items optimally to given positions in the adaptive test and use the responses to update their parameter estimates.

3.1 Bayesian Adaptive Design and MCMC Sampling

The basic idea is to optimize the assignments using (i) the information about the test taker’s θ collected during the test as well as (ii) the currently available information about the parameters of the field-test items. As already explained, the criterion of assignment will be based on the test taker’s expected contribution to the information matrix for the field-test parameters.

The design is implemented using two alternate Markov chain Monte Carlo (MCMC) algorithms for the update of the posterior distributions of one type of parameter while reusing the draws from the previous distributions of the other parameters. More specifically, the algorithm has the following alternating stages:

Stage 1.:

During operational adaptive testing, just before field-test items are to be assigned to a test taker, one version of the MCMC algorithm is run to sample the current posterior distribution of the test taker’s θ while resampling vectors of draws from the posterior distributions of the parameters of the already administered items that are permanently stored in the system. The θs drawn during the stationary part of the chain are saved to decide what field-test items to assign to the current test taker as well as for a later update of the posterior distributions of the parameters of the field-test items in Stage 2.

Stage 2. :

The posterior distributions of the field-test items are periodically updated. In order to do so, another version of the algorithm is run, this time to sample from the updated posterior distributions of the field-test parameters η f while reusing the vectors with the draws from the posterior distributions of the θ parameters for the last batch of test takers collected in Stage 1.

MCMC sampling from posterior distributions has the reputation of being time intensive given our current computational power. But, as will be demonstrated by our later examples, the computation time for the proposed implementations no longer prohibits application in operational testing. Stage 1 involves sampling from the unknown posterior distribution of only one θ parameter along with resampling of the vectors with the draws from the known, highly informative posterior distributions of a limited number of the operational item parameters η i available in the system. Likewise, Stage 2 involves sampling from the posterior distributions of only a few field-test parameters η f in combination with those of a small number of θ parameters with highly informative priors available in the form of the vectors of posterior draws saved from the adaptive test administration.

From a theoretical perspective, updating a field-test parameter immediately each time its item has been administered to a new test taker would be ideal. The assignments of the field-test items would then profit maximally from new response data. In practice, however, the parameters will have to be updated only periodically for batches of test takers with a size determined by such practical factors as the number of testing stations in use for the program, access to the computational resources required for the updates, etc.

4 Detailed Procedure

The calibration procedure is based on a Metropolis–Hastings (MH) within Gibbs algorithm for the 3PL model with blocks of item and ability parameters and symmetric proposal densities. The different algorithms required for the two stages of the procedure are summarized in Appendix A. We first discuss the details of these algorithms and then show that their alternating use does lead to a procedure that does converge to the proper posterior distribution.

4.1 Initialization

Let g(η i ) denote the posterior distributions of the parameters of the current operational items i=1,…,I in the pool upon completion of their calibration. The distributions are assumed to be stored along with the items in the system in the form of vectors of random draws from each of them. The vectors are automatically available if the current operational items were pretested by the system using the same procedure as in this paper and promoted to operational status once their posterior distributions showed sufficient precision.

Let b=1,2,… denote the successive batches of test takers used to update the posterior distributions of the field-test parameters η f . In addition, we use g (b)(η f ), f=1,…,F to denote the posterior density of η f after the update for batch b. The initial prior distribution η f has thus density g (0)(η).

The initial prior distribution is chosen to be the product of independent univariate distributions. The univariate distribution of b f is taken to be normal. As a f and c f are bounded, the distributions for these two parameters are taken to be lognormal and logitnormal, respectively. Such transformations are standard options to produce posterior distributions of parameters on proper domains (e.g., Patz and Junker 1999a).

On the original scale of the parameters, the initial prior densities of a f and c f are

$$ g^{(0)}\bigl(a_{f};\mu _{a_{f}},\sigma _{a_{f}}^{2}\bigr)=\frac{1}{a_{f}\sigma _{a_{f}}\sqrt{2\pi }}\exp \biggl[ - \frac{1}{2} \biggl( \frac{\ln a_{f}-\mu _{a_{f}}}{\sigma _{a_{f}}} \biggr) ^{2} \biggr] $$
(3)

and

$$ g^{(0)}\bigl(c_{f};\mu _{c_{f}},\sigma _{c_{f}}^{2}\bigr)=\frac{1}{c_{f}(1-c_{f})\sigma _{c_{f}}\sqrt{2\pi }}\exp \biggl[ - \frac{1}{2} \biggl( \frac{\ln \frac{c_{f}}{1-c_{f}}-\mu _{c_{f}}}{\sigma _{c_{f}}} \biggr) ^{2} \biggr] ; $$
(4)

that is, normal densities with the Jacobian of the transformation as extra factor. However, the choices are easily implemented as normal distributions for the vector of transformed parameters

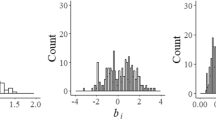
$$ \boldsymbol {\eta }_{f}^{\ast }=(\ln a_{f},b_{f}, \operatorname {logit}c_{f}). $$
(5)

New items for a running testing program are typically written according to the same instructions as for the current operational item pool. It seems therefore appropriate to center the initial prior distributions at the empirical means of the transformed parameters for the operational pool. To avoid optimism about our knowledge about the parameters, however, we recommend choosing them to be much wider than the empirical distributions; except maybe for the c f parameters when convergence of their estimates is an issue (see below). Figure 1 shows the distributions of the original and transformed item parameters in the pool used in the later empirical example in this paper, along with the normal distributions fitted to the latter. The means and variances of the transformed parameters are given in Table 1. The peak at c=0.2 in the distribution of the guessing parameters is due to the fixing of the parameters for some of the five-choice items at this value during the original calibration. With lack of data at the lower end of the scale, the estimates of these parameters have sometimes difficulty converging, and when this happens, it is common practice to fix their values at the reciprocal of the number of response alternatives. We expect optimization of the calibration design to produce a better distribution of the data and the problem to disappear.

Figure 1.
figure 1

Empirical distributions of the original and transformed item parameters in the operational pool, along with the normal distributions fitted to the latter.

Full size image
Table 1. Empirical means and variances of the transformed item parameters in the operational pool.
Full size table

Observe that, although we start from a common prior distribution for the field-test parameters, the first posterior update immediately leads to individual distributions for all item parameters. At this stage of our research, we do not yet want to impose any assumptions on the shapes of these distributions without knowing their impact on the results. This decision has motivated our choice of the MH within Gibbs algorithm with the empirical posterior updates introduced below rather than the more efficient Gibbs sampler with data augmentation for the 3PL model (e.g., Johnson & Albert, 1999, Section 6.9). Using the Gibbs sampler would have restricted the shapes of the posterior distributions to families with conjugacy relationships with the (augmented) 3PL likelihoods throughout the entire calibration process.

4.2 Ability Estimation

Assuming that k−1 items have been administered to test taker j before the field-test items are assigned, the first algorithm in Appendix A is run to sample from the posterior distribution of \(g(\theta _{j}\mid \mathbf{u}_{i_{k-1}})\) in (2) for the test taker. The output is a vector \((\theta _{j}^{(1)},\ldots,\theta _{j}^{(s)},\ldots,\theta _{j}^{(S)})\) with the draws from the posterior distribution of θ j generated by a stationary part of the Markov chain. The vector is stored in the system for reuse when calculating the criterion for the assignment of the field-test items or updating the posterior distributions of their parameters.

The current context allows for an efficient implementation of the algorithm. In the examples reported later in this paper, we used a normal proposal distribution centered at the previously draw θ (r−1),

$$ q\bigl(\theta \mid \theta ^{(r-1)}\bigr)=N\bigl(\theta ^{(r-1)}, \sigma _{q_{\theta }}^{2}\bigr). $$
(6)

The proposal variance \(\sigma _{q_{\theta }}^{2}\) was calculated from the average of the inverse of the Fisher information calculated from simulated administrations of the adaptive test about a well-chosen series of θ values prior to the study. As proposal densities with slightly heavier tails than the posterior distribution that is sampled are generally advantageous, \(\sigma _{q_{\theta }}^{2}\) was set to a value 10 % larger than the average. Further details are provided below.

The prior density g(θ j ) in (A.1) can be taken to be normal with the mean and variance matching our best guess for the population distribution that is tested. Alternatively, an individual prior based on existing empirical information about the test taker (e.g., scores on previous tests in an adaptive test battery) can be used. In fact, the current framework can easily be enhanced to incorporate collateral information about the test taker collected during the test (e.g., response times) in the posterior updates as well. These choices lead to posterior distributions that are both more accurate and less biased. For examples of adaptive testing with empirical individual prior distributions based on collateral information collected during the test, see van der Linden (1999, 2008, 2010).

4.3 Assignment of Field-Test Items

The field-test items are assigned according to a criterion based on the posterior expected contribution by the test taker to the observed information matrix for the item parameters.

For a response u f on field-test item f by a test taker j, the observed information matrix is equal to

$$ J_{u_{f}}(\boldsymbol {\eta }_{f};\theta _{j})=- \biggl\{ \frac{\partial ^{2}}{\partial \eta _{f}\partial \eta _{f^{\prime}}}\ln \bigl[ p(\boldsymbol {\eta }_{f};\theta _{j})^{u_{f}}\bigl(1-p(\boldsymbol {\eta }_{f};\theta_{j})\bigr)^{1-u_{f}} \bigr] \biggr\} . $$
(7)

Taking the posterior expectation over all unknown elements (responses and parameters) is the Bayesian way of allowing for the remaining uncertainty about the item parameters as well as the test taker’s ability. The appropriate posterior distributions are the ones of (i) the field-test parameters η f after the last posterior update, b−1, and (ii) ability parameter θ given the response vector \(\mathbf{u}_{i_{k-1}j}\) for test taker j on the preceding k−1 operational items in the adaptive test. Hence, using \(p(u_{f};\mathbf{u}_{i_{k-1}j},\boldsymbol {\eta }_{f},\theta )=p(u_{f};\boldsymbol {\eta }_{f},\theta )\) (conditional independence),

$$ J_{f}(\mathbf{u}_{i_{k-1}j})= \int\!\!\!\int \sum_{u_{f}}J_{u_{f}}(\boldsymbol {\eta }_{f};\theta _{j})p(u_{f}; \boldsymbol {\eta }_{f},\theta )g^{(b-1)}(\boldsymbol {\eta})g(\theta _{j}\mid \mathbf{u}_{i_{k-1j}}) \,d\boldsymbol {\eta}_{f}\,d\theta _{j}. $$
(8)

Observe that

$$ I_{U_{f}}(\boldsymbol {\eta }_{f};\theta _{j}) =\sum_{u_{f}}J_{u_{f}}(\boldsymbol {\eta}_{f};\theta _{j})p(u_{f};\boldsymbol {\eta}_{f},\theta ) $$
(9)

is the expected information matrix (Fisher’s information). Thus, we can also write (8) as

$$ J_{f}(\mathbf{u}_{i_{k-1}j})= \int \!\!\!\int I_{U_{f}}(\boldsymbol {\eta }_{f};\theta _{j})g^{(b-1)} (\boldsymbol {\eta}_{f})g(\theta _{j}\mid \mathbf{u}_{i_{k-1}j}) \,d\boldsymbol {\eta }_{f}\,d\theta _{j}. $$
(10)

Also, notice that the resulting expression depends only on (i) the candidate field test-item, (ii) the test taker, and (iii) the test taker’s responses to the preceding k−1 items in the adaptive test. It is easily calculated as

$$ J_{f}(\mathbf{u}_{i_{k-1}j})\approx (ST)^{-1}\sum_{S=1}^{S}\sum_{t=1}^{T}I_{U_{f}} \bigl(\boldsymbol {\eta }_{f}^{(b-1,t)};\theta_{j}^{(s)}\bigr), $$
(11)

where \(\theta _{j}^{(s)}\), s=1,…,S, are the draws from the posterior distribution of θ j after the preceding k−1 items in the adaptive test and \(\boldsymbol {\eta }_{f}^{(b-1,t)}\), t−1,…,T, are the saved draws from the update of the posterior distribution of field-test parameter η f after the previous batch of test takers, b−1. The entries of \(I_{U_{f}}(\boldsymbol {\eta }_{f};\theta _{j})\) for the 3PL model are given in (B.7)–(B.12) in Appendix B.

An obvious criterion for the assignment of field-test items is Bayesian D-optimality (for an application to logistic regression, see Chaloner and Larntz 1989). In the current context, the criterion translates into a maximum expected contribution by test taker j across all field-test items to the determinant of the information matrix relative to its current value (i.e., after the update for batch b−1). More formally, we select the item with the maximum of

$$ \gamma _{D}(f,j)= \det \bigl[J_{f}^{(b-1)}+J_{f}(\mathbf{u}_{i_{k-1}j})\bigr] -\det \bigl[J_{f}^{(b-1)}\bigr], $$
(12)

The calculation of observed information matrix \(J_{f}^{(b-1)}\) at update b−1 is explained in the next section; see (17).

The criterion of D-optimality is readily replaced by any of the other alphabetic criteria. For instance, E-optimality involves minimization of the greatest eigenvalue of the inverse of the information matrix (= asymptotic covariance matrix). In the current context, we would assign the item with the largest reduction of its current greatest eigenvalue; that is, with the maximum of

$$ \gamma _{E}(f,j)=\lambda _{\max}\bigl[\bigl(J_{f}^{(b-1)} \bigr)^{-1}\bigr]-\lambda _{\max}\bigl[\bigl\{ J_{f}^{(b-1)}+J_{f}(\mathbf{u}_{i_{k-1}j})\bigr\} ^{-1}\bigr], $$
(13)

where λ max[⋅] denote the greatest eigenvalue of its argument.

The criterion of A-optimality involves minimization of the sum of the expected reductions of the posterior variances of the individual field-test parameters; or, equivalently, selecting the item with the greatest expected reduction of the trace of the inverse of the information matrix:

$$ \gamma _{A}(f,j)=\operatorname {tr}\bigl[\bigl(J_{f}^{(b-1)} \bigr)^{-1}-\bigl\{ J_{f}^{(b-1)}+J_{f}(\mathbf{u}_{i_{k-1}j})\bigr\} ^{-1}\bigr], $$
(14)

Item calibration under the 3PL model is known for occasional different behavior of each of the estimators of its three parameters, typically with less accuracy for the estimators of a i and c i than for b i . Therefore, it sometimes makes sense to control the contributions to the posterior variances by the individual parameters rather than their joint contribution. For parameter η f , this choice amounts to selection of the item that maximizes

$$ \gamma (\eta _{f},j)=\bigl(J_{f}^{(b-1)} \bigr)_{[\eta _{f},\eta _{f}]}^{-1}-\bigl\{ J_{f}^{(b-1)}+J_{f}( \mathbf{u}_{i_{k-1}j})\bigr\} _{[\eta _{f},\eta _{f}]}^{-1}, $$
(15)

where subscript [η f ,η f ] indicates the diagonal element for η f . Formally, the criterion is an instance of the one of c-optimality used when optimizing the contribution to an arbitrary linear combination of all parameters.

All criteria in (12)–(15) evaluate the absolute contribution by test taker j to the current information about the field-test parameters. A possible effect of using an absolute contribution is preference for the field-test items that have recently been added to the pool. We expect this quick initial calibration to be generally desirable. If not, each of the criteria can easily be made relative by dividing the expression in (12)–(15) by that for the previous update.

Again, observe that each of these optimality criteria is a Bayesian version of a classical criterion studied in the current literature on optimal design for item calibration. The essential Bayesian step is integration of the observed information matrix for the item parameters over the posterior distribution of all unknown elements, which enables us to avoid the bias problem inherent in the use of point estimates of θ in the frequentist approach addressed by Stefanski and Carroll (1985). A different option would have been to formulate similar criteria for an expected update of the posterior covariance matrix of the item parameters, with the expectation based on the posterior predictive probability function for the response on the candidate item (“preposterior analysis”). We have left this alternative route for further research.

4.4 Update of Field-Test Parameters

The second version of the MCMC algorithm in Appendix A is to update the posterior distributions of the field-test parameter η f for batches of test takers b f =1,2,…. The size of batch b f is denoted as \(n_{b_{f}}\).

In the current contexts, the choice of a normal proposal density for θ j with mean and variance calculated from the vector \(\boldsymbol {\theta }_{j}^{(s)}= (\theta _{j}^{(1)},\ldots,\theta _{j}^{(S)})\) of draws collected at the end of the adaptive test seems obvious.

For the three-dimensional parameters η f , a multivariate proposal density leads to faster convergence of the Markov chain than independent univariate densities for their components, and the multivariate normal is easy to work with. We therefore suggest a trivariate normal proposal density centered at the previous draw, with a covariance matrix equal to a rescaled version of the posterior covariance matrix derived from the previous update.

Let \(\varSigma _{\eta _{f}}^{(b)}\) denote the covariance matrix of the proposal density for the update of η f after batch b. It can be obtained recursively from the inverse of the posterior expected information matrix at update b−1 as

$$ \varSigma _{\boldsymbol {\eta }_{f}}^{(b)}= \bigl[ \bigl( \varSigma _{\boldsymbol {\eta }_{f}}^{(b-1)}\bigr) ^{-1}+J_{f}^{(b)} \bigr] ^{-1}, $$
(16)

with

$$ J_{f}^{(b)}=(ST)^{-1}\sum_{j\in b_{f}}\sum_{s=1}^{S}\sum_{t=1}^{T}J_{u_{f}} \bigl(\boldsymbol {\eta }_{f}^{(b-1,t)};\theta_{j}^{(s)}\bigr), $$
(17)

where \(J_{u_{f}}(\boldsymbol {\eta }_{f};\theta _{j})\) is the observed information matrix in (7) for item f and test taker j at update b−1. For its elements, see (B.1)–(B.6) in Appendix B.

Let s be the factor we want to use to rescale matrix \(\varSigma _{\boldsymbol {\eta }_{f}}^{(b)}\) in (16). To prevent time-consuming manual tuning of the factor, which has to be repeated after each new batch of test takers, it is tuned adaptively; that is, while the algorithm runs. Adaptive tuning of an MCMC algorithm can be dangerous in that the process may inadvertently distort the ergodicity of the Markov chain, with loss of convergence to the true posterior distribution as a penalty (e.g., Atchadé & Rosenthal, 2005; Rosenthal 2007). However, adaptation with changes in the scale parameter that fade out across the iterations avoids this pitfall.

A simple procedure for this type of adaptation is the following one based on the Robbins–Monro (1951) method of stochastic approximation. Let v=1,2,…,V denote subsequent blocks of iterations of the MH algorithm for the update of η f (e.g., blocks of 200 iterations each). Further, let a v be the acceptance rate after block v. A reasonable target for the three-parameter case is an acceptance probability of 0.40. The proposed procedure adjusts the scale factor as

$$ s_{v+1}=\max \bigl\{ s_{v}+c_{v}(a_{v}-0.40),\varepsilon \bigr\} $$
(18)

where c v , v=1,…,V, is a sequence of step sizes and ε is an arbitrarily small positive lower bound to avoid negative scaling. For a similar application in confirmatory factor analysis, see Cai (2010).

As just noticed, it is critical that the step sizes decrease monotonically to zero across the blocks. In the empirical example later in this paper, we used s 1=1 as the first scale factor with subsequent adjustments after steps with sizes c v =4/v. Table 2 shows the empirical acceptance rates for this choice during the first 20 blocks of 200 iterations of a run of the algorithm for a typical field-test item.

Table 2. Acceptance rates a v in a typical run of the MH algorithm for the posterior updates of the field-test parameters with adaptive scaling of the proposal covariance matrix during 20 blocks of 200 iterations (target acceptance probability equal to 0.40).
Full size table

In order to calculate the acceptance probability in (A.2) and (A.3), we need the prior densities g(θ j ) and g (b−1)(η f ) for each update. As for the former, again the choice of a normal density with mean and variance calculated from the vector \(\boldsymbol {\theta }_{j}^{(s)}= (\theta _{j}^{(1)},\ldots,\theta _{j}^{(S)})\) of draws collected at the end of the adaptive test is natural. The initial densities g (0)(a f ) and g (0)(c f ) were already given in (3) and (4). For the later updates, a kernel density estimate of g (b−1)(η f ) based on the draws \(\boldsymbol {\eta }_{f}^{(b-1,t)}= (\boldsymbol {\eta }_{f}^{(b-1,1)},\ldots,\boldsymbol {\eta }_{f}^{(b-1,T)}) \) is suggested. The recommended estimate is

$$ g^{(b-1)}(\boldsymbol {\eta }_{f})\approx \frac{1}{T} \sum _{t=1}^{T}K\bigl(\boldsymbol {\eta}_{f};\boldsymbol {\eta}_{f}^{(b-1,t)},\mathbf{H}\bigr), $$
(19)

with a trivariate normal kernel function

$$ K\bigl(\boldsymbol {\eta }_{f};\boldsymbol {\eta}_{f}^{(b-1,t)}, \mathbf{H}\bigr)=(2\pi )^{-3/2}\vert H\vert ^{-1/2} \exp \biggl[-\frac{1}{2}\bigl(\boldsymbol {\eta }_{f} -\boldsymbol {\eta }_{f}^{(b-1,t)}\bigr)^{\prime }\mathbf{H}^{-1} \bigl(\boldsymbol {\eta }_{f} -\boldsymbol {\eta }_{f}^{(b-1,t)}\boldsymbol {\bigr)} \biggr], $$
(20)

where H is a diagonal matrix with bandwidths h a , h b , and h c for the item parameters (e.g., Silverman 1986, Section 4.2.1). As the posterior distributions become quite peaked during later updates, we suggest using small bandwidths, for instance, equal to 0.05 times the variance of the samples from the posterior distributions of the item parameters obtained in the current update.

Observe that \(\varSigma _{\boldsymbol {\eta }_{f}}^{(b)}\) in (16) can also be calculated with \(\varSigma _{\boldsymbol {\eta }_{f}}^{(b-1)}\) replaced by an estimate of the covariance matrix of the transformed parameters η f calculated directly from the previous posterior draws \(\boldsymbol {\eta }_{f}^{(b-1,t)}\). As the differences between the results are expected to be minor, the choice between the two options seems just a matter of convenience.

Also, an entirely different, but attractive proposal distribution for the field-test parameters is a trivariate generalization of the earlier log, regular, and logit normal distributions. The option can be realized as a trivariate normal for the transformed parameters \(\boldsymbol {\eta }_{f}^{\ast }\) in (5) centered at the previous draw with an appropriate transformation of the covariance matrix. For this computationally somewhat more intensive alternative, see (B.13)–(B.17) in Appendix B.

4.5 Resampling and Convergence

Resampling of vectors of earlier draws from the posterior distributions of some of the parameters during an MCMC chain is not common. Our argument in support of the claim of convergence of such chains rests on the fact this type of resampling actually amounts to an MH step in the Gibbs algorithm based on an independence sampler. For an introduction to independence samplers, see Gilks, Richardson, and Spiegelhalter (1996).

Generally, an MCMC algorithm produces a sequence of random variables X (r) that behaves as a Markov chain. If properly implemented, it converges to the distribution we are interested in. Let π(⋅) denote the density of this limiting distribution. Rather than sampling each X (r) directly, the MH algorithm samples from proposal densities q(y∣x (r−1)=x) and then accepts the candidate value Y=y as the realization of X (r) with probability

$$ \alpha \bigl(x^{(r-1)},y\bigr)= \min \biggl( 1,\frac{\pi (y)q(x^{(r-1)}\mid y)}{\pi (x^{(r-1)})q(y\mid x^{(r-1)})} \biggr), $$
(21)

but keeps x (r−1) when Y=y is rejected.

An independence sampler uses a proposal density that does not depend on the previous draw, that is, (21) with q(⋅∣⋅)=q(⋅). Now suppose the saved vector of draws for an ability parameter is from a previously converged chain and large enough to represent its marginal posterior distribution, π(⋅). Resampling the vector is then equivalent to the use of an independence sampler with proposal density q(y)=π(y). This choice yields an acceptance probability equal to one; a conclusion that follows immediately upon substitution of π(⋅) for q(⋅) into (21).

An independence sampler works better, the better q(⋅) mimics π(⋅) (Gilks et al. 1996, pp. 9–10). In our application, we have (approximate) equality, which explains the highly efficient behavior of the first algorithm in Appendix A demonstrated in our evaluation study below.

5 A Few Practical Issues

The proposed calibration design can be used in different contexts. One straightforward option is to set a criterion for the posterior accuracy of the field-test parameters and stop assigning an item when it meets the criterion. This setup can be used to create a “self-replenishing item pool”—that is, a procedure that, upon a satisfactory check on its model fit, promotes an item to operational status as soon as it meets the criterion while at the same time retiring the most obsolete operational item from the pool.

The probability of an item to complete field testing depends not only on its true parameter values, but also on those of the other field-test items as well as the distribution of the abilities of the test takers. As a result, some items may spend more time in the calibration procedure than desirable from a practical point of view. Modifications of the procedure to speed up the calibration of such items include temporarily restricting the assignment to a subset of field-test items, the introduction of special weights, minimaxing over the field-test items with respect to their remaining inaccuracy, etc.

Also, in order to prevent undesirable sudden changes in the content in the test, avoid the danger of clues between any of the field-test and operational items, control the time intensity of the complete test, etc., the assignment of field-test items will generally have to be constrained. The proper framework for implementing constrained optimal assignments of field-test items is a shadow-test approach to adaptive testing (van der Linden 2005, Chapter 9), with a common constraint set for the selection of all items but separate objective functions for the selection of the operational and field-test items based on (2) and (12)–(15) (as well as a few extra technical constraints).

Further exploration of these and other more practical issues is beyond the scope of the current paper, though.

6 Simulation Studies

Two different types of simulation studies were conducted. The goal of the first study was to evaluate the two MCMC implementations for their convergence properties and quality of parameter recovery. The goal of the second study was to compare the results by the calibration design for the criteria of D-optimality in (12) and A-optimality in (14), as well as the special case of the criterion of c-optimality in (15) for the a i parameter only. The choice of the last criterion was motivated by the fact that the a i parameters are generally the ones most difficult to estimate (see Figures 4a–4c and 5 below), and we wondered how much we would gain for them and loose for the other parameters if we focused exclusively on the a i parameters.

6.1 General Setup

All results were based on adaptive tests simulated from a pool of 250 items randomly sampled from an inventory of previously calibrated items that had been shown to fit the 3PL response model. Another set of 50 items was randomly selected from the same inventory to serve as the field-test items in the second study.

Each simulated test taker had a true ability θ randomly sampled from N(−0.317,0.998). The distribution was chosen to be the same as the one fitted to the b i parameters in the operational item pool in Figure 1 to reflect the case of an item pool with difficulties roughly matching the population of test takers it was assumed to support.

The posterior distributions of the η i parameters in the operational pool were taken to be normals centered at the available point estimates of the item parameters with variances set equal to their squared standard errors. The standard errors had ranges a i ∈[0.044,0.227], b i ∈[0.032,0.239], and c i ∈[0.012,0.144]. For each item parameter, 5,000 draws from the posterior distribution were stored in the system for resampling during the use of the first MCMC algorithm in Appendix A at the end of adaptive testing.

All simulated adaptive tests had a length of k=25 items. The items were selected to have maximum Fisher information at the expected a posteriori (EAP) estimates of θ, a currently popular criterion in the practice of adaptive testing. As the main focus was on item calibration, the choice of item-selection criterion was hardly consequential, though. The first item was selected to have maximum information at θ=0. The initial EAP estimates were calculated with N(0,1) as the prior distribution.

As initial prior distribution for the estimation of the field-test parameters η f , we followed our earlier recommendation and used the product of the log, regular, and logit normals for the item parameters with the parameter values in Table 1. Because a common prior distribution does not discriminate between any items, each field-test item was assigned to five simulated test takers with θs randomly sampled from the population. Their posterior distributions after these five test takers were the initial prior distributions used in the study.

The final posterior distributions of the ability parameters during adaptive testing were sampled using the first MCMC algorithm in Appendix A with the implementation precisely as described earlier. Candidate values for the proposal variance \(\sigma _{q_{\theta }}^{2}\) in (6) were selected by running the adaptive test before the main study for 500 simulated test takers at θ=−2(0.1)2 each and estimating the variances of the estimates at each of these θ levels. The candidate proposal variances were set to be 10 % larger than these estimates. They were equal to \(\sigma _{q_{\theta }}^{2}=0.179\) (θ=−2), 0.132 (θ=−1), 0.115 (θ=0), 0.143 (θ=1), and 0.218 (θ=2). In the main simulation study, we used the proposal variance at the level closest to the current posterior mean of θ. Prior density g(θ j ) in (A.1) was always N(0,1).

Likewise, the MCMC algorithm for the sampling from the updated posterior distributions of the field-test parameters was implemented precisely as described above. The proposal density was the trivariate normal for the transformed item parameters centered at the previous draw with the adaptive scale factor in (18) for the covariance matrix. The covariance matrix itself was calculated directly from the previous posterior draws of the field-test parameters. The prior densities in (A.2) and (A.3) were normal densities with the means and variances calculated from the vector of posterior draws \(\boldsymbol {\theta }_{j}^{(s)}=(\theta _{j}^{(1)},\ldots,\theta_{j}^{(S)})\) at the end of the adaptive test and the kernel density estimates in (19) with the earlier suggested bandwidths, respectively.

6.2 Evaluation of the Algorithms

The convergence behavior of the MCMC algorithm for the sampling from the posterior density of θ was checked running it for test takers with different abilities. Figure 2 shows the traceplots for test takers at θ=−2(1)2 for 10,000 iterations of the algorithm after adaptive testing for k=25 items. Based on these results, we decided to run the algorithm in the study reported in the next section with 2,000 iterations for burn in and 5,000 additional iterations with results that were stored for the later updates of the field-test parameters.

Figure 2.
figure 2

Examples of traceplots for 10,000 draws from the posterior distribution of θ for an adaptive test of k=25 items.

Full size image

An obvious measure of the quality of the algorithm is its ability to recover the true values of the θ parameters. In order to check the quality of recovery, the algorithm was run for 1,000 test takers with abilities randomly drawn from the simulated population and adaptive testing for k=25 items. Figure 3 shows the average draws from the posterior distributions (EAP estimates) for the simulated test takers plotted against their true θ values. The estimates are generally accurate. The slight inward bias (visible mainly at the upper end of the scale) is typical of adaptive tests of the current length with the first item selected to be optimal at θ=0.

Figure 3.
figure 3

Average draws from the posterior distributions of θ (EAP estimates) for 1,000 simulated test takers for an adaptive test of k=25 items plotted against their true values.

Full size image

All simulations were run in R, with the computationally more intensive procedures programmed in C, on a PC with an Intel CoreTM i5 CPU, 2.67 GHz and 4 GB of RAM. The average running time of the algorithm required for 7,000 draws from the final posterior distribution of each of the θ parameters for the sample of test takers during the evaluation was less than one second.

The same type of evaluation was repeated for the MCMC algorithm for the update of the posterior distributions of the field-test parameters η f . In this evaluation, nine items were chosen from the set of field-test items to have their difficulty parameters closest to b i =−1.6(0.4)1.6; for their actual values, see Table 3. These items were not yet assigned according to any criterion, but their parameters were estimated from a complete set of data for the items. More specifically, we simulated adaptive testing for k=25 items for a sample of N=1,000 test takers from the population, subsequently generated responses on all nine field-test items for each of them, and then estimated their parameters using the MCMC algorithm in Appendix A. The algorithm was run for 12,000 iterations.

Table 3. True parameter values of the field-test items in the simulation study.
Full size table

Figures 4a–4c show the traceplots for the parameters of each of the field-test items. The results reflect our general experience with MCMC estimation of difficulty and discrimination parameters: excellent convergence and small posterior variance for the former but larger posterior variance for the latter. On the other hand, the results for the guessing parameters were surprisingly favorable given their reputation of occasional convergence problems. Based on these results, we decided to run the algorithm in the study reported in the next section with 2,000 iterations for burn in and 10,000 additional iterations for each of the updates of the posterior distributions of the field-test parameters again.

Figure 4a.
figure 4

Traceplots for 12,000 draws from the posterior distributions of the parameters of nine items for a sample 1,000 test takers and an adaptive test of k=25 items.

Full size image
Figure 4b.
figure 5

Traceplots for 12,000 draws from the posterior distributions of the parameters of nine items for a sample 1,000 test takers and an adaptive test of k=25 items.

Full size image
Figure 4c.
figure 6

Traceplots for 12,000 draws from the posterior distributions of the parameters of nine items for a sample 1,000 test takers and an adaptive test of k=25 items.

Full size image

Figure 5 shows the average posterior draws (EAP estimates) for the field-test parameters plotted against their true values for the sample of 1,000 test takers. The results reflect those reported in the previous figure: excellent recovery of the difficulty and guessing parameters but somewhat less accuracy for the discrimination parameters.

Figure 5.
figure 7

Average draws from the posterior distributions of the parameters of nine field-test items (EAP estimates) for a sample 1,000 test takers and an adaptive test of k=25 items plotted against their true values.

Full size image

The average running time of the algorithm for the total of 12,000 draws from the posterior distributions of field-test parameters for the sample of 1,000 test takers was approximately ten seconds per item.

6.3 Assignment of Field-Test Items

The evaluation was for a design with 50 field-test items, adaptive testing for k=25 items, and the assignment of three field-test items to each test taker after adaptive testing. Four different item-assignment criteria were simulated: D-optimality in (12), A-optimality in (14), c-optimality in (15) for the a i parameters, and random assignment. For all four conditions, the posterior distribution of the field-test parameters of each item was updated each time it had been assigned to a batch of 50 test takers. Each of the conditions was studied for two different stopping rules. The first rule retired an item as soon as a predetermined threshold for each of the posterior standard deviations of its parameters had been reached. The second rule retired each item after a fixed number of administrations. In practice, we expect the first type of rule to be most popular, probably in combination with the second rule as back up for more practical reasons (e.g., maximum number of administrations per item permissible given the numbers of field-test items and test takers).

More specifically, the first stopping rule was used with the thresholds for the posterior standard deviations set equal to 0.1 (a i ), 0.1 (b i ), and 0.025 (c i ) and a maximum of 4,000 administrations as back up. Note that these thresholds were rather ambitious given the current practice of item calibration, especially the one for the a i parameters. Figure 6 shows the cumulative numbers of items meeting the thresholds as a function of the number of test takers simulated. The design had 50 field-test items and 5,000 administrations per item as maximum. The experiment stopped after some 22,000 simulated test takers. Except for the last four or five items, the criterion of D-optimality led to much earlier calibration of the items than A-optimality or random assignment. Clearly, a criterion based on the entire posterior information matrix is more effective than one defined on its diagonal only. For roughly 70 % of the field-test items, D-optimality even worked better than c-optimality for the a i parameter. The difference between A-optimality and c-optimality can only be due to the additional enforcement of the thresholds for the b i and c i parameters. Also, the rather vertical shapes of the curves for these two criteria point at their tendency to minimax between the field-test items; consequently, they retired at approximately the same time. The criterion of D-optimality showed much more discriminatory behavior. Random assignment performed slightly better than A-optimality for the majority of the items. We have been unable to find an explanation for this difference.

Figure 6.
figure 8

Cumulative number of field-test items retired after they reached the thresholds for their posterior standard deviations as a function of the number of test takers simulated for the conditions of D-optimality (D), A-optimality (A), c-optimality for the a i -parameters (c), and random assignment (R).

Full size image

Figure 7 shows the same type of plot for the second stopping rule, with each item being retired after 1,000 assignments. As there were 50 field-test items and each test taker received three of them, the experiment stopped after 16,667 simulated test takers. Use of D-optimality now led to earlier retirement of all items. Also, the nature of its curve demonstrates its discriminatory behavior even better: each time the criterion tended to focus on the same three most favorable items; when they retired, it moved on to the next three. The differences between A-optimality for all three parameters and c-optimality for the a i parameters only were much smaller this time. Random assignment of the field-test items led to the worst result. The average posterior standard deviations of the parameters upon retirement of the items are given in Table 4.

Figure 7.
figure 9

Cumulative number of field-test items retired after 1,000 assignments as a function of the number of test takers simulated for the conditions of D-optimality (D), A-optimality (A), c-optimality for the a i -parameters (c), and random assignment (R).

Full size image
Table 4. Average posterior standard deviations of the field-test parameters after 1,000 test takers.
Full size table

Finally, the average running time for the 12,000 draws from the updated posterior distributions of the parameters of a field-test item across the batches of 50 test takers was less than one second per batch.

7 Discussion

Field testing new items during adaptive testing is attractive in that it generates response data collected under exactly the same operational conditions as for the intended use of the items. Equally important, it offers the opportunity to optimize item assignment using the information in the test takers’ ability estimates obtained during adaptive testing.

The main goal of this research was to explore optimal Bayesian design for item calibration in adaptive testing according to different criteria of optimality. A crucial element of our proposed implementation was the use of MCMC sampling in the two alternate stages of updating (i) the posterior distributions of the test takers θs before the assignment of the items and (ii) the posterior distributions of the field-test parameters, η i , after batches of test takers. The vectors of draws from the two stages were saved both to compute the Bayesian criteria for optimal item assignment and for reuse during the next posterior updates.

Our evaluation suggests a procedure that may be ready for use in operational adaptive testing. Due to the reuse of previous draws from either the item or the persons parameters while updating the others, our running times appeared to be extremely favorable relative to the use of MCMC in traditional calibration with both types of parameters unknown. A metaphor that comes to mind is that of traditional calibration with tentative estimates of the person and item parameters dancing around each other, without either taking the lead. Even worse, because of the dependencies between subsequent draws, their moves are extremely slow. Item calibration in the context of adaptive testing as proposed in this study then amounts to a dance with one of them immediately taking the lead, and consequently much quicker stabilization of the moves of other.

Although the behavior of the criterion of D-optimality was clearly superior, our conclusions from the results of the simulation study are only tentative. More definitive conclusions require study of the criteria of optimality as a function of such crucial parameters as the length of the adaptive test prior to the assignment of any field-test items, the number of field-test items in the pool as well as the distribution of their true parameter values, the choice of prior distributions and size of the batches of test takers for the posterior updates of the field-test parameters, use of content constraints on the assignment of the field-test items to better “hide” them among the regular items, the role of item-exposure control, etc. Generally, we expect the gains in accuracy of the field-test parameter estimates (or possible reduction of the sample size) to be more favorable, the longer the adaptive test, the smaller the batch sizes, and the less stringent the content and exposure constraints. In order to get to know the relative impact of each of these factors for different criteria of optimality, additional studies are planned.

As a final advantage of adaptive over traditional item calibration, we point at the fact that the new item parameter estimates are automatically on the same scale as the current operational items. There is thus no need to select any anchor items and conduct a post hoc study linking the new estimates to a previous scale. Alternatively, we may think of adaptive item calibration as calibration with the best implicit set of anchor items possible—the entire operational item pool.