Introduction

The ultimatum (take-it-or-leave-it) bargaining game has been the subject of intense scrutiny by behavioral economists for more than three decades. This two-stage, sequential-move bargaining game begins when a giver offers a taker a share of a monetary pie. If the taker accepts the offer, the game ends and both players receive their share of the proposed distribution. If the taker rejects the offer, the game ends and both players get nothing. Figure 1 illustrates the ultimatum game in which the bargaining set has been normalized to 1. This game has an infinite number of subgames, each corresponding to proffered shares β ∈ [0, 1]. Every decision node between 0 and 1 constitutes an information set that begins a proper subgame.

Fig. 1
figure 1

Ultimatum Game

Full size image

In general, subgame perfection in bargaining games involves two purely rational, risk neutral players with payoffs that are monetary and transferrable, and defines utility as a monotonically increasing function of a player’s share. In Fig. 2, the giver’s utility (U G ) is measured from the lower left-hand corner, and the taker’s utility (U T ) is measured from the upper right-hand corner. In this zero-sum game, an increase in one player’s share of the monetary pie results in an equivalent reduction in the share received by the other player. The bargaining set is the share of distributions along the diagonal line connecting points G and T.

Fig. 2
figure 2

Purely Rational Choice and Players’ Share Distributions

Full size image

If the players in Fig. 2 are purely rational and make decisions that are in their own narrow self-interests, neither player derives utility from the share received by the other player. In the figure, the indifference curves of the giver and the taker are linear, where \( {U_G}>U_G^{\prime } \) and \( {U_T}>U_T^{\prime } \). The giver’s utility is maximized at point G, where the giver gets everything and the taker gets nothing; the taker’s utility is maximized at point T, where the taker gets everything and the giver gets nothing. In games involving multiple offers and counteroffers, where the players have symmetric bargaining power and perfect information and the negotiations are frictionless, the predicted subgame perfect equilibrium is an even split of the monetary pie. This occurs at U G and U T on the diagonal at point E. This equitable distribution is consistent with the prediction of the minimax theorem (Neumann 1928).

By contrast, the predicted subgame perfect equilibrium in the ultimatum game is for a purely rational giver to offer an arbitrarily small share somewhere in neighborhood of point G, and for the taker to accept (Stahl 1972; Rubenstein 1982). This is due to the fact that the taker has two sequentially rational strategies: either (1) accept all offers (β) by the giver, or (2) accept all offers of 0 < β ≤ 1 and reject an offer of β = 0. Subgame perfection requires the taker to reject β = 0 and accept any offer of 0 < β ≤ 1, since every point along the bargaining set is preferred to the disagreement points d. Thus, the taker should accept any positive offer, no matter how small, since something is better than nothing.

Ultimatum Paradox

Analyses of what can be called the ultimatum paradox began with a two-trial experiment by Güth et al. (1982) in which members of a group of proposers (givers) were paired with members of another group of responders (takers). Each giver was told to offer a share of between DM 4 and DM 10 to a taker. If the taker accepted the offer, both players would keep their share of the proposed distribution. If the offer was rejected, the players would receive nothing. Either way, the game ends. Researchers found that proffered shares were inconsistent with predictions based on purely rational behavior. In the first part of the Güth experiment, givers offered takers an even split 7 of 21 times, with a mean offer of 37 %. In only one instance was the proposed distribution rejected. When the experiment was repeated a week later with the same test subjects, givers’ offers were less generous, but still greater than the predicted small amounts. Givers offered takers a 50–50 split in only two instances. The mean offer fell to 32 %, and offers were rejected in 5 of 21 cases. In a separate experiment, a different group of 37 test subjects were told that they would be playing the game twice—first as a giver then as a taker. In this trial, the mean and median offers were 45 and 39 %, respectively.

In the years following publication of the Güth study, numerous experimental trials were conducted controlling for sex, age, social, institutional and cultural factors, degrees of player anonymity, size of the monetary pie, length of the game, etc.Footnote 1 In a study of 15 culturally-diverse tribal societies, Henrich et al. (2005) found that takers tended to reject offers less than 30 %, and sometimes rejected offers less than 40 %. Camerer (2003, Ch. 2) reported that offers of 35 to 45 % were typical, that offers tended to decline over time, and that there was a low and non-negligible frequency of rejection after multiple rounds. Subsequent experimental trials support Güth’s original finding that givers routinely offer shares that are significantly greater than the minimum predicted by purely rational behavior.

Pure versus Bounded Rationality

Many theoretical game theorists were initially skeptical of the experimental evidence of giver generosity and suspected that test subjects were either ill-informed or that the trials were poorly constructed. However, according to Camerer and Thaler (2003), the experimental evidence could be explained in terms of bounded rationalityFootnote 2:

“Economists and game theorists have long used two standard assumptions in modeling behavior: rationality and self-interest. These working assumptions persisted in spite of growing experimental evidence that both rationality and self-interest are ‘bounded.’ In game theoretic contexts, evidence that people care how much others get was abundant: In a standard one-trial prisoner’s dilemma game, where rational selfish choice is to defect, roughly half the players cooperate.” (p. 159)

According to this interpretation, givers make generous offers because they value the approval of others. The assumption of bounded rationality suggests that indifference curves are not linear as in Fig. 2, but convex with respect to the origin as in Fig. 3. For example, suppose that a giver believes that a 70–30 split is fair and the taker believes that a 50–50 split is fair. If negotiations involving multiple rounds of offers and counteroffers are frictionless, and information, bargaining power, and player impatience are symmetrical, subgame perfection will occur somewhere along the diagonal in Fig. 3 in the interval between points A and B, such as point E.

Fig. 3
figure 3

Bounded Rationality

Full size image

The assumption of purely rational behavior is controversial. Critics argue that this is equivalent to assuming that individuals act in their own narrow self interests and that altruism in economic decision-making is anathema. Jean Ensminger commented that proponents of rational choice “…come close to endorsing the caricature of completely rational, perfectly informed, narrowly self-interested homo economicus, maximizing his (sic) way through life by mechanically calculating the narrow costs and benefits of every decision.” (1996, p. 12)

More recently, this dogmatic view has evolved to recognize that economic agents do not always act in their own narrow self-interest (Simon 1957), and that altruism is a by-product of cultural mores and values (see, for example, Hornstein et al. 1968; Hornstein et al. 1971; Kalt and Zupan 1984; North 1990). According to Ensminger, “while rational choice concerns means-ends relationships, economists have used far too narrow a concept of ends, neglecting obvious evidence of considerable behavior motivated by ideological or altruistic ends, and far too broad a concept of means neglecting the costliness of information and the considerable constraints placed on choice by social norms and institutions.” (1996, p. 13) It has even been argued that altruism may, in fact, be genetic (Frank 1988). Whatever the explanation, bounded rationality diverges from narrow self-interest in several interesting ways. In repeated games with an uncertain end, for example, it may be in a player’s long-run best interest to be altruistic if it fosters future cooperation for mutual benefit, even when this results in a less-than-optimal short-run outcome (Axelrod 1984; Taylor 1987).

Part of the debate surrounding the correct interpretation of the experimental data may come from confusing fairness with generosity. Fairness does not imply altruism, although altruism seems to embody a basic sense of fairness. A giver who acts fairly treats all takers equitably, even if this involves small offers. A giver who makes large offers may be described as both fair and generous. This distinction raises an interesting issue. A taker may prefer large shares, but may not reject small but fair offers. Ensminger noted that, “…it is possible that people will accept unequal outcomes, as long as they are the result of fair play within the accepted rules….” (1996, p. 154) A giver who values social approbation may make public offers that are more than fair since being regarded as a generous person generates positive utility. This would also seem to suggest that private offers made to strangers may be less generous, either because there is no good-guy premium, or because parsimonious offers go unpunished.

To control for the effects of peer pressure, several ultimatum game experiments were conducted involving the use of computers (Blount 1995; Rilling et al. 2004; Wout et al. 2006), groups of players (Robert and Carnevale 1997), and autists (Hill and Sally 2002). These experiments support Thaler’s (1988) conclusion that fairness is an important determinant in the size of proffered shares. Interestingly, similar behavior was exhibited by test subjects with a background in game theory for whom the concept of pure rationality is well understood (Carter and Irons 1991; Frank et al. 1993; Kahneman et al. 1986).

Neurological laboratory experiments also support the fairness hypothesis. Zak et al. (2007) found that test subjects tended to make more generous offers after receiving varying doses of oxytocin.Footnote 3 In brain-imaging experiments, Sanfey et al. (2003) attempted to identify the neural correlates of decision-making. They concluded that a basic sense of fairness was fundamental to interpersonal and societal behavior. Crockett et al. (2008) observed that givers with artificially lowered levels of serotonin tended to offer larger shares, and that takers tended to reject a greater proportion of offers without exhibiting changes in mood, fairness judgments, basic reward processing, or response inhibition.Footnote 4 Each of these experiments have led researchers to conclude that rational behavior is tempered by a basic sense of fairness. According to Camerer and Thaler, “…people care how much others get….” (2003, p. 159) In spite of this conclusion, the question remains: were givers being fair, generous, or both?

Uncertainty

If the ultimatum game is characterized by perfect information, it will be in the best interest of a purely rational givers’ to make offers that takers consider fair, since unfair offers will be rejected. Under what circumstances might a purely rational giver offer a more-than-fair (generous) share? To answer this question, it is first necessary to redefine the bargaining surplus in the ultimatum game.

It is typically assumed that the bargaining surplus in the ultimatum game is the entire monetary pie. It can be reasonably argued, however, that the bargaining surplus is only one-half the monetary pie. To see why, consider the bargaining scenario in which management and labor simultaneously submit bids for a share of a firm’s excess profits, as specified in a collective bargaining agreement. If the sum of the bids are equal to, or less than, the total amount of the excess profits, both players receive their bids, with any unclaimed portion distributed to shareholders. If the sum of the bids exceed the bargaining surplus, the bidders receive nothing and must resubmit their bids. To avoid the possibility of this game being infinitely repeated, each bidder is penalized a share of the excess profits for failing to come to an agreement to defray mediation costs.

This bargaining game sounds suspiciously like the ultimatum game, but it has two crucial differences. To begin with, this bargaining game is static, not sequential. Moreover, there are no givers and takers. Unlike ultimatum bargaining, neither player owns the monetary pie at the outset of the game. If information is perfect, bargaining power symmetrical, and negotiations frictionless, the Nash equilibrium strategy profile is for both players to submit bids equal to one-half of the monetary pie, such as point E in Fig. 2.

By contrast, a giver in the ultimatum game dictates a share distribution, which the taker can either accept or reject. The experimental evidence makes it clear that a giver will retain at least half of the monetary pie and offer all or part of what is left over. Thus, the bargaining surplus in the ultimatum game is only one-half the monetary pie. Thus, the sum of the shares of the bargaining surplus is s T  + s G  = ½, where s T and s G are taker’s and giver’s shares, respectively.

In this setting, the giver offers β = s T  ≤ ½ of the monetary pie. If the offer is accepted, the final distribution of the monetary pie is (1–β, β), where the giver’s share is s G  + ½ = (1–β) ≥ ½. For example, if an offer of half of the bargaining surplus is accepted, the taker’s share is β = s T  = ½ · ½ = ¼ and the giver’s share is s G  + ½ = (1 – β) = ¼ + ½ = ¾.

In the ultimatum game, a purely rational giver with narrow self-interests would like to offer a zero share. Since this proposed distribution will be rejected, a purely rational giver will offer the smallest share that will not be rejected. The smallest share that will not be rejected is the taker’s minimum acceptable fair offer. In an ultimatum game with perfect information, the giver will offer the minimum acceptable fair share. On the other hand, if the ultimatum game is characterized by asymmetric information, this minimum fair share is not known by the giver with certainty. The best the giver can do is to infer the cumulative probability distribution of all possible reservation offers. The expected value of the reservations offers approximates the fair-share social norm. This probability distribution, which is determined by nature, may be summarized as

$$ \begin{array}{*{20}{c}} {Pr\left\{ {\left( {{{s}_{T}} + s_{G}^{*}} \right) \le 1/2} \right\} = F\left( {{{s}_{T}} + s_{G}^{*}} \right) = F\left[ {1 - \left( {s_{T}^{*} + {{s}_{G}}} \right)} \right];} \\ {Pr\left\{ {\left( {s_{T}^{*} + {{s}_{G}}} \right) \le 1/2} \right\} = F\left( {s_{T}^{*} + {{s}_{G}}} \right) = 1 - F\left[ {\left( {{{s}_{T}} + s_{G}^{*}} \right)} \right].} \\ \end{array} $$
(1)

Formally, the problem is to simultaneously minimize the taker’s share (s T *) and maximize the giver’s share (s G *) of the bargaining surplus, which is one-half the monetary pie. The subgame perfect strategy profile {s T *, s G *} may be determined by solving the problem

$$ \begin{array}{*{20}c} {\mathop{\min}\limits_{{{s_T}\ }}{s_T} F\left[ {\left( {{s_T}+s_G^{*}} \right)} \right]+s_G^{*}\bullet \left\{ {1-F\left[ {\left( {{s_T}+s_G^{*}} \right)} \right]} \right\};} \hfill \\ {\mathop{\max}\limits_{{{s_G}}}s_G^{*} F\left[ {\left( {s_T^{*}+{s_G}} \right)} \right]+{s_G}\bullet \left\{ {1-F\left[ {\left( {s_T^{*}+{s_G}} \right)} \right]} \right\}.} \hfill \\ \end{array} $$
(2)

By solving the first-order conditions for Equations (2), we obtain

$$ \begin{array}{*{20}c} {F\left[ {\left( {s_T^{*}+s_G^{*}} \right)} \right]=s_G^{*}\bullet f\left[ {\left( {s_T^{*}+s_G^{*}} \right)} \right]-s_T^{*}\bullet f\left[ {\left( {s_T^{*}+s_G^{*}} \right)} \right];} \hfill \\ {1-F\left[ {\left( {s_T^{*}+s_G^{*}} \right)} \right]=s_G^{*}\bullet f\left[ {\left( {s_T^{*}+s_G^{*}} \right)} \right]-s_T^{*}\bullet f\left[ {\left( {s_T^{*}+s_G^{*}} \right)} \right].} \hfill \\ \end{array} $$
(3)

It is a relatively straightforward matter to show that the second-order conditions for this optimization problem are satisfied. By simultaneously solving Equations (3), we obtain the solution values

$$ s_G^{*}-s_T^{*}=\frac{1}{{2f\left( {s_T^{*}+s_G^{*}} \right)}}. $$
(4)

Equation (4) says that the difference in bargaining shares equals one-half the reciprocal of the value of the assumed density function.

To generate more intuitively appealing results, suppose that the giver believes that takers’ reservation offers are normally distributed [s T  ~ N(μ, σ 2)] somewhere in the interval [0, ½] with mean μ and variance σ 2, that is

$$ f\left( {{s_T}+s_G^{*}} \right)=\frac{1}{{\sqrt{{2\pi {\sigma^2}}}}}exp\left\{ {-\frac{1}{{2{\sigma^2}}}{{{\left[ {\left( {{s_T}+s_G^{*}} \right)-\mu } \right]}}^2}} \right\}. $$
(5)

Since fair shares are symmetrically distributed around the mean and median, s T  + s G * = (s T * + s G *)/2, Equation (4) may be rewritten as

$$ s_T^{*}-s_G^{*}=\frac{{\sqrt{{2\pi {\sigma^2}}}}}{2}. $$
(6)

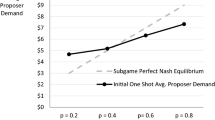
Equation (6) says that the distribution of the bargaining surplus in the ultimatum game depends on the giver’s uncertainty about the taker’s reservation offer. Suppose, for example, that μ = ¼.Footnote 5 If the offer is accepted, the subgame perfect equilibrium shares of the bargaining surplus are

$$ \begin{array}{*{20}c} {S_T^{*}=\frac{1}{4}+\frac{{\sqrt{{2\pi {\sigma^2}}}}}{4};} \hfill \\ {S_G^{*}=\frac{1}{4}-\frac{{\sqrt{{2\pi {\sigma^2}}}}}{4}\ .} \hfill \\ \end{array} $$
(7)

Equation (7) allows us to make predictions about s T that are consistent with the experimental evidence. In particular, these results tell us that even a purely rational giver will offer a more than fair (generous) share when the taker’s reservation offer is not known with certainty. Moreover, this offer becomes more generous the greater the uncertainty. Suppose, for example, that the giver’s uncertainty about the taker’s reservation offer as measured by the variance is σ 2 = 0.02, and the subgame perfect share distribution is (1 – β, β) = (0.62, 0.38). If the giver’s uncertainty about the taker’s reservation offer declines to σ 2 = 0.01, as was observed in repeated experimental trials involving the same test subjects, or the giver has information about the taker’s preferences, the proffered share declines to s T * = 0.31. In this case, the subgame perfect share distribution is (1 – β, β) = (0.69, 0.31).

This analysis offers a complementary explanation of the experimental evidence. Namely, it is not necessary for givers to have a taste for fairness to explain generous offers. This is because it is in the best interest of even purely rational givers, who act in their own narrow self-interests to offer shares that will not be rejected. In ultimatum games characterized by asymmetric information about the taker’s reservation offer, it is in the best interest of all giver types to make more-than-fair (generous) offers, since this decreases the probability of rejection. As a giver’s uncertainty about the taker’s reservation offer declines, proffered shares will approach the taker’s reservation offer.

Summary and Conclusions

The ultimatum (take-it-or-leave-it) bargaining game has been the subject of intense scrutiny by game theorists and behavioral economists for more than three decades. This two-stage, sequential-move bargaining game begins when a giver offers a taker a share of a monetary pie. If the taker accepts the offer, both players receive their share of the proposed distribution. If the taker rejects the offer, both players receive nothing.

If the players are purely rational, the predicted subgame perfect equilibrium is for the giver to make a small offer, and for the taker to accept since something is better than nothing. Experimental trials have demonstrated, however, that givers typically offer generous shares, and that takers almost always reject small offers. A popular interpretation of these results is that givers have a taste for fairness. According to Camerer and Thaler, the “evidence that people care how much others get was abundant.” (2003, p. 159) In other words, the behavior of givers is more properly characterized as boundedly rational.

The analysis presented in this paper argues that it is not necessary for givers to have a taste for fairness to explain the generous offers. In ultimatum games characterized by asymmetric information, even purely rational givers will make more-than-fair (generous) offers to increase the probability that an offer will not be rejected. As a purely rational giver’s uncertainty about the taker’s reservation offer declines, proffered shares approach the taker’s reservation offer.

The main implication of the analysis presented in this paper is not that players in bargaining games have a proclivity for making fair offers. Rather, players in bargaining games expect to be treated fairly. Otherwise, negotiations will break down. An interesting extension to this research is the effect of differential bargaining power on a player’s negotiating strategy. In general, we would expect players with more bargaining power to be less generous. According to Jean Ensminger, “the relationship between distribution and ideology is complex. In cases where the size of the pie remains the same but bargaining power is used to redistribute the shares, we may predict a threat to ideological legitimacy.” (1996, p. 172)