Publication bias is the phrase used to describe the state of affairs when published research on a topic is systematically unrepresentative of the population of completed studies on that topicFootnote 1. Publication bias is problematic, because, when the results of readily available research differ from the results of all the research that has been done in an area, readers and reviewers of that literature may end up drawing an erroneous conclusion about what that body of research shows. At times, this can have serious repercussions, as when an ineffective or dangerous treatment is falsely viewed as safe and effective. This has been shown most clearly in the case of alleged deliberate withholding of negative data by pharmaceutical companies. In 2004, for example, GlaxoSmithKline was sued by Elliott Spitzer, attorney general of New York State, for failing to release data about the lack of efficacy and increased suicide risk associated with the use of Paxil, a selective serotonin reuptake inhibitor (SSRI) antidepressant, by children and teenagers, (NY vs GlaxoSmithKline 2004). In the same year, Merck recalled Vioxx, a popular arthritis drug, because of side effects that included serious kidney and heart problems. Merck maintained that it recalled Vioxx as soon as the data indicated a high prevalence of adverse effects, but it became embroiled in controversy as others claimed that Merck had concealed adverse event data for years (Wall Street Journal, November 1, 2004), a view supported by a meta-analysis of all available randomized trials of adverse effects by researchers from Harvard (Zhang et al. 2006).

In criminology, the effects of publication bias are not likely to be deliberate or as dramatic, but they can still have important consequences for individuals, organizations and society. If, for example, a treatment for incarcerated offenders is less effective than a review shows it is, because unfavorable data do not appear in the review, both the treated individuals and the public may suffer. McCord (2003) has done an excellent job highlighting the fact that interventions in criminal justice intended to help may sometimes harm; to the extent that publication bias exists in systematic reviews in this area, this problem may be more widespread than previously thought.

Publication bias is a potential problem threat to the validity of all types of research, including qualitative research, primary quantitative studies and narrative reviews, not only to meta-analysis. Although publication bias has probably existed since research began to be publicly reported, it has received sustained attention only since meta-analysis became popular. In large part, this is because, as methods of reviewing have become more systematic and quantitative, it has actually become feasible to demonstrate the existence of publication bias and to quantify its impact. Although publication bias is problematic for all types of research, it is particularly problematic for meta-analytic work, since systematic reviewers have claimed that meta-analysis is a more valid means of reviewing research than is a narrative review (e.g., Egger et al. 2000). If, however, the sample of studies retrieved for review is biased, the validity of the meta-analytic results is compromised, no matter how well done it is in other ways. This is not a hypothetical concern: evidence clearly shows that publication bias has had an impact on meta-analyses in many areas.

Dickersin (2005) provides a concise and compelling summary of several decades of research, which shows that publication bias exists in the social and biomedical sciences, for both observational and experimental studies. This research includes direct evidence, including editorial policies, results of surveys of investigators and follow-up of studies registered at inception, all of which indicate that non-statistically significant studies are less likely to be published, and, if they are, they will be published more slowly than significant ones. It also includes indirect evidence that provides convincing evidence of publication bias, including the over-representation of significant results in published studies and negative correlations between sample size and effect size in collections of published studies. Dickersin’s review indicates that researchers themselves appear to be a key source of publication bias, through failure to submit for publication research whose major results do not reach statistical significance. Bias at the editorial level has also been implicated. In addition to the evidence that whole studies are selectively missing are demonstrations by Chan and colleagues (Chan et al. 2004; Chan and Altman 2005) that reporting of outcomes within studies is often incomplete and biased, due to selective withholding of statistically non-significant results.

An informal review of published systematic reviews in the area of crime and justice (including those published in this journal) shows that only a minority has considered publication bias at all, and, of those that did, few conducted any analyses to assess it. To the extent that crime and justice systematic researchers have addressed publication bias, they have generally either compared the magnitude of the effects from published and unpublished studies in their review (cf. Illescas et al. 2001; Losel and Schmucker 2005) or they have conducted a file-drawer analysis and calculated a failsafe N (cf. Deffenbacher et al. 2004; Dreznick 2003; Pratt et al. 2002). While the authors of these reviews are to be commended for attending to the problem of publication bias, comparison of the effect sizes from published and unpublished sources does not provide a complete assessment of the effects of publication bias on the results of a systematic review, since we have no way of determining whether the retrieved unpublished studies are representative of all unpublished studies. It seems likely that the more easily retrieved unpublished studies (such as those presented at conferences, or technical reports) would not be representative of those unpublished studies that were not retrieved (such as those the researchers never made public at all). Furthermore, while file-drawer analysis (failsafe N) was the only statistical technique for assessing publication bias through the mid 1990s, newer and better methods have been available for several years. These newer methods are being used with increasing frequency in healthcare meta-analyses, as well as in psychology and in other areas of scientific research but, apparently, not in criminology. In the only reference I could find to any of these methods in published crime and justice meta-analyses, Braga (2005) mentions that he conducted a trim-and-fill analysis of the hotspots policing data and states that “when a trim-and-fill analysis is run on these data, the random effects model does not generate substantive changes” to his findings, but he does not provide the results in his article. In the same paragraph he voices a widely held misperception of publication bias, namely that if a review includes unpublished studies, then publication bias is not a serious threat.

In the remainder of this paper I offer a brief overview and critique of the failsafe N method, introduce several methods for examining publication bias that are in current use in other areas of social science and in healthcare, and illustrate the application of these methods to a recently published criminology meta-analysis. Finally, I note the shortcomings of current means of publication bias assessment.

The failsafe N (file drawer analysis)

Robert Rosenthal called attention to the “file drawer problem” in 1979, in the very earliest days of meta-analysis. (Rosenthal 1979). He was concerned that meta-analytic results could be wrong, due to non-significant studies that remained in researchers’ file drawers. Specifically, he considered the possibility that the inclusion of these studies would nullify the observed effect (by which he meant that their inclusion would reduce the mean effect to a level not statistically significantly different from zero). To attack this problem empirically, Rosenthal developed a formula to enable meta-analysts to calculate the number of zero-effect studies that would be required to nullify the effect. Rosenthal’s method was based on the test of combined significance (the sum of Zs). Given a sum of Zs for the studies in the meta-analysis that is statistically significant (in other words if Z is larger than the critical value for significance), Rosenthal’s test computes the number of additional studies with Z values averaging zero that would be required to reduce the overall Z to a value lower than the critical value. This number was termed the failsafe N by Rosenthal’s student, Harris Cooper (1979).

While Rosenthal deserves credit for his early attention to the issue of publication bias in meta-analysis, his approach is of limited usefulness for several reasons. First, it focuses on the question of statistical significance rather than practical or theoretical significance. That is, it asks “How many missing studies are needed to reduce the effect to statistical non-significance?” but does not tell us how many missing studies need to exist to reduce the effect to the point that it is not important. Second, the formula assumes that the mean effect size in the hidden studies is zero, although it could as easily be negative (which would require fewer studies to nullify the effect), or positive but small. Third, the failsafe N is based on significance tests that combine P values across studies, as was Rosenthal’s initial approach to meta-analysis. Today, the common practice is to cumulate effect sizes rather than P values, and if a P value is computed at all, it is computed for the mean combined effect. Rosenthal’s failsafe formula is not suitable for this approach. Furthermore, the failsafe N method can be used only with a fixed effect model. Finally, although this method may allow one to conclude that the mean effect is not entirely an artifact of publication bias, it does not provide an estimate of what the mean effect might be once the missing studies are included.

Orwin (1983) proposed a variant on the Rosenthal formula, which addresses two of these issues, in that the Orwin method shifts the focus to practical rather than statistical significance, and that it does not necessarily assume that the mean effect size in the missing studies is zero. This enables the researcher who uses Orwin’s method to determine how many hidden studies would bring the overall effect to any specified level of interest. The researcher can, therefore, select a value that represents the smallest effect considered practically or theoretically important and ask how many missing studies of an average specified effect it would take to bring the mean effect below this point. In theory, this could allow the researcher to model a series of distributions for the missing studies. Orwin’s variant does not, however, address the other criticisms of the failsafe method. While the failsafe N approach may allow us to rule out the possibility that the entire meta-analytic effect is due to bias, this is typically not the (only) question of interest. Newer techniques are available to provide information about the possible existence and impact of publication bias in a meta-analysis and should be used routinely to supplement, or replace, the calculation of failsafe Ns.

Alternative techniques for assessing publication bias

Three types of techniques have been developed to help meta-analysts approach the problem of publication bias. Each type addresses a different aspect of the problem. The first type addresses the question of whether there is evidence that publication bias exists in a given meta-analysis. . Techniques which address this question include a graphical diagnostic called the funnel plot (Light and Pillemer 1984) and two statistical tests (Begg and Mazumdar 1994; Egger et al. 1997). The second type examines whether publication bias has had a noticeable impact on the meta-analytic results. This is a variant of cumulative meta-analysis (Borenstein 2005). The third type asks how the results would change after they had been adjusted for the possible effects of publication bias under some explicit model of publication selection., This type includes Duval and Tweedie’s trim-and-fill method (Duval 2005; Duval and Tweedie 2000a, b), Hedges and Vevea’s general selection model approach (Hedges 1992; Hedges and Vevea 1996, 2005) Copas’ selection model approach (Copas 1999, Copas and Shi 2001) and Richy and Reginster’s (2006) method using the sum of moments of forces. In the current paper, I will provide an introduction to methods representing each type of technique. Criteria for inclusion of specific methods are that: (a) they are in current use in other areas of social science and/or healthcare, (b) their statistical properties are well known, and (c) they are conceptually simple and involve relatively little computation. The Hedges–Vevea and Copas methods have been excluded, as they are not often used, are technically complex and involve considerable computation. The Richy and Reginster method is not included, because it has been tested on only two data sets, its statistical properties are not well known, and it has not been validated against any other approach. Readers interested in advanced selection modeling may wish to consult Hedges and Vevea (2005).

The reader is alerted at the outset that nearly all of these methods use the relationship between sample size and effect size as an indicator of possible bias. This has its basis in the extensive evidence showing that the statistical significance of a study is predictive of publication status, and that the probability of achieving statistically significant results is correlated with sample size (see Dickersin 2005, above). Large studies are likely to achieve statistical significance, even if the effects they demonstrate are relatively small; small studies, on the other hand, will reach statistical significance only if they yield large effects. Of course, smaller studies may show larger effects for a variety of reasons (See Weisburd et al. 1993 for a thorough discussion of what these reasons may be in criminology research) in addition to publication bias. Sterne et al. (2001b) have suggested that the term “small study effect” should be used instead of “publication bias” when describing the results of these methods, in recognition of the fact that, while they may detect a relationship between sample size and effect size, they cannot assign a causal mechanism to it. My view is that finding that sample size and effect size are (negatively) related should be seen as a sign that the researcher needs to (re)examine carefully the data to ascertain whether there are plausible alternative explanations for the small study effects (reflecting true heterogeneity in the effect sizes) or if publication bias seems the likeliest explanation. When no relationship between sample size and effect size is apparent, the researcher can have increased confidence that the validity of the meta-analytic results is not threatened by study selection on the basis of statistical significance.

Techniques used to detect evidence of possible bias

The funnel plot

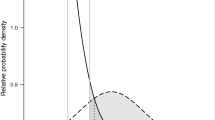
The funnel plot, in its most common form, is a display of an index of study size (usually presented on the vertical axis) as a function of effect size (usually presented on the horizontal axis). Large studies appear toward the top of the graph and generally cluster around the mean effect size. Smaller studies appear toward the bottom of the graph and (since smaller studies have more sampling error variation in effect sizes) tend to be spread across a broad range of values. This pattern resembles a funnel, hence the plot’s name (Light and Pillemer 1984; Light et al. 1994).

This method assumes that, in the absence of publication bias, the studies will be distributed symmetrically about the mean effect size. In the presence of bias, on the other hand, the bottom of the plot will show a larger concentration of studies on one side of the mean than on the other. This reflects the idea that smaller studies (which appear toward the bottom) are more likely to be published if they have larger than average effects, since these studies are likelier to be statistically significant.

Sterne et al. (2005) have noted that the choice of an effect size index may have an effect on the shape and symmetry of the funnel plot. Standardized mean differences may be plotted as they are. Correlations, however, need to be transformed to Fisher’s z before being plotted. The logarithmic odds ratio is preferable to other indices used with binary data, such as the logarithmic risk ratio, and plots of the risk difference are problematic and not recommended. Sterne et al. also point out that the index used to represent study size will affect the way studies are dispersed on the plot and, thus, influence the researcher’s ability to detect bias. They recommend the use of the standard error (rather than sample size or the inverse standard error) for this purpose, although the inverse standard error (precision) seems to be the most frequent choice among social scientists. Finally, they suggest that it may be helpful to superimpose guidelines on the funnel plot to show the expected distribution of studies in the absence of bias. These guidelines can help to identify outliers and facilitate the process of detecting asymmetry. (See also Sterne and Egger 2001).

Figure 1a shows a symmetrical funnel plot of standardized mean differences (d) as a function of precision, while Fig. 1b shows an asymmetrical funnel using the same indices.

Fig. 1
figure 1

Illustration of symmetrical and asymmetrical funnel plots. a Symmetrical funnel plot. b Asymmetrical funnel plot (Std diff standardized difference, Std Err standard error)

Full size image

While the funnel plot is appealing because it offers an immediate visual sense of the relationship between effect size and precision, it is limited by the fact that its interpretation is largely subjective. To address this limitation, two statistical tests have been developed to quantify the amount of bias depicted in the funnel plot.

Statistical tests for the assessment of publication bias

Begg and Mazumdar developed a statistical test to detect publication bias based on the rank correlation (Kendall’s tau) between the standardized effect size and the variances (or standard errors) of these effects (Begg and Berlin 1988; Begg and Mazumdar 1994; Begg 1994). Tau is interpreted as one would interpret any correlation, with a value of zero signifying no relationship between effect size and precision, and departures from zero indicative of the presence of a relationship. If asymmetry is caused by publication bias, we expect that high standard errors (small studies) will be associated with larger effect sizes. The general recommendation is to perform a one-sided significance test., because it increases the statistical power of the test, but a two-sided test is probably more justifiable conceptually. A significant correlation suggests that bias may exist but does not address the consequences of the bias. In particular, it does not suggest what the mean effect would be in the absence of the putative bias. Furthermore, Sterne and Egger (2005) have advised against the use of this test unless the meta-analysis includes a range of study sizes, Based on a simulation, Sterne et al. (2000) reported that there was an inflated type I error rate when the effect size was very large, or when all studies in the meta-analysis had similar sample sizes, or when none of the included studies was medium or large. They also noted that the test has low power unless there is severe bias or the meta-analysis contains a large number of studies (more than 25), and they caution that a non-significant tau should not be taken as proof that bias is absent. Given that most systematic reviews in crime and justice include meta-analyses of fewer than ten studies, and many have fewer than five, it is hard to recommend use of this method in criminology reviews.

Egger has developed a linear regression method (Egger et al. 1997), which, like the rank correlation test, is intended to quantify the bias pictured in a funnel plot. It differs from Begg and Mazumdar’s test in that Egger uses the actual values of the effect sizes and their precision, rather than ranks. Egger’s test uses precision (the inverse of the standard error) to predict the “standardized effect,” In this equation, the size of the standardized effect is captured by the slope of the regression line (B1), while bias is captured by the intercept (B0). The intercept in this regression corresponds to the slope in a weighted regression of the effect size on the standard error. When there is no bias, the intercept is zero. If the intercept is significantly different from zero, there is evidence of asymmetry, suggesting bias. As was true for the rank correlation test, a one-tailed significance test will increase the power of the test, but a two-tailed test has more conceptual justification.

Sterne and Egger (2005) report that power for this test is generally higher than power for the Begg and Mazumdar method but that it is still low, unless there is severe bias or a substantial number of studies (more than ten). The requirement that only ten studies are needed for reasonable statistical power makes Egger’s test a better choice than the Begg and Mazumdar method for most crime and justice meta-analyses, but it will yield less than desired power for some. Sterne and Egger suggest that “the regression method is appropriate in situations in which meta-analysis generally makes sense; in estimating moderate treatment effects, based on a reasonable number of studies. However, to avoid the potential inflation of the Type I error rate described earlier, it should only be used if there is clear variation in study sizes, with one or more trials of medium or large size” (Sterne and Egger 2005, p. 106). An additional benefit of Egger’s test is that the approach can be extended to include more than one predictor variable. This means that one can simultaneously assess the impact of several factors, including sample size (or precision), on the effect size. The ability to examine whether the association between the intervention effect and sample size is affected when other study characteristics are controlled is of particular value when sample size is confounded with substantive and methodological moderators of effect size. This is likely to be the case in most criminology meta-analyses (cf. Lipsey 2003; Weisburd et al. 1993).

As is generally true of significance tests, the point estimate and confidence interval from the Egger test are more informative, and less likely to be misinterpreted, than the significance test. Finally, as was true of the Begg and Mazumdar test, a limitation of the test is that, while the results of Egger’s test may suggest that bias exists, it provides no indication of what the effect might be in the absence of bias.

Assessing the impact of publication bias

Cumulative meta-analysis

A cumulative meta-analysis is a meta-analysis run with one study, then repeated with a second study added, then a third, and so on; in a forest plot of these studies, the first row shows the effect based on one study, the second row shows the cumulative effect based on two studies, etc. (see Lau et al. 1992 for an early example). Borenstein (2005) has pointed out that this technique can be used to assess the potential impact of publication bias, again understood as the relationship between effect size and study size. The studies are sorted from largest to smallest (or from most to least precise), and a cumulative meta-analysis is performed. If the point estimate stabilizes based on the larger studies, and does not shift as smaller studies are added, then there is no evidence that the smaller studies are producing a biased overall effect (it is the smaller studies that are likeliest to be affected by selective publication). If, however, the point estimate does shift when the smaller studies are added, “there is at least a prima facie case for bias” (Borenstein 2005). Figure 2a shows a cumulative funnel plot, where the point estimate does not shift when small studies are added, while Fig. 2b shows a cumulative funnel plot that shifts as small studies are entered. Advantages of this approach are that it provides an estimate of the effect size based only on the larger studies, and that it is totally transparent: The effect based on the larger studies is computed, and, as smaller studies are added, it is possible to see if and how the effect shifts. Borenstein notes that, while a clear distinction between larger and smaller studies will not usually exist, it is not needed.

Fig. 2
figure 2

a Cumulative meta-analysis showing no shift when small studies are added. b Cumulative meta-analysis showing shift when small studies are added (std diff standardized difference, 95% CI 95% confidence interval)

Full size image

Adjusting for publication bias

The trim-and-fill procedure, developed by Duval and Tweedie (Duval 2005; Duval and Tweedie 2000a, b) assesses whether publication bias may be affecting the results of a meta-analysis and estimates how the effect would change if the bias were to be removed. This procedure is based on the notion that, in the absence of bias, a funnel plot will be symmetric about the mean effect. If there are more small studies on one side than on the other side of the bottom of the funnel plot, our concern is that there may be studies that exist but are missing from the analysis. Trim and fill extends this idea by imputing the missing studies, adding them to the analysis, and then re-computing the effect size.

The trim-and-fill method assumes that, in addition to the number of observed studies in a meta-analysis, there are other relevant studies that are not included, due to publication bias. The number of these studies, and the effect sizes associated with them, is unknown but can be estimated. In addition, the uncertainty of these estimates has to be reflected in the (adjusted) meta-analysis result. To adjust for the effect of possibly missing studies, trim and fill uses an iterative procedure to remove the most extreme small studies from the other side of the funnel plot (those without counterparts on the first side) and re-computes the effect size at each iteration, until the funnel plot is symmetric about the (new) effect size. While this “trimming” yields an effect size adjusted for missing studies, it also reduces the variance of the effects, yielding a confidence interval that is too narrow. Therefore, the algorithm then adds the removed studies back into the analysis and imputes a mirror image for each of them. The final estimate of the mean overall effect, as well as its variance, is based on the “filled” funnel plot (Duval and Tweedie 2000a, b). Figure 3 shows a “filled” funnel plot, i.e., one that includes imputed as well as actually observed effects. The clear circles are the original data (from Fig. 2b), and the dark circles are the imputed data.

Fig. 3
figure 3

Illustration of a funnel plot after Trim and Fill has imputed missing studies (open circles original data (from Fig. 2b), filled circles imputed data, Std diff standardized difference, Std Err standard error)

Full size image

Critics of the trim-and-fill approach have noted several problems created by the assumptions it makes. Most notably, this approach assumes that the observed asymmetry is due to publication bias rather than to true differences in the results of the small studies compared to the larger ones. If this assumption is incorrect, imputing “missing” studies is not justified (this issue will be discussed at greater length below). Even when this assumption is correct, an additional problem is that this procedure, as do many of the others, assumes that publication bias follows an orderly pattern, and uses this pattern to detect the number of missing studies. Another assumption underlying trim and fill is that the distribution of effect sizes in the population is relatively homogeneous, that is, sampling error is the key source of variation in a set of studies. This is rarely the case in crime and justice meta-analyses, which are typically quite heterogeneous, due to both methodological and substantive differences among primary studies. Simulations by Terrin et al. (2003) have shown that when trim and fill is applied to heterogeneous data sets, it can adjust for publication bias when none actually exists. Thus, in the application of trim and fill, the researcher might wish to take reasonable steps to eliminate moderators in the distributions of effects, such as choosing to conduct the trim-and-fill analysis on relatively homogeneous subsets of the data, rather on the overall dataset if there is a sufficiently large number of studies to do so. Alternatively, if trim and fill is used on heterogeneous sets of data, positive results should be interpreted cautiously. Of course, if trim and fill shows no studies “missing”, or that “missing studies” do not affect the results of the meta-analysis, the researcher can be confident that the threat to validity of this form of publication bias has been ruled out.

The big advantage of the trim-and-fill approach is that it yields an effect size estimate that is adjusted for bias, something that none of the other methods provides. The mean effect estimated from imputed studies should not be viewed as the best estimate of an intervention’s effectiveness, Instead, the degree of divergence between the original mean effect and the adjusted mean effect serves as a useful sensitivity analysis that estimates the robustness of meta-analytic results to the threat of publication bias and the potential impact of missing studies.

Comparing the results of the various methods

The results obtained from various methods may not be in agreement, because they answer different questions. The traditional failsafe N analysis defines publication bias as the number of studies obtaining no effect that it would take to completely nullify the observed mean effect size; in other words, it answers the question “Is the entire effect due to bias?” Orwin’s variant defines publication bias as the number of studies obtaining a specified low effect that it would take to drop the observed mean effect size below a specified threshold; it, too, answers the question “Is the entire effect due to bias?” Whenever a meta-analysis includes a large number of studies and contains effect sizes far from zero, both versions of failsafe N analyses will yield a conclusion that there is no publication bias.

The funnel plot, Begg and Mazumdar test and Egger test define bias as the relationship between precision (sample size) and effect size, and answers the question “Is there evidence that bias may exist?” Cumulative meta-analysis defines bias as a relationship between sample size and effect size and examines whether the effect, as estimated by the larger studies, shifts as smaller studies are added. It answers the question “How much does the effect size change when smaller studies are added to the meta-analysis?” The trim-and-fill analysis interprets the asymmetry of effect size distribution as evidence of publication bias, and, based on a definition of publication bias as the difference between the original effect size and the recomputed effect size after the “missing” studies have been added to make the distribution symmetrical, answers the question “How much does the effect size shift after adjusting for putative bias?”

Illustrative example

To illustrate the methods of publication bias assessment that are outlined in this article, I will use a data set from a review by Wilson et al. (2006) of the effectiveness of drug courts in reducing criminal behavior.

Publication bias analyses were performed with Comprehensive Meta Analysis, version 2.0 (Borenstein et al. 2005), but all tests can also be run using Metawin version 2 (Rosenberg et al. 2000), while the Egger test, Begg and Mazumdar test, cumulative meta-analysis and trim and fill are also computable using STATA macros (see Sterne et al. (2001a; 2007 for information about using STATA in meta-analysis).

The Wilson et al. drug court meta-analysis

This meta-analysis was conducted to examine the effectiveness of drug courts in reducing criminal behavior. The effect size in this case is the odds ratio, with values above 1 representing a positive effect for drug courts, a value of 1.0 representing no effect, and values below 1 representing a negative effect for drug courts. Using a random effects model, Wilson et al. estimated that the mean odds ratio was 1.66 [95% confidence interval (95% CI) = 1.46, 1.88], based on 55 effects. Figure 4 shows a forest plot of their results. Wilson et al. concluded that drug courts were effective in reducing criminal behavior: the practical effect of drug courts was a 24% reduction in recidivism, relative to the comparison.

Fig. 4
figure 4

Wilson’s forest plot of random effects in the drug court meta-analysis

Full size image

Application of classic failsafe N

Data from the 55 effects comparing the mean percentage of individuals recidivating in the treatment (drug court) group versus the comparison group yielded a z value of 15.365 and corresponding P value of < 0.000 for the combined test of significance. There would need to be a total of 3,326 missing studies with zero effect to yield a combined two-tailed P value exceeding 0.05. Another way of representing this finding is that there would need to be 60.5 missing studies for every observed study for the effect to become non-significant.

Rosenthal suggested that, if the failsafe N is relatively small, then there is cause for concern that publication bias might be responsible for the observed results, but if this number is large, we can have confidence that, although the observed treatment effect might have been inflated by the exclusion of some studies, it is, nevertheless, not likely to be zero. While Rosenthal did not provide specific guidance as to what number of studies might be considered “large” enough to give us confidence that the results have not been nullified by publication bias, he offered a general guideline that a failsafe N equal to or greater than five-times the number of studies in the original meta-analysis, plus ten studies (5K + 10) would indicate that the meta-analytic results were robust to the threat of publication bias. Mullen et al. (2001) proposed Rosenthal’s guideline as a formal rule, and the authors of several recent psychology meta-analyses (Del Vecchio and O’Leary 2004; Rhoades and Eisenberger 2002) have used this formula to assess the results of their file drawer analyses. I used this number as one means of assessing publication bias based on the file drawer analysis results. In this case, 5K + 10 is 285 studies, while the computed failsafe N is 3,326 studies. Using this as a criterion of robustness to the threat of total nullification of the effect due to publication bias, we can conclude that the results of Wilson et al. are unlikely to be totally nullified by missing studies.

Application of Orwin’s failsafe N

Data from the 55 effects yielded an odds ratio of 1.56 under the fixed effects model. (As mentioned earlier, failsafe N can be used only with fixed effects.) Assuming that the smallest non-trivial odds ratio is 1.22 (chosen on the basis of a reduction in offending of 10%, relative to a comparison group recidivism rate of 50%) and that the mean odds ratio in the “missing” studies is 1.0, there would need to be 70 studies for the current odds ratio to be reduced to a “trivial” effect. This number is substantially lower than 5K + 10 (285) studies and would lead us to conclude that there is some likelihood that the effect could be obviated by missing studies. Another, more lenient, rule that has been used is to consider that it is unlikely to expect there to be more missing studies than located studies. Using this as the criterion, we would conclude that it is not likely that the effect would be reduced to a trivial level by missing studies.

Application of the Begg and Mazumdar rank correlation test and Egger’s test

The rank correlation coefficient, Kendall’s tau b (corrected for ties), for the 55 drug court effects is 0.135, with a one-tailed P value of 0.073, or a two-tailed P value of 0.146 (based on continuity corrected normal approximation). Egger’s regression method for the 55 drug court effects produced an intercept (B0) of 1.112 and a 95% confidence interval of 0.009, 2.216, with t = 1.688, df = 53. The one-tailed P value = 0.049; the two-tailed value is 0.10. As might be expected, due to the greater power of the regression method, the P value from Egger’s regression test was smaller than that from the rank correlation test and was statistically significant (one-tailed), while the rank correlation test was not. Using one-tailed statistical significance as the criterion, we would conclude that the Begg and Mazumdar test does not support a conclusion that publication bias is operating, while the Egger test does; the two-tailed test is not significant in either case and, strictly interpreted, would not support a conclusion that publication bias was operating.

Application of cumulative meta-analysis

Figure 5 is a cumulative forest plot of the drug court data. Note the difference between the cumulative plot and the traditional version of a forest plot shown in Fig. 4. In Fig. 4 each study is represented by a line on the graph. In Fig. 5 the studies have been sorted from the most precise to the least precise (roughly corresponding to largest to smallest) and added one at a time, until all studies are included. Thus, each line on the graph represents the cumulative effect of all studies entered to that point. With the 28 largest studies in the analysis, the cumulative odds ratio is 1.57 (1.35, 184). With the addition of the other 27 (smaller) studies, the point estimate shifts to the right, producing an overall odds ratio of 1.66 (1.46, 1.88) As such, the estimate of the odds ratio (and the effectiveness of drug courts) has increased somewhat, due to the smaller studies. Regardless of whether the smaller studies have a truly different effect, or whether they have been affected by publication bias, the point that results from this analysis is that, even if the analysis is limited to the larger studies, the odds ratio still shows that drug courts are effective, and the implications for policy are likely to be the same as when all studies are included.

Fig. 5
figure 5

Cumulative forest plot of Wilson meta-analysis results

Full size image

Application of the trim-and-fill method

Trim-and-fill results suggest that ten studies are missing. Under the random effects model the estimate of the mean odds ratio was 1.66 (95% CI = 1.46, 1.88). Using trim and fill, the estimate of the mean odds ratio, after the ten missing studies had been imputed, dropped to 1.43 (95% CI = 1.25, 1.64). A funnel plot of observed and imputed studies is shown in Fig. 5. These results are concordant with those produced by the cumulative meta-analysis, in that they suggest that, while the results might be inflated somewhat by publication bias or, alternatively, by small study effects, the odds ratio incorporating the imputed studies continues to show that drug courts are effective. Fig. 6.

Fig. 6
figure 6

Trim-and-fill results for the Wilson drug court meta-analysis

Full size image

Limitations of the current assessment methods of publication bias

As I have pointed out throughout this paper, each of the procedures above has limitations. Perhaps the biggest limitation is the inability of most of the methods to distinguish between publication bias and true differences in effect size for small studies compared to large ones. It may be possible, in any given case, to try and attribute a causal mechanism to the bias. For example, in some cases, reviewers may be able to look for a relationship between effect size and sample size within subsets of studies grouped by important methodological features (suggestive of publication bias), or to see if the relationship between sample size and effect size holds within the set of unpublished studies (suggestive that sample size may be a surrogate for other methodological features). If the apparent bias is actually a small study effect, then the larger effect size in the smaller studies reflects legitimate heterogeneity in the effect sizes; this variation in effect needs to be attended to in much the same way as heterogeneity produced by other moderators. Be cautioned, however, that the effects of publication bias can be hard to disentangle from other sources of heterogeneity, and that this does seem to have been fully explored in criminology reviews. For example, although Braga (2005), in his meta-analysis of hotspots policing, found a relationship between sample size and effect size that he suggested was a function of implementation problems in two of the included studies [those from the Repeat Call Address Policing (RECAP) experiment], he did not empirically test this proposition. Along the same lines, Landenberger and Lipsey (2005) found that there was no relationship between publication status and effect size once methodological moderators, such as attrition and fidelity of implementation, had been taken into account, but they did not look at the relationship between sample size and effect size. Ioannidis (2005) has some useful suggestions about how to tackle the difficult jog of disentangling confounding factors from true publication bias.

Conclusion

Over the long run, the best way to deal with publication bias is to prevent it. Toward that end, I encourage criminology researchers to consider sponsor and support the prospective registration of experimental and quasi-experimental studies in trial registries, as researchers in healthcare are currently doing (Krleža-Jeric et al. 2005). At the level of the individual review, publication bias can be minimized by a comprehensive search in which a serious effort is made to retrieve gray and unpublished literature. Nonetheless, the need for statistical techniques to evaluate publication bias will remain for some time into the future. Use of multiple techniques and an integration of their findings can overcome some of the limitations of specific methods. Given what has been found in other areas, such as healthcare meta-analyses, I am optimistic that, in the majority of cases, publication bias analyses will show that publication bias had little impact, thus increasing confidence in the results of these reviews. In cases where publication bias analyses suggest that severe bias may exist, researchers can avoid potentially serious mistakes such as recommending a policy, practice or intervention that could be worthless or problematic. Publishing meta-analyses that ignore the potential for bias (and which may later be found to be incorrect) can only undermine the credibility of meta-analysis as a research method. It is thus important to attend to bias, not only to ensure the integrity of the individual meta-analysis, but also to ensure the integrity of the method.