1 Introduction

Wireless sensor network (WSN) is a cost effective ambiance and many researchers had done work in the past decade. The information in WSN is broadcasted among all the nodes in the network and limited energy resources are the fundamental aspects. Modern technologies in WSN had made sensor nodes to communicate with outside world. The nodes in WSN are connected and shared under common transmission media to exchange data. The applications of WSN include manufacturing productivity, home security, and emergency outlet etc. The responsibility of the sensor nodes is to detect, gather data and transfer to the other network. The battery is the power source for the sensor nodes and some nodes are non-renewable or non-rechargeable. The most issue in a wireless network is maximizing the lifetime of the network and minimizes the coverage loss. The data are broadcasted to all other nodes in the transmission range of sensor node by the evident of wireless multicast advantage (WMA) [22]. Each node in the wireless network has omni-directional antenna and receive data within the transmission range. When a node is in transmission range, it can receive and transmit a signal through multi-hop communication. Multi-hop communication uses rely on nodes as intermediate links to transmit signals. When the transmission range of a node is high it can transmit data to a maximum number of nodes, but it consumes more energy of the wireless node.

In wireless networks, broadcasting involves node with omni-directional antenna under single transmission range. The transmission power of the sensor node is adjusted so that the transmission can reach to the farthest node in the network. So the transmission range will cover all the sensor nodes under WMA. The objective of MEB is to minimize energy consumption transmission range to transfer.

In this work, the author proposed a new variant of Flower pollination algorithm based on Powell’s method proposed called Powell’s Flower pollination algorithm (PFPA). Flower Pollination algorithm (FPA) is adapted to solve NP-hard combinatorial optimization problems by incorporating heuristic method. By embedding conjugate directions in Powell’s method, the basic search pattern was improved towards direct search. In FPA there is inefficiency towards local search process and it result in poor exploitation process. To balance both exploration and exploitation process in FPA the authors incorporated heuristic technique in exploitation process of FPA. Powell’s conjugate gradient descent method is used to find local minimum and it does bi-directional search towards search vector.

Yang [36] evaluated the performance of FPA with genetic algorithm and particle swarm optimization algorithm. The simulation results show that FPA outperforms both and it is successfully used in several fields [4]. However, for larger-scale problems, the performance of FPA degrades substantially due to the higher likelihood of trapping in locally optimal solutions. The proposed method alleviates this drawback by increasing the balance of diversification and intensification of the search process.

The remainder of the paper is organized as follows: Sect. 2 backgrounds the approaches solving MEB to attain optimal solution has discussed. In Sect. 3, the formulation of MEB is presented. In Sect. 4 the proposed flower pollination algorithm based on Powell’s method is discussed. In Sect. 5 applicability of MEB has been explained with experimental result analysis. Finally, Sect. 6 concludes the research work.

2 Literature Review

Over the past decades, various researchers have attempted to solve MEB problems. This problem has been tracked by heuristic, local search, and meta-heuristics algorithms. The simple heuristics to find a minimum spanning tree are proposed based on prim’s algorithm [32] and they used basic greedy search method. Other examples based on heuristic approaches are Greedy Perimeter Broadcast Efficiency (GPBE) [13], Broadcast Incremental Power [33], Adaptive Broadcast Consumption (ABC) [17] and Directed Bee colony algorithm is used to solve scheduling problem [27].

Wieselthier et al. proposed in the wireless network algorithms are based on heuristic methods and in wired network, the algorithms are based on link approaches. The author’s proposed broadcast incremental power (BIP) algorithm with link-based approaches [33]. The BIP will iteratively develop arborescence for each iteration and add a new node to the tree thus results in minimum transmission power into partial arborescence. The non-leaf nodes in the trees are arranged to ascend by the method of sweep procedure to reduce the transmission power to the farthest node. The sweep procedure should be implemented in multiple times and the results show little improvement.

Marks et al. developed an r-shrink procedure for solving MEB problem. In this procedure, the farthest node in the tree is removed one by one and assigned to some other transmission range nearer to so as to reduce the transmission power in the network. The total cost is calculated if the total cost is less than the original cost then arborescence is modified else it is retained. If the arborescence is modified, the whole process is repeated from the new arborescence [7].

Many researchers have also suggested using local search to obtain the near optimal solution like Broadcast Incremental Decremental Power (BIDP) [9]. Čagalj et al. proposed embedded wireless multicast advantage (EWMA). In this procedure, the transmission power of the node is increased to reduce the total cost of the transmission power to stop some other node to transmit entirely [5]. Kang and Poovendra used EWMA in largest expanding sweep search (LESS) procedure to reduce transmission power by increasing the transmission power of a particular node [14]. Raju et al. [28] used bio-inspired algorithm for solving cloud computing environment.

Kang and Poovendran used a perturbation based algorithm and LESS approach for local search to solve MEB in wireless ad-hoc networks [15]. Montemanni et al. proposed simulated annealing based r-shrink to solve MEB. The authors have used sweep procedure based simulated annealing to solve MEB in wireless networks [24]. Al-Shihabi et al. proposed a hybrid algorithm which combines r-shrink based partitioning with LP and integer programming. In this algorithm, nested partitioning part is implemented by generic partitioning [1].

The most recent trends in solving involves utilizing meta-heuristics due to their ability to cope with large-scale problems. Many works related to meta-heuristics algorithm utilizing the benefits of local search methods have done in different applications [12, 19, 23]. Das et al. proposed ant-colony based algorithm to solve MEB in wireless sensor network [6]. Wolf et al. proposed a hybrid algorithm based on evolutionary local search which uses r-shrink and mutation operator to randomly increase the transmission range of the nodes [34]. The results obtained are compared with other localization algorithms and nested partitioning [1] which demonstrated reduced computational time to obtain near optimal solution.

Wu et al. proposed a genetic algorithm which uses permutation encoding and decoding in the broadcast environment for minimum spanning tree problems [35]. They used rank scheme and different crossover operators and compared the result with simulated annealing [24]. Some of the works related to meta-heuristic algorithms on solving MEB includes Hybrid genetic algorithm [31] and Iterated local search algorithm [3]. Singh and Bhukya proposed a hybrid genetic algorithm which uses swap mutation and cycles crossover along with local search algorithm. The authors had used the r-shrink procedure for the local search operation and the combinations of r-shrink with genetic operators are used to achieve the optimal solution [31].

Guo and Yang provided the detailed survey on solving MEB problem with Omni-directional and directional antennas for wireless ad-hoc networks [8]. Sengupta et al. described the objectives to deploy sensor nodes in the wireless network. Before deploying the sensor node have to consider, a number of sensor nodes should be minimized to minimize the cost of deployment. Maximize the coverage area and minimize the energy consumption of the sensor node. The lifetime of the network should be maximized [30].

Enan et al. solved routing problem in wireless sensor network and the authors proposed an evolutionary-based clustering algorithm and the transmission is based on single-hop communication. They formulated the network to achieve maximum stability period until parent node dies and minimized the energy consumption of the network [16].

To minimize energy broadcast problem, the above discussed approaches endured to obtain the optimal solution. Computational time is most needed to validate the performance of the algorithm over the various sized network. The objective of this research is to obtain an optimal solution within an acceptable computational time.

3 Problem Formulation

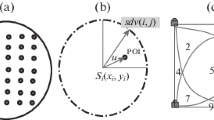
In wireless networks, broadcasting allows all the sensor nodes to share the data proficiently with other nodes in the transmission medium. To construct broadcast trees, there is a limited energy resource because the nodes are operated on the battery. The network consists of a set of nodes, in which a node is considered as a source node, the objective of the minimum energy broadcast (MEB) problem is to minimize the total energy consumption of the network and it has proved to be an NP-Complete problem [5, 20]. In this network, all the nodes have the capacity to regulate their transmission range. The transmission range is assigned to each node in the network and every other node inside the transmission range will receive the message. The goal of the MEB is to assign transmission ranges to the nodes such that the total energy consumption is minimized.

The MEB problem in a wireless network can be stated using directed complete graph \(G = \left( {V,E} \right)\), where \(V\) represents the set of nodes in the wireless network and \(E\) represents set of edges connecting vertices. The energy required to set up a link from node \(i\) to node \(j\) is denoted as \(\varphi_{ij}\) where the node links are the edges of the graph \(ij \in E\). In wireless network the broadcasting done using Omni-directional antenna and nodes are covered in single transmission range. For example if node \(p\) is transmitting data to the node \(q\) then each other node \(i\) in the transmission range will also receive the same data sent by the node \(p\) such that \(\varphi_{pi} \le \varphi_{qj}\).

The objective of the MEB problem is to find the minimum transmission energy broadcast routing tree, source node \(s \in V\) broadcast message either directly or through intermediate nodes to all other remaining nodes of \(V\). The start node of arborescence is responsible to relay the broadcast message to all other terminal nodes of the same directed edge. The transmission energy required for node \(p\) in arborescence is the power of the node to transmit to the farthest child node \(p\) (longest edge) in the tree. The transmission energy required for any leaf node is considered to be zero, since they are not relaying any message to other nodes in the tree.

The energy required to send the packets can be measured using

$$\varphi = \zeta d^{\psi }$$
(1)

To broadcast, the transmission energy required by the node in arborescence can be calculated by adding transmission energy of each parent node in the tree. In a tree, with source node \(s\), the minimum total energy required can be measured by using Eq. (2)

$$TE_{{sol_{i} }} = \mathop \sum \limits_{a \in V} \mathop {\max }\limits_{{\left( {a,b} \right) \in E_{{sol_{i} }} }} d\left( {a,b} \right)^{\psi }$$
(2)

The solution consists of minimum energy broadcast trees which are generated by the algorithm after each iteration. The transmission energy generated by each solution is represented as \(TE_{{sol_{i} }}\) and \(i\) is the index for the solution number. The path loss exponent constant \(\psi\) lies between 2 and 4 [18] and power threshold \(\zeta\) is normalized to 1. \(d\left( {a,b} \right)\) is the distance between the nodes \(a\) and \(b\). The distance \(d\left( {a,b} \right)\) in a transmission, the received power signal at \(b\) varies and can be calculated using Euclidean distance by

$$d\left( {a,b} \right)^{\psi } = \left( {\left[ {\left( {p_{a} - p_{b} } \right)^{2} + \left( {q_{a} - q_{b} } \right)^{2} } \right]^{\frac{1}{2}} } \right)^{\psi }$$
(3)

The Euclidean distance \(\left( {p_{a} ,p_{b} } \right)\) between the nodes \(a\) and \(b\) are the coordinates of the node \(p\) and \(q\). The minimum transmission energy contains the near optimal solution.

4 Flower Pollination Algorithm with Powell’s Method

4.1 Characteristics of Flower Pollination

All flowering plants have a peculiar type of reproduction namely pollination. The exchanges of pollens between the flowers are through insects, birds, etc. Pollination process is made of two types namely biotic and abiotic. Among these types, 0.9 ratio of pollination is done though biotic structure in which insects and birds transfers the pollens to other flowers. A tenth ratio of pollination is done through abiotic pollination, which is the process carried through wind and dissemination offer assistance. Pollen vectors are the pollinator which works in terms of diversity.

In the cross-pollination, biotic occurs at longer distance with the pollinators like bees, birds, insects, and other animals can travel for long geographical region. These types of pollination can be represented as global pollination. A randomized walk is done using Levy flight [25] which also imposes a diversified search in the given region. Objective in flower pollination is to reproduce the production using pollens and to retrieve the best pollinated flowers based on their attributes. Survival of the fittest and providing optimal reproduction in terms of number and fittest. This is the optimization process to achieve optimal reproduction of the flowering plants.

4.2 Flower Pollination Algorithm

Xin-She Yang proposed flower pollination algorithm (FPA) [36], inspired by the natural pollination process of flowering plants.

Rules for the simplicity of FPA:

  1. 1.

    Global pollination process: This process takes place through biotic and cross-pollination, the movement of pollen carrying pollinators obeys Levy flights behavior.

  2. 2.

    Local pollination process: This process takes place through abiotic and self-pollination.

  3. 3.

    Local neighborhood: The pollinators are comparable to offspring probability proportional to the similarity of the two flowers.

  4. 4.

    Switch probability controls the interaction of local and global pollination and lies between o and 1. Here the higher probability is indicated for plants in the neighborhood which mimics local pollination.

In nature, each plant can have many number of flowers and each flower patch will release billions of pollen gametes. For simplicity, the authors assume every plant has single flower and it generate single pollen gamete. Thus there is no need to differentiate a flower, pollen, a plant or solution to the problem. The solution \({\mathcal{F}}_{i }\) is equal to the pollen or flower. In FPA, there are two steps they are global and local pollination.

4.2.1 Global Pollination

In the global pollination, the pollen gametes from the flowers are carried by the pollinators such as birds, bats, and bees are traveled to the longer distance. This process ensures reproduction and pollination of the fittest \({\Psi }_{b}\).

Therefore the Rule 1 and flower constancy in Rule 3 can be mathematically represented as

$${\mathcal{F}}_{i}^{t + 1} = {\mathcal{F}}_{i}^{t} + \varphi Lev\left( \alpha \right)\left( {{\Psi }_{b} - {\mathcal{F}}_{i}^{t} } \right)$$
(4)

where \({\mathcal{F}}_{i}^{t}\) is the solution vector \({\mathcal{F}}_{i}\) at iteration \(t\) for the pollen i, and \({\Psi }_{b}\) is the best solution at current iteration or generation. Here \(\varphi\) is the scaling factor to control step size and \(Lev\left( \alpha \right)\) is the parameter, strength of the pollination which is Levy-flights based step size. Since the insects travel various distance in global pollination, a Levy flight can simulate this behaviour [29]. Xin-she Yang used levy distribution when \(Lev > 0\)

$$Lev\left( \alpha \right) \sim \frac{{\alpha {\Gamma }\left( \alpha \right){\text{sin}}\left( {\frac{\pi \alpha }{2}} \right)}}{\pi }\frac{1}{{s^{1 + \alpha } }},\quad {\text{where}}\;s \gg s_{0} \gg 0$$
(5)

where \({\Gamma }\left( \alpha \right)\) is gamma function and with larger step where \(s > 0\) and the value of \(s_{0}\) is as small as 0.1. To generate a pseudo-random step size which obeys the Levy distribution is not trivial. The random numbers for step size \(s\) are generated by Mantegna algorithm using Gaussian distributions \(G\) and \(H\) can be represented as

$$s = \frac{G}{{\left| H \right|^{1/\alpha } }}, \;G \sim N\left( {0,\sigma^{2} } \right), \;H \sim N\left( {0,1} \right)$$
(6)

where \(G \sim N\left( {0,\sigma^{2} } \right)\) represents Gaussian normal distribution with a variance of \(\sigma^{2}\) and zero mean. The variance for the function can be calculated as

$$\sigma^{2} = \left[ {\frac{{{\Gamma }\left( {1 + \alpha } \right)}}{{\alpha {\Gamma }\left( {\left( {1 + \alpha } \right)/2} \right)}}.\frac{{{\text{sin}}\left( {\frac{\pi \alpha }{2}} \right)}}{{2^{{\left( {\alpha - 1} \right)/2}} }}} \right]^{{\frac{1}{\alpha }}}$$
(7)

Mantegna algorithm is used to produce a random sample which obeys distribution mathematically [21].

4.2.2 Local Pollination

The local pollination process both Rule 2 and Rule 3 can be mathematically represented using Eq. (8)

$${\mathcal{F}}_{i}^{t + 1} = {\mathcal{F}}_{i}^{t} + \eta \left( {{\mathcal{F}}_{k}^{t} - {\mathcal{F}}_{l}^{t} } \right)$$
(8)

where \({\mathcal{F}}_{k}^{n}\) and \({\mathcal{F}}_{l}^{n}\) are the pollen of neighboring flowers of the same plant, that is it is extracted from the same population with less flower constancy in neighborhood. Mathematically, when \({\mathcal{F}}_{k}^{n}\) and \({\mathcal{F}}_{l}^{n}\) comes from the same plant or from same population, then it performs a local random walk \(\eta\) using uniform distribution of [0, 1]. The flower pollination pursuits occur at global and local scales. In nature, the adjacent flower patches or flower in the not-so-far-away neighborhood transfer the pollen grains by local flower pollen than global. To mimic this feature, we switch between local and global pollination. The switch probability Pє[0,1] Rule 4 or proximity probability is used intensively. The probability value \(P = 0.5\) is used as an initial value and \(P = 0.8\) may work better in many applications.

4.3 Powell’s Method

The Powell's method is the extension of the basic pattern search method for direct search and can be improved by the method of conjugate directions. In Powell's method for two variable functions, the function is first minimized towards the direction of coordinates and start with second coordinate thus Powell’s pattern is formed.

There is inefficiency in FPA, which is good at exploration but poor at exploitation process. The local search in FPA increases with increase in a number of iteration. To address this concerning problem, the local pollination phase is done using Powell’s method [26]. M.J.D. Powell proposed Powell’s conjugate gradient descent method to find a local minimum of a function by bi-directional search towards search vector. The new candidate position is in search vector and the displacement vector is added at the end of search list. The best search vector is deleted from the search vector list which contributed mainly towards a new direction.

The conjugate gradient descent method directs towards the nearly given point of search. This proposes strong local search capability and it is incorporated into FPA algorithm to improve the process of local search and increase the convergence speed and accuracy. In every iteration, the population position after updating is not directly fed to the next iteration process. Instead, conjugate gradient descent directions is employed at \({\mathcal{F}}_{i}\) by the conjugate factor \(\beta_{i}\). The population position \({\mathcal{F}}_{i}\) of the flower decreases sufficiently within a predetermined number of iterations. The proposed algorithm combines Powell’s method and FPA algorithm to deliver strong local and global searching capabilities.

Let

$$Y = Y\left( {{\mathcal{F}}_{1} , \ldots , {\mathcal{F}}_{n} } \right)$$
(9)
$$C = \nabla Y = \frac{\partial Y}{{\partial {\mathcal{F}}_{1} }}i_{1} + \frac{\partial Y}{{\partial {\mathcal{F}}_{2} }}i_{2} + \cdots \frac{\partial Y}{{\partial {\mathcal{F}}_{n} }}i_{n}$$
(10)
$$d_{i} = - C_{i} + \beta_{i} d_{i - 1}$$
(11)

where \(d_{i}\) is the deflection parameter, the next iteration is employed by multiplying conjugate factor \(\beta_{i}\) at gradient and adding to the negative gradient.

$$\beta_{i} = \left[ {\frac{{\left| {\left| {C_{i} } \right|} \right|}}{{\left| {\left| {C_{i - 1} } \right|} \right|}}} \right]^{2}$$
(12)
$$\left| {\left| C \right|} \right| = \sqrt[2]{{\frac{\partial Y}{{\partial {\mathcal{F}}_{1} }}^{2} + \cdots \frac{\partial Y}{{\partial {\mathcal{F}}_{n} }}^{2} }}$$
(13)

Evaluate \(\tau ,\)

$${\mathcal{F}}^{0} = \left( {{\mathcal{F}}_{1} , \ldots , {\mathcal{F}}_{n} } \right)^{0}$$
(14)
$${\mathcal{F}}^{1} = {\mathcal{F}}^{0} + \tau d_{0}$$
(15)

Update \(X^{i + 1}\)

$${\mathcal{F}}^{i + 1} = {\mathcal{F}}^{i} + \tau d_{i}$$
(16)

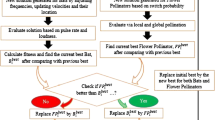
where \({\text{C}}_{{\text{i }}}\) the objective function and this method has the characteristic of the second termination and reaches the minimum point after limited generations or iterations. The pseudo code of Powell’s method and proposed PFPA is shown in Algorithms 1and 2. The workflow of Powell’s method and modified PFPA to solve MEB in wireless sensor network are shown in Figs. 1 and 2.

Fig. 1
figure 1

Workflow of Powell’s method

Full size image
Fig. 2
figure 2

Workflow of PFPA method

Full size image

Algorithm 1 Algorithm for Powell’s method.

figure g

Algorithm 2 Algorithm for PFPA.

figure h

5 Experimental Analysis

5.1 Environment Setup

The performance of the proposed PFPA for solving MEB is evaluated using instances taken from DAG [1] available from http://dag.informatik.uni-kl.de/research/meb/. There are 30 instances of each size with 20, 50 and 100 numbers of nodes, which are randomly scattered in the 1000 × 1000 square. The experimentation to solve MEB was done on different optimization algorithm under similar environment conditions to measure the performance of the proposed algorithm. The algorithm to solve MEB is coded using MATLAB 2012 platform on Windows Intel c2 GHz Core 2 quad processor with 2 GB of RAM. The simulation is done with the parameter setting as shown in Table 1 and appropriate parameter values are assigned based on preliminary experiments. To evaluate the efficiency of the proposed algorithm on solving MEB, competitor algorithms chosen are particle swarm optimization algorithm (PSO) [11], ant colony optimization (ACO) [10], hybrid genetic algorithm (HGA) [31], memetic algorithm (MA) [2], iterated local search (ILS) [15], evolutionary local search (ELS) [34].

Table 1 Parameter setting for experimental evaluation
Full size table

The simulation result for the 10-node network is not given in this work; the proposed algorithm PFPA achieved optimum results for all the nodes. The simulation results for solving MEB using PFPA on varying number of node size are represented in Table. The nodes are randomly distributed and the simulation is done for 20 runs. There is no deviation in results for all executions and the deviation is represented in excess percentage.

5.2 Performance Metrics

The performance of the proposed method PFPA is assessed by comparing with other algorithms. Here, in this work, the authors have considered four performance metrics to calculate the significance of the proposed system.

5.2.1 Found

Found specifies the number of times the algorithm is computed to obtain the best value out of 20 runs. To compute the best solution Euclidian distance is used. The best solutions are considered as the near to obtain best energy consumption value.

5.2.2 Excess (%)

The excess percentage will provide the deviation of solution from the optimal solution. The excess percentage for the solution can be represented by

$$Excess \left( \% \right) = \frac{1}{run}\mathop \sum \limits_{i = 1}^{run} \left[ {\frac{{Best\_value_{i} }}{Optimal\;value} - 1} \right]*100$$
(17)

The excess (%) can be calculated for run number of times and Best_valuei is the best solution obtained at ith iteration and optimal value is the optimum value given in the dataset.

5.2.3 Computational Time

The computational time is the total time taken to complete the runtime of the proposed algorithm. The evaluation is based on random location and best solution is not epoch value for termination.

$$Computational\;time = Runtime\;of\;proposed\;algorithm$$
(18)

5.2.4 Standard Deviation

The standard deviation (SD) is the measure of dispersion of solution from its mean value. The standard deviation can be calculated by

$$SD = \sqrt {\mathop \sum \limits_{i = 1}^{r} \left( {{\text{value in each instance}}_{{\text{i}}} - {\text{mean value}}} \right)^{2} }$$
(19)

The simulation result of PFPA on solving MEB is shown in Table 2. For a 50-node network, out of 30 instances, our proposed algorithm have found best results for 24 instances with 0.06% of excess %, which mean 0.06% of instances deviate from the optimal result. The computation time taken for 50-node instance to obtain an optimal result is 1.53 s. For a 100-node network, our proposed algorithm found best values for 17 instances out of 30 instances with a computational time of 46.54 s. The deviation of solution from the optimal result is given by 0.25%.

Table 2 Simulation results of PFPA
Full size table

The instances for a 50-node network are taken and compared with competitor algorithms on solving MEB. Table 3 reports the detailed performance analysis of proposed PFPA algorithm with other competitor algorithm. The algorithm run for 20 times and excess (%), found, computational times are calculated for all the instances. The performance of the proposed algorithm PFPA on solving MEB is validated by computational time and excess percentage. All the columns in the Table represents performance metrics and ‘–’ shows that the algorithm had obtained best value for the corresponding instances. The comparison is made for seven algorithms; ILO performs worst in terms of excess percentage and computational time. ELS performs worst in deviating the result and better with computational time. ACO performs better than MA and HGA with respect to both computational time and excess percentage. Still, there is a gap between the proposed algorithm and existing algorithm. PSO achieved a better result than other existing algorithm but when compared with proposed PFPA achieved six better results with marginal computational time and lesser excess percentage.

Table 3 Performance analysis of PFPA with other algorithms solving MEB for 50 nodes
Full size table

The simulation results and the performance evaluation of proposed algorithm with other existing algorithm on solving MEB for 100-node network are tabulated in Table 4. From the previous simulation result for 50 runs, only ACO, HGA and PSO gave a marginal result with proposed PFPA. So for 100-node network, the authors have considered ACO, HGA, and PSO to measure the performance of PFPA. Among these algorithms, HGA shows poor performance in terms of computational time and excess percentage. ACO achieved results in lesser computational time but the excess percentage is more compared to other algorithms. The proposed algorithm PFPA shows five best results than PSO algorithm with better computational time.

Table 4 Comparison of PFPA and other algorithms solving MEB for 100 nodes
Full size table

The overall performance analysis of the proposed algorithm PFPA with other algorithms on solving MEB over 50 and 100-node networks is shown in Table 5.

Table 5 Comparison of PFPA with Competitor Algorithms
Full size table

Figure 3 shows the comparison of performance analysis for proposed algorithm with existing algorithm. For a 50-node network, Fig. 3a shows the average excess % of PFPA compared with other algorithm. Figure 3b shows the average number of times the best solution is found by the proposed algorithm and other algorithm. Figure 3c shows the average computation time availed by the proposed algorithm PFPA for 20 independent runs. Inspecting the results in Fig. 3, it is evident that PFPA produce near optimal solutions in reduced generations for medium sized network.

Fig. 3
figure 3

The performance analysis for 50 node network

Full size image

For 100 node network the comparison of performance analysis for proposed algorithm with existing algorithm is shown in Fig. 4. Figure 4a shows the average excess % of PFPA compared with competitor algorithms. Figure 4b shows the average standard deviation of the proposed algorithm and other algorithm. Figure 4c shows the average computation time consumed by the proposed algorithm PFPA for 20 independent runs. From the Figs. 3 and 4 it is evident that PFPA produce near optimal solutions in reduced generations for both medium and large sized network.

Fig. 4
figure 4

The performance analysis for 100 node network

Full size image

The research for solving NP-hard combinatorial optimization problem of MEB is carried out by the proposed algorithm PFPA. Various meta-heuristic algorithms are chosen for solving MEB and the results obtained are compared with proposed algorithm PFPA. The obtained results are compared with competitor methods and tabulated in Tables 3, 4 and 5. Investigating from Figs. 3 and 4, it is evident our proposed PFPA shows best value on performance metrics for a 50-node and a 100-node network compared with other competitor algorithms. Comparing with other metaheuristic algorithms, for a 50-nodes the excess percentage was reduced to 0.06%, the computation time to obtain best results was 1.53 ms and out of 30 solutions 24 solutions obtained best results. For a 100-node instance, PFPA excess percentage was reduced to 0.25% the computation time taken was 46.54 ms and out of 30 instances 17 instances found best solution.

The proposed PFPA algorithm is tested on various sized datasets and from the result it is proved PFPA outperforms well than other competitor algorithms. The incorporation of conjugate based Powell’s method as local search algorithm in FPA increases the process of exploitation and thus it balanced in biased nature. PFPA shows higher convergence rate towards optimal solution and the computational results over other competitor algorithm for solving MEB. Embedment of Powell’s method in FPA shows higher computational complexity and other existing exact methods to solve MEB in terms of time complexity.

6 Conclusion

This paper proposes a variant of Flower pollination algorithm based on Powell’s method to solve minimum energy broadcast problem in wireless sensor network. The proposed algorithm is compared with other state-of-the-art heuristic existing algorithms.

  • To solve MEB efficiently FPA is used as a global search and conjugated Powell’s method is used as a local search. This incorporation balances the process of both exploration and exploitation technique. The proposed PFPA was compared with three existing competitor algorithms using instances taken from DAG.

  • The simulation results show the performance of the proposed algorithm reduces over existing algorithms. The empirical result validates the efficiency of the proposed algorithm to MEB problem in smaller and larger sized networks. Thus our algorithm does both deterministic and heuristic search towards obtaining optimal solution in solving MEB.

The future work of this research can be extended to

  1. (a)

    adapting PFPA for solving various NP-hard combinatorial problems,

  2. (b)

    further tuning the heuristic function and balancing exploration and exploitation process,

  3. (c)

    investigating to apply in various coverage problems in wireless sensor networks,

  4. (d)

    exploring unfeasible solution in the search space to emulate optimal solutions.