1 Introduction

DOA estimation algorithms are widely used in wireless communication applications including radar [1, 2], cellular communication [2] and sonar [3, 4], etc. Most of the research work in literature use a ULA for spectral estimation of desired signals since DOA estimation using a UCA is always a challenging thing [5, 6]. Recently, large scale UCA has been considered as one the most promising methods in array signal processing (e.g., millimeter-wave and massive MIMO communication) [7].

Single snapshot spectrum estimation methods are attractive in the wireless communication application due to the following reasons.

  1. 1.

    The time of computation and execution can be reduced by using a single snapshot.

  2. 2.

    Some added simplifications are possible by the use of a single signal sample.

  3. 3.

    The reaction speed can be increased instantaneously after measurement without waiting for large snapshots.

  4. 4.

    Frequency interferer may distort many samples which will not contribute to the estimation.

  5. 5.

    Clutter can superpose a few samples. Such samples cannot be used for DOA estimation.

Most of the research work [8,9,10,11,12] especially for DOA estimation using a single snapshot uses a uniform linear array (ULA) as an array configuration. However, most of the practical applications require UCAs. The key feature is, UCAs can provide 360° coverage in azimuth and 180° coverage in elevation [13]. DOA estimation using UCAs is an attractive solution antenna array configurations for performance-driven communication systems. Multipath propagation or intentional jamming in mobile communication yields coherent signals [9, 14, 15]. The ESPRIT and the root-MUSIC algorithms might not work well to estimate the DOA of coherent signals. To overcome this problem, spatial smoothing and subspace smoothing have developed. But these methods require a large number of snapshots, this increases the computational burden. As a result of this, it requires more time to execute [16, 17].

Most of the classical and recent DOA algorithms require large antenna array samples (snapshots), which increases the computational load of the system [18]. Most of the time few snapshots may available at the receiver, especially in driver assistant systems, for which few or in the worst case only one sample is available for estimation of the incoming signal [19].

In such cases, single snapshot-based algorithms play a vital role. We proposed the new method which does not require the use of forward or backward spatial smoothing of SCM. This minimizes the complexity of computation and enhances the speed of execution.

In this work, the DOA method of [6] is modified to overcome the aforementioned drawbacks. The proposed spectral estimation technique for DOA estimation is the enhanced version of the aforementioned work, which gives 360° signal detection and estimation efficiently. The performance of the proposed algorithm with a single snapshot is compared with spatial smoothing methods with 100 snapshots.

The computation time is decreased as the single snapshot case allows some additional simplifications in DOA estimation

2 Array Signal Model

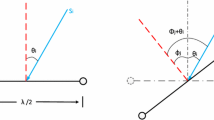
Consider a UCA with M antenna elements as shown in Fig. 1. Consider these antenna elements are identical, unidirectional and distributed uniformly over a UCA with the radius of circle \(r = \lambda .\) Let us assume that at time n, p(p < M) narrow-band signals impinge the UCA with elevation angle \(\theta\) and azimuth angle \(\Phi\) in far fields. Let N represents the number of snapshots observed by the array.

Fig. 1
figure 1

Uniform circular array

Full size image

The signal output at the m-th antenna can be expressed as

$${\mathbf{x}}(n) = \sum\limits_{p = 1}^{P} {{\mathbf{a}}_{m} \left( {\theta_{p} } \right)} \;{\mathbf{s}}_{p} \left( n \right) + {\mathbf{n}}\left( n \right)$$
(1)

where \({\mathbf{s}}\left( n \right),\,{\mathbf{a}}\left( \theta \right)\,{\text{and}}\;{\mathbf{n}}\left( n \right)\) are the desired signal, the steering vector and the noise signal respectively. Now, the Eq. (1) can be represented as

$${\mathbf{x}}\left( k \right) = {\mathbf{A}}\left( \theta \right)\,{\mathbf{s}}\left( n \right) + {\mathbf{n}}\left( n \right)$$
(2)

where

$${\mathbf{A}}\left( \theta \right) = \left[ {{\mathbf{a}}\left( {\theta_{1} } \right),{\mathbf{a}}\left( {\theta_{2} } \right), \ldots ,{\mathbf{a}}\left( {\theta_{p} } \right)} \right]^{T}$$
$${\mathbf{s}}\left( n \right) = \left[ {{\mathbf{s}}_{1} \left( n \right),{\mathbf{s}}_{2} \left( n \right), \ldots ,{\mathbf{s}}_{p} \left( n \right)} \right]^{T}$$
$${\mathbf{x}}\left( n \right) = \left[ {{\mathbf{x}}_{1} \left( n \right),{\mathbf{x}}_{2} \left( n \right), \ldots ,{\mathbf{x}}_{p} \left( n \right)} \right]^{T}$$
$${\mathbf{n}}\left( n \right) = \left[ {{\mathbf{n}}_{1} \left( n \right),{\mathbf{n}}_{2} \left( n \right), \ldots ,{\mathbf{n}}_{M - 1} \left( n \right)} \right]^{T}$$

Now, the matrix form of the received signal can be represented as

$${\mathbf{X}} = {\mathbf{AS}} + {\mathbf{W}}$$
(3)

where X represents the M × 1 signal vector, S represents the p × 1 envelopes of complex signal and W is the noise matrix.

The array manifold vector which is responsible for steering is represented as

$${\mathbf{A}} = \left[ {{\mathbf{a}}_{1} \left( {\xi ,\Phi } \right), \ldots ,{\mathbf{a}}_{P} \left( {\xi ,\Phi } \right)} \right]$$
(4)

where each column is of form

$${\mathbf{a}}\left( \theta \right) = \left[ \begin{aligned} \exp \left( {j\xi \cos \left( {\Phi_{p} - v_{0} } \right)} \right), \ldots \hfill \\ \exp \left( {j\xi \cos \left( {\Phi_{p} - v_{M - 1} } \right)} \right) \hfill \\ \end{aligned} \right]$$
(5)

here \(\theta = \left( {\xi ,\Phi } \right)\) represents the elevation angle which depends on \(\xi\). This is utilized to represent the directions of arriving sources. Let \(\xi = \vartheta \,r\,\sin \theta\), where r denotes the radius, \(\vartheta = \left( {2\pi /\lambda } \right)\) represents the wavenumber and \(v_{n} = \left( {2\pi n} \right)/M\) represents the location of array for \(n = 0,1, \ldots ,M - 1.\)

The azimuth angle is measured counter clockwise from the axis. Let the noise is white Gaussian with zero mean and variance.

Since Vandermonde structure [6] does not agree with the A (array manifold vector), decorrelated algorithms cannot be used to the uniform circular array. In our approach, we have transformed the virtual UCA (VUCA) into a 2 h + 1 virtual array. This form of structure can be applied to the decorrelated algorithms. Let us use the transformation matrix \(\Im\) to apply the mode excitation technique.

We know that the observation vector is

$${\mathbf{x}}\left( n \right) = {\mathbf{A}}\left( \Phi \right)\;{\mathbf{s}}(n) + {\mathbf{n}}\left( n \right)$$
(6)

Let us define the matrix \(\Im\) as

$$\Im = \aleph \zeta$$

where \(\zeta\) denotes the (2 h + 1) × M submatrix of the spatial discrete Fourier transform, which is expressed as

$$\zeta = \frac{1}{{\sqrt{M}}}\left({\begin{array}{*{20}c} 1 & {w^{- h}} & {w^{- 2h}} & \cdots & {w^{{-\left({M - 1} \right)h}}} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & {w^{- h}} & {w^{- 2}} & \cdots & {w^{{- \left({M - 1} \right)}}} \\ 1 & 1 & 1 & \cdots & 1 \\ 1 & {w^{1}} & {w^{2}} & \cdots & {w^{{\left({M - 1} \right)}}} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & {w^{h}} & {w^{2h}} & \cdots & {w^{{- \left({M - 1} \right)h}}} \\ \end{array}} \right)$$
(7)

and \(\aleph\) is the diagonal matrix of size (2 h + 1) × (2 h + 1), which is expressed as

$$\aleph = diag\left\{ {\frac{1}{{\sqrt M j^{n} \aleph_{n} \left( {vr} \right)}}} \right\},\quad n = - h, \ldots ,0, \ldots ,h.$$
(8)

A UCA can intrigue maximum of \(h \approx v_{o} r\) mode numbers.

This matrix is very helpful for protecting the angle-dependent phase. In (8), \(\aleph_{n} \left( {vr} \right)\) represents the n-order first kind of the Bessel function.

The array manifold vector of VULA if \(\left( {2h + 1} \right) \le M\) can be expressed as

$${\mathbf{A}}\left( \Phi \right) = \left( {\begin{array}{*{20}c} {e^{{ - jh\Phi_{1} }} } & \cdots & {e^{{ - jh\Phi_{P} }} } \\ \cdots & \cdots & \cdots \\ {e^{{jh\Phi_{1} }} } & \cdots & {e^{{jh\Phi_{P} }} } \\ \end{array} } \right)$$
(9)

where \({\mathbf{A}}\left( \Phi \right)\) has a size of (2 h + 1) × p.

3 Proposed Methods

For the 2D- DOA estimation we consider the following array signal model using a UCA. Assume that p(p < M) uncorrelated narrowband signals are received at the UCA composed of M sensors with half-wavelength spacing from \(\left[ {\left( {\theta_{1} ,\varphi_{1} } \right), \ldots ,\left( {\theta_{p} ,\varphi_{p} } \right)} \right]\). The signal received at the UCA is described as

$${\mathbf{X}}\left( n \right) = {\mathbf{As}}(n) + {\mathbf{n}}\left( n \right)$$
(10)

where \({\mathbf{x}}(n) = \left[ {{\mathbf{x}}_{1} \left( n \right),{\mathbf{x}}_{2} \left( n \right), \ldots ,{\mathbf{x}}_{M} \left( n \right)} \right]\) denotes the n-th snapshot of the impinging signal at the considered UCA. \(\left( \cdot \right)^{T}\) is the transpose of the matrix.

\({\mathbf{A}}\) is the array manifold which is expressed for 2D-DOA as

$${\mathbf{A}}\left( \theta \right) = \left[ {{\mathbf{a}}\left( {\theta_{1} ,\varphi_{1} } \right),{\mathbf{a}}\left( {\theta_{2} ,\varphi_{2} } \right), \ldots ,{\mathbf{a}}\left( {\theta_{p} ,\varphi_{p} } \right)} \right]^{T}$$
(11)

This steering matrix is the full column rank matrix with the following steering vector.

$${\mathbf{a}}\left( {\theta_{i} ,\varphi_{i} } \right) = \left[ {{\mathbf{a}}_{1} \left( {\theta_{1} ,\varphi_{1} } \right),{\mathbf{a}}_{2} \left( {\theta_{i} ,\varphi_{i} } \right), \ldots ,{\mathbf{a}}_{p} \left( {\theta_{i} ,\varphi_{i} } \right)} \right]$$
(12)

here \(i = 1,2, \ldots ,p\) and \(\theta_{i} \;and\;\varphi_{i}\) are respectively the elevation and the azimuth angles of the i-th received signal.

\({\mathbf{s}}\left( n \right)\) denotes the vector of the incident signal and \({\mathbf{n}}\left( n \right)\) is the white Gaussian noise with zero mean \(\sigma_{n}^{2}\) variance.

We should set the array manifold vector to \({\mathbf{a}}\left( {\theta ,\phi } \right) = \left[ {{\mathbf{a}}_{1} \left( {\theta ,\phi } \right),{\mathbf{a}}_{2} \left( {\theta ,\phi } \right), \ldots ,{\mathbf{a}}_{M} \left( {\theta ,\phi } \right)} \right]\)if the DOAs of the impinging signals are \(\left( {\theta ,\phi } \right).\) Here \(a_{m} \left( {\theta ,\phi } \right) = e^{{j2\pi \left( {R/\lambda } \right)\sin \left( \theta \right)\cos \left( {2\pi m/M - \phi } \right)}}\)

Now the covariance matrix of the received signal is written as

$${\tilde{\mathbf{R}}} = {\rm E}\left[ {{\mathbf{x}}_{1} (n){\mathbf{x}}_{1}^{\rm H} (n)} \right] = {\mathbf{AR}}_{S} {\mathbf{A}}^{\rm H} + \sigma^{2} {\mathbf{I}}$$
(13)

where \({\mathbf{R}}_{{\mathbf{s}}} = {\rm E}\left[ {{\mathbf{s}}(n){\mathbf{s}}^{\rm H} (n)} \right]\) is the covariance matrix of the incident signal. Finally, the DOAs can be obtained by deploying the ESPRIT algorithm for the considered UCA using single snapshot.

3.1 The UCA-ESPRIT Algorithm

Using the doublet structure array antenna, mathematical representations for the signals received is described as

$${\mathbf{x}}_{1} \left( n \right) = {\mathbf{A}}_{1} \left( \Phi \right){\mathbf{s}}(n) + {\mathbf{n}}_{1} \left( n \right) = {\mathbf{A}}_{1} {\mathbf{s}}(n) + {\mathbf{n}}_{1} \left( n \right)$$
(14)
$${\mathbf{x}}_{2} \left( n \right) = {\mathbf{A}}_{2} \left( \Phi \right){\mathbf{s}}(n) + {\mathbf{n}}_{2} \left( n \right) = {\mathbf{A}}_{2} {\mathbf{s}}(n) + {\mathbf{n}}_{2} \left( n \right)$$
(15)

here \({\mathbf{A}}_{2}\) and \({\mathbf{A}}_{2}\) are steering vectors. For the simplification purpose, we have considered \({\mathbf{A}}\left( \Phi \right) = {\mathbf{A}}\)

Now, the array correlation matrix is expressed as

The correlation matrices of doublet structure can be represented as

$${\mathbf{R}} = {\rm E}\left[ {{\mathbf{x}}(n){\mathbf{x}}^{\rm H} (n)} \right]$$
(16)

The above correlation can also be represented as

$${\mathbf{R}} = {\mathbf{AR}}_{S} {\mathbf{A}}^{\rm H} + \sigma^{2} {\mathbf{I}}_{n}$$
(17)

In the above expression, \({\mathbf{R}}_{s}\) denotes the impinging signal’s covariance matrix which is expressed as

$${\mathbf{R}}_{s} = E\left[ {\Phi \;\Phi^{H} } \right].$$
(18)

Now, for the ESPRIT algorithm, the covariance matrices are associated with the array 1 and array 2 as

$${\mathbf{R}}_{1} = {\rm E}\left[ {{\mathbf{x}}_{1} (n){\mathbf{x}}_{1}^{\rm H} (n)} \right] = {\mathbf{AR}}_{S} {\mathbf{A}}^{\rm H} + \sigma^{2} {\mathbf{I}}_{n}$$
(19)
$${\mathbf{R}}_{2} = {\rm E}\left[ {{\mathbf{x}}_{2} (n){\mathbf{x}}_{2}^{\rm H} (n)} \right] = {\mathbf{A}}\Phi \;{\mathbf{R}}_{S} \Phi^{H} {\mathbf{A}}^{\rm H} + \sigma^{2} {\mathbf{I}}_{n}$$
(20)

The array antennas are translationally related to each other by non-singular transformation matrix as

$${\mathbf{E}}_{1} \psi = {\mathbf{E}}_{2}$$
(21)

There must also exist a unique non-singular transformation matrix \({\mathbf{U}}\) such that

$${\mathbf{E}}_{1} = {\mathbf{AU}}$$
(22)

and

$${\mathbf{E}}_{2} = {\mathbf{A}}\Phi {\mathbf{U}}$$
(23)

Now, let us substitute (17) and (18) in (19) by using that the array manifold is of a full rank matrix to obtain the following relationship

$${\mathbf{U}}\psi \,{\mathbf{U}}^{ - 1} = \Phi$$
(24)

Finally, the DOAs by exploiting the doublet array configuration can be obtained for the ESPRIT algorithm as

$$\theta_{p} = \cos^{ - 1} \left\{ {\frac{{Arg\left( {\lambda_{p} } \right)}}{2\pi \delta }} \right\},$$
(25)

here \(p = 1,2, \ldots ,m\).

3.2 The UCA-Modified MUSIC Algorithm

In this algorithm, we exploit the ensemble-averaged correlation matrix \({\mathbf{R}}_{{{\mathbf{xx}}}}\) [20] for the array outputs. The eigendecomposition of the \({\mathbf{R}}_{{{\mathbf{xx}}}}\) is given as

$${\mathbf{R}}_{{{\mathbf{xx}}}} = \sum\limits_{i = 1}^{M} {\lambda_{i} {\mathbf{e}}_{i} {\mathbf{e}}_{i}^{H} }$$
(26)

where \({\mathbf{e}}_{i}\) denotes the eigenvector of the correlation matrix \({\mathbf{R}}_{{{\mathbf{xx}}}} .\)

Finally, the DOAs are estimated using the modified MUSIC algorithm by separring the noise subspace from the signal subspace and it is given as

$${\mathbf{P}}\left( {\theta ,\phi } \right) = \frac{1}{{\left| {{\mathbf{a}}\left( {\theta ,\varphi } \right){\mathbf{C}}} \right|^{2} }}$$
(27)

where C and a respectively represent the eigenvectors of the noise and signal vector.

4 Results and Discussion

Let us consider a UCA as an antenna array configuration for simulation of the proposed algorithm. Let the size of the received signal matrix ‘X’ can be calculated as

  • The size of matrix ‘X’ for the classical method = (2 h + 1) × 100( snapshots) = 9 × 100 = 900.

  • The size of matrix ‘X’ for the proposed methods = (2 h + 1) × 1( snapshot) = 9 × 1 = 9.

Root mean square error (RMSE) performance of DOA algorithms can be analyzed using Monte Carlo simulations, which is expressed as [21,22,23,24]

$$RMSE = \sqrt {\sum\limits_{l = 1}^{L} {\frac{{\left( {\Phi_{\ell }^{ * } - \Phi_{\ell } } \right)^{2} }}{L - 1}} }$$
(27)

where \(\Phi_{l}^{ * }\) is the estimated DOA at each trail, \(\Phi_{l}\) is the actual DOA and ‘L’ is the total number of trails.

Let us study the performance of the proposed algorithm for widely spaced and closely spaced targets.

Let us consider the two coherent sources impinge a UCA consisting of M = 10 antenna elements at 50o and 250o. Let the noise be additive white Gaussian with zero mean \(\sigma^{2}\) variance, SNR = 10 dB, N = 1(single snapshot) and d = λ/2. In this experiment, L = 200 Monte Carlo trails are used for each SNR.

Figures 2 and 3 show the histogram and RMSE performance of the proposed UCA-DOA method for two widely spaced targets [50o and 250o]. Now let us consider coherent sources impinge a UCA at 10o and 30o keeping other parameters unchanged. Computer simulations of this case are shown in Figs. 4 and 5. Figure 4 is the histogram and Fig. 5 is the RMSE performance for two closely spaced [10o and 30o] targets.

Fig. 2
figure 2

DoA Estimation of proposed UCA-DOA METHOD [M = 10, N = 1, p = 2 for targets 50o and 250o]

Full size image
Fig. 3
figure 3

RMSE angle error performance of modified UCA -DOA METHOD [for M = 10, N = 1, p = 2, Targets 50o and 250o]

Full size image
Fig. 4
figure 4

DoA Estimation of proposed UCA-DOA METHOD [M = 10, N = 1, p = 2 for targets 10o and 30o]

Full size image
Fig. 5
figure 5

RMSE performance of proposed UCA -DOA METHOD [M = 10, N = 1, p = 2 for targets 10o and 30o]

Full size image

In Fig. 6, we have examined the performance probability resolution of the proposed methods and compared them with classical MUSIC, the root-MUSIC, and the ESPRIT algorithm. We have considered three narrowband uncorrelated signal sources that are received from [20o, 30o, and 50o] at the 10 element array antenna with half-wavelength spacing. We assume the noise is white with zero means. We used one snapshot per antenna for the proposed method and 100 snapshots to the other methods. It is seen that the performance of the proposed method with one sample per antenna does not affect the performance of PR over a wide range of SNRs.

Fig. 6
figure 6

PR performances versus SNR

Full size image

It is observed that the performances of both ESPTIR using 100 samples and the performance of the proposed method show the almost same resolution from SNR is 10 dB onwards. This experiment illustrates that the proposed method is more efficient and less complex than the other three methods. This certainly reduces the computational burden of the processor and saves a lot of time. In the next experiment, we have analyzed the computational complexity of the proposed method.

As illustrated in Fig. 7, the processing time of each algorithm is calculated using the previous example. As seen in this Figure, the proposed method significantly has reduced time computation as compared to the MUSIC, the root-MUISC, and the ESPRIT methods. This experiment is based on the Intel Core i5 3470 Processor. Hence it is proved that the proposed method using just one sample per antenna can achieve the same performance as that of classical methods using 100 samples per antenna.

Fig. 7
figure 7

Analysis of CPU time (computational time in second versus antenna elements)

Full size image

Consider two uncorrelated signal sources from far directions − 38° azimuth, 0° elevation and 18° azimuth, 20° with the frequencies 1.5 kHz and 2.5 kHz impinge a UCA composed of 8 antenna elements separated by 0.45 wavelength. Let the SNR and snapshots are fixed to 20 dB and 1 respectively. The array operating frequency is 300 MHz. The 2D- pseudo spectrum using modified MUSIC by deploying a single snapshot is depicted in Fig. 8.

Fig. 8
figure 8

2-D spatial spectrum of Modified MUSIC using single snapshot

Full size image

5 Conclusion

In this work, a single snapshot direction of arrival estimation by using a UCA-DOA is devised. This method focus on the worst-case scenario in wireless communication application wherein a very few snapshots or single snapshots are available at the receiver end to estimation the required DOAs. This is the most important advantage of this work since it is highly useful for real-time practical applications. The performance of the proposed algorithm with a single snapshot is similar to the classical methods, namely, MUSIC, root-MUSIC, and the ESPRIT algorithm using 100 snapshots. Furthermore, the computational complexity of the proposed algorithm in terms of CPU time is presented. The proposed method shows a significant reduction in the time as it exploits one snapshot of antenna element as compared to 100 snapshots used for the other methods.