1 Introduction

The exploration of chaotic systems started some 200 years ago. A system whose current state cannot be determined by initial conditions is known as chaotic system. The current state of the system is the consequence of the past initial conditions, medium of communication, the noise and external circumstances beyond the control of the observer. Hence randomness, ergodicity and sensitivity to initial conditions are ultimate topographies of chaotic system. These features attract cryptographers to use such system for secure communications of media using cryptographic algorithms. The purpose of cryptography in secure transmission is to convert valuable and meaningfull messages into the bogus ones. Such targets are achieved specifically in symmetric key cryptography and assymetric key cryptography, the two main divisions of cryptography. This paper make use of symmetric key cryptography. These are further divided by gauging mode of applications like block ciphers and stream ciphers.

Block cryptosytem works by selecting blocks of input data for further application of cryptographic procedures. The two main objectives of block cryotograms are to induce confusion and diffusion in the plain-text message. This was the idea introduced by Shannon [1]. Diffusion is attained by distorting the statistical configuration i.e. the original bits are scattered in cipher text. While confusion is achieved by modification of original bits. These two are attained in many block cryptosystems by means of round repetition of an algorithm. The four steps of recent block cryptograms include permutation, substitution, addition of key and mixing [2,3,4,5].

The usage of chaotic systems in cryptography specifically in block cryptosystems like the case here in this article is due to the fact of their pecuiler behaviour. These systems exhibt random behaviour, unpredictability and sensitivity towards initial inputs and parameters [6, 7]. An assaulter can not predict the chaotic system and the results obtained from this without having the knowledge of initial conditions. Chaotic dynamical systems are useful in the the design of cryptostem for acquiring confusion and dissusuion in the ciphered text. Henceforth, chaos is getting place in recent cryptosystem [8,9,10,11,12].

Secure communication using wireless channels is mandatory since cryptanalysts are always in line to extract the vital information. Thus, use of cryptography is only way to tackle such situations. The main aim of cryptographic algorithms is to create ambiguity in the enciphered information which is achieved using substitution boxes. These are only nonlinear components of block ciphers generating pandemonium in cryptosystems. Many articles are available in literature to construct such non-linear components utilizing different algebraic and chaotic maps, some of them are listed here. [13,14,15,16,17,18], but the chaotic dynamical systems are utilized very often in the field of cryptography.

The motivation behind the utilization of chaotic dynamical systems like double pendulum in the design of cryptosystems is due to the fact of the unpredictability and complex behaviour of the system. These systems are governed by the differential equtions. A physical system is modelled initially by finding derivatives of the function. These systems are key sensitive i.e. for a different set of initial conditions and parameters, a totally dissimilar chaotic trajectory is obtained. Moreover, with the involvement of numerous equations and conditions, chaotic dynamical systems are having enriched key space as compared to one dimensional systems like [7, 10, 15, 16, 19].

2 Double Pendulum

The simplest chaotic dynamical system is double pendulum. Whenever initial angels are slightly changed, the bifurcation pattern of this system changes exponentially. Being sensitive to initial conditions, the chaotic dynamical system is found prolific in generating confusion and diffusion in the cryptosystem. In this article, two double pendulums having same inclinations initially are used to generate integer values to design the non-linear components of block cipher. The mathematical formulation of a double pendulum shown in Fig. 1 is explained as follow

$$x_{1} = l_{1} \sin \varphi_{1}$$
(1)
$$x_{2} = l_{1} \sin \varphi_{1} + l_{2} \sin \varphi_{2}$$
(2)
$$y_{1} = - l_{1} \cos \varphi_{1}$$
(3)
$$y_{2} = - l_{1} \cos \varphi_{1} - l_{2} \cos \varphi_{2}$$
(4)

where \(x_{1}\) and \(x_{2}\) are horizontal components and \(y_{1}\) and \(y_{2}\) are vertical components of masses \(m_{1}\) and \(m_{2 }\) respectively. Now the potential energy \(P\) for case of double pendulum is given as

Fig. 1
figure 1

Double pendulum attached end to end

Full size image
$$P = - m_{1} gl_{1} \cos \varphi_{1} - m_{2} g\left( {l_{1} \cos \varphi_{1} + l_{2} \cos \varphi_{2} } \right)$$
(5)

And kinetic energy \(K\) is obtained by finding derivatives of Eqs. (1)–(4), we get

$$K = \frac{1}{2}m_{1} \left( {\dot{\varphi }_{1}^{2} l_{1}^{2} } \right) + \frac{1}{2}m_{2} \left( {\dot{\varphi }_{1}^{2} l_{1}^{2} + \dot{\varphi }_{2}^{2} l_{2}^{2} + 2\dot{\varphi }_{1} l_{1} \dot{\theta }_{2} l_{2} \cos \left( {\varphi_{1} - \varphi_{2} } \right)} \right)$$
(6)

The Langrangian (L) of a system is defined as the difference of kinetic energy and potential energy, which, for the case of a double pendulum is

$$\begin{aligned} L & = \frac{1}{2}\left( {m_{1} + m_{2} } \right)L_{1}^{2} \dot{\varphi }_{1}^{2} + \frac{1}{2}m_{2} L_{2}^{2} \dot{\varphi }_{2}^{2} + m_{2} L_{1} L_{2} \dot{\varphi }_{1} \dot{\varphi }_{2} \cos \left( {\varphi_{1} + \varphi_{2} } \right) \\ & \quad + \,\left( {m_{1} + m_{2} } \right)gL_{1} \cos \varphi_{1} + m_{2} gL_{2} \cos \varphi_{2} \\ \end{aligned}$$
(7)

Then,

$$\frac{\partial L}{{\partial \varphi_{1} }} = - L_{1} g\left( {m_{1} + m_{2} } \right)\sin \varphi_{1} - m_{2} L_{1} L_{2} \dot{\varphi }_{1} \dot{\varphi }_{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right)$$
(8)
$$\frac{\partial L}{{\partial \dot{\varphi }_{1} }} = \left( {m_{1} + m_{2} } \right)L_{1}^{2} \dot{\varphi }_{1} + m_{2} L_{1} L_{2} \dot{\varphi }_{2} \cos \left( {\varphi_{1} - \varphi_{2} } \right)$$
(9)
$$\frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{\varphi }_{1} }}} \right) = \left( {m_{1} + m_{2} } \right)L_{1}^{2} \ddot{\varphi }_{1} + m_{2} L_{1} L_{2} \ddot{\theta }_{2} \cos \left( {\varphi_{1} - \varphi_{2} } \right) - m_{2} L_{1} L_{2} \ddot{\varphi }_{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right)\left( {\ddot{\varphi }_{1} - \ddot{\varphi }_{2} } \right)$$
(10)

Since Langrangian of a system satisfies the Euler-Langrange differential equation

$$\frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{\varphi }_{1} }}} \right) - \frac{\partial L}{{\partial \varphi_{1} }} = 0 .$$
(11)

Substituting Eqs. (9) and (10) in above equation we get

$$\left( {m_{1} + m_{2} } \right)L_{1}^{2} \ddot{\varphi }_{1} + m_{2} L_{1} L_{2} \ddot{\theta }_{2} \cos \left( {\varphi_{1} - \varphi_{2} } \right) - m_{2} L_{1} L_{2} \ddot{\varphi }_{2}^{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right) + gL_{1} \left( {m_{1} + m_{2} } \right)\sin \varphi_{1} = 0$$
(12)

Extracting \(\ddot{\varphi }_{1}\) from the above equ, we get:

$$\ddot{\varphi }_{1} = \frac{{ - m_{2} L_{2} \ddot{\varphi }_{2} \cos \left( {\varphi_{1} - \varphi_{2} } \right) - m_{2} L_{2} \ddot{\varphi }_{2}^{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right) - g\left( {m_{1} + m_{2} } \right)\sin \varphi_{1} }}{{\left( {m_{1} + m_{2} } \right)L_{1} }}$$
(13)

Similarly, we can derive an equation using Euler–Langrange equation for \(\varphi_{2}\), which is as follow

$$\ddot{\varphi }_{2} = \frac{{ - L_{1} \ddot{\varphi }_{1} \cos \left( {\varphi_{1} - \varphi_{2} } \right) - L_{1} \ddot{\varphi }_{1}^{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right) - g\sin \varphi_{2} }}{{L_{2} }}$$
(14)

Solving above two equations simultaneously to derive the following differential equations

$$\ddot{\varphi }_{1} = \frac{{ - m_{2} L_{1} \ddot{\varphi }_{1}^{2} { \sin }\left( {\varphi_{1} - \varphi_{2} } \right)\cos \left( {\varphi_{1} - \varphi_{2} } \right) - m_{2} L_{2} \ddot{\varphi }_{2}^{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right) + m_{2} gsin\left( {\varphi_{2} } \right){ \cos }\left( {\varphi_{1} - \varphi_{2} } \right) - g\left( {m_{1} + m_{2} } \right)\sin \varphi_{1} }}{{\left( {m_{1} + m_{2} } \right)L_{1} - m_{2} L_{1} \cos^{2} \left( {\varphi_{1} - \varphi_{2} } \right)}}$$
$$\ddot{\varphi }_{2} = \frac{{m_{2} L_{2} \ddot{\varphi }_{2}^{2} { \sin }\left( {\varphi_{1} - \varphi_{2} } \right)\cos \left( {\varphi_{1} - \varphi_{2} } \right) + L_{1} \ddot{\varphi }_{1}^{2} \sin \left( {\varphi_{1} - \varphi_{2} } \right)\left( {m_{1} + m_{2} } \right) + gsin\left( {\varphi_{1} } \right)\cos \left( {\varphi_{1} - \varphi_{2} } \right)\left( {m_{1} + m_{2} } \right) - g\left( {m_{1} + m_{2} } \right)\sin \varphi_{1} }}{{\left( {m_{1} + m_{2} } \right)L_{2} - m_{2} L_{2} \cos^{2} \left( {\varphi_{1} - \varphi_{2} } \right)}}$$

Now replacing \(\varphi_{1} , \varphi_{2} , \ddot{\varphi }_{1} {\rm and} \, \ddot{\varphi }_{1}\) by \(\zeta_{1} , \zeta_{2} ,\zeta_{3} ,and \zeta_{4}\) respectively. Differentiation of these yields the following four first order differential equations after substituting \(\ddot{\varphi }_{1}\) and \(\ddot{\varphi }_{2}\):

$$\dot{\zeta }_{1} = \ddot{\varphi }_{1}$$
$$\dot{\zeta }_{2} = \ddot{\varphi }_{2}$$
$$\dot{\zeta }_{3} = \frac{{ - m_{2} L_{1} \zeta_{3}^{2} { \sin }\left( {\zeta_{1} - \zeta_{2} } \right)\cos \left( {\zeta_{1} - \zeta_{2} } \right) - m_{2} L_{2} \zeta_{4}^{2} \sin \left( {\zeta_{1} - \zeta_{2} } \right) + m_{2} gsin\left( {\zeta_{2} } \right){ \cos }\left( {\zeta_{1} - \zeta_{2} } \right) - g\left( {m_{1} + m_{2} } \right)\sin \zeta_{1} }}{{\left( {m_{1} + m_{2} } \right)L_{1} - m_{2} L_{1} \cos^{2} \left( {\zeta_{1} - \zeta_{2} } \right)}}$$
$$\dot{\zeta }_{4} = \frac{{m_{2} L_{2} \zeta_{4}^{2} { \sin }\left( {\zeta_{1} - \zeta_{2} } \right)\cos \left( {\zeta_{1} - \zeta_{2} } \right) + L_{1} \zeta_{4}^{2} \sin \left( {\zeta_{1} - \zeta_{2} } \right)\left( {m_{1} + m_{2} } \right) + gsin\left( {\zeta_{1} } \right){ \cos }\left( {\zeta_{1} - \zeta_{2} } \right)\left( {m_{1} + m_{2} } \right) - g\left( {m_{1} + m_{2} } \right)\sin \zeta_{2} }}{{\left( {m_{1} + m_{2} } \right)L_{2} - m_{2} L_{2} \cos^{2} \left( {\zeta_{1} - \zeta_{2} } \right)}}$$

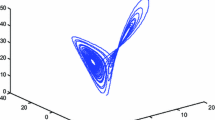
Solving the above four first order differential equations for two double pendulums in MATLAB for 50 s. The graph given in Fig. 2 depicts the chaotic nature of this dynamical system. The trajectories of two double pendulums are represented by colors in figure i.e. blue and red.

Fig. 2
figure 2

Bifurcation diagram for double pendulum. (Color figure online)

Full size image

The initial inclinations of two double pendulums along with initial conditions of differential equations are responsible to determine the chaotic trajectory of dynamical system. A slight change in their values generate a different bifurcation pattern as demonstarted in Fig. 3. In other words, the solution space is sensitive to initial keys. This concept is very useful in cryptography for the generation of S-boxes. The robustness of the scheme based on such systems increases exponentially. For the case of two double pendulums, slight variation in initial parameters generated the following different bifurcation pattern. It implies that with theses values one can generate a totally different substitution box. Hence the suggested method is key sensitive.

The dominance of chaotic dynamical systems over low dimensional discrete chaotic systems is due to the fact that they have larger and complex solution space. Their larger key space and key sensitivity are also contributing in their supremacy. Moreover, chaotic range of continuous chaotic systems is bigger than discrete systems. Additionally, with the invention of modern computing devices, the chance of resistance attacks like brute force etc. are minimum for chaotic dynamical systems as compared to 1D and 2D systems.

Fig. 3
figure 3

Trajectory plot of the system for different initial conditions

Full size image

3 Review of S-Boxes Connected to the Suggested Scheme

This section includes the contextual background regarding the suggested scheme. System of differential equations like Chaotic Lorenz system and Rabionvich–Fabrikant system is used by [13, 20, 21] to generate S-box. Khan et al. used multi chaotic systems for the construction of block cipher in [22]. The chaotic maps with improved chaotic range are utilized in [7] to synthesize nonlinear component of block cipher. The chaotic behavior of tent and sine maps are used to encipher the image by Zhou et al. in [5] and Attaullah et al. in [23]. Chaotic Gingerbreadman and symmetric group of order 8 was used for the design of an S-box in [24]. Authors used ABC optimization [25] and three dimensional baker maps for the production of S-boxes [17]. In [26] authors used the concept of coset diagram with bijecteive map and in [27] primitive irreducible polynomials over the field Z2 for the construction of S-boxes. There is enough relevant material available in literature for the construction of S-boxes based on chaotic maps [19, 28,29,30,31] but chaotic dynamical systems are less utilized in cybersecurity.

4 Construction of Substitution Box

The confidentiality in any cryptosystem is increased utilizing substitution boxes. We suggest a new scheme for the design of S-box based on chaotic dynamical system. The simplest chaotic dynamical system is double pendulum. Two double pendulums making an extreme chaotic trajectory are used to construct S-box in this scheme. The result analysis of nonlinearity, strict avalanche criterion (SAC), bit independence criterion (BIC) and linear and differential approximation probability validates the proficiency of the suggested S-box. Substitution box construction involves the following steps.

  • Initially, from the solution space of two double pendulums a chaotic sequence \(U\left( {1 \times 256} \right)\) of integers is generated using MATLAB.

  • Find the sequence \(V\left( {1 \times 256} \right)\) as follow.

    $$V\left( i \right) = U\left( {256} \right) - U\left( i \right) 1 \le i \le 256$$

  • Arranging \(V\left( i \right)\) in ascending order to obtain \(W\left( i \right)\).

  • After that each element of \(W\left( i \right)\) is replaced by its order in \(U\left( i \right)\) to obtain \(Z\left( i \right)\).

  • A new sequence \(Z^{\prime}\left( i \right)\) is obtained by the following relation

    $$Z^{\prime}\left( i \right) = Z\left( 1 \right) - Z\left( i \right) 1 \le i \le 256$$

  • Permuting the position of \(Z^{\prime}\left( i \right)\) with random permutation generated by MATLAB to obtain the \(16 \times 16\) matrix \(M_{16}\) given in Table 1.

    Table 1 \(16 \times 16\) matrix
    Full size table

  • In the last step, a permutation \(\mu\) from symmetric group \(S_{256}\), containing only two cycles, is utilized for permuting the entries of \(M_{16}\). This process leads us to obtain the desired substitution box given in Table 2.

    $$\begin{aligned} & \mu = (0\; 125\; 171\; 106\; 242\; 81 \;164\; 217\; 138\; 244\; 187\; 201\; 13\; 224\; 253\; 226\; 41\; 50\; 216\; 129\; 20 \\ & 194 \;205 \;60\; 99\; 37\; 67\; 150 \;240 \;114\; 246\; 118\; 198\; 113\; 97\; 57\; 69\; 119\; 191\; 117\; 18\; 51\;1 \;64\; 94 \\ & 241\; 115\; 210\; 12\; 59\; 124\; 111\;131\; 74\; 228\; 248\; 123\; 31\; 104\; 245\; 25\; 102\; 86\; 10\; 32\; 197\; 44\; 128 \\ & 48\;239\;151\; 7\; 130\; 89\; 196\;168\; 229\; 8 \;172\; 93\; 61\; 126\; 52\; 178\; 160\; 193\; 180\; 73\; 146\; 225\; 66\; 170 \\ & 212\; 163\; 71\; 213\; 127\; 14 \;211 \;254\; 42\; 70\; 38\; 159\; 219\; 87\; 153\; 101\; 207\; 9\; 157\; 62\; 108\; 195\; 83 \\ & 47\; 223\; 218 \;182 \;252\; 133\; 92\; 88\; 165\; 96\; 147\; 58\; 17\; 177\; 214\; 39\; 233\; 121\; 43\; 166 \;189 \;215 \\ & 179\; 137\; 134\; 152\; 135\; 149\; 162\; 200\; 103) \;(2 \;155 \;255\; 91\; 227\; 26\; 95\; 145\; 183\; 65\; 192\; 105 \\ & 110\; 49\; 85\; 72\; 243\; 45\; 63\; 174\; 167\; 132\; 29\; 176\; 84\; 22\; 231\; 53\; 75\; 156\; 190\; 33\; 21\; 79\; 112\; 158 \\ & 140\; 36\; 15 \;186 \;181\; 208\; 238\; 30\; 78\; 5\; 175\; 230\; 169\; 6\; 54 \;209\; 202\; 40\; 204\; 188\; 247\; 251\; 142 \\ & 55 \;221\; 232\; 107\; 235\; 35\; 143\; 56\; 34\; 19\; 220\; 4 \;236\; 122\; 109\; 3\; 11\; 234\; 68\; 139\; 46\; 24\; 120\; 250 \\ & 27\; 206 \;185\; 154\; 249\; 80\; 100\; 77\; 28\; 16 \;90 \;237\; 136\; 161\; 76 \;199\; 148\; 184\; 173\; 23\; 82\; 116\; 144 \\ & 222\; 203\; 98\, 141) \\ \end{aligned}$$
    Table 2 Designed substitution box
    Full size table

4.1 Nonlinearity

It is the most imperative property of a cryptosystem. Principally, the nonlinearity of an outstanding cryptographic system is higher. It measures the confrontation of a system against linear cryptanalysis as given in Table 3. For a set of affine Boolean functions \(f_{j}\), the following equation describes the nonlinearity of a Boolean function \(v\):

Table 3 Evaluation of suggested S-box for nonlinearity analysis
Full size table
$$NL_{u} = d\left( {v,f_{j} } \right) = \hbox{min} \;\;d\left( {v,\delta } \right); \quad \delta \in f_{j}$$

4.2 Bit Independence Criterion

The statistical property of output bit independent criterion (BIC) for an S-box given by Webster and Tavares [32] is delineated as, for a certain collection of avalanche vectors, altogether the avalanche variables should be pairwise autonomous. This principle highlights the efficacy of confusion function. BIC values for the suggested S-box are tabultaed in Table 4.

Table 4 Evaluation of suggested S-box for average values
Full size table

4.3 Strict Avalanche Criterion

The Strict avalanche effect (SAC) introduced by Webster and Tavares in 1985, basically elaborates the generality of avalanche effect and completeness given in Table 5. It states that the chances of variation in output bits must by 0.5 for alteration of sole input bit. Mathematically, for

Table 5 Evaluation of suggested S-box for SAC analysis
Full size table
$$h:GF\left( 2 \right)^{n} \to GF\left( 2 \right)^{m}$$
$$Prob\left( {h\left( {x^{j} } \right)} \right)_{i} \ne Prob\left( {g\left( x \right)} \right)_{i} = \frac{1}{2}\quad \quad \forall \quad j \in \left[ {1,n} \right] \quad and\quad i \in \left[ {1,m} \right]$$

4.4 Linear Approximation Probability

The linear approximation probability (LAP) is used to measure the maximum amount of discrepancy of an event. For a set \(S\) containing total members \(2^{p}\) of possible input bits. If \(\tau_{i} \;and\; \tau_{o}\) are denoting input and output values respectively, then (LAP) values for the proposed S-box given in Table 6, is explained by the following equation:

Table 6 Evaluation of suggested S-box for LP analysis
Full size table
$$LAP = \mathop {\hbox{max} }\limits_{{\tau_{i} ,\tau_{o} \ne 0}} \left| {\frac{{\# \left\{ {u/u.u = \tau \left( u \right).\tau_{o} } \right\}}}{{2^{p} }} - \frac{1}{2}} \right|$$

4.5 Differential Approximation Probability

The differential homogeneity is an ultimate trait of a substitution box. The degree of a differential equality is also known as differential approximation probability. The corresponding values of DP are depicted in Table 7. Mathemaitcally, it is defined as follow:

$$DP_{f} = \left( {\frac{{\# \left\{ {u \in U \wedge f(u) \oplus f(u \oplus \Delta u) = \Delta z} \right\}}}{{2^{k} }}} \right)$$

5 Majority Logic Criterion

Majority logic criterion (MLC) is used to gauge the texture of an encrypted image after enciphering of an input image by an S-box. It includes the analyses like homogeneity, contrast, correlation, entropy and energy [33]. These analyses are used to establish the statistical strength of nonlinear component of block ciphers by measuring the amount of alterations occurred in an image after encryption. Some very brief details of these analysis are given hereafter.

5.1 Information Entropy Analysis

The rate of disorder in the cipher image gives the information entropy. The entropy for an image having total pixels \(N\) and the probability \(p\left( {u_{j} } \right)\) for the pixel \(u_{j}\) will be calculated by:

$${\text{E}}\left( {\text{U}} \right) = \mathop \sum \limits_{j = 1}^{N} p\left( {u_{j} } \right)\log_{2} p\left( {u_{j} } \right)$$

For a grayscale image, if \(p\left( {u_{j} } \right)\) of occurance for any pixel \(u_{j}\) is equal then the hypothetical value of entropy is 8. Hence, the information entropy for the suggested scheme should approximately be 8, to validate its efficacy. Table 7 compares the entropy outcomes for the suggested scheme with [4, 7, 34].

Table 7 Assessment of DP entities for various S-boxes
Full size table

5.2 Correlation Analysis

The adjoining pixels (horizontally, vertically and diagonally) of the host image are highly correlated. A secure and robust encryption procedure make these adjacent pixels unrelated, i.e. the correlation of adjacent pixels approaches to zero of an enciphered image. The correlation for the neighbouring pixels \(r\) and \(s\) for a grayscale image is given by:

$$\Lambda _{rs} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\left\{ {r_{i} - \bar{r}} \right\}\left\{ {s_{i} - \bar{s}} \right\}} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {r_{i} - \bar{r}} \right)^{2} } \sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {s_{i} - \bar{s}} \right)^{2} } }}$$

The outcomes generated by above relation are shown in Table 8. The correlation values of the processed image is almost zero as required.

Table 8 Evaluation of the proposed S-box for the Cameraman Image in comparison of varous S-boxes
Full size table

5.3 Contrast, Homogeneity and Energy Analyses

An appropriate amount of brightness is present in the host image, which vanishes in the enciphered image. This loss is measured by the contrast analysis. The secure encryption yields the higher values of contrast for the encrypted image. Furthermore, the texture of an encrypted image is measured utilizing homogeneity and energy analysis (Figs. 4, 5).

Fig. 4
figure 4

Original and the processed cameraman image

Full size image
Fig. 5
figure 5

Histogram of the Host and encrypted cameraman image

Full size image

6 Conclusion

To increase the vagueness of a cryptosystem, use of chaotic maps in the construction of a substitution box is a recent trend. In this paper, the simplest chaotic dynamical system i.e. double pendulum is used for the first time to generate integer values along with the application of symmetric group in construction of non-linear components of block cipher. The amalgamation of these two yields confusion and diffusion in the suggested cryptosystem. For a practical application, an image is encrypted afterwards with the designed S-box. The standard algebraic and statistical analyses available in literature validate the efficacy of the proposed system for the safe communication of data. Hence, designed chaotic S-box generated by means of chaotic dynamical system and symmetric group has the ability to become hurdle in the path of cryptanalysts.