Outage Capacity Analysis of a Cooperative Relaying Scheme in Interference Limited Cognitive Radio Networks

Abstract

In this study, we investigate the outage capacity of a cooperative relaying based cognitive radio network in slow fading channel. Our network scenario consists of a primary transmitter (PT) and primary receiver (PR) as well as a group of $M$ secondary transmitter (ST)–receiver (SR) pairs. We grouped STs into active and inactive. Only one active ST may transmit data at a time in parallel with the PT satisfying a predefined interference threshold $I_{th}$ to the PR. Due to fading/shadowing or interference caused by ST to the PR, primary user (PU) may fail to achieve its target rate $R_{{\textit{PT}}}$ over a direct link. To overcome this, we can boost up primary capacity by using inactive STs as cooperative relay (Re) nodes for the PU. In addition, one of the inactive STs that achieves $R_{{\textit{PT}}}$ will be act as a best decode-and-forward relay to forward the primary information. In this paper, a closed-form expression of the outage capacity is derived. Results show that outage capacity improves with increasing cooperative nodes as well as when the active ST is located farther away from the PR.

1 Introduction

Cognitive radio (CR) is an exciting and emerging technology to solve the spectrum inefficiency problem. It has attracted a great deal of attention in recent years to enhance the utilization of limited resources [1]. In CR network, secondary (unlicensed) users (SUs) or CR users may coexist with the primary (licensed) users (PUs) either on non-interference basis (in white spaces) [2] or interference tolerant basis (in gray spaces) [3, 4].

In communication systems, capacity is one of the most important metric for performance measure in fading channels. Basically, there are two types of capacity: ergodic capacity and outage capacity. Ergodic capacity is defined as the maximum achievable long term rate without considering any delay constraint and specifically chosen for the fast fading channels. On the contrary, outage capacity can be defined as the data rate that can be achieved if outage is allowed to occur with probability $\varepsilon$. Moreover, outage capacity is more practical performance metric for slow fading channels and the main focus of this paper. In slow fading channel with interference limited environment, when fading level is very high or the channel is in deep fade, capacity at that time degrades rapidly. Hence, in such scenario, ergodic capacity does not give any significance of the system performance. But, outage capacity is the important performance metric because it excludes those deep fading scenarios. Furthermore, if link gain between PT and PR over direct link reduces due to fading/shadowing or the interference gain between ST and PR increases then the outage probability of the PU increases. Though, the calculation of ergodic capacity is much easier than the outage capacity but ergodic capacity is not a good performance metric in that case. That is why, we consider outage capacity and derive a closed-form expression.

In [5], the authors evaluate the outage probability and outage capacity for three relaying schemes such as fixed selective decode-and-forward (FSDF) with and without direct link (DL) combining as well as small selective decode-and-forward (SSDF). Although, they derive exact expression for outage capacity under Rayleigh fading channel but did not consider any interference link. Moreover, the CR network scenario is not considered in [5]. Outage capacity of interference temperature-limited CR multi-input multi-output (MIMO) channel is investigated in [6]. Two schemes such as space-time coding (STC) based simultaneous transmission and transmit antenna selection (TAS) based transmission are considered. In this work, the authors did not consider any cooperative link when the DL fails to achieve target rate due to fading or shadowing. Outage capacity of spectrum sharing system along with optimal power allocation policies for Rayleigh fading channel is derived in [4, 7]. Outage capacity of the SU fading channel with optimal power allocation under different types of fading channel models and power constraints are investigated in [4]. In [7], the authors proposed a spectrum sharing model where a SU is allowed to use the licensed spectrum of the PU satisfying a predefined interference threshold to the PR on the average and peak powers. But, in [4, 7], no relay or cooperative nodes are considered either for primary or secondary system. However, SUs do not cooperate the PU for the primary transmission. In [8], the authors propose a discrete stochastic optimization algorithm to maximize the outage capacity for CR network with cooperative communication under Rayleigh flat-fading environments. In the proposed system, it is assumed that SU can sense the licensed spectrum of the PU with imperfect channel sensing. However, any interference caused by SUs to the PR is not considered in [8]. Moreover, SUs do not cooperate the PU for the primary transmission as well as interference limited environment is not considered in [8]. In [9], the authors investigate the capacity of SUs equipped with multi-antenna through the selection of a simple antenna in the spectrum-sharing environment. But the authors did not consider any cooperative link where neither any relays nor SUs cooperative the PU to forward the primary information if the DL fails to achieve target rate. No cooperative link is also considered between ST and SR.

In this paper, we evaluate the outage capacity of a cooperative relaying scheme in interference limited CR networks under Rayleigh fading channel. In the proposed CR network scenario, SU coexist with the PU. It is assumed that only one ST active in parallel with the PU at a time. Other idle or inactive STs can be used as cooperative relays for the PU. Thus, by using inactive STs as cooperative relays for the PU, we can improve the performance of PU. Moreover, due to interference caused by ST to the PU, primary capacity may be reduced. But, PU will not allow this degradation because it is the licensed user. As a solution of this problem, we can boost up primary capacity by using inactive STs as cooperative nodes for the PU.

In this paper, our work is different from existing works. Some distinguishable features or the main contributions of this work are summarized as follows:

• We analyze the outage capacity of a cooperative relaying based CR network where inactive STs act as cooperative relays for the PU and the active ST coexist with PU satisfying $I_{th}$ to the PR. Closed-form expression of the outage capacity is also derived.

• We show how the position of the active ST with respect to PR impact on the performance of outage capacity. However, we show that outage capacity improves with increasing the number of cooperative nodes (relays) as well as when the active ST is located farther away from the PR.

The decode-and-forward (DF) relaying scheme proposed in [10] has been incorporated in this research paper for the clarity of the presentation of this work. But the notable differences between this work and [10] are as follows. In [10], we proposed a cooperative SU selection scheme for an underlay CR network and investigated only the ergodic capacity. But in this work, we have analyzed the outage capacity with the derivation of closed-form expression in slow fading channel of the DF scheme proposed in [10]. However, the main contributions of the current work have been summarized above.

The rest of this paper is organized as follows. In Sect. 2, we introduce the system model. In Sect. 3, closed-form expression of the outage capacity is derived. Results are presented in Sect. 4 to show the effectiveness of the proposed scheme and finally we conclude this paper in Sect. 5.

2 System Description

In this section, we provide a detail description of the system model of our considered cooperative CR network. The channel model considered in this work is also presented.

2.1 System Model

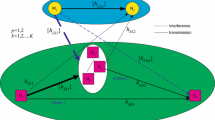
We consider a CR network which is shown in Fig. 1. The primary system consists of a PT–PR pair and the secondary system consists of a group of $M$ ST–SR pairs within the transmission range of the primary system. We divide the group of STs into two sub groups. The first sub group consists of $K (K \in M)$ active secondary transmitters whereas the second sub group consists of $N=M-K$ inactive secondary transmitters. An active ST is denoted as $\hbox {ST}_\mathrm{i},i \in \{1, 2,\ldots , K\}$ and an inactive ST is denoted as $\hbox {ST}_\mathrm{j},\; j \in \{1, 2,\ldots , N\}$. A $\hbox {ST}_\mathrm{i}$ may transmit data in parallel with the PT satisfying a predefined interference threshold $I_{\mathbf {th}}$ to the PR. On the contrary, inactive or idle STs may assist the primary system by acting as relays to forward the primary information. When the data rate between PT to PR over the DL achieves $R_{{\textit{PT}}}$ then the PT directly transmits to the PR which is shown in Fig. 1a. Moreover, when the data rate over the DL between PT to PR falls below $R_{{\textit{PT}}}$ then the primary transmission is performed over two transmission phases via the help of the best ST$_\mathrm{j} (\hbox {Re}_\mathrm{j})$ which acts as a DF relay to the primary system shown in Fig. 1b. In our proposed method, only $\hbox {ST}_\mathrm{j}$ will participate in the relay selection procedure to cooperate the PU and a $\hbox {ST}_\mathrm{i}$ may transmit data to the corresponding receiver causing interference below the certain threshold $I_{th}$to the PR at the same time. So, $\hbox {ST}_{\mathrm {i}}$ causes interference to the PR when the DL between PT and PR exist or to $\hbox {ST}_{\mathrm {j}}$ as well as the PR during cooperation. Similarly, the PT causes interference to the SR when $\hbox {ST}_{\mathrm {i}}$ transmits data to its corresponding receiver.

Fig. 1

System model. a Direct transmission b transmission using best inactive ST. The dashed dotted line indicates that best relay transmits only when the cooperation is required. The SRs, the link between each ST to its corresponding SR and interference link from PT to SR are not shown in the figure for simplicity

2.2 Channel Model

The term channel refers to the medium between the transmitting antenna and the receiving antenna. Rayleigh fading models assume that the magnitude of a signal passing through a communication channel will vary randomly, or fade, according to a Rayleigh distribution. In addition, additive white Gaussian noise (AWGN) is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density and a Gaussian distribution of amplitude [11].

Assume that the channels over all links are subject to Rayleigh flat fading plus AWGN because large-scale fading is almost constant and can be mitigated by the power control over a long period of time whereas small-scale fading can’t. Each node is a single antenna system and a half duplex radio. Also assume that the channel coefficients remain static during the both transmission phases. For Rayleigh flat fading $\alpha _{{{\textit{PT}}}{\text {-}}{{\textit{PR}}}}, \alpha _{{\textit{PT}}{\text {-}}{\textit{ST}}_{j}(\mathrm{Re}_{j} )} ,\alpha _{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}} , \alpha _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}}$ and $\alpha _{{\textit{ST}}_{i}{\text {-}}\mathrm{Re}_{j} }$ are the link gains over links $\hbox {PT}\rightarrow \hbox {PR}, \hbox {PT} \rightarrow \hbox {ST}_\mathrm{j} (\mathrm{Re}_\mathrm{j}), \mathrm{Re}_\mathrm{j} \rightarrow \hbox {PR}, \hbox {ST}_\mathrm{i} \rightarrow \hbox {PR}, \hbox {and}\, \hbox {ST}_\mathrm{i} \rightarrow \hbox {ST}_\mathrm{j} (\mathrm{Re}_\mathrm{j})$ respectively. We assume that the channel coefficient $h_{\textit{PT}{\text {-}}\textit{PR}} , h_{{\textit{PT}}{\text {-}}{\textit{ST}}_{j} (\mathrm{Re}_{j} )} ,h_{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}}, h_{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}}$ and $h_{{\textit{ST}}_{i}{\text {-}}\mathrm{Re}_{j} }$ are distributed in complex Gaussian distribution with zero mean and variance $\lambda _{\textit{PT}{\text {-}}\textit{PR}} , \lambda _{{\textit{PT}}{\text {-}}{\textit{ST}}_{j} (\mathrm{Re}_{j} )} ,\lambda _{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}} ,\lambda _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}}$ and $\lambda _{{\textit{ST}}_{i} -\mathrm{Re}_{j} }$ respectively i.e. $h_{i,j} \thicksim {\textit{CN}}(0, \lambda _{i,j})$ . Therefore, the link gains are denoted as

$$\begin{aligned}&\alpha _{\textit{PT}{\text {-}}\textit{PR}} = |h_{\textit{PT}{\text {-}}\textit{PR}} |^\mathrm{2},\alpha _{{\textit{PT}}{\text {-}}{\textit{ST}}_{j} (\mathrm{Re}_{j} )} =|h_{{\textit{PT}}{\text {-}}{\textit{ST}}_{j} (\mathrm{Re}_{j})} |^{\mathrm{2}}, {\alpha _{\mathrm{Re}_{j} -PR}} = |h_{\mathrm{Re}_{j} -PR} |^\mathrm{2}\!: {\text {data links}},\\&\alpha _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}} = |h_{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}} |^\mathrm{2}, \alpha _{{\textit{ST}}_{i}{\text {-}}\mathrm{Re}_{j} } =|h_{{\textit{ST}}_{i}{\text {-}}\mathrm{Re}_{j} } |^\mathrm{2}\!: {\text {interference links}}, \end{aligned}$$

where these gains are exponentially distributed random variable with mean values $\lambda _{\textit{PT}{\text {-}}\textit{PR}} , \lambda _{{\textit{PT}}{\text {-}}{\textit{ST}}_{j} (\mathrm{Re}_{j} )},\lambda _{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}},\lambda _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}}$ and $\lambda _{{\textit{ST}}_{i} -\mathrm{Re}_{j} }$ respectively [12]. To get the desired effect of the position of the active secondary transmitter with respect to the PR, we consider $\lambda _{i,j} =(1/ d_{i,j} )^\mathrm{n}$ where $n$ is the path loss exponent and $d_{i,j}$ denotes the distance between node $i$ and $j$. The transmit power at PT, ST$_\mathrm{i}$ and ST$_\mathrm{j}$ is denoted as $P_{{\textit{PT}}}, P_{{\textit{ST}}_{i} }$ and $P_{{\textit{ST}}_{j} }$ respectively. In addition, we consider signal to interference ratio (SIR) over the links PT–PR, PT–ST $_\mathrm{{j}} (\mathrm{Re}_\mathrm{j} )$, and $\hbox {ST}_\mathrm{j}$–PR.

3 Outage Capacity Analysis

In this section, we focus on the outage capacity of the proposed system (i) when only DL is considered as well as (ii) when only relaying or cooperative link is considered (no DL). Therefore, the outage capacity of the primary system is calculated as follows.

3.1 Direct Transmission

When the data rate between PT to PR over the DL achieves $R_{{\textit{PT}}}$ then the PT directly transmits to the PR. We assume that only one active ST (i.e., $K=1$) may transmit data with the co-existence of PU below a certain interference threshold to the PR at a time when PU is active. However, we allow multiple secondary nodes to transmit in the same channel but only one secondary node can access the channel at a time. All secondary nodes compete for spectrum access considering CSMA/CA like random access protocol [13]. Moreover, in our work, we have considered interference limited environment where interference dominates over noise. In interference limited environment, noise power is negligible [14]. The achievable data rate of the DL is therefore given by

$$\begin{aligned} R_{\textit{PT}{\text {-}}\textit{PR}} =\log _{2} (1+{\textit{SIR}}_{\textit{PT}{\text {-}}\textit{PR}} ) \end{aligned}$$

(1)

The SIR of the PT–PR link can be approximates as follows

$$\begin{aligned} {\textit{SIR}}_{\textit{PT}{\text {-}}\textit{PR}} \cong \frac{\alpha _{\textit{PT}{\text {-}}\textit{PR}} P_{{\textit{PT}}} }{\alpha _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}} P_{{\textit{ST}}_{i} } } \end{aligned}$$

(2)

The outage probability of the DL is therefore written as

$$\begin{aligned} P_{r} \left\{ {R_{\textit{PT}{\text {-}}\textit{PR}} <\hbox {R}_\mathrm{PT} } \right\} =P_{r} \left\{ {\frac{\alpha _{\textit{PT}{\text {-}}\textit{PR}} }{\alpha _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}} }<\rho _\mathrm{\textit{PT}{\text {-}}\textit{PR}} } \right\} \end{aligned}$$

(3)

where $\rho _\mathrm{{\textit{PT}{\text {-}}\textit{PR}}} =(2^{R_{{\textit{PT}}} }-1)\times \left( 1/\frac{P_{{\textit{PT}}} }{P_{{\textit{ST}}_{i} } }\right)$

Let, $g_{o}$ and $g_{1}$ are exponential random variables with means $\lambda _{0}$ and $\lambda _{1}$ respectively. Then, the probability density function (PDF) of $X=g_{0} /g_{1}$ is expressed as [9].

$$\begin{aligned} {f_{X}} (x)=\frac{\lambda _{0} \lambda _{1} }{\left( {\lambda _{0} +\lambda _{1} x} \right) ^{2}} \end{aligned}$$

Similarly, all the link gains assumed in this paper are exponentially distributed random variables with their corresponding mean values which are defined in Sect. 2. Thus, the outage probability for the links PT–PR can be derived as

$$\begin{aligned} P_{{\textit{OUT}}}^{{\textit{DT}}} = P_{r} \left\{ {R_{\textit{PT}{\text {-}}\textit{PR}} <\hbox {R}_\mathrm{PT} } \right\}&= \int _0^{\rho _{\textit{PT}{\text {-}}\textit{PR}} } {\frac{\lambda _{\textit{PT}{\text {-}}\textit{PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }{\left( {\lambda _{\textit{PT}{\text {-}}\textit{PR}} +\lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} x} \right) ^{2}}} dx \nonumber \\&= \frac{\rho _{\textit{PT}{\text {-}}\textit{PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }{\lambda _{\textit{PT}{\text {-}}\textit{PR}} +\rho _{\textit{PT}{\text {-}}\textit{PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} } \end{aligned}$$

(4)

Now, the outage capacity [6] associated with given outage probability $\varepsilon$ is given as

$$\begin{aligned} C_{\varepsilon }^{DT} =\log _{2} \left( 1+{\rho }'_\mathrm{\textit{PT}{\text {-}}\textit{PR}} \frac{P_{{\textit{PT}}} }{P_{{\textit{ST}}_{i} } }\right) (1-\varepsilon ) \end{aligned}$$

(5)

Where the value of ${\rho }'_{\mathrm{PT}{\text {-}}\mathrm{PR}}$ can be calculated as follows

$$\begin{aligned}&\varepsilon =\frac{{\rho }'_{\mathrm{PT}-\mathrm{PR}}\lambda _{{{\textit{ST}}_i}-{PR}}}{\lambda _{\text {PT}{\text {-}}\text {PR}} +{\rho }'_ {\text {PT}{\text {-}}\text {PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }\nonumber \\&{\rho }'_{\text {PT}{\text {-}}\text {PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} = \varepsilon (\lambda _{\textit{PT}{\text {-}}\textit{PR}} +{\rho }'_ {\textit{PT}{\text {-}}\text {PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} )\nonumber \\&{\rho }'_{\text {PT}{\text {-}}\text {PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} -\varepsilon {\rho }'_{\text {PT}{\text {-}}\text {PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} =\varepsilon \lambda _{\textit{PT}{\text {-}}\textit{PR}}\nonumber \\&{\rho }'_{\text {PT}{\text {-}}\text {PR}} =\frac{\varepsilon \lambda _{\textit{PT}{\text {-}}\textit{PR}} }{(1-\varepsilon )\lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }=\frac{\lambda _{\textit{PT}{\text {-}}\textit{PR}} }{\lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }\times \frac{\varepsilon }{(1-\varepsilon )} \end{aligned}$$

(6)

The value of ${\rho }'_{\text {PT}{\text {-}}\text {PR}}$ in Eq. (6) is the solution of Eq. (4) for the target outage probability $\varepsilon$ of the direct transmission (DT).

3.2 Decode-and-Forward (DF) Relay Transmission

In this section, we first describe the best inactive ST (relay) selection to forward the primary information then derive the closed-form expression of the outage capacity of the cooperative relaying scheme. When the data rate of the PU over DL falls below $R_{{\textit{PT}}}$ then one of the $\hbox {ST}_\mathrm{j}$ acts as a best cooperative relay to forward the primary information. We propose a similar approach as in [10] to select the best inactive ST as a DF relay from $N$ available nodes. The achievable rate of the links $\hbox {PT-to-Re}_\mathrm{j}$ and $\hbox {Re}_\mathrm{j}$-to-PR are given by

$$\begin{aligned} R_{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{j}}&= \frac{1}{2}\log _{2} (1+{\textit{SIR}}_{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{j} } )\end{aligned}$$

(7)

$$\begin{aligned} R_{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}}&= \frac{1}{2}\log _{2} (1+{\textit{SIR}}_{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}} ) \end{aligned}$$

(8)

where the scaling factor $1/2$ in Eqs. (7) and (8) is due to the fact that the overall transmission is divided into two transmission phases. The first phase is from PT to Re$_{\mathrm {j}}$ and the second phase is from $\hbox {Re}_\mathrm{j}$ to PR. Since, we assume $K=1$ and noise powers are negligible in the interference limited environment [14], so SIR in Eqs. (7) and (8) can be approximated as follows

$$\begin{aligned} {\textit{SIR}}_{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{j} }&\cong \frac{\alpha _{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{j} } P_{{\textit{PT}}} }{\alpha _{{\textit{ST}}_{i}{\text {-}}{\mathrm{Re}_{j}} } P_{{\textit{ST}}_{i} } }\end{aligned}$$

(9)

$$\begin{aligned} {\textit{SIR}}_{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}}&\cong \frac{\alpha _{\mathrm{Re}_{j}{\text {-}}{\textit{PR}}} P_{{\textit{ST}}_{j} } }{\alpha _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}} P_{{\textit{ST}}_{i} } } \end{aligned}$$

(10)

The equivalent end-to-end data rate of the two hop cooperative link is the minimum one of the two hops [15]. We denote $S$, the set of relays that can be considered for relay selection as

$$\begin{aligned} S=\{j\,\big \vert \, j\in N,\min \{R_{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{j} }, R_{\mathrm{Re}_j{\text {-}}{\textit{PR}}} \}>R_{{\textit{PT}}} \} \end{aligned}$$

(11)

We consider a similar relay selection procedure as [10]. So, our proposed protocol selects the best relay $\hbox {Re}_{\mathrm {best}}$ if it satisfies the following condition

$$\begin{aligned} \mathrm{Re}_{best} =\arg \hbox {max}_{m\in \{S\}} (\min \{R_{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{m} } ,R_{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} \}) \end{aligned}$$

(12)

After the selection of the best inactive ST (best relay), the PT transmits the message to the best relay in the first time slot. If the best relay is able to decode the message successfully then it will forward this message to the PR in the second time slot. Otherwise, the best relay remains silent and the system declares an outage.

The primary system with cooperative relaying is in outage if none of the inactive secondary nodes achieves $R_{{\textit{PT}}}$ i.e. $|S|=0$. So, the outage probability of the primary system with cooperative relaying is expressed as [16]

$$\begin{aligned} P_{\textit{OUT}}^\mathrm{Re}&= P_{r} \left\{ {\vert S\vert =0} \right\} \nonumber \\&= P_{r} \left\{ {\hbox {max}_{{m}\in {N}}} (\min \{R_{{\textit{PT}}{\text {-}}\mathrm{Re}_{m} }, R_{\mathrm{Re}_{m} {\text {-}}{\textit{PR}}}\})<\hbox {R}_\mathrm{PT} \right\} \nonumber \\&= \prod \limits _{m=1}^N {\left\{ {P_{r} \left\{ {\left( \min \left\{ R_{{\textit{PT}}{\text {-}}\mathrm{Re}_{m} } ,R_{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} \right\} \right) <\hbox {R}_\mathrm{PT} } \right\} } \right\} }\nonumber \\&= \prod \limits _{m=1}^N {\left[ {1-\left( {1-P_{r} \left\{ {R_{{\textit{PT}}{\text {-}}\mathrm{Re}_{m} } <\hbox {R}_\mathrm{PT} } \right\} } \right) \left( {1-P_{r} \left\{ {R_{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} <\hbox {R}_\mathrm{PT} } \right\} } \right) } \right] } \end{aligned}$$

(13)

In Eq. (13), the outage probability for the links PT-to-Re$_{\mathrm {m}}$ and Re$_{\mathrm {m}}$-to-PR are given by

$$\begin{aligned} P_{r} \left\{ {R_{{{\textit{PT}}}-{\mathrm{Re}_{m}} } <\hbox {R}_\mathrm{PT} } \right\}&= P_{r} \left\{ {\frac{\alpha _{{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{m}} } }{\alpha _{{\textit{ST}}_{i} -{\mathrm{Re}_{m}} } }<{\rho _{\mathrm{PT}{\text {-}}\mathrm{Re}_\mathrm{m}} }} \right\} \end{aligned}$$

(14)

$$\begin{aligned} P_{r} \left\{ {R_{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} <\hbox {R}_\mathrm{PT} } \right\}&= P_{r} \left\{ {\frac{\alpha _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} }{\alpha _{{\textit{ST}}_{i}{\text {-}}{\textit{PR}}} }<{\rho _{\mathrm{Re}_\mathrm{m}{\text {-}}{\textit{PR}}}}} \right\} \end{aligned}$$

(15)

where $\rho _{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}} } =(2^{2R_{{\textit{PT}}} }-1)\times \left( 1/\frac{P_{{\textit{PT}}} }{P_{{\textit{ST}}_{i} } }\right)$ and $\rho _{\mathrm{Re}_{\mathrm{m}}{\text {-}}{\textit{PR}}} =(2^{2R_{{\textit{PT}}} }-1)\times \left( 1/\frac{P_{{\textit{ST}}_{m} } }{P_{{\textit{ST}}_{i} } }\right)$

Now, the outage probability according to Eq. (4) for the links $\hbox {PT-to-Re}_\mathrm{m}$ and $\hbox {Re}_\mathrm{m}\hbox {-to-PR}$ can be derived as

$$\begin{aligned} P_{r} \left\{ {R_{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m} }} < \hbox {R}_\mathrm{PT} } \right\}&= \frac{\rho _{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}} } \lambda _{{\textit{ST}}_i-{\mathrm{Re}_{m} }} }{\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m} }} + \rho _{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m} }} \lambda _{{{\textit{ST}}_i}{\text {-}}{\mathrm{Re}_{m}} }} \end{aligned}$$

(16)

$$\begin{aligned} P_{r} \left\{ {R_{\mathrm{Re}_{m}{\text {-}}{{\textit{PR}}}}} < \hbox {R}_\mathrm{PT} \right\}&= \frac{\rho _{\mathrm{Re}_\mathrm{m}{\text {-}}{\textit{PR}}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }{\lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} +\rho _{\mathrm{Re}_\mathrm{m}{\text {-}}{\textit{PR}}} \lambda _{{{\textit{ST}}_i}{\text {-}}{{\textit{PR}}}} } \end{aligned}$$

(17)

Therefore, the outage capacity [6] associated with given outage probability $\varepsilon$ is given as

$$\begin{aligned} C_{\varepsilon }^{\mathrm{Re}} =\log _{2} \left( 1+{\rho }'_{\mathrm{PT}{\text {-}}{{\mathrm{Re}_\mathrm{m}}}{\text {-}}\mathrm{PR}} \frac{P_{{\textit{PT}}} }{P_{{\textit{ST}}_{i} } }\right) (1-\varepsilon ) \end{aligned}$$

(18)

Where the value of ${\rho }'_{\mathrm{PT}{\text {-}}\text {Re}_\mathrm{m}{\text {-}} \mathrm{PR}}$ can be calculated as follows

$$\begin{aligned} \varepsilon&= \prod \limits _{m=1}^N {\left[ {1-\left( {1-P_{r} \left\{ {R_{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}} }} <{\hbox {R}_\mathrm{PT}} \right\} } \right) \left( {1-P_{r} \left\{ {R_{\mathrm{Re}_{m}{\text {-}}{{\textit{PR}}}}}<\hbox {R}_\mathrm{PT} \right\} } \right) } \right] }\\ \root n \of {\varepsilon }&= 1-\left( {1-P_{r} \left\{ {R_{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}} } <\hbox {R}_{\mathrm{PT}} } \right\} } \right) \left( {1-P_{r} \left\{ {R_{\mathrm{Re}_{m}{\text {-}}{{\textit{PR}}}} <\hbox {R}_\mathrm{PT}} \right\} } \right) \\ {\varepsilon }'&= 1-\left( {1-P_{r} \left\{ {R_{{{{\textit{PT}}}-\mathrm{Re}_{m}} } <\hbox {R}_\mathrm{PT} } \right\} } \right) \left( {1-P_{r} \left\{ {R_{{\mathrm{Re}_{m}}{\text {-}}{{\textit{PR}}}} <\hbox {R}_\mathrm{PT} } \right\} } \right) [\hbox {Let},{\varepsilon }'=\root n \of {\varepsilon }]\\&= 1-\left( 1-\frac{\rho _{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}}\lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}}}}{\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}}}+\rho _{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}} \lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m} }}} \right) \left( 1-\frac{\rho _{\mathrm{Re}_\mathrm{m}{\text {-}}{{\textit{PR}}}}\lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}}}{\lambda _{{{\mathrm{Re}_{m}}{\text {-}}{{\textit{PR}}}}} +\rho _{{\mathrm{Re}_\mathrm{m}}{\text {-}}{{\textit{PR}}}} \lambda _{{{\textit{ST}}_i}{\text {-}}{{\textit{PR}}}}} \right) \end{aligned}$$

Since $\mathrm{Re}_\mathrm{m}$ uses the same transmit power as the PT during cooperative relaying of the primary information, we assume that $\rho _{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}} =\rho _{{\mathrm{Re}_\mathrm{m}}{\text {-}}{{\textit{PR}}}} ={\rho }'_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}{\text {-}}\mathrm{PR}}$. Therefore,

$$\begin{aligned}&{\varepsilon }^{\prime }=1-\left( 1-\frac{{\rho }^{\prime }_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}{\text {-}}\mathrm{PR}}} {\lambda _{{{\textit{ST}}_i}{\text {-}}{\mathrm{Re}_{m}}}}}{\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}}} +{{\rho }^{\prime }_{{{\mathrm{PT}-{\mathrm{Re}_\mathrm{m}}}}{\text {-}}\mathrm{PR}}} \lambda _{{{\textit{ST}}_i}{\text {-}}{\mathrm{Re}_{m}}}} \right) \left( 1-\frac{{\rho ^{\prime }_\mathrm{{PT}\mathrm{-Re}_\mathrm{m}{\text {-}}\mathrm {PR}}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} }{\lambda _{\mathrm{Re}_{m}{\text {-}}{{\textit{PR}}}} +{\rho }'_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}} {\text {-}}\mathrm{PR}} \lambda _{{{\textit{ST}}_i}{\text {-}}{{\textit{PR}}}}}\right) \nonumber \\&\quad = 1-\left( \frac{\lambda _{{\textit{PT}}{\text {-}}{\mathrm{Re}_{m}}}}{\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}}} +{\rho }^{\prime }_{\mathrm{PT}{\text {-}}{{\mathrm{Re}_\mathrm{m}} {\text {-}}\mathrm{PR}}} \lambda _{{{\textit{ST}}_i}{\text {-}}{\mathrm{Re}_{m}}}} \right) \left( \frac{\lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}}}{\lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} +{\rho }^{\prime }_{\mathrm{PT}{\text {-}}{{\mathrm{Re}_\mathrm{m}}}{\text {-}} \mathrm{PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}}} \right) \nonumber \\&\quad 1-{\varepsilon }^{\prime }=\left( \frac{\lambda _{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{m}} }{\lambda _{{{\textit{PT}}}{\text {-}}\mathrm{Re}_{m}} +{\rho }'_{{\mathrm{PT} {\text {-}}\mathrm{Re}_\mathrm{m}{\text {-}}\mathrm{PR}}} \lambda _{{{{\textit{ST}}_i}{\text {-}}\mathrm{Re}_{m} }}} \right) \left( \frac{\lambda _{\mathrm{Re}_{m}{\text {-}}{{\textit{PR}}}} }{\lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} +{\rho }^{\prime }_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}{\text {-}}\mathrm{PR}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}}} \right) \nonumber \\&\quad \left( \lambda _{{{\textit{PT}}{\text {-}}{\mathrm{Re}_m}}} +{\rho }^{\prime }_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}{\text {-}}\mathrm{PR}}\lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}}} \right) \left( {\lambda _{{{\mathrm{Re}_{m}}{\text {-}}{{\textit{PR}}}}}} +{\rho }^{\prime }_{{\mathrm{PT}{\text {-}}\mathrm{Re}_\mathrm{m}{\text {-}}\mathrm{PR}}} \lambda _{{{\textit{ST}}_i}{\text {-}}{\textit{PR}}} \right) \nonumber \\&\quad =\frac{\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}}} \lambda _{{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} }}{1-{\varepsilon }'}\nonumber \\&\quad \lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} {\rho }^{\prime {2}}_{\mathrm{{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}{\text {-}}\mathrm{PR}}}} +\left( {{\lambda _{{\textit{PT}}{\text {-}}{\mathrm{Re}_{m}}}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} +\lambda _{{\textit{ST}}_i-{\mathrm{Re}_{m}}} \lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} } \right) {\rho }^{\prime }_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}{\text {-}}{\textit{PR}}}}\nonumber \\&\qquad +\left( {\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}}}} \lambda _{{\mathrm{Re}_{m}} {\text {-}}{\textit{PR}}} -\frac{\lambda _{{\textit{PT}}{\text {-}}{\mathrm{Re}_{m}}} \lambda _{{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} }}{1-{\varepsilon }^{\prime }} \right) =0\nonumber \\&\quad \lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}}} {\lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} {\rho }^{\prime {2}}}_{\mathrm{PT}{\text {-}} {\mathrm{Re}_\mathrm{m}} -\mathrm{PR}}+\left( \lambda _{{\textit{PT}}{\text {-}}{\mathrm{Re}_{m}}} \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} +\lambda _{{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}} } \lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} } \right) {\rho }^{\prime }_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{m}}{\text {-}}\mathrm{PR}}\nonumber \\&\quad +\left( {-\frac{\lambda _{{{\textit{PT}}}{\text {-}}{\mathrm{Re}_{m}}} \lambda _{{\mathrm{Re}_{m}}{\text {-}}{\textit{PR}}} {\varepsilon }'}{1-{\varepsilon }'}} \right) =0 \end{aligned}$$

(19)

From Eq. (19), the value of ${\rho }'_\mathrm{{PT}{\text {-}}{\mathrm{Re}_\mathrm{{m}}{\text {-}}\mathrm {PR}} }$ which is the solution of Eq. (13) for the target outage probability $\varepsilon$ of the cooperative transmission can be calculated as follows.

Let, $\,\lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}} } \lambda _{{{\textit{ST}}_i}{\text {-}}{\textit{PR}}} =A,\,\left( {\lambda _{PT{\text {-}}{\mathrm{Re}_{m}} } \lambda _{{\textit{ST}_i}{\text {-}}{\textit{PR}}} +\lambda _{{\textit{ST}}_i{\text {-}}{\mathrm{Re}_{m}} } \lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} } \right) =B$ and $\left( {-\frac{\lambda _{{\textit{PT}}{\text {-}}{\mathrm{Re}_{m} }} \lambda _{\mathrm{Re}_{m}{\text {-}}{\textit{PR}}} {\varepsilon }'}{1-{\varepsilon }^{\prime }}} \right) =C$

So, Eq. (19) can be written as

$$\begin{aligned} {A{\rho }'^{2}_{{\mathrm{{PT}{\text {-}}\mathrm{Re}}_{\mathrm{m}}}{\text {-}}\mathrm{PR}}} +B{\rho }'_{\mathrm{PT}{\text {-}}\mathrm{Re}_\mathrm{{m}}{\text {-}}\mathrm {PR}} +C=0 \end{aligned}$$

(20)

Solving Eq. (20) we get

$$\begin{aligned} {\rho }'_{\mathrm{PT}{\text {-}}\mathrm{Re}_\mathrm{m}{\text {-}}\mathrm{PR}} =\frac{-B\pm \sqrt{B^{2}-4AC} }{2A} \end{aligned}$$

(21)

Since the outage capacity cannot be negative, Eq. (21) can be simplified as

$$\begin{aligned} {\rho }'_{\mathrm{PT}{\text {-}}{\mathrm{Re}_\mathrm{{m}}}{\text {-}}\mathrm{PR}} =\frac{-B+\sqrt{B^{2}-4AC} }{2A} \end{aligned}$$

(22)

4 Results and Discussions

In this section, we provide the numerical results of the outage capacity to evaluate the performance of the cooperative relaying scheme presented in this work. Assume that, PT and PR are located at (0, 40) and (100, 40) respectively. So, for our analysis we considered an instance of environment where a set of SUs are located in between PT and PR. Moreover, according to the principle of CR network design, we need to know the location as well as the transmission range of the PT. Once we know this, SUs are located within the transmission range of the primary system. Although, we have assumed some fixed locations of PT, $\hbox {ST}_{{\mathbf {i}}}$ and $\hbox {ST}_{{\mathbf {j}}}$ but our scheme works for any location of $\hbox {PT},\,\hbox {ST}_{{\mathbf {i}}}$ and $\hbox {ST}_{{\mathbf {j}}}$ as well as any distance among PT, PR, $\hbox {ST}_{{\mathbf {j}}}$ and $\hbox {ST}_{{\mathbf {i}}}$.

As in [17], to reduce the numbers of model parameters, the position of all the relays are considered at approximately the same distance between PT and PR. Moreover, we consider variable location of active ST to show that the outage capacity is affected by the position of the active ST with respect to the PR. Furthermore, slow fading is considered in this paper. So, to get the effect of all relays, fading co-efficient of each relay is independent to each other. Assume, path loss exponent $n=2$ and meter is the unit of distance here.

In Fig. 2, we show the outage probability of the primary system with cooperative relaying ${(P_{{\textit{OUT}}}=P_{{\textit{OUT}}}^{{\textit{DT}}}\times P_{{\textit{OUT}}}^\mathrm{Re})}$ as well as without cooperative relaying ${(P_{{\textit{OUT}}}^{{\textit{DT}}})}$ as a function of SIR in dB. Here, we assume $\hbox {SIR}=P_{{\textit{PT}}} /P_{{\textit{ST}}_{i} } =P_{{\textit{ST}}_{j} }/P_{{\textit{ST}}_{i} }$ where, SIR varies from 0 to 18 dB. In each case, Monte Carlo simulation (Sim) results are well matched with the numerical (Num) results. Figure 2 shows the outage probability decreases with increasing SIR as well as $N$. It can be observed that the proposed cooperative relaying scheme shows better outage performance than non-cooperative network. It is noted that in non-cooperative network only DT is considered. Moreover, both simulation and numerical results clearly indicate the improvement of transmission opportunity as the number of relays increase.

Fig. 2

Outage probability of the primary network with or without cooperative relaying. Active secondary transmitter is located at (20, 20) and inactive secondary transmitters (relay sets) are located at (60, 40)

In Fig. 2, outage probability is shown for validating the accuracy of the mathematical analysis derived in Sect. 3 with the simulation results. To describe the characteristics of CR network, outage probability is important but not enough. Therefore, plotting of outage capacity gives us in depth analysis of CR network.

In Figs. 3, 4 and 5, we show the outage capacity of the primary system over DL as well as relaying link as a function of SIR. We assume, ${\textit{SIR}}=P_{{\textit{PT}}} /P_{{\textit{ST}}_{i}} =P_{{\textit{ST}}_{j}}/P_{{\textit{ST}}_{i} }$ and SIR varies from 2 to 18 dB. Figure 3 shows the outage capacity for DL as well as cooperative link with different number of secondary relays for a given outage probability $\varepsilon =0.01.$ It can be observed from Fig. 3 that outage capacity monotonically increases with increasing SIR as well as with the number of cooperating secondary nodes $(N)$. Better outage capacity can be found for the DL than the cooperative link when $N=1$. This is because when $N=1$, the cooperative link shows the same diversity as in DL i.e., diversity $=1$. When diversity is the same then the capacity depends on path loss only. Moreover, we have considered half duplex radio for each link and according to Eqs. (7) and (8) the outage capacity of the PU over cooperative link must be less than the DL when $N=1$. On the contrary, when $N$ becomes two or more then the cooperative link shows greater diversity than the DL. That is why, outage capacity of the PU over cooperative link outperforms DL when the number of cooperating nodes becomes 2 or more i.e., $N\ge 2$. However, we have considered interference limited environment in CR network where a SU transmits in parallel with the PU. As expected, outage capacity of the PU over DL in non-interference limited environment $(DT_{\mathbf {NonInt}})$ outperforms the outage capacity with interference limited environment. But, in CR network, this degradation is not allowed. As a solution of this problem, we can use appropriate number of cooperative secondary nodes $(N\ge 2)$ to improve the outage capacity of the PU which is shown in Fig. 3. It is also observed that the increasing rate of the outage capacity becomes slower when $N$ closes to a large value. Importantly, outage capacity of the cooperative relaying scheme with multiple relays, always perform better than the single relay based 2-hop scheme.

Fig. 3

SIR versus outage capacity. Active ST is located at (20, 20) and inactive STs (relay sets) are located at (60, 40)

Fig. 4

SIR versus outage capacity for different values of $\varepsilon$. Active ST is located at (20, 20) and inactive STs are located at (60, 40)

Fig. 5

SIR versus Outage capacity with varying position of the active ST. Inactive STs (relay sets) are located at (60, 40)

In Fig. 4, we show the outage capacity of the DL as well as cooperative links $(N=4)$ for the different values of $\varepsilon$. We consider three cases of $\varepsilon$ where $\varepsilon =0.1,\varepsilon =0.01$ and $\varepsilon =0.001$. It is clear from Fig. 4 that outage capacity increases with SIR as well as with increasing $\varepsilon$ as expected. Figure 5 shows the outage capacity with the varying position of the active ST for a given outage probability $\varepsilon =0.001.$ It can be observed that outage capacity decreases as the active ST becomes closer to the PR. This is because if two active STs have the same transmit power then the closer one with respect to PR causes more interference to the PR which is clear from Fig. 5. On the contrary, we can say that if each active ST satisfy a fixed interference threshold i.e., $\alpha _{{\textit{ST}}_{i}{\text {-}}PR} P_{{\textit{ST}}_{i}} \le I_{th}$ or, $\alpha _{{\textit{ST}}_{i}{\text {-}}{\mathrm{Re}_{j}} } P_{{\textit{ST}}_{i} } \le I_{th}$ then their position with respect to the PR as well as relay nodes do not impact on the performance of the outage capacity which is clear from Eqs. (2), (9) and (10).

Figure 6 shows the outage capacity of the cooperative link with respect to $N$ for different values of $\varepsilon$. We consider three cases of $\varepsilon$ where $\varepsilon =0.1,\varepsilon =0.01$ and $\varepsilon =0.001$. As expected, the outage capacity increases with increasing $N$ as well as with increasing of $\varepsilon$. Here, we assume ${\text {SIR}}=12$ dB. It is clear from Fig. 6 that the increasing rate of the outage capacity becomes slower when $N$ closes to a large value.

Fig. 6

$N$ versus Outage capacity for different values of $\varepsilon$. Active ST is located at (60, 50) and inactive STs are located at (60, 40)

5 Conclusion

In this paper, we investigate the outage capacity of the primary system in interference limited CR network for both the DL as well as cooperative link. We also derived closed-form expression of the outage capacity. The derived expression is simple and can be applied to any cooperative relaying based network. We found that outage capacity of the cooperative link improves when the number of cooperative nodes increases as well as with increasing of $\varepsilon$. We also found that at the cost of overall complexity, the cooperative link outperforms the DL in terms of outage capacity when $N$ becomes two or more. The other expenses for this improvement are implementation of cooperative communication i.e., dividing the primary transmission into two transmission phases where the first phase is from PT to relay and the second phase is from relay to PR, dividing STs into active and inactive groups, best relay selection procedure as well as coordination and synchronization among PT, PR & relays. Moreover, the outage capacity of PU over DL as well as cooperative link improves when the active ST is located farther away from the PR.