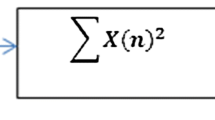Energy Detection Approach for Spectrum Sensing in Cognitive Radio Systems with the Use of Random Sampling

Abstract

In radiomobile contexte, radio frequency spectrum is a ressource that needs to be used with appropriate efficiency. This can be achieved by the mean of spectrum sensing operation. This function consists to analyze the occupancy of the radio frequency spectrum in order to detect which bands are unused. This concept is largely appreciated in cognitive radio where more flexibility is required to adapt to the communication environment. Different techniques are presented in the literature. In this paper, we are interested by the application of the energy detector method for spectrum sensing. This application is performed in cognitive radio systems with the use of random sampling. The performance of this approach is evaluated in term of its receiver operating characteristic curve and compared to the uniform sampling case.

1 Introduction

A cognitive radio (CR) [1] is a device that is aware of its radio environment and transmits only in frequency bands that are not being used by a primary user. A crucial first step in enabling CR systems is spectrum sensing (SS), where the goal is the detection of presence or absence of a signal from a primary transmitter. The main challenge in SS is to quickly detect the signal in a very low signal to noise ratio (SNR) environment, with high reliability.

Various techniques used for SS can be broadly classified into three types: energy detector (ED), matched filter detector (MFD) and cyclostationary feature detector (CFD). In this paper we are interested by the Energy Detector based approach, which is the most common way of spectrum sensing due to its low computational and implementation complexities [2].

Energy detection is a technique proposed to detect the presence of unknown signals [3]. Therefore it is used in spectrum sensing to detect the occupancy of the radio frequency spectrum without a priori knowledge of these signals. The energy in the band of interest is compared to a detection threshold to decide if this band is occupied or not. The block diagram of a temporal domain energy detector is shown in Fig. 1.

Fig. 1

Block diagram of an energy detector

The input band pass filter removes the out of band signals by selecting the central frequency $f_{c}$, and the bandwidth of interest. After the signal is digitized by an analog to digital converter (ADC), a simple square and average device is used to estimate the received signal energy. The estimated energy, $T$, is then compared with a threshold, $\lambda _{E}$, to decide whether a signal is present $H_{1}$ or not $H_{0}$ [4, 5].

In the literature different works on energy detector sensing method are presented. To our knowledge, these works are always based on uniform sampling. The application of a random sampling sequence in cognitive radio systems seems to present several advantages compared to the uniform sampling case [6]: there is more flexibility in sampling frequencies, the constraints on signal filtering operation are reduced and the aliases of the spectrum are attenuated (or completely eliminated in the case of a stationary sampling sequence) [7, p. 36].

In this work, we propose an approach based on random sampling as a sampling mode [8], on the energy detector method as the method of spectrum sensing and on the direct algorithm singular value decomposition (SVD) [6] as a method of reconstruction and channel filtering. The performance of the proposed approach will be evaluated and compared to those of the uniform sampling case.

The rest of this article is organized as follows. Section 2 presents signal reconstruction and channel selection in random sampling mode using the SVD algorithm. In Sect. 3, the Energy Detector sensing method is introduced. Section 4 evaluates the performance of the proposed approach in term of its ROC curve and compares it to the uniform sampling case. Finally, conclusions are drawn in the Sect. 5.

2 Signal Reconstruction and Channel Selection in Random Sampling Mode

Random sampling process consists in converting a continuous analog signal x(t) into a discrete time representation $x_{s}(t)$ (Fig. 2) where the sampling instants are not uniformly distributed.

Fig. 2

Ideal sampler

We propose to use an ARS sequence of random sampling (additive random sampling) [9], among the most used in the literature.

Consider a multiband signal x(t) with effective band $I=UI_{i}$ [6]. The $I_{i}$ represent the different signal subbands and U is the union operator. The samples are identified by a sample time ($t_{i}$), and a value $x_{i}=$ x ($t_{i}$) with i varying from 1 to N.

For sample rates higher than the average Nyquist frequency (defined by the effective bandwidth) the orthogonal basis of complex exponential functions is an appropriate choice for the reconstruction process [10]. Therefore, each element of the matrix A is given by:

$$\begin{aligned} \mathbf A _{ik}=\exp (2{\pi }jf_{k}t_{i}) \end{aligned}$$

(1)

The reconstructed signal is defined by the following expression:

$$\begin{aligned} \widehat{\mathbf{x }}(t)=\sum \limits _{k=1}^M c_{k}\exp (2{\pi }jf_{k}t_{i}) \end{aligned}$$

(2)

The $f_{k}$ are chosen in the signal bandwidth and the $c_{k}$ coefficients are calculated from the minimization of the squared error defined by:

$$\begin{aligned} E_{q}^{2}=\Vert \mathbf A \mathbf c -\mathbf x _{s}\Vert ^{2} \end{aligned}$$

(3)

where:

• ${\varvec{x}}_{s}(t)=[x(t_{1}), x(t_{2}),\ldots , x(t_{N})]$ is a vector of dimension equal to the number of samples N.

• A is a matrix of dimension $N \times M$ formed by the elements of the base $\mathbf A _{m}(t_{n})$.

• c is a vector of dimension M with the complex elements $c_{k}$ to calculate.

The minimum of the Eq. (3) is obtained by the solution to a system of linear equations:

$$\begin{aligned} \mathbf A ^{H}\mathbf A \mathbf c =\mathbf A ^{H}\mathbf x _{s} \end{aligned}$$

(4)

To solve this problem, SVD direct algorithm [6] is performed.

Once the coefficients $c_{k}$ are calculated, the signal can be reconstructed from the formula (2) and compared to the original signal through the formula (5):

$$\begin{aligned} E_{m}^{2}=\frac{\sum \nolimits _{k}\vert x(t_{k})-\widehat{x}(t_{k})\vert ^{2}}{\sum \nolimits _{k}\vert x(t_{k})\vert ^{2}} \end{aligned}$$

(5)

From this value, we can define the SNR of reconstruction as: $-10 log_{10}(E_{m}^{2})$.

The channel selection is achieved as shown in Fig. 3 in two steps: the calculation of all the frequency components of the multiband signal followed by the reconstruction of the baseband channel using only the corresponding $c_{k}$ coefficients associated to their frequencies as developed in [8].

Fig. 3

The proposed structure for channel selection

3 Spectrum Sensing Based on the Energy Detector Method

The goal of spectrum sensing is to determine if a licensed band is currently used by its primary owner or not.

Let us assume that the received signal has the following simple form:

$$\begin{aligned} x_{n}=s_{n}+\omega _{n} \end{aligned}$$

(6)

where $s_{n}$ is the signal to be detected, $\omega _{n}$ is an additive white Gaussian noise (AWGN) sample, and n is the sample index. Note that $s_{n}=0$ when there is no transmission by primary user. The decision metric for the energy detector can be written as:

$$\begin{aligned} T=\frac{1}{N}\sum \limits _{k=1}^{N}\vert x_{k}\vert ^{2} \end{aligned}$$

(7)

N is the number of samples. The decision of the occupancy of a band can be obtained by comparing the decision metric T against a fixed threshold $\lambda _{E}$. This is equivalent to distinguishing between the two following hypothesis:

$$\begin{aligned} \begin{aligned} H_{0}: x_{n}&= \omega _{n} \qquad (vacant) \\ H_{1}: x_{n}&= s_{n}+ \omega _{n} \quad (occupied) \end{aligned} \end{aligned}$$

(8)

The performance of a detection algorithm can be summarized with the probability of detection $P_{D}$ and the probability of false alarm $P_{FA}$, which are defined as [2]:

$$\begin{aligned} \begin{aligned}&P_{FA}: Prob\lbrace T\;\rangle \;\lambda _{E} / H_{0} \rbrace \\&P_{D}\;\;: Prob\lbrace T\;\rangle \;\lambda _{E}/H_{1}\rbrace \end{aligned} \end{aligned}$$

(9)

$P_{D}$ is the probability of detecting a signal on the considered frequency when it is truly present and $P_{FA}$ is the probability that the test incorrectly decides that the considered frequency is occupied when it is not.

To formulate the mathematical equation for the energy detector, the decision metric T should be investigated. Under $H_{0}$, T follows a central Chi-square ($\chi ^{2}$) distribution with 2N degrees of freedom and under $H_{1}$, the decision statistic T has a non central distribution with the same degrees of freedom and a non centrality parameter equal to $2\gamma$ [11], where $\gamma$ denotes the SNR which is defined as the ratio of the signal variance $\sigma _{s}^{2}$ to the noise variance $\sigma _{\omega }^{2}$.

$$\begin{aligned} \gamma =\frac{\sigma _{s}^{2}}{\sigma _{\omega }^{2}} \end{aligned}$$

(10)

So, the decision metric T can be described by:

$$\begin{aligned} T \sim \left\{ \begin{array}{l@{\quad }l} \chi _{2N}^{2} &{} H_{0}\\ \chi _{2N}^{2}(2\gamma ) &{} H_{1} \end{array} \right. \end{aligned}$$

(11)

Hence, the probability of false alarm $P_{FA}$ and the probability of detection $P_{D}$ for the ED over AWGN channels are given respectively by [11]:

$$\begin{aligned} P_{\textit{FA}}&= \frac{\varGamma ({N,\lambda _{E}/2})}{\varGamma (N)} \end{aligned}$$

(12)

$$\begin{aligned} P_{D}&= Q_{N}({\sqrt{2\gamma },\sqrt{\lambda }_{E}}) \end{aligned}$$

(13)

where $\lambda _{E}$ denotes the threshold, $\varGamma (a,x)$ is the incomplete gamma function, $\varGamma (a)$ is the gamma function and $Q_{N}(a,b)$ is the generalized Marcum Q-function.

4 Application and Simulation Results

In this section, the performance of the ED method associated with random sampling is evaluated and compared with the uniform sampling case. The case-study signal is sampled, reconstructed and the occupancy of the radio frequency spectrum is analyzed. The Monte Carlo method is performed to evaluate the receiver operating characteristic (ROC). We consider an AWGN channel and the reconstruction of a randomly sampled signal is achieved by using the SVD direct algorithm.

The analysis is made for different central frequency values. The block diagram for the simulations is shown in Fig. 4.

Fig. 4

Block diagram for simulation

4.1 Generation of the Test Signal

We consider the reconstruction of a group of five carriers, each at a symbol rate $Rsym=4.10^{5}$symb/s and with a raised cosine filter excess bandwidth factor of 0.5. The carriers are separated by 0.8 MHz.

In simulation, the multiband signal is constructed using a regular oversampling with $f_{e}=100$ MHz.

The uniform sampled signal is obtained by decimating the original signal by a factor $M=10$ (classical decimation), which leads to a sampling frequency of $f_{e}=10$ MHz. The non uniformely sampled signal consists to apply to the original signal an ARS sampling sequence of length N, of average periode $T_{1}=1/f_{s}$ and whose random variables are generated by a normal distribution with a standard deviation equal to $0.3T_{1}$. Let’s $T_{0}$ the time of observation. In both cases (uniform and non uniform sampling), the number of samples obtained during $T_{0}$ is approximately the same: $N=T_{0}.f_{s}$.

For the non uniformely sampled signal, both signal reconstruction and channel selection operations are performed by applying SVD algorithm. The spectrum sensing operation is done based on energy detection method.

We note that in the case study signal, the central frequencies are ranging from 6 to 40 MHz (for both random and uniform sampling modes).

In the case of uniform sampling with a sampling rate of 10 MHz, the allowed bands [6] are defined for central frequency values (in MHz) located within: [7, 8], [12, 13], [17, 18], [22, 23], [27, 28], [32,33], [37,38]...

In the random sampling case, for an average sampling rate slightly higher than the Nyquist rate, the signal can be efficiently reconstructed without forbidden bands constaint.

4.2 Monte Carlo Simulation for the Proposed Energy Detector Approach

Monte Carlo method is used in our application to estimate both the detection and false alarm probabilities for channel occupancy in order to characterize the receiver detection performance.

The receiver performance is evaluated with its operating characteristic curves ($P_{D}$ versus $P_{FA}$). Figures 5 and 6 illustrate the ROC curves over an AWGN channel for different central frequency values: two central frequencies are chosen in two allowed bands ($f_{c}=12.5$ MHz and $f_{c}=32.5$ MHz) and two others are located out of the allowed bands (in forbidden bands) ($f_{c}=15$ MHz and $f_{c}=35$ MHz) and using both sampling modes: uniform sampling (Fig. 5) and random sampling (Fig. 6). For these simulations, the number of samples is set to 1,024, i.e. $N=1{,}024$ in (8) and the $\gamma$ is of $-60$ dB.

Fig. 5

ROC curves in the case of uniform sampling at different $f_{c}$ values

Fig. 6

ROC curves in the case of random sampling at different $f_{c}$ values

From Fig. 5, we can note that, in the case of uniform sampling, we have two cases of ROC curves:

• For central frequency values that are inside the allowed bands, good performance is obtained as it is possible to find a trade-off between $P_{FA}$ and $P_{D}$ which explains the ROC curves form inside these bands.

• For central frequency values inside the forbidden bands, a spectrum aliasing occurs within the channel of interest and hence a great energy is present within this channel even if this channel is free. This explains the obtained ROC curves which are reduced to a unique point $(P_{D}=P_{FA}=1)$ meaning that the energy detector does not work properly

However, with the use of random sampling (Fig. 6), we have a good performance (the reconstruction process is efficient) whatever the value of the central frequency. The use of the random sampling overcomes the constraint of the forbidden bands imposed in the uniform sampling case. This explains the obtained ROC curves which are almost similar.

5 Conclusion

In this work, we were interested in spectrum sensing which is the key function of the cognitive radio. The proposed approach is based on the energy detector method as the sensing method and on the random sampling as a sampling mode. The performance of this proposed approach in term of the ROC curve is evaluated for different values of central frequencies and then compared to the uniform sampling case.

Random sampling makes it possible to overcome forbidden band restriction encountered with uniform sampling mode.

We can deduce that random sampling associated with energy detector represents an interesting solution in cognitive radio due to a large flexibility it offers in sampling rates.