Optimization of Cluster-Based Cooperative Spectrum Sensing Scheme in Cognitive Radio Networks with Soft Data Fusion

Abstract

This paper investigates cluster-based cooperative spectrum sensing issues in two-layer hierarchical cognitive radio networks with soft data fusion. We first define a two-phase reporting protocol in the paper. In the first phase, secondary users forward their soft sensing information to cluster heads (CHs) over large-scale fading. In the second phase, all CHs transmit the aggregated soft energy information to the fusion center (FC) with different weights. Thus we derive the network false alarm (FA) and the detection probabilities as functions of the FC decision threshold, the clustering algorithm and different weights. Given a target on the detection probability, minimizing the FA probability is then formulated as a constraint optimization problem within two scenarios including additive white Gaussian noise environment and Rayleigh fading environment. A close-form upper bound of the FA probability is derived and a novel clustering scheme is also proposed for each scenario. Numerical results show that the proposed schemes achieve a satisfying performance.

1 Introduction

With the rapid development of new wireless devices and services, the scarcity of spectrum becomes one of the most imperative challenges for designing future wireless communication systems [1]. Cognitive radio (CR), which can utilize the licensed spectrum in a much more efficient manner, has attracted significant attention to solve the spectrum shortage problem. In CR networks (CRNs), secondary users (SUs) have opportunities to utilize spectrum holes without causing interference to primary users (PUs) by sensing the radio environment. However, due to the intrinsic instability of wireless channels, i.e., penetration loss, shadowing, and multipath fading, it is difficult for an SU to obtain an accurate sensing result in cognitive radio networks (CRNs). In order to improve sensing performance, cooperative spectrum sensing (CSS) [2, 3], which allows multiple SUs to share sensing data to improve performance in the detection of a PU, is proposed thereafter.

Recently, two categories of CRN infrastructures, namely. centralized CRNs (CCRNs) [4] and distributed CRNs (DCRNs) [5], take our attention. With respect to (w.r.t.) the CCRNs, there existing a fusion center (FC) to decide the status of PUs based on the collected sensing information from SUs. In the DCRNs however, no FC exists and SUs should exchange sensing information with each other for the final decision. There are also two kinds of fusion methods in the CRNs including (1) decision fusion method, in which SUs decide the presence of primary activity and send 1-bit result to the FC, (2) data fusion method in which SUs transmit sensing information to the FC. The performance of the decision ability of data fusion method is superior to decision fusion method at expense of further reporting bandwidth. In this paper, soft data fusion method is considered in the CCRNs.

In order to sufficiently protect PU, It is preferable to minimize the probability of false alarm (FA) given a target detection probability. In [6] an optimal number of SUs and a sensing threshold are derived by minimizing the sum of FA probability and missing(failing to detection) probability, conditioned on identical sensing channels between SUs and PU as well as perfect reporting channels. In [7], the imperfect issue of sensing and reporting channels is investigated for CCRNs. Furthermore, the performance of log-normal sensing and reporting channels is also studied for CCRNs in [8].

In cooperative CCRNs, the more number of cooperative SUs increases, the further performance improvement can be achieved. However, too many cooperative SUs negatively affects gathering global sensing data at a local place [9]. And results in higher overhead in sensing result collection and less time allocated to data transmission. In order to address such challenge, cluster-based CSS approach is proposed to ease the traffic load of the reporting channel in [10].

There are several previous studies on cluster-based CRNs in the literature. In [10], performance of hard and soft fusion rules are studied, respectively. Different clustering algorithms are also in Malady and da Silva [11]. In [12–14], the fusion rules and optimal parameter setup are investigated. In [15], a multi-cluster multi-group based cooperative spectrum sensing scheme is proposed, which pursued the optimal cluster number by minimizing the error rate of each cluster. In [16], a weighted cooperative sensing framework is proposed to increase spectrum sensing accuracy. In [17], the performance for log-normal channels with noise uncertainty is investigated. In [18], a time division multiplex access(TDMA)-based protocol is proposed to manage spectrum sensing data and exploit cooperative sensing benefit. In [19–21], some hard decision fusion rules are investigated to improve sensing performance. In [22–24], some schemes are presented to optimize sensing efficiency/reliability and reduce power consumption. In [25–27], the reduction of overhead and detection expenditure is investigated specifically. From the perspective of data transmission, [28] proposes a TDMA reporting frame structure and investigates a sensing-throughput tradeoff issue.

In this paper, we present a two-phase reporting protocol. In the first phase, SUs forward their soft sensing information to their cluster heads (CHs) over large-scale fading reporting channels. In the second phase, all CHs transmit the aggregated soft energy information to the FC with different weights. The FC makes a final decision and broadcasts it to all the SUs.

Given such protocol, the contributions of this paper are listed in the following:

(1):

Both FA and detection probabilities are derived as functions of the FC decision threshold, cluster number and weights.

(2):

A set of optimal weights is derived by minimizing the FA probability given a target detection probability.

(3):

A close-form upper bound of the FA probability is derived given a target detection probability in both the AWGN environment and the Rayleigh fading environment. Importantly, based on the above derivations, two efficient and effective clustering schemes are proposed to achieve a satisfying performance.

The rest of the paper is organized as follows. In Sect. 2, system model and assumptions are introduced. The optimization problem is then formulated to minimize the FA probability given a target detection probability in Sect. 3. Solution of the optimization problem w.r.t. the AWGN environment and the Rayleigh fading environment are derived accordingly in Sect. 4. The simulation results are given in Sect. 5. Finally, we draw our conclusion in Sect. 6.

2 System Model and Assumptions

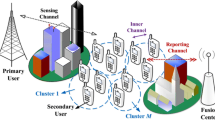
Figure 1 shows the system model of a cluster-based two-layer hierarchical CCRN. There is one FC in the SU network. Without loss of generality, we assume there are $K$ CHs and $N$ SUs which are divided into $K$ clusters in the CCRN. We denote that the $k$-th cluster has $n_k$ ($n_k\ge 0$ and $n_k$ is an integer) SUs, which subjects to $\sum _{k=1}^K{n_k}=N$. In each cluster, CHs collect the soft sensing information forwarded by their cluster members (CMs).

Fig. 1

System model of a two-layer hierarchical CRN

In a cluster-based CCRN, the $i$-th SU conducting local spectrum sensing is formulated in the following:

$$\begin{aligned} y_i(m)&= \left\{ \begin{array}{l@{\quad }l} n_i(m), &{} \mathcal {H}_0 \\ h_i*s(m)+n_i(m), &{} \mathcal {H}_1 \end{array} \right. \end{aligned}$$

(1)

where $\mathcal {H}_0$ and $\mathcal {H}_1$ denote the absence and the presence of the PU, respectively. $y_i(m)$ represents the $m$-th received signal sample by the $i$-th SU, $s(m)$ represents the $m$-th transmitted signal sample from the PU and $\sigma _s^2$ represents covariance of $s(m)$. $n_i(m)$ represents the received noise sample at the $i$-th SU which follows circular symmetric complex Gaussian (CSCG) distribution denoted as $\mathcal {N}(0,\sigma _n^2)$ for all SUs. $h_i$ represents the transmitted signal sample complex channel gain of the sensing channel between the PU and the $i$-th SU. The instantaneous detection signal-to-noise ratio (SNR) at the $i$-th SU is given as $\gamma _i=\frac{|h_i|^2\sigma _s^2}{\sigma _u^2}$. Herein, we also assume that the FC has perfect knowledge of the instantaneous detection SNR $\gamma _i$, and this can be realized by direct feedback from the SUs.

In the AWGN environment, all SUs have the same channel coefficient $h_i$ because they have the identical path loss. Therefore all SUs have the same instantaneous detection SNR ($\gamma _i=\gamma _j, 1\le i,j\le N$).

In the Rayleigh fading environment, the channel coefficient $|h_i|^2$ follows the exponential distribution. As a result, the instantaneous detection SNR of each SU is an exponentially distributed random variable with the same $\overline{\gamma }$ accordingly.

Given the above hypothetical problem, the testing statistic for energy detector denoted as $v_i$ is in the following

$$\begin{aligned} v_i = \frac{1}{M}\sum _{m = 1}^M {|y_i(m)|^2 }, \end{aligned}$$

(2)

where the received signal is sampled at the sampling frequency $f_s$ within the sensing time $\tau _s$. And $M$ is the maximum integer not greater than $f_s\tau _s$.

When $M$ is large, given Central Limit Theorem (CLT), $v_i$ can be approximated to follow a Gaussian distribution denoted as $\mathcal {N}(\mu _0,\sigma _0^2)$ with

$$\begin{aligned} \mu _0,\sigma _0^2&= \left\{ \begin{array}{ll} \sigma _n^2,\frac{1}{M}\sigma _n^4 &{} \mathcal {H}_0 \\ (1+\gamma _i)\sigma _n^2, \frac{1}{M}(2\gamma _i + 1)\sigma _n^4. &{}\mathcal {H}_1 \\ \end{array} \right. \end{aligned}$$

(3)

3 Optimization Problem Formulation

In this section, we first introduce a cluster-based CSS framework and then formulate an optimization problem by minimizing the FA probability given the target detection probability.

3.1 Cluster-Based CSS Framework

We consider a two-phase reporting protocol in a cluster-based CCRN. In the first phase, the CMs in the same cluster forward their soft sensing information to their CH, and the aggregated sensing information received by the $k$-th CH is denoted as $V_k$. We assign each SU to a certain cluster, denoted as $\varvec{\rho }=\{\rho _{k,i} \in \{0,1\}|k \in \{1,2,\ldots ,K\},\;i \in \{1,2,\ldots ,N\}\}$ in which $\rho _{k,i}=1$ means the $i$-th SU is assigned to the $k$-th cluster, $\rho _{k,i}=0$ otherwise. In this setting, we have $n_k=\sum _{i=1}^{N}{\rho _{k,i}}$. In other words, $n_k$ in the following discussion is equivalent to $\sum _{i=1}^N{\rho _{k,i}}$.

For simplicity, we assume that the $i$-th SU forward its soft sensing information $v_i$ to the $k$-th CH over large-scale fading denoted as $g_{k,i}$. We have $g_{k,i}\!=\!d_{k,i}^{-\alpha }, k\in \{1,2,\ldots ,K\}, i\in \{1,2,\ldots ,N\}$, where $\alpha$ is the path loss exponent and $d_{k,i}$ is the normalized distance between the $k$-th CH and the $i$-th SU. Since $v_i$ and $g_{k,i}$ are statistically independent from each other, $V_k$ also follows the Gaussian distribution denoted by $V_k\sim \mathcal {CN}(\mu _k,\sigma _k^2)$. When $n_k>0$, we have

$$\begin{aligned} V_k = \frac{1}{n_k}\sum _{i=1}^{N} \rho _{k,i}d_{k,i}^{-\alpha }v_i , 1\le k \le K \end{aligned}$$

(4)

with

$$\begin{aligned} \mu _k&= \frac{1}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\mu _0},\end{aligned}$$

(5)

$$\begin{aligned} \sigma _k^2&= \frac{1}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }\sigma _0^2}, \end{aligned}$$

(6)

and $V_k=0$, otherwise.

In the second transmission phase, all CHs transmit the aggregated soft energy information through the reporting channels to the FC with different weights. Let’s use $\mathbf {w}=\{w_k|k \in \{1,2,\ldots ,K\}\}$ to define a weight coefficient set where $\sum _{k=1}^K{w_k}=1$, the energy information received at the FC is in the following:

$$\begin{aligned} V =\sum _{k=1}^K {w_k V_kd_{k,fc}^{-\alpha }}, \end{aligned}$$

(7)

where $w_k$ denotes the weight factor of the $k$-th CH valued at the the corresponding contribution to the performance. In addition, $n_k=0$ means no information transmitted from the $k$-th CH to the FC. For ease of discussion, let’s assume $n_k>0$ and $V$ therefore follows the Gaussian distribution with

$$\begin{aligned} \mu&= \frac{1}{K}\sum _{k=1}^K{\frac{w_kd_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\mu _0}},\end{aligned}$$

(8)

$$\begin{aligned} \sigma ^2&= \frac{1}{K^2}\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }\sigma _0^2}}. \end{aligned}$$

(9)

Given a detection threshold $\lambda$, the FA probability denoted as $P_f$ and the detection probability denoted as $P_d$ are given by

$$\begin{aligned} P_f(\lambda )&= Q\left( \frac{\lambda -\frac{1}{K}\sum _{k=1}^K{\frac{w_kd_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\sigma _n^2}}}{\sqrt{\frac{1}{K^2}\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }\frac{\sigma _n^4}{M}}}}}\right) ,\end{aligned}$$

(10)

$$\begin{aligned} P_d(\lambda )&= Q\left( \frac{\lambda -\frac{1}{K}\sum _{k=1}^K{\frac{w_kd_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }(1+\gamma _i)\sigma _n^2}}}{\sqrt{\frac{1}{K^2}\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }(1+2\gamma _i)\frac{\sigma _n^4}{M}}}}}\right) . \end{aligned}$$

(11)

with

$$\begin{aligned} Q(x)=\frac{1}{\sqrt{2\pi }}\int \limits _{x}^{\infty }exp\left( -\frac{t^2}{2} \right) dt. \end{aligned}$$

(12)

3.2 Problem Formulation

Given a target detection probability, minimizing the FA probability is formulated a constrained optimization problem in the following:

Problem P1:

$$\begin{aligned} \mathop {\min }\limits _{\{\lambda ,\varvec{\rho },\varvec{w}\}} P_f\end{aligned}$$

(13a)

$$\begin{aligned} s.t. P_d\ge \overline{P}_d, \end{aligned}$$

(13b)

$$\begin{aligned} \sum _{k=1}^K{w_k}=1,\end{aligned}$$

(13c)

$$\begin{aligned} \sum _{k=1}^K{\rho _{k,i}}=1, \end{aligned}$$

(13d)

where $\overline{P}_d$ denotes as the target detection probability.

Obviously the optimal solution occurs when $P_d=\overline{P}_d$. Thus we are able to derive

$$\begin{aligned} \lambda ^{*}&= \frac{1}{K}\sum _{k=1}^K{\frac{w_kd_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }(1+\gamma _i)\sigma _n^2}}\\ \nonumber&\quad +Q^{-1}(\overline{P}_d)\sqrt{\frac{1}{K^2}\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }(1+2\gamma _i)\frac{\sigma _n^4}{M}}}}. \end{aligned}$$

(14)

In CCRN, $\gamma _i\ll 1, i\in \{1,2,\ldots ,N\}$ because the strength of PU’s signal power received by SUs is very low. Thus the FA probability is further approximated in the following:

$$\begin{aligned}&P_f(\varvec{\rho },\mathbf {w})\nonumber \\&\quad =Q\left( Q^{-1}(\overline{P}_d)\sqrt{\frac{\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }(1+2\gamma _i)}}}{\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{n_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}}}+\frac{\sum _{k=1}^K{\frac{w_kd_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-v}\gamma _i}}}{\sqrt{\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{Mn_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}}}\right) \nonumber \\&\quad \approx Q\left( Q^{-1}(\overline{P}_d)+\frac{\sum _{k=1}^K{\frac{w_kd_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-v}\gamma _i}}}{\sqrt{\sum _{k=1}^K{\frac{w_k^2d_{k,fc}^{-2\alpha }}{Mn_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}}}\right) . \end{aligned}$$

(15)

4 Solution of Optimization Problem

Problem (13) involves both discrete and continuous variables which is difficult to be solved. In this paper, a reasonable weight fusion rule is first derived. The optimization problem is then transformed into a discrete optimization problem. An exhausting search is generally used to find the optimization solution for such discrete problem at expense of high computation complexity. In order to more efficiently and effectively solve such problem, two clustering schemes are then proposed in both AWGN environment and Rayleigh fading environment.

4.1 Weight Fusion Rule

Proposition 1

The optimal value of $\mathbf {w}$ with specific $\varvec{\rho }$ for Problem (13) is in the following:

$$\begin{aligned} w_k^{*}=\frac{\left( n_kd_{k,fc}^{\alpha }\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) /\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}\right) }{\sum _{k=1}^K{\left( n_kd_{k,fc}^{\alpha }\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) /\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}\right) }}.1\le k \le K \end{aligned}$$

(16)

Proof

Since minimizing $Q(x)$ is equal to maximizing $x$, Problem (13) w.r.t. $\mathbf {w}$ under specific $\varvec{\rho }$ can be reformulated as

$$\begin{aligned} P_f(\mathbf {w})=\mathop {\max }\limits _{\{\mathbf {w}\}} \frac{\sum _{k=1}^K{w_kB_k}}{\sqrt{\sum _{k=1}^K{w_k^2A_k}}}\end{aligned}$$

(17a)

$$\begin{aligned} s.t. \sum _{k=1}^K{w_k}=1, \end{aligned}$$

(17b)

with

$$\begin{aligned} A_k&= \frac{d_{k,fc}^{-2\alpha }}{Mn_k^2}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }},\end{aligned}$$

(18)

$$\begin{aligned} B_k&= \frac{d_{k,fc}^{-\alpha }}{n_k}\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}. \end{aligned}$$

(19)

Hence we have

$$\begin{aligned}&\frac{dP_f}{dw_k} = 0 \Rightarrow \frac{B_k \sqrt{\sum _{k=1}^K{w_k^2A_k}}-\frac{w_kA_k\sum _{k=1}^K{w_k\ B_k}}{\sqrt{\sum _{k=1}^K{w_k^2A_k}}}}{\sum _{k=1}^K{w_k^2A_k}} = 0\nonumber \\&\quad \Rightarrow B_k\left( \sum _{k=1}^K{w_k^2A_k}\right) =w_kA_k\left( \sum _{k=1}^K{w_kB_k}\right) . \end{aligned}$$

(20)

Let’s further define

$$\begin{aligned} \mathbf {B}&= \{B_1,B_2,\ldots ,B_K\}. \nonumber \\ \mathbf {A}&= \left( \begin{array}{cccc} A_1 &{}\quad 0 &{}\quad 0 &{}\quad \ldots \\ 0 &{}\quad A_2 &{}\quad 0 &{}\quad \ldots \\ \vdots &{}\quad \vdots &{}\quad \ddots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad A_K \end{array} \right) .\nonumber \end{aligned}$$

Then

$$\begin{aligned}&B_k \mathbf {w} \mathbf {A} \mathbf {w}^T=w_k A_k \mathbf {B} \mathbf {w}^T \nonumber \\ \Rightarrow&\frac{B_k}{A_k} \mathbf {w} \mathbf {A}=w_k \mathbf {B}\nonumber \\ \Rightarrow&\sum _{k=1}^K{\frac{B_k}{A_k} \mathbf {w} \mathbf {A}}=\sum _{k=1}^K{w_k \mathbf {B}}=\left( \sum _{k=1}^K{w_k}\right) \mathbf {B}=\mathbf {B}\nonumber \\ \Rightarrow&\sum _{k=1}^K{\frac{B_k}{A_k}}\mathbf {w} \mathbf {A}=\left( \sum _{k=1}^K{\frac{B_k}{A_k}}\right) (w_1A_1,w_2A_2,\ldots ,w_KA_K)=(B_1,B_2,\ldots ,B_K)=\mathbf {B}\nonumber \end{aligned}$$

Therefore

$$\begin{aligned} w_k^{*}&= \frac{B_k/A_k}{\sum _{k=1}^K{B_k/A_k}}\nonumber \\&= \frac{\left( n_kd_{k,fc}^{\alpha }\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) \big /\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}\right) }{\sum _{k=1}^K{\left( n_kd_{k,fc}^{\alpha }\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) {\big /}\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}\right) }}. \end{aligned}$$

(21)

$\square$

4.2 Scenario 1: Sensing Channels in the AWGN Environment

In the AWGN environment, all SUs have the same instantaneous detection SNR ($\gamma _i=\gamma$ for $i\in \{1,2,\ldots ,N\}$). Therefore

$$\begin{aligned} w_k^{*}=\frac{\left( n_kd_{k,fc}^{\alpha }\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }}\right) /\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}\right) }{\sum _{k=1}^K{\left( n_kd_{k,fc}^{\alpha }\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }}\right) /\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}\right) }}, 1\le k \le K. \end{aligned}$$

(22)

Then

$$\begin{aligned} P_f(w^{*},\varvec{\rho })\approx Q\left( Q^{-1}(\overline{P}_d)+\gamma \sqrt{M}\sqrt{\sum _{k=1}^K\frac{\left( \sum _{i=1}^N {\rho _{k,i}d_{k,i}^{-\alpha }}\right) ^2}{\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}}\right) . \end{aligned}$$

(23)

Thus, Problem (13) in scenario 1 can be reformulated as

$$\begin{aligned} \mathop {\max }\limits _{\{\varvec{\rho }\}}\sum _{k=1}^K{\frac{\left( \sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-\alpha }}\right) ^2}{\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}} \end{aligned}$$

(24a)

$$\begin{aligned} s.t. \sum _{k=1}^K{\rho _{k,i}}=1. \end{aligned}$$

(24b)

For ease of presentation, we denote by

$$\begin{aligned}&\psi _{k,i}=\rho _{k,i}d_{k,i}^{-\alpha },\end{aligned}$$

(25)

$$\begin{aligned}&\psi _{k,i}^2=\rho _{k,i}^2d_{k,i}^{-2\alpha }=\rho _{k,i}d_{k,i}^{-2\alpha }. \end{aligned}$$

(26)

Then

$$\begin{aligned} P_f(w^{*},\varvec{\rho })&= \sum _{k=1}^K{\frac{\left( \sum _{i=1}^N{\psi _{k,i}}\right) ^2}{\sum _{i=1}^N{\psi _{k,i}^2}}}=\sum _{k=1}^K{g(k)}. \end{aligned}$$

(27)

Because $g(k_1)$ is irrelevant from $g(k_2)$ when $k_1\ne k_2$, we can optimize $g(k)$ for each $k$ independently. Given $n_k=\sum _{i=1}^N\rho _{k,i}, \rho _{k,i}\in \{0,1\}$, Let’s use $\{\xi _{k,m}\ne 0,m=1,2,\ldots ,n_k\}$ to represent the nonzero subset of $\{\psi _{k,i},1\le i\le N\}$ and then,

$$\begin{aligned} g(k)&= \frac{\left( \sum _{i=1}^{N}{\psi _{k,i}}\right) ^2}{\sum _{i=1}^{N}{\psi _{k,i}^2}}=\frac{\left( \sum _{m=1}^{n_k}{\xi _{k,m}}\right) ^2}{\sum _{m=1}^{n_k}{\xi _{k,m}^2}}=\frac{\sum _{m=1}^{n_k}{\xi _{k,m}^2}+\sum _{j=1}^{n_k}{\sum _{l\ne j}\xi _{k,j}\xi _{k,l}}}{\sum _{m=1}^{n_k}{\xi _{k,m}^2}}\nonumber \\&\le \frac{\sum _{m=1}^{n_k}{\xi _{k,m}^2}+\frac{1}{2}\sum _{j=1}^{n_k}{\sum _{l\ne j}(\xi _{k,j}^2+\xi _{k,l}^2)}}{\sum _{m=1}^{n_k}{\xi _{k,m}^2}}\nonumber \\&= \frac{\sum _{m=1}^{n_k}{\xi _{k,m}^2}+\frac{1}{2}\sum _{j=1}^{n_k}{2(n_k-1)\xi _{k,j}^2}}{\sum _{i=m}^{n_k}{\xi _{k,i}^2}}=\frac{n_k\sum _{m=1}^{n_k}{\xi _{k,m}^2}}{\sum _{m=1}^{n_k}{\xi _{k,m}^2}}=n_k. \end{aligned}$$

(28)

Hence, $g(k)$ is maximized when $\xi _{k,1}=\xi _{k,2}=\cdots =\xi _{k,n_k}$, which means the $k$-th CH selects $n_k$ SUs with the same distances away from itself and

$$\begin{aligned}&\sum _{k=1}^K{g(k)}\le \sum _{k=1}^K{n_k}=N.\nonumber \\&\quad \Rightarrow P_f \le Q\left( Q^{-1}(\overline{P}_d)+\gamma \sqrt{MN}\right) . \end{aligned}$$

(29)

Given the above discussion, the procedures of clustering scheme in scenario 1 is given in the following:

4.3 Scenario 2: Sensing Channels in the Rayleigh fading Environment

In the Rayleigh fading environment, $P_f$ is approximated in the following:

$$\begin{aligned} P_f(\varvec{\rho })\approx Q\left( Q^{-1}(\overline{P}_d)+\sqrt{M}\sqrt{\sum _{k=1}^K\frac{\left( \sum _{i=1}^N {\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) ^2}{\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}}\right) . \end{aligned}$$

(30)

And Problem (13) is reformulated in the following:

$$\begin{aligned} \mathop {\max }\limits _{\{\varvec{\rho }\}}\sum _{k=1}^K\frac{\left( \sum _{i=1}^N {\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) ^2}{\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}\end{aligned}$$

(31a)

$$\begin{aligned} s.t. \sum _{k=1}^K{\rho _{k,i}}=1. \end{aligned}$$

(31b)

According to Cauchy-Schwarz Inequality, we can derive

$$\begin{aligned} q(\varvec{\rho })&= \sum _{k=1}^K\frac{\left( \sum _{i=1}^N {\rho _{k,i}d_{k,i}^{-\alpha }\gamma _i}\right) ^2}{\sum _{i=1}^N{\rho _{k,i}d_{k,i}^{-2\alpha }}}=\sum _{k=1}^K\frac{\left( \sum _{i=1}^{n_k} {\xi _{k,m}\gamma _m}\right) ^2}{\sum _{m=1}^{n_k}{\xi _{k,m}^{2}}}\nonumber \\&\le \sum _{k=1}^K\frac{\left( \sum _{m=1}^{n_k}{\xi _{k,m}^{2}}\right) \left( \sum _{m=1}^{n_k}{\gamma _m^2}\right) }{\sum _{m=1}^{n_k}{\xi _{k,m}^{2}}}=\sum _{k=1}^{K}\sum _{m=1}^{n_k}{\gamma _m^2}\nonumber \\&= \sum _{i=1}^N{\gamma _i^2}. \end{aligned}$$

(32)

And $q(\varvec{\rho })=\sum _{i=1}^N{\gamma _i^2}$ when $\frac{\xi _{k,1}}{\gamma _1}=\frac{\xi _{k,2}}{\gamma _2}=\cdots =\frac{\xi _{k,n_k}}{\gamma _{n_k}}, k\in \{1,2,\ldots ,K\}$ is satisfied. Therefore

$$\begin{aligned} P_f \le Q\left( Q^{-1}(\overline{P}_d)+\sqrt{M\sum _{i=1}^N{\gamma _i^2}}\right) . \end{aligned}$$

(33)

And the clustering scheme in the scenario 2 is given in the following:

5 Numerical Results and Discussions

5.1 Simulation Setup

In this section, numerical results and discussions are presented to evaluate the effectiveness of our proposed clustering schemes in the two-layer CCRN. We assume the distances between all the SUs and CHs are normalized and we choose the path loss exponent $\alpha =4$. The sampling frequency and the fixed sensing time are assumed to be $f_s=4MHz,\tau _s=0.5s$, respectively. And the sampling times can be obtained by $M=f_s\tau _s=2000$. Furthermore, the SNR for the PU measured at the SUs is $SNR=\gamma$ in the AWGN environment, and $SNR=\overline{\gamma }$ in the Rayleigh fading environment.

5.2 Scenario 1: Sensing Channels in the AWGN Environment

In the scenario 1, we first show the clustering results proposed in Algorithm 1 and then demonstrate several numerical results on effectiveness of different setups for $\gamma ,\overline{P}_d,K$ in scenario 1.

Figure 2 shows the clustering result of Algorithm 1 in the scenario 1. The simulation setup is given including $N=200,K=4$. For ease of discussion, we consider a system topology in a two-dimensional X-Y plane, where the FC and $K$ CHs are located at points (0, 0), ($-$0.5, 0.5), (0.5, 0.5), ($-$0.5, $-$0.5) and (0.5, $-$0.5), respectively. The locations of SUs are uniformly distributed in the simulation area. From the simulation results, we can observe that each cluster almost guarantee the same distances between CHs and their CMs, which demonstrates the theoretical clustering result agrees well with the simulation results proposed in the Algorithm 1.

Fig. 2

Clustering result in the AWGN environment

Figure 3 depicts the correlation between $N$ and $P_f$ under different $K$ in the AWGN environment. The simulation setup is given including $\overline{P}_d=0.9, \gamma =-20dB$. Obviously, we can observe that $P_f$ significantly decreases conditioned on $N\le 60$ and almost keep constant conditioned on $N\ge 100$ with the increasing number of cooperative SUs. Moreover, we can see no difference between the curves of the upper bound on $P_f$ under different $K$. Since the upper bound of $P_f$ is irrelevant to the number of clusters obtained from the exact expression(i.e., (28)). Importantly, we can also see that the simulation performance with the clustering scheme is nearly identical to that achievable of the upper bound when the number of cooperative SUs or the number of clusters achieve a certain quantity ($N\ge 80$ for $K=4$) or ($N\ge 30$ for $K=8$). This implies that the design of clustering scheme will favor in a large-scale SUs CCRN.

Fig. 3

$P_f$ versus $N$ under different $K$ in the AWGN environment

Figures 4 and 5 illustrate the correlation between $N$ and $P_f$ in the AWGN environment with varying $\overline{P}_d$ and $\gamma$, given simulation setups of $K=4, \gamma =-20dB$ and $K=4, \overline{P}_d=0.9$, respectively. We can obviously observe that $P_f$ is decreasing along with the increasing number of cooperative SUs under different $\overline{P}_d$ and $\gamma$. Similarly for Fig. 3, the gaps between the upper bounds on $P_f$ and the performance of the proposed clustering scheme are bigger with higher $\overline{P}_d$ and lower $\gamma$. Specifically, for larger $N$, the gaps become smaller. This again implies that the design of clustering scheme will be beneficial in a large-scale SUs CCRN.

Fig. 4

$P_f$ versus $N$ under different $\overline{P}_d$ in the AWGN environment

Fig. 5

$P_f$ versus $N$ under different $\gamma$ in the AWGN environment

5.3 Scenario 2: Sensing Channels in the Rayleigh Fading Environment

Figure 6 shows the clustering result of Algorithm 2. The simulation setup is given including $N=200,K=4$. And the system topology in a two-dimensional X-Y plane is similar to that introduced in Fig. 2. From the simulation results, we can observe that unlike Algorithm 1, the clustering scheme in the scenario 2 involves not only the locations of all SUs but also the instantaneous detection SNRs of all the SUs.

Fig. 6

Clustering result in the Rayleigh fading environment

Figure 7 shows the relationship between $N$ and $P_f$ under different $K$ in the Rayleigh fading environment. The simulation setup is given including $\overline{P}_d=0.9, \overline{\gamma }=-20dB$. Similarly for Fig. 3, we can obtain that $P_f$ decreases with the increasing number of cooperative SUs and the upper bound on $P_f$ is irrelevant to the number of clusters according to Eq. (33). Specially, from the simulation results, the gap between the upper bound on $P_f$ and the performance of the proposed scheme is bigger than that in the scenario 1 shown in Fig. 3. It is because that the instantaneous SNRs in the Rayleigh fading environment lead to the result that the upper bound on $P_f$ in the scenario 2 is harder to achieve.

Fig. 7

$P_f$ versus $N$ under different $K$ in the Rayleigh fading environment

Figures 8 and 9 investigate the relationship between $N$ and $P_f$ in the Rayleigh fading environment with varying $\overline{P}_d$ and $\overline{\gamma }$, given simulation setups of $K=4, \overline{\gamma }=-20dB$ and $K=4, \overline{P}_d=0.9$, respectively. Similarly for Figs. 4 and 5, it is obvious to again observe that the gaps between the upper bounds on $P_f$ and the proposed clustering scheme in the scenario 2 are bigger than those in the scenario 1.

Fig. 8

$P_f$ versus $N$ under different $\overline{P}_d$ in the Rayleigh fading environment

Fig. 9

$P_f$ versus $N$ under different $\overline{\gamma }$ in the Rayleigh fading environment

5.4 Complexity Analysis

In the subsection, the complexity of proposed algorithms is analyzed by the times of operations. It is assumed that calculating a subtraction and comparing with the threshold needs about 1 operation. Moreover, it is obvious to obtain that the complexity of Algorithm 1 is same as Algorithm 2. Specially, for a predefined threshold, the complexity of proposed algorithms is in the following:

$$\begin{aligned} \sum _{k=1}^K{\left( N-\sum _{i=1}^k{n_i}\right) \left( N-\sum _{i=1}^k{n_i}-1\right) }+N(N-1)\sim N^2+O(N^2). \end{aligned}$$

(34)

In addition, the iterative times of proposed algorithms depend on $\epsilon ,\Delta \epsilon$. With the decreasing value of $\epsilon ,\Delta \epsilon$, the proposed algorithms can achieve a better performance but at the expense of higher complexity.

6 Conclusion

In this paper, we investigate optimization of cluster-based CSS schemes in two-layer cognitive radio networks with soft data fusion. A two-phase reporting protocol is presented. Thus we derive the FA probability given target detection probability as functions of the FC decision threshold, cluster parameters and weights in a cluster-based CCRN. Minimizing the FA probability given a target detection probability is then formulated as a constrained optimization problem in both AWGN environment and Rayleigh fading environment. And two efficient and effective clustering schemes are further proposed for both environments, respectively. Numerical results show that the proposed schemes achieve a satisfying performance.