Outage Performance of Underlay Cognitive Opportunistic Multi-relay Networks in the Presence of Interference from Primary User

Abstract

In this paper, considering the interferences from primary transmitter to secondary receiver and from secondary transmitter to primary receiver, we derive the upper and lower bounds of outage probability for underlay cognitive opportunistic multi-relay networks. Theoretical and simulation results show the upper and lower bounds converge to the exact outage probability at high interference-to-noise (INR) region. Because the interference from primary transmitter to secondary receiver is considered, an outage floor at high signal-to-noise ratio (SNR) occurs when INR increases proportionally with SNR.

1 Introduction

Cognitive radio is considered as an efficient technology to solve the spectrum scarcity problem. In cognitive radio, the secondary users (SUs) and primary users (PUs) can share the spectrum with underlay or overlay model [1, 2]. In underlay model, the SU is allowed to transmit concurrently with the PU provided that the cochannel interference from SU to PU is below a tolerable threshold. Due to the interference power constraint and the wireless channel fading, the quality of service (QoS) of the SU cannot be guaranteed. To improve the performance of SU, cognitive relay networks which provide extra spatial diversity [3, 4] for the SU has been proposed in [5–13].

In [7] and [8], considering the dependence introduced by the interference power constraint, a tight lower bound and the exact outage probability (OP) are derived for decode-and-forward (DF) underlay cognitive relay networks, respectively. In [9] and [10], a closed-form OP of amplify-and-forward (AF) cognitive relay networks is obtained under average and maximum interference power constraint, respectively. In [11], a tight approximate OP is derived for AF cognitive two-way relay networks. However, the interference from primary transmitter to secondary receiver is not considered in the above mentioned literatures. In fact, when the secondary receiver is near to the primary transmitter, the cochannel interference from the primary transmitter may be too strong to be ignored.

Recently, the effect of PU interference on the secondary AF and DF cognitive radio networks has been investigated in [12] and [13], respectively, assuming that only single relay is involved and direct link is not available. However, multi-relay networks are more general in practical situation and direct link should be considered in some scenario. In this paper, considering the interferences from primary transmitter to secondary receiver and from secondary transmitter to primary receiver, the maximum transmit power constraint of SU, and the dependence introduced due to interference power constraint, we derive the upper and lower bound expressions of the OP for the underlay cognitive opportunistic multi-relay networks with direct link. The opportunistic relaying scheme [14, 15], where only the “best” relay is selected to forward message and the “best” relay can be selected with a distributed algorithm, is employed in this paper. Furthermore, we obtain the approximate OP at high signal-to-noise ratio (SNR) to find the diversity order of cognitive multi-relay networks.

The rest of the paper is organized as follows. The system model is described in Sect. 2. The upper and lower bounds outage probability are derived in Sect. 3. In Sect. 4, the asymptotic outage performance is investigated. The simulation results are illustrated in Sect. 5, and the conclusions are provided in Section 6.

2 System Model

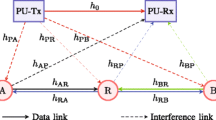
Consider an underlay cognitive multi-relay network with the coexistence of primary and secondary links, as illustrated in Fig. 1 [7, 8]. The primary link employs the direct transmission while the secondary link employs opportunistic decode-and-forward (DF) relaying transmission. The primary link consists of a transmitter $(c)$ and a receiver $(p)$. The secondary link consists of a source $(s)$, $K$ relays $(r_1,r_2,\ldots ,r_K)$, and a destination $(d)$. For the secondary link, the DF cooperative relaying protocol and half-duplex mode are adopted. The transmission of secondary link is divided into two phases. In the first phase, the source $(s)$ broadcasts its message to the $K$ relays and the destination $(d)$. In the second phase, only the relay in the successfully decoding relay set which has maximum signal-to-interference-plus-noise ratio (SINR) is selected to forward the message to the destination $(d)$. The destination combines the messages of the direct link and opportunistic relaying link with maximum ratio combining (MRC) scheme [16]. To ensure the QoS of PU, the transmit power of SU should satisfy both the maximum transmit power constraint $Q$ and maximum tolerable interference power constraint $I_p$. The wireless channel between transmitter node $i (c, s, r_{1}, \ldots , r_{K})$ and receiver node $j (p, r_{1}, \ldots , r_{K}, d)$ is independent Rayleigh flat fading channel with variance $1/\lambda _{ij}$. Thus, the channel gain $g_{ij}=|h_{ij}|^2$ is exponential distributed with probability density function (PDF) $f_{g_{ij}}(x)=\lambda _{ij}\exp (-\lambda _{ij}x)u(x)$ $\left( g_{ij}\sim \mathcal{E }(\lambda _{ij}) \right)$, where $u(x)$ is the Heaviside (unit) step function, i.e., $u(x)=1$ for $x\ge 0$ and $u(x)=0$ for $x<0$. In this paper, we assume that all relays are located close to one another (optimal clustering) [17], which implies $\lambda _{sr_{k}}=\lambda _{sr}$, $\lambda _{r_{k}d}=\lambda _{rd},\, \lambda _{cr_{k}}=\lambda _{cr}$, and $\lambda _{r_{k}p}=\lambda _{rp},\, k\in \{1,2,\ldots ,K\}$.

Fig. 1

The system model of the underlay cognitive opportunistic multi-relay network

3 Outage Performance Analysis

3.1 Outage Probability

Under both the maximum transmit power constraint $Q$ and maximum tolerable interference power constraint $I_p$, the allowed maximum instantaneous transmit powers of the source $(s)$ and the $k^{th}$ relay $(r_{k}),\, k\in \{1,2,\ldots ,K\}$, are $P_{s}=\min \{I_{p}/g_{sp},Q\}$ and $P_{r_{k}}=\min \{I_{p}/g_{r_{k}p},Q\}$, respectively. Taking the interference from PU into account, the SINR of the link from transmitter node $i (s, r_{1}, \ldots , r_{K})$ and receiver node $j (r_{1}, \ldots , r_{K}, d)$ is given by

$$\begin{aligned} \gamma _{ij}=\frac{P_i g_{ij}}{N_0+P_c g_{cj}}=\frac{\min \{\gamma /g_{ip}, \gamma _{Q}\}\cdot g_{ij}}{\gamma _I\left( g_{cj}+\frac{1}{\gamma _I}\right) }, \end{aligned}$$

(1)

where $P_{c}$ is the transmit power of PU transmitter; $N_{0}$ is the variance of Gaussian noise at receiver node $j$; $\gamma _{Q}=Q/N_0$; $\gamma =I_ {p}/N_ {0}$ and $\gamma _{I}=P_c/N_0$ are defined as the average signal-to-noise ratio (SNR) and average interference-to-noise ratio (INR), respectively.

From (1), it is noted that $\gamma _{sd},\, \gamma _{s r_k}, \,\gamma _{r_{k}d}$, and $\gamma _{r_{m}d}\, (k\ne m, k, m\in \{1,2,\ldots , K\})$ are dependent because of the common interference power constraint as shown in [8] and the interference from PU.

Define $\gamma _{\text{ th }}$ to be the outage threshold SINR for SU. In the first phase of relaying transmission, the successful decoding set, denoted as $\mathcal{D }_{l}$, is defined as $\mathcal{D }_{l}=\{r_{k}: \gamma _{sr_{k}} \ge \gamma _{\text{ th }}, k\in \{1,2,\ldots ,K\}\}$, where the cardinality of $\mathcal{D }_{l}$ is $l$. The probability of $\mathcal{D }_{l}$ is given by [15]

$$\begin{aligned} \Pr [\mathcal{D }_{l}] = \Pr \left[ \bigcap \limits _{{r_k} \in {\mathcal{D }_{l}}} {{\gamma _{s{r_k}}} \ge {\gamma _{\text{ th }}},} \bigcap \limits _{{r_k} \notin {\mathcal{D }_{l}}} {{\gamma _{s{r_k}}} < {\gamma _{\text{ th }}}} \right] . \end{aligned}$$

(2)

In the second phase of relaying transmission, the relay which has the maximum $\gamma _{r_{k}d}$, denoted as $r_b$, is selected from $\mathcal{D }_{l}$ to forward the message, i.e., $r_b = \arg \mathop {\max \limits _{{r_k} \in \mathcal{D }_{l}}} {\gamma _{{r_k}d}}$. According to the total probability law, the OP is given by [7, 15]

$$\begin{aligned} P_{\text{ out }} = \sum \limits _{l = 0}^K \underbrace{\Pr [{\gamma _{sd}} + {\gamma _{{r_b}d}} < {\gamma _{\text{ th }}},{\mathcal{D }_{l}}]}_{I_{1}(l)}, \end{aligned}$$

(3)

where $I_{1}(l)$ denotes the outage probability given the cardinality of $\mathcal{D }_{l}$.

For notational convenience, let $X=g_{cd}+1/\gamma _I,\, Y=g_{sp}, \,Z_k=g_{sr_k}/(g_{cr_k}+1/\gamma _I),\, V=\mathop {\max }\limits _{{r_k} \in {\mathcal{D }_{l}}} \min \{\gamma /g_{r_kp}, \gamma _{Q}\}\cdot g_{r_kd}$. Then, $\gamma _{sr_{k}}=\min \{\gamma /Y, \gamma _{Q}\}Z_k/\gamma _I,\, \gamma _{sd}=\min \{\gamma /Y, \gamma _{Q}\}\cdot g_{sd}/(\gamma _I X)$, and $\gamma _{r_{b}d}=V/(\gamma _I X)$. The PDF of $X$ is $f_{X}(x)=\lambda _{cd}\exp (-\lambda _{cd}(x-1/\gamma _I))u(x-1/\gamma _I)$. According to [7, 8], the cumulative distribution function (CDF) of $Z_{k}$ and $V$ are

$$\begin{aligned} F_{Z_{k}}(z)&= 1-\frac{\lambda _{cr}}{\lambda _{sr}z+\lambda _{cr}} e^{-\frac{\lambda _{sr} z}{\gamma _I}},\end{aligned}$$

(4)

$$\begin{aligned} F_V(v)&= \left[ 1-e^{-\frac{\lambda _{rd}v}{\gamma _{Q}}}+ \frac{v}{\frac{\lambda _{rp}\gamma }{\lambda _{rd}}+v} e^{-\frac{\lambda _{rp} \gamma +\lambda _{rd} v }{\gamma _{Q}}}\right] ^l \nonumber \\&= \sum \limits _{i=0}^{l}\sum \limits _{j=0}^{i}\sum \limits _{m=0}^{j} \left( {\begin{array}{c}l\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \left( {\begin{array}{c}j\\ m\end{array}}\right) (-1)^{i+j+m}\left( \frac{\lambda _{rp} \gamma }{\lambda _{rd}}\right) ^{m} \nonumber \\&\cdot \frac{1}{(v+\lambda _{rp} \gamma /\lambda _{rd})^m} e^{- \frac{\lambda _{rp} \gamma j+\lambda _{rd} v i}{\gamma _{Q}}}. \end{aligned}$$

(5)

Substituting (2) into (3), $I_{1}(l)$ is rewritten as

$$\begin{aligned} I_{1}(l)&= \text{ Pr }\Bigg [\frac{\min \{\gamma /Y, \gamma _{Q}\} g_{sd}}{\gamma _I X} + \frac{V}{\gamma _I X} < \gamma _{\text{ th }}, \bigcap \limits _{{r_k} \in {\mathcal{D }_{l}}} {\left( {\frac{\min \{\gamma /Y, \gamma _{Q}\}Z_k}{\gamma _I}} \ge \gamma _{\text{ th }}\right) ,} \nonumber \\&\bigcap \limits _{{r_k} \notin {\mathcal{D }_{l}}} {\left( {\frac{\min \{\gamma /Y, \gamma _{Q}\}Z_p}{\gamma _I}} < {\gamma _{\text{ th }}}\right) }\Bigg ]. \end{aligned}$$

(6)

Now, relaying on the relation between $\gamma _{Q}$ and $\gamma /Y$, (6) can further be written as

$$\begin{aligned} I_{1}(l)=\left( {\begin{array}{c}K\\ l\end{array}}\right) \left( I_2\cdot I_3+I_4 \right) , \end{aligned}$$

(7)

where

$$\begin{aligned} I_2&= \int \limits _{\frac{1}{\gamma _I}}^{\infty } \int \limits _{0}^{\gamma _{\text{ th }}\gamma _{I}x}\!\!\text{ Pr }\left[ \frac{\gamma _{Q} g_{sd}}{\gamma _I x}\!+\!\frac{v}{\gamma _I x}\!<\! \gamma _{\text{ th }}\right] \!f_V(v)f_X(x)dvdx, \end{aligned}$$

(8)

$$\begin{aligned} I_3&= \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma _{Q} Z_k}{\gamma _I} \!\ge \! \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma _{Q} Z_k}{\gamma _I} \!<\! \gamma _{\text{ th }} \right] \text{ Pr }\left[ Y\!<\!\frac{\gamma }{\gamma _{Q}}\right] , \end{aligned}$$

(9)

$$\begin{aligned} I_4&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{\frac{1}{\gamma _I}}^{\infty }\int \limits _{0}^{\gamma _{\text{ th }}\!\gamma _{I}x} \text{ Pr }\left[ \frac{\gamma g_{sd}}{\gamma _I y x}+\frac{v}{\gamma _I x}< \gamma _{\text{ th }}\right] f_V(v)f_X(x)dvdx \nonumber \\&\cdot \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(10)

To facilitate the subsequent analysis, the following lemmas are presented.

Lemma 1

Let $m \in \mathbb N ,\, u, p \in \mathbb R$, and $a > b$. The integral $\mathcal{J }(a,b,u,m,p)=\int _{a}^{b} e^{-p x}/{(x+u)^m} dx$ is

$$\begin{aligned} p^{m-1} e^{pu} \left[ \varGamma (1-m, (a+u)p)-\varGamma (1-m, (b+u)p) \right] \end{aligned}$$

for $p>0$;

$$\begin{aligned}&\sum \limits _{k=0}^{m-1} \frac{(-p)^{k-1} \varGamma (m-k)}{\varGamma (m)} \left[ \frac{e^{-p a}}{(a+u)^{m-k}}-\frac{e^{-p b}}{(b+u)^{m-k}}\right] \\&\quad +\frac{(-p)^{m-1} e^{pu}}{\varGamma (m)} \left[ \text{ Ei }(-p(b+u))-\text{ Ei }(-p(a+u))\right] \end{aligned}$$

for $p\le 0, m\ne 0$;

$$\begin{aligned} b-a \end{aligned}$$

for $p=0, m=0$;

$$\begin{aligned} \left( e^{-pa}-e^{-pb} \right) / p \end{aligned}$$

for $p<0, m=0$,

where $\text{ Ei }(\bullet )$ is the exponential integral function [18, Eq. (8.211)] and $\varGamma (\bullet ,\bullet )$ is the upper incomplete gamma function [18, Eq. (8.350.2)].

Proof

When $p>0$, replacing $(x+u)p$ with $t$ and following [18, Eq. (8.350.2)], the final result is obtained. When $p\le 0, m\ne 0$, replacing $x+u$ with $t$ and following [18, Eq. (2.324.2)], the final result is obtained. $\square$

Lemma 2

Let $m \in \{0,1\},\, n \in \mathbb N$. The integral $\mathcal{L }(a,u,w,m,n,p)=\int _{a}^{\infty } \frac{e^{-p x}}{(x+u)^m (y+w)^n} dx$ is

$$\begin{aligned} \frac{\mathcal{J }(a,\infty ,u,1,p)}{(w-u)^n}+\sum \limits _{q=1}^{n}\frac{(-1)^{n-q}}{(u-w)^{n-q+1}} \mathcal{J }(a,\infty ,w,q,p) \end{aligned}$$

for $u\ne w, m=1, n\ne 0$;

$$\begin{aligned} \mathcal{J }(a,\infty ,w,n,p) \end{aligned}$$

for $u\ne w, m=0$;

$$\begin{aligned} \mathcal{J }(a,\infty ,u,m+n,p) \end{aligned}$$

for the others.

Proof

By employing the partial fraction expansion method and Lemma 1, the final result is derived. $\square$

Lemma 3

Let $u \in \mathbb R$, and $a > b$. The integral $\mathcal K (a,b,p)=\int _{a}^{b} e^{-p x} f_V(x) dx$ is

$$\begin{aligned}&e^{-pb}F_V(b)-e^{-pa}F_V(a)+\sum \limits _{i=0}^{l}\sum \limits _{j=0}^{i}\sum \limits _{m=0}^{j}\left( {\begin{array}{c}l\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \left( {\begin{array}{c}j\\ m\end{array}}\right) p\nonumber \\&\cdot (-1)^{i+j+m} \left( \frac{\lambda _{rp} \gamma }{\lambda _{rd}}\right) ^{m} e^{-\frac{\lambda _{rp}\gamma j}{\gamma _Q}} \nonumber \mathcal{J }\left( a,b,\frac{\lambda _{rp} \gamma }{\lambda _{rd}},m,\frac{\lambda _{rd}i}{\gamma _Q}+p\right) . \end{aligned}$$

Proof

By employing the integration-by-parts method and Lemma 1, the final result can be obtained. $\square$

By interchanging the order of integration, $I_2$ in (8) can be expressed as

$$\begin{aligned} I_2&= \int \limits _{0}^{\gamma _{\text{ th }}}\int \limits _{\frac{1}{\gamma _{I}}}^{\infty }\text{ Pr }\left[ g_{sd}< \frac{\gamma _{\text{ th }}\gamma _{I}x-v}{\gamma _{Q}}\right] f_X(x)dxf_V(v)dv \nonumber \\&\quad +\int \limits _{\gamma _{\text{ th }}}^{\infty }\int \limits _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty }\text{ Pr }\left[ g_{sd}< \frac{\gamma _{\text{ th }}\gamma _{I}x-v}{\gamma _{Q}}\right] f_X(x)dxf_V(v)dv \nonumber \\&= F_V(\gamma _{\text{ th }})-\frac{a_1}{1+a_1} \int \limits _{0}^{\gamma _{\text{ th }}}\exp \left( -\frac{\lambda _{sd}(\gamma _{\text{ th }}-v)}{\gamma _Q}\right) dF_{V}(v) \nonumber \\&\quad +\frac{1}{1+a_1} \int \limits _{\gamma _{\text{ th }}}^{\infty }\exp \left( -\frac{\lambda _{cd}(v-\gamma _{\text{ th }})}{\gamma _{\text{ th }} \gamma _I}\right) dF_{V}(v) \nonumber \\&= F_V(\gamma _{\text{ th }})-\frac{a_1}{1+a_1} \exp \left( -\frac{\lambda _{sd}\gamma _{\text{ th }}}{\gamma _Q }\right) \mathcal K \left( 0,\gamma _{\text{ th }},-\frac{\lambda _{sd}}{\gamma _Q}\right) \nonumber \\&\quad +\frac{1}{1+a_1} \exp \left( \frac{\lambda _{cd}}{\gamma _I} \right) \mathcal K \left( \gamma _{\text{ th }},\infty , \frac{\lambda _{cd}}{\gamma _{\text{ th }}\gamma _I} \right) , \end{aligned}$$

(11)

where $a_1=\frac{\lambda _{cd}\gamma _{Q}}{\lambda _{rd}\gamma _{\text{ th }} \gamma _{I}}$ and the last equality stems from Lemma 3.

Substituting (4) into $I_3,\, I_3$ is expressed as

$$\begin{aligned} I_3=\left( \frac{b_1 e^{-\frac{\lambda _{sr}\gamma _{\text{ th }}}{\gamma _Q}}}{1+b_1}\right) ^l \left( 1-\frac{b_1 e^{-\frac{\lambda _{sr}\gamma _{\text{ th }}}{\gamma _Q}}}{1+b_1}\right) ^{K-l} \left( 1-e^{-\frac{\lambda _{sp}\gamma }{\gamma _{Q}}}\right) , \end{aligned}$$

(12)

where $b_1=\frac{\lambda _{cr}\gamma _{Q}}{\lambda _{sr} \gamma _{\text{ th }}\gamma _{I}}$.

Define the VOX plane as the plane spanned by the $X$ and the $V$ axes. The integral region of $I_4$ on the VOX plane is ABDE, where ABDE denotes the region bounded by the lines $x=1/\gamma _I,\, v=0$, and $v=\gamma _{\text{ th }}\gamma _I x$, as shown in Fig. 2. It is noted that the integral region ABDE can be divided into the regions ABF and FBDE. By interchanging the order of integration, $I_4$ can be expressed as

$$\begin{aligned} I_4&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \left\{ \int \limits _{\gamma _{\text{ th }}}^{\infty } \int \limits _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\!\frac{(\gamma _{I}\gamma _{\text{ th }} x-v)y}{\gamma }\right] \!f_X(x)dx f_V(v)dv \right. \nonumber \\&\left. \quad + \int \limits _{0}^{\gamma _{\text{ th }}}\int \limits _{\frac{1}{\gamma _I}}^{\infty } \text{ Pr }\left[ g_{sd}<\!\frac{(\gamma _{I} \gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx f_V(v)dv \right\} \nonumber \\&\quad \cdot \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(13)

Unfortunately, there is no closed-form expression for $I_4$ due to the correlation between $Y$ and $V$. However, by slightly enlarging and shrinking the integration regions of $I_4$, the following results can be obtained.

Fig. 2

The integration region of $I_4$

Lemma 4

By slightly enlarging the integration region of $I_4$ from $\varOmega _1=\{\gamma /\gamma _Q \le y < \infty , ABDE\}$ to $\varOmega _2=\{\gamma /\gamma _Q \le y < \infty , AOE\}$ and shrinking the integration region of $I_4$ to $\varOmega _3=\{\gamma /\gamma _Q \le y < \infty , ABCDE\}$ as shown in Fig. 2, the upper and lower bounds of $I_4$ are obtained as

$$\begin{aligned} I_4^{\text{ UB }}&= \sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n} \lambda _{sp}a_{2}^{n} b_{2}^{k+l} \exp \left( \frac{\lambda _{cd}}{\gamma _I} \right) \nonumber \\&\quad \cdot \mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma }+ \lambda _{sp}\right) \mathcal K \left( 0,\infty , \frac{\lambda _{cd}}{\gamma _{\text{ th }}\gamma _I}\right) , \end{aligned}$$

(14)

$$\begin{aligned} I_4^{\text{ LB }}&= \sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n} \lambda _{sp}a_{2}^{n} b_{2}^{k+l} \nonumber \\&\quad \cdot \Bigg [ \exp \left( \frac{\lambda _{cd}}{\gamma _I} \right) \mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma } +\lambda _{sp}\right) \mathcal K \left( \gamma _{\text{ th }},\infty , \frac{\lambda _{cd}}{\gamma _{\text{ th }}\gamma _I} \right) \nonumber \\&\quad +\mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sd}\gamma _{\text{ th }}n}{\gamma } +\frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma } +\lambda _{sp}\right) \mathcal K \left( 0,\gamma _{\text{ th }}, \frac{\lambda _{cd}}{\gamma _{\text{ th }}\gamma _I}\right) \Bigg ], \nonumber \\ \end{aligned}$$

(15)

where $a_2=\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{th}\gamma _{I}}$ and $b_2=\frac{\lambda _{cr}\gamma }{\lambda _{sr}\gamma _{th}\gamma _{I}}$.

Proof

See Appendix 1. $\square$

Now, combining (3), (11), (12), (14), and (15), the upper and lower bounds on the OP for underlay cognitive opportunistic multi-relay networks are

$$\begin{aligned} P_{\text{ out }}^{\text{ UB }}&\triangleq \sum _{l=0}^{K}\left( {\begin{array}{c}K\\ l\end{array}}\right) \left( I_2 \cdot I_3+I_4^{\text{ UB }}\right) , \end{aligned}$$

(16)

$$\begin{aligned} P_{\text{ out }}^{\text{ LB }}&\triangleq \sum _{l=0}^{K}\left( {\begin{array}{c}K\\ l\end{array}}\right) \left( I_2 \cdot I_3+I_4^{\text{ LB }}\right) . \end{aligned}$$

(17)

To reveal how the interference caused by PU impacts the performance of SU, we investigate the asymptotic behavior of OP.

Theorem 1

The relationship between the lower bound OP and the upper bound OP at high INR region is

$$\begin{aligned} \lim _{\gamma _I \rightarrow \infty } \left( P_{\text{ out }}^{\text{ UB }} -P_{\text{ out }}^{\text{ LB }}\right) =0 \end{aligned}$$

(18)

when $\gamma$ and $\gamma _{Q}$ are fixed or $\rho =\gamma /\gamma _{I}$ and $\rho _Q=\gamma _{Q}/\gamma _I$ are fixed.

Proof

See Appendix 2. $\square$

Theorem 1 states that the lower and upper bounds of OP converge to the exact OP at high INR region. This is because that the gap between the lower bound and the upper bound is determined by the area of $\varOmega _2-\varOmega _3=\{\gamma /\gamma _Q \le y < \infty , \text{ BODC }\}$. It is noted that the area of $\varOmega _2-\varOmega _3$ decreases with the increase of $\gamma _I$, which implies the gap tends to 0 with the increase of $\gamma _I$.

3.2 Approximate Outage Probability at High SNR

In this subsection, a simple expression of $P_{\text{ out }}$ is derived at high SNR.

Let $\gamma _{Q}=\mu \gamma$ [10], where $\mu$ is a constant. When $\gamma \rightarrow \infty$, in (11), using the Taylor expansion,

$$\begin{aligned} I_2 \approx \frac{a_2}{\mu }\left( \frac{\lambda _{rd} \gamma _{\text{ th }}\gamma _{I}}{\lambda _{rp} \lambda _{cd}\gamma }\right) ^l \left( \frac{\lambda _{rp}}{\mu }+e^{-\frac{\lambda _{rp}}{\mu }}\right) ^{l}\Bigg [ \frac{1}{l+1} \left( \frac{\lambda _{cd}}{\gamma _I}\right) ^{l+1} +e^{\frac{\lambda _{cd}}{\gamma _I}}\varGamma \left( l+1, \frac{\lambda _{cd}}{\gamma _I}\right) \Bigg ]. \end{aligned}$$

(19)

When $\gamma \rightarrow \infty$, in (12),

$$\begin{aligned} I_3 \approx \frac{1}{b_{1}^{K-l}} \left( 1+\frac{\lambda _{cr}}{\gamma _I}\right) ^{K-l}\left( 1-e^{-\frac{\lambda _{sp}\gamma }{\gamma _{Q}}}\right) . \end{aligned}$$

(20)

After some mathematical manipulation, when $\gamma \rightarrow \infty$, OP is approximated as

$$\begin{aligned} P_{\text{ out }}^{\tau }&\approx \sum \limits _{l=0}^{K}\left( {\begin{array}{c}K\\ l\end{array}}\right) \left( 1+\frac{\lambda _{cr}}{\gamma _I}\right) ^{K-l} \left( \frac{\lambda _{rp}}{\mu }+e^{-\frac{\lambda _{rp}}{\mu }}\right) ^{l} \left( \frac{b_3}{c_3}\right) ^{l} \nonumber \\&\quad \cdot \Bigg \{ \delta (\tau ) +\Bigg [ \frac{1}{l+1} \left( \frac{\lambda _{cd}}{\gamma _I}\right) ^{l+1} +e^{\frac{\lambda _{cd}}{\gamma _I}}\varGamma \left( l+1,\frac{\lambda _{cd}}{\gamma _I}\right) \Bigg ] \nonumber \\&\quad \cdot \left( \frac{\lambda _{sp}}{\mu }\right) ^{K-l+1}\left( 1-e^{-\frac{\lambda _{sp}}{\mu }}\right) \Bigg \}\frac{1}{a_{3} b_{3}^{K}}, \end{aligned}$$

(21)

where $\tau \in \{\text{ UB },\text{ LB } \}$, $a_3=\frac{\lambda _{sp}\lambda _{cd}\gamma }{\lambda _{sd} \gamma _{\text{ th }}\gamma _{I}}$ and $b_3=\frac{\lambda _{sp}\lambda _{cr}\gamma }{\lambda _{sr} \gamma _{\text{ th }}\gamma _{I}}$, $c_3=\frac{\lambda _{rp}\lambda _{cd}\gamma }{\lambda _{rd} \gamma _{\text{ th }}\gamma _{I}}$, $\delta (\text{ UB })=\varGamma (l+1)\varGamma (K-l+2, \frac{\lambda _{sp}}{\mu })e^{\frac{\lambda _{cd}}{\gamma _I}}$, $\delta (\text{ LB })=\varGamma (l+1,\frac{\lambda _{cd}}{\gamma _I})\varGamma (K-l+2, \frac{\lambda _{sp}}{\mu })e^{\frac{\lambda _{cd}}{\gamma _I}} -(\frac{\lambda _{cd}}{\gamma _I})^{l} \varGamma (K-l+2, \frac{\lambda _{sp}}{\mu }) +\varGamma (K-l+2, \frac{\lambda _{sp}}{\mu }) (1+\frac{\lambda _{cd}}{\gamma _I}) [(\frac{\lambda _{cd}}{\gamma _I})^{l}e^{-\frac{\lambda _{cd}}{\gamma _I}}+\gamma (l+1,\frac{\lambda _{cd}}{\gamma _I})]$, and $\gamma (\bullet ,\bullet )$ is the lower incomplete gamma function [18, Eq. (8.350.1)]. (21) implies the full diversity order of $K+1$ is achieved.

4 Simulation Results

In this section, we present Monte Carlo simulation results to verify our analysis. The simulation tool is MATLAB. In the simulations, as shown in Fig. 3, a two dimensional network topology is assumed where the primary transmitter $(c)$, the primary receiver $(p)$, the secondary source $(s)$, the secondary relays, and the secondary destination $(d)$ are located at the coordinates $(0.7,0.7),\, (0.5,0.5),\, (0,0),\, (0.5,0)$, and $(1,0)$, respectively [12]. The fading variances are assigned by adopting a path loss model of the form $\lambda _{ij}=d_{ij}^{-4}$ where $d_{ij}$ is the distance between the transmitter node $i \,(c,\, s,\, r_{1}, \ldots ,\, r_{K})$ and receiver node $j (p, r_{1}, \ldots , r_{K}, d)$. We assume that all the relays are located close to one another (optimal clustering) [17]. The distance between any two relays is negligible compared with that between the relays and the nodes $c,\, p,\, s$, and $d$. Thus, we have $\lambda _{sr_{k}}=\lambda _{sr},\, \lambda _{r_{k}d}=\lambda _{rd},\, \lambda _{cr_{k}}=\lambda _{cr}$, and $\lambda _{r_{k}p}=\lambda _{rp}, \,k\in \{1,2,\ldots ,K\}$. We also assume that the PU always transmits signals and the interference caused by the PU is always exist [12, 13, 19]. In all cases, $\gamma _{\text{ th }}=3$ and the OP is averaged over $10^7$ different channel realizations. The simulation steps are provided in detail in Algorithm 1.

Fig. 3

The positions of primary transmitter $(c)$, primary receiver $(p)$, secondary source $(s)$, secondary relays, and secondary destination $(d)$ in the simulations

Algorithm 1: Simulation method to obtain the secondary OP of cognitive multi-relay network
(1) Initialization
a) Initialize the secondary OP count, $count=0$.
b) Initialize the channel realizations, $l=0$.
(2) Until $l\le 10^7$, repeat
a) Generate the Rayleigh fading channels according to $h_{ij}\sim \mathcal{CN }(0, 1/\lambda _{ij})$.
b) Obtain the successful decoding set $\mathcal{D }_l$ by judging whether the $k^{th}$ relay satisfies $\gamma _{sr_{k}} \ge \gamma _{\text{ th }}$.
c) Select the best relay in $\mathcal{D }_l$ based on $r_b = \arg \mathop {\max \limits _{{r_k} \in \mathcal{D }_{l}}} {\gamma _{{r_k}d}}$.
d) If $\gamma _{{sd}}+\gamma _{{r_b}d}<\gamma _{\text{ th }},\, count=count+1$.
It is noted that in the computation of $\gamma _{sr_{k}},\, \gamma _{{r_k}d}$ and $\gamma _{{sd}}$, the interference from PU is
included through (1).
e) $l=l+1$.
(3) Obtain the secondary OP, $P_{\text{ out }}=count/10^7$.

In Fig. 4, we present the analytical and simulated OP versus average SNR for different values of $K$ and $\gamma _{I}$. From Fig. 4, it is observed that the OP improves with the increase of $K$ when the average INR $\gamma _{I}$ is fixed. It is also found that only when $\gamma _I<-8$ dB or $\gamma <10$ dB, the proposed upper and lower bounds have noticeable difference with the simulation results.

Fig. 4

Analytical and simulated OP versus average SNR for different values of $K$ and $\gamma _{I}$ where $\mu =\gamma _{Q}/\gamma =0$ dB. Solid curves with marker correspond to upper bound OP (16). Solid curves correspond to lower bound OP (17). Dotted curves correspond to approximate upper bound OP at high SNR (21). The dashed curves correspond to approximate lower bound OP at high SNR (21)

In Fig. 4, OP is presented where the PU’s interference $\gamma _{I}$ is fixed. Let $\rho =\gamma /\gamma _{I}$ and $\rho _{Q}=\gamma _Q /\gamma _{I}$. When $\rho$ and $\rho _{Q}$ are fixed, i.e., the signal-to-interference ratio (SIR) is fixed, we present the analytical and simulated OP versus average INR for different values of $K$ in Fig. 5. From Fig. 5, it is found that an outage floor at high INR occurs in contrast to the results in [7–11]. This is because the interference from PU is considered. It is also observed that the gap between the upper bound and the simulation values decreases with the increase of $\gamma _I$. The reason is that the increment area from enlarging the integration region of $I_4$ decreases with the increase of $\gamma _I$. It is also observed that the gap between the lower and upper bounds OP is approximately equal to 0 when $\gamma _I > 0$ dB, which implies the lower and upper OP can be regard as the exact OP as long as $\gamma _I$ is moderately large. When $\rho _Q$ and $K$ is fixed, the OP improves with the increase of $\rho$. This is because that in (1), $\min \{\rho /g_{ip}, \rho _{Q}\}\approx \rho /g_{ip}$ for small $\lambda _{ip},\, i \in \{s, r_1, \ldots , r_K\}$, which implies the OP is dominated by $\rho$.

Fig. 5

Analytical and simulated OP versus average INR when $\rho =\gamma /\gamma _{I}$ and $\rho _Q=\gamma _{Q} /\gamma _I$ are fixed. Solid curves with marker correspond to upper bound OP (16). Solid curves correspond to lower bound OP (17)

5 Conclusions

In this paper, we theoretically derive the upper and lower bounds of OP for the underlay cognitive opportunistic multi-relay networks considering the interferences from primary transmitter to secondary receiver and from the secondary transmitter to the primary receiver, the maximum transmit power constraint of SU, and the dependence introduced due to interference power constraint. The upper and lower bounds of OP are derived by enlarging and shrinking the integration regions. It is found that the gap between the upper and lower bounds tends to 0 when the INR is large. It is also found that because the interference from primary transmitter to secondary receiver is considered, an outage floor at high SNR occurs when the INR increases proportionally with SNR.

Appendices

Appendix 1: Proof of Lemma 4

Note that $I_4$ in (10) can be rewritten as

$$\begin{aligned} I_4=\int \!\!\int \!\!\int _{\varOmega _1}\psi (x,y,z)dxdydz \end{aligned}$$

(22)

where

$$\begin{aligned} \psi (x,y,z)&= \text{ Pr }\left[ \frac{\gamma g_{sd}}{\gamma _I y x}+\frac{v}{\gamma _I x}< \gamma _{\text{ th }}\right] f_V(v)f_X(x)f_Y(y) \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \nonumber \\&\prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] \end{aligned}$$

(23)

and $\varOmega _1=\{\gamma /\gamma _Q \le y < \infty , \text{ ABDE }\}$. It is noted that $0 \le \psi (x,y,z)<\infty$ and $\psi (x,y,z)$ is a continuous function. According to additivity of integration on intervals [20, Theorem 6.12], the integral $\int \!\!\int \!\!\int _{\varOmega _1}\psi (x,y,z)dxdydz$ increases with the increase of the area of $\varOmega _1$ when $\varOmega _1\in \varOmega =\{ 0 \le x,y,z<\infty \}$. Thus, by enlarging the integration region from $\varOmega _1$ to $\varOmega _2=\{\gamma /\gamma _Q \le y < \infty , \text{ AOE }\}$ shown in Fig. 2 and interchanging the order of integration, $I_4$ is upper bounded by

$$\begin{aligned} I_4^{\text{ UB }}&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{0}^{\infty }\underbrace{\int \limits _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx}_{\varphi } \nonumber \\&\quad \cdot f_V(v)dv \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(24)

Integrating with respect to $x,\, \varphi$ is expressed as

$$\begin{aligned} \varphi =\left[ 1-\frac{1}{\frac{\lambda _{sd}\gamma _{\text{ th }}\gamma _{I}y}{\lambda _{cd}\gamma }+1}\right] \exp \left( -\frac{\lambda _{cd}(v-\gamma _{\text{ th }})}{\gamma _{\text{ th }}\gamma _{I}}\right) \end{aligned}$$

(25)

where the correlation between $Y$ and $V$ is decoupled due to the integration regions enlarging. Substituting (4) and (25) into (24), $I_4$ is expressed as

$$\begin{aligned} I_4^{\text{ UB }}=J_1 \cdot J_2, \end{aligned}$$

(26)

where

$$\begin{aligned} J_1&= \int \limits _{0}^{\infty }\exp \left( -\frac{\lambda _{cd}(v-\gamma _{\text{ th }})}{\gamma _{\text{ th }} \gamma _I}\right) dF_{V}(v), \end{aligned}$$

(27)

$$\begin{aligned} J_2&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty }\frac{y}{y+a_2} \bigg ( 1-\frac{b_2}{y+b_2}e^{-\frac{\lambda _{sr}\gamma _{\text{ th }} y}{\gamma }}\bigg )^{K-l} \bigg (\frac{b_2}{y+b_2}e^{-\frac{\lambda _{sr}\gamma _{\text{ th }} y}{\gamma }}\bigg )^l \lambda _{sp}e^{-\lambda _{sp}y}dy \end{aligned}$$

(28)

in which $a_2=\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{th}\gamma _{I}}$ and $b_2=\frac{\lambda _{cr}\gamma }{\lambda _{sr}\gamma _{th}\gamma _{I}}$. Using Lemma 3, $J_1$ can be expressed as

$$\begin{aligned} J_1=\exp \left( \lambda _{cd}/\gamma _I \right) \mathcal K (0,\infty , \lambda _{cd}/(\gamma _{\text{ th }}\gamma _I) ). \end{aligned}$$

(29)

Using the binomial theorem, $J_2$ is given as

$$\begin{aligned} J_2=\int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n} \left( \frac{a_2}{y+a_2}\right) ^n \left( \frac{b_2}{y+b_2}e^{-\frac{\lambda _{sr}\gamma _{\text{ th }}y }{\gamma }}\right) ^{k+l}\lambda _{sp}e^{-\lambda _{sp}y}dy.\nonumber \\ \end{aligned}$$

(30)

By invoking Lemma 2, $J_2$ can be obtained as

$$\begin{aligned} J_2&=\sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n}\lambda _{sp}a_{2}^{n} b_{2}^{k+l} \mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma } +\lambda _{sp}\right) . \end{aligned}$$

(31)

Substituting (29) and (31) into (26), the upper bound of $I_4$ is obtained.

Furthermore, by shrinking the integration region of $I_4$ to $\varOmega _3=\{\gamma /\gamma _Q \le y < \infty , \text{ ABCDE }\}$, $I_4$ is lower bounded by

$$\begin{aligned} I_4^{\text{ LB }}=O_1+O_2, \end{aligned}$$

(32)

where

$$\begin{aligned} O_1=&\int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{0}^{\gamma _{\text{ th }}}\int \limits _{\frac{v+\gamma _{\text{ th }}}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx f_V(v)dv \nonumber \\&\cdot \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy, \end{aligned}$$

(33)

$$\begin{aligned} O_2=&\int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{\gamma _{\text{ th }}}^{\infty }\int \limits _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\infty } \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx f_V(v)dv \nonumber \\&\cdot \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(34)

Following the derivation of $I_4^{\text{ UB }}$, we obtain $O_1=O_3 \cdot O_4$ and $O_2=O_5 \cdot J_2$, where

$$\begin{aligned} O_3&= \mathcal K \left( 0,\gamma _{\text{ th }}, \lambda _{cd}/(\gamma _{\text{ th }}\gamma _I) \right) , \end{aligned}$$

(35)

$$\begin{aligned} O_4&= \sum \limits _{k=0}^{K-l}\sum \limits _{n=0}^{1}\left( {\begin{array}{c}K-l\\ k\end{array}}\right) \left( {\begin{array}{c}1\\ n\end{array}}\right) (-1)^{k+n}\lambda _{sp}a_{2}^{n} b_{2}^{k+l} \nonumber \\&\quad \cdot \mathcal{L }\left( \frac{\gamma }{\gamma _{Q}},a_2,b_2,n,k+l, \frac{\lambda _{sd}\gamma _{\text{ th }}n}{\gamma } +\frac{\lambda _{sr}\gamma _{\text{ th }}(k+l)}{\gamma } +\lambda _{sp}\right) ,\end{aligned}$$

(36)

$$\begin{aligned} O_5&= \exp \left( \lambda _{cd}/\gamma _I \right) \mathcal K (\gamma _{\text{ th }},\infty , \lambda _{cd}/(\gamma _{\text{ th }}\gamma _I) ). \end{aligned}$$

(37)

Substituting (35)-(37) into (32), the lower bound of $I_4$ is obtained.

Appendix 2: Proof of Theorem 1

From (16) and (17), the outage gap between the lower and upper bounds is formulated as

$$\begin{aligned} P_{\text{ out }}^{\text{ UB }}-P_{\text{ out }}^{\text{ LB }}&= \sum _{l=0}^K \left( {\begin{array}{c}K\\ l\end{array}}\right) \left( I_4^{\text{ UB }}-I_4^{\text{ LB }}\right) \nonumber \\&= \sum _{l=0}^K \left( {\begin{array}{c}K\\ l\end{array}}\right) \underbrace{\int \!\!\int \!\!\int _{\varOmega _2-\varOmega _3}\psi (x,y,z)dxdydz}_{\varDelta I_4}. \end{aligned}$$

(38)

It is noted that $\varOmega _2-\varOmega _3=\{\gamma /\gamma _Q \le y < \infty , \text{ BODC }\}$ and interchanging the order of integration, $\varDelta I_4$ can be expressed as

$$\begin{aligned} \varDelta I_4&= \int \limits _{\frac{\gamma }{\gamma _{Q}}}^{\infty } \int \limits _{0}^{\gamma _{\text{ th }}}\underbrace{\int _{\frac{v}{\gamma _{\text{ th }}\gamma _{I}}}^{\frac{v+\gamma _{\text{ th }}}{\gamma _{\text{ th }}\gamma _{I}}} \text{ Pr }\left[ g_{sd}<\frac{(\gamma _{I}\gamma _{\text{ th }}x-v)y}{\gamma }\right] f_X(x)dx}_{\chi } \nonumber \\&\quad \cdot f_V(v)dv \prod \limits _{{r_k} \in {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} \ge \gamma _{\text{ th }}\right] \prod \limits _{{r_k} \notin {\mathcal{D }_{l}}}\text{ Pr }\left[ \frac{\gamma Z_k}{\gamma _I y} < \gamma _{\text{ th }} \right] f_Y(y)dy. \end{aligned}$$

(39)

Integrating with respect to $x,\, \chi$ is expressed as

$$\begin{aligned} \chi =\frac{\lambda _{sd}\gamma _{\text{ th }}\gamma _I y}{\lambda _{sd}\gamma _{\text{ th }}\gamma _I y+\lambda _{cd}\gamma }e^{-\frac{\lambda _{cd}(\gamma _{\text{ th }}-v)}{\gamma _{\text{ th }}\gamma _I}}- e^{-\frac{\lambda _{cd} v}{\gamma _{\text{ th }}\gamma _I}} \left( 1-\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{\text{ th }}\gamma _I y+\lambda _{cd}\gamma }e^{-\frac{\lambda _{sd}\gamma _{\text{ th }} y}{\gamma }}\right) . \end{aligned}$$

(40)

When $\gamma$ and $\gamma _{Q}$ are fixed, $\gamma _I \rightarrow \infty$, using the Taylor expansion, $\chi$ is approximated as

$$\begin{aligned} \chi \approx \left[ \frac{\lambda _{cd}(\gamma _{\text{ th }}-v)}{\gamma _{\text{ th }}}-\frac{\lambda _{cd}\gamma }{\lambda _{sd}\gamma _{\text{ th }}y}\left( 1-e^{-\frac{\lambda _{sd}\gamma _{\text{ th }} y}{\gamma }}\right) \right] \frac{1}{\gamma _I}. \end{aligned}$$

(41)

Substituting (41) into (39), we obtain

$$\begin{aligned} \lim _{\gamma _I \rightarrow \infty } \varDelta I_4=0, \end{aligned}$$

(42)

which implies $\mathop {\lim }\limits _{\gamma _I \rightarrow \infty } \left( P_{out}^{\text{ UB }}-P_{out}^{\text{ LB }} \right) =0$. When $\rho =\gamma /\gamma _{I}$ and $\rho _Q=\gamma _{Q}/\gamma _I$ are fixed, the similar result can be obtained.