Performance Analysis of Downlink W-CDMA Systems in Weibull and Lognormal Fading Channels Using Chaotic Codes

Abstract

In this paper, a subspace based blind channel estimation scheme for downlink W-CDMA systems using chaotic codes under Weibull and Lognormal fading channel conditions is proposed and compared with W-CDMA system using PN codes. The algorithm provides estimates of multiuser channels by exploiting the structural information of the data output. The subspace of the (data + noise) matrix contains sufficient information for unique determination of channels and, hence, the signature waveforms and signal constellations. The proposed channel estimation algorithm is also implemented for multiuser—orthogonal frequency division multiplexing (OFDM) system. Performance measures like bit error rate (BER) and root mean square error (RMSE) are plotted for Weibull and Lognormal fading channels. Signal constellations under Weibull and Lognormal channels are also plotted. Analytical and Simulation results for BER and RMSE are compared for W-CDMA system using PN codes and chaotic codes. Simulation results show that, chaos-based W-CDMA outperforms the PN-based W-CDMA in terms BER and RMSE. Simulation results of multiuser-OFDM system shows that performance is further improved when compared to the W-CDMA system.

1 Introduction

1.1 Overview

W-CDMA is an air interface standard found in 3G mobile communication networks. It utilizes the DS-CDMA channel access method and the frequency division duplexing method to achieve higher speeds and supports more users compared to most Time Division Multiple Access (TDMA) schemes used today. It uses a pair of 5 MHz spectrum, one for uplink and one for downlink. Uplink refers to remote subscribers to the Base Station (BS) and downlink refers to transmission of signal from the base station to remote subscribers.

In a CDMA environment, the receiver requires suppression of multipath induced ICI which causes the ISI and highly structured Multiple User Interference (MUI). In [1], Honig et al. introduced a blind adaptive receiver that is potentially of great importance to practical applications in multiuser detection. Although the adaptive receiver eliminates the need for training sequences for every user, the adaptive detection algorithm still requires knowledge of the desired user’s signature waveform and associated timing.

1.2 Literature Review

The estimation of channel parameters for CDMA systems operating over fading channels with either single or multiple propagation paths using subspace-based approach was considered in [2]. In [3], it was shown that under signal subspace estimation scheme, both decorrelating detector and the linear minimum-mean-square-error (MMSE) detector can be obtained blindly. Improved subspace based algorithms [4–7] have been developed for DS-CDMA systems which eliminate the use of training sequences and also combat fast fading channels. In [8], Torlak and Xu developed a blind estimation scheme in the case of A-CDMA systems. Subspace based algorithms for different CDMA schemes under various channel fading conditions which eliminate the use of training sequence have been proposed [9–11].

Chaos-based CDMA communication has opened up a new category for spread spectrum communication, where the spreading code that is used to scramble data in CDMA systems can be generated using a single mathematical relationship of a chaotic generator instead of using the Pseudo-Noise (PN) generator [12]. Simulation results show that for blind adaptive filtering and matched filtering schemes, chaos-based CDMA outperforms the PN-based CDMA in terms of BER and Mean-Squared Error (MSE).

In [13], a blind channel equalization technique for chaotic communications based on particle filtering is proposed. Particularly, we consider the problem of combating various channel distortions from time-varying or slow multipath fading. Assuming that the channel coefficients of fading are unknown parameters, blind equalization can be formulated as an estimation problem of mixed nonlinear parameters and states. The problem of blind identification of Finite Impulse Response (FIR) system driven by a stochastic chaotic signal was considered in [14]. It was observed that the equalization performance of the chaotic approach was superior to the conventional statistical method. This is another benefit for using chaos in a spread spectrum communication system. The problem of robust CDMA signal detection in a chaotic communication system transmitting across a non-Gaussian fading channel was investigated in [15]. Since the performance of robust multiuser detector depends on the selection of M-estimator and the spreading sequences, a new influence function was used to derive an improved robust detector for the problem of data detection in CDMA impulsive fading channels using chaotic spreading. Numerical results showed that the proposed robustification outperforms the DPSK de-correlating detector particularly when the channel is highly impulsive.

Lucaino et al. [16] proposed two novel blind receivers for multiple-input-multiple-output orthogonal frequency division multiplexing (MIMO–OFDM) wireless communication systems using independent component analysis (ICA). A non-redundant linear precoder for MIMO–OFDM systems that enables blind channel estimation is proposed in [17]. Due to the structure introduced by the precoding matrix, the channel can be estimated based on general SVD. The asymptotic performance of the proposed estimation method is presented.

The BER of OFDM system with pulse shaping for ICI reduction, employing $L$th-order maximal ratio combining (MRC) diversity in Rayleigh fading environments was derived in [18]. The probability density function (PDF) of the signal-to-interference ratio (SINR) per bit,$\gamma$, in the presence of the total average inter-carrier interference (ICI) power was also derived. Khoa [19] introduced a new hyperbolic distribution and hyperbolic mask for edge detection. Edge-detection error probability as a function of the half-mask size $m$ was estimated using both masks in Gaussian- and hyperbolic-distributed pixel-intensity images. Advantages and disadvantages of the masks and both distributions were discussed.

Investigations on the hyperbolic kernel family by giving a mathematical insight into auto-term and noise robustness properties of the first-order hyperbolic, Choi-Williams (CW) and nth-order hyperbolic kernels was presented in [20]. In [21] and [22], the upper and lower bounds on ICI power, $\text{ P }_{\mathrm{ICI}}$, OFDM systems in a Gaussian scattering channel and uniform scattering channel was derived. The bounds were computed as functions of $\text{ f }_{\mathrm{d}}\text{ T }_{\mathrm{s}}$, the product of the maximum Doppler spread, $\text{ f }_{\mathrm{d}}$, and symbol duration, Ts, frequency tracking, $\xi$, and mobile travelling direction,$\varepsilon$.

In our work, the primary task is to eliminate the undesired user’s signal from the received signal in downlink W-CDMA systems using chaotic codes. The estimation is accomplished by exploiting the fact that user’s signature waveform is confined to a subspace defined by its associated code. The blind channel estimation algorithm is implemented for a SISO–OFDM system. We evaluate system performance in terms of BER and RMSE for varying system parameters like Channel order (L), Smoothing Factor (K) under Weibull and Lognormal fading channel conditions. The validation of the simulation results is done by comparing the analytical BER expression for subspace based channel estimation algorithm for W-CDMA system. Using the proposed algorithm, the performance of the W-CDMA system is compared between PN codes and Chaotic codes. The performance of a multiuser SISO–OFDM system is also analyzed.

1.3 Organization of the Paper

The paper is organized as follows: Section 2 briefly describes a W-CDMA system using PN/Chaotic codes and Data formulation. Section 3, describes Subspace based channel estimation. Section 4 presents the implementation of Blind Channel algorithm for a multiuser-OFDM system. Section 5 discusses the simulation results obtained for both PN and chaotic codes and multiuser-OFDM system in detail. Finally, Sect. 6 presents the Conclusions.

2 Downlink W-CDMA System Model and Data Formulation

2.1 W-CDMA System Description

Downlink CDMA system involves transmission of signals from the base station which mixes and broadcasts the spread spectrum modulated signals designated for different users. The spreading codes used can be PN or Chaotic sequences. Individual data sequences are first spread by PN codes/Chaotic sequences and then transmitted. Downlink signal reception is usually performed in two steps:

• Channel equalization that compensates the common multipath channel effects and restores the orthogonality,

• Despreading that extracts the desired signal.

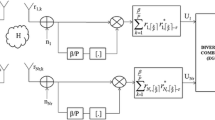
The block diagram of a downlink W-CDMA system using PN codes/Chaotic codes is shown in Fig. 1.

Fig. 1

Block diagram of downlink W-CDMA system using PN codes/chaotic codes

The system specifications are shown below:

• P is the number of users,

• N is the number of information symbols from the users,

• $\text{ b }_{\mathrm{i}}\text{(k) }$ is the information symbols from the $\text{ i }$th user, $\forall \text{ i } = 1, 2, {\ldots }, \text{ P }$,

• $\text{ L }_{\mathrm{c}}$ is the spreading code length,

• C is the spreading code PN codes (Walsh codes) / Chaotic Codes (Logistic Map)

• $\text{ s }_\mathrm{i}\text{(n) }$ is the modulated chip sequence of the $\text{ i }$th user,

• X(n) is the transmitted signal at the base station,

• L is the channel order,

• M is the number of sub-channels,

• $\text{ h }_{\mathrm{m}}\text{(n) }$ is the $\text{ m }$th channel impulse response, $\forall \text{ m } = 1, 2, {\ldots }, \text{ M }$,

• $\text{ v }_{\mathrm{m}}\text{(n) }$ is the thermal noise of the $\text{ m }$th subchannel,

• $\text{ y }_{\mathrm{m}}\text{(n) }$ is the received signal at the $\text{ m }$th subchannel,

• $\hat{{q}}_m \left( n \right)$ is the channel equalizer of the $\text{ m }$th multipath subchannel $\text{ h }_{\mathrm{m}}\text{(n) }$.

2.2 W-CDMA Data Formulation

The data structure of the W-CDMA system is given by [23]

$$\begin{aligned} \mathbf{X}_\mathrm{m} = \mathbf{G}_\mathrm{m}\;\mathbf{S}, \end{aligned}$$

(1)

where

$$\begin{aligned} \mathbf{G}_\mathrm{m} = \left[ {\mathbf{G}_{\mathrm{1m}} \quad \mathbf{G}_{\mathrm{2m}} \quad \cdots \quad \mathbf{G}_{\mathrm{Pm}}} \right] _{K L_c \times (K+1) L P},\quad \mathbf{S} = \left[ {\begin{array}{c} \text{ S }_1 \left( r\right) \\ \text{ S }_2 \left( r\right) \\ \vdots \\ \text{ S }_\mathrm{P} \left( r\right) \\ \end{array}} \right] _{(K+1)L P \times (N-(K+1) L+1)} \end{aligned}$$

(2)

$\forall \text{ i }=1,2, \ldots , \text{ P }; \text{ m } = 1,2, \ldots , \text{ M }$, where subscript i denotes the user index, M denotes the number of subchannels and $K$ is defined as the smoothing factor [23]. Smoothing factor provides an efficient method for stacking more information symbols on the data matrix leading to a type of data diversity. As $K$ increases, the (data + noise) matrix appears with more signal vectors. Hence, the probability that the signal vectors are affected by multipath fading is reduced. The signature waveform matrix associated with user i in the $\text{ m }$th subchannel is defined as

$$\begin{aligned} \mathbf{G}_\mathbf{m} =\left[ {\begin{array}{ccccc} \mathbf{c}_\mathbf{i}\mathbf{(2)}\quad &{} \mathbf{c}_\mathbf{i}\mathbf{(1)}\quad &{}\mathbf{0}\quad &{} \cdots \quad &{}\mathbf{0} \\ \quad \mathbf{0} \quad \quad &{} \mathbf{c}_\mathbf{i}\mathbf{(2)}\quad &{}\mathbf{c}_\mathbf{i}\mathbf{(1)}\quad &{}\cdots \quad &{} \mathbf{0} \\ \vdots \quad &{} \vdots \quad &{}\ddots \quad &{}\ddots \quad &{} \vdots \\ \mathbf{0} \quad &{}\cdots \quad &{}\mathbf{0} \quad &{}\mathbf{c}_\mathbf{i} \mathbf{(2)} &{}\mathbf{c}_\mathbf{i} \mathbf{(1)} \\ \end{array}}\right] _{K L_{c} \times (K+1)L} \quad \left[ \begin{array}{cccc} \mathbf{h}_{\mathrm{i,m}}&{}\mathbf{0} &{}\cdots &{}\mathbf{0} \\ \mathbf{0}&{}\mathbf{h}_{\mathrm{i,m}}&{} \vdots &{}\vdots \\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \mathbf{0}&{}\cdots &{}\mathbf{0}&{}\mathbf{h}_{\mathrm{i,m}}\end{array} \right] _{(K+1)L \times (K+1)L} \end{aligned}$$

(3)

and denoted by $\mathbf{G}_{\mathrm{m}} = \mathbf{C}_{\mathrm{i}}\mathbf{h}_{\mathrm{i,m.\;.}}$ Assume that $\{\text{ c }_{\mathrm{i}}(1),\,\text{ c }_{\mathrm{i}}(2),\ldots , \text{ c }_{\mathrm{i}}(\text{ L }_{\mathrm{c}})$; $\text{ c }_{\mathrm{i}}\text{(k) } = \pm 1\}$ is the pre-assigned Walsh spreading code of the $\text{ i }$th user. The chaotic code for the $\text{ i }$th user is generated by the Logistic map which provides best system performance under a multiuser environment [24], and is given as $c_{n+1} =\;\lambda c_{n} (1-c_n)\quad \forall \;0 \le \;c_{n} \le 1$, where $\lambda$ is the bifurcation parameter. Depending on the values of $\lambda$, system dynamics can be changed dramatically, exhibiting periodicity or chaos. For $3.5 \le \lambda \le 4$, the sequence is aperiodic and diverging.

$$\begin{aligned} \mathbf{c}_\mathbf{i}\left( \text{ j }\right) = \left[ {\begin{array}{c} \mathbf{c}_\mathrm{i} \left( 1\right) \\ \mathbf{c}_\mathrm{i} \left( 2\right) \\ \end{array}} \right] _{{2}L_{c} \times L},\,\mathbf{c}_\mathrm{i} \left( \text{ j }\right) \text{ is } \text{ of } \text{ dimension } L_{c} \times L, \text{ where } \text{ j } \text{= } \text{1, } \text{2 }. \end{aligned}$$

(4)

It is evident that

$$\begin{aligned} \mathbf{g}_{i,m} =\mathbf{c}_\mathrm{i} \left( \text{ j }\right) \;\mathbf{h}_{i, m}, \quad \forall \text{ j }= 1, 2, \end{aligned}$$

(5)

and $\mathbf{h}_{\mathrm{i,m}}$ is the channel response of the $\text{ i }$th user, and $\text{ m }$th sub-channel, and is of order $\text{ L }\times 1 \quad \forall \text{ i }=\;1,\;2\;\ldots \text{ P }; \text{ m }\;=\;1 , 2\; \ldots \;\text{ M }$. Moreover, information symbol of the $\text{ i }^{\mathrm{th}}$ user can be arranged as

$$\begin{aligned} \mathbf{S}_\mathbf{i} \left( r\right) = \left[ {\begin{array}{cccc} \!\!\!\!\!s_{i} \left( 1\right) &{} s_i \left( 2 \right) \quad \quad &{}\cdots &{} s_i \left( {N-r+1} \right) \\ s_{i} \left( 2 \right) \quad \; \;&{} s_i \left( 3 \right) \quad \quad &{}\cdots &{}\quad s_i \left( {N-r+2} \right) \\ \vdots &{}\vdots &{}\cdots &{}\vdots \\ s_i \left( r \right) \quad \; &{}s_i \left( {r+1} \right) \quad &{}\cdots &{}s_i \left( N \right) \\ \end{array}} \right] _{(K+1) L \times (N- (K+1) L+1 )}, \end{aligned}$$

(6a)

where $s_i \left( r\right)$ is the information symbol of the $\text{ r }$th sample of the $\text{ i }$th user. In our model, we arrange the data vectors such that the data matrix has a Hankel block structure [8]. This enables us to smooth output data vectors to restore the rank of G up to $\text{ P } \approx \text{ L }_{\mathrm{c}}$ so that we can accommodate more users than the existing techniques.

3 Subspace Based Channel Estimation

In Section 2, we have shown that $\mathbf{G}_{\mathrm{m}}$ has a restrictive structure, and is given as $\mathbf{G}_{\mathrm{m}} = \mathbf{C}_{\mathrm{i}}\mathbf{h}_{\mathrm{i,m}}$. Therefore, the estimation of signature vectors is equivalent to the determination of channel vectors.

3.1 Algorithm

In the presence of additive white noise, the data matrix becomes

$$\begin{aligned} \mathbf{X}_m + \mathbf{N}=\mathbf{G}_\mathrm{m} \mathbf{S} + \mathbf{N}. \end{aligned}$$

(6b)

As in [23], a subspace decomposition can be performed on $\mathbf{X}_{m}$ in (1) by Singular Value Decomposition (SVD) [25] to obtain the following channel estimates:

$$\begin{aligned} \hat{{\mathbf{h}}}_{\mathbf{i,m}}&= \; \arg \mathop {\min }\limits _{\left\| {hi} \right\| =1} \;\;\mathbf{h}_{i,m}^{H}\;\mathbf{c}_{i}^{H} \;\;\left[ {\sum _{l = 1}^{K L_c -P (K+1)} {\;\tilde{U}l \tilde{U}_{l}^{H}}} \right] \nonumber \\ \mathbf{c}_\mathrm{i} \;\mathbf{h}_{i,m} \forall \text{ i }&= \;1, 2,\;\ldots \text{ P } ;\; \text{ m }\;=\;1, 2, \ldots ,\text{ M } , \end{aligned}$$

(7)

where

$$\begin{aligned} \tilde{U}_l&= \left[ {\begin{array}{c} \!\!\!\!u_1^{\left( l\right) } \;\!u_2^{(l)} \;\;\cdots \;\;u_K^{(l)} \;\;\; 0 \\ 0\;\;\;u_1^{(l)} \;\;u_2^{(l)} \;\;\cdots \;\;\;u_K^{(l)} \\ \end{array}}\right] _{2L_c \times (K+1)} ,\nonumber \\ U_l \;&= \;\left[ {\begin{array}{c} u_1^{\left( l \right) } \\ u_2^{\left( l \right) } \\ \vdots \\ u_K^{(l)} \\ \end{array}} \right] _{K L_c \times \;K\;L_c -P \left( {K+1} \right) L} u_k^{(l)} \text{ is } \text{ L }_{\mathrm{c}} \times 1, \text{ k }= 1, 2\ldots , \text{ K }. \end{aligned}$$

(8)

This algorithm exploits the important fact that each signature vector is a linear function of a unique spreading code, and thus, its is possible to perfectly determine $\hat{{\mathbf{h}}}_{i,m}$ by linear operations on noise-free data vectors.

3.2 Minimum Mean Square Error (MMSE) Detector

A MMSE detector is employed to estimates the signal powers and gains. We assume that both signal and noise symbols in S are independent and identically distributed (i.i.d) with variance, $\sigma _{s}^{2}$, and $\sigma _{n}^{2}$, respectively. Note that

$$\begin{aligned} \tilde{\mathbf{R}}_\mathrm{X} = \frac{1}{N}\left( {\mathbf{X+N}} \right) \;\left( {\mathbf{X+N}} \right) ^{H}= \hat{{\mathbf{G}}}_m \;\displaystyle \tilde{\sum }_s^2 \;\hat{{\mathbf{G}}}_\mathrm{m}^\mathrm{H} +\sigma _n^2 \mathbf{I}, \end{aligned}$$

(9)

where $\tilde{\mathbf{R}}_\mathrm{X}$ is the sample data covariance matrix, $\sum _{s}^{2}$ is the diagonal matrix containing singular values pertaining to signal subspace, and $\sigma _{n}^{2}$ is the noise power that can be determined by the least significant eigenvalue of $\tilde{\mathbf{R}}_\mathrm{X}$. The MSE of the signature estimate can be expressed as [23]

$$\begin{aligned} \text{ RMSE }=\frac{\sigma _{n}^2}{\text{ N }\sigma _{s}^2}\left\| {\mathbf{c}_\mathrm{i} \mathbf{T}_{\mathrm{i}}^{+}} \right\| ^{2} \;\forall \text{ i }=1, 2, \ldots , \text{ P }, \end{aligned}$$

(10)

where N is the number of information symbols, $\sigma _{s}^2$ is the signal power, $\frac{\sigma _{s}^{2} }{\sigma _{n}^2}$ is the average received SNR, $\mathbf{T}_\mathrm{i} =\mathbf{c}_{i}^{H} \text{ U }_{\mathrm{o}}$ and $\mathbf{T}_{\mathrm{i}}^{+}$ is the left pseudo inverse of $\mathbf{T}_i$ [8].

The analytical RMSE expression can obtain by substituting for $\text{ T }_{\mathrm{i}}$ in (10) and taking expectation for the random quantities in the expression. So,

$$\begin{aligned} \text{ RMSE }&= \frac{1}{N \times SNR}\;E\;\left[ {\left( {\mathbf{c}_\mathrm{i} \mathbf{T}_\mathbf{i}^+} \right) \;\left( {\mathbf{c}_\mathrm{i} \mathbf{T}_\mathbf{i}^+} \right) ^{\mathrm{H}}} \right] \nonumber \\&= \;\frac{1}{N \times SNR}\;\mathbf{c}_\mathrm{i} E \left[ {\mathbf{T}_\mathbf{i}^+ \mathbf{T}_\mathrm{i}^{+^{\mathrm{H}}} } \right] \mathbf{c_{i}^H} \nonumber \\&= \frac{1}{N \times SNR}\;\mathbf{c}_\mathrm{i} \;E \left[ {\mathrm{U}_\mathrm{o}^+ \left( {\left( {\mathbf{c}_i^+ } \right) ^{\mathrm{H}}\mathbf{c}_i^+}\right) \left( {\text{ U }_\mathrm{o}^+} \right) ^{\mathrm{H}}} \right] \mathbf{c_{i}^{H}} \end{aligned}$$

(11)

$$\begin{aligned} \text{ i.e., } \text{ RMSE }&= \;\frac{1}{N \times SNR}\;\mathbf{c}_\mathrm{i} \;\left( {\left( {\mathbf{c}_\mathrm{i}^+} \right) ^{\mathrm{H}}\mathbf{c}_i^+ } \right) E \left[ {\text{ U }_\mathrm{o}^+ \text{ U }_\mathrm{o}^{+^{\mathrm{H}}}} \right] \;\mathbf{c_i^H}. \end{aligned}$$

(12)

3.3 Analytical Expression for BER

The analytical expression for BER in the subspace based asynchronous W-CDMA system is given in [26] as

$$\begin{aligned} \mathrm{P}_\mathrm{b} \left( \text{ e }\right)&= Q\left( {\sqrt{\gamma }} \right) \;, \nonumber \\ \mathrm{where} \;\quad \gamma&= \frac{\left( {\mathbf{w}_1^\mathrm{H} \tilde{\mathbf{c}}_1} \right) ^{2}}{\sum \limits _{\mathrm{i=2}}^P {\;\left[ \mathfrak{R \;\left( {\text{ w }_1^\mathrm{H} \tilde{\mathbf{c}}_\mathrm{i}} \right) }\right] }^{2}\;+\;\frac{\eta }{2}\;\left\| {\mathbf{w}_1} \right\| ^{2}\;+\;\frac{1}{\mathrm{2 N}}\;\mathrm{tr}\;\left[ \mathfrak{R \left( {\bar{{\mathbf{B}}}_\mathbf{w}}^{\mathrm{o}*} \;\bar{{\mathbf{B}}}_\mathbf{r} \right) \;+\;\mathbf{B}_\mathrm{w}^\mathrm{o} \text{ B }_\mathrm{r}}\right] }, \nonumber \\ \end{aligned}$$

(13)

$\mathbf{B_{r}}$ is the autocorrelation matrix of the received signal, Y, and its SVD is given by

$$\begin{aligned} \mathbf{B_{r}} \;\underline{\underline{\Delta }} \;E \left[ {\mathbf{Y}\;\mathbf{Y}^{\mathrm{H}}} \right] \;=\;\tilde{C}\tilde{C}^{H}+\;\upeta \mathbf{I_{N}} =\mathbf{U}_\mathrm{s} \sum \nolimits _\mathrm{s} \mathbf{U}_\mathrm{s}^\mathrm{H} +\eta \mathbf{U}_\mathrm{n} \mathbf{U}_\mathrm{n}^\mathrm{H}. \end{aligned}$$

(14)

In (14), $\sum _\mathrm{s}$ is a diagonal matrix containing the P largest singular values of $\mathbf{B_{r}},\,\mathbf{U}_\mathrm{s}$ contains the eigenvectors corresponding to eigenvalues in $\sum _\mathrm{s}$, and $\mathbf{U}_\mathrm{n}$ contains the (N–P) eigenvectors corresponding to the smallest eigenvalue, $\eta$, of $\mathbf{B_{r}}$. Suppose that user 1 is the user of interest. Since $\tilde{\mathbf{c}}_1 \;=\;\mathbf{C}_1 \;\mathbf{h}_1$, and $\mathbf{U}_\mathrm{n}^\mathrm{H} \tilde{\mathbf{c}}_1 =0$, it follows that $\mathbf{h}_{1}$ can be obtained from the quadratic optimization problem defined in (7). To obtain the BER expression in (13), the following notations were used:

$$\begin{aligned} {\tilde{\mathbf{c}}}_\mathbf{i} \;&= \;\mathbf{C}_{\mathbf{i}} \mathbf{h}_\mathbf{i} ;\;\text{ C }_\mathrm{i} \;\underline{\underline{\Delta }} \;\left[ {\mathbf{c}_{\mathrm{1,i}} , \mathbf{c}_{\mathrm{2,i}} , \ldots , \mathbf{c}_{\mathrm{L,i}}} \right] \;;\;\mathbf{h}_\mathbf{i} \;\underline{\underline{\Delta }} \;\left[ {\mathbf{h}_{\mathrm{1,i}} , \mathbf{h}_{\mathrm{2,i}} , \ldots , \mathbf{h}_{\mathrm{L,i}} } \right] ^{T}; \nonumber \\&\quad \bar{{\mathbf{c}}}_\mathrm{i} \;\underline{\underline{\Delta }} \;\mathbf{C}_{\mathrm{i}} \mathbf{h}_{\mathrm{i}} \;;\;\mathbf{C}\;=\;\left[ {\bar{{\mathbf{c}}}_1 , \bar{{\mathbf{c}}}_2 , \ldots , \bar{{\mathbf{c}}}_\mathrm{P} } \right] . \end{aligned}$$

(15)

As already mentioned in Sect. 2, $\mathbf{C}_{\mathrm{i}}$ denotes the code matrix of the $\text{ i }$th user, which can be PN or Chaotic codes. In (15), the terms inside $\mathbf{C}_\mathrm{i}$ are denoted by $\mathbf{c}_{l,i}$ which is a column vector, the terms inside $\mathbf{h}_\mathbf{i}$ are denoted by $\text{ h }_{l, i}$ which is the Weibull/Lognormal fading channel coefficient $\forall \;l\;=\;1 , 2 , \ldots , \text{ L } , \;\forall \text{ i }=1, 2, \ldots , \text{ P }$ and C denotes the code matrix containing all P users’ codes. The exact linear MMSE detector for user is given as [26]

$$\begin{aligned} \text{ w }_1 \;=\;\mathbf{B}_r^{-1} \;\tilde{\mathbf{c}}_1 \;=\;\mathbf{U}_\mathrm{s} \;\sum \nolimits _s^{-1} \;\mathbf{U}_\mathrm{s}^\mathrm{H} \;\mathbf{C}_1 \;\mathbf{h}_1 \;. \end{aligned}$$

(16)

The variables $\bar{{\mathbf{B}}}_\mathrm{w}^\mathrm{o} ,\bar{{\mathbf{B}}}_\mathrm{r} \text{ and } \mathbf{B}_\mathrm{w}^\mathrm{o}$ in the third term of the denominator in (13) are defined as [26]

$$\begin{aligned}&\bar{{\mathbf{B}}}_\mathbf{w}^{\mathbf{o}} \;=\;\mathbf{w}_{1}{}{\mathbf{w}_{1}^\mathrm{T}} +\;\mathbf{U}_s {\varvec{\Sigma }}_s^{-1} \mathbf{U}_s^H \tilde{\mathbf{C}}\;\left[ {\mu \;\left( {\mathbf{w}_1^T \tilde{\mathbf{C}}^{*}\tilde{\mathbf{C}}{}^{\mathbf{H}}\mathbf{w}_{1}} \right) \;\mathbf{I_{P}} +\upsilon \;\bar{{\mathbf{D}}}} \right] \;\tilde{\mathbf{C}}^{\mathbf{T}}\mathbf{U}_\mathrm{s}^*\Sigma _s^{-1} \mathbf{U}_s^H \;, \end{aligned}$$

(17)

$$\begin{aligned}&\bar{{\mathbf{B}}}_\mathbf{r} \;\underline{\underline{\Delta }} \;E \left[ {\mathbf{Y}\;\mathbf{Y}^{T}} \right] ,\end{aligned}$$

(18)

$$\begin{aligned}&\mathbf{B}_\mathrm{w}^{\mathrm{o}} \;=\;\left( {\mathbf{w}_1^\mathrm{H} \tilde{\mathbf{c}}_1 } \right) \;\mathbf{U}_s \Sigma _s^{-1} \mathbf{U}_s^H +\mathbf{U}_s \Sigma _s^{-1} \mathbf{U}_s^H \tilde{\mathbf{C}} \left[ {\mu \;\left( {\tilde{\mathbf{C}}^{\mathrm{T}}\text{ w }_1^*\text{ w }_1^\mathrm{H} \tilde{\mathbf{C}}^{*}} \right) +\upsilon \;\mathbf{D}} \right] \;\tilde{\mathbf{C}}^{\mathbf{H}}\mathbf{U}_s \Sigma _s^{-1} \mathbf{U}_s^H \;, \nonumber \\ \end{aligned}$$

(19)

where

$$\begin{aligned}&\mathbf{D} \underline{\underline{\Delta }} \;\text{ diag }\;\left\{ {\;\left| {\tilde{\mathbf{c}}_1^\mathrm{H} \mathbf{w}_1 } \right| ^{2},\;\left| {\tilde{\mathbf{c}}_2^\mathrm{H} \mathbf{w}_1 } \right| ^{2},\;\ldots \;,\;\left| {\tilde{\mathbf{c}}_\mathrm{P}^\mathrm{H} \mathbf{w}_1 } \right| ^{2}} \right\} \;, \end{aligned}$$

(20)

$$\begin{aligned}&\mathbf{D} \underline{\underline{\Delta }} \;\text{ diag }\;\left\{ { \left( {\tilde{\mathbf{c}}_1^\mathrm{H} \mathbf{w}_1 } \right) ^{2},\;\left( {\tilde{\mathbf{c}}_2^\mathrm{H} \mathbf{w}_1 } \right) ^{2},\;\ldots \;,\;\left( {\tilde{\mathbf{c}}_\mathrm{P}^\mathrm{H} \mathbf{w}_1 } \right) ^{2}} \right\} \;, \end{aligned}$$

(21)

$$\begin{aligned}&\mu \;\underline{\underline{\Delta }} \;\left| { E\left\{ {b^{2}} \right\} } \right| ^{2} \text{ and } \upsilon \;=\;\text{ E }\;\left\{ { \left| \text{ b } \right| ^{4}} \right\} \;-\;\text{2 } \text{ E }\;\left\{ { \left| \text{ b } \right| ^{2}} \right\} ^{2}-\left| { E\left\{ {b^{2}} \right\} } \right| ^{2}. \end{aligned}$$

(22)

For BPSK modulation, $b\;\in \;\left\{ {+1, -1}\right\}$, then $\mu = 1 \text{ and } \upsilon = -2$.

3.4 Identifiability

In order to determine the number of users, P, the constraint $\text{ P }< \text{ KL }_{\mathrm{c}}- \text{ P } (\text{ K }+\text{1 }) \text{ L }$ must be satisfied. But, this is only the necessary condition to estimate a channel vector. From (7), it is clear that the determination of the signature vector for the noise-free case is simply a matter of finding a vector {$\hat{{\mathbf{G}}}_m: \hat{{\mathbf{G}}}_\mathrm{m}\;\bot \;\mathbf{U}_{\mathrm{o}},\,\hat{{\mathbf{G}}}_m \in \;span\;(C_i )\}\; \forall \text{ i } = 1, 2, {\ldots }, \text{ P }; \text{ m }= 1, 2, {\ldots }, \text{ M }$, where span (.) denotes the column range span.

4 Blind Channel Estimation Algorithm for Multiuser OFDM System

In this section, we present the extended work of implementing blind channel estimation algorithm for multiuser OFDM system. Basically, OFDM is a method of encoding digital data on multiple carrier frequencies. OFDM has developed into a popular scheme for wideband digital communications, and is widely used in applications such as digital television and audio broadcasting, DSL broadband internet access, and 4G mobile networks. The primary advantage of OFDM over single-carrier schemes is its ability to cope with severe channel conditions, for example, attenuation of high frequencies in a long copper wire, narrowband interference and frequency-selective fading due to multipath without complex equalization filters. Channel equalization is simplified because OFDM may be viewed as using many slowly modulated narrowband signals rather than one rapidly modulated wideband signal [27].

4.1 Data Formulation

The received signal vector is a combination of transmitted signal vector from all users through all subcarriers, and is given as [28]

$$\begin{aligned} \mathbf{R}=\left[ \mathbf{R}_1^{\mathbf{T}} \quad \cdots {\mathbf{R}_\mathbf{i}^\mathbf{T} \cdots }\quad {\mathbf{R}_\mathbf{P}^\mathbf{T}} \right] ^{\mathbf{T}}, \end{aligned}$$

(23)

where the signal vector from the $\text{ i }$th user is

$$\begin{aligned} \mathbf{R}_i =\left[ {\mathbf{R}_i (0)^{T}\;\mathbf{R}_i (1)^{T} \cdots \mathbf{R}_i \left( {N_c -1} \right) ^{T}} \right] ^{T}. \end{aligned}$$

(24)

Here, $\text{ R }_\mathrm{i}\left( \text{ k }\right) \;=\;\text{ X }_\mathrm{i} \left( \text{ k }\right) \;\text{ H }_\mathrm{i} \left( \text{ k }\right) \;\!+\!\;\text{ N(k) }$ is the $\text{ k }$th subcarrier of the $\text{ i }$th user received signal vector,

$$\begin{aligned} \text{ X }_\mathrm{i}(\text{ k })=\left[ {{\begin{array}{c} {\text{ X }^{\mathrm{k}}(\text{ N })} \\ {\text{ X }^{\mathrm{k}}(\text{ N }-1)} \\ \vdots \\ {\text{ X }^{\mathrm{k}}(\text{ N }-\mathrm{K+1})} \end{array}}}\right] _{\text{ KL }_{\mathrm{c}} \times \text{ N }} \quad \mathbf{H}_\mathbf{i} \left( \mathbf{k}\right) =\mathop \sum \limits _{(\mathbf{l=0})}^{(\mathbf{L-1})} \mathbf{H}_\mathbf{l}^{\left( \mathbf{i}\right) } \mathbf{exp}(-\mathbf{j}2\mathbf{\uppi } \mathbf{kl}/\mathbf{N}_\mathbf{c}) \end{aligned}$$

and N(k) is the AWGN noise associated with the $\text{ k }$th subcarrier. Similarly, the transmitted signal matrix is a combination of signal through all subcarriers of each user and is given as [28]

$$\begin{aligned} \mathbf{X}=\left[ {\mathbf{X}_1^{\mathbf{T}} \quad \cdots {\mathbf{X}_\mathbf{i}^\mathbf{T} \cdots } \quad {\mathbf{X}_\mathbf{P}^\mathbf{T}}} \right] ^{\mathbf{T}}, \end{aligned}$$

(25a)

where the signal-vector from the $\text{ i }$th user is given as

$$\begin{aligned} \mathbf{X}_\mathbf{i} =\left[ {\mathbf{X}_\mathbf{i} \left( \mathbf{0}\right) ^{\mathbf{T}}\ldots }\quad {\mathbf{X}_\mathbf{i} \left( \mathbf{k} \right) ^{\mathbf{T}}\ldots }\quad {\mathbf{X}_\mathbf{P} \left( {\mathbf{N}_\mathbf{c} -1} \right) ^{\mathbf{T}}} \right] ^{\mathbf{T}}, \end{aligned}$$

(25b)

and $\mathbf{X}_\mathbf{i} \left( \mathbf{k} \right)$ is the $\text{ k }^{\mathrm{th}}$ subcarrier, $\text{ i }$th user received signal vector. The code matrix, C, is given as

(26)

where $\mathbf{C}_\mathrm{i}\text{(k) }$ is the block diagonal code matrix of the $\text{ i }$th user in the $\text{ k }$th subcarrier. Now, the code matrix of the $\text{ i }$th user for all subcarriers is given by

$$\begin{aligned} \mathbf{C}_\mathbf{i} =\left[ {\mathbf{C}_1 \left( \mathbf{0} \right) \ldots }\quad {\mathbf{C}_\mathbf{i} \left( \mathbf{k} \right) \ldots }\quad {\mathbf{C}_\mathbf{P} \left( {\mathbf{N}_\mathbf{c} -1} \right) }\right] ^{\mathbf{T}}. \end{aligned}$$

(27)

The channel matrix H is a $PN_c \times PN_c$ block diagonal matrix that can be represented as

$$\begin{aligned} \mathbf{H}=\mathbf{diag}\{\mathbf{H}^{(\mathbf{i})}(\mathbf{exp}\;(\mathbf{j2\mathbf{\uppi } k/N_c}))\}\forall \; \mathbf{k=1,2,\ldots ,}(\mathbf{N}_\mathbf{{c} -1}),\forall \;\mathbf{i=1,2,\ldots , P}. \end{aligned}$$

(28)

We have

$$\begin{aligned} \mathbf{H}^\mathbf{(i)}(\mathbf{exp}\;(\mathbf{j2\mathbf{\uppi } k/N_c })) = \mathbf{H}^{(\mathbf{i})}(\mathbf{k}) = {\varvec{\sum \nolimits _{{(1=0)}}^{(\mathbf{L-1})}} }\mathbf{H}_1 ^{(\mathbf{i})}\mathbf{exp} (\mathbf{-j2\mathrm{\uppi } kl/N_c }). \end{aligned}$$

(29)

In (29), $\mathbf{H}_l^{(i)}$is a $\mathbf{1\times 1}$ complex Gaussian random matrix denoting the $l$th tap of the fading channel impulse response of the $\text{ i }$th user. Thus, the channel matrix for 0th subcarrier through the 0th path of the first user is $\mathbf{H}_\mathbf{0}\mathbf{(0) = [h(0)]}$. The channel matrix for the individual subcarriers is the sum of channel matrices of the corresponding subcarrier for different paths between transmit and receive antennas. Therefore, for user 1, $\mathbf{H}^{(1)}\left( 0 \right) \;=\;\mathbf{H}_0^{(1)} \left( 0 \right) \;+\;\mathbf{H}_1^{(1)} \left( 0 \right) \;+\;\cdots \;+\mathbf{H}_l^{(1)} \left( 0 \right) \;+\;\cdots \;\mathbf{H}_{(L-1)}^{(1)} \left( 0\right) \;,$ where L is the number of resolvable paths. Hence, each element in $\mathbf{H}^{(\mathrm{i})}(\mathrm{k})$ matrix is the sum of fading impulse response in different paths between transmit and receive antennas. The entries of $\mathbf{H}_l^{(\mathrm{i})}$ have non-zero mean for Weibull fading channel conditions. Hence, channel matrix can be obtained as given below:

(30)

4.2 Downlink OFDM Data Formulation

To reveal the relations between input and output data structures, $x(t)$ can be represented in discrete-form (Fig. 2). Sampling $x(t)$ at chip rate, we obtain

$$\begin{aligned} \text{ x }(1)=\sum _{\mathrm{i=1}}^\mathrm{p} \sum _{\mathrm{n}=-\infty }^\infty \text{ S }_\mathrm{i}\text{(n) }\text{ g }_\mathrm{ij}(\text{ l }-\text{ n }\text{ L }_\mathrm{c}). \end{aligned}$$

(31)

The discrete counterpart of signature waveform can be represented as

$$\begin{aligned} \text{ g }_{\mathrm{ij}} (1)&= \sum _{\text{ k=1 }}^{\mathrm{2L_c}} {\text{ c }_\mathrm{i}} (\text{ k }-\text{ k }_\mathrm{i})\text{ h }_{\mathrm{ij}} (1-\text{ k }). \nonumber \\&= \sum _{\mathrm{k=1}}^\mathrm{L} {\text{ h }_{\mathrm{ij}} (\text{ k })\text{ c }_\mathrm{i} (\mathrm{1-k}+\text{ k }_\mathrm{i}), \qquad 1=1,2,\ldots ,2\text{ L }_\mathrm{c}} \end{aligned}$$

(32a)

The RHS of the above convolution can be represented as

$$\begin{aligned} \left[ \begin{array}{ccccc} \mathbf{c}_\mathbf{i} \left( \mathbf{k}_\mathbf{i} \right) &{} \mathbf{c}_\mathbf{i} \left( \mathbf{k}_\mathbf{i -1} \right) &{} \mathbf{c}_\mathbf{i} \left( \mathbf{k}_\mathbf{i} -\mathbf{2} \right) &{} {\ldots } &{} \mathbf{c}_\mathbf{i} \left( \mathbf{k}_\mathbf{i} +\mathbf{1}-\mathbf{L} \right) \\ {\mathbf{c}_\mathbf{i} \left( {\mathbf{k}_\mathbf{i +1}} \right) }&{} \ldots &{} \ldots &{} \ldots &{} {\mathbf{c}_\mathbf{i} \left( {\mathbf{k}_\mathbf{i}+\mathbf{2}-\mathbf{L}} \right) } \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {\mathbf{c}_\mathbf{i} \left( {\mathbf{k}_\mathbf{i} +\mathbf{2}\mathbf{L}_\mathbf{c} -1} \right) }&{} {\mathbf{c}_\mathbf{i} \left( {\mathbf{k}_\mathbf{i} +2\mathbf{L}_\mathbf{c} -2} \right) }&{} \ldots &{} \ldots &{} {\mathbf{c}_\mathbf{i} \left( {\mathbf{k}_\mathbf{i} +\mathbf{2}\mathbf{L}_\mathbf{c} -\mathbf{L}} \right) } \\ \end{array} \right] _{2\text{ L }_\mathrm{c} \times \text{ L }} \left[ {{\begin{array}{c} {\text{ h }_{\mathrm{ij}} (1)} \\ {\text{ h }_{\mathrm{ij}} (2)} \\ \vdots \\ {\text{ h }_{\mathrm{ij}} (\text{ L })} \\ \end{array}}} \right] _{\text{ L }\times 1} \nonumber \\ \end{aligned}$$

(32b)

Fig. 2

Block diagram of multiuser OFDM system

where $\mathbf{c}_\mathrm{i} \left( {\text{ j }_1} \right)$ is the kernel matrix with dimension $2L_c \times L$. If we partition

$$\begin{aligned} \mathbf{c}_\mathrm{i} \left( {\text{ j }_1} \right) = \left[ {\begin{array}{c} \mathbf{c}_\mathrm{i} \left( 1\right) \\ \mathbf{c}_\mathrm{i} \left( 2\right) \\ \end{array}} \right] _{2 L_c \times L}, \quad \mathbf{c}_\mathrm{i} \left( {\text{ j }_1} \right) \text{ is } \text{ of } \text{ dimension } \text{ L }_\mathrm{c} \times \text{ L }, \text{ where } j_1 =1, 2. \end{aligned}$$

(33)

It is evident that

$$\begin{aligned} \mathbf{g}_{\mathrm{ij}} \left( {\text{ j }_1} \right) \;=\;\mathbf{c}_\mathrm{i} \left( {\text{ j }_1} \right) \;\mathbf{h}_{\mathrm{ij}} \;, \quad j_1 =1,\;2. \end{aligned}$$

(34)

Stacking $KL_c$ successive samples in vector form, we have

$$\begin{aligned} \text{ X }_{\mathrm{j}} =\left[ {{\begin{array}{c} {\text{ X }^{\mathrm{j}}(\text{ N })} \\ {\text{ X }^{\mathrm{j}}(\text{ N }-1)} \\ \vdots \\ {\text{ X }^{\mathrm{j}}(\text{ N }-\mathrm{K+1})} \\ \end{array}}}\right] _{\mathrm{KL}_{\mathrm{c}} \times \text{ N }} =\mathop \sum \limits _{\mathrm{i}=1}^\mathrm{P} \text{ X }_{\mathrm{ij}} =\mathop \sum \limits _{\mathrm{i}=1}^\mathrm{P} \text{ g }_{\mathrm{ij}} \text{ S }_\mathrm{i} \left( \text{ r } \right) . \end{aligned}$$

(35)

Thus, the signature waveform matrix associated with $\text{ j }^{\mathrm{th}}$ subcarrier of $i$th user can be given as

$$\begin{aligned} \mathbf{g}_{\mathbf{ij}} =\left[ {{\begin{array}{ccccc} {\mathbf{c}_\mathbf{i} \mathbf{(2)}}&{} {\mathbf{c}_\mathbf{i} \mathbf{(1)}}&{} 0&{} \ldots &{} 0 \\ 0&{} {\mathbf{c}_\mathbf{i} \mathbf{(2)}}&{} {\mathbf{c}_\mathbf{i} \mathbf{(1)}}&{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \vdots \\ 0&{} 0&{} 0&{} {\mathbf{c}_\mathbf{i} \mathbf{(2)}}&{} {\mathbf{c}_\mathbf{i} \mathbf{(1)}} \\ \end{array}}}\right] _{\mathrm{KL}_{\mathrm{c}} \times \left( \text{ K }+1\right) \text{ L }}\quad \left[ {{\begin{array}{cccc} {\mathbf{h}_{\mathbf{ij}} }&{} 0&{} \ldots &{} 0 \\ 0&{} {\mathbf{h}_{\mathbf{ij}} }&{} \vdots &{} \vdots \\ \vdots &{} 0&{} \ddots &{} 0 \\ 0&{} \ldots &{} 0&{} {\mathbf{h}_{\mathbf{ij}} } \\ \end{array}}} \right] _{\left( {\text{ K }+1} \right) \text{ L }\times (\text{ K }+1)\text{ L }} \end{aligned}$$

(36)

and the signature waveform matrix associated with the $i$th user comprising $N_c$ subcarriers, and where $i=1,2,\ldots ,P$, can be represented as

(37)

where $\mathbf{g}_{ij}$ is the signature waveform matrix associated with $j$th subcarrier of $i$th user $j=0,1,\ldots ,(\text{ N }_\mathrm{c} -1)$. In general,

$$\begin{aligned} \mathbf{G}_\mathbf{i} =\mathbf{C}_{\mathbf{i}} \times \mathbf{H}_\mathbf{i}. \end{aligned}$$

(38)

The data structure is given by

$$\begin{aligned} \mathbf{X}=\mathbf{G S}, \end{aligned}$$

(39)

where G is given as [28]

(40)

The information symbol of $i$th user on $j$th subcarrier can be arranged as

$$\begin{aligned} \mathbf{S}_{\mathbf{ij}} (\mathbf{r})=\left[ {{\begin{array}{ccccc} {\mathbf{S}_{\mathbf{ij (1)}}}&{} {\mathbf{S}_{\mathbf{ij (2)}}}&{} \ldots &{} \ldots &{} {\mathbf{S}_{\mathbf{ij}} (\mathbf{N}-\mathbf{r}+1)} \\ {\mathbf{S}_{\mathbf{ij (2)}}}&{} \ldots &{} \ldots &{} \ldots &{} {\mathbf{S}_{\mathbf{ij}} (\mathbf{N}-\mathbf{r+2})} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ {\mathbf{S}_{\mathbf{ij}} (\mathbf{r})}&{} {\mathbf{S}_{\mathbf{ij}} (\mathbf{r+1})}&{} \ldots &{} \ldots &{} {\mathbf{S}_{\mathbf{ij}} (\mathbf{N})} \\ \end{array} }} \right] _{(\text{ K }+1)\text{ L }\times (\text{ N }-\left( {\text{ K }+1} \right) \text{ L }+1)} \end{aligned}$$

(41)

Hence, the information symbol of the $i$th user having $\text{ N }_{\mathrm{c}}$ subcarriers is $\mathbf{S}_{\mathrm{i}}\text{(r) }$

$$\begin{aligned} \mathbf{S}_\mathbf{i} (\mathbf{r})=\left[ {{\begin{array}{cccc} {\mathbf{S}_{\mathbf{i}0} (\mathbf{r})}&{} \mathbf{0}&{} \ldots &{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{S}_{\mathbf{i}1} (\mathbf{r})}&{} \vdots &{} \vdots \\ \vdots &{} \mathbf{0}&{} \ddots &{} \mathbf{0} \\ \mathbf{0}&{} \ldots &{} \mathbf{0}&{} {\mathbf{S}_{\mathbf{i}(\mathbf{N}_\mathbf{c} -1)} } \\ \end{array} }} \right] _{\mathrm{N}_\mathrm{c} (\text{ K }+1)\text{ L }\times \text{ N }_\mathrm{c} (\text{ N }-\left( {\text{ K }+1} \right) \text{ L }+1)} \end{aligned}$$

(42)

The overall information matrix S of P-user OFDM system having $\text{ N }_{\mathrm{c}}$ subcarriers is given as [28]

(43)

4.3 Subspace Based Channel Estimation Algorithm for OFDM System

In the presence of additive white noise, the data matrix becomes

$$\begin{aligned} \mathbf{X}+\mathbf{N}=\mathbf{GS} + \mathbf{N}. \end{aligned}$$

(44)

On applying SVD to (44), we obtain

$$\begin{aligned} \mathbf{X}+\mathbf{N=}\left( {\mathbf{Us}\quad \;\mathbf{Uo}} \right) \quad \left( {\begin{array}{cc} \sum \nolimits _\mathrm{s} \quad \quad 0 \\ 0\;\quad \quad \sum \nolimits _\mathrm{o} \\ \end{array}} \right) \quad \left( {\begin{array}{c} \mathbf{V}_\mathrm{s}^\mathbf{H} \\ \mathbf{V}_\mathrm{o}^\mathbf{H} \\ \end{array}} \right) \;, \end{aligned}$$

(45)

• $\mathbf{U}_{\mathrm{s}}$ is the signal subspace of dimension $\text{ P } \text{ K } \text{ L }_\mathrm{c} \text{ N }_\mathrm{c} \;\times \;\text{ P } \text{ N }_\mathrm{c} \left( {\text{ K+1 }} \right) \text{ L }$.

• $\mathbf{U}_{\mathrm{o}}$ is the noise subspace of dimension $\text{ P } \text{ K } \text{ L }_\mathrm{c} \text{ N }_\mathrm{c}\;\times \;\text{ P } \text{ K } \text{ L }_\mathrm{c} \text{ N }_\mathrm{c} -\text{ P } \text{ N }_\mathrm{c} \left( {\text{ K+1 }} \right) \text{ L }$.

The noise subspace is given by

$$\begin{aligned} \mathbf{U}_{\mathrm{o}}&= \left[ {\mathbf{U}_{1}\quad \mathbf{U}_{2}\quad \cdots \quad \mathbf{U}\text{ KP } \text{ N }_{\mathrm{c}} \text{ L }_\mathrm{c}-(\text{ PN }_{\mathrm{c}}(\text{ K+1 })\text{ L })}\right] . \end{aligned}$$

(46)

$$\begin{aligned} \hat{{\mathbf{h}}}_\mathrm{i}&= \; \arg \;\mathop {\min }\limits _{\left\| {hi} \right\| =1} \;\;\mathbf{h}_i^H \;\mathbf{c}_i^H \;\;\left[ {\sum _{l = 1}^{KP N_c L_c -P N_{c} (K+1)L} {\;\tilde{U}l \tilde{U}_l^H } } \right] \;\;\mathbf{c}_\mathrm{i} \;\mathbf{h}_i ,\;\forall \text{ i }=\;1, 2,\;\ldots \text{ P }.\nonumber \\ \end{aligned}$$

(47)

where

$$\begin{aligned} \tilde{U}_l&= \left[ {\begin{array}{ccccc} u_1^{\left( l \right) } \;u_2^{(l)} \;\;\ldots \;\;u_K^{(l)} \;\;\; 0 \\ 0\;\;\;u_1^{(l)} \;\;u_2^{(l)} \;\;\ldots \;\;\;u_K^{(l)} \\ \end{array}} \right] _{2\text{ N }_\mathrm{c} \text{ L }_\mathrm{c} \times \text{ K }} , \nonumber \\ U_l \;&= \;\left[ {\begin{array}{c} u_1^{\left( l \right) } \\ u_2^{\left( l \right) } \\ \vdots \\ u_K^{(l)} \\ \end{array}} \right] _{\text{ K } \text{ PL }_\mathrm{c} \text{ N }_\mathrm{c} \times \; \text{ K } \text{ PN }_\mathrm{c} \;\text{ L }_\mathrm{c} -\mathrm{P} \text{ N }_\mathrm{c} \left( {\text{ K }+1 } \right) L} u_k^{(l)} \text{ is } \text{ L }_{\mathrm{c}} \times 1, \text{ k }= 1, 2\ldots , \text{ K }. \end{aligned}$$

(48)

Each signature vector is a linear function of a unique spreading code, and thus, it is possible to perfectly determine $\hat{{\mathbf{h}}}_i\;$.

5 Simulation Results

In this section, we present analytical and simulated results to analyze the performance of downlink W-CDMA system using PN and Chaotic codes in terms of BER and RMSE for Weibull and Lognormal fading channels. The system parameters are chosen based on the theoretical bounds obtained for number of users (P), smoothing factor (K) and Channel order (L). The bounds are as follows:

• (a) The number of users $\text{ P }\;<\;\text{ K }\;\text{ L }_\mathrm{c} \;-\;\text{ P }\;(\text{ K }+\text{1 })\;\text{ L }$.

• (b) Channel order $\text{ L }<\frac{\text{ K } \text{ L }_\mathrm{c} -\text{ P }}{\text{ P } \left( {\text{ K }+\text{1 }} \right) }$ and $\text{ L }\;<<\;\text{ L }_\mathrm{c}$.

• (c) The channel orders for all users are equal.

• (d) The channel order L is known.

• (e) Smoothing factor $\text{ K }>>\frac{\text{ P } \text{ L }}{\text{ L }_\mathrm{c} \;-\;\text{ P } \text{ L }}$.

We use a single receiver W-CDMA system with $\text{ L }_{\mathrm{c}} = 63, \text{ K } = 2$ and channel order L = 4. On applying the system parameters in the bound for P, we obtain $P\;<\;9$. In simulation, we use P = 3. For the chosen value of P = 3, the bound for K is $\text{ K }\;>>0.23529$. The number of data vectors for the proposed channel estimation is $\text{ N } = 10^{4}$.

Figure 3a shows the real and imaginary parts of the estimated channel response of subchannels 1, 2, 3, and 4 for user 1 under Weibull fading channel conditions. For each user, the channel vector $\{\hat{{\mathbf{h}}}_{i,m}\}$ is estimated as in (7). For each user, user delay, multipath delay, and the number of multipath components is uniformly distributed in [1 $\text{ L }_{\mathrm{c}}$], [0 3T], and [1, 6], respectively. The real part of the estimated channel response of subchannel 1 with channel order L is denoted by $\underline{\alpha }\;=\;\left\{ {\alpha _1 , \alpha _2 , \ldots , \alpha _L } \right\} \;,$ the imaginary part is denoted by $\underline{\beta }\;=\;\left\{ {\beta _1 , \beta _2 , \ldots , \beta _L } \right\} \;,$ and the complex estimated channel response is given by $\underline{Z}\;=\;\underline{\alpha }\;+\;j \underline{\beta }$. In simulation, we use L = 4, and the coefficients are $\underline{\alpha }\;=\;\left\{ {-0.0228, \;0.7067 ,\;-0.0228, \;0.7067} \right\} \;$ and $\underline{\beta }=\left\{ {0.0052,\;0,\;0.0052,\;0} \right\} \;$. Taking the norm of the channel response, we have $\left\| {\hat{{h}}_1 } \right\| ^{2}=\sqrt{\left( {\left( {-0.0228} \right) ^{2}+\left( {0.0052} \right) ^{2}} \right) +\left( {0.7067} \right) ^{2}+\left( {\left( {-0.0228} \right) ^{2}+\left( {0.0052} \right) ^{2}} \right) +\left( {0.7067} \right) ^{2}}=$ $0.99997 \cong \;1$, which satisfies the requirement for unit norm of the estimated channel vector in the quadratic optimization problem shown in (7). Similarly, the norm of the channel response of subchannel 2, 3 and 4 can be proved. For subchannel 2, the real and imaginary part of the channel responses are $\underline{\alpha }\;=\;\left\{ {0.6787,\;0.1944,\;0.6787,\;0.1944} \right\} \text{ and } \underline{\beta }\;=\;\left\{ {0, - 0.0391,\;0,\;- 0.0391} \right\} \;$. Taking the norm of the channel response, we have

$$\begin{aligned} \left\| {\hat{{h}}_2 } \right\| ^{2}\;&= \;\sqrt{\left( {0.6787} \right) ^{2}+\left( {\left( {0.1944} \right) ^{2}+\left( {-0.0391} \right) ^{2}} \right) +\left( {0.6787} \right) ^{2}+\left( {\left( {0.1944} \right) ^{2}+\left( {-0.0391} \right) ^{2}} \right) }\\&= \;0.9999\;\cong \;1. \end{aligned}$$

Fig. 3

Estimated channel response of subchannel 1, 2, 3 and 4 of user 1 in a Weibull fading channel (a), Lognormal fading channel (b)

For subchannel 3, $\underline{\alpha }=\left\{ {0.0081, 0.6960, 0.0081, 0.6960} \right\} \text{ and } \underline{\beta }=\left\{ {0.1244, 0,0.1244,0} \right\}$.

Taking the norm of the channel response, we have

$$\begin{aligned} \left\| {\hat{{h}}_3 } \right\| ^{2}\;&= \sqrt{\left( {\left( {0.0081} \right) ^{2}+\left( {0.1244} \right) ^{2}} \right) +\left( {0.6960} \right) ^{2}+\left( {\left( {0.0081} \right) ^{2}+\left( {0.1244} \right) ^{2}} \right) +\left( {0.6960} \right) ^{2}}\;\;\\&= 0.99995\;\cong \;1. \end{aligned}$$

For subchannel 4, $\underline{\alpha }\;=\;\left\{ {-0.0698 ,\;0.7028,\;-0.0698 ,\;0.7028} \right\}$ and $\underline{\beta }\;=\;\left\{ - 0.0325,0,\right. \left. \;- 0.0325,\;0\right\}$. Taking the norm of the channel response, we have

$$\begin{aligned} \left\| {\hat{{h}}_4 } \right\| ^{2}\;&= \;\sqrt{\left( {\left( {-0.0698} \right) ^{2}+\left( {-0.0325} \right) ^{2}} \right) +\left( {0.7028} \right) ^{2}+\left( {\left( {-0.0698} \right) ^{2}+\left( {-0.0325} \right) ^{2}} \right) +\left( {0.7028} \right) ^{2}}\\&= 0.9998\cong \;1. \end{aligned}$$

Figure 3b shows the real and imaginary parts of the estimated channel response of subchannels 1, 2, 3, and 4 for user 3 under Lognormal fading channel conditions. The effect of Lognormal fading on the channel impulse response is lower compared to other fading channels. So, the estimated channel response will be better compared to Weibull fading channel conditions. The real part of the channel coefficients with channel order $\text{ L }=4$ is $\underline{\alpha }\;=\;\left\{ {-0.0570,\;0.7048,\;-0.0570,\;0.7048} \right\}$ and $\underline{\beta }\;=\;\left\{ {0.0001,\;0,\;\text{0.0001, }\;\text{0 }} \right\} \;$. Taking norm of the channel coefficients, we have

$$\begin{aligned} \left\| {\hat{{h}}_1 } \right\| ^{2}\;&= \;\sqrt{\left( {\left( {-0.0570} \right) ^{2}+\left( {0.0001} \right) ^{2}} \right) +\left( {0.7048} \right) ^{2}+\left( {\left( {-0.0570} \right) ^{2}+\left( {0.0001} \right) ^{2}} \right) +\left( {0.7048} \right) ^{2}} \\&= 0.9999 \cong \;1. \end{aligned}$$

For subchanne1 2, the estimated channel coefficients are $\underline{\alpha }\!=\!\left\{ {0.6799, 0.1944, 0.6799, 0.1944} \right\}$ and $\underline{\beta }=\left\{ {\;0,\;\text{0.0025, }\;\text{0, }\;\text{0.0025 }} \right\} \;$. Taking norm of the channel coefficients, we have

$$\begin{aligned} \left\| {\hat{{h}}_2 } \right\| ^{2}\;&= \;\sqrt{\left( {0.6799} \right) ^{2}+\left( {\left( {0.1944} \right) ^{2}+\left( {0.0025} \right) ^{2}} \right) +\left( {0.6799} \right) ^{2}+\left( {\left( {0.1944} \right) ^{2}+\left( {0.0025} \right) ^{2}} \right) }\\&= 1. \end{aligned}$$

For subchannel 3, the estimated channel coefficients are $\underline{\alpha }=\left\{ -0.3458,\;0.6168, -0.3458 ,\right.$ $\left. 0.6168 \right\}$ and $\underline{\beta }\;=\;\left\{ {0.0042,\;0,\;0.0042,\;0} \right\}$. Taking norm of the channel coefficients, we have

$$\begin{aligned} \left\| {\hat{{h}}_3 } \right\| \;&= \;\sqrt{\left( {\left( {-0.3458} \right) ^{2}+\left( {0.0042} \right) ^{2}} \right) +\left( {0.6168} \right) ^{2}+\left( {\left( {-0.3458} \right) ^{2}+\left( {0.0042} \right) ^{2}} \right) +\left( {0.6168} \right) ^{2}}\\&= 1. \end{aligned}$$

For subchannel 4, the estimated channel coefficients are $\underline{\alpha }\;=\;\left\{ -0.1012 ,\;0.6667, -0.1012 ,\right.$ $\left. 0.6667 \right\}$ and $\underline{\beta }\;=\;\left\{ {-0.2129,\;0,\;-0.2129,\;0} \right\}$. Taking norm of the channel coefficients, we have

$$\begin{aligned} \left\| {\hat{{h}}_4 } \right\| =\sqrt{\left( {\left( {-0.1012} \right) ^{2}+\left( {-0.2129} \right) ^{2}} \right) +\left( {0.6667} \right) ^{2}+\left( {\left( {-0.1012} \right) ^{2}+\left( {-0.2129} \right) ^{2}} \right) +\left( {0.6667} \right) ^{2}}=1. \end{aligned}$$

Figure 4 shows the analytical and simulated BER performance comparison of Downlink W-CDMA system using PN codes and chaotic codes under Weibull fading channel conditions. It is evident that BER improves as SNR increases and the performance of W-CDMA system using chaotic codes outperforms PN codes in a significant manner. The performance of chaotic codes is further verified by plotting the signal constellation of the desired user, user 1 for PN codes and chaotic codes in Figs. 5 and 6a, b, respectively. The estimated channel response $\{\hat{{\mathbf{h}}}_{i,m} \} ,$is used to reconstruct the signature vectors $\{\hat{{\mathbf{g}}}_{i,m} \}$using (5). We then construct a zero-forcing equalizer to recover the information signals of each user. When compared to the signal constellation of the system using PN codes in Fig. 5, in Fig. 6a, we observe that the transmitted bits are very much closer to $\pm 1$ in the presence of Weibull fading effects and other channel impairments. Figure 6b shows the signal constellation of user 1 under Lognormal fading channel conditions. All these figures show that the proposed algorithm successfully determine the signature waveforms and recovers the message signal. Also, the system performance using chaotic codes outperforms that of PN codes. Moreover, Weibull fading channel conditions provide improvement in BER when compared to Lognormal channel conditions.

Fig. 4

Comparison of analytical BER versus simulated BER for a downlink W-CDMA system incorporating PN codes and Chaotic codes in a Weibull fading channel

Fig. 5

Estimated signal constellation for user 1 using PN codes in a Weibull fading channel

Fig. 6

Estimated signal constellation for user 1 using chaotic codes in a Weibull fading channel (a), Lognormal fading channel (b)

Figure 7 shows the plot of BER versus SNR for varying Weibull fading parameter k. As the fading parameter k increases, fading severity decreases and hence the system performance improves. The value of k is varied from 2 to 3 in steps of 0.25 for k = 2.5, both analytical and simulated BER values are plotted. The analytical BER at SNR = 7 dB is 0.0024, whereas the simulated BER is 0.0021 which are almost similar to each other. Figure 8 shows the analytical versus simulated BER performance comparison of W-CDMA system using chaotic codes under Weibull and Lognormal fading channel condition. It is observed that the analytical and simulated BER performance of the system is better for Weibull fading channel conditions.

Fig. 7

Comparison of analytical BER and simulated BER for a downlink W-CDMA system incorporating PN codes in a Weibull fading channel for fading parameters, $\text{ k } (= 2, 2.25, 2.5, 2.75, 3)$

Fig. 8

Comparison of analytical BER and simulated BER for a downlink W-CDMA system incorporating chaotic codes under Weibull and Lognormal fading conditions

Another interesting observation of this algorithm is shown in Fig. 9a where we increase the channel order L from 2 to 10. For analysis purposes, $\text{ P } = 3, \text{ L }_{\mathrm{c}} = 63$ and $\text{ K } = 2$ are chosen. On applying the above specification in the bounds for Channel order L, we obtain $\text{ L } < 13.66$. So, the range for L is justified. When the channel order increases, the effect of impulse response of the channel will be more on the signature waveforms, thereby increasing the BER. After certain value of L, the BER is extremely high and reaches saturation. This interesting observation of the algorithm is shown in Fig. 9a when the channel order is increased to 10.

Fig. 9

BER performance analysis of a downlink W-CDMA system incorporating chaotic codes for varying, a channel orders (L), b smoothing factors (K) under Lognormal and Weibull fading channels

Furthermore, we perform another simulation by varying K from 2 to 6 and obtain both analytical and simulated BER for Weibull and Lognormal fading channel conditions. In this example, we use 1000 symbols to estimate the signature waveforms while SNR = 6 dB. As K increases, more and more data vectors are stacked into the $\mathbf{X}_m$ matrix, making the (data + noise) matrix appear with more signal vectors. Hence, the probability of the signal vectors affected by multipath fading is reduced, thus reducing the BER. In Fig. 9b, the performance improvement due to the smoothing of the data matrix is evident especially when K is relatively small. For higher value of K the BER reaches saturation.

The next performance measure metric is RMSE of the signature waveform estimate. The simulated RMSE is determined as in (10) and plotted for various SNR dB in Fig. 10. It is shown that the average RMSE improves with increase in SNR. The solid line represents the theoretical RMSE and the symbol * shows the simulated RMSE. Theoretically, $\mathbf{U}_\mathrm{o}{}^\mathrm{H} \mathbf{U}_o = \mathbf{I}$ [8] whereas in the simulation, $\mathbf{U}_\mathrm{o}^\mathrm{H} \mathbf{U}_\mathrm{o} =1.000065504$, which makes analytical and simulated RMSE to have excellent agreement between each other.

Fig. 10

Analytical versus simulated RMSE of a downlink W-CDMA system using chaotic codes in a Weibull fading channel for varying SNRs (dB)

Figure 11a, b show the RMSE for varying L and K, respectively, under Weibull and Lognormal fading channel conditions. Figure 11a indicates that the new algorithm is indeed robust to channel order selection upto a reasonable extent and performance is better for Weibull fading channel conditions. Fig. 11b shows that the RMSE improves with increasing K providing data diversity to W-CDMA systems using chaotic codes.

Fig. 11

RMSE performance analysis of a downlink W-CDMA system incorporating chaotic codes for varying, a channel orders (L), b smoothing factors (K) under Lognormal and Weibull fading channels

The subspace based blind channel algorithm is implemented for multiuser OFDM system. Figure 12 shows the estimated channel vector of user 1 with $\text{ N }_{\mathrm{c}}= 4$ subcarriers which is a vector of dimension 12 x 1. The real part of the channel coefficients are

$$\begin{aligned} \underline{\alpha \;}\;=\;\left\{ {\begin{array}{l} -0.0146 ,\;0.0140 ,\;-0.0145 ,\; -0.0520 ,\;0.0534 ,\;-0.0595 , \;0.5453,\;-0.5534 ,\;0.5627, \\ \; 0.0022 ,\;-0.0043 ,\;0.0045 \\ \end{array}} \right\} \end{aligned}$$

and the imaginary part of the channel coefficients are

$$\begin{aligned} \underline{\beta }=\left\{ {0, 0.0177, 0.0165, 0.1517, 0.0534, 0.1595, 0.0044, 0.0087, 0, 0.0008, 0.0005, 0.0001} \right\} . \end{aligned}$$

Taking norm of the estimated channel vector, we have

$$\begin{aligned} \left\| {\hat{{h}}_1 } \right\| \;=\;\sqrt{{\begin{array}{l} \left( {-0.0146} \right) ^{2}+\left( {\left( {0.0140} \right) ^{2}+\left( {0.0177} \right) ^{2}} \right) +\left( {\left( {-0.0145} \right) ^{2}+\left( {0.0165} \right) ^{2}} \right) \\ \quad +\left( {\left( {-0.0520} \right) ^{2}+\left( {0.1517} \right) ^{2}} \right) \\ \left( {\left( {0.0534} \right) ^{2}+\left( {0.0534} \right) ^{2}} \right) +\left( {\left( {-0.0595} \right) ^{2}+\left( {0.1595} \right) ^{2}} \right) +\left( {\left( {0.5453} \right) ^{2}+\left( {0.0044} \right) ^{2}} \right) \\ \left( {\left( {-0.5534} \right) ^{2}+\left( {0.0087} \right) ^{2}} \right) +\left( {0.5627} \right) ^{2}+\left( {\left( {0.0022} \right) ^{2}+\left( {0.0008} \right) ^{2}} \right) \\ \quad +\left( {\left( {-0.0043} \right) ^{2}+\left( {0.0005} \right) ^{2}} \right) \\ \left( {\left( {0.0045} \right) ^{2}+\left( {0.0001} \right) ^{2}} \right) \\ \end{array}}} \end{aligned}$$

$=$ 1.00003570, which satisfies the square of the unit norm of the estimated channel vector in the quadratic optimization problem shown in (47). Figure 13 shows the BER performance analysis of subspace based channel estimation for multiuser OFDM system using PN codes. It is observed that the BER improves much better for OFDM system when compared to single carrier modulation scheme, thereby proving that the proposed subspace based channel estimation algorithm works well for OFDM system.

Fig. 12

Estimated channel response of user 1 having $\text{ N }_{\mathrm{c}} = 4$ subcarriers under Weibull fading channel

Fig. 13

BER performance analysis of multiuser OFDM system under Weibull and Lognormal fading channels

6 Conclusions

A subspace-based approach for blind multiuser channel estimation in W-CDMA system using chaotic codes has been presented and compared with the system using PN codes. The subspace based algorithm exploits the fact that the signature waveform is the intersection of the signal subspace and the noise subspace, thus allowing it to be uniquely determined without the knowledge of the input signal. The analytical and simulated BER and RMSE performance of the system due to incorporation of signature waveform estimates in detection is presented for Weibull and Lognormal fading channel conditions

From the results, we observe that the signal constellation for each user shows that the proposed method clearly accomplishes satisfactory channel estimation. The system performance is evaluated by varying parameters like smoothing factor (K), channel order (L) and received SNR. The average RMSE and BER improves gradually when K is increased while RMSE and BER degrade when L is increased. The system provides satisfactory results when SNR is increased. It is observed that the analytical performance matches very well with the simulated performance. Finally, we have extended our analysis to a SISO–OFDM system and obtained the corresponding results, which prove that the proposed algorithm works well with the OFDM system, and thereby provides better system performance.