Coverage analysis of ultra-dense heterogeneous cellular networks with interference management

Abstract

Deploying ultra-dense small base stations (SBSs) in the coverage umbrella of a macro base station (MBS) requires proactive users offloading form MBS to SBSs to achieve maximum performance gain in heterogeneous cellular networks. However, it degrades the signal-to-interference-plus-noise ratio (SINR) of the offloaded users due to strong interference received from MBS. To improve users’ SINR, an efficient interference mitigation scheme is required to be used in conjunction with users offloading. Soft frequency reuse (SFR) is an attractive and spectrally efficient interference mitigation scheme that allocates available bandwidth among all cell users associated with $k{\text{BS}}$, where $k\in ({\text{M}},{\text{S}})$. To address the problem of interference, we use the SFR scheme together with power control factor $(\beta )$ to transmit at different power levels for interior and edge regions of $k{\text{BS}}$, i.e., $r^i_{k} \,{\text{and}}\, r^e_{k}$, respectively. We further consider uniform and nonuniform SBS distribution in the premises of MBS and analyse the effect of the SFR scheme on the proposed model with the help of Stochastic geometry. Mathematical expressions for coverage probabilities are derived and validated through simulations. Numerical results show that the proposed model achieves better coverage probability due to reduced interference. Moreover, nonuniform SBS distribution together with the SFR scheme further improves the performance gain of the proposed model.

1 Introduction

The demand for ubiquitous coverage with high data rates is increasing exponentially, which forces the cellular network operators to increase the capacity as well as improve the efficiency of networks. Mobile data usage has increased by 200% in recent years [2]. One of the cost effective and efficient schemes for increasing the network capacity is the ultra-dense deployment of small base stations (SBSs) inside the coverage umbrella of a macro base station (MBS) [3]. Poisson point process (PPP) has been extensively used to model and analyse heterogeneous cellular networks (HCNs) due to its tractability and accuracy [4, 5]. MBSs and SBSs are, therefore, spatially distributed using independent PPPs.

In HCNs, a user associates itself with $k{\text{BS}}$, where $k\in ({\text{M}},{\text{S}})$, based on maximum long term received power. An MBS transmits with higher power as opposed to SBSs and, thus, causes more users to get associated with it. This results in an imbalanced user distribution across HCNs and an inefficient resource utilization [6, 7]. To address this problem, the authors in [8] offload users from MBSs to low power SBSs for better resource utilization in HCNs. However, this results in reduce signal-to-interference-plus-noise ratio (SINR) due to strong interference received from offloaded base station, i.e., MBS, and thus acts as a limiting factor for performance gain of HCNs [9]. Hence, a proactive interference abating scheme is required together with the users offloading. In state-of-the-art, one of the potential interference abating schemes is the fractional frequency reuse (FFR) [10], where the entire frequency band, W, of the system is partitioned into small sub-bands to mitigate interference and, thus, improve coverage. However, only a fraction of W is allocated to each tier of BSs, therefore, this scheme proves to be spectrally inefficient. Another such interference abating scheme is the soft frequency reuse (SFR) [11]. SFR is spectrally more efficient, compared with FFR, because all bandwidth is made available for each tier of BSs.

In [12, 13], the authors divide MBS coverage region into two sub-regions, i.e., cell edge region and cell interior region for better coverage analysis. Users located in the edge region experience low SINR due to their distant locations [12]. However, users offloading in the cell interior region encounter severe interference due to close proximity of users to MBS that transmits with high power [13]. Additionally, SBSs in cell interior region have reduced coverage area due to strong signals received form MBS [12].

In [14], analytical models for FFR and SFR schemes, based on spatial PPP, are proposed. Furthermore, tractable expressions for each scheme are derived. The authors show that SFR is spectrally more efficient, whereas FFR provides highest gains in the lowest average SINR scenario. In [15], downlink multichannel model for SFR is analysed along with average user rate. Moreover, optimal combinations of association bias and SFR parameters are investigated. The authors show that SFR outperforms FFR in different load conditions. In [16], general mathematical models are developed for load balancing both with FFR and SFR while considering downlink transmission for HCNs. The authors show that FFR outperforms SFR in terms of SINR and rate coverage. However, it fails to provide the same spectral efficiency as that of SFR. Furthermore, the authors reduce the complex general mathematical expressions to simple closed-forms for rate and coverage analyses. In [17], load balancing together with reverse frequency allocation (RFA) scheme are analysed while considering two tier HCNs. Expressions for coverage probability while assuming both interior and edge regions of MBS are derived. There is significant improvement in coverage by using RFA with load balancing. In [18], RFA along with nonuniform SBS deployment are considered. SBSs are muted in cell interior region while they remain active in cell edge region. Expressions for both coverage probability and average rate are derived. Numerical results indicate that nonuniform SBS deployment in MBS coverage region shows significant improvement in rate coverage. Similarly, in [19] energy efficient user association and power allocation in millimeter wave-based HCNs are proposed while focusing on load balancing, energy harvesting, quality of service, and interference. Moreover, the complexity of the proposed model is analyzed and compared with existing schemes via simulations.

In this paper, we propose a nonuniform SBS deployment strategy where SBSs provide service to the users in cell edge region, $r^e_{{\text{M}}}$, and are assumed to be muted in cell interior region, $r^i_{{\text{M}}}$. Furthermore, we employ SFR, which is spectrally more efficient due to availability of entire bandwidth to the users of both MBS and SBSs.The major contributions of this paper are as follows:

• (1) Received SINR of the offloaded users degrades due to strong interference received from MBS. Therefore, we propose SFR employment to effectively mitigate the interference and use the spectrum efficiently.

• (2) To the best of our knowledge, SFR has been studied independently without considering nonuniform SBS distribution scenario. Therefore, we propose a unified model for nonuniform SBS deployment along with SFR to mitigate interference with optimal resource utilization while considering Rayleigh fading as a special case of Nakagami-m distribution.

• (3) Universal bottleneck in cellular networks is the edge user performance due to its distant location from serving BS. The results show that the proposed model reduces interference and, thus, significantly increases edge user performance gain.

• (4) Coverage probability is analysed against signal-to-noise ratio (SNR) value, SINR threshold, and MBS and SBS densities.

• (5) Results demonstrate that the SFR employment together with nonuniform SBS distribution requires fewer SBSs, which results in reduced interference and, hence, improves coverage probability.

The rest of the paper is organized as follows. In Sect. 2, network model for both uniform and nonuniform SBS deployment in MBS coverage area together with SFR is presented. In Sect. 3, coverage probability of the proposed scheme is analysed. In Sect. 4, numerical results are presented with discussion, and Sect. 5, concludes the paper. The notations used in the paper are listed in Table 1.

Table 1 Notation summary

2 System model

This section focuses on both uniform and nonuniform ultra-dense SBS deployment in the coverage area of MBS along with the SFR scheme and Nakagami-m fading. Furthermore, we develop mathematical preliminaries, which will be used in Sect. 3 to derive coverage probability expressions.

Fig. 1

SBS deployment scenario using SFR

Fig. 2

Ultra-dense uniform SBS deployment scenario using SFR. Here triangles denote the users associated with MBS and dots denote the users associated with SBS

Fig. 3

Ultra-dense uniform SBS deployment scenario using SFR. Here triangles denote the users associated with MBS, dots denote the users associated with SBS and red small circles represents the muted SBSs

2.1 Network model

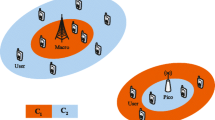
We consider two tier network model, where SBSs are overlaid in the coverage region of MBS to increase network capacity. SFR is used to mitigate interference caused by user offloading. Figure 1 shows the multi-tier BSs deployment along with SFR. Here R denotes the radius for entire coverage region of MBS. Coverage region of each tier is divided into two sub-regions, i.e., interior region, $r^i_c$, and edge region $r^e_c$ where $c\in ({\text{M}},{\text{S}})$. Moreover, due to SFR employment, the frequencies used by MBS in $r^i_{\text{M}}$ and $r^e_{\text{M}}$ are used by SBS in $r^e_{\text{S}}$ and $r^i_{\text{S}}$, respectively. According to SFR, total bandwidth F is divided into two identical sub-bands $F^{r^i_k}$ and $F^{r^e_\tau }$ [14], where $\tau \in ({\text{M}},{\text{S}}) \,{\text{and}}\, k\in ({\text{M}},{\text{S}}) \; \forall \; \tau \ne k$, s.t., $F^{r^i_k} =F^{r^e_\tau }$ and $F^{r^i_k} \bigcap F^{r^e_\tau } = \phi$, as shown in Table 2. The SFR sub-bands are used in alternate regions by $k{\text{BS}}$ and ${ \tau {\text{BS}} }$, s.t., complete frequency band $F = F^{r^i_\tau } \bigcup F ^{r^e_k}$ [15]. We consider a two-tier cellular network model employing SFR while assuming uniform and nonuniform SBS deployment scenarios as shown in Figs. 2 and 3, respectively. MBSs are considered as first tier, while SBSs as second tier. MBS, SBSs and users are spatially distributed using independent PPPs, $\psi _{\text{M}}$, $\psi _{\text{S}}$, and $\psi _u$, respectively. For co-channel network deployment, all available sub-channels are shared by both tiers. Analysis are performed on typical user ${\text{T}}_u$ located at the origin, which is allowed by Slivnyak theorem [18]. For the sake of tractability, standard path loss model is assumed with path loss exponent $\alpha > 2$, whereas noise is considered as additive with power $\sigma ^2$. Furthermore, we assume that $\alpha _k$ = $\alpha _{\text{S}}$ = $\alpha$. Fading is modeled using Nakagami-m distribution with Rayleigh fading as a special case when ${\text{m}}=1$. To address coverage issues in cell edge region, $r^e_k$, we use power control factor, $\beta$, to transmit high power in $r^e_k$ as compared to cell interior region, $r^i_k$, where, $k\in ({\text{M}},{\text{S}})$ [14]. Users in $r^i_k$ are served with low transmit power, i.e, $\beta P_t$ with $\beta =1$, whereas users in $r^e_k$ are served with high transmit power level, i.e., $\beta P_t$ with $\beta > 1$.

2.2 System model with uniform and nonuniform SBS deployment scenario

Coverage areas of each tier BSs are divided into $r^i_k$ and $r^e_k$ with frequency bands distributed using SFR. SBSs are uniformly deployed via PPP with density $\rho _{\text{S}}$, throughout the coverage area of MBS, as shown in Fig. 2. Similarly, Fig. 3 shows nonuniform SBS distribution scenario where SBSs in $r^i_{\text{M}}$ are muted due to reasonable MBS coverage, severe interference received by offloaded user, reduced SBS coverage and fewer SBS user associations [12, 13]. Here, red circular discs show the muted SBSs. Furthermore, triangles and dots represent the user’s association with MBS and SBSs, respectively, and $d_1$ and $d_2$ represent the radii of $r^i_{\text{M}}$ and $r^e_{\text{M}}$, respectively.

Table 2 Frequency distribution using SFR

2.3 Downlink and uplink SINR analysis

Downlink ($D_L$) and uplink ($U_L$) SINR received at ${\text{T}}_{u}^{r^{e}_{k}}$ and $k{\text{BS}}$, respectively, while considering both uniform (U) and nonuniform (NU) SBS distribution are calculated, respectively, as

$$\begin{aligned} \varGamma ^{r^{e}_k}_{D_L,k}({\mathcal { S}},U)&= \frac{ P_{r,D_L,{\mathcal { S}}} }{I_{tot,D_L}^{r^e_k} (U)+\sigma ^2}, \end{aligned}$$

(1)

$$\begin{aligned} \varGamma ^{r^{e}_k}_{U_L,k}({\mathcal { S}},U)&= \frac{ P_{r,U_L,{\mathcal { S}}}}{I_{tot, U_L}^{r^e_k}(U) +\sigma ^2}, \end{aligned}$$

(2)

$$\begin{aligned} \varGamma ^{r^{e}_k}_{D_L,k}({\mathcal { S}},NU) &= \frac{ P_{r,D_L,{\mathcal { S}}} }{I_{tot,D_L}^{r^e_k} (NU)+\sigma ^2}, \end{aligned}$$

(3)

and

$$\begin{aligned} \varGamma ^{r^{e}_k}_{U_L,k}({\mathcal { S}},NU) = \frac{ P_{r,U_L,{\mathcal { S}}}}{I_{tot, U_L}^{r^e_k}(NU) +\sigma ^2}. \end{aligned}$$

(4)

Here $\varGamma ({\varvec{\cdot }})$ represents the received SINR at ${\text{T}}_u$, ${\mathcal { S}}$ denotes the distance between $k{\text{BS}}$ and ${\text{T}}_u$. $P_{r,D_L,{\mathcal { S}}}$ is the power received by ${\text{T}}_u$ from $k{\text{BS}}$ in $D_L$ direction, while $P_{r,U_L,{\mathcal { S}}}$ is the power received by $k{\text{BS}}$ from ${\text{T}}_u$ in $U_L$ direction.

Table 3 Interference distribution using SFR for Uniform SBS Deployment

Table 4 Interference distribution using SFR for nonuniform SBS deployment

Interference distribution scenarios of ${\text{T}}_u$ associated with $k{\text{BS}}$ while assuming uniform and nonuniform SBS deployment scenarios are given in Tables 3 and 4, respectively. For uniform deployment scenario, SBSs are distributed using independent PPP in the region R(U) of MBS, where $R(U)=\bigcup _{j\in \{i,e\}} r^j_{\text{M}}$ with density $\rho _{\text{S}}^{R(U)} \in \bigcup _{j\in \{i,e\}} r^j_{\text{M}}$. Similarly, for nonuniform deployment scenario, SBSs are randomly distributed using independent PPP in the region R(NU) s.t., $R(NU)=r^e_{\text{M}}$ with $\rho _{\text{S}}^{R(NU)} \in r^e_{\text{M}}$.

Total $D_L$ and $U_L$ interference received at ${\text{T}}_{u}^{r^{e}_{k}}$, while considering uniform SBS deployment scenario, is the sum of $U_L$ and $D_L$ interference received from users located in $r^e_k$ while associated with $k{\text{BS}}$ and from users located in $r^i_\tau$ while associated with $\tau$BS. Total $D_L$ and $U_L$ interference, i.e., $I_{tot,D_L}^{r^e_k} (U)$ and $I_{tot, U_L}^{r^e_k}(U)$, are therefore given respectively as

$$\begin{aligned} I_{tot,D_L}^{r^e_k} (U) &= I_{D_L}^{r^e_k} + I_{U_L}^{r^e_k} + I_{D_L }^{r^i_\tau }+I_{U_L }^{r^i_\tau }, \;\; \forall \;\rho _{\text{S}}^{R(U)}, \end{aligned}$$

(5)

$$\begin{aligned} I_{tot, U_L}^{r^e_k}(U)&= I_{U_L}^{r^e_k} + I_{D_L}^{r^e_k} + I_{U_L }^{r^i_\tau }+I_{D_L }^{r^i_\tau }, \;\; \forall \;\rho _{\text{S}}^{R(U)}. \end{aligned}$$

(6)

Similarly, total $D_L$ and $U_L$ interference received at ${\text{T}}_{u}^{r^{e}_{k}}$, i.e., $I_{tot,D_L}^{r^e_k} (NU)$ and $I_{tot, U_L}^{r^e_k}(NU)$, respectively, while considering nonuniform SBS deployment scenario, is the sum of $U_L$ and $D_L$ interference received from users located in $r^e_k$ while associated with $k{\text{BS}}$ and from users located in $r^i_\tau$ while associated with $\tau$BS, and can be written as

$$\begin{aligned} I_{tot,D_L}^{r^e_k} (NU) &= I_{D_L}^{r^e_k} + I_{U_L}^{r^e_k} + I_{D_L }^{r^i_\tau }+I_{U_L }^{r^i_\tau },\;\; \forall \;\rho _{\text{S}}^{R(NU)}, \end{aligned}$$

(7)

$$\begin{aligned} I_{tot, U_L}^{r^e_k}(NU) &= I_{U_L}^{r^e_k} + I_{D_L}^{r^e_k} + I_{U_L }^{r^i_\tau }+I_{D_L }^{r^i_\tau },\;\; \forall \;\rho _{\text{S}}^{R(NU)}. \end{aligned}$$

(8)

Here $k\in ({\text{M}},{\text{S}}) \,{\text{and}}\, \tau \in ({\text{M}},{\text{S}})$$\forall \; k \ne \tau$. $I_{D_L}^{r^e_k} (\cdot )$ is the $D_L$ interference received by ${\text{T}}_{u}^{r^{e}_{k}}$ from $k{\text{BS}}$, $I_{U_L}^{r^e_k}(\cdot )$ is the $U_L$ interference received by $k{\text{BS}}$ from ${\text{T}}_{u}^{r^{e}_{k}}$, $I_{D_L }^{r^i_\tau }(\cdot )$ is the $D_L$ interference received by ${\text{T}}_u^{r^i_\tau }$ from $\tau$BS, and $I_{U_L }^{r^i_\tau }(\cdot )$ is the $U_L$ interference received by $\tau$BS from ${\text{T}}_u^{r^i_\tau }$.

The total interference expressions of Eqs. (5) and (6) can be rewritten as

$$\begin{aligned} \begin{aligned} I_{tot,D_L}^{r^e_k}(U)&= \sum _{x_k\in \varPsi ^{r^e_k}_k {\backslash d_k}} \beta {\text{P}}_{t,D_L}^{k}{\text{h}}_{x_k}^{r^e_k}||x_k||^{-\alpha } +\sum _{y_k\in \varPsi ^{r^e_k}_u} {\text{P}}_{t,U_L}^u{\text{h}}_{y_k}^{r^e_k}||y_k||^{-\alpha }\\&\quad +\,\sum _{x_\tau \in \varPsi ^{R(U)}_\tau } {\text{P}}_{t,D_L}^{\tau }{\text{h}}_{x_\tau }^{r^i_\tau }||x_\tau ||^{-\alpha } +\sum _{y_\tau \in \varPsi ^{r^i_\tau }_u } {\text{P}}_{t,U_L}^{u}{\text{h}}_{y_\tau }^{r^i_\tau }||y_\tau ||^{-\alpha }\;\forall \;\rho _{\text{S}}^{R(U)}, \end{aligned} \end{aligned}$$

(9)

and

$$\begin{aligned} \begin{aligned} I_{tot,U_L}^{r^e_k}(U)&= \sum _{y_k\in \varPsi ^{r^e_k}_u{\backslash d_k}} {\text{P}}_{t,U_L}^u{\text{h}}_{y_k}^{r^e_k}||y_k||^{-\alpha } +\sum _{x_k\in \varPsi ^{r^e_k}_k } \beta {\text{P}}_{t,D_L}^{k}{\text{h}}_{x_k}^{r^e_k}||x_k||^{-\alpha }\\&\quad +\sum _{y_\tau \in \varPsi ^{r^i_\tau }_u } {\text{P}}_{t,U_L}^{u}{\text{h}}_{y_\tau }^{r^i_\tau }||y_\tau ||^{-\alpha } +\sum _{x_\tau \in \varPsi ^{R(U)}_\tau } {\text{P}}_{t,D_L}^{\tau }{\text{h}}_{x_\tau }^{r^i_\tau }||x_\tau ||^{-\alpha }\;\forall \;\rho _{\text{S}}^{R(U)}. \end{aligned} \end{aligned}$$

(10)

where $x_k$ is the distance between $k{\text{BS}}$ and users in $D_L$ direction, $x_\tau$ is the distance between $\tau$BS and users in $D_L$ direction, $y_k$ is the distance between $k{\text{BS}}$ and users in $U_L$ direction, and $y_\tau$ is the distance between $\tau$BS and users in $U_L$ direction.

Similarly, total $D_L$ and $U_L$ interference received by ${\text{T}}_{u}^{r^{e}_{k}}$, i.e., $I_{tot, D_L}^{r^e_k}(NU)$ and $I_{tot, U_L}^{r^e_k}(NU)$, while considering nonuniform SBS deployment scenario can be derived in a similar way as Eqs. (9) and (10), and are given by

$$\begin{aligned} \begin{aligned} I_{tot, D_L}^{r^e_k}(NU)\,&= \sum _{x_k\in \varPsi ^{r^e_k}_k {\backslash d_k}} \beta {\text{P}}_{t,D_L}^{k}{\text{h}}_{x_k}^{r^e_k}||x_k||^{-\alpha } + \sum _{y_k\in \varPsi ^{r^e_k}_u} {\text{P}}_{t,U_L}^u{\text{h}}_{y_k}^{r^e_k}||y_k||^{-\alpha }\\&\quad +\,\sum _{x_\tau \in \varPsi ^{R(NU)}_\tau } {\text{P}}_{t,D_L}^{\tau }{\text{h}}_{x_\tau }^{r^i_\tau }||x_\tau ||^{-\alpha } +\sum _{y_\tau \in \varPsi ^{r^i_\tau }_u } {\text{P}}_{t,U_L}^{u}{\text{h}}_{y_\tau }^{r^i_\tau }||y_\tau ||^{-\alpha }\;\;\forall \;\rho _{\text{S}}^{R(NU)}, \end{aligned} \end{aligned}$$

(11)

and

$$\begin{aligned} \begin{aligned} I_{tot, U_L}^{r^e_k}(NU)\,&= \sum _{y_k\in \varPsi ^{r^e_k}_u{\backslash d_k}} {\text{P}}_{t,U_L}^u{\text{h}}_{y_k}^{r^e_k}||y_k||^{-\alpha } +\sum _{x_k\in \varPsi ^{r^e_k}_k } \beta {\text{P}}_{t,D_L}^{k}{\text{h}}_{x_k}^{r^e_k}||x_k||^{-\alpha }\\&\quad +\sum _{y_\tau \in \varPsi ^{r^i_\tau }_u } {\text{P}}_{t,U_L}^{u}{\text{h}}_{y_\tau }^{r^i_\tau }||y_\tau ||^{-\alpha } +\sum _{x_\tau \in \varPsi ^{R(NU)}_\tau } {\text{P}}_{t,D_L}^{\tau }{\text{h}}_{x_\tau }^{r^i_\tau }||x_\tau ||^{-\alpha }\;\;\forall \;\rho _{\text{S}}^{R(NU)}. \end{aligned} \end{aligned}$$

(12)

Equations (9) and (10) are similar to Eqs. (11) and (12), respectively, except the main difference of SBS density, which ultimately reduces interference in nonuniform SBS deployment scenario. Here ${\text{h}}_{x_k}^{r^e_k}$, ${\text{h}}_{y_k}^{r^e_k}$, ${\text{h}}_{x_\tau }^{r^i_\tau }$ and ${\text{h}}_{y_\tau }^{r^i_\tau }$ are the fading coefficients that follow Nakagami-m distribution. It is worth mentioning here that Nakagami-m is more suitable to be used for mobile applications [20]. It also has the inherent ability to model a wide variety of other fading environments, such as one-sided Gaussian distribution (${\text{m}}=1/2$) and Rayliegh distribution (${\text{m}}=1$). It closely matches the Rician distribution $({\text{m}} > 1)$ and no fading (${\text{m}}=\infty$) [20]. Signals to the users in $r^e_k$ are transmitted with high power, i.e., $\beta P_{t,k }$ where $\beta > 1$, whereas signals to users in $r^i _k$ are fed with low power, i.e., $\beta P_{t,k }$ with power control factor, $\beta = 1$.

2.4 Distribution of statistical distances ${Y}_{k}$ between associated $k{\text{BS}}$ to the ${\text{T}}_{u}$

Based on the model we have developed above, the distribution of distances ${Y}_{k}$ between associated $k{\text{BS}}$ and the ${\text{T}}_u$ is derived in the following.

Considering void probability property of PPP [21, 22], the probabilities that ${\text{T}}_u$ is located in $r^e_{\text{M}}$ and $r^i_{\text{M}}$, i.e., ${\text{P}}_{ {\text{T}}_{u}^{r^{e}_{\text{M}}} }$ and ${\text{P}}_{ {\text{T}}_u^{r^{i}_{\text{M}}} }$, repectively, are

$$\begin{aligned} \begin{aligned} {\text{P}}_{ {\text{T}}_u^{r^e_k} }={\text{exp}}\bigg ({-\rho _{k}\pi \big ({d_{1}^{r_k^i}}\big )^{2}}\bigg ), \end{aligned} \end{aligned}$$

(13)

and

$$\begin{aligned} \begin{aligned}&{\text{P}}_{ {\text{T}}_u^{r^{i}_{k}} }=1-{\text{P}}_{ {\text{T}}_u^{r^{e}_{k}} } \;\;\; \forall \;\;k\in \{{\text{M}}\}. \end{aligned} \end{aligned}$$

(14)

Here $\pi ({d_{1}^{r_k^i}})^{2}$ and $d_{1}^{r_k^i}$ denote the area and radius of $r^i_k$, respectively, with $\rho _{k}$ represents the $k{\text{BS}}$ density.

Assuming user association scheme, based on maximum received power,¹ PDF of association distances for $k{\text{BS}}$, located at $y_{k}$ to the ${\text{T}}_u$, i.e, $f_{Y_{k}}(y_{k})$, is given as [23]

$$\begin{aligned} f_{Y_{k}}(y_{k}) = 2\pi \rho _{k}y_{k}{\text{exp}} {(-\,\pi \rho _{k}y_{k}^2)}. \end{aligned}$$

(15)

Similarly, conditional PDF of the distances for ${\text{T}}_u$ in $r^i_k$ and $r^e_k$ of each tier, while associated with $k{\text{BS}}$, i.e., $f_{Y_{k}|{ {\text{T}}_u^{r^i_k}}}(y_{k})$ and $f_{Y_{k}|{ {\text{T}}_u^{ r^e_k}}}(y_{k})$, are given, respectively, as [24, 25]

$$\begin{aligned} f_{Y_{k}|{ {\text{T}}_u^{r^i_k}}}(y_{k})=\frac{2\pi \rho _{k}y_{k}{\text{exp}}{(-\,\rho _{k}\pi y_{k}^{2})}}{1-{\text{exp}}\left( {-\,\rho _{\text{M}}\pi \left( {d_{1}^{r_{\text{M}}^i}}\right) ^{2}}\right) }, \end{aligned}$$

(16)

and

$$\begin{aligned} f_{Y_{k}|{ {\text{T}}_u^{ r^e_k}}}(y_{k})=\frac{2\pi \rho _{k}y_{k}{\text{exp}}{(-\,\rho _{k}\pi y_{k}^{2})}}{{\text{exp}}\left( {-\,\rho _{\text{M}}\pi \left( {d_{1}^{r_{\text{M}}^i}}\right) ^{2}}\right) }. \end{aligned}$$

(17)

3 Coverage probability

Definition 1

(Coverage Probability) Downlink coverage probability can be defined as the successful communication between users and associated $k{\text{BS}}$, provided that received SINR, $\varGamma _{k}$, at user is greater then its predefined threshold, $\gamma _k$ [26], i.e.,

$${\text{P}}_{{k,D_{L} }}^{{r_{k}^{e} }} (\gamma _{k} ) \triangleq P\left[{\varGamma _{k}^{{r_{k}^{e} }} (y_{k} ) > \gamma _{k} |{\text{T}}_{u}^{{r_{k}^{e} }} } \right] = {\text{E}}\left[ {P\left[{\varGamma _{k}^{{r_{k}^{e} }} (y_{k} ) > \gamma _{k} |{\text{T}}_{u}^{{r_{k}^{e} }} } \right]} \right].$$

Users with similar frequency bands in the cell receive increased interference, which ultimately degrades the received SINR and, hence, the coverage probability. In this section, we develop expressions for coverage probability assuming ${\text{T}}_u$ located in $r^e_k$, while considering both the uniform and nonuniform system models derived in the previous section.

3.1 Coverage probability for uniform SBS distribution scenario

$D_L$ and $U_L$ coverage probabilities of ${\text{T}}_u^{ r^e_k}$ associated with $k{\text{BS}}$ along with uniform SBS distribution, i.e., ${\text{P}}^{ r^e_k }_{k,D_L}{(\gamma _{k},U)}$ and ${\text{P}}^{ r^e_k }_{k,U_L}{(\gamma _{k},U)}$ are given, respectively, as

$$\begin{aligned} \begin{aligned} {\text{P}}^{ r^e_k }_{k,D_L}{(\gamma _{k},U)}&={\frac{1}{{{\text{exp}}\left( -\,\rho _{\text{M}}\pi r{_{1}^{2}}\right) }}}\int _{d_1^{r^e_k}}^{d_2^{r^e_k}}{\text{exp}}\left( \frac{-\,\gamma _k}{\eta _k}\right) {\text{exp}}{\left( -\,2\pi \left[ \rho _{k}^{ r^e_k} {\text{O}}_{k}^{ r^e_k}+\rho _{u}^{ r^e_k} {\text{O}}_{u}^{ r^e_k}+\rho _{\tau }^{ R(U)} {\text{O}}_{\tau }^{r^i_\tau } +\rho _{u}^{ r^{i}_\tau } {\text{O}}_{u}^{r^i_\tau } \right] \right) }\\&\quad \times \,\left( {2\pi \rho _{k}y_{k}{\text{exp}}{(-\,\rho _{k}\pi y_{k}^{2})}}\right) dy_k, \end{aligned} \end{aligned}$$

(18)

and

$$\begin{aligned} \begin{aligned} {\text{P}}^{ r^e_k }_{k,U_L}{(\gamma _{k},U)}&={\frac{1}{{{\text{exp}}(-\rho _{\text{M}}\pi r{_{1}^{2}})}}}\int _{d_1^{r^e_k}}^{d_2^{r^e_k}}{\text{exp}}\left( \frac{-\gamma _k}{\eta _k}\right) {\text{exp}}{\left( -2\pi \left[ \rho _{u}^{ r^e_k} {\text{O}}_{u}^{ r^e_k}+\rho _{k}^{ r^e_k} {\text{O}}_{k}^{ r^e_k}+\rho _{u}^{ r^{i}_\tau } {\text{O}}_{u}^{r^i_\tau }+\rho _{\tau }^{ R(U)} {\text{O}}_{\tau }^{r^i_\tau } \right] \right) }\\&\quad \times \left( {2\pi \rho _{k}y_{k}{\text{exp}}{(-\rho _{k}\pi y_{k}^{2})}}\right) dy_k, \end{aligned} \end{aligned}$$

(19)

where $\eta _k$ is the $k{\text{BS}}$ transmitted SNR, and $\rho _{k}$ and $\rho _{\tau }$ represent the densities of $k{\text{BS}}$ and $\tau$BS, respectively. Similarly ${\text{O}}_{k}^{ r^e_k}$, ${\text{O}}_{u}^{ r^e_k}$, ${\text{O}}_{\tau }^{r^i_\tau }$ and ${\text{O}}_{u}^{r^i_\tau }$, are given, respectively, as

$$\begin{aligned} {\text{O}}_{k}^{ r^e_k} &= \int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{x_{k}}{1+\left( s\beta {\text{P}}_{t,D_L}^{k}\right) ^{-1}||x_{k}||^{\alpha }}\right) dx_{k}, \end{aligned}$$

(20)

$$\begin{aligned} {\text{O}}_{u}^{ r^e_k} &= int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{y_{k}}{1+\left( s{\text{P}}_{t,U_L}^u\right) ^{-1}||y_{k}||^{\alpha }}\right) dy_{k}, \end{aligned}$$

(21)

$$\begin{aligned} {\text{O}}_{\tau }^{r^i_\tau } &= \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{x_\tau }{1+\left( s {\text{P}}_{t,D_L}^{\tau }\right) ^{-1}||x_{\tau }||^{\alpha }} \right) dx_{\tau }, \end{aligned}$$

(22)

and

$$\begin{aligned} {\text{O}}_{u}^{r^i_\tau } = \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{y_\tau }{1+\left( s {\text{P}}_{t,U_L}^{u}\right) ^{-1}||y_{\tau }||^{\alpha }} \right) dy_{\tau }. \end{aligned}$$

(23)

Here ${\text{P}}_{t}^{k}$, ${\text{P}}_{t}^{\tau }$ and ${\text{P}}_{t}^{u}$ are the power transmitted by $k{\text{BS}}$, $\tau$BS and users, respectively, where $k\in ({\text{M}},{\text{S}})$ and $\tau \in ({\text{M}},{\text{S}})$$\forall \; k\ne \tau$.

3.2 Coverage probability for nonuniform SBS distribution scenario

$D_L$ and $U_L$ coverage probability of ${\text{T}}_u^{ r^e_k}$ associated with $k{\text{BS}}$, along with nonuniform SBS distribution, ${\text{P}}^{ r^e_k }_{k,D_L}{(\gamma _{k},NU)}$, ${\text{P}}^{ r^e_k }_{k,U_L}{(\gamma _{k},NU)}$ are given, respectively, as

$$\begin{aligned} \begin{aligned} {\text{P}}^{ r^e_k }_{k,D_L}{(\gamma _{k},NU)}&={\frac{1}{{{\text{exp}}(-\rho _{\text{M}}\pi r{_{1}^{2}})}}}\int _{d_1^{r^e_k}}^{d_2^{r^e_k}}{\text{exp}}\left( \frac{-\gamma _k}{\eta _k}\right) {\text{exp}}{\left( -2\pi \left[ \rho _{k}^{ r^e_k} {\text{O}}_{k}^{ r^e_k}+\rho _{u}^{ r^e_k} {\text{O}}_{u}^{ r^e_k}+\rho _{\tau }^{ R(NU)} {\text{O}}_{\tau }^{r^i_\tau } +\rho _{u}^{ r^{i}_\tau } {\text{O}}_{u}^{r^i_\tau } \right] \right) }\\&\quad \times \left( {2\pi \rho _{k}y_{k}{\text{exp}}{(-\rho _{k}\pi y_{k}^{2})}}\right) dy_k, \end{aligned} \end{aligned}$$

(24)

and

$$\begin{aligned} \begin{aligned} {\text{P}}^{ r^e_k }_{k,U_L}{(\gamma _{k},NU)}&={\frac{1}{{{\text{exp}}(-\rho _{\text{M}}\pi r{_{1}^{2}})}}}\int _{d_1^{r^e_k}}^{d_2^{r^e_k}}{\text{exp}}\left( \frac{-\gamma _k}{\eta _k}\right) {\text{exp}}{\left( -2\pi \left[ \rho _{u}^{ r^e_k} {\text{O}}_{u}^{ r^e_k}+\rho _{k}^{ r^e_k} {\text{O}}_{k}^{ r^e_k}+\rho _{u}^{ r^{i}_\tau } {\text{O}}_{u}^{r^i_\tau }+\rho _{\tau }^{R(NU)} {\text{O}}_{\tau }^{r^i_\tau } \right] \right) }\\&\quad \times \left( {2\pi \rho _{k}y_{k}{\text{exp}}{(-\rho _{k}\pi y_{k}^{2})}}\right) dy_k, \end{aligned} \end{aligned}$$

(25)

where $\rho ^{R(NU)}_\tau$ denotes nonuniform SBS distribution, and ${\text{O}}_{k}^{ r^e_k}$, ${\text{O}}_{u}^{ r^e_k}$, ${\text{O}}_{\tau }^{r^i_\tau }$ and ${\text{O}}_{u}^{r^i_\tau }$ are defined, respectively, as

$$\begin{aligned} {\text{O}}_{k}^{ r^e_k}&= \int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{x_{k}}{1+\left( s\beta {\text{P}}_{t,D_L}^{k}\right) ^{-1}||x_{k}||^{\alpha }}\right) dx_{k}, \end{aligned}$$

(26)

$$\begin{aligned} {\text{O}}_{u}^{ r^e_k}&= \int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{y_{k}}{1+\left( s{\text{P}}_{t,U_L}^u\right) ^{-1}||y_{k}||^{\alpha }}\right) dy_{k}, \end{aligned}$$

(27)

$$\begin{aligned} {\text{O}}_{\tau }^{r^i_\tau }&= \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{x_\tau }{1+\left( s {\text{P}}_{t,D_L}^{\tau }\right) ^{-1}||x_{\tau }||^{\alpha }} \right) dx_{\tau }, \end{aligned}$$

(28)

and

$$\begin{aligned} {\text{O}}_{u}^{r^i_\tau } = \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{y_\tau }{1+\left( s {\text{P}}_{t,U_L}^{u}\right) ^{-1}||y_{\tau }||^{\alpha }} \right) dy_{\tau }. \end{aligned}$$

(29)

Expressions for coverage probabilities obtained in this section are based on the mathematical preliminaries derived for the SFR scheme in Sect. 2.3. Numerical results for the above expressions are discussed in Sect. 4. Proof of Eq. 24) is given in Appendix.

4 Results and discussion

In this section, we provide discussion on different numerical results for the employment of SFR while considering both uniform and nonuniform SBS distribution scenario in the coverage region of MBS. The results are derived using Matlab (Version 2017a) with parameters listed in Table 5.

Figure 4 presents MBS coverage probability against different values of the SINR thresholds. There are three types of comparisons in this result, i.e., the proposed model is used: (1) with SFR scheme and load balancing, (2) without SFR scheme while considering load balancing, and (3) without SFR scheme and no load balancing. The result demonstrates that increasing SBS power in $r^e_{\text{M}}$ results in improved coverage due to load balancing across the network. Moreover, SFR with $\beta = 5$ dB outperforms rest of the analysis scenarios.

Figure 5 presents coverage probability against $\rho _{\text{M}}$ for uniform and nonuniform SBS distribution scenarios with and without employing SFR. These results are drawn using $D_L$ coverage probability Eqs. (18) and (24) for both uniform and nonunifrom SBS deployment scenarios while assuming SINR threshold, $\gamma _k = -25$ dB. We observe significant degradation in the coverage probability when there is no SFR employed. However, with the introduction of SFR, our proposed model becomes more resilient to interference and, therefore, coverage probability is notably improved. Furthermore, it can be observed from the figure that nonuniform SBS deployment results in better coverage probability against other aforementioned scenarios. This coverage improvement is due to reduced interference caused by fewer number of active SBSs. It can be deduced from the figure that $\rho _{\text{M}}(NU) \approx 4-8\; {{\text{MBSs}}}/( \pi (R(U))^2 )\;{\text{km}}^{2}$ gives the optimum coverage for the proposed model.

Fig. 4

Coverage probability versus SINR threshold

Fig. 5

Coverage probability versus $\rho _{\text{M}}$

Fig. 6

Coverage probability versus SINR threshold in $r^e_{\text{M}}$

Fig. 7

Coverage probability versus received SNR in $r^e_{\text{M}}$

Fig. 8

Coverage probability versus SBS density in $r^e_{\text{M}}$

Figure 6 compares the coverage probability with SINR threshold, $\gamma _k$, for the ${\text{T}}_u$ located in $r^e_{\text{M}}$ using Eqs. (18) and (24). The figure also compares uniform and nonuniform SBS distribution scenarios while assuming both SFR and no SFR for interference mitigation with $\rho _{\text{M}}(U)= 6\;{{\text{MBSs}}}/( \pi (R(U))^2 )\;{\text{km}}^2$, $\rho _{\text{M}}(NU) = 3\;{{\text{MBSs}}}/( \pi (R(NU))^2 )\;{\text{km}}^2$, $\rho _{\text{S}}(U) = 16\;{{\text{SBSs}}}/( \pi (R(U))^2 )\;{\text{km}}^2$, $\rho _{\text{S}}(NU) = 8\;{{\text{SBSs}}}/( \pi (R(NU))^2 )\;{\text{km}}^2$, and $\rho _{u}(U) = 45\; {\text{users}}/( \pi (R(U))^2 )\;{\text{km}}^2$. The plots show that SFR along with nonuniform SBS deployment has significant impact on interference reduction and, thus, results in improved coverage probability. Furthermore, it can be observed that higher values of $\gamma _{k }$ lead to degradation in coverage probability due to reduced user association with $k{\text{BS}}$.

In Fig. 7, coverage probability is compared with SNR (MBS signal power affected by noise $\sigma ^2$). Here $\gamma _k = -25$ dB. As depicted in the figure, nonuniform SBS distribution scenario outperforms uniform SBS distribution scenario in terms of better coverage probability for different values of $\eta _{k}$. Furthermore, the results in this figure establish the fact that increasing the value of $\eta _{k}$ produces better coverage probability due to reduced interference.

In Fig. 8, coverage probabilities are presented against SBS densities for $\gamma _{k} =-25$ dB, while considering both uniform and nonuniform SBS distribution scenarios. This figure shows that increasing number of SBSs deployed inside the coverage area of MBS results in decreased coverage probability, which is due to increased interference received from dense SBS deployment. Furthermore, degradation in coverage probability is smaller as compared with Fig. 5. This is due to higher transmitted power by MBS compared with SBS. Here, ${\text{P}}_t^{\text{M}}$, ${\text{P}}_t^{\text{S}}$ and ${\text{P}}_t^u$ are set to 40 dB, 20 dB and 20 dB, respectively.

Fig. 9

Coverage probability versus $r^{i}_{\text{M}}$ radius

Table 5 Simulation parameters

Figure 9 compares coverage probability with radius of $r^i_{\text{M}}$ for $\gamma _k= -20$ dB. From the figure it can be observed that the optimum value of $d_1^{r^i_{\text{M}}}$ is approximately 70% of $d_2^{r^e_{\text{M}}}$. It can also be observed from the figure that beyond this point, performance improvement, in terms of coverage probability, degrades. Furthermore, nonuniform SBS deployment with SFR scheme outperforms rest of the simulation scenarios.

5 Conclusion

In ultra-dense SBS deployment, offloading of users from MBS to SBSs in edge coverage region of MBS has a significant impact on SINR degradation due to increased interference received from offloaded MBS users. For interference mitigation, the proposed model considers the SFR scheme along with nonuniform SBS distribution scenario. Expressions for coverage probabilities are derived for both uniform and nonuniform distribution scenarios. Numerical results indicate that the proposed model becomes more resilient to interference by using the SFR scheme. Similarly, analysis of SFR with nonuniform SBS deployment shows significant improvement in coverage probability due to reduced interference and efficient utilization of SBS resources. Results also show that optimum radius for interior coverage region of MBS is about 70% of radius for edge coverage region of MBS. Furthermore, increasing the densities of MBS and SBS adversely affect the coverage probability due to increased interference, while decreasing the value of SINR threshold results in improved coverage due to more number of associated users. As a future direction, this work can be extended to find the most favorable value of $\beta$ in the proposed model to achieve optimal load balancing among MBS and SBSs.

Appendix

Proof

Proof of Eq. (24)

$$\begin{aligned}&{\text{P}}^{ r^e_k }_{k,D_L}{(\gamma _{k},NU)} ={\text{E}}\left[P\left[ \varGamma _{k}^{r^e_k}(y_{k})>\gamma _{k}|{\text{T}}_{u}^{r^e_k}\right] \right] \\&\quad =\int _{d_{1}^{r_{\text{M}}^e}}^{d_{2}^{r_{\text{M}}^e}}P\left[ \varGamma _{k }^{r^e_k}(y_{k})>\gamma _{k}|{\text{T}}_u^{r^e_k}\right] f_{Y_{k}|{{\text{T}}_u^{r^e_k} }}(y_{k})dy_{k}, \end{aligned}$$

(30)

where $\varGamma _{k}$ and $\gamma _{k}$ are, respectively, the SINR and its threshold for $k{\text{BS}}$. $P[\varGamma _{k }^{r^e_k}(y_{k})>\gamma _{k}|{\text{T}}_u^{r^e_k}]$ denotes the success probability, which is defined as the received SINR greater than $\gamma _{k}$ at ${\text{T}}_u^{r^e_k}$, while associated with $k{\text{BS}}$. It can be further written as

$$\begin{aligned}&P[\varGamma _{k}^{r^e_k}(y_{k})>\gamma _{k}|{\text{T}}_u^{r^e_k}]\nonumber \\&\quad {\mathop { = }\limits ^{i}}\,\text {E}_{I_{tot, D_L}^{r^e_k}(NU)}\bigg [\bigg ( \dfrac{ P_k h_r r^{-\alpha }}{I_{tot, D_L}^{r^e_k}(NU) +\sigma ^2} \bigg )>\gamma _{k}|{\text{T}}_u^{r^e_k}\bigg ]\nonumber \\&\quad {\mathop { = }\limits ^{ii}}\, \text {exp}\bigg (\dfrac{-\gamma _{k}}{\eta _k}\bigg ) \text {E}_{I_{tot, D_L}^{r^e_k}(NU)}[\text {exp}(-s{I_{tot, D_L}^{r^e_k}(NU)})]\nonumber \\&\quad {\mathop { = }\limits ^{iii}}\, \text {exp}\bigg (\dfrac{-\gamma _{k}}{\eta _k}\bigg ){\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s), \end{aligned}$$

(31)

where $I_{tot, D_L}^{r^e_k}(NU)$ is the total interference received at ${\text{T}}_u^{r^e_k}$ associated with $k{\text{BS}}$, and $s =\frac{\gamma _{k}||y_{k}||^{\alpha }}{ {\text{P}}_{t,k}}$. Step (i) is obtained by substituting the value of $\eta _k$. Similarly, we obtain step (ii) by substituting Eqs. (3) into (31), using independence of interferences, and Nakagami-m fading assumption for all the links. In Step (iii) , ${\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s)$ is the moment generating functional (MGF) [15] of $I_{tot, D_L}^{r^e_k}(NU)$. Using Eq. (11), ${\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s)$ can be calculated as

$$\begin{aligned}&{\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s)\, {\mathop { = }\limits ^{iv}}\, {\text{E}}_{(\varPsi ^{r^e_k}_k {\backslash d_k},\varPsi ^{r^e_k}_u, \varPsi ^{R(NU)}_\tau , \varPsi ^{r^i_\tau }_u,{\text{h}}_{x_k}^{r^e_k},{\text{h}}_{y_k}^{r^e_k}, {\text{h}}_{x_\tau }^{r^i_\tau }, {\text{h}}_{y_\tau }^{r^i_\tau })}\nonumber \\&\quad \Bigg [ {\text{exp}}\Bigg ( -s\Bigg ( \sum _{x_k\in \varPsi ^{r^e_k}_k {\backslash d_k}} \beta {\text{P}}_{t,D_L}^{k}{\text{h}}_{x_k}^{r^e_k}||x_k||^{-\alpha } + \sum _{y_k\in \varPsi ^{r^e_k}_u} {\text{P}}_{t,U_L}^u{\text{h}}_{y_k}^{r^e_k}||y_k||^{-\alpha }\nonumber \\&\qquad +\sum _{x_\tau \in \varPsi ^{R(NU)}_\tau } {\text{P}}_{t,D_L}^{\tau }{\text{h}}_{x_\tau }^{r^i_\tau }||x_\tau ||^{-\alpha } + \sum _{y_\tau \in \varPsi ^{r^i_\tau }_u } {\text{P}}_{t,U_L}^{u}{\text{h}}_{y_\tau }^{r^i_\tau }||y_\tau ||^{-\alpha } \Bigg )\Bigg ) \Bigg ], \end{aligned}$$

(32)

where ${\text{E}}_{(\varPsi ^{r^e_k}_k {\backslash d_k},\varPsi ^{r^e_k}_u, \varPsi ^{R(NU)}_\tau , \varPsi ^{r^i_\tau }_u,{\text{h}}_{x_k}^{r^e_k},{\text{h}}_{y_k}^{r^e_k}, {\text{h}}_{x_\tau }^{r^i_\tau }, {\text{h}}_{y_\tau }^{r^i_\tau })}[\cdot ]$ denotes the expected value of interference with respect to PPPs and fading coefficients, and $\varPsi ^{r^e_k}_k {\backslash d_k},\varPsi ^{r^e_k}_u, \varPsi ^{R(NU)}_\tau \,{\text{and}}\, \varPsi ^{r^i_\tau }_u$ represent the distribution of BSs and users using PPP in $r^e_k$ and $r^i_\tau$, respectively. By using Nakagami-m fading coefficients for channel estimation and independence assumptions of the PPPs, Step (iv) can be obtained. Further simplification of Eq. (32) leads to

$$\begin{aligned} \begin{aligned} &{\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s)={\text{exp}}\left( { -2\pi \rho ^{r^e_k}_k\int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}}\left\{ 1-{\text{M}}_{{\text{h}}_{x_k}^{r^e_k}}( \beta {\text{P}}_{t,D_L}^{k}{\text{h}}_{x_k}^{r^e_k}||x_k||^{-\alpha })\right\} x_{k} dx_{k}}\right) \\&\quad \times \,{\text{exp}}\left( { -2\pi \rho ^{r^e_k}_u\int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}}\left\{ 1-{\text{M}}_{{\text{h}}_{y_k}^{r^e_k}}( {\text{P}}_{t,U_L}^u{\text{h}}_{y_k}^{r^e_k}||y_k||^{-\alpha })\right\} y_{k} dy_{k}}\right) \\&\quad \times \,{\text{exp}}\left( { -2\pi \rho ^{R(NU)}_\tau \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }}\left\{ 1-{\text{M}}_{{\text{h}}_{x_\tau }^{r^i_\tau }}( {\text{P}}_{t,D_L}^{\tau }{\text{h}}_{x_\tau }^{r^i_\tau }||x_\tau ||^{-\alpha })\right\} x_{\tau } dx_{\tau }}\right) \\&\quad \times \,{\text{exp}}\left( { -2\pi \rho ^{r^i_\tau }_u\int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }}\left\{ 1-{\text{M}}_{{\text{h}}_{y_\tau }^{r^i_\tau } }( {\text{P}}_{t,U_L}^{u}{\text{h}}_{y_\tau }^{r^i_\tau } ||y_\tau ||^{-\alpha })\right\} y_{\tau } dy_{\tau }}\right) . \end{aligned} \end{aligned}$$

(33)

Here $d_{1}^{r^e_k}$ and $< d_{2}^{r^e_k}$ define the lower and higher limits of $r^e_k$, while $0^{r^i_\tau }$ and $d_{1}^{r^i_\tau }$ define the lower and higher boundaries of $r^i_\tau$, respectively. $\{{\text{M}}_{{\text{h}}_{x_k}^{r^e_k}}(\cdot )$, ${\text{M}}_{{\text{h}}_{y_k}^{r^e_k}}(\cdot )\}$ and $\{{\text{M}}_{{\text{h}}_{x_\tau }^{r^i_\tau }}(\cdot )$${\text{M}}_{{\text{h}}_{y_\tau }^{r^i_\tau } } (\cdot )\}$ are the sets of MGF with respect to fading coefficients for $r^e_k$ and $r^i_\tau$, respectively. Moreover, using the Nakagami-m fading assumption, a simplified form of Eq. (33) can be written as

$$\begin{aligned} \begin{aligned} &{\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s)={\text{exp}}{\left( -2\pi \rho ^{r^e_k}_k\int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{x_{k}}{1+\left( s\beta {\text{P}}_{t,D_L}^{k}\right) ^{-1}||x_{k}||^{\alpha }}\right) dx_{k}\right) }\\&\quad \times \,{\text{exp}}{\left( -2\pi \rho ^{r^e_k}_u\int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{y_{k}}{1+\left( s{\text{P}}_{t,U_L}^u\right) ^{-1}||y_{k}||^{\alpha }}\right) dy_{k}\right) }\\&\quad \times \,{\text{exp}}{\left( -2\pi \rho ^{R(NU)}_\tau \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{x_\tau }{1+\left( s {\text{P}}_{t,D_L}^{\tau }\right) ^{-1}||x_{\tau }||^{\alpha }} \right) dx_{\tau }\right) }\\&\quad \times \,{\text{exp}}{\left( -2\pi \rho ^{r^i_\tau }_u\int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{y_\tau }{1+\left( s {\text{P}}_{t,U_L}^{u}\right) ^{-1}||y_{\tau }||^{\alpha }} \right) dy_{\tau }\right) }. \end{aligned} \end{aligned}$$

(34)

Equation (34) can be rewritten as

$$\begin{aligned}&{\text{M}}_{I_{tot, D_L}^{r^e_k}(NU)}(s) ={\text{exp}}{\left( -\,2\pi \left[ \rho _{k}^{ r^e_k} {\text{O}}_{k}^{ r^e_k}+\rho _{u}^{ r^e_k} {\text{O}}_{u}^{ r^e_k}+\rho _{\tau }^{R{(NU)}} {\text{O}}_{\tau }^{r^i_\tau } +\rho _{u}^{ r^{i}_\tau } {\text{O}}_{u}^{r^i_\tau } \right] \right) }, \end{aligned}$$

(35)

where

$$\begin{aligned} {\text{O}}_{k}^{ r^e_k}&= \int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{x_{k}}{1+\left( s\beta {\text{P}}_{t,D_L}^{k}\right) ^{-1}||x_{k}||^{\alpha }}\right) dx_{k}, \end{aligned}$$

(36)

$$\begin{aligned} {\text{O}}_{u}^{ r^e_k}&= \int _{d_{1}^{r^e_k}}^{d_{2}^{r^e_k}} \left( \frac{y_{k}}{1+\left( s{\text{P}}_{t,U_L}^u\right) ^{-1}||y_{k}||^{\alpha }}\right) dy_{k}, \end{aligned}$$

(37)

$$\begin{aligned} {\text{O}}_{\tau }^{r^i_\tau }&= \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{x_\tau }{1+\left( s {\text{P}}_{t,D_L}^{\tau }\right) ^{-1}||x_{\tau }||^{\alpha }} \right) dx_{\tau }, \end{aligned}$$

(38)

and

$$\begin{aligned} {\text{O}}_{u}^{r^i_\tau } = \int _{0^{r^i_\tau }}^{d_{1}^{r^i_\tau }} \left( \frac{y_\tau }{1+\left( s {\text{P}}_{t,U_L}^{u}\right) ^{-1}||y_{\tau }||^{\alpha }} \right) dy_{\tau }. \end{aligned}$$

(39)

Substituting Eqs. (35) into (31), the success probability that $\varGamma _k$ is greater than $\gamma _k$ can be obtained as

$$\begin{aligned} \begin{aligned}&P[\varGamma ^{r^e_k}_k(y_{k})>\gamma _{k}|{\text{T}}_u^{r^e_k}] ={\text{exp}}\left( \frac{-\gamma _{k}}{\eta _k}\right) \times {\text{exp}}{\left( -2\pi \left[ \rho _{k}^{ r^e_k} {\text{O}}_{k}^{ r^e_k}+\rho _{u}^{ r^e_k} {\text{O}}_{u}^{ r^e_k}+\rho _{\tau }^{R(NU)} {\text{O}}_{\tau }^{r^i_\tau } +\rho _{u}^{ r^{i}_\tau } {\text{O}}_{u}^{r^i_\tau }\right] \right) }. \end{aligned} \end{aligned}$$

(40)

Finally, we obtain Eq. (24) by substituting Eqs. (17) and (40) into (30).

Similarly, proof of Eq. (18) can be obtained by using the same approach as for the proof of Eq. (24). $\square$