1 Introduction

The heterogeneity of networks is the main feature of the next mobile communication system [1]. In heterogeneous networks, some small base stations with low transmit power are deployed in the coverage area of the macrocell base station (MBS). Small base stations with the small coverage area can improve the data traffic and the spatial multiplexing, and then promote the capacity of cellular networks [2]. Moreover, heterogeneous cellular networks (HCNs) can improve the performance of macro cell edge users and the capacity of the hot-spot region by utilizing the spectrum resource effectively. It cannot be denied that the deployment of small cell base stations (SCBSs) also brings great challenges, such as interference management, power control and handoff between wireless networks [3].

Matching problems in the realm of game theory originate with the seminal paper by Gale and Shapley for solving the “marriage” problem [4]. In the “marriage” problem, there are two distinct sets and the objective is to form suitable pairs containing one from each set [5, 6]. Therefore, the matching game is seen as a powerful and efficient framework to model conflicting objectives between two sets of participators [7, 8]. Fortunately, the discrete resource allocation problem can be exactly regarded as a marriage problem between two sets of resources and its users [9, 10]. In matching games, one-to-one matching scenario is especially suitable for the resource allocation problem since a participator of one set in this game can be matched with one participator of another set [11]. What’s more, most matching algorithms are fully distributed and only need to capture the preference list in the iteration.

In this paper, we consider the HCN with one MBS and multiple SCBSs, and derive the expression of overall outage probability of the system. To further improve the system performance, we propose a resource allocation problem to reduce the outage probability of the HCN. Taking the mutual effect into account, matching game is a powerful tool to address this problem. Therefore, we formulate the resource block (RB) allocation problem as a matching game with SCUE-specific utility functions and propose a distributed iterative algorithm to find the stable matching.

The main contributions of this paper are summarized as follows:

  • We derive the outage probability of the HCN and formulate a RB allocation problem to optimize the outage performance of the system.

  • The resource allocation problem is modeled as a one-to-one matching game which captures the preferences of both small cell user equipments (SCUEs) and RBs to select their optimum partners in the HCN. Then we propose novel and well-defined utility functions to capture the preferences of SCUEs and RBs.

  • We propose a distributed algorithm to solve the matching game that converges to a stable matching between two sets of SCUEs and RBs.

The rest of this paper is organized as follows. In Sect. 2, related works are introduced. In Sect. 3, the system model is presented and the outage probability of the system is derived. To improve the overall outage performance, Sect. 4 establishes the matching game framework and then proposes a algorithm which can find a stable matching. Finally, numerical results and discussion are presented in Sects. 5, and  6 concludes this paper.

2 Related work

In this section, we give a brief review of the works related to ours. More related works on the performance analysis and resource allocation for HCNs can be found in [3, 12, 13].

Recently, the performance analysis for HCNs has attracted more and more attention [12]. Since SCBS communications reuse the cellular frequency resource, the co-channel interference between the macrocell and the small cell (SC) exists and can dramatically degrade the network performance. Some interference management techniques are introduced to mitigate the interference, such as interference cancellation and interference alignment [13]. In [14], the authors analyzed the ergodic achievable rate of a device-to-device communication system for both beamforming and interference cancellation strategies and verified that the ergodic rate under the interference cancellation strategy was always better than that under the beamforming strategy. A novel interference cancellation algorithm in [15] was proposed to mitigate the interference of HCNs and its performance was robust. A generalized interference alignment and cancellation scheme was introduced in [16], and an interference alignment scheme for HCNs was proposed which could be applicable to the network with arbitrary number of picocells and macro users [17].

Moreover, these two techniques have some deficiencies particularly in the dense network, of which the transmitter or the receiver needs the exact channel state information and their designs are with high complexity. For practical applications, there are many issues which should be considered, e.g., synchronization, channel estimated errors, spectrum-sensing errors and so on. In [18], the joint subchannel and power allocation algorithm was proposed for cognitive femtocells by considering imperfect spectrum sensing, since fairness and spectrum sensing errors were ignored in most of the existing studies and perfect spectrum sensing was extremely difficult to achieve in practical cognitive wireless communications. In [19], using the out-of-band emissions and imperfect-spectrum-sensing-based interference model, a computationally efficient algorithm for downlink and uplink subcarriers and power allocation in an OFDMA-based cognitive radio network was proposed and achieved a near-optimal performance over a wide range of values for different cognitive radio network parameters.

Motivated by these problems, we need to find a much simpler and more efficient way to mitigate the cross-tier interference and improve the entire system performance. The resource optimization approach is a very efficient and practical method to mitigate the interference and increase the spectral efficiency. The resource allocation problem has been extensively studied to improve the performance of heterogeneous networks [20]. In [21], joint uplink subchannel and power allocation problem was investigated in cognitive small cells using cooperative Nash bargaining game theory, and then a game-based resource allocation algorithm was developed and shown to converge to a Pareto-optimal equilibrium. [22] investigated the joint subchannel and power allocation in both the uplink and the downlink for two-tier networks comprising spectrum-sharing femtocells and macrocells, and introduced an interference temperature limit to protect the macrocell from co-channel femtocell transmissions.

Nevertheless, the outage performance expression for HCNs is extremely complicated and brings a great challenge to the optimization of the resource allocation problem [23, 24]. Hence, traditional optimization methods are not suitable for optimizing the outage performance of HCNs. Different from these work in the literature, our proposed scheme applies the matching game to address the problem of resource allocation for reducing the outage probability of the system and promoting the utilization rate of the spectrum resource.

3 System model and problem formulation

In this section, we first introduce the network model, then give the outage probability analysis and the formulation of the resource allocation problem.

For convenience, we present lower case, boldface lower case and calligraphic symbols to denote scalars, vectors (matrixes) and sets, respectively. \(\times\) denotes Cartesian product. \(|\cdot |\) represents the absolute value of a complex-valued scalar. \({\mathbb {E}}\{\cdot \}\) is the statistical expectation. Additionally, \({\mathbb {I}}_{\lbrace condition \rbrace }\) represents an indicator function, and it equals 1 if condition is true; otherwise 0.

3.1 System model

Fig. 1
figure 1

System model (Suppose that SCBS 2 occupies the same RB as that of MUE 3 for data transmission while SCBS 1 selects other RBs rather than that of MUE 5)

Full size image

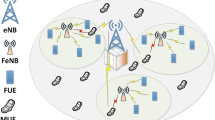
Consider the downlink of a HCN consisting of one MBS with N transmit antennas and F overlaid single antenna SCBSs, illustrated by Fig. 1. The indices of these F SCBSs are orderly included in a set \({\mathcal {B}}=\{1,2,\dots ,F\}\). Moreover, suppose that there aren’t overlapped coverage areas among SCBSs and there are \(S_{k}\) SCUEs associated with SCBS k for \(\forall k\in {\mathcal {B}}\), coexisting with M macrocell user equipments (MUEs) (\(S_{k}<M\)). Assume that the network employs an orthogonal frequency division multiple access (OFDMA) or single-carrier frequency division multiple access (SC-FDMA) strategy for transmitting information, and there are M RBs where each RB is considered as flat fading and occupied by one different MUE. Here, \({\mathcal {M}}=\{1,2,\dots ,M\}\) represents the set of all RBs or MUEs, and assume that MUE \(i\in {\mathcal {M}}\) selects RB \(i\in {\mathcal {M}}\) for signal transmission without loss of generality.

Let \(x_{k}(n)\) be the transmitted signal on RB n for \(\forall k\in {\mathcal {B}}\), and it is normalized and satisfies the following power constraint:

$$\begin{aligned} {\mathbb {E}}\left\{ \Vert x_{k}\Vert ^{2}\right\} =1. \end{aligned}$$
(1)

Denote the channel gain from MBS to MUE i (SCUE j) by \(\varvec{h}_{0,i}\) (\(\varvec{g}_{0,j}\)), and the channel gain from SCBS k to MUE i (SCUE j) by \(h_{k,i}\) (\(g_{k,j}\)) for \(\forall i\in {\mathcal {M}}\), \(\forall k\in {\mathcal {B}}\) and \(\forall j\in {\mathcal {S}}_{k}\). Let entries of each channel gain be modeled as independent and identically distributed (i.i.d.) zero mean and unit variance complex Gaussian variables, i.e., \(\varvec{h}_{0,i},\varvec{g}_{0,j}\sim \mathcal {CN}(\varvec{0},\varvec{I}_{N})\), \(h_{k,i},g_{k,j}\sim \mathcal {CN}(0,1)\). Therefore, the received signal at the MUE i or SCUE j for \(\forall i\in {\mathcal {M}}\), \(\forall k\in {\mathcal {B}}\) and \(\forall j\in {\mathcal {S}}_{k}\) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} y_{0,i} = &\sqrt{p_{0,i}\alpha _{0,i}}\varvec{h}_{0,i}\varvec{w}_{i}x_{i}\\ & \quad +\,\sum _{k\in {\mathcal {B}}}\sqrt{p_{k}\alpha _{k,i}}h_{k,i}x_{j}{\mathbb {I}}_{\{\beta _{ki}^{0}\}}+z_{0,i},\\ y_{k,j} = &\sum _{i\in {\mathcal {M}}}\sqrt{p_{0,i}\alpha _{0,j}}\varvec{g}_{0,j}\varvec{w}_{i}x_{i}{\mathbb {I}}_{\{\beta _{ij}^{1}\}}\\ &\quad +\,\sqrt{p_{k}\alpha _{k,j}}g_{k,j}x_{j}+z_{k,j}, \end{array}\right. } \end{aligned}$$
(2)

where \(p_{0,i}\) is the transmit power of MBS in RB i, \(p_{k}\) is the transmit power of SCBS k, \(\beta _{ki}^{0}\) represents that i locates in the coverage area of SCBS k and k occupies the same RB as that of i, \(\beta _{ij}^{1}\) represents that SCUE j selects the same RB as that of i to transmit information to its associated SCBS, and \(z_{0,i}\) and \(z_{k,j}\) are the normalized additive Gaussian noise with zero mean.

Here, we assume that MBS preforms the maximum ratio transmission (MRT) as the precoding vector, namely, \(\varvec{w}_{i}=\frac{\varvec{h}_{0,i}^{H}}{\Vert \varvec{h}_{0,i}\Vert }\). According to (2), the received signal-to-noise-plus-interference ratios (SINRs) at MUE \(i\in {\mathcal {M}}\) and SCUE \(j\in {\mathcal {S}}_{k}\) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma _{0,i}&=\frac{p_{0,i}\alpha _{0,i}|\varvec{h}_{0,i} \varvec{w}_{i}|^{2}}{\sum _{k\in {\mathcal {B}}} p_{k}\alpha _{k,i}|h_{k,i}|^{2}{\mathbb {I}}_{\{\beta _{ki}^{0}\}}+1}, \forall i\in {\mathcal {M}},\\ \gamma _{k,j}&=\frac{p_{k}\alpha _{k,j}|g_{k,j}|^{2}}{\sum _{i\in {\mathcal {M}}}p_{0,i}\alpha _{0,j}|\varvec{g}_{0,j} \varvec{w}_{i}|^{2}{\mathbb {I}}_{\{\beta _{ij}^{1}\}}+1}, \forall k\in {\mathcal {B}}, \forall j\in {\mathcal {S}}_{k}. \end{array}\right. } \end{aligned}$$
(3)

3.2 Outage probability analysis

In this subsection, we give the closed-form expression of overall outage probability of the system, and then propose the resource allocation problem.

Based on the precoding vector, we have the following distribution results:

$$\begin{aligned} {\left\{ \begin{array}{ll} |\varvec{h}_{0,i}\varvec{w}_{i}|^{2}\sim \varGamma \left( N,\frac{1}{2}\right) ,\\ |\varvec{g}_{0,j}\varvec{w}_{i}|^{2},|h_{k,i}|^{2}, |g_{k,j}|^{2}\sim \varGamma \left( 1,\frac{1}{2}\right) ,\\ \end{array}\right. } \end{aligned}$$
(4)

where \(\varGamma (\cdot )\) represents the Gamma random variable.

To obtain the outage probability of the system, we need to derive cumulative distribution functions (CDFs) of \(\gamma _{0,i}\) and \(\gamma _{k,j}\) for \(\forall i\in {\mathcal {M}}\), \(\forall k\in {\mathcal {B}}\) and \(\forall j\in {\mathcal {S}}_{k}\).

3.2.1 CDF of \(\gamma _{0,i}\)

From (4), the probability density function (PDF) and CDF of \(|\varvec{h}_{0,i}\varvec{w}_{i}|^{2}\) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} f_{|\varvec{h}_{0,i}\varvec{w}_{i}|^{2}}(x)=\frac{2^{N}x^{N-1}}{\varGamma (N)}\exp (-2x),\\ F_{|\varvec{h}_{0,i}\varvec{w}_{i}|^{2}}(x)=\frac{1}{\varGamma (N)}\gamma \left( N,2x\right) , \end{array}\right. } \end{aligned}$$
(5)

and the PDF and CDF of \(|h_{k,i}|^{2}\) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} f_{|h_{k,i}|^{2}}(x)=2\exp (-2x),\\ F_{|h_{k,i}|^{2}}(x)=\gamma \left( 1,2x\right) =1-\exp (-2x). \end{array}\right. } \end{aligned}$$
(6)

Before starting the performance analysis, we first present the following lemma:

Lemma 1

For two independent distributed random variables \(X\sim \varGamma (m_{1},\theta _{1})\), \(Y\sim \varGamma (m_{2},\theta _{2})\), and positive constants a, b and c, we let \(Z=\frac{aX}{bY+c}\) and get its PDF as follows:

$$\begin{aligned} \begin{aligned} p_{Z}(z)&= \frac{z^{m_{1}-1}\exp (-\frac{cz}{a\theta _{1}})}{\varGamma (m_{1})\varGamma (m_{2})\theta _{1}^{m_{1}}\theta _{2}^{m_{2}}a^{m_{1}} b^{m_{2}}}\\&\quad \times \, \sum _{m=0}^{m_{1}} \begin{pmatrix} m_{1} \\ m \end{pmatrix} \frac{c^{m_{1}-m}}{\left( \frac{z}{a\theta _{1}}+\frac{1}{b\theta _{2}}\right) ^{m_{2}+m}}\varGamma (m_{2}+m). \end{aligned} \end{aligned}$$
(7)

Proof

Since \(X\sim \varGamma (m_{1},\theta _{1})\) and \(Y\sim \varGamma (m_{2},\theta _{2})\) are independent distributed, the joint probability density function of X and Y is written as

$$\begin{aligned} p_{XY}(x,y)=\frac{x^{m_{1}-1}y^{m_{2}-1}}{\varGamma (m_{1}) \varGamma (m_{2})\theta _{1}^{m_{1}}\theta _{2}^{m_{2}}}\exp (-\frac{x}{\theta _{1}}-\frac{y}{\theta _{2}}). \end{aligned}$$
(8)

Let \(z=\frac{ax}{by+c}\) and \(w=by\). The Jacobian determinant of (x, y) is that \(\det (J(z,w))=\frac{w+c}{ab}\). Then, the joint probability density function of Z and W is expressed as

$$\begin{aligned} \begin{aligned} p_{ZW}(z,w)&= \frac{\det (J(z,w))}{\varGamma (m_{1})\varGamma (m_{2})\theta _{1}^{m_{1}} \theta _{2}^{m_{2}}}\left( \frac{z(w+c)}{a}\right) ^{m_{1}-1}\\&\quad \times \, \left( \frac{w}{b}\right) ^{m_{2}-1}\exp \left( -\frac{z(w+c)}{a\theta _{1}}-\frac{w}{b\theta _{2}}\right) . \end{aligned} \end{aligned}$$
(9)

Thus, the probability distribution of Z can be derived as follows

$$\begin{aligned} \begin{aligned}&p_{Z}(z)\\&= \int _{0}^{\infty }p_{ZW}(z,w)\,dw\\&=\frac{z^{m_{1}-1}\exp (-\frac{cz}{a\theta _{1}})}{\varGamma (m_{1})\varGamma (m_{2})\theta _{1}^{m_{1}}\theta _{2}^{m_{2}} a^{m_{1}}b^{m_{2}}}\sum _{m=0}^{m_{1}}\begin{pmatrix} m_{1} \\ m \end{pmatrix}c^{m_{1}-m}\\&\quad \times \, \int _{0}^{\infty }w^{m+m_{2}-1}\exp \left( -\frac{zw}{a\theta _{1}}-\frac{w}{b\theta _{2}}\right) \,dw. \end{aligned} \end{aligned}$$
(10)

Finally, we can derive Eq. (7) by integrating in Eq. (10) and the proof is completed. \(\square\)

The derivation process of CDF of \(\gamma _{0,i}\) is divided the following two cases: \({\mathbb {I}}_{\{\beta _{ki}^{0}\}}=1\) and \({\mathbb {I}}_{\{\beta _{ki}^{0}\}}=0\).

(i) When \({\mathbb {I}}_{\{\beta _{ki}^{0}\}}=1\) for a certain SCBS \(k\in {\mathcal {B}}\), the PDF of \(\gamma _{0,i}\) can be obtained by Lemma 1, given by

$$\begin{aligned} \begin{aligned} p_{\gamma _{0,i}}^{1}(z)=&\frac{2^{N+1}\exp (-\frac{2z}{p_{0,i}\alpha _{0,i}})}{\varGamma (N)(p_{0,i}\alpha _{0,i})^{N}p_{k}\alpha _{k,i}}\\&\times \sum _{m=0}^{N} \begin{pmatrix} N \\ m \end{pmatrix} \frac{z^{N-1}}{\left( \frac{2z}{p_{0,i}\alpha _{0,i}}+\frac{2}{p_{k}\alpha _{k,i}}\right) ^{m+1}}\varGamma (m+1). \end{aligned} \end{aligned}$$
(11)

Some fractions containing the variable z in Eq. (11) can be rewritten as

$$\begin{aligned} \frac{z^{N-1}}{\left( \frac{2z}{p_{0,i}\alpha _{0,i}} +\frac{2}{p_{k}\alpha _{k,i}}\right) ^{m+1}}=\sum _{n=1}^{m+1} \frac{d_{n}^{m}}{\left( \frac{2z}{p_{0,i}\alpha _{0,i}} +\frac{2}{p_{k}\alpha _{k,i}}\right) ^{n}}, \end{aligned}$$
(12)

where \(d_{n}^{m}\) be constant and can be solved by residue theorem.

According to Eqs. 3.352.1, 3.353.3, 3.353.2 and 8.211 in [25], we can get the CDF of \(\gamma _{0,i}\) from (11) and (12)

$$\begin{aligned} \begin{aligned} P_{\gamma _{0,i}}^{1}(z)=&\frac{2^{N+1}\exp \left( -\frac{2z}{p_{0,i}\alpha _{0,i}}\right) }{\varGamma (N)(p_{0,i}\alpha _{0,i})^{N}p_{k}\alpha _{k,i}}\times \\&\sum _{m=0}^{N} \begin{pmatrix} N \\ m \end{pmatrix} \sum _{n=1}^{m+1}d_{n}^{m}L_{n}(z)\varGamma (m+1), \end{aligned} \end{aligned}$$
(13)

where \(\lambda =\frac{2}{p_{0,i}\alpha _{0,i}}, \mu =\frac{p_{0,i}\alpha _{0,i}}{p_{k}\alpha _{k,i}}\) and \(L_{n}(z)\) is given in Eq. (14).

$$\begin{aligned} L_{n}(z)= {\left\{ \begin{array}{ll} \exp (\lambda \mu )\left[ Ei(-\lambda z-\lambda \mu )-Ei(-\lambda \mu )\right] ,n=1,\\ \begin{aligned} &{} \frac{1}{(n-1)!}\sum _{l=1}^{n-1}(l-1)!(-\lambda )^{n-l-1}\mu ^{-l} -\frac{(-\lambda )^{n-1}}{(n-1)!}\exp (\lambda \mu )Ei(-\lambda \mu )\\ &{} -\exp (-\lambda z)\sum _{l=1}^{n-1}\frac{(l-1)!(-\lambda )^{n-l-1}}{(n-1)!(\mu +z)^{l}} +\frac{(-\lambda )^{n-1}}{(n-1)!}\exp (\lambda \mu )Ei [-\lambda (z+\mu )],n=2,3,\dots , \end{aligned} \end{array}\right. } \end{aligned}$$
(14)

(ii) When \({\mathbb {I}}_{\{\beta _{ki}^{0}\}}=0\) for all \(k\in {\mathcal {B}}\), the CDF of \(\gamma _{0,i}\) is calculated as follows.

$$\begin{aligned} P_{\gamma _{0,i}}^{0}(z)=\frac{1}{\varGamma (N)}\gamma \left( N,\frac{2z}{p_{0,i}\alpha _{0,i}}\right) . \end{aligned}$$
(15)

As a result, we summarize the CDF of \(\gamma _{0,i}\) for \(i\in {\mathcal {M}}\) below

$$\begin{aligned} P_{\gamma _{0,i}}(z)= {\left\{ \begin{array}{ll} P_{\gamma _{0,i}}^{0}(z), \,\text {if}\,{\mathbb {I}}_{\{\beta _{ki}^{0}\}}=0 \,\text {for} \,\forall k\in {\mathcal {B}},\\ P_{\gamma _{0,i}}^{1}(z), \,\text {if}\,{\mathbb {I}}_{\{\beta _{ki}^{0}\}}=1 \,\text {for a ceratin}\,k \in {\mathcal {B}}. \end{array}\right. } \end{aligned}$$
(16)

3.2.2 CDF of \(\gamma _{k,j}\)

When \({\mathbb {I}}_{\{\beta _{ij}^{1}\}}=1\) for a certain MUE \(i\in {\mathcal {M}}\), the CDF of \(\gamma _{k,j}\) is get in a similar way as described above.

$$\begin{aligned} \begin{aligned}&P_{\gamma _{k,j}}(z)\\&=\frac{4\exp (-\frac{2z}{p_{k}\alpha _{k,j}})}{p_{k} \alpha _{k,j}p_{0,i}\alpha _{0,j}}\sum _{m=0}^{1} \begin{pmatrix} 1 \\ m \end{pmatrix} \sum _{n=1}^{m+1}d_{n}^{m}L_{n}(z)\varGamma (m+1)\\&=\frac{4\exp (-\frac{2z}{p_{k}\alpha _{k,j}})}{p_{k}\alpha _{k,j} p_{0,i}\alpha _{0,j}}\left( L_{1}(z)+L_{2}(z)\right) , \end{aligned} \end{aligned}$$
(17)

where \(\lambda =\frac{2}{p_{k}\alpha _{k,j}}\) and \(\mu =\frac{p_{k}\alpha _{k,j}}{p_{0,i}\alpha _{0,j}}\).

3.3 Problem formulation and transformation

Let \(\gamma _{th}\) be the minimum SINR requirement for each user and according to Eqs. (16) and (17), the outage probability of the system is given in Eq. (18).

$$\begin{aligned} \begin{aligned} P_{out}&=Pr\left\{ \min \left( \{\gamma _{0,i},i\in {\mathcal {M}}\},\{\gamma _{k,j}, k\in {\mathcal {B}},j\in {\mathcal {S}}_{k}\}\right) <\gamma _{th}\right\} \\&=1-Pr\left\{ \{\gamma _{0,i},i\in {\mathcal {M}}\}>\gamma _{th}, \{\gamma _{k,j},k\in {\mathcal {B}},j\in {\mathcal {S}}_{k}\}> \gamma _{th}\right\} \\&=1-\prod _{i\in {\mathcal {M}}}Pr\left\{ \gamma _{0,i}>\gamma _{th}\right\} \prod _{k\in {\mathcal {B}}}\prod _{j\in {\mathcal {S}}_{k}} Pr\left\{ \gamma _{k,j}>\gamma _{th}\right\} \\&=1-\prod _{i\in {\mathcal {M}}}\left( 1-\sum _{k\in {\mathcal {B}}} P_{\gamma _{0,i}}(\gamma _{th}){\mathbb{I}}_{\{\beta _{ki}^{0}\}}\right) \prod _{k\in {\mathcal {B}}}\prod _{j\in {\mathcal {S}}_{k}}\left( 1-\sum _{i\in {\mathcal {M}}}P_{\gamma _{k,j}}(\gamma _{th}) {\mathbb {I}}_{\{\beta _{ij}^{1}\}}\right) .\\ \end{aligned} \end{aligned}$$
(18)

Then, we propose the RB allocation problem to decrease the outage probability of the whole HCN. The strategy profile of all SCUEs is represented as \(\varvec{a}=(\varvec{a}_{1},\varvec{a}_{2},\dots ,\varvec{a}_{F})\) where \(\varvec{a}_{k}=(a_{k}^{(1)},a_{k}^{(2)},\dots ,a_{k}^{(S_{k})})\), and P is defined as follows

$$\begin{aligned} \begin{aligned} P&=\ln (1-P_{out})=\sum _{i\in {\mathcal {M}}}\ln \left( 1-\sum _{k\in {\mathcal {B}}}P_{\gamma _{0,i}}(\gamma _{th}){\mathbb {I}}_{\{\beta _{ki}^{0}\}}\right) \\&\quad +\,\sum _{k\in {\mathcal {B}}}\sum _{j\in {\mathcal {S}}_{k}}\ln \left( 1-\sum _{i\in {\mathcal {M}}}P_{\gamma _{k,j}}(\gamma _{th}){\mathbb {I}}_{\{\beta _{ij}^{1}\}}\right) . \end{aligned} \end{aligned}$$
(19)

Therefore, the RB optimization problem for the overall outage probability of the system can be expressed as

$$\begin{aligned} P1: \max \limits _{\varvec{a}\in {\mathcal {A}}} P(\varvec{a}) \end{aligned}$$
(20)

Since there aren’t overlapped coverage areas among SCBSs, P1 is rewritten as P2.

$$\begin{aligned} P2: \sum _{k\in {\mathcal {B}}}\max \limits _{\varvec{a}_{k}\in {\mathcal {A}}_{k}} P_{k}(\varvec{a}_{k}) \end{aligned}$$
(21)

where \(P_{k}=\frac{1}{F}\sum _{i\in {\mathcal {M}}}\ln \left( 1-\sum _{k\in {\mathcal {B}}}P_{\gamma _{0,i}}(\gamma _{th}){\mathbb {I}}_{\{\beta _{ki}^{0}\}}\right) +\sum _{j\in {\mathcal {S}}_{k}}\ln \left( 1-\sum _{i\in {\mathcal {M}}}P_{\gamma _{k,j}}(\gamma _{th}){\mathbb {I}}_{\{\beta _{ij}^{1}\}}\right)\).

4 Matching theory for outage performance

4.1 Game-theoretic analysis

Since SCUEs associated with the same SCBS occupy different RBs for receiving information, the RB allocation problem for outage performance can be posed as a one-to-one marriage problem. To address this problem, matching theory is a suitable approach to model the interactions among participators with conflicting interests. Moreover, matching game is proved to be successful in explaining the allocation mechanisms in decentralized markets. As a result, the matching problem between SCUEs and RBs is solved by using a matching game framework. Formally, we define the matching game as follows:

Definition 1

(Matching Game) Let \({\mathcal {S}}\) and \({\mathcal {M}}\) be the two disjoint finite sets of SCUEs in a SC and RBs respectively, and \({\mathcal {G}}=(\mathcal {V},\mathcal {E})\) be a simple connected graph, where \(\mathcal {V}=\{{\mathcal {S}},{\mathcal {M}}\}\) is the vertex set and \(\mathcal {E}\) is the edge set. A matching \(\nu \subseteq \mathcal {E}\) is defined as a function from \({\mathcal {S}}\cup {\mathcal {M}}\) to itself such that: 1) \(\nu (m)=s\) if and only if \(\nu (s)=m\), and 2) \(\nu (m)\in {\mathcal {S}}\cup \emptyset\) and \(\nu (s)\in {\mathcal {M}}\cup \emptyset\). Thus, \({\mathcal {G}}\) with the matching behavior is a matching game.

A matching is essentially an allocation between SCUEs and RBs and the basic solution concept for matching game is the stable matching. Let \(\succ _{s}\) denotes the ordering relationship of s and \(m\succ _{s}m^{'}\) means that s prefers m over \(m^{'}\). The stable matching is defined as follows:

Definition 2

(Stable Matching) A one-to-one matching \(\nu\) is blocked if \(\nu (s)\ne m\) and if \(s\succ _{m}\nu (m)\) and \(m\succ _{s}\nu (s)\). One-to-one matching is stable if there is no subset of \({\mathcal {S}}\) and \({\mathcal {M}}\) in which the matching is blocked.

To obtain the stable matching, we propose a preference relation among RBs by defining a utility function of each SCUE. Each SCUE builds a ranking of RBs using the preference relations and forms a preference list. SCUEs are considered as individual selfish and the utility function is given by

$$\begin{aligned} u_{j,k}^{S}=\ln \left( 1-\sum _{i\in {\mathcal {M}}} P_{\gamma _{k,j}}(\gamma _{th}){\mathbb {I}}_{\{\beta _{ij}^{1}\} }\right) . \end{aligned}$$
(22)

If SCUE j’s utility for receiving useful information on RB i is obviously larger than that of RB \(i^{'}\), it is shown that \(i\succ _{j}i^{'}\). Based on Eq. (22), we can define their preference relations and form a preference list. However, the preference relation of between i and \(i^{'}\) may be weak or nonexistent when they have nearly equal utility values. This weak preference relation of between i and \(i^{'}\) is represented as \(i\succeq _{j}i^{'}\). This phenomenon usually occurs in the hyper-dense networks and poses an obstacle to obtain the stable matching. To overcome this challenge, we need to switch weak preference relations into strong preference relations using the local information. Let \(\gamma _{k}^{j}(i)\) be the received SINR at SCBS \(k\in {\mathcal {B}}\) when \(j\in {\mathcal {S}}_{k}\) selects RB i to transmit signal. When \(i\succeq _{j}i^{'}\) from Eq. (22), we need to redefine the preference relation based on the received SINR at the SCBS, i.e., \(i\succ _{j}i^{'}\) if \(\gamma _{k}^{j}(i)>\gamma _{k}^{j}(i^{'})\). As a result, we can make sure that preference relations in the preference list are all strong.

In most prior research, each participator is regarded as selfish and only following individual benefit. This self-interested action is short-sighted and blocks the further enhancement of the system performance. Certainly, a fully altruistic action is also inadvisable since it needs a great deal of timely information exchange and increases the calculation burden. This inspires we to make a tradeoff between self-interested and fully altruistic schemes by designing utility function of each RB. Since physical locations of users are regarded as stationary in the implement of algorithm, we design a local altruistic utility function based on neighbors’ topology.

$$\begin{aligned} \begin{aligned} u_{j,k}^{R} =&\sum _{i\in \bar{{\mathcal {M}}}_{j}}\ln \left( 1-\sum _{i\in {\mathcal {B}}}P_{\gamma _{0,i}}(\gamma _{th}) {\mathbb {I}}_{\{\beta _{ki}^{0}\}}\right) \\&+\omega _{j,k}\ln \left( 1-\sum _{i\in {\mathcal {M}}}P_{\gamma _{k,j}} (\gamma _{th}){\mathbb {I}}_{\{\beta _{ij}^{1}\}}\right) , \end{aligned} \end{aligned}$$
(23)

where \(\omega _{j,k}\) is a weight factor and \(\bar{{\mathcal {M}}}_{j}=\{m|d_{j,m}\le L_{th},m\in {\mathcal {M}}\}\) where \(d_{j,m}\) and \(L_{th}\) denote the physical distance and the maximum distance requirement between j and m, respectively.

Therefore, each RB’s preferences for different SCUEs at the SCBS can be obtained according to Eq. (22).

4.2 Decentralized algorithm

figure a

To obtain the stable matching of \({\mathcal {G}}\), we propose a distributed algorithm shown in Algorithm 1. Algorithm 1 is an improved approach of the deferred acceptance algorithm, which is proposed by Gale and Shapley to solve the marriage problem in which preferences are static and independent of the matching [4]. Unfortunately, the conventional deferred acceptance algorithm is not applicable to our matching problem since the presence of externalities alters the preferences of participators. To guarantee that Algorithm 1 can lead to a stable matching when it converges, an iterative approach is employed and the preferences of participators in each step depend on the current matching. In each step, the utilities are updated based on the matching received by the previous step and the preference lists are updated accordingly. According to current preference lists, a new temporal matching is obtained by using the deferred acceptance algorithm. The algorithm proceeds to the next iteration based on the previous temporal matching. The proposed algorithm converges when two sequent temporal matchings are the same. The property of convergence is discussed in [26].

However, the preferences of participators obtained by Eqs. (22) and (23) in game \({\mathcal {G}}\) may contain weak preference relations. Hence, the classical deferred acceptance algorithm cannot be used here directly. To overcome this drawback, we redefine these weak preference relations by means of comparing the received SINR on one RB with that on another RB in the uplink transmission. This manipulation not only enhances preference relations among RBs but also improves the uplink performance. Moreover, this manipulation is performed in the associated SCBS with the purpose of low computational complexity and less information exchange. Since SCUEs request RBs according to their preference relations in Algorithm 1, RBs are chosen by SCUEs and RBs accept request according to their preferences. The eventual matching is optimal from the SCUEs’ points of view. It has been proved that the deferred acceptance algorithm can converge to a stable matching for any initial conditions. Since the weak preference relations have been reassigned as strong preference relations, the proposed algorithm converges to a stable matching in each iteration.

4.3 Computational complexity analysis

The complexity depends on the set of SCUEs in the SC as well as the number of RBs. In each iteration, the preference lists are updated based on the previous matching, and then a new matching is obtained by using the deferred acceptance approach. As for the computation of the preferences, the utility values are computed with a complexity of \({\mathcal {O}}(M)\) and it needs \(M\mid {\mathcal {S}}_{k}\mid\) computations of utility values and multiple comparisons to form the preference lists. Thus, the total complexity for updating the preference lists is \({\mathcal {O}}(M^{2}\mid {\mathcal {S}}_{k}\mid )\). According to the updated preference lists, a new stable matching is found in at most \(M^{2}-2M+2\) stages and its complexity is \({\mathcal {O}}(M^{2})\). The above analysis provides the computational complexity for each iteration of the proposed algorithm. Moreover, the whole computational complexity also relies on the number of iterations needed for convergence, which is not unlimited because of a finite number of possible matchings.

5 Simulation results and discussion

Table 1 Simulation parameters
Full size table

5.1 Scenario setup

In this section, the objective is to validate the outage performance of the system and the efficiency and performance of the proposed matching algorithm based on resource allocation procedure in a heterogeneous network scenario. Consider one MBS with hexagonal coverage area where there are randomly layouts of \(F=2\) SCBSs and their coverage areas are not overlap with each other. For convenience, we assume that there are 2 SCUEs randomly located within each SC, and the other 5 MUEs in the MBS, two of which locate in the coverage area of SCBSs. For the sake of simplicity, all deployed SCBSs are assumed to be always active. Each SCUE receives data through one RB in each SCBS. Here, we suppose that MBS and each SCBS have the same downlink transmission power on each RB which are set to 20 dBm and 14 dBm, respectively. Consider 5 MHz bandwidth in this heterogeneous network which constitutes a total of 5 RBs with the same 110 kHz bandwidth. Specifically, simulation parameters and values are listed in Table 1, which is partially in accordance with the 3GPP simulation assumption case 1.

5.2 Outage performance analysis

Fig. 2
figure 2

Outage performance versus transmit power of SCBS with the fixed RBs allocation when MUEs locate in the coverage area of SC

Full size image
Fig. 3
figure 3

Outage performance versus transmit power of MBS with the fixed RBs allocation when MUEs locate in the coverage area of SC

Full size image
Fig. 4
figure 4

Outage performance versus transmit power of SCBS/MBS with the fixed RBs allocation when not MUE locates in the coverage area of SC

Full size image

To verify the theoretical analysis of outage probability, Figs. 2 and  3 compare theoretical analysis with numerical results of MUE, SCUEs or their overall performance (labeled as HN) when these users share a certain RB. It is shown from Figs. 2 and  3 that the outage performance of the system by theoretical derivation is consistent with that of the actual scenario by simulation. The simulation validates the correctness of theoretical deduction.

In addition, Fig. 2 gives the outage performance versus transmit power of SCBS with the fixed RBs allocation when SCUE occupies the resource of MUE and MUE locates in the coverage area of SC. Figure 3 shows the outage performance versus transmit power of MBS under the same condition. As the transmit power of SCBS increases, the outage performance of the system becomes poorer and is largely influenced by that of MUE. This is mainly because MUE suffers more serious interference for sharing the same RB by SCUE. Similarly, the increment of the transmit power of MBS can promote the outage performance of the system while this enhancement is limited because of cross-tier interferences. Figure 4 shows outage performance versus transmit power of SCBS/MBS with the fixed RBs allocation when not MUE locates in the coverage area of SC. The outage performance loss caused by interferences is not serious as the transmit power of SCBS/MBS increases. It can be concluded from overall analysis that the resource allocation is important to enhance the communication quality of the HCN.

5.3 Convergence behavior and optimality of this algorithm

Fig. 5
figure 5

Outage performance of MUE and SCUEs sharing the same resource for different number of SCUEs located in each SC by performing the matching algorithm or not

Full size image
Fig. 6
figure 6

Overall outage performance of the system for different number of SCUEs located in each SC by performing the matching algorithm or not

Full size image

Figure 5 gives the outage performance of users sharing the same resource for different number of SCUEs located in each SC by performing the matching algorithm or not. Figure 6 shows the outage performance of the system for different number of SCUEs in each SC by performing the matching algorithm or not. It is given in Figs. 5 and  6 that the resource allocation approach by using the matching game can efficiently improve the outage performance of the system. If the resource allocation is not performed in this paper, the outage performance of the system is reduced and it results in the degradation of system performance as users are densely deployed in this heterogeneous network.

6 Conclusion

In this paper, we have proposed a novel spectrum sharing approach to improve the downlink outage performance of HCNs. Specifically, we have derived PDFs and CDFs of the received SINRs of both MUEs and SCUEs, and obtained the outage probability of HCNs. By defining utility functions, we model the resource allocation problem as a one-to-one matching game which optimizes the outage probability of HCNs. To solve the presented matching game, we have proposed a distributed algorithm that converges to a stable matching between SCBSs and RBs. Simulation results show that the effectiveness of the derived outage probability and the proposed matching algorithm.