1 Background and motivation

Wireless sensor networks (WSNs) have many applications such as environmental monitoring, conferencing, disaster relief, rescue operations, and police operations. This paper models traffic in a WSN using the IEEE 802.15.4 protocol with N-to-one data aggregation, where C of the N active nodes (0 ≤ C ≤ N) each generate a packet containing sensed data to be transmitted during the next superframe. No more than one packet can be sent by each node during each superframe. This is called batched arrivals [1], where many nodes each attempt to transmit a packet at the same time, possibly resulting in severe collisions [2]. This type of data traffic is also known as one-shot data [3], and arises with many sensor network applications [4–6]. This data aggregation model is based on a star topology where all the sensor nodes are one hop from the cluster head (PAN Coordinator) which performs aggregation. In multihop cases, similar traffic model analysis could be applied to each hop.

The model determines the statistical distribution of S F , the number of timeslots taken for all C active nodes either to finish their transmissions (either successfully or with a collision) or to discard their packets. The mean is also determined. This model can determine parameters such as the length of IEEE 802.15.4 Contention Access Period necessary for acceptable packet loss, making it a potentially useful tool for WSN design and dimensioning.

The remainder of this Section discusses the details of the IEEE 802.15.4 protocol and relevant prior work in this area. The new 4D Markov chain model is explained and discussed in Sect. 2, with the analytical results being presented and compared with simulations running on OPNET (Optimized Network Engineering Tools) in Sect. 3. Finally, Sect. 4 concludes the paper.

1.1 Modeling scenario for the IEEE 802.15.4 protocol

It is assumed that beacon enabled mode (slotted CSMA/CA) is used, without acknowledgement (NACK mode), in the 2.4 GHz frequency band with a data rate of 250 kb/s. In beacon enabled mode, each node senses the target area and can generate a data packet at any time, during either the active or inactive period of a superframe. The node then queues the packet to await transmission. Upon receiving the beacon frame from the PAN Coordinator, the node chooses a random slot from the backoff window W, which is initially equal to macMinBE. If the contention window CW is equal to 1, it senses the channel once using Clear Channel Assessment (CCA). If the channel is busy, the node performs another backoff and tries to sense the channel again for another single CCA, repeating this until the end of the Contention Access Period (CAP) until it senses a clear channel and sends the packet. On the mth attempt to sense the channel, the backoff window W = min (2m+macMinBE, 2macMaxBE), where 0 ≤ m ≤ M − 1. If the node senses a busy channel during its last (Mth) attempt, the packet is discarded. If multiple nodes sense a clear channel during the same slot and then send their packets simultaneously, their transmissions collide, and the packets are lost without retransmission.

The standard defines CW = 2 [7], meaning that a transmitter node performs the CCA twice in succession, in order to protect acknowledgment (ACK) packet transmission. Each CCA occurs at the boundary of a backoff slot, where 8 of the 20 physical-layer symbols in a backoff slot are monitored. Once a packet is received, the receiver sends the ACK after 12 to 31 symbols. Performing only a single CCA (with CW = 1) could cause a collision between a newly-transmitted packet and an ACK. Setting CW >2 would waste channel throughput without providing any benefit.

However for data transmission without acknowledgements, performing a single CCA (CW = 1) is sufficient, and setting CW to 2 is unnecessary [8]. This assumption is made in this paper; acknowledgements are assumed to be unnecessary because packets containing similar data are being transmitted by many nodes, so packet loss is assumed to have little effect on sensing integrity or accuracy. This simplifies the mathematical analysis, while not transmitting acknowledgements also saves power [9]. It is also assumed that each slave node has at most one packet to send during each superframe, and that the packet length L is constant. (In IEEE 802.15.4, a slave node is defined as a node associated with a PAN Coordinator.)

When CW = 2, it generally takes slightly longer before all transmissions have taken place than when CW = 1, due to the delay introduced by having two CCAs instead of one. However, simulations show that this difference is very small, indeed the analytical results from the new 4D model correspond closely with the simulations, justifying its correctness.

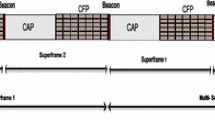
The MAC protocol defined in the IEEE 802.15.4 standard [7] includes a duty cycling operation. The MAC attributes macBeaconOrder (BO) and macSuperframeOrder (SO) determine the lengths of the Beacon Interval (BI) and Superfame Duration (SD), respectively, where BO and SO are integers and 0 ≤ SO ≤ BO ≤ 14. The time during a Contention Access Period (CAP) is slotted, and each slot is of duration aUnitBackoffPeriod (equal to 20 symbols). A slave node starts with a random backoff, the length of which (measured in slots) is randomly chosen in the range [0, 2BE − 1] with a uniform distribution. BE is the backoff exponent, which takes an initial value of macMinBE.

In the 2.4 GHz frequency band with a data rate of 250 kb/s (sample rate: 62.5 ksymbols/s), 10 bytes (80 bits) can be transmitted during each slot (aUnitBackoffPeriod = 20 symbols). Each data packet is between 9 and 127 bytes long, occupying between 1 and 13 slots.

1.2 Related work and motivation for model

There are simulation studies of the IEEE 802.15.4 protocol in small star-topology networks under low loads [10], and studies of energy efficiency in a dense wireless network [11], while ns2 simulations have evaluated delay and other performance aspects [12]. Analytical models exist for beacon enabled mode with slotted CSMA/CA during the Contention Access Period (CAP) [13–18]. One model represents the behavior of individual nodes by a three-level renewal process [13], while another Markov model provides accurate evaluation of throughput under saturation [14]. The access delay of uplink transmissions in a beacon-enabled PAN has been evaluated through an M/G/1/K queuing model [16], assuming Poisson arrivals. A further Markov chain model operates on a per-user basis [17]. In this existing research, the probability that each node starts sensing the medium in a randomly chosen slot is assumed to be constant and independent, regardless of the number of retransmissions that have already taken place. This probability is dependent on assumptions about channel access probability [19].

This paper proposes a new 4D Markov chain model. It is an extension of an existing 3D model [20] which captures the state of the whole star network rather than the state of each individual node. In this paper, the probability that the mth attempt to sense the channel takes place during timeslot n [P n (m) in the “Appendix”] is no longer independent of m, yielding more accurate results. Furthermore, the states are denoted by ψ n (c, r, t, u) where there is an additional parameter t which was not present in the 3D model—it captures the fact that a node cannot stay in backoff state for more than 2BE slots. Because of this shortcoming of the 3D model, the Markov chain could enter states which should not have existed, generating erroneous results. Furthermore, in the 3D model, the area under the curve representing the probability that transmission finishes by a particular slot did not sum to unity. The 4D model introduced here overcomes these fundamental shortcomings.

2 New 4D Markov chain model

The following variables are used in this model—they are presented below in order of their first appearance:

  • BE: Backoff Exponent

  • macMinBE: minimum Backoff Exponent

  • macMaxBE: maximum Backoff Exponent

  • W: backoff window size, where W = min(2 m+macMinBE, 2macMaxBE)

  • M: maximum number of attempts made by a node to sense the channel

  • MaxN: largest numbered timeslot during which a node can make its Mth attempt to sense the channel

  • C: total number of slave nodes associated with the PAN Coordinator

  • L: packet length in slots

  • n: number of the current timeslot in the Contention Access Period (CAP)

  • c: number of nodes in the backoff state during timeslot n

  • r: number of slots that have elapsed since a node starting transmitting a packet – several nodes may have done so simultaneously, resulting in a collision

  • u: number of nodes finished transmission successfully, or transmitting without collision

  • t: number of idle slots since the last transmission (1 ≤ t ≤ 2BE)

  • ψ n (c, r, t, u): state in the 4D Markov chain model

  • \( S_{c}^{k} (n,t) \) : time-varying transition probability that k out of the c backoff nodes start transmission

  • P (n, t): probability that a node attempts to sense the idle channel at timeslot n after t idle slots

  • P W (n, t): probability that a node attempts to sense the channel at any slot which is both numbered no less than n, and before the end of the backoff window W

  • Q (n, t): conditional probability for P (n, t) given the condition of P W (n, t)

  • P n (i): probability of the ith attempt to sense the channel at timeslot n, (i = 0, 1, … M)

  • \( G_{c}^{k} (n) \): probability that k out of c nodes make their Mth attempt to sense the busy channel given that none of the c nodes has done so before timeslot n

  • Q n (M): probability that any one of the c nodes makes its Mth attempt to sense the channel during timeslot n given that it has not done so before timeslot n

  • S F : timeslot during which the last transmission is completed

  • H n : probability that timeslot n is idle

  • I: total number of idle timeslots before all transmissions are completed

  • B: total number of timeslots during which the medium is busy (successful transmission or collision)

  • P n : probability that a node senses the channel or makes an attempt to access it in a particular slot n

In the Markov chain, a contention state is one in which the channel is clear, i.e. r = 0. The contention state transitions for the 4D Markov chain model are shown in Fig. 1(a), and assuming that k out of the c backoff nodes (nodes in backoff state) start transmission, the corresponding transitions are:

$$ \psi_{n} (c,0,t,u)\mathop{\longrightarrow}\limits^{{S_{c}^{k} (n,t)}}\left\{ {\begin{array}{*{20}c} {\psi_{n + 1} (c,0,\min (t + 1,2^{BE} ),u)} \hfill & {{\text{if }}k = 0.} \hfill \\ {\psi_{n + 1} (c - k,1,0,u + 1)} \hfill & {{\text{if }}k = 1.} \hfill \\ {\psi_{n + 1} (c - k,1,0,u)} \hfill & {{\text{if }}k > 1.} \hfill \\ {\psi_{n + 1} (0,0,0,u)} \hfill & {{\text{if }}c = 0{\text{ and }}t = 0.} \hfill \\ \end{array} } \right. $$
(1)

In timeslot n, c is the number of nodes in backoff state, t is the number of idle slots since the last transmission, and u is the number of nodes with have either finished transmission successfully or are transmitting without collision. The time-varying transition probability that k out of the c backoff nodes start transmission is:

$$ S_{c}^{k} (n,t) = \left\{ {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} c \\ k \\ \end{array} } \right)\left[ {Q\left( {n,t} \right)} \right]^{k} \left[ {1 - Q\left( {n,t} \right)} \right]^{c - k} \, } \hfill & {{\text{if }}0 \, \le \, k \, \le \, c \, and \, 0 \, \le \, n \, \le {\text{ MaxN}}.} \hfill \\ 0 \hfill & {{\text{if }}k \, < \, c{\text{ and }}n \, > {\text{ MaxN}}.} \hfill \\ 1 \hfill & {i{\text{f }}k \, = \, c{\text{ and }}n \, > {\text{ MaxN}}.} \hfill \\ \end{array} } \right. $$
(2)

Q (n,t) is the probability that any one of the c backoff nodes attempts to sense the idle channel during timeslot n given that the last transmission finished at timeslot n − t, so that the channel was idle for t slots before timeslot n:

$$ Q\left( {n,t} \right) = \, {{P(n,t)} \mathord{\left/ {\vphantom {{P(n,t)} {P_{W} (n,t)}}} \right. \kern-\nulldelimiterspace} {P_{W} (n,t)}} $$
(3)

MaxN is the largest numbered timeslot during which a node can make its last (Mth) attempt to sense the channel with non-zero probability P MaxN(M). P n (i) (i = 0, 1, … M) is the probability that the ith attempt to sense the channel takes place during timeslot n; it is defined in the “Appendix”.

$$ P(n,t) = \left\{ {\begin{array}{lll} {P_{n} (0)} & {{\text{if }}n \le t{\text{ and }}t < W.} \\ {P_{n} (0) + \frac{1}{W}\sum\limits_{m = 1}^{M} {\left( {\sum\limits_{{k = \max \left( {0,n - W} \right)}}^{n - t} {P_{k} \left( {m - 1} \right)} } \right)} } & {{\text{if }}n > \, t.} \\ \end{array} } \right. $$
(4)
$$ P(n,t) = \sum\limits_{N = n}^{n - t + W} {P(N,\;t + N - n)} $$
(5)

The time-varying transition probability ψ n (c, r, u) in the 3D model for transmission states (states having r > 0 i.e. in which one or more nodes are transmitting) is replaced in the 4D model by ψ n (c, r, 0, u). The variable r is the number of slots that have elapsed since a node starting transmitting a packet—several nodes may have done so simultaneously, resulting in a collision. \( G_{c}^{k} (n) \) in the 4D model is the probability that k out of the c backoff nodes make their Mth attempt to sense the busy channel during timeslot n, given that none of them has done so before. Figure 1(b) shows the transmission state transitions for 4D Markov chain model.

$$ \psi_{n} (c,r,0,u)\mathop{\longrightarrow}\limits^{{G_{c}^{k} (n)}}\psi_{n + 1} (c - k,r^{\prime} = \min (r + 1,\;L + 1),0,u) $$
(6)
$$ G_{c}^{k} (n) = \left[ {Q_{n} (M)} \right]^{k} \left[ {1 - Q_{n} (M)} \right]^{c - k} ,\quad 0 \le k \le c. $$
(7)
$$ Q_{n} (M) = {{P_{n} (M)} \mathord{\left/ {\vphantom {{P_{n} (M)} {\sum\limits_{N = n}^{{{\text{Max}}N}} {P_{N} (M)} }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{N = n}^{{{\text{Max}}N}} {P_{N} (M)} }} $$
(8)

\( \sum\limits_{N = n}^{\text{MaxN}} {P_{N} (M)} \) is the probability that the node makes its last (Mth) attempt to sense the busy channel during or after timeslot n.Therefore the state vector at timeslot n is:

$$ \begin{array}{*{20}c} {\Uppsi_{n} = \left\{ {\psi_{n} (C,0, \, 0,0),\psi_{n} (C,0, \, 1,0), \ldots ,\psi_{n} (C,0, \, 2^{BE } - 1,0),} \right.} \\ {\left. {\psi_{n} (C - 1,1, \, 0,1), \ldots ,\psi_{n} (C - 1,L, \, 0,1),\psi_{n} (C - 1,0, \, 0,1), \ldots ,\psi_{n} (0,0, \, 0,C)} \right\}.} \\ \end{array} $$
(9)
Fig. 1
figure 1

a Contention state transitions for the 4D Markov chain model for BE = 3. b Transmission state transitions for the 4D Markov chain model

Full size image

The initial value of Ψ 0 at the beginning of a Contention Access Period (CAP) is {1, 0, 0, …, 0}, because all the C nodes are in backoff state and contending for the channel (i.e. c = C). It is often the case that a closed-form solution is not possible due to the complexity of the model, and state probabilities have to be evaluated by computer. Here, the time-varying transition matrix T n is generated by a MATLAB program which employs Eqs. 1 and 6, where:

$$ \Uppsi_{n + 1} = \Uppsi_{n} T_{n} $$
(10)

The random variable S F is the timeslot during which the last transmission is completed. The 4D Markov chain model can be used to derive the probability that all C nodes have finished transmitting by timeslot n, which is the probability that no node is in backoff or transmission state at timeslot n + 1.

$$ P(S_{F} \le n) = \sum\limits_{u = 0}^{C} {\psi_{n + 1} (0,0,0,u)} $$
(11)

Then P (S F  = n) can be derived, namely the probability of all transmissions finishing exactly at timeslot n:

$$ P(S_{F} = n) = P(S_{F} \le n) - P(S_{F} \le n - 1) $$
(12)

The mean time taken for all transmissions to complete is thus:

$$ E(S_{F} ) = \sum\limits_{n = 0}^{\infty } {n \cdot P(S_{F} = n)} $$
(13)

The random variable H n is the probability that timeslot n is idle:

$$ H_{n} = \left\{ {\begin{array}{ll} {\sum\limits_{c = 1}^{C} {\sum\limits_{t = 0}^{{2^{\text{BE}} - \, 1}} {\sum\limits_{u = 0}^{C - c} {\psi_{n} (c,0,t,u)} } } } & {{\text{if }}n < S_{F} } \\ 1 & {{\text{if }}n \ge S_{F} } \\ \end{array} } \right. $$
(14)

The random variable I is the total number of idle slots before all transmissions are completed, so the mean number of idle slots is therefore:

$$ E(I) = \sum\limits_{n = 0}^{MaxN} {H_{n} } $$
(15)

The random variable B is the number of timeslots during which the medium is busy—because of either a successful transmission or a packet collision. Its mean value is the expected number of timeslots required to finish the transmission, minus the expected number of idle slots:

$$ E(B) = E(S_{F} ) - E(I) $$

3 Calculation and simulation results

Figure 2 shows simulation results from OPNET Version 11.5, incorporating the open-ZB toolset for IEEE 802.15.4 with beacon enabled mode (Version 2.0) [21]. The original source code with contention window CW = 2 was modified to CW = 1, and some bugs were fixed so that backoff nodes discard packets correctly after the number of transmission attempts exceeds MacMaxbackoff.

Fig. 2
figure 2

a Comparison between the 3D model, the 4D model, and OPNET simulation with C = 5 active nodes, of the probability P(S F  = n) that the last transmission finishes at slot n. b Comparison between the 3D model, the 4D model, and OPNET simulation with C = 15 active nodes, of the probability P (S F  = n) that the last transmission finishes at slot n

Full size image

Simulations took place with a range of values for the number of slave nodes C and the packet length L. During each simulation run, each slave node clears its buffer and generates a data packet at the beginning of each superframe. After receiving the beacon frame, it then chooses a random slot during the Contention Access Period (CAP) during which it senses the channel and tries to send the packet. If the channel is busy, the node performs another backoff and senses the channel again, repeating this procedure until it senses a clear channel and sends the packet. If several nodes sense a clear channel and send packets simultaneously, then a collision results and the packets are lost without re-transmission. Also, if a slave node detects a busy channel after the maximum number of retries (MacMaxbackoff), it discards its packet.

Figure 2 shows P(S F  = n), namely the probability that the last transmission finishes exactly at slot n. Calculations confirm that the sum of this probability over all values of n is unity in both the simulation (10,000 simulation runs) and the 4D Markov chain model, as expected. However with the 3D model [20], it is only 0.906 for C = 5 and L = 5 [Fig. 2(a)], so there appears to be a probability of 0.094 that the last transmission finishes after n = MaxN + L, which is of course incorrect. For more nodes C, the area under the curve with the 3D model decreases even further [0.335 for C = 15 and L = 5 as shown in Fig. 2(b)]. However with the 4D model, it remains at unity—also, 4D model agrees well with the simulation results whereas the 3D model does not.

However, there is a slight difference between the results from the 4D model and the simulations. This is because the attempt probability P n (as described in the “Appendix”) is based on the assumption that the channel was always busy before the current timeslot n. In reality there is always at least one idle slot between any two transmissions, so the real attempt probability is smaller than P n , and the expected time required to finish all transmissions is slightly longer than the analytical result suggests. This reasoning is confirmed by Fig. 2, where the difference between analytical results and simulation results in Fig. 2(b) is smaller than in Fig. 2(a). This is because there are more slave nodes in Fig. 2(b), so the channel is generally busier than in Fig. 2(a), providing a closer approximation to the assumption underlying the attempt probability model in the “Appendix”.

Figure 3(a) shows P (S F  = n) against n for different numbers of nodes C with constant packet length L; Fig. 3(b) shows this for different packet lengths L but constant number of nodes C. As expected, the mean number of timeslots required to complete transmission increases either with more contending nodes C or longer packet length L. Figure 3 also shows that the increase in the mean number of timeslots required to complete transmission becomes less pronounced when C ≥ 10 or L ≥ 8. Under either condition contention becomes more severe, so more nodes fail to access the transmission medium and thus cannot send their packets by their last attempt.

Fig. 3
figure 3

a Probability P (S F  = n) that the last transmission finishes at slot n for different numbers of nodes C but constant packet length L = 10. b Probability P (S F  = n) that the last transmission finishes at slot n for a constant number of nodes C = 10 but different packet lengths L

Full size image

Figure 4 shows that as expected E(S F ), the mean number of timeslots required to finish all transmission, increases with either the number of nodes C, or the packet length L.

Fig. 4
figure 4

E(S F ), mean number of timeslots required to finish transmission

Full size image

Figure 5 shows E(I), the mean number of idle slots before all transmissions are complete. With few slave nodes (C = 2 or 3), E(I) increases with packet length L because for longer packets, it is more likely that backoff nodes will sense a busy channel and select a longer backoff for the next transmission attempt, resulting in general in larger idle gaps between transmissions. With more nodes (C > 7), the situation is reversed and E (I) decreases with L, because longer packets imply that the channel is busy for longer, so there are more nodes which are already transmitting which can contend even after backoff nodes have increased their backoff exponential number (BE). Therefore in this case, the number of idle slots decreases as the number of nodes increases.

Fig. 5
figure 5

E(I), mean number of idle timeslots before the last transmission

Full size image

Figure 6 shows E(B), the mean number of timeslots during which the timeslot is busy due to either successful transmission, or packet loss due to collision. The trend is similar to Fig. 4, which shows the expected number of timeslots required to complete transmission. E (B) increases with increasing packet length L or number of initial nodes C. However the mean number of actual packets transmitted decreases for longer packet lengths L. For example, for the same initial number of nodes (C = 16), the expected number of packets transmitted is 10.5 (42 slots divided by 4 slots) for L = 4, but this decreases to 7.2 (72 slots divided by 10 slots) for L = 10, because longer packets imply that the channel is busy for longer, and there is hence a higher probability of backoff nodes discarding packets once the number of attempts becomes larger than MacMaxbackoff.

Fig. 6
figure 6

E(B), mean number of busy timeslots (either successful transmission, or collision)

Full size image

Figure 7 shows the probability that the channel is idle at a given number of timeslots after the beacon is transmitted at timeslot 0; once the curve has decreased to zero, all nodes have transmitted. For fewer nodes (C = 5) and shorter packets (L = 5), transmission is complete after approximately 70 slots, while for more nodes (C = 10) and longer packets (L = 10), more than 100 slots are required. (Fig. 4 has already provided confirmation that for larger C and L, more timeslots are required for transmission to complete.)

Fig. 7
figure 7

H n , Probability that the channel is idle during timeslot n

Full size image

The distance between peaks in the curve for C = 10 and L = 10 increases with time in Fig. 7, whereas the peaks themselves decrease in size. This is because as time passes, the number of backoff nodes contending for access to the transmission medium decreases because more nodes have finished their transmission. Hence the gap between peaks in the curve increases, but the probability of finishing the next transmission in a given timeslot decreases (value of each peak in the curve) because there are more timeslots available to start (and finish) the next transmission. Another interesting characteristic is that the total number of peaks in the curve is equal to the total number of packet transmissions. For example, the total number of such peaks is six for C = 10 and L = 10, which agrees with the expected number of packets transmitted in Fig. 6. This can be calculated as the expected number of busy timeslots divided by packet length (62/10 = 6.2, shown in Fig. 6).

Figures 8 and 9 show the probability P (S F  ≤ n) that transmission is complete before the end of a superframe with SO = 0 and SO = 1 respectively. (As described above, SO is a MAC attribute which determines the superframe duration.) When the number of nodes or the packet length increases, the probability P (S F  ≤ n) decreases. Figure 8 shows for more than three nodes (C > 3), the probability of finishing transmission at the end of the CAP (48 slots) for BO = 0 decreases dramatically for packet lengths of L ≥ 8, which indicates SO should be larger than 0 in order to finish all transmissions. However in Fig. 9, P (S F  ≤ n) decreases more slowly for C < 8 and L ≥ 8, and for L = 2, P (S F  ≤ n) is always larger than 98% for C ≤ 20, which indicates SO = 1 is sufficient in such cases. For SO ≥ 2, P (S F  ≤ n) = 1 because the number of slots in the superframe is larger than MaxN + L, which means SO = 2 is sufficient to finish one-shot transmission with any number of slave nodes C and any packet length L.

Fig. 8
figure 8

P(S F  ≤ n), probability of finishing transmission before timeslot n for SO = 0

Full size image
Fig. 9
figure 9

P(S F  ≤ n), probability of finishing transmission before timeslot n for SO = 1

Full size image

These graphs can be used to determine the optimum value of SO in order to save energy, and the shortest duration required in order to have an acceptable probability of receiving all packets. For example, Fig. 9 shows that, for C < 19 and L = 4, and for C < 12 and L = 6, the probability of finishing transmission with SO = 1 is more than 95%; in such cases the optimum value SO = 1 would be selected to avoid longer data aggregation delay, and to avoid wasting energy by having a larger SO.

The discussion earlier implies that if at least one slave node generates a packet before the start of a superframe, node S will be able to generate a packet through its data fusion algorithm. If the statistics of these processes were known, a traffic model could then be developed based upon the analysis in this paper. Such a model would specify the statistics of the aggregated data traffic generated by the coordination node S after receiving all packets from adjacent slave nodes. Furthermore, once the optimum value of SO is selected, the data aggregation delay at the coordination node S can be calculated, which is equal to the superframe duration (SD), or the Contention Access Period (CAP) assuming the contention free period (CFP) is zero. After a superframe duration (SD), coordination node S can aggregate all received packets during the last SD to generate an aggregated packet, and forward it to the base station directly or via other intermediate nodes.

Problems may arise if a large number of slave nodes generate data packets before the start of a superframe. The simplest solution would be to increase the backoff window size W, in order to decrease the probability of collision due to multiple nodes choosing the same time slot. However the maximum value of W is determined by macMaxBE, which cannot be larger than 2macMaxBE according to the standard. Therefore it may be necessary to reduce the number of nodes which have a packet to send after receiving the beacon frame. In low-duty cycle applications, the inactive portion of a superframe is much longer than the active period (SD). Therefore most of the sensing data could be generated during the inactive period. A possible solution would be to send the data as soon as possible once the data packet is generated, rather than sending it after the start of a superframe. To achieve this goal, a proposed Enhanced Beacon-Enabled Mode incorporates optional Periodic Wakeup (PW) by the associated slave nodes, and listening by the PAN Coordinator during the inactive period. Hence not only queued data, but also newly generated data during the inactive period can be sent to the PAN coordinator with low latency [22]. The method is backward compatible and inter-operable with the original IEEE 802.15.4 standard.

4 Conclusions

This paper introduced a 4D Markov chain model to calculate both the probability distribution function and mean number of timeslots required to finish all transmissions. It is assumed that C nodes contend for the channel at the beginning of a superframe and each transmits a packet of length L using beacon mode in the IEEE 802.15.4 standard without acknowledgement (NACK mode). This 4D model was developed by extending an existing 3D Markov chain model [20], rectifying errors, and providing a more accurate and meaningful result.

This model can be used to decide the optimum value of SO to save energy, and can determine the length of IEEE 802.15.4 Contention Access Period necessary for packets to be received with an acceptable probability. Furthermore, based upon the results in this paper, an analytical model could be derived for the aggregated data traffic that the coordination node generates upon receiving packets from adjacent slave nodes.