1 Introduction

Shortage of the available water resources in Iran which has an arid and semi-arid climate, along with increasing water demand due to the expansion of agricultural, urban, and industrial activities has always been considered one of the most critical challenges of the water sector. Therefore, optimal control and use of water resources and water resources management, in general, are of high priority. Surface reservoirs are among the structures used in the field of water resources for storing and using surface water resources. For the optimal operation of a reservoir, the objective function value and the considered variables are optimized to supply the demands. In real cases, different objectives such as supplying drinking, agricultural, industrial, and environmental water in downstream areas, generating hydropower energy, and controlling flood are usually defined, which can be either consistent or inconsistent with each other. Therefore, to consider all the above-mentioned objectives simultaneously, the system defined for the optimal operation of the reservoir is considered as a multi-objective one.

Optimization problems for water resources systems may include a large number of different decision variables and constraints, which cannot be solved by the conventional mathematical methods. In recent decades, various methods have been proposed for optimizing complex problems. Quantification methods for defining and evaluating different water problems include a variety of different mathematical techniques. These techniques are a part of important research topics such as systems analysis, systems engineering, operations research (OR), or management science, all of which have similar objectives (Wurbs 1993).

During the last decades, several evolutionary algorithms (EAs) including genetic algorithm (GA) (Chang et al. 2005), water cycle algorithm (WCA) (Qaderi et al. 2018), shark algorithm (SA) (Ehteram et al. 2017), symbiotic organisms search (SOS) (Bozorg-Haddad et al. 2017; Akbarifard and Radmanesh 2018; Madadi et al. 2020a, b), particle swarm optimization (PSO) (Baltar and Fontane 2008; Bozorg-Haddad et al. 2020), and moth swarm algorithm (MSA) (Madadi et al. 2020a, b) have been applied for solving water engineering optimization problems.

The necessity of solving the problems that address several different objectives simultaneously has led to forming algorithms with this capability. Algorithms such as non-dominated sorting genetic algorithm-II (NSGA-II), Pareto envelope-based selection algorithm-II (PESA-II), strength Pareto evolutionary algorithm-2 (SPEA2), multi-objective particle swarm optimization (MOPSO), etc. have been developed in this regard. In the present study, the MOWCA algorithm is used in the optimal operation of multi-reservoir, multi-objective water resources systems for the first time.

Reddy and Kumar (2006) proposed a multi-objective evolutionary algorithm to derive a set of optimal operation policies for a multi-objective reservoir system. They used the multi-objective genetic algorithm (MOGA) in a real reservoir system (i.e. Bhadra Reservoir) in India and found that MOGA was useful for multi-objective optimization problems. Deep et al. (2009) proposed a fuzzy interaction method for efficient management of multi-objective multi-reservoir problems and demonstrated the performance of the proposed method based on the mathematical model of a real-world multi-objective multi-reservoir system. Noori et al. (2013) developed the genetic algorithm in their study for the optimal operation of multi-objective multi-reservoir water resources in Ghezel Ozen Basin used for the generation of power plants and control of flood. Model performance for 12 months of the year showed that the release rate in the flooding months was higher than that in in other months. Guo et al. (2013) proposed a multi-reservoir application policy to supply water by combining parametric and hedging rules. To maintain the diversity of non-dominant solutions for the multi-objective optimization problem and bringing them closer to the optimal alternative surfaces, they incorporated a multi-population mechanism into the non-dominated sorting particle swarm optimization (NSPSO) algorithm to develop an improved NSPSO algorithm (I-NSPSO). The performance of I-NSPSO on two benchmark functions represented it had good ability in finding Pareto optimal sets. I-NSPSO also showed good performance in multi-objective optimization of the proposed policy. Sadollah et al. (2015a) developed the MOWCA to solve multi-objective bound problems. Their research proved MOWCA's exploration capability compared to other efficient methods. Using MOWCA has been mainly in cases such as the problem of optimal design for the simultaneous finding of a unified power flow controller and power system stabilizer (Khodabakhshian et al. 2016) and finding efficient boundaries associated with the optimization model (Moradi et al. 2017). In order for the optimal operation of reservoir systems, Qaderi et al. (2018) used the water cycle algorithm (WCA). In the problem of operating Gorganrood basin system, the results showed the superiority of the water cycling algorithm to other investigated algorithms such as GA and PSO algorithms. Feng et al. (2017) investigated the optimal operation of Guizhou hydropower system in China using an orthogonal discrete differential dynamic programming (ODDDP) algorithm. The results showed that the ODDDP method, with only 0.37% of computational time, achieved 99.75% generation in the examined hydropower system. Afshar and Hajiabadi (2018) presented a new approach of parallel cellular automaton (PCA) to optimize the operation of the multi-objective reservoir in their study. They also used the NSGA-II to solve the problems and compare the results. The superiority of the method proposed to NSGA-II was shown by increasing the problem scale. Also, Feng et al. (2017) used a parallel genetic algorithm for the Wu hydropower system in China and showed that the proposed method can use expensive computational resources to improve population performance. Xu (2020) applied the NSGA-II algorithm to multi-objective operation strategy for multi-reservoirs in small-scaled watershed. Akbarifard et al. (2020) used the MSA to optimize the complex problem of 4-reservoir and 10-reservoir systems operation. Also, Sharifi et al. (2021) developed a new fitness-distance-balance (FDB) selection method in the MSA to achieve promoted FDB-MSA for optimizing the hydropower generation of a multi-reservoir system along Karun River in Iran. The results showed that the FDB-MSA could successfully increase the hydropower generation.

A multi-objective optimization problem (MOP) is a multi-criteria decision-making domain that contains more than one objective function optimized simultaneously. Pareto dominance is the most common relationship used to compare solutions in MOPs. However, as the number of objectives grows beyond three, Pareto dominance alone is no longer satisfactory. Performance metric parameters are widely used to make fair quantitative evaluations and judgments among different types of multi-objective algorithms. In this paper, four performance parameters including generational distance (GD), metric of spacing (S), spread (Δ), and maximum spread (MS) criteria that are widely used to evaluate the performance of metaheuristic algorithms are investigated.

The need to solve problems that address several different objectives simultaneously has led to developing algorithms with such capabilities, i.e. NSGA-II and MOWCA. In the present study, the MOWCA algorithm was used to solve several hydrology and water resources problems for the first time. Also, due to the well-known NSGA-II algorithm and its current use in various multi-objective problems, especially multi-objective reservoir systems, in this study, the NSGA-II algorithm was compared with the MOWCA algorithm.

To the authors’ knowledge, this is the first application of MOWCA algorithm in optimal operation of multi-reservoirs systems with different objectives. The limitations and advantages of the utilized algorithms for handling constrained MOPs are presented in Table 1.

Table 1 Main advantages and limitations of the utilized algorithms
Full size table

2 Materials and Methods

Halilrood basin is one of the main sub-basins of Hamoun-Jazmourian, which plays a major role in its annual stream generation, and is located in the western part of Hamoun-Jazmourian, between longitude 56° -51′ to 61° 30′ east and latitude 26° 18′ to 29° 30′ north. This basin has areas of south and east of Kerman Province, including Baft, Jiroft, and Kohnuj and areas of west of Sistan and Baluchestan Province including Iranshahr. The main dams in the western part of the catchment include Baft Earth Dam (Asyab Jofte) constructed for agricultural, drinking, and industrial purposes, Jiroft double curvature concrete arch dam h constructed for drinking, industrial, agricultural, electricity generation, and flood control purposes, and Safarood Dam (under construction) constructed for agricultural, drinking, and industrial purposes. Figure 1 shows the position of the above-mentioned dams in the western part of Jazmourian basin (Halilrood catchment). Despite the construction of numerous dams on the main rivers supplying wetlands and their stream, the increasing trend of studying and constructing new dams in this basin still continues. As a result, with increasing construction of dams and planning river water extraction in the basin, it is clear that the inflow of water into the wetland will be greatly reduced through the surface water resources of the wetland. Indeed, the role of Jiroft Dam located on Halilrood River in the western part of Jazmourian is more prominent than that of others.

Fig. 1
figure 1

Location of Jiroft Dam in Hamoun-Jazmourian basin

Full size image

By constructing the above-mentioned dams, the inflows through the rivers to the Jazmourian wetland have almost discontinued. Therefore, increasing construction of dams and water extraction for various uses as well as lack of proper allocation of water as the result of the environmental water demand have a significant impact on the reduction of wetland area. If proper dam management planning is not devoted for the environment in the dams planning management and the construction process of new dams in the basin continues further, a more undesirable condition would be expected. Therefore, it is necessary to do more management studies on surface water resources and explore different scenarios for optimal operation of these resources and existing dams, which is the purpose of this study.

2.1 Multi-objective Optimization Problems (MOPs)

An MOP is a multi-criteria decision-making domain that contains more than one objective function optimized simultaneously:

$$F\left(X\right)={[{F}_{1}\left(X\right), {F}_{2}\left(X\right), \dots , {F}_{m}\left(X\right),]}^{T}$$
(1)

where X =  × 1, × 2, × 3,…, xd are a vector of variables, and d and m are the number of variables and objectives, respectively. A simple approach to solving MOPs is to use a variety of weight to transform MOPs into a single-objective optimization problem. This problem can be formulated based on Eq. (2):

$$F=\sum_{i=1}^{m}{w}_{i}.{f}_{i}$$
(2)

where m is the number of objective functions, and \({w}_{i}\) and \({f}_{i}\) are weight factors and objective functions, respectively. However, this is time-consuming and considered a major drawback of the method. The most common solution for MOPs is to keep a list of the best solutions in an archive and update it in each iteration. In this method, the best solutions are defined as non-dominated solutions or optimal Pareto solutions. A solution can be considered as a non-dominated solution if and only if it fulfills the following conditions (Coello 2000):

  1. A)

    Pareto dominance: \(U=\left(u1, u2, u3,\dots , un\right)<V=(v1, v2, v3,\dots ,vn)\) if and only if U is less than V in the objective space, which means that:

    $$\left\{\begin{array}{*{20}c}{f}_{i}\left(U\right)\le {f}_{i}\left(V\right) \forall i\\ {f}_{i}\left(U\right){f}_{i}\left(V\right) \exists i\end{array}\right. i=1, 2, 3,\dots , m.$$
    (3)
  2. B)

    Pareto optimal solution: Vector U is an optimal solution if and only if none of the other solutions can dominate U. A set of optimal Pareto solutions is called Pareto optimal front (\({PF}_{optimal}\)).

Figure 2 shows that, among three solutions of A, B, and C, solution C has the highest value for f1 and f2. Thus, it is considered the dominant solution. In contrast, both solutions A and B can be considered as non-dominated solutions (Sadollah et al. 2015a, b).

Fig. 2
figure 2

Pareto optimal solutions (A and B) for two-dimensional space (Sadollah et al. 2015a, b)

Full size image

Performance Criteria for MOPs

In this study, four performance parameters are used to evaluate the performance of the algorithms: generational distance (GD), metric of spacing (S), spread (Δ), and maximum spread (MS) criteria (Sadollah et al. 2015a, b).

Van Veldhuizen and Lamont (1998) introduced the GD criterion, which represented the distance of the solutions obtained by the Pareto line. This criterion specified the ability of different algorithms to find a set of non-dominant solutions with the least distance from the optimal Pareto front. An algorithm with minimum GD had the best convergence with the Pareto optimal front. This evaluation is defined as follows:

$$GD={\frac{1}{NPF}(\sum_{i=1}^{NPF}{d}_{i}^{2})}^{\frac{1}{2}}$$
(4)

where NPF is the number of members obtained on the Pareto front (PF) and d is the Euclidean distance between the ith member at PFg and the closest member at PFoptimal. Figure 3 shows a schematic overview of the two-dimensional GD evaluation criterion. The best criterion obtained for GD is zero; i.e. PFgis exactly on the optimal or PFoptimalline.

Fig. 3
figure 3

Schematic overview of the GD criterion for MOPs (Van Veldhuizen and Lamont 1998)

Full size image

Schott (1995) introduced the distance criterion between the obtained solutions (S), which represented the distribution of non-dominated solutions using a specific algorithm (Schott 1995). This criterion can show how the solutions were distributed among each other and can be defined as:

$$S=\sqrt{{\frac{1}{NPF-1}\sum_{i=1}^{NPF}({d}_{i}\stackrel{-}{d})}^{2}}$$
(5)

In Eq. (5), \({d}_{i}={min}_{j}(\left|{f}_{1}^{i}\left(x\right)-{f}_{1}^{j}\left(x\right)\right|+\left|{f}_{2}^{i}\left(x\right)-{f}_{2}^{j}\left(x\right)\right|\), i,j = 1,2,…,NPF and \(\stackrel{-}{d}\) is the mean of all di. The least value of S yields the best uniform distribution in PFg. If all non-dominated solutions are uniformly distributed in PFg, the values of di and d are similar. Thus, the value of criterion S is zero. Figure 4 shows a schematic view of the distance criterion.

Fig. 4
figure 4

Schematic overview of evaluators for MOPs (Schott 1995)

Full size image

Deb (2001) proposed the criterion of spread (Δ). This criterion shows the expansion extent of non-dominated solutions derived from a given algorithm (Deb 2001). This criterion represents how solutions are expanded around PFoptimal and is defined as follows:

$$\Delta =\frac{{d}_{f}+{d}_{l}+\sum_{i=1}^{NPF}\left|{d}_{i}\stackrel{-}{d}\right|}{{d}_{f}+{d}_{l}+(NPF-1)\stackrel{-}{d}}$$
(6)

where df and dl are the distance between the extremum solutions (starting and ending points) at PFoptimal and PFg. di is the distance between any point at PFg, and the closest point at PFoptimal.

This criterion is the point-to-point distance of the diagrams. The benchmark value of Δ is always greater than zero and its lower value means the best distribution and expanding solutions. When Δ is equal to zero, the condition is excellent, indicating that for all the non-dominated points, \({d}_{i}=\stackrel{-}{d}.\) Figure 5 shows a schematic overview of the benchmark criterion of Δ for a Pareto optimal front.

Fig. 5
figure 5

Schematic overview of the spread criterion (Δ) for MOPs (Deb 2001; Deb et al. 2002)

Full size image

The maximum spread (MS) criterion indicates how far the starting and ending points of the PFg line overlap similar points on the PFoptimal line and, to this end, measures the proximity of two extrema at PFoptimal and PFg. This criterion shows how far the non-dominated solutions lines cover the Pareto line. Naturally, it is better if the speed is higher. This criterion is defined as Eq. (7):

$$MS={\left[\frac{1}{m}\sum_{i=1}^{m}{\left[\frac{\mathrm{min}\left({f}_{i}^{max},{F}_{i}^{max}\right)-\mathrm{max}({f}_{i}^{min},{F}_{i}^{min})}{{F}_{i}^{max}-{F}_{i}^{min}}\right]}^{2}\right]}^{\frac{1}{2}}$$
(7)

where \({f}_{i}^{max}\) and \({f}_{i}^{min}\) are the maximum and minimum ith target at PFg, and \({F}_{i}^{max}\) and \({F}_{i}^{min}\) are the maximum and minimum ith target at PFoptimal, respectively. A larger amount of MS means better expansion of solutions (Sadollah et al. 2015a, b.

2.2 Water Cycle Algorithm (WCA)

The WCA was developed by Eskandar et al. (2012) based on the water cycle or hydrological cycle in nature (Eskandar et al. 2012). Similar to other meta-heuristic algorithms, the WCA method starts with the initial population, so-called raindrops. At first, it is assumed that there is rain or precipitation. The best person (the best water drop) is chosen as the sea. Thereafter, some good raindrops are considered as rivers and the remaining ones as streams that flow into rivers and seas. In the WCA method, a single solution is called a "raindrop". In the GA method, such an array is called a "chromosome". In a multi-dimensional optimization problem, a raindrop is an Nvar × 1 array, defined as Eq. (8).

$$Raindrop = [{X}_{1}, {X}_{2}, {X}_{3}, . . . , {X}_{Nvar}]$$
(8)

where X1 to XNvar represent the decision variables. To begin with, a sample of the raindrop matrix with the size of Npop × Nvar is randomly generated.

$$Population of raindrops=\left[\begin{bmatrix}{Raindrop}_{1}\\ {Raindrop}_{2}\\ \vdots \\ {Raindrop}_{{N}_{pop}} \end{bmatrix} \right]= \left[\begin{bmatrix}{X}_{1}^{1}{X}_{2}^{1}{X}_{3}^{1}& \cdots &{X}_{{N}_{var}}^{1}\\ \vdots & \ddots & \vdots \\ {X}_{1}^{{N}_{pop}}{X}_{2}^{{N}_{pop}}{X}_{3}^{{N}_{pop}}& \cdots &{X}_{{N}_{var}}^{{N}_{pop}}\end{bmatrix} \right]$$
(9)

where Npop and Nvar are the number of raindrops (initial population) and number of design variables, respectively. The values of the given cost function (C) are obtained from Eq. (10).

$${C}_{i}={Cost}_{i}=f\left({X}_{1}^{i}, {X}_{2}^{i}, {X}_{3}^{i},\dots , {X}_{{N}_{var}}^{i}\right) , i=1, 2, 3,\dots , {N}_{pop}$$
(10)

where Ci is the target value of each drop. In the first step, the Npop number of raindrops is created and, then, the NSR number of the best droplets (minimum value) is selected as the sea and river. Raindrops with the smallest amount are regarded as the sea. NSR is the sum of the rivers (which is an applied parameter) and a sea (Eq. 11). The rest of the population (streams that may flow into rivers or directly into the sea) is calculated using Eq. (12).

(11)
$${N}_{Raindrops}={N}_{pop}-{N}_{SR}$$
(12)

Equation (13) is employed to determine or assign raindrops to rivers and seas, depending on the flow intensity.

$${NS}_{n}=round\left\{\left|\frac{{Cost}_{n}}{{\sum }_{i=1}^{{N}_{SR}}{Cost}_{i}}\right|\times {N}_{Raindrops}\right\} , n=1, 2,\dots , {N}_{SR}$$
(13)

where NSn is the number of streams that flow into specific rivers or seas. A stream flows up to the river along with a connection between them using the randomly selected distance, which is determined by Eq. (14).

$$X\in \left(0, C\times d\right), C>1$$
(14)

where C has a value between one and two (close to two) and the best value for C is considered two (Eskandar et al. 2012). d is the current distance between the stream and the river. The value of X in Eq. (14) is a random number distributed (uniformly or any other appropriate distribution) between zero and (C × d). The new position of streams and rivers can be calculated by Eqs. (15) and (16).

$${X}_{Stream}^{i+1}={X}_{Stream}^{i}+rand\times C\times ({X}_{River}^{i}-{X}_{Stream}^{i})$$
(15)
$${X}_{River}^{i+1}={X}_{River}^{i}+rand\times C\times ({X}_{Sea}^{i}-{X}_{River}^{i})$$
(16)

where rand is a uniform random number distributed between zero and one. If the solution provided by a stream is better than the river connected to it, the position of the river and stream will change. This change can also happen in the same way for rivers and seas. Evaporation is one of the most important factors preventing the rapid convergence of the algorithm and being trapped in the local minima. The process of evaporation causes the seawater to evaporate again as it flows into rivers or streams. The pseudo-code (17) shows how to determine whether a river flows into the sea or not.

$$if \left|{X}_{Sea}^{i}-{X}_{River}^{i}\right|<{d}_{max} , i=\mathrm{1,2},3\dots ,{N}_{SR}-1\to \mathrm{Evaporation and rain process}\to \mathrm{End}$$
(17)

where dmax is a small number (close to zero). Therefore, if the distance between the river and the sea is less than dmax, then, the river has reached the sea. In this situation, the evaporation process is affected and, after sufficient evaporation, precipitation will begin. dmax controls the intensity of the search near the sea (optimal solution). The value of dmax is reduced by Eq. (18) in each step.

$${d}_{max}^{i+1}={d}_{max}^{i}-\frac{{d}_{max}^{i}}{\mathit{max}iteration}$$
(18)

Rainfall is applied after evaporation is met. In the precipitation process, new raindrops form streams at different locations (similar to the GA jump operator). Equation 19 shows the new location of the newly formed streams.

$${X}_{Stream}^{new}=LB+rand\times (UB-LB)$$
(19)

where LB and UB are the upper and lower bounds defined by the problem, respectively. The best new raindrops formed are considered as rivers and the rest of the raindrops as new streams flowing into the rivers. To increase the convergence speed and computational performance of the algorithm for constrained problems, Eq. (20) is used.

$${X}_{Stream}^{new}={X}_{Sea}+\sqrt{\mu }\times randn(1,{N}_{var})$$
(20)

where μ is a factor that represents the search range near the sea. randn is the random number of the normal distribution. Large values of µ increase the probability of leaving the possible area, and small values of µ lead to the search of the algorithm in a smaller area near the sea. The appropriate value of µ is set to 0.1 (Eskandar et al. 2012).

2.3 Developing Multi-objective Water Cycle Algorithm (MOWCA)

To convert WCA into an efficient multi-objective optimization algorithm, the dominant features of the algorithm (such as the sea and rivers) must be properly defined. In normal optimization problems for WCA, only one objective function should be either minimized or maximized. In this situation, some of the best solutions are considered as a sea (for example, the best solution so far) and rivers. For the first time, Sadollah et al. (2015a) presented an MOWCA version to solve multi-objective constrained problems.

However, more than one function should be maximized (minimized) in MOPs, so the definition of choosing sea and rivers in the WCA should be changed to a multi-objective space. The distance density mechanism is used to select the most efficient (best) solutions in the population as a sea and a river. Initially, Deb et al. (2002) defined the mechanism of density-distance from Pareto (Deb et al. 2002). This criterion shows the distribution of non-dominated solutions around a non-dominated solution. Figure 6 illustrates how to calculate the distance density (i.e. the average cubic length) for point i. The lower value for the distance density indicates greater distribution of solutions in a given area. In MOPs, this parameter is calculated in the target spaces, so all the non-dominated solutions must be classified based on the values ​​for one of the target functions. It is necessary to calculate these parameters for each non-dominated solution. An essential step in MOWCA is to select the sea and rivers from the population obtained as the best solution for the other solutions in each iteration. This affects the synchronization capability of MOWCA and maintains good spread of non-dominated solutions.

Fig. 6
figure 6

Schematic overview of computing distance density (Deb 2001; Deb et al. 2002)

Full size image

The distance density must be calculated for all the non-dominant solutions in all iterations. It is necessary to determine which solutions have the highest values of distance density. Afterwards, the obtained non-dominated solutions are considered as seas and rivers. In addition, the flow intensity of rivers and seas is calculated on the basis of distance density values. Some non-dominated solutions are likely to occur near the rivers and seas in the next iteration and their distance values will be lost and reduced.

It is important to store non-dominated solutions in an archive to access the Pareto front series. This archive is updated in each iteration and the dominant solutions are removed from it. So, whenever the number of members in the Pareto archive becomes larger than its size, the density of distance is used to eliminate the non-dominated solutions with the least density values of the distance among the members of the Pareto archive. MOWCA has a high capacity for operation in the design space, as it focuses on near-optimal solutions and extracts the long-distance ones.

Mostly, MOWCA starts with the operation approach, the streams move to the river, and the rivers to the sea. however, in the initial iteration, these movements act as an exploratory factor due to the spread of the initial population. This trend can be seen as MOWCA's potential to finding a wide range of design space while focusing on close optimal non-dominant solutions (Sadollah et. al. 2015b).

Many MOPs are subject to a set of constraints (e.g. inequality, equality, linearity, nonlinearity, etc.). Therefore, it is important to find good and simple strategies for managing constraints and identifying solutions in the possible space. Hence, a simple approach is defined here for applying MOWCA. After obtaining a set of solutions in each iteration, all the constraints are checked and some solutions that are in the possible space are chosen. Then, non-dominant solutions are selected from the possible solutions and enter the Pareto archive. Finally, the seas and rivers are selected from this archive for the subsequent iteration (Sadollah et al. 2015b).

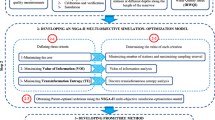
Multi-objective multi-reservoirs long-term simulation optimization model:

The decision variables in the multi-objective reservoirs optimization model are the monthly optimum release values from the dams' reservoirs, which include releasing values to supply downstream demand and flood control in Baft, Safarood, and Jiroft dams as well as releasing of hydropower supply of Jiroft Dam. The planning horizon of this study is 223 months (from 2000 to 2019). So, the MOWCA algorithm has 892 decision variables in the system. The release of the reservoirs in each period is the decision variable, and the storage and input volume to the reservoirs in each period is the variable of state. Input data include river flow volume, evaporation altitude, rainfall height, and volume of requirements on the monthly basis.

In reservoir problems, the usual objective function for definite optimization of the reservoir system can be expressed as follows:

$$Min\left(Max\right) Z=\sum_{t=1}^{T}f({S}_{t},{Re}_{t})$$
(21)

where t is the index of the desired period, T is the number of periods of operation, Z is the objective to be maximized or minimized, \({Re}_{t}\) is the rate of release, and \({S}_{t}\) is the storage volume of the reservoir in period t. State-location equations based on maintaining the mass conservation of the system are considered as a fundamental equation as follows:

$${S}_{t+1}={S}_{t}+{Q}_{t}-{Re}_{t}-{Sp}_{t}-{Loss}_{t}$$
(22)

where \({Q}_{t}\) is reservoir inflow in the tth period, \({Sp}_{t}\) is overflow in the tth period, and \({Loss}_{t}\) is the total water loss in the tth period. The upper and lower ranges of the storage volume should be such that they provide recreational and renewable purposes of flood control volume and minimum level for the dead volume of the reservoir and hydropower plant operation.

$${S}_{Min}\le {S}_{t}\le {S}_{Max}$$
(23)
$${Re}_{Min}\le {Re}_{t}\le {Re}_{Max}$$
(24)

where \({S}_{Min}\) is the minimum storage volume, \({S}_{Max}\) is the maximum storage volume, \({Re}_{Min}\) is the minimum volume of release, and \({Re}_{Max}\) is the maximum volume of release.

Loss from the reservoir is calculated as evaporation given the nonlinear relationship of the surface and volume of the reservoir based on Eqs. (25) to (26):

$${Loss}_{t}={Ev}_{t}\times \stackrel{-}{{A}_{t}}/1000$$
(25)
$$\stackrel{-}{{A}_{t}}=({A}_{t}+{A}_{t+1})/2$$
(26)
$${A}_{t}=a\times {{S}_{t}}^{2}+b\times {S}_{t}+c$$
(27)

where \({Ev}_{t}\) is the mean drop value of the tth period (evaporation minus precipitation) in millimeters, \(\stackrel{-}{{A}_{t}}\) is the mean water level of the reservoir in the tth period in terms of square kilometers, \({A}_{t}\) and \({A}_{t+1}\) are reservoir level per square kilometer at the beginning and end of the period tth, a, b, and c are the constant coefficients of conversion of the reservoir volume into the corresponding level of the reservoir.

The objectives include supplying downstream demand, flood control, and hydropower energy generation for the optimal operation of the multi-reservoir system. Three outputs of hydropower energy, downstream demand supply, and flood control are considered for the reservoir system. In different operation modes, the release of water is initially performed from the hydropower output, then, from the demanded supply output, and finally, from flood control output. As a result, the other two outputs are not used as long as the hydropower output is not used to its maximum capacity. The flood control output is also employed after using the required supply output to its maximum capacity. \({Re}_{Max}^{Power}\) is the maximum output capacity, \({Re}_{Max}^{De}\) is the maximum output supply capacity, and \({Re}_{Max}^{FC}\) is the maximum flood control output capacity, all in million cubic meter (MCM). It should be noted that \({Re}_{t}\) is between zero and the sum of the maximum outputs of the reservoir in this case, \({Re}_{t}^{Power}\), \({Re}_{t}^{De}\), and \({Re}_{t}^{FC}\) are the rates of release from the hydropower output, demand supply, and flood control in each t period in terms of millions of cubic meters, respectively.

2.4 Optimal Operation of Reservoir System to Supply Downstream Demand

In this case, the objective function is to minimize the sum of the squared difference of the demands in period t expressed as:

$$Min {f}_{1}=\sum_{t=1}^{T}{(\frac{{Re}_{t}^{Power}+{Re}_{t}^{De}-{De}_{t}}{{De}_{Max}})}^{2}$$
(28)

where \({f}_{1}\) is the sum of the squares of the monthly release difference (\({Re}_{t}^{Power}+{Re}_{t}^{De}\)) of the demands in period t, \({De}_{Max}\) is the maximum monthly demands of the reservoir, and \({De}_{t}\) is the downstream demands in period t.

2.5 Optimal Operation of Reservoir System for Flood Control Purposes

In the operations with this objective, all the relationships are similar to the operation aiming to supply the downstream demands and only the objective function is as follows:

$$Min {f}_{2}=\sum_{t=1}^{T}{(\frac{{S}_{t}-{S}_{t}^{target}}{{S}_{Max}})}^{2}$$
(29)

where \({S}_{t}^{target}\) is the volume of flood control required in the tth period in million cubic meter (MCM). In the objective function introduced, the goal is to maintain the volume constant around \({S}_{t}^{target}\) during all the operation periods. In fact, if the reservoir volume is greater than the intended target volume, the target is to control flood. If it is below that, it fails to supply the downstream demands and will deviate from \({S}_{t}^{target}\) in each period.

2.6 Optimal Operation of Reservoir System to Supply Hydropower Energy

In this section, the complexity of the problem, especially in terms of constraints and nonlinear conditions, is added and the target function is presented as follows:

$$Min {f}_{3}=\sum_{t=1}^{T}(1-\frac{{P}_{t}}{PPC})$$
(30)

where \({P}_{t}\) is the generation capacity in the tth period in terms of MW and PPC is the capacity of the reservoir installation in terms of MW.

Other dominant relations are as follows:

$${P}_{t}=g\times {e}_{t}\times \frac{{RP}_{t}}{PF}/{Mul}_{t}\times (\stackrel{-}{{H}_{t}}-{TW}_{t})/1000$$
(31)
$$\stackrel{-}{{H}_{t}}=({H}_{t}+{H}_{t+1})/2$$
(32)
$${H}_{t}={a}_{0}+{a}_{1}.{S}_{t}+{a}_{2}.{S}_{t}^{2}+{a}_{3}.{S}_{t}^{3}$$
(33)
$${TW}_{t}={b}_{0}+{b}_{1}.{Re}_{t}^{Power}+{b}_{2}.{({Re}_{t}^{Power})}^{2}+{b}_{3}.{({Re}_{t}^{Power})}^{3}$$
(34)
$${RPS}_{t}={Re}_{t}^{Power}-{RP}_{t}$$
(35)
$$0\le {P}_{t}\le PPC$$
(36)

where \(g\) is the gravity acceleration, \({e}_{t}\) is hydropower plant efficiency assumed constant for all periods, PF is hydropower plant function coefficient,\({Mul}_{t}\) is the conversion factor of million cubic meter per cubic meter per s in the tth period, \(\stackrel{-}{{H}_{t}}\) is the average reservoir water level in the tth period, \({H}_{t}\) is the water level at the beginning of the tth period, \({H}_{t+1}\) is the water level at the end of the tth period in meters, \({TW}_{t}\) is the downstream water level in the tth period in meter, \({a}_{0}\), \({a}_{1}\), \({a}_{2}\), and \({a}_{3}\), are constant coefficients of converting the reservoir volume into the corresponding height, \({b}_{0}\), \({b}_{1}\), \({b}_{2}\), and \({b}_{3},\) are constant coefficients of converting the output water from the hydropower plant into downstream water level, \({RP}_{t}\) is the rate of release of hydropower output to generate power in the tth period in million cubic meter, and \({RPS}_{t}\) is the rate of overflow from the hydropower output in the tth period in million cubic meter.

3 Discussion and Results

In this research, the developed multi-objective simulation–optimization model of the Halilrood catchment reservoir system was coded and compared for the long-term (19 years) using MOWCA and NSGA-II multi-objective algorithms in MATLAB. For this model, three objective functions were defined as follows: the first objective function minimized the sum of deficiency in supplying downstream demands; the second objective function minimized the total volume difference of the reservoir volume from the volume needed for flood control; and the third objective function maximized the total power generation of Jiroft Dam (minimizing the total difference between generated power and capacity of the hydropower plant installation). These objective functions are usually inversely correlated, so that one may inevitably be distanced from one objective when trying to achieve another. This can be resolved to some extent by using multi-objective optimization techniques and achieving the optimum case for all the objectives.

To have a reliable and fair comparison, the maximum number of objective function evaluations (NFEs) and the number of iterations in the investigated algorithms were the same and equal to 50,000 and 1000, respectively. The best values of the initial parameters of the algorithms investigated in the multi-objective operation problem of the Halilrood reservoir system obtained by sensitivity analysis are shown in Tables 2 and 3.

Table 2 MOWCA Algorithm parameter values for multi-objective optimal operation
Full size table

The multi-objective optimization problem of the Halilrood catchment system using a multi-objective water cycle and genetic algorithms with non-dominated sorting for 19-year period (October 2000 to March 2019) were solved from the available statistics and values of parameters in Tables 2 and 3

Table 3 Values of NSGA-II algorithm parameters in multi objective optimal operation problem
Full size table

Table 4 shows the best values of the Pareto front corresponding functions derived from the MOWCA and NSGA-II algorithms.

Table 4 Corresponding Pareto front objective functions derived from algorithms
Full size table

According to the results presented in Table 4, the best optimal point in the Pareto front was selected to minimize the total of the objective functions and somehow approximate all the three objectives simultaneously to the optimal value. The results showed that the MOWCA algorithm performed better with OF1 = 60.02, OF2 = 98.08, OF3 = 77.97 and total objectives of 236.07 than the NSGA-II algorithm with OF1 = 40.04, OF2 = 108.71, OF3 = 119.26 and total objectives of 268.01.

Considering the three objectives of downstream demand supply, flood control, and energy generation in the problem, the superiority of the objective function in the MOWCA algorithm showed several advantages simultaneously. This superiority demonstrated that in all situations, especially in the critical ones, the scenarios obtained from the algorithm can better supply the demands. Also, while controlling the possible floods in real conditions, these scenarios could generate more energy. As a result, according to using real long-term data, the dynamic process of hydrological dispatching conformed to reality.

The Pareto front derived from the values of the three objective functions of supplying downstream demands, hydropower generation, and flood control by each of the multi-objective algorithms used is shown in 3D in Fig. 7.

Fig. 7
figure 7

Pareto front derived from different objective functions in 3D a MOWCA algorithm b NSGA-II algorithm

Full size image

Also, to compare the different objectives obtained from the multi-objective algorithms investigated in pairs and schematic comparison of the results of both MOWCA and NSGA-II algorithms, the Pareto front of two-dimensional objective values is shown in Fig. 8.

Fig. 8
figure 8

Pareto front derived from two-dimensional objective functions by MOWCA and NSGA-II algorithms. a Objective functions of supplying downstream demands—flood control. b Objective functions of supplying demands—hydropower energy generation. c Objective functions of flood control—hydropower energy generation

Full size image

As seen in Fig. 8, in all the three investigated objective functions, the Pareto front derived from the MOWCA algorithm was more regular than the NSGA-II algorithm and at a better level, indicating the complete superiority of the MOWCA algorithm in solving the multi-objective problem of the Halilrood reservoir system operation.

In this study, four evaluation criteria including generational distance (GD), metric of spacing (S), spread (Δ), and maximum spread (MS) were widely used in multi-objective optimization problems to evaluate the efficiency of algorithms. MOWCA and NSGA-II were applied and the results of the evaluation criteria of the multi-objective algorithms used are presented in Table 5.

Table 5 Optimization results of algorithms with evaluation criteria
Full size table

As seen in Table 5, the MOWCA algorithm with GD of 183.81 had the best convergence with the Pareto front compared to the NSGA-II algorithm with GD of 187.98. The metric of spacing criterion (S) in the MOWCA and NSGA-II algorithms was 23.35 and 6.33, respectively, indicating a more uniform distribution of solutions obtained by the NSGA-II algorithm. Also, the spread criterion (Δ) of the MOWCA and NSGA-II algorithms was 0.87 and 0.95, respectively, indicating better distribution and expansion of the solutions in the MOWCA algorithm. Finally, the maximum spread criterion (MS) obtained from MOWCA and NSGA-II algorithms was 151.21 and 47.38, respectively, indicating greater speed of the Pareto line by solutions derived from the MOWCA algorithm.

Figure 9 shows the release values obtained from the MOWCA and NSGA-II algorithms over the long-term (223 months) statistical period for Baft, Jiroft, and Safarood dams. The quantities of hydropower energy generated by the algorithms mentioned for Jiroft Dam are shown in Fig. 10.

Fig. 9
figure 9

Values of water released from reservoirs in the long-term statistical period for 223 months. a Baft Dam. b Jiroft Dam. c Safarood Dam

Full size image
Fig. 10
figure 10

Values of energy generated in the long-term statistical period for 223 months in Jiroft Dam

Full size image

As shown in Fig. 9, the release rate of the MOWCA algorithm was higher than the NSGA-II algorithm in all three reservoirs studied and was able to better supply the demands. Also, according to Fig. 10, the amount of energy produced by the MOWCA algorithm was higher than that of the NSGA-II algorithm; in some months, it was equal to the plant’s generation capacity. The amount of energy produced by the MOWCA and NSGA-II algorithms was 4278.69 and 3138.55 MW over the 223-month period, respectively (from October 2000 to April 2019), indicating the superiority of the multi-objective water cycle algorithm in generating hydropower energy of multi-objective multi-reservoir systems.

4 Conclusion

The WCA is based on the simulation of the hydrological cycle in nature, which has been proven to solve optimization problems in various articles. In this research, due to the superiority of the water cycle algorithm in various single- and multi-objective engineering problems, it was developed and used to solve the complex problem of optimal multi-objective multi-reservoir operation of the Halilrood catchment system. Coding and modeling the objective functions and multi-objective problem constraints with the targets, minimizing the total deficiencies in supplying downstream demands, minimizing the total difference of reservoir volume required for flood control, and minimizing the total difference in power generation of hydropower plant installation capacity were performed in MATLAB software. To evaluate the efficiency of the MOWCA, four performance evaluation criteria including Pareto distance criterion, distance between solutions, speed, and spread criteria were used and compared with the known NSGA-II algorithm.

The results of applying the multi-objective algorithms investigated showed that the MOWCA algorithm with the total objectives of 236.07 had better performance than the NSGA-II algorithm with the total objectives of 268.01. Also, the Pareto front derived from the MOWCA algorithm was more regular and at a better level than the NSGA-II algorithm. The results of applying multi-objective performance evaluation criteria showed that the MOWCA algorithm was superior in three criteria of distance, spread, and maximum spread; the NSGA-II algorithm was superior only in metric of spacing (S) criterion than MOWCA. Given the importance of hydropower energy generation in hydropower systems, maximizing hydropower energy generation as one of the important targets of the simulation–optimization model of Halilrood catchment was also analyzed with the mentioned algorithms. The results showed that the MOWCA algorithm with the generation of 4278.69 compared to the NSGA-II algorithm with the generation of 3138.55 MW during 223 months period (from October 2000 to April 2019) was also superior in this respect and had higher capability. Finally, due to the superiority of the MOWCA algorithm in optimal operation of Halilrood multi-reservoirs system and its limited application as a new multi-objective optimization method, it is recommended to use this algorithm in hydrology and water resources problems, especially multi-objective, multi-reservoir systems.