1 Introduction

Influenced by economic development and population explosion, in recent years, total available fresh water resources have sharply decreased globally. Spatial-temporal differences, together with global climate change and high-intensive anthropogenic activities have exacerbated the shortfall (Zhou et al. 2015; Lu et al. 2019; Chen et al. 2020). Moreover, water demands for diversity of water-using sectors such as industry, domesticity, ecology and agriculture are continuing to grow (Coulibaly et al. 2014; Liu et al. 2019; Chen et al. 2019). It has become important for humans to lessen the seriousness of water scarcity caused by imbalanced supply and demand, which has stimulated attempts to address limited water resources, including the greater utilization of surface water and groundwater (Gupta et al. 1985). Meanwhile, reclaimed water reuse one way to recycle water resources that is inexpensive and environmentally friendly (Woltersdorf et al. 2016). Furthermore, inter-basin water transfer can provide an effective approach to address regional water shortages (Sun et al. 2017; Rogers et al. 2020). Thus, how to achieve scientific allocation between multiple water supplies and customers following fairness and rationality is a difficult problem to address.

Research on water resources optimal allocation (WROA) began in the 1950s. During the past few decades, it has become a focus of a growing number of scholars. To promote optimal allocation and efficient utilization of limited water, mathematical methods (Mohammad et al. 2015) including linear programming (LP), dynamic programming (DP), non-linear programming (NLP), goal programming (GP) and multi-objective programming (MOP), have been employed (Ghahraman and Sepaskhah 2004; Ahmad and Tang 2016; Nasiri-Gheidari et al. 2018; Alahdin et al. 2019; Musa 2020). These models commonly take economic, society, environment and power generation benefits into account during the water supply process, but seldom consider uncertainties existing in WROA. Uncertain factors are widespread in water resources management systems, such as seasonal changes in water supply, conflicts of goals in water allocation, water supply efficiency, cost efficiency, and water requirements. All these phenomena and parameters are non-determinate and measureless and may influence the model’s comprehensive benefits. In this case, the adoption of deterministic parameters or models may cause deviations in the results. Consequently, uncertain optimization techniques have become important in WROA. In earlier studies, indeterminate information is usually quantified as a random variable, fuzzy number or fuzzy random variable, and various optimal allocation models have been developed.

For single reservoir operation, Wang and Adams (1986) constructed a two-phase optimization-based theoretical structure in which the inflows of the reservoir are considered periodically changing Markov processes caused by hydrological and seasonal factors. Butcher (2010) designed optimization policies for a multi-purpose single reservoir by means of a stochastic dynamic programming (SDP) approach. Moreover, targeting the infeasibility drawback in SDP, Saadat and Asghari (2019) established an improved SDP model through appropriate adjustment of the reservoir volume interval indices. To guarantee that the performance of water supply can satisfy given reliability and vulnerability (RV), Chen et al. (2018) incorporated RV constraints into the reservoir operation and formulated a stochastic linear programming (SLP) model. In WROA, the combined mode of water supply by multiple reservoirs within a region is common. Higgins et al. (2008) constructed a NLP-based stochastic model considering uncertainty in reservoir inflow measurement to relieve the pressure of the water supply from three reservoirs in Brisbane. Lee et al. (2008) suggested that the non-determinacy of future inflow in reservoir group planning was influenced by rainfall-runoff, and they constructed a multi-period stochastic linear programming (MSLP) model in possible scenarios based on weather prediction information. To effectively incorporate streamflow uncertainty in distributing surface and ground water resources, an integrated SDP method was presented by Jafarzadegan et al. (2014). For agricultural irrigation, the optimal strategy for different crops in the presence of multiple water supply sources was obtained by proposing a robust model, which combined two-stage stochastic programming with interval numbers (Fu et al. 2018). Taking reused wastewater and harvested rainwater in water system, Wei et al. (2020) suggested that these supplementary water sources could lessen costs, and they established a multi-stage stochastic programming (MSP) model under bounded-but-unknown uncertainty to achieve harmony between social and ecosystem in WROA. Most of the above models are effective and can be utilized only when the parameter uncertainties, such as inflows, water supply and demand, can be quantified via distribution functions. Taking into account the circumstances under which the decision may not satisfy the constraints when an unfavourable situation occurs, chance-constrained programming (CCP) and dependent chance programming (DCP) have also been applied to WROA (Edirisinghe et al. 2000; Li and Guo 2014; Dai et al. 2018).

Fuzzy programming is a frequently used inexact optimization technique based on fuzzy theory. Tan and Cruz (2004) utilized a symmetric fuzzy linear optimization method to describe the operation of water reuse networks. On the condition that the satisfaction degree of water supply and demand is greater than a certain level under fuzzy environment, a seven-objective dependent-chance model and an acceptable water allocation plan for an oceanic coastal city were conducted by Peng and Zhou (2011). In view of the double uncertainties, which are regarded as fuzzy boundary interval numbers, a hybrid stochastic approach built by Wang and Huang (2012) enables managers to identify the most beneficial allocation strategy. Fan et al. (2015) utilized fuzzy random variables to describe dual uncertainties in water allocation system, and generalized the traditional MSP. When only double sides uncertainties knowledge is accessible, Cheng et al. (2018) created a fuzzy CCP method to simultaneously assess the possibilities of unsatisfied constraints. Moreover, for total water consumption control, Ji et al. (2018) formulated a theoretical framework of inexact fuzzy chance-constrained programming (IFCCP). In addition, when multiple parameters uncertainties and random disturbance exist simultaneously, Khosrojerdi et al. (2019) established an extend MSP model with interval and fuzzy numbers. Faced with different water shortage scenarios, Fatemeh et al. (2020) analysed water allocation strategies through proposing a robust fuzzy stochastic programming model.

The stochastic, fuzzy and interval parameter programming models are all effective approaches to address objective uncertainties in WROA systems. However, stochastic programming models work only when uncertainties can be expressed via random variables with certain known distribution functions obtained from massive quantities of data. Interval parameters can quantify the uncertainties with unknown distribution functions, but the upper and lower bounds may vary over time. Furthermore, fuzzy measures do not stress on the logic rules of excluded middle and contradiction from a theoretical perspective. Considering the parameters and phenomena with uncertain characters and not fuzziness nor randomness, uncertainty theory, which is defined based on rigorous mathematical axioms by Liu (2007), can provide an alternative to counteract these difficulties. Through leading uncertain variables into mathematical models, uncertain programming (Zhang et al. 2015), uncertain MOP (Ning et al. 2017), uncertain GP (Li and Liu 2017) and uncertain multi-level programming (He et al. 2020) have been applied to various fields. In the field of WROA, Guo et al. (2016) characterized water supply and demand with uncertain variables in an emergency scenario and proposed an optimal framework of dependent-chance goal programming.

This paper considers the uncertainties of human consciousness and model parameters and introduces uncertain variables obtained by experts’ experience to the WROA system. Then, chance of event happening is quantified via an uncertain measure. Moreover, the target is to search for a tread-off among the conflicting objectives of economy, society and ecology when subject to satisfying water supply and demand. Taking the impact of uncertain factors into consideration, the outcome may not satisfy the constraints when adverse situations occur. Therefore, the approach can be used to make decisions when the possibilities of the establishing constraints are not less than certain confidence levels. Following that, an uncertain chance-constrained programming model in WROA process is established. The followings represent structure of this article. The second section introduces some theoretical supporting preliminaries, based on which, next part formulates a multi-objective uncertain chance-constrained programming (MUCCP) framework for WROA. Then, as to model solving, Section 4 presents a conversion technology, by which the MUCCP is transformed into a single-objective LP version combined with a weighted summation method. In Section 5, this MUCCP model with solution technique is employed for determining water system distribution strategy of Handan City, China. Finally, the main contribution and advantages of the built model are summarized in Conclusions part.

2 Preliminaries

Here, we will make a simplified briefing about needful definitions, theorems and basis programming models in uncertainty theory.

2.1 Uncertainty Theory

Definition 1

Assume that \({\mathscr{L}}\) is a σ-algebra over nonempty set Γ, every element Λ in \({\mathcal {L}}\) is an event with possibility of occurrence \(\mathcal M \{\Lambda \}\), in which uncertain measure ℳ possesses mathematical properties of normality, duality and subadditivity (Liu 2007), i.e.

  1. i)

    ℳ{Γ} = 1.

  2. ii)

    ℳ{Λ} + ℳ{Λc} = 1 for any event Λ.

  3. iii)

    \(\mathcal M\left \{\bigcup _{i=1}^{\infty }{\Lambda }_{i}\right \} \leq {\sum }_{i=1}^{\infty }\mathcal M\{{\Lambda }_{i}\}\), if \({\Lambda }_{i} \in {\mathcal {L}}, i=1, 2, 3,\cdots \)In this case, the measurable space \(({\Gamma }, {\mathcal {L}}, \mathcal M)\) is named uncertainty space.

    Moreover, Liu defined the following product axiom for clarification operational rules of uncertain measures.

  4. iv)

    For \(({\Gamma }_{k}, {\mathcal {L}}_{k}, \mathcal M_{k}) (k=1, 2, \cdots )\), the product uncertain measure ℳ satisfies

    $$ \mathcal M\left\{\prod\limits_{k=1}^{\infty}{\Lambda}_{k}\right\} =\bigwedge_{k=1}^{\infty}\mathcal M_{k}\{{\Lambda}_{k}\}, \forall {\Lambda}_{k} \in {\mathcal {L}}_{k}. $$

Definition 2

Let ξ denote an uncertain variable, then it is defined as \(({\Gamma }, {\mathcal {L}}, \mathcal M) \stackrel {\xi }{\longrightarrow }R\) (ξ is measurable, R is a real number set) (Liu 2007). That is, {ξ ∈ B} is an event for any Borel set B.

Definition 3

(Liu 2007) Assume that x is arbitrarily chosen from R, then Φ(x) = ℳ{ξ ≤ x} is defined to be the distribution function of ξ.

Definition 4

(Liu 2007) If Φ(x) ∈ (0,1) is continuous and monotonically increasing with respect to x and \(\underset {x\rightarrow -\infty }{\lim }{\varPhi }(x)=0, \underset {x\rightarrow +\infty }{\lim }{\varPhi }(x)=1,\) then we say Φ(x) is regular.

Definition 5

(Liu 2007) Φ− 1(α) denotes the inverse uncertainty distribution of ξ, when Φ(x) is a regular distribution function of ξ and α ∈ [0, 1].

Example 1

Let \({\mathcal {L}}(m,n) (m, n \in R, m<n)\) be a linear uncertain variable, then it has a linear distribution function

$$ {\varPhi}(x)=\left\{\begin{array}{cl} 0,&\text{} x\leq m\\ \frac{x-m}{n-m},&\text{} m\leq x\leq n\\ 1,&\text{} x\geq n \end{array} \right. $$

and an inverse distribution Φ− 1(α) = α(n − m) + m, α ∈ [0,1].

Definition 6

(Liu 2007) The optimistic value and pessimistic value to an uncertain variable ξ at a given level 0 < α < 1 are defined as ξsup(α) = sup{γ|ℳ{ξ ≥ γ}≥ α} and ξinf(α) = inf{γ|ℳ{ξ ≤ γ}≥ α}. If ξ has a regular uncertainty distributions Φ, then we have \(\xi _{sup}(\alpha )={\varPhi }^{-1}(1-\alpha )\) and \(\xi _{inf}(\alpha )={\varPhi }^{-1}(\alpha )\).

Definition 7

(Liu 2007) Assume that ξi(i = 1, 2, ⋯ , n) are uncertain variables. If for any Borel sets Bi(i = 1, 2, ⋯ , n) of real numbers, it holds that

$$\mathcal M\left\{\bigcap_{i=1}^{n}(\xi_{i}\in B_{i})\right\} =\bigwedge_{i=1}^{n}\mathcal M\{\xi_{i}\in B_{i}\},$$

then ξ1, ξ2, ⋯ , ξn are said to be independent.

Theorem 1

(Liu 2007) Let ξ1, ξ2, ⋯ , ξn be uncertain variables, and let f be a real-valued measurable function. Then f(ξ1, ξ2, ⋯ , ξn) is an uncertain variable.

Theorem 2

(Liu 2007) Assume that ξ1, ξ2, ⋯ , ξn are independent uncertain variables with regular distribution functions Φ1, Φ2, ⋯ , Φn. If f(x1, x2, ⋯ , xn) strongly increases with respect to x1, x2, ⋯ , xs and strongly decreases with respect to xs+ 1, xs+ 2, ⋯ , xn, then we get \({\varPsi }^{-1}(\alpha )=f({\varPhi }^{-1}_{1}(\alpha ),\cdots ,{\varPhi }^{-1}_{s}(\alpha ),{\varPhi }^{-1}_{s+1}(1-\alpha ),\cdots ,{\varPhi }^{-1}_{n}(1-\alpha )),\) which represents the inverse distribution of ξ = f(ξ1, ξ2, ⋯ , ξn).

2.2 Uncertain Programming Model

Uncertain programming (Liu 2009) is an optimization method involving uncertain variables under uncertain environments. Notice that the constraints may not be met simultaneously when faced with unwise decision. So this occasion calls for a principle to broaden the constrain conditions. Similarly, aim at maximization of f(x,ξ) at a guaranteed confidence level β, the general form of uncertain CCP (UCCP) is written as:

$$\left\{\begin{array}{l} \underset{\mathbf{x}}{\max} \overline{f} \\ \textup{s.t.} \\ \quad \mathcal M \{f(\mathbf{x,\xi})\geq \overline{f}\}\geq \beta \\ \quad \mathcal M \{g_{j}(\mathbf{x,\xi})\geq 0\}\geq \alpha_{j}, j=1, 2,\cdots,m \end{array}\right. $$

where x is a decision vector, and ξ is an uncertain vector, f(x,ξ) is an uncertain objective function, \(\overline {f}\) is the β-optimistic value of f(x,ξ), and gj(x,ξ) ≥ 0 are uncertain constraint conditions. ℳ presents the possibility that the event in {⋅} may take place. Since the constraints may lead to an empty feasible region, we hope they can hold with chance α. In this model, parameters α and β are given confidence levels of constraint function and objective function, respectively.

As an extension of single-objective UCCP, a multi-objective form is constructed as following:

$$ \left\{\begin{array}{l} \max_{\mathbf{x}} [\overline{f_{1}}, \overline{f_{2}}, \cdots, \overline{f_{n}}]\\ \textup{subject to:} \\ \quad \mathcal M \{f_{i}(\mathbf{x,\xi})\geq \overline{f_{i}}\}\geq \beta_{i}, i=1, 2,\cdots,n \\ \quad \mathcal M \{g_{j}(\mathbf{x,\xi})\geq 0\}\geq \alpha_{j}, j=1, 2,\cdots,m \end{array}\right. $$

where αj and βi are confidence levels of the j-th objective function and the i-th constraint condition. \(\overline {f_{i}}\) is the βi-optimistic value of fi(x,ξ).

Theorem 3

(Liu 2007) Let g(x, ξ1, ξ2, ⋯ , ξn) be a constrain function, in which ξ1, ξ2, ⋯ , ξn are independent, with uncertainty distributions Φ1, Φ2,⋯Φn. If g(x, ξ) strongly increases with respect to ξ1, ξ2, ⋯ , ξt and strongly decreases with respect to ξt+ 1, ξt+ 2, ⋯ , ξn, then

$$\mathcal M\{g(\textbf{x}, \xi_{1},\xi_{2},\cdots,\xi_{n})\leq 0\}\geq \alpha$$

is equivalent to

$$ g(\textbf{x},{\varPhi}^{-1}_{1}(\alpha),\cdots,{\varPhi}^{-1}_{t}(\alpha),{\varPhi}^{-1}_{t+1}(1-\alpha),\cdots,{\varPhi}^{-1}_{n}(1-\alpha))\leq 0. $$

3 Multi-objective Uncertain Chance-Constrained Programming Model for WROA

WROA is a process of scientifically allocating depletable multiple water resources to each water user through engineering or non-engineering measures according to the principles of effectiveness, impartiality and sustainability in a certain drainage basin or domain. Mathematical programming model for WROA provides an approach to optimizing water supply and discharge process by maximizing the total benefits to society, economy and ecology while simultaneously minimizing the unbalance between water supply and demand. During WROA, water resource systems are affected by various uncertainties, including model uncertainty and parameter uncertainty, which can be described by uncertain variables. With the deepening research on water resource system operation, models proposed for the water supply problem from multiple suppliers to multiple users are becoming increasingly sophisticated. The complexities of the practical models and system make many constraints difficult to satisfy. The introduction of UCCP model can transform the tight and strong features of the constraints of conventional programming models into ones with flexibility and adjustability. To achieve a compromise between optimization of objective functions and satisfaction of constraint conditions and provide decision makers with a trade-off between system cost-effectiveness and default risk under uncertainty, the MUCCP model for WROA is studied in this section.

Target area contains K sub-regions by geographic division. Water supply is provided by I types of water resources. And the demand system contains J water consumers, such as industry, domestic users, agriculture and ecology. The simplified structure of water distribution systems from multiple sources to users is shown in Fig. 1. The purpose is choosing the best allocation schedule via MUCCP model, i.e., the value of xijk(i = 1, 2, ⋯ , I, j = 1, 2, ⋯ , J, k = 1, 2, ⋯ , K), which denotes the quantity supplied from water source i to user j in sub-region k. As shown, the detailed MUCCP model for WROA is established as below.

Fig. 1
figure 1

The simplified structure of water distribution systems

Full size image

3.1 Objective Functions

In consideration of the influences of uncertain parameters on WROA, this programming model sets a goal of coordinated development of economic, social and environmental benefits, for this purpose, net income from water supply, water deficit and total quantities of major pollutants discharged are objective functions, and by reasonably allocating the multiple water sources to different water users, the overall maximum benefit at a given confidence level can be obtained.

  1. (1)

    Maximum total income net from water supply

The total net profits of water supply are the total difference between the benefits and costs of water supply. The net profits function can be formulated as

$$\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}(\tilde{b_{ijk}}-\tilde{c_{ijk}})a_{i}b_{j}\omega_{k}r_{ij}x_{ijk},$$

where (i = 1, 2, ⋯ , I, j = 1, 2, ⋯ , J, k = 1, 2, ⋯ , K)xijk: in the k − th sub-region, the water quantity supplied from i to user j;\(\tilde {b_{ijk}}\): profit coefficients of unit water supply defined as independent uncertain variables with distribution \({\varPhi }_{\tilde {b_{ijk}}}(x)\);\(\tilde {c_{ijk}}\): cost coefficients of unit water supply defined as independent uncertain variables with distribution \({\varPhi }_{\tilde {c_{ijk}}}(x)\);ai: water supply priority coefficient of water source i;bj: fairness index of water use of user j;ωk: weight of sub-region k;rij: the relationship between water source i and user j, and

$$ r_{ij}=\left\{\begin{array}{cl} 0,&\text{if } x_{ijk}=0, \forall k \\ 1,&\text{otherwise, } \forall k. \end{array} \right. $$

To maximize the β1 −optimistic value of income net function \(\overline {f_{1}}\), then we obtain

$$\max \left\{\overline{f_{1}}\bigg| \mathcal M \left\{\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}(\tilde{b_{ijk}}-\tilde{c_{ijk}})a_{i}b_{j}\omega_{k}r_{ij}x_{ijk}\geq \overline{f_{1}}\right\}\geq \beta_{1}\right\}.$$
  1. (2)

    Minimum total water deficit

Water shortages negatively affect people’s survival, quality of life and social stability. Thus, water shortage can be employed as an index to characterize the social benefits of water supply. Social benefits optimization can be considered equivalent to minimization of total water deficit in a certain region, which is denoted by the difference between demand and supply. Then total water deficit can be expressed as

$$ \sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}(\tilde{D_{kj}}-\sum\limits_{i=1}^{I}r_{ij}x_{ijk}), $$

where \(\tilde {D_{kj}}\) denotes demand of j in the k − th sub-region, which are defined by independent uncertain variables with uncertainty distribution \({\varPhi }_{\tilde {D_{kj}}}(x)\).

To minimize the β2 −pessimistic value of the water deficit function \(\overline {f_{2}}\), that is, maximize the social benefits, then we obtain

$$ \min \left\{\overline{f_{2}}\bigg| \mathcal M \left\{\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}(\tilde{D_{kj}}-\sum\limits_{i=1}^{I}r_{ij}x_{ijk})\leq \overline{f_{2}}\right\}\geq \beta_{2}\right\}. $$
  1. (3)

    Minimum total amount of major pollutant emission

In recent years, during the processes of industrial production and human life, a large amount of solid waste and waste water have been produced and have led to the deterioration of the ecological environment, especially water pollution. For instance, the high concentration of ammonia nitrogen from industrial waste water and sewage water directly causes water quality eutrophication, which results in serious damage to the ecological balance of water bodies. Therefore, the amount of pollutants in waste water should be controlled. Minimization of the total quantity of major pollutants discharged is treated as an environmental target, which will be maximized. The total quantity of major pollutants discharged is

$$ \sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\tilde{d_{kj}}p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk}, $$

where \(\tilde {d_{kj}}\) denotes concentration of major pollutant in a unit of waste water, which is characterized as independent uncertain variable with distribution \({\varPhi }_{\tilde {d_{kj}}}\), and pkj is the waste water discharge coefficient of j in sub-region k.

To minimize the β3 −pessimistic value in the water deficit function \(\overline {f_{3}}\), that is, maximize the environmental benefits, then we have

$$ \min \left\{\overline{f_{3}}\bigg| \mathcal M \left\{\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\tilde{d_{kj}}p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\leq \overline{f_{3}}\right\}\geq \beta_{3}\right\}. $$

3.2 Chance Constraint Conditions

Various constraints exist in the WROA process that cannot be neglected. To avoid obtaining a conservative optimization strategy when the constraint conditions are not satisfied, chance constraint conditions (where i = 1, 2, ⋯ , I, j = 1, 2, ⋯ , J, k = 1, 2, ⋯ , K) are introduced as follows. They make it possible for the constraint conditions to not be satisfied within a range of possibility.

  1. (1)

    Non-negative constraint

$$x_{ijk}\geq 0, \forall \ i,\ j,\ k$$

where xijk is the quantity supplied from i to j in sub-region k.

  1. (2)

    Supply capacity constraints of water resources

$$ \mathcal M \left\{\sum\limits_{j=1}^{J}r_{ij}x_{ijk}\leq \tilde{Q_{ik}}\right\}\geq \alpha_{ik}, \forall \ i,\ k $$

where \(\tilde {Q_{ik}}\) is the available water supply from i to sub-region k, characterized as an independent uncertain variable with distribution \({\varPhi }_{\tilde {Q_{ik}}}\); and αik is the confidence level predetermined by experts.

  1. (3)

    Demand capacity constraints of water users

$$ \mathcal M \left\{\tilde{W_{jkmin}}\leq\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right\}\geq \gamma_{jk}, \ \forall \ j,\ k $$

and

$$ \mathcal M \left\{\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\leq \tilde{W_{jkmax}}\right\}\geq \gamma_{jk}, \ \forall \ j,\ k, $$

where \(\tilde {W_{jkmin}}\) and \(\tilde {W_{jkmax}}\) are minimum and maximum water demand of j in k, which are quantified as independent uncertain variables with distributions \({\varPhi }_{\tilde {W_{jkmin}}}\) and \({\varPhi }_{\tilde {W_{jkmax}}}\), respectively, and γjk is a given confidence level.

Based on the analysis above, MUCCP framework during WROA process is integrated into

$$ \left\{\begin{array}{l} \max \overline{f_{1}}\\ \min \overline{f_{2}}\\ \min \overline{f_{3}}\\ \textup{subject to:} \\ \quad \mathcal M \left\{\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}(\tilde{b_{ijk}}-\tilde{c_{ijk}})a_{i}b_{j}\omega_{k}r_{ij}x_{ijk}\geq \overline{f_{1}}\right\}\geq \beta_{1}, \\ \quad \mathcal M \left\{\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}(\tilde{D_{kj}}-\sum\limits_{i=1}^{I}r_{ij}x_{ijk})\leq \overline{f_{2}}\right\}\geq \beta_{2}, \\ \quad \mathcal M \left\{\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\tilde{d_{kj}}p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\leq \overline{f_{3}}\right\}\geq \beta_{3}, \\ \quad \mathcal M \left\{\sum\limits_{j=1}^{J}r_{ij}x_{ijk}\leq \tilde{Q_{ik}}\right\}\geq \alpha_{ik}, \\ \quad \mathcal M \left\{\tilde{W_{jkmin}}\leq\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right\}\geq \gamma_{jk}, \\ \quad \mathcal M \left\{\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\leq \tilde{W_{jkmax}}\right\}\geq \gamma_{jk}, \\ \quad x_{ijk}\geq 0, \\ \quad r_{ij}=\left\{ \begin{array}{ll} 0, & \ if \ x_{ijk}=0, \\ 1, & \ otherwise. \end{array} \right.\\ \quad i=1, 2,\cdots,I, j=1, 2,\cdots,J, k=1, 2,\cdots,K. \end{array}\right. $$
(1)

4 Model Transformation and Solution

For the sake of convenience in the process of model solving, the MUCCP model can be transformed into a crisp version via uncertain measures and operation algorithms of uncertain variables, as indicated in Theorem 4.

Theorem 4

The multi-objective uncertain chance-constrained programming model (1) involving uncertain variables is equivalent to the following crisp multi-objective programming model (2).

$$ \left\{\begin{array}{l} \min -\overline{f_{1}}^{\prime}\\ \min \overline{f_{2}}^{\prime}\\ \min \overline{f_{3}}^{\prime}\\ \textup{subject to:} \\ \quad \overline{f_{1}}^{\prime}=\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}\left[{\varPhi}^{-1}_{\tilde{b_{ijk}}}(1-\beta_{1})-{\varPhi}^{-1}_{\tilde{c_{ijk}}}(\beta_{1})\right]a_{i}b_{j}\omega_{k}r_{ij}x_{ijk},\\ \quad \overline{f_{2}}^{\prime}=\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\left[{\varPhi}^{-1}_{\tilde{D_{kj}}}(\beta_{2})-\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right],\\ \quad \overline{f_{3}}^{\prime}=\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}{\varPhi}^{-1}_{\tilde{d_{kj}}}(\beta_{3})p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk},\\ \quad \sum\limits_{j=1}^{J}r_{ij}x_{ijk}\leq {\varPhi}_{\tilde{Q_{ik}}}^{-1}(1-\alpha_{ik}),\\ \quad \sum\limits_{i=1}^{I}r_{ij}x_{ijk} \geq {\varPhi}_{\tilde{W_{jkmin}}}^{-1}(\gamma_{jk}),\\ \quad \sum\limits_{i=1}^{I}r_{ij}x_{ijk} \leq {\varPhi}_{\tilde{W_{jkmax}}}^{-1}(1-\gamma_{jk}),\\ \quad x_{ijk}\geq 0,\\ \quad r_{ij}=\left\{ \begin{array}{ll} 0, & \ if \ x_{ijk}=0,\\ 1, & \ otherwise. \end{array} \right.\\ \quad i=1, 2,\cdots,I, j=1, 2,\cdots,J, k=1, 2,\cdots,K. \end{array}\right. $$
(2)

Proof

First, the determined equivalent forms of the objective functions are proved.

  1. (1)

    For the objective function of net economic benefit

Since \(\tilde {b_{ijk}}\) and \(\tilde {c_{ijk}}\) are regular uncertain variables with distributions \({\varPhi }_{\tilde {b_{ijk}}}(x)\) and \({\varPhi }_{\tilde {c_{ijk}}}(x)\), for any i = 1, 2, ⋯ , I, j = 1, 2, ⋯ , J, k = 1, 2, ⋯ , K, it follows from Theorem 1 that

$$ g_{1}=\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}(\tilde{b_{ijk}}-\tilde{c_{ijk}})a_{i}b_{j}\omega_{k}r_{ij}x_{ijk} $$

is an uncertain variable.

Since aibjωkrijxijk ≥ 0, we know that g1 strongly increases with respect to \(\tilde {b_{ijk}}\) and strongly decreases with respect to \(\tilde {c_{ijk}}\). By Theorem 2, g1 has following inverse uncertainty distribution

$$ \begin{array}{@{}rcl@{}} {\varPsi}_{1}^{-1}(\alpha)&=&\overline{f_{1}}({\varPhi}^{-1}_{\tilde{b_{ijk}}}(\alpha),{\varPhi}^{-1}_{\tilde{c_{ijk}}}(\alpha))\\ &=&\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}\left[{\varPhi}^{-1}_{\tilde{b_{ijk}}}(\alpha)-{\varPhi}^{-1}_{\tilde{c_{ijk}}}(1-\alpha)\right]a_{i}b_{j}\omega_{k}r_{ij}x_{ijk}. \end{array} $$

And from Definition 6, the β1-optimistic value of g1 is

$$ \begin{array}{@{}rcl@{}} \overline{f_{1}}^{\prime}&=& {\varPsi}_{1}^{-1}(1-\beta_{1})\\ &=&\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\sum\limits_{i=1}^{I}\left[{\varPhi}^{-1}_{\tilde{b_{ijk}}}(1-\beta_{1})-{\varPhi}^{-1}_{\tilde{c_{ijk}}}(\beta_{1})\right]a_{i}b_{j}\omega_{k}r_{ij}x_{ijk}. \end{array} $$

Then, we obtain \({\max \limits } \overline {f_{1}}^{\prime }\), which is equivalent to \({\min \limits } -\overline {f_{1}}^{\prime }\).

  1. (2)

    For the objective function of social benefit

In uncertainty theory, the constant number rijxijk is treated as a special regular uncertain variable with inverse uncertain distribution rijxijk and \(\tilde {D_{kj}}\) is a regular uncertain variable with distribution \({\varPhi }_{\tilde {D_{kj}}}(x)\), for any i = 1, 2, ⋯ , I, j = 1, 2, ⋯ , J, k = 1, 2, ⋯ , K. Therefore, it follows from Theorem 1 that

$$ g_{2}=\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\left( \tilde{D_{kj}}-\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right) $$

is an uncertain variable.

g2 strongly increases with respect to \(\tilde {D_{kj}}\) and strongly decreases with respect to rijxijk. Thus, by Theorem 2, g2 has following inverse uncertainty distribution

$$ \begin{array}{@{}rcl@{}} {\varPsi}_{2}^{-1}(\alpha)&=&\overline{f_{2}}({\varPhi}^{-1}_{\tilde{D_{kj}}}(\alpha),{\varPhi}^{-1}_{r_{ij}x_{ijk}}(\alpha))\\ &=&\overline{f_{2}}({\varPhi}^{-1}_{\tilde{D_{kj}}}(\alpha),r_{ij}x_{ijk})\\ &=&\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\left( {\varPhi}^{-1}_{\tilde{D_{kj}}}(\alpha)-\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right). \end{array} $$

And from Definition 6, we get the β2-pessimistic value of g2

$$ \begin{array}{@{}rcl@{}} \overline{f_{2}}^{\prime}&=& {\varPsi}_{2}^{-1}(\beta_{2})\\ &=&\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\left[{\varPhi}^{-1}_{\tilde{D_{kj}}}(\beta_{2})-\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right]. \end{array} $$
  1. (3)

    For the objective function of ecological benefit

\(\tilde {d_{kj}}\) is regular with uncertainty distribution function \({\varPhi }_{\tilde {d_{kj}}}(x)\), it follows from Theorem 1 that

$$g_{3}=\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}\tilde{d_{kj}}p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk}$$

is an uncertain variable.

Since \(p_{kj}{\sum }_{i=1}^{I}r_{ij}x_{ijk}\geq 0\), we know that g3 strongly increases with respect to \(\tilde {d_{kj}}\). By Theorem 2, g3 has following inverse uncertainty distribution

$$ \begin{array}{@{}rcl@{}} {\varPsi}_{3}^{-1}(\alpha)&=&\overline{f_{3}}({\varPhi}^{-1}_{\tilde{d_{kj}}}(\alpha))\\ &=&\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J} {\varPhi}^{-1}_{\tilde{d_{kj}}}(\alpha)p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk}. \end{array} $$

And from Definition 6, we have the β3-pessimistic value of g3

$$ \begin{array}{@{}rcl@{}} \overline{f_{3}}^{\prime}&=& {\varPsi}_{3}^{-1}(\beta_{3})\\ &=&\sum\limits_{k=1}^{K}\sum\limits_{j=1}^{J}{\varPhi}^{-1}_{\tilde{d_{kj}}}(\beta_{3})p_{kj}\sum\limits_{i=1}^{I}r_{ij}x_{ijk}. \end{array} $$

Second, the determined equivalent forms of the constraint conditions are proved.

  1. (4)

    For the supply capacity constraints of water resources

By Theorem 3, we have

$$ \begin{array}{@{}rcl@{}} \mathcal M \left\{\sum\limits_{j=1}^{J}r_{ij}x_{ijk}\leq \tilde{Q_{ik}}\right\}\geq \alpha_{ik}&& \Leftrightarrow \mathcal M \left\{\tilde{Q_{ik}} \geq \sum\limits_{j=1}^{J}r_{ij}x_{ijk}\right\}\geq \alpha_{ik}\\ & &\Leftrightarrow 1-\mathcal M \left\{\tilde{Q_{ik}} \leq \sum\limits_{j=1}^{J}r_{ij}x_{ijk}\right\}\geq \alpha_{ik}\\ & &\Leftrightarrow \mathcal M \left\{\tilde{Q_{ik}} \leq \sum\limits_{j=1}^{J}r_{ij}x_{ijk}\right\}\leq 1-\alpha_{ik}\\ & &\Leftrightarrow {\varPhi}_{\tilde{Q_{ik}}}(\sum\limits_{j=1}^{J}r_{ij}x_{ijk})\leq 1-\alpha_{ik}. \end{array} $$

Taking the inverse uncertain distribution on both sides of the above equation, we obtain

$$\sum\limits_{j=1}^{J}r_{ij}x_{ijk}\leq {\varPhi}_{\tilde{Q_{ik}}}^{-1}(1-\alpha_{ik}).$$
  1. (5)

    For the demand capacity constraints of water users

By Theorem 3, we have

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{array}{l} \mathcal M \left\{\tilde{W_{jkmin}}\leq \sum\limits_{i=1}^{I}r_{ij}x_{ijk}\right\}\geq \gamma_{jk} \\ \mathcal M \left\{\sum\limits_{i=1}^{I}r_{ij}x_{ijk}\leq \tilde{W_{jkmax}}\right\}\geq \gamma_{jk} \end{array} \right. &&\Leftrightarrow \left\{ \begin{array}{l} {\varPhi}_{\tilde{W_{jkmin}}}(\sum\limits_{i=1}^{I}r_{ij}x_{ijk})\geq \gamma_{jk} \\ {\varPhi}_{\tilde{W_{jkmax}}}(\sum\limits_{i=1}^{I}r_{ij}x_{ijk})\leq 1-\gamma_{jk} \end{array} \right.\\ &&\Leftrightarrow \left\{ \begin{array}{l} \sum\limits_{i=1}^{I}r_{ij}x_{ijk} \geq {\varPhi}_{\tilde{W_{jkmin}}}^{-1}(\gamma_{jk}) \\ \sum\limits_{i=1}^{I}r_{ij}x_{ijk} \leq {\varPhi}_{\tilde{W_{jkmax}}}^{-1}(1-\gamma_{jk}) \end{array} \right.\\ \end{array} $$

As mentioned above, Model (1) is transformed into Model (2). Thus, the theorem is verified. □

To solve this problem, the linear weighted sum method is an essential approach to transform from a multi-objective programming model to a single-objective form. Assume that \(\overline {f_{1}},\overline {f_{2}},\cdots ,\overline {f_{S}}\) are objective functions with weight set Λ = (λ1, λ2, ⋯ , λS)T, where λs ≥ 0 and \({\sum }_{s=1}^{S} \lambda _{s}=1\). Then, we introduce the following evaluation function

$$\overline{f(F)}=\sum\limits_{s=1}^{S}\lambda_{s}\overline{f_{s}}.$$

Thus, the optimal solution of the model with objective \(\overline {f(F)}\) is seen as a Pareto-optimal solution of the MUCCP model.

5 Case Study

5.1 Study Area

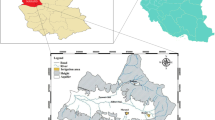
China is suffering from severe drought and water shortage. It possesses nearly 5% of the global drinking freshwater to supply about 20% of the whole population on earth. Moreover, water waste and serious pollution make the situation worse. One of the most significant features between the South and the North is distribution differentiation. So, our majority cities in the North face water scarcity caused by lacking enough surface and underground fresh water, as well as huge water demand. Located in North China, Handan City (113°28′− 115°28′ east longitude and 36°04′− 37°01′ north latitude) of Hebei Province, is a city with a serious water crisis. Until 2016, groundwater and surface reservoirs have been the main water supply sources of Handan. A long-term water shortage has caused serious overexploitation of groundwater, and the continuous decline of the groundwater level will not only cause deterioration of water quality, land subsidence, ground fissure, soil desertification, and abandonment of pumped wells but also increase the risk of other geological disasters. Moreover, meteorological factors have an immediate impact on the storage capacity of surface reservoirs, and exposure to the surface makes the reservoirs extremely vulnerable to contamination. Undoubtedly, China’s South-North Water Transfer Project provides an alternative high-quality water source. Thus far, Handan City has formed a water supply system composed of South-to-North water, Yangjiaopu groundwater and the Yuecheng reservoir with continuous improvement of the water supply emergency system. In general, the three water sources all supply water to the urban district and operate together. Moreover, the East Sewage Treatment Plants and West Sewage Treatment Plants in Handan City have a total daily waste water treatment capacity of 20 million cubic meters. At present, reclaimed water has been used for urban heat and power supply, agricultural irrigation and landscaping but not domestic water. However, to fundamentally solve the water shortage issue in Handan, there is an urgent need to improve the reasonable utilization of multiple water sources while strengthening water saving management. Thus, how to effectively use the limited water during WROA is an urgent concern for the city.

5.2 WROA Based on the MUCCP Model

In this research, parameter i, which represents the water supply source, takes values from 1 to 4, respectively, corresponding to south water, surface water, groundwater and reclaimed water. Additionally, the water demands are classified into domestic, industry, agriculture and ecology, denoted by j = 1, 2,3,4, respectively. Then, we can build the following MUCCP model.

$$ \left\{\begin{array}{l} \min [-\overline{f_{1}}, \overline{f_{2}}, \overline{f_{3}}]\\ \textup{subject to} \\ \quad \mathcal M \left\{\sum\limits_{j=1}^{4}\sum\limits_{i=1}^{4}(\tilde{b_{ij}}-\tilde{c_{ij}})a_{i}b_{j}r_{ij}x_{ij}\geq \overline{f_{1}}\right\}\geq \beta_{1} \\ \quad \mathcal M \left\{\sum\limits_{j=1}^{4}(\tilde{D_{j}}-\sum\limits_{i=1}^{4}r_{ij}x_{ij})\leq \overline{f_{2}}\right\}\geq \beta_{2} \\ \quad \mathcal M \left\{\sum\limits_{j=1}^{4}\tilde{d_{j}}p_{j}\sum\limits_{i=1}^{4}r_{ij}x_{ij}\leq \overline{f_{3}}\right\}\geq \beta_{3} \\ \quad \mathcal M \left\{\sum\limits_{j=1}^{4}r_{ij}x_{ij}\leq \tilde{Q_{i}}\right\}\geq \alpha_{i} \\ \quad \mathcal M \left\{\tilde{W_{jmin}}\leq\sum\limits_{i=1}^{4}r_{ij}x_{ij}\right\}\geq \gamma_{j} \ and \ \mathcal M \left\{\sum\limits_{i=1}^{4}r_{ij}x_{ij}\leq \tilde{W_{jmax}}\right\}\geq \gamma_{j}\\ \quad x_{ij}\geq 0\\ \quad r_{ij}=\left\{ \begin{array}{ll} 0, & \ \ if \ i=4,\ j=1 \\ 1, & \ otherwise \end{array} \right.\\ \quad i=1, 2,3,4, j=1, 2,3,4. \end{array}\right. $$
(3)

From Theorem 4, model (3) is converted to an equivalent crisp multiple-objective linear programming model (4).

$$ \left\{\begin{array}{l} \min [-\overline{f_{1}}^{\prime}, \overline{f_{2}}^{\prime}, \overline{f_{3}}^{\prime}]\\ \textup{subject to} \\ \quad \overline{f_{1}}^{\prime}=\sum\limits_{j=1}^{4}\sum\limits_{i=1}^{4}{\varPhi}^{-1}_{\tilde{b_{ij}}}(1-\beta_{1})a_{i}b_{j}r_{ij}x_{ij}-\sum\limits_{j=1}^{4}\sum\limits_{i=1}^{4}{\varPhi}^{-1}_{\tilde{c_{ij}}}(\beta_{1})a_{i}b_{j}r_{ij}x_{ij}\\ \quad \overline{f_{2}}^{\prime}=\sum\limits_{j=1}^{4}{\varPhi}^{-1}_{\tilde{D_{j}}}(\beta_{2})-\sum\limits_{j=1}^{4}\sum\limits_{i=1}^{4}r_{ij}x_{ij}\\ \quad \overline{f_{3}}^{\prime}=\sum\limits_{j=1}^{4}{\varPhi}^{-1}_{\tilde{d_{j}}}(\beta_{3})p_{j}\sum\limits_{i=1}^{4}r_{ij}x_{ij}\\ \quad \sum\limits_{j=1}^{4}r_{ij}x_{ij}\leq {\varPhi}^{-1}_{\tilde{Q_{i}}}(1-\alpha_{i})\\ \quad \sum\limits_{i=1}^{4}r_{ij}x_{ij}\leq {\varPhi}^{-1}_{\tilde{W_{jmax}}}(1-\gamma_{j})\\ \quad \sum\limits_{i=1}^{4}r_{ij}x_{ij}\geq {\varPhi}^{-1}_{\tilde{W_{jmin}}}(\gamma_{j})\\ \quad x_{ij}\geq 0\\ \quad r_{ij}=\left\{ \begin{array}{ll} 0, & \ \ if \ i=4,\ j=1 \\ 1, & \ otherwise \end{array} \right.\\ \quad i=1, 2,3,4, j=1, 2,3,4. \end{array}\right. $$
(4)

5.3 Parameter Description

The relevant parameters are computed as follows and the main uncertain parameters in the case study are listed in Table 1.

Table 1 Main uncertain parameters
Full size table

During water allocation, the priorities of water supply for different water sources are different. In addition, the water-use priorities of different water departments are not the same. Thus, we can calculate the priority water supply coefficient ai of water source i and the fairness index bj of the water supply of user j by

$$a_{i}=\frac{1+n_{imax}-n_{i}}{{\sum}_{i=1}^{I}(1+n_{imax}-n_{i})}$$

and

$$b_{j}=\frac{1+n_{jmax}-n_{j}}{{\sum}_{j=1}^{J}(1+n_{jmax}-n_{j})},$$

where ni is the supply order of i and nimax is the largest order of water supply. nj is the order for water use of user j, and njmax is the largest order of water use.

5.4 Results and Discussion

Let Λ = (λ1, λ2, λ3) = (0.4,0.4,0.2) be the weight vector of the objective functions. By means of the linear weighting method, we obtain the evaluation function

$$ f(F)=-\lambda_{1}\overline{f_{1}}^{\prime}+\lambda_{2}\overline{f_{2}}^{\prime}+\lambda_{3}\overline{f_{3}}^{\prime}. $$

Taking αi = 0.85,(i = 1, 2, 3, 4), β1 = β2 = β3 = 0.8, γ1 = γ3 = γ4 = 0.85, γ2 = 0.7, we obtain the following optimal water supply scheme

$$ \left\{\begin{array}{l} x_{11}=6280\times 10^{4} \text{m}^{3}\\ x_{21}=3393.8\times 10^{4} \text{m}^{3}, x_{22}=6880.7\times 10^{4} \text{m}^{3} \\ x_{32}=5980\times 10^{4} \text{m}^{3} \\ x_{42}=715.2\times 10^{4} \text{m}^{3}, x_{43}=4628.9\times 10^{4} \text{m}^{3}, x_{44}=1564\times 10^{4} \text{m}^{3}. \end{array}\right. $$
(5)

At this time, \(\overline {f_{1}}^{\prime }=25305.63\times 10^{4} \text {RMB}, \overline {f_{2}}^{\prime }=6369.20\times 10^{4} \text {m}^{3}, \overline {f_{3}}^{\prime }=22916.46 \text {t}\) and the objective value is \(\overline {f(F)}=450754.2\).

If we take β1 = β2 = β3 = 0.8, αi = γj = 1.0, then MUCCP model will degenerate to a multi-objective programming form, in which chance-constrained conditions turn into hard constraints. In this case, the optimal water supply strategy is

$$ \left\{\begin{array}{l} x_{11}=6700\times 10^{4} \text{m}^{3}\\ x_{21}=3800\times 10^{4} \text{m}^{3}, x_{22}=8880\times 10^{4} \text{m}^{3} \\ x_{32}=5358\times 10^{4} \text{m}^{3}, x_{33}=27\times 10^{4} \text{m}^{3}, x_{34}=1615\times 10^{4} \text{m}^{3} \\ x_{43}=4760\times 10^{4} \text{m}^{3}. \end{array}\right. $$
(6)

Thus, \(\overline {f_{1}}^{\prime }=26929.10\times 10^{4} \text {RMB}, \overline {f_{2}}^{\prime }=5211.80\times 10^{4} \text {m}^{3}, \overline {f_{3}}^{\prime }=23888.51\text {t}\), and the objective value is \(\overline {f(F)}=469083.2\).

In the proposed model, the smaller the value of β is, the smaller the objective function value; that is, the greater the economic benefit is, the smaller the water shortage and the lower the pollutant emissions. Conversely, the possibility of satisfying constraints is increased. α = γ = 1.0 corresponds to the decision in a conservative situation. At this time, the risk level is reduced, and the opportunity to obtain more benefits from the above results comparison is lost. Compared with deterministic programming models, the MUCCP method can provide decision makers the output that achieves a balance between the benefits and risks to avoid the emergence of non-optimal or even erroneous decisions.

6 Conclusions

WROA, a necessary measure, has become popular among water-starved cities with the increasing contradiction between water supply and usage. A reasonable allocation for water consumption of different users can provide assistance for water plants to determine exact amount of water production and minimize water supply costs so that the system can run more efficiently under the premise of guaranteeing sustainability and stability of the water supply.

Uncertainty is a major challenge in allocating limited water quantities. This study found a novel MUCCP model for optimal assignment of restricted water based on uncertainty theory. In this model, uncertain variable is introduced to handle the parameter uncertainty. The uncertain measure is applied to assess probabilities of indeterminate events occurrence. Additionally, we take three objective functions, namely, economic benefit, social benefit and ecological benefit, into consideration concurrently, and solve for the optimal strategy of water supply under the premise of satisfying the chance-constraint conditions. Moreover, a crisp equivalent programming model is established. The obtained results can provide managers with a trade-off analysis between system cost-effectiveness and default risk. Eventually, a case study of Handan City verifies the model validity.

In brief, this paper makes main contributions on the following aspects. i) Uncertain variable as a vehicle is introduced to addressing uncertain information existing in model parameters under uncertain circumstances. ii) For WROA, this paper build a new MUCCP framework, in which not only three kinds of objectives are considered, but also the scenario that the rigid constraints cannot be satisfied in a complex water distribution system. iii) For model solution, a transformation technology is provided and proved. iv) The results provide support for decision making in water allocation process about how much water to release for distribution from water sources to water consumers.

The MUCCP model can be implemented as an efficient tool to relieve water shortage threats and avoid the excessively conservative plan obtained from traditional deterministic models. It can overcome the limitation caused by a lack of samples obtained from independent repeated trials. In contrast to fuzzy programming methods, this model is based on rigorous mathematical axioms. The established model has relatively strong practicability and applicability. In each stage of the actual water supply process, when adverse events occur, decision makers can constantly adjust the water supply target based on the combination of dynamic changes in the available water supply, the water demand and the implementation of water supply scheme in the previous stage. To develop the current water supply strategy, we can minimize the losses caused by unfavourable events and achieve the optimal trade-off between overall benefits and risk.