1 Introduction

Urbanization has been taking place worldwide since the 1950s, leading to rapid change of city land use, increasing runoff discharges, and high risk of flooding (Lu et al. 2019). As one of the strategies for controlling urban floods, the use of low impact development (LID) was codified in legislation in North America (United States of America 2007; Toronto Region Conservation Authority 2010). It involves a series of decentralized stormwater management practices, such as green roof (GR), pervious pavement (PP) and bio-retention cell (BC), with focuses on water quality and quantity control (Noordhoek 2014). A representative GR normally includes vegetation cover, growing medium and drainage layer and is capable of retaining stormwater on the roof surface to relieve the stress of urban drainage system (UDS) (Getter and Rowe 2006). A PP system consists of multiple pervious layers (e.g. surface, base and geotextile layers), and could manage runoff at its earliest condition (Jato-Espino et al. 2014). A BC normally uses a shallow depression to slow down and treat on-site stormwater runoff (Lakesuperiorstreams 2009).

In recent years, with the aid of hydrological modeling tools such as Storm Water Management Model (SWMM) (Rossman 2010) and Flo-2D model (Hu et al. 2017), LIDs are proven effective on retaining rainwater and mitigating urban flood (Noordhoek 2014; Chui et al. 2016). However, the reliability of LID design is affected by a variety of uncertainties (Vogel et al. 2015; Duan et al. 2016). Many previous studies have investigated various kinds of uncertainties associated with different components of LID design, such as rainfall design and economic statistics. In 2013, Qin et al. (2013) discussed the effects of LIDs on urban flooding under different rainfall characteristics; later on, Chui et al. (2016) discussed the cost-effectiveness of specific LIDs among different regions; most recently, Lu et al. (2019) discussed the tradeoff between investment of LIDs and mitigation of urban flood damage.

Nevertheless, few studies in urban drainage and LID design attempted to address uncertainties associated with model parameters. One example work was reported by Fu et al. (2011), who tried to investigate uncertainties arising from model parameters of roughness coefficient for conduits and runoff coefficient, and their influence on modeling output of sewer flooding; Fu and Kapelan (2013) combined probabilistic rainfall and fuzzy model parameters to calculate the lower and upper exceedance probabilities of flood depths. However, in these two studies, the concerned model parameters were both predetermined and short of a selection process. A framework that is capable of sorting out key model parameters and tackling uncertainties arising from these parameters is desired for more feasible LID designs.

Besides uncertainty analysis, optimization technique is also imperative for facilitating cost-effective design of UDS and LIDs. Previously, a number of studies were reported in dealing with uncertainties arising from urban drainage modelling and optimization. In earlier years, Chang et al. (2011) discussed the optimization of GRs for water conservation and energy savings under uncertainties originated from rainfall and economic statistics; Dotto et al. (2012) discussed four different techniques dealing with uncertainty issues in UDS modeling; Yazdi et al. (2014) presented an optimization approach for drainage rehabilitation by integrating copula function, Monte Carlo Simulation (MCS), hydrological modelling and optimization algorithm. More recently, Duan et al. (2016) established different types of distribution functions to address various uncertainties in UDS (e.g. rainfall intensity and conduit roughness), and adopted MCS for stochastic analysis. Yu et al. (2017) proposed a chance-constrained programming (CCP) model to optimize drainage design and used MCS to deal with the violation risk of constraints containing stochastic variables (Charnes and Cooper 1959). Ronalds and Zhang (2019) discussed impact of rainfall pattern uncertainty on regional hydrographs by carrying out MCS on a runoff-routing model. Li et al. (2019) developed a multi-objective optimization framework for supporting robust designs of detention tanks and LIDs in UDS.

Among the above-mentioned studies, it was found that the stochastic-theory-based approaches such as MCS and CCP were popularly adopted for characterizing uncertainties. One drawback of traditional stochastic theory is that the probabilistic distributions of stochastic model parameters are difficult to obtain if the related data is limited or unreliable (He et al. 2008). Moreover, some types of uncertainty may not be suitable to be described as stochastic, such as the vagueness originated from subjective knowledge (Ross et al. 2009). Fuzzy set theory is an alternative tool in handling uncertainty. It can be used to capture expert knowledge and imprecise data, and is relatively flexible in defining uncertain parameters using the concept of fuzzy membership function (MF) (Zadeh 1965).

Fuzzy set theory has been widely used in applications of hydraulic structure design and water resources management (e.g. Mooselu et al. 2019; Banihabib et al. 2019). However, in the field of LID design or UDS modeling, the relevant studies are rather limited. Yazdi and Neyshabouri (2014) presented an approach to deal with both hydrological uncertainties and curve number (CN) parameter uncertainties in search of optimal implementation plans of LIDs. The performance of LIDs was affected by CN parameters, which were characterized by using fuzzy MF. Another study tried to use analytic hierarchy process to capture the vagueness of subjective knowledge and convert the judgment of experts into fuzzy sets (Jato-Espino et al. 2014). These fuzzy sets were combined with MCS to evaluate the aggregate performance (e.g., cost, flexibility and aesthetic) of three types of PPs. Nevertheless, both of the mentioned studies were in absence of a physical simulation model and did not consider the selection of LID parameters during evaluation or optimization processes.

To fill the above-mentioned research gaps, this study aims to propose a fuzzy-based, simulation-aided optimization model, namely fuzzy simulation-optimization model (FSOM), for supporting optimal design of LIDs and addressing uncertainties arising from hydrological model parameters. The model integrates hydrological simulation, fuzzy sets, fuzzy simulation (FS), CCP and evolutionary algorithm into a general modeling framework. The main novelty of FSOM is that it could offer cost-effective schemes of LIDs for controlling the flood risks at various confidence levels, which reflect the degree of system uncertainty handled by fuzzy sets. Through a case study of a small urban catchment, the applicability and efficiency of the proposed FSOM will be compared with two traditional models (i.e., deterministic and stochastic models) under various scenarios.

2 Methodology

2.1 System Framework

Figure 1 illustrates the overall flow of the proposed model and its individual components. In general, physical model is established first, followed by the formulation of the optimization problem. Then, the simulation-optimization model needs to run under predefined parameters (e.g. confidence levels) to yield the optimal solutions under various scenarios.

Fig. 1
figure 1

Flowchart of the proposed model

Full size image

To be more specific, firstly, necessary data should be collected for the study area, which may include specifications of drainage network (e.g., layout of conduits), configuration of land use, the potential types and locations of LIDs in each subcatchment and long-term meteorological data (e.g. rainfall and evaporation). Secondly, initial LID schemes are generated by random sampling and simulated by the hydrological model. Uncertain model parameters are sorted out and described by fuzzy sets. Thirdly, a design rainfall is used to reflect extreme rainfall condition and drive the model. Finally, the objective function, FS process and constraints are formulated for building the FSOM, where the output of hydrological model provides runoff and flood information for checking the violation of constraints. A few parameters need to be predefined, including (1) total acceptable flood volume of the system and allowable flood volumes for sensitive junctions (e.g. commercial areas and heavy traffic roads), (2) confidence levels of constraint satisfaction, and (3) configuration parameters of optimization algorithm.

Genetic algorithm (GA) is employed to solve the FSOM. It is a widely adopted algorithm based on the evolutionary idea of natural selection (Xu and Qin 2013). During GA operation, the candidate children (i.e., solutions) are generated by applying three major rules to their parent generation, including: (i) selection, which selects parents for the next generation based on suitable fitness values; (ii) crossover, which combines two parents to form a new child for the next generation; (iii) mutation, which triggers small random changes to parents to increase genetic diversity in searching (MATLAB 2015). These candidate children are then evaluated by FS process to check the probability of constraint satisfaction. Generally, a penalty (i.e., a large real number) is added to the fitness score to reject any candidate solution that is in violation of the constraints. The optimal solution is acquired only when the stopping criteria are satisfied (i.e. either the maximum number of generation is exceeded, or the fitness score no longer progress to a certain degree). More technical details of GA can be referred to Dhingra and Lee (1994).

2.2 FSOM Model Formulation

The SWMM model is selected as the hydrological model for this study, due to its popularity in urban hydrological modeling (Rossman 2010; US EPA 2019) and flexibility of linking with optimization components (e.g., MATLAB) (Chui et al. 2016). Dealing with parameter uncertainties and their impact on model performance is an important task in hydrological modeling. Previously, Krebs et al. (2013) carried out calibration and parameter sensitivity analysis of a high-resolution SWMM model, and identified two pivotal parameters (i.e., roughness coefficient for conduits and depression storage) through optimization. However, the study did not further analyze the impact of parameter uncertainty on modelling output. The proposed fuzzy simulation-optimization model (FSOM) screens out key parameters based on sensitivity analysis, and adopts fuzzification to tackle the uncertainties arising from these key parameters.

A general FSOM embedded with CCP can be formulated as follows (Huang 1998):

$$ Minf\left(\overrightarrow{x},\xi \right) $$
(1a)

subject to:

$$ Poss\left\{{h}_i\left(\overrightarrow{x},\xi \right)\le 0\left|\xi \right.\right\}\ge {\alpha}_i,i=1,2,\dots m $$
(1b)
$$ {g}_j\left(\overrightarrow{x}\right)\le 0,j=1,2,\dots n $$
(1c)

where f is objective function with vector of decision variables\( \overrightarrow{x} \)and matrix of fuzzy parameters ξ; h and g are constraint functions with and without fuzzy parameters, respectively; Poss{∙} is possibility of fuzzy events in {·}; αi is predetermined confidence level in ith fuzzy chance constraints; m and n are total numbers of i and j, respectively.

Specifically, FSOM for LID design and optimization subjected to uncertainty could be formulated as follows (Dai et al. 2018; Yu et al. 2017):

$$ MinC=\sum \left({c}_p^c+\varphi \cdot {c}_p^m\right)+{\pi}_1+{\pi}_2,p=1,2,\dots v $$
(2a)

subject to:

$$ {c}_p^c=\sum {x}_{p,q}\cdot {u}_q,q=1,2,\dots w,\forall p $$
(2b)
$$ {c}_p^{\mathrm{m}}=\lambda \cdot {c}_p^c,\forall p $$
(2c)
$$ Poss\left\{Q= SWMM\left(\overrightarrow{x},r,\xi \right)\le \gamma \left|r,\xi \right.\right\}\ge \alpha $$
(2d)
$$ {s}_i\le {\omega}_i,i=1,2,\dots, n $$
(2e)
$$ 0\le \overrightarrow{x}\le {x}_{\mathrm{max}} $$
(2f)

where C is total cost of LID design, which consists of construction cost, maintenance cost and penalty factors; p is index of subcatchment; v is number of subcatchment; \( {c}_p^c \) and \( {c}_p^m \) are construction and maintenance costs of LIDs for pth subcatchment, respectively. \( {c}_p^m \) is defined as a certain ratio λ to \( {c}_p^c \); φ is the discount factor; π1 is penalty factor for violation of fuzzy constraints (2d); π2 is penalty factor for violation of deterministic constraints (2e) or (2f); xp,q is decision variable which represents the implementation level (e.g. unit size) of the qth type of LID for the pth subcatchment (as it is assumed that the number of each type of LID facilities for each subcatchment is predefined, and these facilities would share the same xp,q); uq is unit cost of the qth type of LID; Q is total flood volume with a threshold of γ; Q is the output of SWMM model, which is driven by its input rainfall (r) and vector of decision variables (\( \overrightarrow{x} \)); ξ is matrix of fuzzy parameters (e.g., roughness coefficients); i denotes index of junctions which locate in important areas (e.g. subway entrance, school and hospital) and have special requests of preventing flood risks; n is the total number of i; si is surcharge volume at the ith junction; ωi is threshold level of si; xmax is vector confines the maximum value of\( \overrightarrow{x} \).

Generally, to solve model (2), the fuzzy constraint (2d) needs to be converted to its crisp equivalent. This is particularly efficient when the fuzzy constraint is linear, and the fuzzy MF μ(ξ) have specific shapes like triangular or trapezoidal (Liu and Iwamura 1998). In this study, as the fuzzy constraint is interweaved with simulation model which is highly non-linear, it is infeasible to convert the constraint to its crisp equivalent (i.e., deterministic). To solve this problem, a fuzzy simulation (FS) approach proposed by Liu and Iwamura (1998) is introduced to compute the possibility under fuzziness (Poss). Taking constraint (2d) as an example, the steps of FS are briefly summarized as follows:

  1. Step 1:

    Set Poss = 0;

  2. Step 2:

    Generate a vector ξ0 uniformly from the α-cut of ξ;

  3. Step 3:

    Compute the total flood volume Q0 under the realization of ξ0. If Q0 ≤ γ then set μ = min (ξ0), otherwise, set μ = 0;

  4. Step 4:

    If Poss < μ, then set Poss = μ, otherwise, Poss remains unchanged;

  5. Step 5:

    Repeat Step 2 to Step 4 for a given number of cycle n. Finally, Poss will be compared with pre-determined confidence level α for checking violation of fuzzy constraint.

For numerical examples of FS, readers can refer to He et al. (2008) and Xu and Qin et al. (2013). The computational time of FS is mainly determined by a predetermined number of cycle c. After the FS process, π1 will be added into fitness score if fuzzy constraint (2d) is not satisfied.

3 Case Study

3.1 Case Background and Model Setup

3.1.1 Description of the Study Site

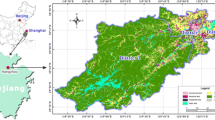
A hypothetical urban catchment adapted from a real tropical urban area is selected to demonstrate applicability of the proposed framework. Figure 2 shows its land use map and layout of the drainage network. The site area is about 98 ha and mainly characterized by urban commercial and residential areas under a tropical climate with mean annual rainfall around 2166 mm (Meteorological Service Singapore 2019). An urban hydrological model is established based on SWMM, which consists of 10 subcatchments, 21 junctions, 21 conduits and 1 outfall.

Fig. 2
figure 2

Drainage system and land use of the study area

Full size image

3.1.2 Design Rainfall

The designed rainfall is based on local intensity-duration-frequency (IDF) curve and Huff storm distribution. The IDF curves reveal the characteristics of the rainfall extremes, which are established based on annual maximum rainfalls with various durations (Arnbjerg-Nielsen 2012). The Huff storm distribution (Huff 1967) includes four types of rainfall patterns, where the peak intensity of each pattern would occur in different quarters of the rainfall duration. For this study, we assume a 1-h design rainfall with a total depth at 92 mm (i.e. 10-year return) and a Type-II Huff distribution (Jun et al. 2019). The design rainfall is used to set up the model and generate flood scenarios. Readers can refer to the Online Resource Fig. S1 for the corresponding hyetograph.

3.1.3 Sensitivity Test

Sensitivity tests are needed to identify key model parameters that may cause notable impact on flooding results and are necessary to be addressed as uncertainty factors (i.e., fuzzy parameters). Based on the pervious works (Krebs et al. 2013; Yu et al. 2017) and local hydrological conditions, six candidate parameters are selected for sensitivity test. They include: (i) subcatchment properties: slope, impervious depression storage and overland flow width, which are highly diverse even within single subcatchment; (ii) hydraulic roughness for conduits (Revelli and Ridolfi 2002) and overland flows, which may change with time and difficult to estimate. Based on their default values, these parameters are allowed to vary within their corresponding sampling range following a fixed sampling step. Based on the test results, the conduit roughness nc, the Manning’s n for pervious overland flow np and the width of overland flow path Wf are determined to be the most sensitive parameters in SWMM. For detailed information about candidate parameters and their test results, please refer to Online Resource (Table S1 and Fig. S2).

3.1.4 Properties and Layouts of LIDs

Three types of LIDs are proposed, including green roof (GR), bio-retention cell (BC) and permeable pavement (PP). As shown in Fig. 2, areas within subcatchment S3, S5, S6 and S8 are classified as commercial areas (CA) with busy roads, while the rest 6 subcatchments are residential areas (RA). GR and BC are applicable on both CA and RA, as they can reduce the overall peak and have aesthetic benefits for the city landscape. PP is assumed only applicable on RA as it is considered not suitable for roads with large traffic volume (Hu et al. 2017).

The detailed properties about LIDs are provided in Online Resource Table S2 and S3. Some of these values are referred to Rossman (2010) and Chui et al. (2016). Note that the soil layer properties of BC and PP are the same as GR, except that the thicknesses of soil layers are 700 mm and 200 mm for BC and PP, respectively. Considering the fact that the area of each subcatchment is significantly larger than the unit size of each LID facility, there will be multiple facilities (with the same unit size) of the same type of LID deployed in one catchment. The detailed allocation of the LID numbers in each subcatchments can be referred to Online Resource Table S4. The decision variables are the unit sizes of GR, BC and PP facilities in different subcatchments. Thus, there are 26 (i.e. 4 CA × 2 types of LIDs +6 RA × 3 types of LIDs) continuous decision variables in total.

3.1.5 Setup of FSOM Framework

Configuration of the optimization framework is: (i) according to Chui et al. (2016), the unit construction costs (uq) of GR, BC and PP = 152, 153 and 61 US$/m2; (ii) the discount factor (φ) = 11.1, which is a function of design life and interest rate; (iii) the ratio of maintenance to construction cost (λ) = 0.03; (iv) the threshold of total flood volume (γ) = [35,000, 40,000, 45,000, 50,000] m3, and each junction is equally important in the case area (i.e., n = 0 for Eq. 2e); (v) confidence level (α) = [0.55, 0.75, 0.95]; (vi) the maximum unit size (xmax) for GR, BC and PP are all set to 500 m2. From sensitivity test, nc, np and Wf are assumed as fuzzy sets. For simplicity of calculation, these fuzzy sets are denoted as triangle or trapezoid-shaped MF (as shown in Online Resource Fig. S3). Generally, the shapes of fuzzy sets could be more specific (e.g., exponential or Gaussian) based on actual survey or data analysis, as the FS process is applicable to any kinds of MF (Xu and Qin 2013).

The SWMM model is directly linked with MATLAB GA toolbox (version of 2015b). Processes of candidate generation, file reading, model calling, fuzzy simulation, and fitness calculation are all carried out under the MATLAB platform. Some main parameters are set as follows: (i) maximum number of generation = 30 (selected according to the convergence speed of minimum fitness value); (ii) population size = 50 (chosen to have an affordable computational cost of FSOM while maintaining the diversity of population in each generation); (iii) crossover fraction = 0.8 (adopted the default value in MATLAB); (v) penalty factor π1 = 1 × 108 and π2 = 1 × 108 (selected to be notably larger than the maximum fitness value to ensure rejection of unqualified solutions); (vi) the cycle number c = 500 for FS process (selected to have reliable results with affordable computational cost). The GA operation is carried out on a 32-core AMD Opteron 2.6 GHz workstation and it takes approximately 30 h to solve FSOM in a single run. In comparison, a deterministic model with all parameters fixed at their default values takes about 1.5 h on the same machine.

3.2 Result Analysis

Figure 3 shows the optimized total costs of LIDs (C, unit in million US$) from the FSOM and the deterministic model under various confidence levels (α) and thresholds of system flood volume (γ) (unit in 103 m3, the same hereinafter). It implies that for the FSOM, α and γ determine the strictness of LID implementation: a higher α or a lower γ normally leads to a higher C and vice versa. Particularly, when α increases from 0.75 to 0.95, C would increase from 83.47 to 96.08 with γ = 35 and from 50.27 to 58.58 with γ = 50. For deterministic model, C would fall between the FSOM results with confidence levels of 0.75 and 0.95 under most γ levels (except for γ = 45). In general, FSOM and deterministic models achieve comparable costs under various conditions. The advantage of FSOM lies in that, with various confidence levels being considered, it could offer a spectrum of solutions for decision makers who could eventually determine a suitable tradeoff between risk and cost.

Fig. 3
figure 3

Optimized total cost of LIDs from FSOM and deterministic model with different confidence levels (alpha) and thresholds of system flood volume

Full size image

Since a higher confidence level generally corresponds to a more reliable system, the result from the confidence level of 0.95 will be focused on. Figure 4 shows the maps with optimal coverage areas of LIDs and the percentages of vacant areas (i.e., area free of LIDs) marked in different subcatchments under different γ levels. Subplots (a) to (d) represent the scenarios with γ = 35, 40, 45 and 50, respectively. Generally, Fig. 4 shows that, for most subcatchments, the percentage of vacant area would increase with the increase of γ, and this leads to a lower C. The only exception is subcatchment S7, where the LID coverage percentages are 53.95% and 59.08% under γ = 35 and 50, respectively. Besides, in some subcatchments, some specific types of LID tend to be dominant (e.g., GR for S5, BC for S3 and S8, and PP for S2 and S7), while some prefer a more balanced implementation among three types of LIDs (e.g., S1 and S10).

Fig. 4
figure 4

Maps with coverage area of GR (vertical line), BC (horizontal line), PP (cross line) and percentage of the vacant area marked in different subcatchments. Optimized by FSOM under confidence level of 0.95 and system flood volume threshold of (a) 35,000 (b) 40,000 (c) 45,000 and (d) 50,000 m3

Full size image

Under the four optimal layouts of LIDs illustrated in Fig. 4, the SWMM model (embedded with fuzzy parameters) has run another 1000 times for each layout. Figure 5 uses box plots to show the variation of flood volume at individual junctions (with a threshold of 1000 m3 for extreme flood volume) based on the simulation results. The purpose is to investigate the impact of parameter uncertainties on model performance after the implementation of LIDs. It is indicated from Fig. 5 that the uncertainty associated with SWMM parameters may lead to spatial variations of flooding. In terms of extreme flood conditions, the outliers of some junctions are well outside their normal ranges. For instance, the median flood volume of J13 is 2110 m3 (γ = 35), but the outliers may reach up to 4437 m3 (210.3% of median); whereas one outlier of J6 (483 m3, γ = 35) is only 31.8% of its median (1521 m3, γ = 35). In terms of heavily flooded junctions whose maximum flood volumes are over 4000 m3, some are subjected to higher uncertainties (e.g., J13 and J17, but only when γ is relatively small), and some are much more stable (e.g., J14 and J19) under all γ levels. The less flooded junctions (e.g., J12 and J21) witness a variety of degree of uncertainties, but the measures to match their maximum outliers are affordable. For these junctions, the absolute increases of flood volumes are limited and thus manageable by extra LID implementations nearby. These results may help decision makers understand the potential extreme flood risks in specific areas after adopting the optimal solutions, and take necessary actions by adjusting local settings (Yu et al. 2017).

Fig. 5
figure 5

Boxplot of flood volume at individual junctions (with a threshold of 1000 m3). LIDs are optimized by FSOM under confidence level of 0.95 and system flood volume threshold of (a) 35,000 (b) 40,000 (c) 45,000 and (d) 50,000 m3

Full size image

3.3 Comparison with a Traditional Stochastic Model

In order to demonstrate the applicability of FSOM, a traditional MCS-based stochastic model (e.g., Duan et al. 2016) is also applied to solve the problem under similar setup (i.e., α = 0.95 and the same options of GA). Instead of defining uncertainty parameters (i.e., Wf, np and nc) as fuzzy sets, they are assumed as stochastic variables with normal distributions. The corresponding distribution information (e.g., mean and standard deviation) can be referred to the Online Resource Table S5. Figure 6 shows a comparison of the iteration processes between FSOM (denoted as F) and stochastic model (denoted as S). Subplots (a) to (d) represent the processes with γ = 35, 40, 45 and 50 (unit in 103 m3, the same hereinafter), respectively. In each subplot, solid lines and dash lines are used to represent the minimum and mean fitness value in each generation of GA, respectively.

Fig. 6
figure 6

Comparisons between iteration processes (solid line: min fitness value; dash line: mean fitness value) of FSOM (denoted as F) and stochastic model (denoted as S). Both under confidence level of 0.95 and system flood volume threshold of (a) 35,000 (b) 40,000 (c) 45,000 and (d) 50,000 m3

Full size image

Figure 6 shows that the stochastic model outperforms FSOM with respect to mean fitness value under various γ; in other words, the gap between the mean and the minimum values for stochastic model is usually narrower than that of FSOM. Taking γ = 45 as an example, the mean values of FSOM would fluctuate between 125.7 and 158.8 million $, which are much larger than the corresponding minimum values (63.1 to 75.9 million $). This may because the FS process is sensitive to not only the simulation model, but also the number of fuzzy parameters. When there are more than one fuzzy parameter (e.g., three in this case study), FS adopts the minimum α-cut of these parameters as the possibility (i.e. Poss) under fuzziness. Therefore, under a high confidence level (i.e., α = 0.95), FS is relatively difficult to acquire a Poss that is larger than α when the cycle number is reached, which would bring penalties (π1, 100.0 million $) into fitness values of candidates. As a result, the mean values of FSOM would increase in each generation. On the other hand, there is no concept of α-cut for stochastic model, and Poss is calculated by the proportion of candidates that satisfy the flood constraint, which reduces the risk of constraint violation.

In terms of minimum value, which is deemed as a practical criterion for optimization models, FSOM and stochastic model achieve very close results in their final generations in subplots (b) (γ = 40) and (d) (γ = 50), and the relative differences are 2.5% and 2.8%, respectively. For the rest two subplots, in subplot (a) (γ = 35), FSOM is defeated with a relative difference of 7.3%, whereas in subplot (c) (γ = 45), FSOM surpasses stochastic model with a relative difference of 9.0%. It is worth noting that both models have drawbacks regarding the iterative processes. Stochastic model has the risk of deviation in the last few generations in subplot (c); FSOM gains no feasible candidate (i.e., candidate without penalty) in both 9th and 20th generations in subplot (d), which endangers the feasibility of the following generations. In general, the two models achieve comparable performances based on minimum fitness values and both models could be considered as feasible alternatives to deal with uncertainty issues addressed in the study case. However, by adopting MF and FS, it is believed that FSOM could address the imprecision and vagueness arising from the modeling process and expert knowledge in a more flexible way.

3.4 Further Discussions

This work attempts to integrate various techniques into FSOM for supporting LID design under uncertainty. These techniques involve urban hydrological modeling, chance-constrained programming, fuzzy simulation and an evolutionary algorithm. The model allows generation of robust optimal solutions that could achieve tradeoffs between the flood risks (e.g., thresholds of system flood volume and corresponding confidence levels) and the total cost of LIDs. More importantly, the framework of FSOM is flexible for various practical problems, such as hydrological model for other locations and additional types of LIDs (e.g., rain garden and vegetative swale). The performance of the proposed FSOM is justified by comparing it to the traditional deterministic and stochastic models, and it is a feasible alternative to the traditional optimization models.

As the first attempt in proposing FSOM, we also encountered some limitations. Firstly, the decision variables (i.e., implementation levels of LIDs) are set as the unit area of each LID facility in each subcatchment, and the numbers of these facilities are fixed in all subcatchments. In this way, the coverage of LIDs could be adjusted, and the number of decision variables could be limited to the product of subcatchment number and number of LID types. In practical design, the number of LID facilities in each subcatchment may also be considered as decision variables. Secondly, the computational burden for FSOM is much higher than the traditional deterministic model, as FS requires repetitive execution of hydrological model for a cycle number of times. Surrogate approaches such as artificial neural network (ANN) (He et al. 2008; Lu et al. 2017) may be a promising solution to help alleviate computational cost by explicitly mimicking the relationships between decision variables and system responses. Moreover, the flood risk is controlled by the system flood volume. It is believed that, with the support of further geographical data and social economic input, a two-dimensional inundation model could further improve the accuracy of flood risk assessment.

4 Conclusion

An integrated fuzzy simulation-optimization model (FSOM) for supporting low impact development (LID) design was proposed. FSOM integrated techniques of fuzzy simulation, chance-constrained programming, hydrological modeling and evolutionary algorithm to achieve trade-offs between investments of LIDs and flood risks. The performance of the proposed FSOM were tested through a case study of a hypothetical urban catchment. FSOM applied a simulation-based iteration process, which could effectively address the uncertainty associated with hydrological model. Meanwhile, the constraints with fuzzy variables were allowed to be satisfied at specified confidence levels. It was shown that a higher confidence level and a lower threshold of flood volume would bring a more reliable system but a less economically attractive plan. The applicability of FSOM was also demonstrated through comparison to a MCS-based traditional stochastic model. The heavy computational burden of FS process is a major limitation of this work. In addition, the absence of surficial inundation modeling may limit the precision of flood risk assessment. Both issues are desired to be tackled in future works.