1 Introduction

Water management covers a wide range of activities, in which technical, economic, environmental and social issues are involved (Anagnostopoulos et al. 2005). Therefore, to select the best alternative, it is necessary to consider all of these activities in integrated water resources management. One of the most important tasks in water resources management is improving decision making on the projects by using multiple attribute decision making (MADM) methods. These methods provide a framework to help water managers to identify critical criteria and select best alternatives. Many different MADM methods were used in water management fields as follows: ranking projects in Krishna basin (Raj and Kumar 1999), using fuzzy compromise approach in water resource system planning (Bender and Simonovic 2000), developing sustainable water resources management by MADM (Connell et al. 2000), ranking water resources projects in Spain by PROMETHEE-2, ELECTRE-3, Compromise Programming (CP), EXPROM-2, and ELECTRE-4 (Raju et al. 2000), using Fuzzy CP in water resources (Prodanovic and Simonovic, 2002; 2003), ranking alternatives by TOPSIS and CP methods (Srdjevic et al. 2004), review of multiple criteria analysis for water resources management (Hajkowicz and Collins 2007), fuzzy AHP methods (Srdjevic and Medeiros 2008), using multi-criteria decision making method for integrated urban water management (Zarghami et al. 2008), ranking water transfer projects by different fuzzy MADM methods (Razavi Toosi et al. 2009), assessing global water productivity of irrigation networks in Iran (Montazar and Zadbagher 2010), ranking urban watershed management alternatives (Chung et al. 2011), ranking water transfer projects by ANP method (Razavi Toosi and Samani 2012), introducing a new group decision making aid in urban water supply management (Roozbahani et al. 2012), using MADM to integrated water resources management (Geng and Wardlaw 2013), using AHP and GIS for watershed prioritization (Chowdary et al. 2013), evaluating the power of water users in inter-basin water allocation system by AHP, ANP, TOPSIS, ER (Evidential Reasoning) and PROMETHEE II (Abed-Elmdoust and Kerachian 2014), using AHP based decision support for watershed prioritization (Jaiswal et al. 2014) and etc.

This paper proposed an integrated model that incorporates several criteria in benefit, cost and risk clusters within a network construction that provides a comprehensive evaluation of group decision making able of selecting the best water transfer project. The procedure integrates the ANP, fuzzy TOPSIS and fuzzy max-min set methods. In MADM problems, the decision maker’ preference information is often used. However, the decision makers’ judgments are different in form and depth. The proposed method can overcome errors arising from arithmetic or geometric mean when all decision maker judgments’ are not of equal importance. When the weights of decision makers’ are different, the arithmetic mean is not a suitable method for aggregating and therefore it is important to consider decision makers’ judgments weighs and quantify the effects of the decision makers’ judgments on final ranking. The proposed model not only evaluates complex network relations but also obtain the final ranking by considering the weighs of each decision maker judgments. The alternatives include four water transfer projects that accomplished higher scores in the previous study (Razavi Toosi and Samani 2012). As described there, the alternatives need more criteria for evaluation due to their close estimated scores. Therefore, in this paper, compared to the previous one conducted by Razavi Toosi and Samani (2012), a comprehensive model with more effective criteria for selecting the best alternative in group decision making problem is developed. The main novelty of this paper is its ability to model the complex relations among different clusters, criteria and alternatives, quantifying the effects of the various decision makers’ judgments on the final ranking in fuzzy environment as well. In addition, the influences of decision maker judgments weights on the alternatives’ scores are evaluated by fuzzy max-min method. This paper is organized as follows: the methodology is described in section 2. In section 3, the case study is introduced and all the criteria, sub criteria and alternatives are defined. The results are described in section 4. Finally, the conclusion is presented in section 5.

2 Methodology

Multiple criteria decision making refers to the process of screening, prioritizing, ranking, or selecting a set of alternatives under usually independent, incommensurate and conflicting criteria (Afshar et al. 2011). Group decision making is usually understood as aggregating different individual preferences on a given set of alternatives to a single collective preference. A group decision making involves different decision makers with different skills, experience and knowledge. One of the problems in group decision making is how to aggregate individual judgments and how these influence the final ranking (Saaty and Vargas 2006). In this paper, a new framework is proposed by combining ANP, fuzzy TOPSIS and fuzzy max-min set method for group decision making. The procedure of this integrated method is shown in Fig. 1. This procedure is described as follows.

Fig. 1
figure 1

The procedure of the proposed model

Full size image

2.1 ANP Method

The theory of ANP was first introduced by Saaty (1980) as a new essential phase in decision making theory. It is an extension of AHP. The ANP method is used as a flexible model for demonstrating the mutual interactions among different factors in the decision making procedure.

In AHP, the decision maker framework is modeled by unidirectional hierarchal connections but in ANP the connections are more complex based on a network structure. At first, the alternatives, criteria and sub criteria are defined. The network structure is constructed by creating the relationship and connections between elements. The network structure can be obtained by decision makers through brainstorming or other appropriate methods. Figure 2 shows different relations in network structure.

Fig. 2
figure 2

Different relations in network structure (Horenbeek and Pintelon 2014)

Full size image

After setting up the network structure and element’s connections, the pairwise comparisons are performed by preparing questionnaire for each decision maker. The preference value of pairwise comparisons which was proposed by Saaty (1996) is used. In ANP method, the decision maker is asked to answer the question as: “how much the importance does the sub criterion have compared to another sub criterion with respect to the specific cluster criterion?” if two criteria are of equal importance, the value 1 is given in the comparison. The value 9 shows extreme importance of one criterion overall. This comparison matrix is then checked for consistency. The consistency index (CI) is calculated as follows:

$$ CI=\frac{\lambda_{\max }- n}{n-1} $$
(1)

where λmax is the maximum eigenvalue of the judgment matrix (n × n). The CI can be compared with the random index value, RI. The consistency ratio (CR) is defined as CI/RI. Saaty (1980) suggests the value of CR to be less than 0.1 (Bhushan and Rai 2004). Numerical weights are assigned to each element of the comparison matrix, based on their relative importance, where the total sum of weights of all alternatives in a criterion must equal one. This could be accomplished using one of several available methods. The most common one is the Eigenvector Method (EM). Priorities are then derived for each alternative (Javadi and Dambatta 2008).

The supermatrix is used in ANP method to deal with the relationship of feedback and interdependence among the criteria. If no interdependent relationship exists, the pairwise comparison value would be 0. In contrast, if an interdependent and feedback relationship exists among the criteria, then such value would no longer be 0 and an unweighted supermatrix will be obtained (Tseng et al. 2009). The general form of supermatrix is as follows (Saaty 1996).

(2)

where Cn denotes the nth cluster, enm denotes the mth element in nth cluster and Wij is the principle eigenvector of the influence of the elements compared in the jth cluster to the ith cluster (Yang and Tzeng 2011). The components of the unweighted supermatrix are multiplied by the corresponding cluster weights to obtain the weighted supermatrix and normalize it. Generally, the columns of the unweighted supermatrix do not sum to 1, whereas in the weighted supermatrix they do (Razavi Toosi and Samani 2012). It is important that the weighted supermatrix be always the stochastic matrix. Finally, by calculating the limiting power of the weighted supermatrix, the limiting supermatrix is obtained. All the columns of the limit supermatrix are similar. Therefore, the global priorities of alternatives will be determined. In this study the group decision making is considered by ANP method. Therefore, the ANP results and the priority of each alternative are changed based on each decision makers’ judgments. The final result for each decision maker is shown as follows:

$$ D{M}^{\ell }=\left\{{S}^{\ell}\left({A}_1\right),{S}^{\ell}\left({A}_2\right),\dots, {S}^{\ell}\left({A}_n\right)\right\},\kern0.36em \ell =1,2,\dots, L $$
(3)

where S ℓ(A n ) is the priority of alternative (An) that obtained by decision maker ℓ by ANP method.

2.2 Proposed Method: Combination of Fuzzy TOPSIS and Fuzzy max-min set Method for Group Decision Making

The initial information is obtained by ANP method as described above. In this section, the ANP results are used to construct matrix for fuzzy TOPSIS and fuzzy max-min set method. The proposed method is described as follows: At first, decision making matrix is constructed for decision makers and criteria:

$$ \tilde{D}=\left[\begin{array}{cccc}\hfill {\tilde{x}}_{11}\hfill & \hfill {\tilde{x}}_{12}\hfill & \hfill \cdots \hfill & \hfill {\tilde{x}}_{1 n}\hfill \\ {}\hfill {\tilde{x}}_{21}\hfill & \hfill {\tilde{x}}_{22}\hfill & \hfill \cdots \hfill & \hfill {\tilde{x}}_{2 n}\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \vdots \hfill \\ {}\hfill {\tilde{x}}_{m1}\hfill & \hfill {\tilde{x}}_{m2}\hfill & \hfill \cdots \hfill & \hfill {\tilde{x}}_{m3}\hfill \end{array}\right]\kern0.36em $$
(4)

The elements of this matrix (\( {\tilde{x}}_{ij} \)), show the rating of ith decision maker with respect to the jth criteria. i and j are numbers of decision makers and criteria, respectively. The weight of each criterion is assigned in conceptual form. Then these conceptual phrases were replaced with triangular fuzzy numbers as shown in Table 1.

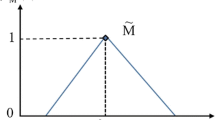
Table 1 Linguistic variables for ratings and the importance weight of each criterion (Chen 2000)
Full size table

The membership function of fuzzy triangular number \( \tilde{n}=\left({n}_1,{n}_2,{n}_3\right) \) is defined as follows:

$$ {\mu}_{\tilde{n}}(x)=\left\{\begin{array}{l}0\kern4.56em x<{n}_1\\ {}\frac{x-{n}_1}{n_2-{n}_1}\kern2.76em {n}_1\le x\le {n}_2\\ {}\frac{x-{n}_3}{n_2-{n}_3}\kern2.52em {n}_2\le x\le {n}_3\\ {}0\kern4.2em x>{n}_3\end{array}\right. $$
(5)

The criteria are classified in two groups, benefits and costs. The benefit criterion means that a higher value is better while for the cost criterion is vice versa. The data of decision matrix come from different sources so it is necessary to have the data normalized. The weighted normalized fuzzy decision matrix is constructed by multiplying the normalized fuzzy decision matrix by its associated weights (\( {\tilde{v}}_{ij} \)). In the next step, the positive ideal solution (A+) and the negative ideal solution (A−) are calculated as follows (Krohling and Campanharo 2011):

$$ {A}^{+}=\left({\tilde{v}}_1^{+},{\tilde{v}}_2^{+},\dots, {\tilde{v}}_n^{+}\right)\kern0.48em ,\kern0.6em {A}^{-}=\left({\tilde{v}}_1^{-},{\tilde{v}}_2^{-},\dots, {\tilde{v}}_n^{-}\right) $$
(6)

and

$$ {\tilde{v}}_j^{+}=\left(\underset{i}{ \max}\;{\tilde{v}}_{i j}, j\in {J}_1;\underset{i}{ \min}\;{\tilde{v}}_{i j}, j\in {J}_2\right)\kern0.36em ,\kern0.48em {\tilde{v}}_j^{-}=\left(\underset{i}{ \min}\;{\tilde{v}}_{i j}, j\in {J}_1;\underset{i}{ \max}\;{\tilde{v}}_{i j}, j\in {J}_2\right) $$
(7)

where j1 and j2 are the benefit and cost criteria, respectively. Then the Euclidean distance is calculated from A+ and A− for each alternative:

$$ {d}_i^{+}={\displaystyle \sum_{j=1}^n d\left({\tilde{v}}_{i j},{\tilde{v}}_j^{+}\right)}\kern0.6em ,\kern0.6em {d}_i^{-}={\displaystyle \sum_{j=1}^n d\left({\tilde{v}}_{i j},{\tilde{v}}_j^{-}\right),\kern0.36em i=1,2,\dots, m} $$
(8)

Finally, the closeness coefficient (CCi) is obtained as:

$$ C{C}_i=\frac{d_i^{-}}{d_i^{+}+{d}_i^{-}}, i=1,2,\dots, m $$
(9)

Therefore the score of each decision maker (w) is obtained as follows:

$$ {w}^{\ell }=\left\{ c{c}_1, c{c}_2,\dots, c{c}_{\ell}\right\}\kern0.72em ,\ell =1,2,\dots, L $$
(10)

In next step, the priority of each alternative by ANP and decision makers’ judgments weights through fuzzy TOPSIS method are converted to trapezoidal fuzzy number for using in fuzzy max-min set method as input data. As shown in Eq. 11, \( {\tilde{S}}^{\ell}\left({A}_n\right) \) and \( c{\tilde{c}}_{\ell } \) are the trapezoidal fuzzy numbers that show the priority of each alternative (An) by decision maker ℓ and the score of each decision maker, respectively.

$$ \begin{array}{l} D{\tilde{M}}^{\ell }=\left\{{\tilde{S}}^{\ell}\left({A}_1\right),{\tilde{S}}^{\ell}\left({A}_2\right),\dots, {\tilde{S}}^{\ell}\left({A}_n\right)\right\}\\ {}{\tilde{S}}^{\ell}\left({A}_i\right)=\left({\alpha}_i^{\ell },{\beta}_i^{\ell },{\gamma}_i^{\ell}\;{\delta}_i^{\ell}\right), i=1,2,\dots, n\\ {}{\tilde{w}}^{\ell }=\left\{ c{\tilde{c}}_1, c{\tilde{c}}_2,\dots, c{\tilde{c}}_{\ell}\right\},\ell =1,2,\dots, L\\ {} c{\tilde{c}}_{\ell }=\left({\varepsilon}_{\ell },{\zeta}_{\ell },{\eta}_{\ell },{\theta}_{\ell}\right)\end{array} $$
(11)

Therefore, the initial matrix is constructed for fuzzy max-min set method as follow:

$$ \tilde{R}=\left[\begin{array}{cccc}\hfill {\tilde{S}}^1\left({A}_1\right)\hfill & \hfill {\tilde{S}}^2\left({A}_1\right)\hfill & \hfill \cdots \hfill & \hfill {\tilde{S}}^L\left({A}_1\right)\hfill \\ {}\hfill {\tilde{S}}^1\left({A}_2\right)\hfill & \hfill {\tilde{S}}^2\left({A}_2\right)\hfill & \hfill \cdots \hfill & \hfill {\tilde{S}}^L\left({A}_2\right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill {\tilde{S}}^1\left({A}_n\right)\hfill & \hfill {\tilde{S}}^2\left({A}_n\right)\hfill & \hfill \cdots \hfill & \hfill {\tilde{S}}^L\left({A}_n\right)\hfill \end{array}\right] $$
(12)

Where \( {\tilde{S}}^1\left({A}_i\right) \) is the priority of alternative Ai based on judgments of DM1 and represented by trapezoidal fuzzy number. L and n indicate the number of decision makers and alternatives, respectively. The membership function of trapezoidal fuzzy number (α ℓ i , β ℓ i , γ ℓ i   δ ℓ i ) is defined as follows:

$$ {\mu}_{{\tilde{S}}^{\ell }}(x)=\left\{\begin{array}{l}0\kern3.96em x<{\alpha}_i^{\ell}\\ {}\frac{x-{\alpha}_i^{\ell }}{\beta_i^{\ell }-{\alpha}_i^{\ell }}\kern2.04em {\alpha}_i^{\ell }< x<{\beta}_i^{\ell}\\ {}1\kern3.72em {\beta}_i^{\ell }< x<{\gamma}_i^{\ell}\\ {}\frac{\delta_i^{\ell }- x}{\delta_i^{\ell }-{\gamma}_i^{\ell }}\kern2.16em {\gamma}_i^{\ell }< x<{\delta}_i^{\ell}\\ {}0\kern3.72em x>{\delta}_i^{\ell}\end{array}\right. $$
(13)

In next step, the weight for above matrix is assigned by multiplying two trapezoidal fuzzy numbers \( {\tilde{S}}^{\ell}\left({A}_i\right)=\left({\alpha}_i^{\ell },{\beta}_i^{\ell },{\gamma}_i^{\ell}\;{\delta}_i^{\ell}\right) \) and \( c{\tilde{c}}_{\ell }=\left({\varepsilon}_{\ell },{\zeta}_{\ell },{\eta}_{\ell },{\theta}_{\ell}\right) \). The final weight in fuzzy form is shown as follow:

$$ {\tilde{w}}_i=\left({\alpha}_i\left[{L}_{i1},{L}_{i2}\right],{\beta}_i,{\gamma}_i,{\delta}_i\;\left[{U}_{i1},{U}_{i2}\right]\;\right) $$
(14)

Where

$$ \kern0.6em {\alpha}_i={\displaystyle \sum {\alpha}_i^{\ell }{\varepsilon}_{\ell }}/ K\; L\kern0.6em ,\kern0.6em {\beta}_i={\displaystyle \sum {\beta}_i^{\ell }{\zeta}_{\ell }}/ K\; L\kern0.6em ,\kern0.6em {\gamma}_i={\displaystyle \sum {\gamma}_i^{\ell }{\eta}_{\ell }}/ K\; L\kern0.6em ,\kern0.6em {\delta}_i={\displaystyle \sum {\delta}_i^{\ell }{\theta}_{\ell }}/ K\; L $$
(15)

And

$$ {L}_{i1}=\left\{{\displaystyle \sum \left({\beta}_i^{\ell }-{\alpha}_i^{\ell}\right)\left({\zeta}_{\ell }-{\varepsilon}_{\ell}\right)}\right\}/ K\; L\kern0.6em ,\kern0.72em {L}_{i2}=\left[{\displaystyle \sum \left\{{\alpha}_i^{\ell}\left({\zeta}_{\ell }-{\varepsilon}_{\ell}\right)+{\varepsilon}_{\ell}\left({\beta}_i^{\ell }-{\alpha}_i^{\ell}\right)\right\}}\right]/ K\; L $$
(16)
$$ {U}_{i1}=\left\{{\displaystyle \sum \left({\delta}_i^{\ell }-{\gamma}_i^{\ell}\right)\left({\theta}_{\ell }-{\eta}_{\ell}\right)}\right\}/ K\; L\kern0.6em ,\kern0.6em {U}_{i2}=-\left[{\displaystyle \sum \left\{{\delta}_i^{\ell}\left({\theta}_{\ell }-{\eta}_{\ell}\right)+{\theta}_{\ell}\left({\delta}_i^{\ell }-{\gamma}_i^{\ell}\right)\right\}}\right]/ K\; L $$
(17)

L is the number of decision makers and K refers to the best condition (K = 10). Finally, the total utility (UT) is obtained as follows:

$$ {U}_T\left({A}_i\right)=\left\{{U}_M\left({A}_i\right)+1-{U}_m\left({A}_i\right)\right\}/2 $$
(18)

And

$$ {U}_M\left({A}_i\right)=\underset{x}{Supremum}\left\{{\mu}_{\tilde{w} i}(x)\cap {\mu}_{\tilde{M}}(x)\right\}\kern0.6em ,\kern0.6em {U}_m\left({A}_i\right)=\underset{x}{Supremum}\left\{{\mu}_{\tilde{w} i}(x)\cap {\mu}_{\tilde{m}}(x)\right\} $$
(19)

where \( {\mu}_{\tilde{M}}(x) \) and \( {\mu}_{\tilde{m}}(x) \) are the membership function of maximum and minimum groups, respectively. \( {\mu}_{\tilde{w} i}(x) \) is the membership function of \( {\tilde{w}}_i \) that introduced in Eq. 14 (Razavi Toosi et al. 2009) and UT (Ai) is the final score of each alternative with respect to different criteria and by considering decision makers’ judgments weights. For more details on fuzzy max-min set see Raj and Kumar (1999).

3 Case Study

Water scarcity is one of the important problems among many water problems that are presented today and will be even more noticeable in the future (Ghassemi and White 2007). In Iran, the non uniform distribution of water in terms of space and time and the fast growth of the population have led to the present water shortages in major parts of the country, especially in the central zone and in the southeastern regions. One of the proposed solutions for this problem is inter-basin water transfer. The inter-basin water transfer project is an alternative to balance the non uniform spatial distribution of water resources and water demands (Abrishamchi and Tajrishy 2005). There is no enough financial capability to execute all water resources projects, therefore among several water transfer projects, it is necessary to rank execution projects on the basis of different criteria evaluation. In this paper, a new MADM method is introduced by combination of ANP, fuzzy TOPSIS and fuzzy max-min set methods. The aim of this model is to rank water transfer projects under different criteria in group decision making environment. Four water transfer projects in Karun River are investigated as alternatives by considering over 60 criteria in benefit, cost and risk cluster. The questionnaires are completed by three water resources experts. Regarding the aggregation of the group decisions, the new method is introduced.

3.1 Alternatives and Criteria

In this paper, four water transfer projects with high priority in the previous work (Razavi Toosi and Samani 2012) are selected to be investigated by considering over 60 criteria and sub criteria in group decision making environment. The projects are included Kohrang tunnel 1 (A1), Kohrang tunnel 2 (A2), Langan source (A3) and Gukan (A4). Different criteria are classified in economic, social-cultural and environmental clusters that defined under benefit, cost and risk model named BCR model. Also, the importance rating of the BCR model is determined by the strategic criteria. These criteria include employment and migration, benefit cost ratio, crisis management and environmental impacts. All the alternatives, clusters and criteria as well as their relations are shown in Fig. 3. Over 88 questionnaires are provided as pairwise comparison matrix for network structure. Three experts in water management were asked to fill out the questionnaires, separately.

Fig. 3
figure 3

The network structure for BCR model

Full size image

4 Result and Discussion

The results are presented in three sections as follows:

Section1: the ANP model is used based on three decision makers’ judgments and the alternatives priorities are obtained. Due to space limitation, all the supermatrices are not shown in this paper. For instance, the weighted supermatrix in benefit cluster under social-cultural based on the first decision maker’s judgment (DM1) is illustrated in Table 2. The priority of each alternatives are obtained in benefit, cost and risk cluster based on DM1’s judgments as shown in Table 3. Also, the weights of benefit, cost and risk in BCR model are obtained based on four strategic criteria.

Table 2 Supermatrix in social- cultural sub network of benefit model
Full size table
Table 3 The priorities of alternatives under BCR model
Full size table

Finally, based on each decision maker judgments, the alternatives priorities are obtained by ANP method. The ideal priorities of alternatives based on three decision makers’ judgments are obtained as follows.

  • DM1: Kohrang2 (0.276) > Langan (0.27) > Kohrang1 (0.254) > Gukan (0.198)

  • DM2: Langan (0.27) > Kohrang2 (0.255) > Gukan (0.242) > Kohrang1 (0.23)

  • DM3: Kohrang2 (0.267) > Langan (0.25) > Kohrang1 (0.246) > Gukan (0.236)

Section2: the weight of each decision maker judgments is obtained by fuzzy TOPSIS method. Five criteria are considered including being professional in operation evaluation (C1), vulnerability (C2), related educational requirement (C3), acquaintance of country water laws and acts (C4) and practical experience (C5). Table 4 shows the weighted fuzzy decision matrix in fuzzy TOPSIS method. di +,di − are the distance of each decision maker from positive and negative ideal solutions, respectively. The scores of each decision maker are determined by calculating CCi as a closeness coefficient.

Table 4 The weighted fuzzy decision making matrix, di+, di− and CCi in fuzzy TOPSIS method
Full size table

Section3: the fuzzy max-min set method is used to investigate the influence of decision makers’ judgments weights in final results. For this reason, the decision making matrix is provided by using alternative priorities (results of ANP method) and decision makers’ judgments weight (results of fuzzy TOPSIS method). Therefore, the alternatives’ priorities and decision making judgments’ weights are converted to trapezoidal fuzzy number based on Table 5.

Table 5 Trapezoidal fuzzy number for converting ANP and fuzzy TOPSIS results
Full size table

The decision making matrix and weights of decision makers’ judgments in trapezoidal fuzzy number are illustrated in Table 6.

Table 6 Decision making matrix and weights
Full size table

Then, the fuzzy weight by considering alternatives and decision makers’ judgments weights is calculated by Eq. 14 as follow:

$$ \begin{array}{l}{\tilde{w}}_1=\left(2\kern0.24em \left[0.066,0.73\right],2.8,3.93,5.3\;\left[0.1,1.46\right]\;\right)\kern0.36em ,{\tilde{w}}_2=\left(2.33\;\left[0.066,0.8\right],3.2,4.86,5.9\;\left[0.033,1.06\right]\right)\\ {}{\tilde{w}}_3=\left(1.46\;\left[0.066,0.63\right],2.16,3.03,4.3\;\left[0.1,1.36\right]\;\right)\kern0.36em ,{\tilde{w}}_4=\left(2.2\;\left[0.066,0.76\right],3.03,4.67,5.8\;\left[0.033,1.16\right]\;\right)\end{array} $$
(20)

where \( {\tilde{w}}_i \) is the weight of alternative Ai. Finally, the final ranking is obtained as follows:

$$ \mathrm{Gukan}<\mathrm{Kohrang}1<\mathrm{Langan}<\mathrm{Kohrang}2 $$

4.1 Sensitivity Analysis

The sensitivity analysis is conducted to investigate the influence of decision maker’s judgments weights on the final results as shown in Fig. 4. It is seen that the variations of decision makers’ judgments weights could change the final ranking. For example, when the weight of DM3 is increased, Kohrang2 will have a high score than others. On the other hand, by increasing the weight of DM1, Langan will be the best alternative in contrast Gukan as a worst alternative. Therefore, it is important to consider decision makers’ judgments weights to evaluate the final scores of alternatives instead of the arithmetic or geometric mean which is not suitable in this condition. As results show, the new method based on combination of ANP, fuzzy TOPSIS and fuzzy max-min set method can be assigned as an effective tool for evaluating alternatives in group decision making problems with respect to different criteria.

Fig. 4
figure 4

Sensitivity analysis of decision makers’ judgments weights

Full size image

On the other hand, the sensitivity analysis has conducted for ANP results that are based on decision maker judgment with higher score. The results are shown in Fig. 5. It is seen that the weights of economic, social- cultural and environmental have been changed in each cluster. In benefit cluster, when the local weight of environmental is between 0 and 0.192, Langan is the best alternative in the ranking but that is the worst alternative in the weight between 0.744 and 1. Also, by changing the weights of social-cultural and environmental criteria, the alternatives’ rankings are changed in the cost cluster although the different weight of economic criteria in cost cluster have no effect on ranking. By changing the economic weight in cost cluster the alternatives are ranked as: Kohrang2, Langan, Kohrang1 and Gukan. In risk cluster, different weights of economic and environmental criteria have no effect on ranking. In contrast, the social- cultural weight could change ranking.

Fig. 5
figure 5

Sensitivity analysis of criteria weights in BCR model

Full size image

5 Conclusion

In this study, a new multiple attribute decision maker method based on ANP, fuzzy TOPSIS and fuzzy max-min set method is proposed for ranking water transfer projects in group decision making problem. Four water transfer projects with respect to 61 criteria are evaluated in group decision making problem. Due to complex interaction and dependence between criteria and sub criteria, the network structure is constructed and the alternatives priorities are obtained by ANP. Then, to obtain the weights of decision makers’ judgments, fuzzy TOPSIS method is used. Finally, by combination of ANP and fuzzy TOPSIS results, the decision matrix is constructed for fuzzy max-min set method and the final ranking is obtained by evaluating the influence of decision makers’ judgments weights on alternatives priorities.